Abstract
The Ca2+-sensitive regulatory switch of cardiac muscle is a paradigmatic example of protein assemblies that communicate ligand binding through allosteric change. The switch is a dimeric complex of troponin C (TnC), an allosteric sensor for Ca2+, and troponin I (TnI), an allosteric reporter. Time-resolved equilibrium Förster resonance energy transfer (FRET) measurements suggest that the switch activates in two steps: a TnI-independent Ca2+-priming step followed by TnI-dependent opening. To resolve the mechanistic role of TnI in activation we performed stopped-flow FRET measurements of activation after rapid addition of a lacking component (Ca2+ or TnI) and deactivation after rapid chelation of Ca2+. Time-resolved measurements, stopped-flow measurements, and Ca2+-titration measurements were globally analyzed in terms of a new quantitative dynamic model of TnC-TnI allostery. The analysis provided a mesoscopic parameterization of distance changes, free energy changes, and transition rates among the accessible coarse-grained states of the system. The results reveal that 1), the Ca2+-induced priming step, which precedes opening, is the rate-limiting step in activation; 2), closing is the rate-limiting step in de-activation; 3), TnI induces opening; 4), there is an incompletely deactivated population when regulatory Ca2+ is not bound, which generates an accessory pathway of activation; and 5), there is incomplete activation by Ca2+—when regulatory Ca2+ is bound, a 3:2 mixture of dynamically interconverting open (active) and primed-closed (partially active) conformers is observed (15°C). Temperature-dependent stopped-flow FRET experiments provide a near complete thermokinetic parameterization of opening: the enthalpy change (ΔH = −33.4 kJ/mol), entropy change (ΔS = −0.110 kJ/mol/K), heat capacity change (ΔCp = −7.6 kJ/mol/K), the enthalpy of activation (δ‡ = 10.6 kJ/mol) and the effective barrier crossing attempt frequency (νadj = 1.8 × 104 s−1).
INTRODUCTION
The periodic contraction and relaxation of the heart is regulated by cytosolic Ca2+ through the myofilament, an assembly of proteins comprised of troponin C (TnC), troponin I (TnI), troponin T, tropomyosin, filamentous actin, and the head of myosin—an actin-binding ATPase (1–3). The TnC-TnI complex functions as a Ca2+-sensitive regulatory switch as part of the larger myofilament assembly. Ca2+ binding to the single functional regulatory site (site II) of the Ca2+-receptor, TnC, is transduced as a delayed stochastic change in the isomerization state of TnI. The TnI isomerization event relieves contractile inhibition through the release of the inhibitory region of TnI (TnI-I, residues 130–149) from actin (4). Inhibition is due to the regulated association of TnI-I with actin, which places tropomyosin in a position that inhibits inorganic phosphate release from myosin. Inorganic phosphate release is required to form the strongly bound, force-generating, acto-myosin complex (5). Activation of the TnC-TnI assembly involves an interhelical rearrangement, called “opening”, in the Ca2+-binding EF-hand (helix-loop-helix) motifs in the N-domain of TnC. The pivoting of helices B and C away from the central helix (D) (6) enables previously buried hydrophobic residues in the B, C, and D helices to associate with hydrophobic residues in the regulatory helix of TnI (TnI-R, residues 150–165) that is contiguous with TnI-I. In the cardiac system TnI-R is required for TnC to open (7,8).
Allostery is the long-range coupling between distinct regions of a macromolecule. Cardiac TnC-TnI is an assembly of two allosteric proteins. Classical models of allostery, such as the Monod-Wyman-Changeux model (9), the Koshland-Nemethy-Filmer (10) model, and generalized models using linked functions (11) or conditional free energies (12), only consider systems that are in equilibrium. The classic requirements that an allosteric system be oligomeric and symmetric have given way to a new definition of allosteric systems—systems where the binding of one ligand affects the affinity of a second ligand. This definition includes monomeric multidomain proteins, where the second ligand is second protein. This definition also includes macromolecular assemblies, where the second ligand is another member of the assembly. The cardiac TnC-TnI assembly belongs to this last class.
Over the past decade, the role of dynamics in allosteric regulation has drawn increasing interest (13). The protein is now seen as a fluctuating entity that dynamically exchanges among a large number of microstates (13,14). These microstates can be organized into regions of local stability, called “conformational substates” (15) or “macrostates”, that correlate with functional activity. Dynamics within a macrostate involves fluctuating motions of individual atoms, residues, and groups of residues on the picosecond-to-microsecond timescale. These fluctuations are the basis for the entropy of a macrostate (16). A second class of dynamics, which we call “allosteric dynamics”, involves random jumplike transitions among macrostates on the microsecond-to-second timescale. The focus of this study is the allosteric dynamics of the cardiac TnC-TnI assembly.
Förster resonance energy transfer (FRET) provides a powerful tool to study ligand binding-induced interdomain distance changes (on the near Å scale) in protein assemblies in their native environment (17,18). In contrast to conventional fluorescent assays that report change in the local environment of the probe, FRET provides a clear metric for allosteric change—a change in the mean interprobe distance. Time-resolved FRET measurements can quantitate the distribution of interprobe distances (19). Used in experiments involving dynamic change through some perturbation of the system, FRET provides what has been termed “structural kinetics” (20) with structural monitoring of Ca2+ regulated allosteric dynamics of the TnC-TnI assembly.
An unfortunate property of measured perturbation-induced relaxation rates is that they are functions of the elementary forward and backward transition rate constants that govern the allosteric dynamics of a system (21). One approach to resolving the component elementary rate constants from observed relaxation rates is to perform a set of kinetic experiments that contain overlapping information. When two or more experiments jointly depend on underlying elementary transition rate parameters, a combined (or global) analysis of the experiments may resolve the rate parameters (22,23). This resolution is usually not possible when experiments are analyzed independently and empirically.
Here, we have pursued such a global strategy by using a previously characterized FRET reporter system on TnC (8) in a set of experiments to parameterize the structural kinetics of the cardiac TnC-TnI assembly. (See Fig. 1 for FRET assay.) Global analysis of the experiments required that we formulate a mesoscopic model of TnC-TnI allosteric dynamics during the activation and deactivation stages of the signaling cycle. We performed time-resolved FRET measurements of Mg2+- or Ca2+-saturated (apo/holo) and TnI bound/unbound samples of TnC; stopped-flow FRET measurements of Ca2+-induced activation, TnI-induced activation, and Ca2+-chelation induced deactivation; and a FRET-monitored Ca2+-titration measurement of TnC-TnI. The measurements were analyzed in terms of the allosteric model to provide distance changes, free energy changes, and the elementary rate constants for transitions among the accessible coarse-grained states of the system. The analysis was used to differentiate between two mechanistic models of TnC-TnI activation/deactivation. The experiments were used to construct the macroscopic free energy landscape that governs signaling. To obtain a more complete thermokinetic parameterization of the TnC opening transition, the stopped-flow FRET measurements were repeated for a set of temperatures. The recovered transition rates for opening/closing were subjected to van 't Hoff and modified Arrhenius analyses that quantitated the heat capacity change, enthalpy change and entropy change of opening, the forward and backward enthalpy of activation, and the forward and backward effective barrier crossing attempt frequencies. Our measurements suggest that the cardiac TnC-TnI assembly is in dynamic equilibrium among its macrostates both when regulatory Ca2+ is bound and unbound. When Ca2+ is bound, the probability that the TnC-TnI complex is active is only 60%.
FIGURE 1.
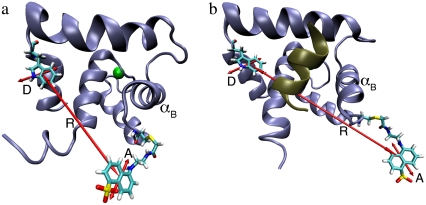
N-terminal portion of TnC, showing engineered FRET donor Trp-12 (D) and FRET acceptor Cys-51-labeled AEDANS (A). (a) Ca2+-bound TnC in the absence of TnI (modified from PDB ID code 1AP4). (b) The Ca2+-bound TnC with bound TnI-R (brown helix) (modified from PDB ID code 1J1E). The efficiency of photon transfer between the emission dipole of Trp-12 and the absorption dipole of AEDANS (shown) depends on the interprobe distance (R), which changes upon hingelike movement of helix B of TnC (αB) during activation.
METHODS
Sample preparation
The construction, purification methods, and validation of TnC(F12W/N51C/C35S/C84S) (abbreviated name, TnC(12W/51C)) as well as tryptophan-less cardiac troponin I, TnI(W192F) (abbreviated name, TnI(W-)), used in this study have been described (8). To remove unlabeled protein from the reaction mixture (i.e., obtain 100% labeling efficiency) the mixture was fractionated as described in the literature (24). The binary troponin complex was prepared by incubating TnC(12W/51C ± AEDANS) (2 μM) with a twofold excess of TnI(W-) (4 μM) on ice for 20 min.
Spectroscopic measurements
Except where noted, all measurements were performed at 15 ± 0.1°C. Samples were prepared in standard buffer (SB): 50 mM 3-(n-morpholino)propanesulfonic acid, pH 7.0, 1 mM dithiothreitol, 5 mM MgCl2, 0.2 M KCl; working buffer (WB): SB + 2 mM ethylene glycol-bis-(β-aminoethyl ether)-n,n,n′,n′-tetraacetic acid (EGTA); or activating buffer (AB): SB + 160 μM Ca2+ (pCa, 3.8). A stable TnC-TnI complex is formed in WB with twofold molar excess TnI as shown previously (25), where, using an engineered TnI(W150), TnI-binding-induced changes in the Trp lifetime were saturated with a 1.2 molar excess of TnC in the absence of Ca2+. Ca2+ titrations of the FRET distance were performed as described (1) with the following modifications. A microtitrator (ISS, Champaign, IL) delivered 90 successive 5-μL injections of a Ca2+-EGTA solution into reconstituted binary troponin complex ([TnC] = 1 μM) in WB (1.0 mL starting volume). The FRET donor, tryptophan, was excited at 295 nm; the FRET-quenched donor fluorescence was monitored at 340 nm (monochromator slit width, 2 μm).
The ensemble distribution of the interprobe distance was obtained from the time-resolved multiexponential decay of the FRET donor Trp-12 as described in detail (1) with the following modifications. The time-resolved fluorescent decays of Trp-12 were collected using an IBH 5000U single-photon counting time domain fluorescent lifetime instrument (HORIBA Jobin Yvon, Edison, NJ). Excitation was with a 295-nm pulsed LED. Isolated TnI(W-) in WB provided background fluorescence and scattering, which was subtracted from donor-containing samples. (Failure to subtract background fluorescence, which is particularly problematic when using Trp as a FRET donor, produces reported FRET distances that are artificially low.)
Perturbation-induced time-dependent FRET distances were obtained as described (26) using a KinTek F2004 stopped flow mixing spectrometer (1.8-ms instrument dead time, KinTek, Austin, TX). Deactivation kinetics: rapid mixing of the binary troponin complex in AB with an equal volume of WB (postmixing: 2 μM TnC, 1 mM EGTA). Ca2+-induced activation: rapid mixing of the binary troponin complex in SB + minimally buffered 30 μM EGTA was mixed with an equal volume of SB + 500 μM Ca2+ (postmixing: 2 μM TnC, 250 μM Ca2+). TnI-induced activation: rapid mixing of a Ca2+-saturated TnC in AB with an equal volume of TnI in AB. A reduced concentration of TnI (postmixing: 0.5 μM TnC, 1 μM TnI) was used due to the low solubility of TnI in 0.2 M KCl. FRET distances were calculated from the average of 8–10 tracings of concentration matched donor-only and donor-acceptor samples. Mean FRET distances recovered from the time-resolved data provided distance calibration standards for the stopped-flow measurements. Mock injections, where the protein was mixed with the same buffer, were used for calibration and to exclude the possibility of dilution-induced artifacts in the measured fluorescence.
Data analysis
The time-resolved FRET experiments were fit as described (1). Using the extensible global analysis software, GlobalCurve (27), the stopped flow FRET data were first independently fit to an empirical sum of exponentials then globally fit to the kinetically coupled models of activation and deactivation (Eqs. 14a, 14b, and 15). Global fitting required custom-written routines to solve the set of master equations (coupled ordinary differential equations) for the probability 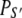 of finding the system in system state
of finding the system in system state 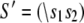 during activation (a) and deactivation (d),
during activation (a) and deactivation (d),
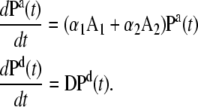 |
(1) |
αi is the relative species flux through path i. 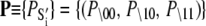 is the time-dependent marginalized probability distribution for finding TnC in state s1 and TnI in state s2,
is the time-dependent marginalized probability distribution for finding TnC in state s1 and TnI in state s2,
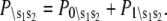 |
(2) |
The distribution is normalized, 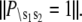 The kinetic transition matrix for the first path of activation is
The kinetic transition matrix for the first path of activation is
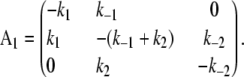 |
(3) |
The kinetic transition matrix for deactivation and the second path of activation (with k′−3 = 0.1 s−1 substituted for k−3) is
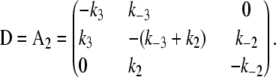 |
(4) |
The equations were numerically integrated (Gear method, IMSL, Visual Numerics, Houston, TX) subject to the following initial conditions. The initial condition for the Ca2+-induced activation kinetics is the equilibrated system under deactivating conditions, 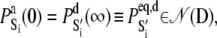 where 𝒩(D) is the null space of D, obtained from the singular value decomposition of D, and
where 𝒩(D) is the null space of D, obtained from the singular value decomposition of D, and  is the equilibrium probability for finding the protein in state S′i under deactivating [Ca2+]. The initial condition for TnI-induced activation is obtained by setting k2 = 0 in A1, giving
is the equilibrium probability for finding the protein in state S′i under deactivating [Ca2+]. The initial condition for TnI-induced activation is obtained by setting k2 = 0 in A1, giving 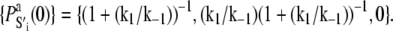 The initial condition for the Ca2+-chelation-induced deactivation kinetics is the equilibrium distribution under saturating [Ca2+],
The initial condition for the Ca2+-chelation-induced deactivation kinetics is the equilibrium distribution under saturating [Ca2+], 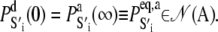 To deal with calibration error caused by noise in the stopped flow measurements and experimental error in the recovered mean FRET distance from the time-resolved measurements, small adjustable distance correction factors were added to the models during global fitting.
To deal with calibration error caused by noise in the stopped flow measurements and experimental error in the recovered mean FRET distance from the time-resolved measurements, small adjustable distance correction factors were added to the models during global fitting.
The observed FRET distance in the stopped flow measurements and in the Ca2+-titration measurement is the population-weighted average
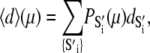 |
(5) |
where 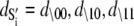 are the species-associated FRET distances. The equilibrium system-state distribution at the Ca2+ chemical potential μ is given by the Boltzmann equation
are the species-associated FRET distances. The equilibrium system-state distribution at the Ca2+ chemical potential μ is given by the Boltzmann equation
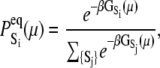 |
(6) |
where β = 1/RT, R is the Boltzmann gas constant, and T is absolute temperature in K. The set of free energies of the accessible system-states 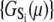 parameterize the macroscopic free energy landscape.
parameterize the macroscopic free energy landscape.
MODELING
We have developed a mesoscopically resolved theory of nonequilibrium allostery suitable for describing the isomerization dynamics of TnC and TnI as part of the cardiac TnC-TnI assembly. The theory provides linked models of the activation and deactivation components of the signaling cycle, and it can be used to combine both structural and kinetic information into an integrated analysis of Ca2+-mediated signaling. To construct a model of TnC-TnI allostery, assumptions must be made about the nature and number of allosteric transitions within the system. Many allosteric proteins, including TnC and TnI, are adequately described as bi-meta-stable (28,29), meaning they possess two macrostates: an active and an inactive isomer. The kinetics of Ca2+-induced structural changes in TnC-TnI are well fit by a three-state sequential model involving two isomerization steps (30). The two isomerization steps can be interpreted as individual two-state isomerization events in the component proteins TnC and TnI.
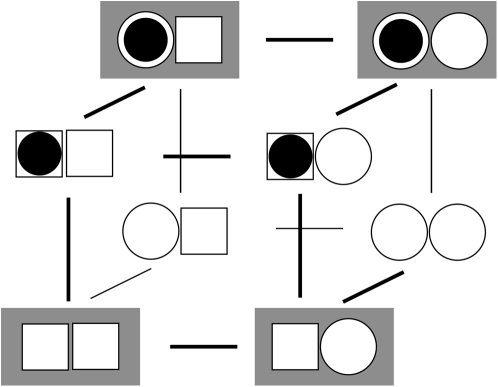
We represent the allosteric protein as a union of two domains—an input domain and an output domain. Each domain can be in one of two macrostates. Ligand binding to the input domain involves direct steric interaction, while the interaction between the input and output domains is allosteric. From the steric effects of molecular association (31), the state of the input domain is absolutely correlated with ligand binding. This assumed correlation satisfies the lock-and-key (32) and induced-fit (10) models. (The lock-and-key process is just an induced-fit process without structural change.) Scheme I summarizes our model of an allosteric protein. All possible combinations of the state of the input domain, the state of the output domain, and the ligand binding status of the input domain are enumerated. Each domain is either inactive (square) or active (circle). The input domain appears on the left, the output domain appears on the right. Bound ligand is represented as a solid circle. Of the eight possible states, the four that are allowed are shown with a shaded background. For these, the active input state (circle) is ligand-bound and the inactive input state (square) is ligand-unbound—the state of input domain is absolutely correlated with ligand binding. In contrast, the output domain can be either active (circle) or inactive (square) both when ligand is bound or unbound—it is a preexisting equilibrium process (12,33). Our model of allostery is thus a hybrid of preexisting equilibrium and induced-fit models. The model describes allostery in all members of an assembly of allosteric proteins, provided that the output of a protein is viewed as the input ligand for the immediately downstream protein. In this way, intermolecular signaling is treated as a steric interaction. For members of an allosteric assembly that do not function as the principal ligand receptor, only the output state of the protein needs to be specified because the state of its input is inferred from the state of the output of the immediately upstream protein.
Scheme 1.
The TnC-TnI complex is a thermodynamic system of three components: one Ca2+, one TnC, and one TnI. The configuration of the entire system, called the system-state, is represented as a binary string, S = (s0\s1s2), which is a labeling scheme comprised of bits that specify the state of each component. The 0th bit s0 gives the ligand binding status of the Ca2+-regulatory site (loop II) of TnC (0 = Ca2+-not bound; 1 = Ca2+-bound); the first bit specifies the output state of TnC, and the second (terminal) bit specifies the output state of TnI. For bits representing the output state of a protein (bits to the right of \), 0 denotes the inactive state and 1 denotes the active state.
At the mesoscopic level, allosteric signaling in the TnC-TnI assembly is a stochastic process because ligand-binding and protein isomerization events are random thermally activated transitions. Continuous-time random processes are governed by an evolution equation, called the master equation, for the probability PS(t) to find the system in state S at time t (34)
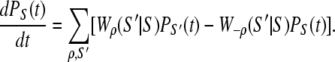 |
(7) |
The quantities Wρ(S′|S) and W–ρ(S′|S) = Wρ(S|S′) denote, respectively, the rates of the transitions 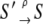 and
and 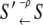 for the elementary processes ρ = 1, 2, …, r, of which there are r = 8 × 7/2 = 28. Many of the fundamental properties of the nonequilibrium behavior of the TnC-TnI assembly can be investigated and understood in terms of the Markov network of the system—a graph associated with the master equation (Eq. 7). In a Markov network, system-states S are represented as vertices (nodes), and the elementary (bi-directional) transitions ρ are represented as edges.
for the elementary processes ρ = 1, 2, …, r, of which there are r = 8 × 7/2 = 28. Many of the fundamental properties of the nonequilibrium behavior of the TnC-TnI assembly can be investigated and understood in terms of the Markov network of the system—a graph associated with the master equation (Eq. 7). In a Markov network, system-states S are represented as vertices (nodes), and the elementary (bi-directional) transitions ρ are represented as edges.
Four carefully considered assumptions afford a significant reduction in the number of elementary transitions and the number of independent kinetic/thermodynamic parameters needed to describe Ca2+-induced signaling in the TnC-TnI assembly.
Only one component can switch at a time. Thus, system-state changes S′ → S involve transitions in a single bit sj. Single bit transitions are represented by
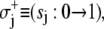 and
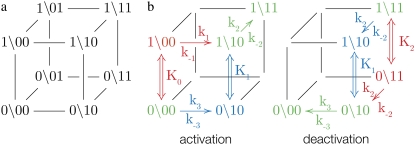
and 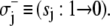 The Markov network of the TnC-TnI assembly undergoing only single bit transitions is shown in Fig. 2 a. The number of elementary transitions are reduced to r = 8 × 3/2 = 12.
The Markov network of the TnC-TnI assembly undergoing only single bit transitions is shown in Fig. 2 a. The number of elementary transitions are reduced to r = 8 × 3/2 = 12.-
The rate constants for each elementary transition ρ obey detailed balance
where from Eq. 6,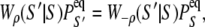
(8) 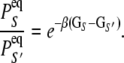
(9) 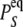 is the probability that the equilibrated system occupies the system-state S. We can identify a set of six minimal network circuits {𝒞1, 𝒞2, … 𝒞6}, where travel along allowed elementary transitions ρ returns the system to its starting position. Each minimal circuit contains four nodes and consists of transitions in two bits. The cyclic flows
is the probability that the equilibrated system occupies the system-state S. We can identify a set of six minimal network circuits {𝒞1, 𝒞2, … 𝒞6}, where travel along allowed elementary transitions ρ returns the system to its starting position. Each minimal circuit contains four nodes and consists of transitions in two bits. The cyclic flows 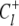 and
and 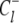 on the circuit 𝒞l involve, respectively, clockwise and counterclockwise travel in the circuit. Conservation of free energy dictates that the net free energy change along each circuit 𝒞l is zero. From conservation of free energy, Eqs. 8 and 9, we find that for each circuit 𝒞l the product of transition rates for
on the circuit 𝒞l involve, respectively, clockwise and counterclockwise travel in the circuit. Conservation of free energy dictates that the net free energy change along each circuit 𝒞l is zero. From conservation of free energy, Eqs. 8 and 9, we find that for each circuit 𝒞l the product of transition rates for 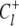 must balance the product of transition rates for
must balance the product of transition rates for 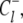
Transition rates are thus macroscopically detail-balanced. Circuits that involve transitions in all three bits can be defined, but they do not provide additional restraints on the transition rates.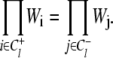
(10) Constraints 1 and 2 apply to both simple systems, such as coupled chemical reactions, and more complex systems, such as assemblies of allosteric proteins. The TnC-TnI assembly, being a complex spatially extended system, is subject to two additional constraints.
- Each component of the assembly knows only its local environment. This is a defining feature of complex systems (35). It implies, for example, that TnI has no direct knowledge of whether regulatory Ca2+ is bound to TnC; rather, Ca2+ binding is communicated to TnI by an allosteric change in TnC. Incomplete knowledge manifests as nearest-neighbor-limited influence, causing certain transition probabilities to be degenerate,
where n = 3. Here, the rate of the transition involving bit sj,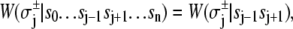
(11) 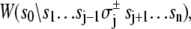 has been rewritten to show explicitly how the rate depends on the remaining bits sk ≠ j:
has been rewritten to show explicitly how the rate depends on the remaining bits sk ≠ j: 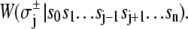 In the TnC-TnI complex, the nearest-neighbor assumption (Eq. 11) dictates that the transition rates for TnI switching do not directly depend on whether regulatory Ca2+ is bound to TnC (i.e.,
In the TnC-TnI complex, the nearest-neighbor assumption (Eq. 11) dictates that the transition rates for TnI switching do not directly depend on whether regulatory Ca2+ is bound to TnC (i.e., 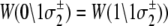 and that the transition rates for Ca2+ binding/release do not directly depend on the isomerization state of TnI (i.e.,
and that the transition rates for Ca2+ binding/release do not directly depend on the isomerization state of TnI (i.e., 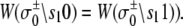 Degenerate transition rates evidently originate in the constrained topology of the free energy landscape of the system. The forward and reverse transition probabilities Wρ, W–ρ along each edge ρ depend on the geometry of the two-basin free energy surface of that edge (see Supplementary Material, Fig. S1, in Data S1) as well as the basin-associated friction coefficients (36,37). The concept of a one-dimensional free energy surface along the reaction coordinate of a transition is generalized to the composite free energy landscape, consisting of the set of free energy surfaces over the reaction coordinates of all transitions ρ in the Markov network.
Degenerate transition rates evidently originate in the constrained topology of the free energy landscape of the system. The forward and reverse transition probabilities Wρ, W–ρ along each edge ρ depend on the geometry of the two-basin free energy surface of that edge (see Supplementary Material, Fig. S1, in Data S1) as well as the basin-associated friction coefficients (36,37). The concept of a one-dimensional free energy surface along the reaction coordinate of a transition is generalized to the composite free energy landscape, consisting of the set of free energy surfaces over the reaction coordinates of all transitions ρ in the Markov network. The two system-states with inactive TnC but active TnI—(0\01), (1\01)—are recognized as high energy states, where the TnI-R is inserted into an unexposed hydrophobic pocket on TnC. Because of their high energies, the probability that these states are visited is negligible. These states are deleted from the network, as are the transitions involving them.
FIGURE 2.
The TnC-TnI assembly represented as a Markov network (see text). (a) The parent network with system-states (s0\s1s2) as nodes and bi-directional transitions as edges. (b) Reduced models of activation and deactivation showing transition rates ki, i = 1, 2, 3, Ca2+ affinity constants Kj, j = 0, 1, 2, kinetic linkages between activation and deactivation, and degeneracy in k2 and k−2. Dominant (red) are minor (blue) pathways and common portions (green) are shown. Double arrows indicate transitions with the reversible binding of Ca2+. For protein isomerizations, single arrows indicate the direction of net probability flux.
In summary, we have introduced four assumptions that reduce the number of accessible network states from eight to six and constrain the transition rates that govern system dynamics.
We assume that transition rates {W±ρ} are governed by the law of mass action and that the transition rates obey the empirical Arrhenius Law—an exponential dependence of the transition rate on the free energy of activation. Out of convenience we assume that the rate of Ca2+ dissociation from partially activated TnC-TnI and fully activated TnC-TnI is intermediate (∼10/μs). Below, we relax this assumption and show that the assumption does not restrict the results. In Fig. 2 b, the parent Markov network (Fig. 2 a) is divided into two sub-networks—networks for the activation and deactivation components of the signaling cycle. The transition rates {W±ρ} for the protein isomerizations are given in terms of the kinetic rate constants k±i, i = 1, 2, 3. The activation and deactivation sub-networks are kinetically linked through common k2, k−2, k3, and k−3. System states (0\01) and (1\01) are eliminated and degenerate transition rates are shown—the transition rates of TnI activation ((0\10) → (0\11)) and ((1\10) → (1\11)) are a common k2; the transition rates of TnI deactivation ((0\10) ← (0\11)) and ((1\10) ← (1\11)) are a common k−2. W±ρ for the elementary Ca2+ binding transitions are not considered. Instead, their quotients, the bi-molecular association constants K0, K1, and K2 (in M−1), are defined (see Appendix B) for Ca2+ binding/release, to the system-states (\00), (\10), and (\11). For both activation and deactivation, two pathways, the anticipated dominant (red) and minor (blue) pathways, are identified. Transitions common to both pathways are shown in green. The minor pathway for activation (deactivation) involves the binding (release) of Ca2+ from a partially activated (deactivated) TnC-TnI complex. The dominant and minor pathways of activation are given, respectively, by the kinetic schemes
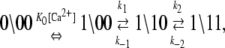 |
(12a) |
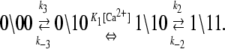 |
(12b) |
The dominant and minor pathways of deactivation are given, respectively, by
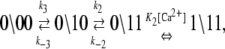 |
(13a) |
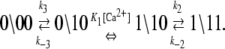 |
(13b) |
The double arrow (⇔) indicates reversible binding and release of regulatory Ca2+ by TnC. Activation is rightward; deactivation is leftward.
The kinetic schemes (Eqs. 12 and 13) simplify for experiments that involve rapid perturbations of [Ca2+] between the extremes of activation—full saturation and full desaturation. In the first path of activation (Eq. 12a), a high [Ca2+] strongly favors (1\00) over (0\00), and Ca2+ binding is rapid, so (0\00) can be ignored on the millisecond and longer timescale. In the second path of activation (Eq. 12b), rapid Ca2+ binding to (0\10) out-competes the deactivation of TnC through k−3. The first two steps can be approximated by a single transition with a forward rate constant k3 and a backward rate constant k′−3 that is small. In the first path of deactivation (Eq. 13a), a low [Ca2+] strongly favors (0\11) over (1\11), and the step of Ca2+ release is assumed to not be rate-limiting, so (1\11) can be ignored. In the second path of deactivation (Eq. 13b), a low [Ca2+] strongly favors (0\10) over (1\10). The step of Ca2+ release is assumed not to be rate-limiting, so (1\10) can be ignored. Considering only the protein components (\s1s2), the schemes for the two activation pathways simplify:
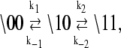 |
(14a) |
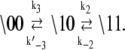 |
(14b) |
The two pathways of activation will relax with different rates from differences between k1 and k3 and between k−1 and k′−3 ≃ 0. The relative flux between the two pathways of activation depends on the underlying rate constants for K0 and K1 as well as k1, k−1, k3, and k−3 in Eqs. 12. Relative flux cannot be predicted from the reduced models (Eqs. 14a).
In the two schemes for deactivation (Eq. 13), the protein system-states (\s1s2) and the kinetic transition rates are identical. The schemes are equivalent with respect to the measured FRET distance, which depends only on the states of the proteins. Considering only the protein components (\s1s2), deactivation through either (or both) pathway(s) will procede according to the scheme
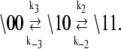 |
(15) |
The assumed ∼10/μs transition rate for Ca2+ release from partially activated TnC-TnI and fully activated TnC-TnI can be relaxed to allow faster dissociation rates. This leads to more complicated kinetic schemes, where Ca2+ can undergo one or more cycles of binding/release during activation or deactivation. In one such kinetic scheme of TnC-TnI activation, TnI activation 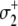 occurs after Ca2+ has transiently dissociated from TnC:
occurs after Ca2+ has transiently dissociated from TnC:
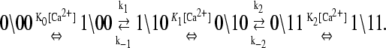 |
(16) |
This scheme extends the dominant pathway of activation (Eq. 12a) by including additional transitions of Ca2+ binding and release, but it differs from Eq. 12a because 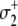 occurs when Ca2+ is not bound. Because the transition rates k2 and k−2 are degenerate (i.e., independent of whether Ca2+ is bound to TnC) the schemes in Eq. 12a and Eq. 16 are kinetically equivalent with respect to the isomerization dynamics of TnC-TnI (Eq. 14a). Our current measurements cannot distinguish between the activation schemes in Eq. 12a and Eq. 16 because their isomerization dynamics are given identically by Eq. 14a. The same arguments apply to other complicated kinetic schemes.
occurs when Ca2+ is not bound. Because the transition rates k2 and k−2 are degenerate (i.e., independent of whether Ca2+ is bound to TnC) the schemes in Eq. 12a and Eq. 16 are kinetically equivalent with respect to the isomerization dynamics of TnC-TnI (Eq. 14a). Our current measurements cannot distinguish between the activation schemes in Eq. 12a and Eq. 16 because their isomerization dynamics are given identically by Eq. 14a. The same arguments apply to other complicated kinetic schemes.
Equations 14 and 15 are rationally reduced models for the isomerization dynamics of TnC and TnI during the activation and deactivation components of the signaling cycle when the TnC-TnI assembly is driven by step changes in Ca2+ between fully saturating and fully de-saturating conditions. Eq. 14b represents a possible accessory pathway of activation that may be experimentally resolved. The signaling cycle dynamics at the extremes of activation are determined by six rate constants: k1, k−1, k2, k−2, k3, and k−3. Three structural configurations of TnC-TnI are accessible: (\00), (\10), and (\11).
RESULTS
Time-resolved FRET
We employed a previously characterized FRET reporter system TnC(12W/51C*AEDANS) (8) to follow structural changes in the TnC-TnI assembly during the signaling cycle. The FRET assay, shown in Fig. 1, is sensitive to TnC opening—the interhelical rearrangement in TnC of helices B and C relative to the central helix D. The time-resolved decays of donor-only TnC(12W/51C) and donor-acceptor TnC(12W/51C*AEDANS) have been reported (8) for isolated TnC and the TnC-TnI complex. In this study we repeated and extended the measurements to include the addition of TnI to Ca2+-saturated TnC. The multiexponential decays (Fig. S1 in Data S1) were fit to a static Gaussian-distributed interprobe distance model, as described in the literature (1,8). The recovered mean 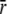 and the standard deviation σ of the interprobe distance distribution are shown in Fig. 3. Here, but not in Dong et al. (8), background fluorescence was subtracted from the decays. Background subtraction resulted in small increases in
and the standard deviation σ of the interprobe distance distribution are shown in Fig. 3. Here, but not in Dong et al. (8), background fluorescence was subtracted from the decays. Background subtraction resulted in small increases in  and a reduction in σ of the distance distribution (σ = 1.18hw) compared to previous measurements. The quantity hw is the half-width at half-maximum that was used to quantify the breadth of the distribution in our previous work.
and a reduction in σ of the distance distribution (σ = 1.18hw) compared to previous measurements. The quantity hw is the half-width at half-maximum that was used to quantify the breadth of the distribution in our previous work.
FIGURE 3.
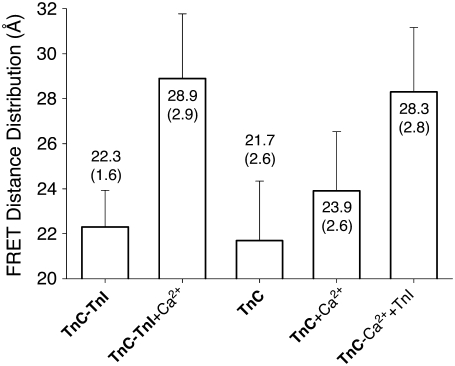
Recovered FRET distance distribution. Background-corrected, time-resolved, donor-only and donor-acceptor decays were fit to a Gaussian-distributed population of interprobe distances with mean (bar) and standard deviation (shown as an error bar). Samples: starting Ca2+-free samples of TnC-TnI complex or isolated TnC (bold) with addition of saturating Ca2+ or sequential addition of saturating Ca2+ then TnI.
In Fig. 3, Ca2+-induced structural changes are apparent in both isolated TnC and in the binary TnC-TnI complex. Starting with the preformed Ca2+-depleted TnC-TnI complex, saturation with Ca2+ caused an apparent mean 6.6 Å change in the interprobe distance. Ca2+ saturation of the previously Ca2+-depleted TnC-only sample caused a small 2.2 Å increase in the mean FRET distance. NMR measurements of the N-domain of cardiac TnC have shown a subtle 12° change in the C/D interhelical angle (7). The observed 2.2 Å change in our FRET measurement, where the acceptor C51*AEDANS is in the short loop that connects the B and C helices (the B/C linker), is evidently sensitive to this structural change. Other possibilities for the apparent 2.2 Å interprobe distance change, such as partial opening of TnC, or altered fluorophore mobility, cannot be ruled out. Subsequent addition of TnI generated a larger 4.4 Å increase in the mean FRET distance. The sequential addition of Ca2+ and TnI produced a distance change (6.6 Å) of equal magnitude to the Ca2+-induced change in the binary complex, although absolute distances were 0.6 Å less than for the preformed complex. These results demonstrate that activation is commutative—the order of Ca2+ and TnI addition is not important. In the analysis that follows, we take 28.9 Å as the apparent mean interprobe distance in the fully activated binary complex. The standard deviation of the interprobe distance distribution for the apo TnC-TnI complex is narrower than the other samples (by ∼1 Å).
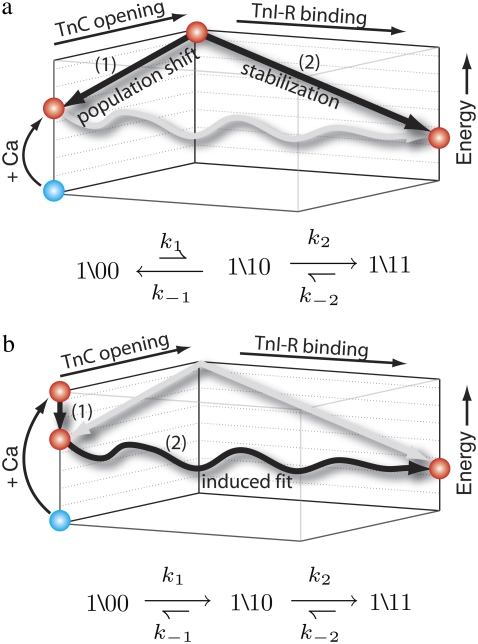
Fig. 4 shows two mechanistic models of activation that can account for the small change in distance observed after Ca2+ is added to isolated TnC and the large change in distance that is observed after the addition of Ca2+ to the binary TnC-TnI complex. The mechanistic models provide different structural interpretations of the allosteric transitions of TnC and TnI in the model of system dynamics (Fig. 2). In the population-shift-stabilization model (Fig. 4 a), when TnI is not present, Ca2+ binding to TnC fails to appreciably activate TnC because the transition is energetically unfavorable, 𝒦1 ≡ k1/k−1 < 1. Here, TnC activation is equated with TnC opening; that is, exposure of the hydrophobic pocket. Binding of TnI-R to the exposed hydrophobic pocket stabilizes an otherwise energetically unfavorable TnC opening event. Without TnI, Ca2+-bound TnC remains predominantly deactivated in the (1\00) state. Viewed kinetically, upon TnI addition most Ca2+-bound TnC-TnI must first proceed through the rate-limiting transition k1 before becoming stabilized through the k2 transition that out-competes the back reaction governed by k−1: k2 > k−1. Combining these results, we find that both Ca2+-induced and TnI-induced activation are rate-limited by k1: k2 > k−1 > k1. If TnC-TnI switching is a population-shift-stabilization process, then the rate of Ca2+-induced activation and the rate of TnI-induced activation will be equal. Equality applies to the slowest relaxation rate of a multiexponential decay.
FIGURE 4.
Mechanistic models of TnC-TnI activation consistent with the distance changes in Fig. 3. (a) Population-shift-stabilization model: TnC first undergoes an energetically unfavorable opening event (1), which is subsequently stabilized by TnI-R binding (2). (b) Induced-fit model: Ca2+ binding produces an energetically favorable Ca2+-primed species that is not open (1). In the presence of TnI, the Ca2+-primed complex undergoes concerted TnC opening and TnI-R binding (2). The kinetic signatures of each model are shown, with relative arrow length indicating relative transition probabilities.
The induced-fit model interprets differently the small change in distance that is observed after adding Ca2+ to isolated TnC compared to the large change in distance that is observed after adding Ca2+ to the binary TnC-TnI complex. In this model, Ca2+ binding directly and favorably activates TnC, 𝒦1 > 1, but the TnC activation event, (\00) → (\10), does not involve appreciable structural change (opening). Because of the large 𝒦1, Ca2+-binding strongly shifts the distribution of states toward an energetically favorable Ca2+-primed state of TnC (\10) that we call the “primed-closed state”. TnI subsequently induces structural opening as TnI-R migrates between the B/C and D helices of TnC, which forces TnC to open. With TnC predominantly in the primed-closed state, activation flux in TnI-induced activation (TnI addition to Ca2+-bound TnC) is rate-limited only by the opening step that is governed by k2. The kinetic rate of a sequential reaction scheme cannot exceed the kinetic rate of any component reaction. Therefore, the rate of TnI-induced activation must be greater than or equal to the rate of Ca2+-induced activation, which contains the isomerization steps of both TnC and TnI. For the observed Ca2+-induced and TnI-induced distance changes (Fig. 3), the induced-fit mechanism allows the rate of TnI-induced activation to exceed the rate of Ca2+-induced activation. This is not the case for the population-shift-stabilization mechanism for which both TnI-induced and Ca2+-induced activation are limited by k1.
Stopped flow kinetics
To determine which of the two mechanistic models correctly describes activation of the TnC-TnI assembly, we performed a series of stopped-flow measurements of the activation and deactivation components of the signaling cycle. In each experiment, the mean time-dependent FRET distance was calculated from the transient donor probe fluorescence of independently measured concentration-matched preparations of donor-only and donor-acceptor samples, as described in Dong et al. (26). Trp-12 fluorescence in mock-injected and actual samples were converted into time-dependent mean interprobe distance using the mean distances that were recovered from the time-resolved FRET experiments (Fig. 3).
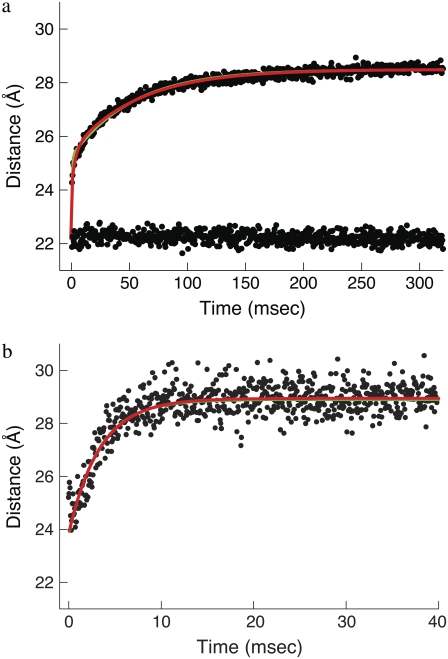
Activation kinetics were monitored in two sets of stopped-flow measurements (Fig. 5). For Ca2+-induced activation (Fig. 5 a), distance changes were obtained after rapidly mixing preformed binary TnC-TnI in a minimally Ca2+-buffered solution (30 μM EGTA) with buffer containing sufficient Ca2+ to saturate the sample (500 μM). Empirically, the FRET relaxation is a bi-exponential process consisting of a very rapid transient (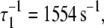 48% amplitude) followed by much slower transition (
48% amplitude) followed by much slower transition (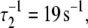 52% amplitude). The reduced (unweighted) χ2,
52% amplitude). The reduced (unweighted) χ2, 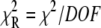 was 2.9 × 10−5. A fit to a three-exponential function (not shown;
was 2.9 × 10−5. A fit to a three-exponential function (not shown; 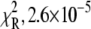 ) did not provide a statistically significant improvement in the residuals,
) did not provide a statistically significant improvement in the residuals, 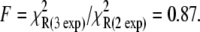 The 68% confidence level is reached when F < 0.68.
The 68% confidence level is reached when F < 0.68.
FIGURE 5.
Activation kinetics. FRET optical distance versus time, 15 C. (a) Ca2+-induced activation: change after rapid mixing of preformed binary TnC-TnI complex with Ca2+ solution (top dotted trace) or with buffer (mock injection, bottom trace). Empirical double exponential fit (green): 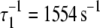 (48% amplitude),
(48% amplitude), 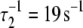 (52%). Global model-based fit (red) with derived parameters in Table 1. (b) TnI-induced activation: change after rapid mixing of TnI into Ca2+-presaturated TnC. Empirical single exponential fit (green): τ−1 = 305 s−1. Global model-based fit (red) with derived parameters in Table 1.
(52%). Global model-based fit (red) with derived parameters in Table 1. (b) TnI-induced activation: change after rapid mixing of TnI into Ca2+-presaturated TnC. Empirical single exponential fit (green): τ−1 = 305 s−1. Global model-based fit (red) with derived parameters in Table 1.
For TnI-induced activation (Fig. 5 b) distance changes were obtained from samples of Ca2+-presaturated TnC that were rapidly mixed with a twofold excess of isolated TnI. Rapid single-exponential kinetics were observed (τ−1 = 305 s−1, 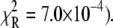 A two-exponential fit (not shown;
A two-exponential fit (not shown; 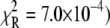 did not improve the fitting, F = 0.99. We find that the rate of TnI-induced activation (τ−1 = 305 s−1) greatly exceeds the rate of Ca2+-induced activation
did not improve the fitting, F = 0.99. We find that the rate of TnI-induced activation (τ−1 = 305 s−1) greatly exceeds the rate of Ca2+-induced activation 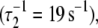 a rate that is sensitive to both Ca2+- and TnI-activating steps. This finding is consistent with the induced-fit model, which, of the two mechanistic models, is the only one that allows the rate of cTnI-induced activation to exceed the rate of Ca2+-induced activation. If the transition proceeded through a population-shift-stabilization mechanism then the rate of TnI-induced activation would be rate-limited to 19 s−1. The rate of overall association between TnC and TnI is apparently much faster than the rate of TnI-induced activation. The observed rapid single-exponential transient for TnI-induced activation indicates that saturation with Ca2+ places TnC predominantly in the primed-closed state (1\10) that precedes opening. From the Ca2+-primed state, the TnC-TnI assembly rapidly undergoes an induced-fit opening through k2. We conclude that the Ca2+-priming step (with k1 < 19 s−1) is the rate-limiting step in the activation of the TnC-TnI assembly. The Ca2+-priming step is energetically favorable, 𝒦1 ≫ 1, because there is no slow phase in TnI-induced activation (from a population that must undergo a slow k1 transition before opening through k2). This implies that reverse reaction rate of Ca2+-priming is very slow: k−1 = k1/𝒦1 ≃ 0 s−1.
a rate that is sensitive to both Ca2+- and TnI-activating steps. This finding is consistent with the induced-fit model, which, of the two mechanistic models, is the only one that allows the rate of cTnI-induced activation to exceed the rate of Ca2+-induced activation. If the transition proceeded through a population-shift-stabilization mechanism then the rate of TnI-induced activation would be rate-limited to 19 s−1. The rate of overall association between TnC and TnI is apparently much faster than the rate of TnI-induced activation. The observed rapid single-exponential transient for TnI-induced activation indicates that saturation with Ca2+ places TnC predominantly in the primed-closed state (1\10) that precedes opening. From the Ca2+-primed state, the TnC-TnI assembly rapidly undergoes an induced-fit opening through k2. We conclude that the Ca2+-priming step (with k1 < 19 s−1) is the rate-limiting step in the activation of the TnC-TnI assembly. The Ca2+-priming step is energetically favorable, 𝒦1 ≫ 1, because there is no slow phase in TnI-induced activation (from a population that must undergo a slow k1 transition before opening through k2). This implies that reverse reaction rate of Ca2+-priming is very slow: k−1 = k1/𝒦1 ≃ 0 s−1.
The allosteric model of activation (Fig. 2 b; Eqs. 14a and 14b) provides a straightforward explanation of the two-exponential process of Ca2+-activation. The two-exponential process is interpreted as the superposition of two populations of TnC-TnI, each relaxing through one of the two distinct pathways of activation. The values for k−1 and k′−3 that were obtained above afford preliminary estimates of k1 and k3. For the first pathway of activation (Eq. 14a), the dominant eigenvalue of its rate matrix (Eq. 3) is
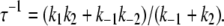 |
(17) |
With k−1 ≃ 0, this simplifies to τ−1 ≃ k1 = 19 s−1. For the second pathway of activation (Eq. 14b), the dominant eigenvalue of its rate matrix (Eq. 4) is
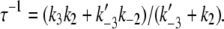 |
(18) |
With k′−3 ≃ 0, this simplifies to τ−1 ≃ k3 = 1554 s−1. The activation models provide a simple expression for the observed rate for TnI-induced activation,
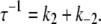 |
(19) |
Additional information needed to resolve k2 and k−2 is provided by the kinetics of deactivation.
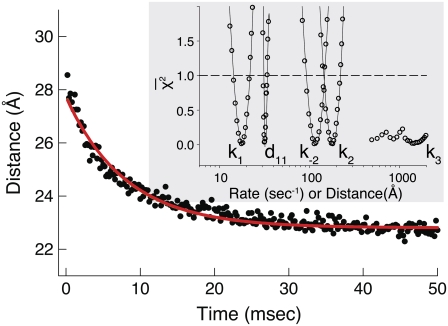
Deactivation of the TnC-TnI assembly was monitored after rapidly mixing the Ca2+-saturated sample of TnC-TnI with a solution containing the Ca2+ chelator EGTA (2 mM) (Fig. 6). The relaxation transient was empirically fit as a single-exponential decay process (τ−1 = 125 s−1, 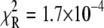 ). A two-exponential fit (not shown) did not statistically improve the fitting (F = 0.76). Because the scheme for deactivation is kinetically linked with the scheme for TnI-induced activation (Eqs. 14 and 15), the information in the two experiments can be combined to resolve k2 and k−2. The dominant eigenvalue of the scheme of deactivation (Eq. 15) is
). A two-exponential fit (not shown) did not statistically improve the fitting (F = 0.76). Because the scheme for deactivation is kinetically linked with the scheme for TnI-induced activation (Eqs. 14 and 15), the information in the two experiments can be combined to resolve k2 and k−2. The dominant eigenvalue of the scheme of deactivation (Eq. 15) is
 |
(20) |
For the system to deactivate upon the release of Ca2+, the system must preferentially exit the primed-closed state (\10) to the left; this implies that k−3 ≫ k2. The expression for the observed rate simplifies to
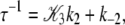 |
(21) |
where 𝒦3 ≡ k3/k−3. Equations 19 and 21 explain why the rate of relaxation for deactivation (125 s−1) is slower than the rate of TnI-induced activation (305 s−1). In Eq. 21, k2 is premultiplied by a 𝒦3 < 1. 𝒦3 must be less than unity for TnC to switch off during deactivation. Assuming that 𝒦3 = 0.1, we obtain estimates for k2 (200 s−1) and k−2 (105 s−1). The backward reaction rate k−2 approaches the forward reaction rate k2, making induced-fit TnC opening highly reversible. Under saturating Ca2+ (15°C), the system is an ∼2:1 mixture of rapidly interconverting, fully activated (open) and partially activated (primed-closed) species. The finding that the TnC-TnI does not fully activate upon Ca2+ binding implies that the mean FRET distance of the Ca2+ saturated TnC-TnI assembly (Fig. 3) is a weighted mixture of the FRET distances from primed-closed and open populations.
FIGURE 6.
Deactivation kinetics after Ca2+ removal, 15°C. FRET optical distance change after rapid mixing of Ca2+-saturated TnC-TnI with buffer containing Ca2+ chelator, EGTA. Empirical single-exponential fit (green, obscured by red trace): τ−1 = 125 s−1. Global model-based fit (red) with derived parameters in Table 1. (Inset) 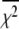 (Eq. 22), the normalized adiabatic projection of the global χ2 hypersurface on a model parameter (labeled) axis.
(Eq. 22), the normalized adiabatic projection of the global χ2 hypersurface on a model parameter (labeled) axis.
Global analysis of equilibrium and transient FRET distances
Initial estimates for the rate parameters that govern the model of TnC-TnI allostery (Eqs. 14 and 15) were obtained from the observed relaxation rates in the stopped-flow FRET measurements and assumed equilibrium constants. The structural information provided by FRET was ignored. To realize the full potential of the experimental information, we performed a global analysis of the three stopped-flow FRET measurements. The main task of the global fitting was to resolve the species-associated FRET distances and the microscopic transition rates that cause system-state populations to evolve after perturbation of the system. The results of the global fitting are shown in Figs. 5 and 6. Recovered values of the model parameters k1, k2, k−2, k3, d\00, and d\11 are given in Table 1. To provide stable convergence, k−1, k−3, and d\10 were assigned fixed values. The FRET distance d\10 was fixed at 23.9 Å, the mean FRET distance of the Ca2+-saturated TnC-only sample from the time-resolved measurements. Parameters k−1 and k−3 were assigned fixed values of 1.0 s−1 and 31000 s−1 because they were, respectively, too slow or too fast to be resolved by the data. Values were assigned based on the preliminary estimates of k1 and k3, the requirement that the primed-closed state is favored over the closed state when Ca2+ is bound, 𝒦1 > 1, and the requirement that closed state is favored over the primed-closed state when Ca2+ is not bound, 𝒦3 < 1.
TABLE 1.
Mesoscopic parameterization of the Ca2+-signaling cycle
| Parameter | Global fit |
|---|---|
| k1 (s−1) | 18.0 ± {14.4, 21.9} |
| k−1 | 1.0* |
| k2 | 181 ± {145, 222} |
| k−2 | 117± {93,148} |
| k3 | 1618† |
| k−3 | 31,000* |
| d00 (Å) | 21.4‡ |
| d10 | 23.9 ± 2.6§ |
| d11 | 32.2 ± {31.3, 34.5} |
Parameter values are from a global fit of activation and deactivation stopped flow FRET data (compare to Figs. 5 and 6) to the model of the signaling cycle (Fig. 2, Eqs. 14 and 15) (15°C). Reported values are mean ± precision. Precision is expressed as {le, ue}, where le and ue are the respective lower and upper 68% (1 σ) confidence estimates of the parameter, obtained from a one-dimensional adiabatic grid search.
Fixed (see text).
Poorly resolved, confidence estimates unavailable.
Precision not determined because value depends on assumed k−1.
Fixed to value measured from time-resolved FRET (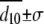 ).
).
The ability of the experimental information to specify values for the model parameters is quantitated by the recovered precision of the model parameters. The precision of the parameters k1, k2, k−2, k3, and d\11 were determined by projecting the 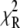 hypersurface (measure of deviation between model and data as a function of parameter values) along the individual parameter axes in a series of one-dimensional adiabatic grid searches (Fig. 6, inset; Table 1). The grid search results are reported as a normalized χ2
hypersurface (measure of deviation between model and data as a function of parameter values) along the individual parameter axes in a series of one-dimensional adiabatic grid searches (Fig. 6, inset; Table 1). The grid search results are reported as a normalized χ2
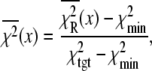 |
(22) |
where 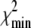 is the
is the 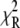 at the converged minimum. The quantities
at the converged minimum. The quantities 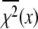 are
are 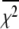 values at grid search points. The target χ2,
values at grid search points. The target χ2, 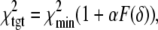 is a function of the F-statistic F(δ), where δ is the confidence level (taken as 68%), and
is a function of the F-statistic F(δ), where δ is the confidence level (taken as 68%), and 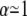 accounts for the loss of one degree of freedom in the grid search. Intersection of
accounts for the loss of one degree of freedom in the grid search. Intersection of 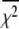 with unity (dashed line) provides the upper and lower 68% (one standard deviation) error estimates of the parameter. In general, parameter error is non-Gaussian, and it is preferable to express parameter precision using upper and lower limits that nonsymmetrically bracket the 68% confidence interval. The values of parameters k1, k2, k−2, and d\11 are determined with high precision (Fig. 6, inset). The parameter k3 is poorly resolved because the
with unity (dashed line) provides the upper and lower 68% (one standard deviation) error estimates of the parameter. In general, parameter error is non-Gaussian, and it is preferable to express parameter precision using upper and lower limits that nonsymmetrically bracket the 68% confidence interval. The values of parameters k1, k2, k−2, and d\11 are determined with high precision (Fig. 6, inset). The parameter k3 is poorly resolved because the 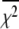 curve for k3 is shallow; it also has more than one local minimum. This is expected, because k3 = 1618 s−1 exceeds the resolution of the stopped flow instrument (1/1.8 ms dead-time = 555 s−1). The value of the species-associated distance d\00 depends on the assumed value for k−1. Since the accuracy of d\00 is conditional, its precision was not determined.
curve for k3 is shallow; it also has more than one local minimum. This is expected, because k3 = 1618 s−1 exceeds the resolution of the stopped flow instrument (1/1.8 ms dead-time = 555 s−1). The value of the species-associated distance d\00 depends on the assumed value for k−1. Since the accuracy of d\00 is conditional, its precision was not determined.
The refined values of parameters k2 (181 s−1) and k−2 (117 s−1) confirmed the preliminary observation that Ca2+-bound TnC-TnI is in dynamic equilibrium between the primed-closed and open conformations. The microequilibrium constant of TnI-facilitated TnC opening is rigorously determined, 𝒦2 ≡ k2/k−2 = 1.55 (15°C). Estimates for the microassociation constants that govern Ca2+-induced TnC priming (isomerization of s1), 𝒦1 ≡ k1/k−1 = 18.0 and 𝒦3 ≡ k3/k−3 = 0.052, are less reliable because k−1 and k−3 were assigned fixed values; they are, nevertheless, consistent with the data. The mean observed FRET distance of Ca2+-saturated TnC-TnI from the time-resolved measurements (28.9 Å) is a 1.55:1 mixture of species-associated interprobe distances for the primed-closed state d\10 (mean, 23.9 Å) and the open state d\11 (mean, 32.2 Å). The mean interprobe distance change for TnC opening is 8.3 Å.
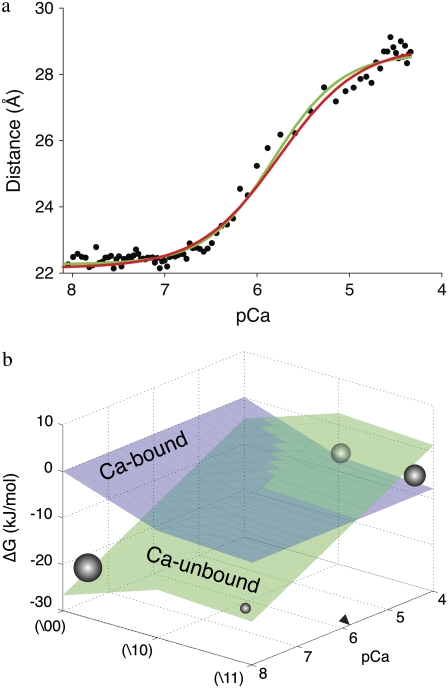
FRET-Ca2+ titration
From free energy conservation, the three microequilibrium constants that govern the protein isomerizations 𝒦1, 𝒦2, and 𝒦3, along with any of the three equilibrium constants for Ca2+ binding to closed (\00), primed-closed (\10), or open (\11) system states (respectively, K0, K1, and K2), provide a complete parameterization of the free energies 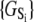 of the relevant system-states in the macroscopic free energy landscape
of the relevant system-states in the macroscopic free energy landscape 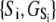 of the TnC-TnI assembly. To complete the thermodynamic parameterization of the TnC-TnI landscape, we performed an equilibrium Ca2+ titration of the FRET distance (Fig. 7 a). For reference, the data were empirically fit to the Hill equation,
of the TnC-TnI assembly. To complete the thermodynamic parameterization of the TnC-TnI landscape, we performed an equilibrium Ca2+ titration of the FRET distance (Fig. 7 a). For reference, the data were empirically fit to the Hill equation, 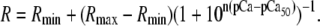 The recovered parameters (n = 1.18, pCa50 = 5.82) are consistent with previous measurements (1,26). Through the Boltzmann equation (Eq. 6), the
The recovered parameters (n = 1.18, pCa50 = 5.82) are consistent with previous measurements (1,26). Through the Boltzmann equation (Eq. 6), the 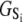 determine how the system will equilibrate among all system-states Si at a given [Ca2+]. As discussed in Appendix B, the free energies of the ligand-unbound species depend linearly on the Ca2+ chemical potential,
determine how the system will equilibrate among all system-states Si at a given [Ca2+]. As discussed in Appendix B, the free energies of the ligand-unbound species depend linearly on the Ca2+ chemical potential, 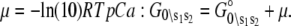 The free energies of the ligand-bound species are independent of μ:
The free energies of the ligand-bound species are independent of μ: 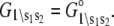 The relative free energies of the ligand-bound species are calculated from k2, k−2, k3, and k−3 using
The relative free energies of the ligand-bound species are calculated from k2, k−2, k3, and k−3 using
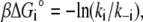 |
(23) |
where β = 1/RT and we assign βG°1\00 = 0. From the rate constants in Table 1, we obtain 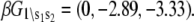 The relative free energies of the ligand-unbound species
The relative free energies of the ligand-unbound species 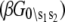 were calculated from k1, k−1, k2, and k−2 after assigning G°0\00 = μ′, where μ′ is a chemical potential offset that specifies when G°0\00 = G°1\00. From Eq. 23 and the rates in Table 1, we obtain
were calculated from k1, k−1, k2, and k−2 after assigning G°0\00 = μ′, where μ′ is a chemical potential offset that specifies when G°0\00 = G°1\00. From Eq. 23 and the rates in Table 1, we obtain 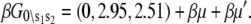 A fit to the Ca2+-FRET titration data using Eqs 2, 5, 6 (Fig. 7 a) provided the value for βμ′ (9.56)—the remaining parameter needed to parameterize the landscape (Fig. 7 b). The datum is sufficient to determine the remaining microequilibrium constants K0, K1, and K2 that, respectively, determine the affinity of Ca2+ for the system states (\00), (\10), (\11) (compare to Fig. 2). K0 = exp(βμ′) = exp(9.56) = 1.4 × 104 M−1. From conservation of free energy and considering the energy changes corresponding to
A fit to the Ca2+-FRET titration data using Eqs 2, 5, 6 (Fig. 7 a) provided the value for βμ′ (9.56)—the remaining parameter needed to parameterize the landscape (Fig. 7 b). The datum is sufficient to determine the remaining microequilibrium constants K0, K1, and K2 that, respectively, determine the affinity of Ca2+ for the system states (\00), (\10), (\11) (compare to Fig. 2). K0 = exp(βμ′) = exp(9.56) = 1.4 × 104 M−1. From conservation of free energy and considering the energy changes corresponding to 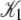 and
and 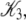 we obtain K1 = exp(9.56 + 2.95 + 2.89) = 4.9 × 106 M−1. We conclude that the primed-closed state has K1/K0 ≅ 300-times higher affinity for Ca2+ than the closed state. Due to nearest-neighbor-limited influence, there is no relative free energy difference between the Ca2+-bound and Ca2+-unbound surfaces for the opening transition, so K2 = K1 = 4.9 × 106 M−1. Kapp, the net (or apparent) affinity of Ca2+ for the regulatory site on TnC in the TnC-TnI assembly can be calculated from the recovered landscape
we obtain K1 = exp(9.56 + 2.95 + 2.89) = 4.9 × 106 M−1. We conclude that the primed-closed state has K1/K0 ≅ 300-times higher affinity for Ca2+ than the closed state. Due to nearest-neighbor-limited influence, there is no relative free energy difference between the Ca2+-bound and Ca2+-unbound surfaces for the opening transition, so K2 = K1 = 4.9 × 106 M−1. Kapp, the net (or apparent) affinity of Ca2+ for the regulatory site on TnC in the TnC-TnI assembly can be calculated from the recovered landscape 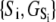 using Eqs. 27, 29, and 6 (see Discussion).
using Eqs. 27, 29, and 6 (see Discussion). 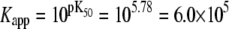 is a function of the entire landscape
is a function of the entire landscape 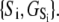 The pCa50 (5.82) from the fit to the Hill equation closely corresponds to the recovered pK50 (5.78).
The pCa50 (5.82) from the fit to the Hill equation closely corresponds to the recovered pK50 (5.78).
FIGURE 7.
System response to a change in [Ca2+]. (a) Ca2+ titration, mean FRET distance versus pCa (−log([Ca2+])). Empirical fit to the Hill equation (green) (n = 1.18; pCa50 = 5.82). Global fit to the model (Eqs. 2, 5, and 6) (red) (βΔμ′ = 22.9 kJ/mol). (b) The experiment-resolved macroscopic free energy landscape (see text, T = 15 C). Ca2+-unbound system-states (green). Ca2+-bound system-states (blue). Population density (spheres, radius represents magnitude) at the extremes of activation. pCa50 (labeled as a right arrowhead).
Temperature-dependent kinetics
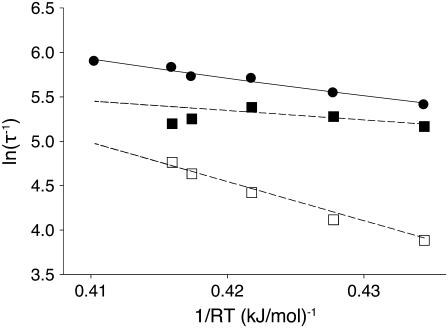
To further parameterize the kinetics and thermodynamics of the opening step in activation, we repeated the stopped flow measurements (Figs. 5 and 6) for a range of temperatures T = {3.7,8,12,15,16,20} C. TnI-induced activation was single-exponential at all temperatures with recovered τ−1 = {222,254,299,305,338,362} s−1. The kinetic transients were globally analyzed to obtain k2(T) and k−2(T) (Fig. 8). Noise increased with temperature (data not shown), and the global analysis failed to converge for 20 C. The backward rate constant k−2 showed upward deviation from a logarithmic dependence with temperature: k−2 {49,61,83,103,117} s−1 for T = {3.7,8,12,15,16} C. The forward rate constant k2 showed downward deviation from a logarithmic dependence on temperature: k2 = {175,196,218,191,181} s−1 for T = {3.7,8,12,15,16} C. These deviations from Arrhenius Law behavior cannot be attributed solely to a temperature-dependent energy (or enthalpy) of activation, which would cause k2 and k−2 to deviate in the same direction.
FIGURE 8.
Arrhenius analysis of the induced-fit opening step of activation. The rate of TnI-induced activation (circles), τ−1 = k2 + k−2, at T = {3.7,10,15,16,20} C (compare to Fig. 5 b) were fit to Eq. 26 (solid line) to recover the enthalpy of activation δ‡ and the entropy-adjusted barrier crossing attempt frequency νadj for the opening transition (Table 2). Also shown (squares) are the k2(T) (solid) and k−2(T) (open) values recovered from global analysis of relaxation data at T = {3.7,10,15,16} C (compare to Figs. 5 and 6) and calculated k2 and k−2 (dashed lines) from the recovered values νadj, 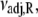 δ‡, and
δ‡, and 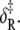
In an Arrhenius analysis of a reversible first-order process, the logarithm of the observed relaxation rate τ−1 = k2 + k−2 is plotted against inverse temperature β = 1/RT. The slope (see Appendix A),
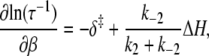 |
(24) |
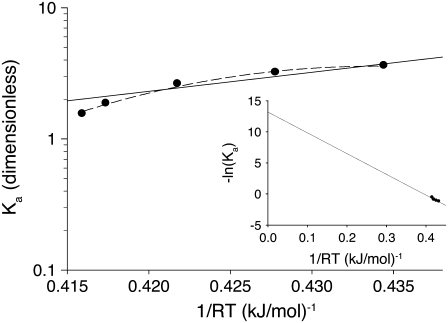
depends on the enthalpy of activation of the forward reaction δ‡ and the net enthalpy change of opening ΔH. In the derivation of Eq. 24, ΔH and the net entropy of opening ΔS were assumed to be temperature-independent. The second term in Eq. 24, which arises from reaction reversibility, can produce curvature in an Arrhenius plot. To recover the enthalpy ΔH and entropy ΔS of the opening process, we performed a van 't Hoff analysis (Fig. 9) of the recovered temperature-dependent k2(T) and k−2(T) by fitting to
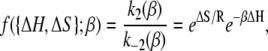 |
(25) |
where 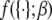 indicates that parameters {·} are being fit to a function f that depends on β. The rates at 16 C were excluded from the fitting. Opening is exothermic (ΔH, −33.4 kJ/mol) and is balanced by a loss of entropy (ΔS, −0.110 kJ/mol/K). Curvature in the data points in Fig. 9 suggested that ΔH and ΔS undergo temperature-dependent change over the experimental temperature range. The data were refit to Eq. 25 using temperature-dependent expressions for enthalpy and entropy,
indicates that parameters {·} are being fit to a function f that depends on β. The rates at 16 C were excluded from the fitting. Opening is exothermic (ΔH, −33.4 kJ/mol) and is balanced by a loss of entropy (ΔS, −0.110 kJ/mol/K). Curvature in the data points in Fig. 9 suggested that ΔH and ΔS undergo temperature-dependent change over the experimental temperature range. The data were refit to Eq. 25 using temperature-dependent expressions for enthalpy and entropy,
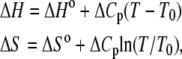 |
where ΔHo = ΔH(T0), ΔSo = ΔS(T0), and the heat capacity difference between the open and closed-primed states ΔCp is assumed to be temperature-independent. Fitting (Fig. 9, dashed line) produced maximum likelihood estimates for ΔHo (−33.1 KJ/mol), ΔSo (−0.108 KJ/mol/K), ΔCp (−7.6 kJ/mol/K), and T0 (282 K). The fit suggests that the temperature dependence of K2 = k2/k−2 can be attributed to a large negative ΔCp. The recovered ΔHo and ΔSo are within 2% of the recovered temperature-independent ΔH and ΔS.
FIGURE 9.
Thermodynamic analysis of the induced fit opening step of activation. The temperature-dependent equilibrium constant, Ka = k2/k−2, (circles) from k2(T) and k−2(T) (Fig. 8) were fit using Eq 28 with temperature-independent ΔH and ΔS (solid line) and temperature-dependent ΔH and ΔS (dashed line). Recovered ΔH, ΔS, and ΔCp are given in Table 2. (Inset) van 't Hoff plot showing extrapolated results from fit to temperature-independent ΔH and ΔS. The y intercept and slope provide –ΔS/R and ΔH, respectively.
To recover δ‡ and the entropy-adjusted barrier crossing attempt frequency νadj ≡ exp(σ‡/R) (where ν is the attempt frequency, and σ‡ is the entropy of activation of the forward reaction), the observed temperature-dependent rates τ−1 = k2 + k−2 for TnI-induced activation (compare to Fig. 5 b), were fit to (see Appendix A)
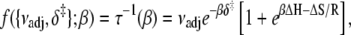 |
(26) |
using the temperature-independent ΔH and ΔS obtained from the van 't Hoff analysis. The fitting (Fig. 8, solid line) provided values for νadj (1.8 × 104 s−1) and δ‡ (10.6 kJ/mol). Here, as indicated by Eq. 24, curvature in the slope is caused by reaction reversibility, a nonzero ΔH, and shifting balance of forward k2 and reverse k−2 reaction rates. The data are well fit by Eq. 26, which does not include temperature-dependent changes in ΔH and ΔS. Using a more complicated expression with temperature-dependent ΔH and ΔS is unlikely to improve the fitting results.
The combined results of the van 't Hoff and Arrhenius analyses provide the reaction enthalpy ΔH (−33.4 kJ/mol), the reaction entropy ΔS (−0.110 kJ/mol/K), the enthalpy of activation of the forward reaction δ‡ (10.6 kJ/mol), and the entropy-adjusted barrier crossing attempt frequency for the forward reaction νadj (1.8 × 104 s−1). From these values we obtain the enthalpy of activation of the reverse reaction, 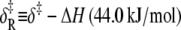 and the entropy-adjusted barrier crossing attempt frequency for the reverse reaction, νadj,R ≡ ν exp(
and the entropy-adjusted barrier crossing attempt frequency for the reverse reaction, νadj,R ≡ ν exp(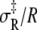 ) (1.0 × 1010 s−1), where
) (1.0 × 1010 s−1), where 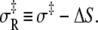 It is calculated from νadj,R = νadj exp(−ΔS/R). To confirm the fitting and calculations, k2 = νadj exp(–βδ‡) and
It is calculated from νadj,R = νadj exp(−ΔS/R). To confirm the fitting and calculations, k2 = νadj exp(–βδ‡) and 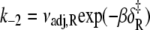 were calculated from the recovered parameters νadj,
were calculated from the recovered parameters νadj, 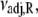 δ‡, and
δ‡, and 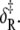 In Fig. 8, the calculated rates (dashed lines) are plotted along with the observed k2(T), k−2(T) (squares). The recovered thermokinetic parameters for the opening/closing transition are summarized in Table 2.
In Fig. 8, the calculated rates (dashed lines) are plotted along with the observed k2(T), k−2(T) (squares). The recovered thermokinetic parameters for the opening/closing transition are summarized in Table 2.
TABLE 2.
Thermokinetic parameterization of the opening/closing transition of cardiac TnC-TnI
| Parameter | Value |
|---|---|
| ΔH (kJ/mol) | −33.4 |
| δ‡ | 10.6 |
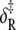 |
44.0 |
| ΔS (kJ/mol/K) | −0.110 |
| ΔCp | −7.6 |
| νadj (s−1) | 1.8 × 104 |
| νadj,R | 1.0 × 1010 |
For opening: ΔH, net enthalpy change; ΔCp, heat capacity change; ΔS, net entropy change; δ‡, enthalpy of activation; and νadj = ν exp(σ‡/R), entropy-adjusted barrier crossing attempt frequency (ν, barrier crossing attempt frequency; σ‡, entropy of activation). For closing: 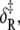 enthalpy of activation; and νadj,R entropy-adjusted barrier crossing attempt frequency.
enthalpy of activation; and νadj,R entropy-adjusted barrier crossing attempt frequency.
DISCUSSION
A previously characterized FRET reporter system TnC(12W/51C*AEDANS) (8) was used to probe the structural kinetics of the cardiac TnC-TnI assembly during rapid activation and deactivation. In stopped-flow kinetic measurements, FRET provides a meaningful measure of interprobe distance in addition to relaxation rates. The data were analyzed in terms of a new nonequilibrium mesoscopic (coarse-grained) model of allosteric transitions in the TnC-TnI assembly. The model captures the functional dynamics of the TnC-TnI assembly in two kinetically linked allosteric models for the activation and deactivation stages of the signaling cycle.
Dynamic conformational equilibrium
Our measurements provide structural and kinetic evidence for the existence of a dynamic equilibrium of macrostates in the TnC-TnI assembly when Ca2+ is bound and when Ca2+ is not bound to the regulatory site (loop II) of TnC. These results provide mechanistic insight into the phenomenon of “incomplete myofilament activation by Ca2+” (1,38). In addition, the results provide, apparently, the first reported evidence of incomplete deactivation of cardiac troponin. The structural transition from the primed-closed state to the open state is governed by the forward rate constant k2 (181 ± {145,222}s−1) and backward rate constant k−2 (117 ± {93,148}s−1). Parameter precision ±{le,ue} is quantified by the lower and upper estimates for the 68% confidence interval. We conclude that Ca2+-bound TnC-TnI rapidly interconverts between the primed-closed and open structural conformations, spending ∼65% of the time in the open state (T = 15 C). This finding is consistent with previously reported energetic measurements of Ca2+-dependent changes in the affinity of TnC for TnI (39) and by high resolution structural studies of Ca2+-saturated TnC (7,40). The affinity constants 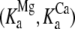 of native TnI for TnC under Mg2+-saturated and Ca2+-saturated conditions (400 mM KCl, 20 C) have been reported by Liao et al. (39). The ratio
of native TnI for TnC under Mg2+-saturated and Ca2+-saturated conditions (400 mM KCl, 20 C) have been reported by Liao et al. (39). The ratio 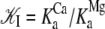 provides an estimate of the Ca2+-sensitive component of TnC-TnI interaction. Equating the Ca2+-sensitive TnC-TnI interaction with the TnC opening transition, we calculate 𝒦I = 127.0 × 106 M−1/41.7 × 106 M−1 = 3.04 (400 mM KCl, 20 C). This is in general agreement with the isomerization constant for TnC opening obtained in this study, 𝒦2 = k2/k−2 = 1.55 (200 mM KCl, 15 C).
provides an estimate of the Ca2+-sensitive component of TnC-TnI interaction. Equating the Ca2+-sensitive TnC-TnI interaction with the TnC opening transition, we calculate 𝒦I = 127.0 × 106 M−1/41.7 × 106 M−1 = 3.04 (400 mM KCl, 20 C). This is in general agreement with the isomerization constant for TnC opening obtained in this study, 𝒦2 = k2/k−2 = 1.55 (200 mM KCl, 15 C).
Our measurements and analysis indicate that the TnC opening causes an 8.3 Å change in the mean interprobe distance. This distance change is statistically indistinguishable from the interprobe distance change (9.2 Å) calculated from the NMR-derived, Ca2+-bound, primed-closed structure (PDB ID code 1AP4) (7) and x-ray crystallography-derived, Ca2+-bound, open structure (PDB ID code 1J1E) (40) structure (J. M. Robinson, unpublished). The interprobe distance was obtained by modifying the high-resolution primed-closed and open structures in silico to incorporate the donor and acceptor FRET probes (Fig. 1) and performing all-atom molecular dynamics simulations to sample the conformations of the FRET probes.
When regulatory Ca2+ is not bound to TnC, the TnC-TnI assembly may exist in the partially activated primed-closed state in addition to the closed state. Activation through the accessory pathway in our allosteric model (Fig. 2 b (blue); Eq 12b) occurs through Ca2+-binding to a preexisting population of TnC-TnI in the primed-closed state. Our kinetic measurements detect activation through this pathway. Solzin et al. (41), using an environmentally sensitive fluorophore to monitor activation kinetics, also detected a rapid transient during Ca2+-activation . They interpreted this transient as an additional step that precedes the rate-limiting (Ca2+-priming) step in a serial reaction scheme for Ca2+-activation. From the FRET-provided distance information in our measurements, we found that the rapid Ca2+-induced transient (1554 s−1) involves substantial (48% of 6.6 Å) distance change. This large distance change is associated with opening (not priming). We have shown that opening temporally follows the slow priming transition. The accessory pathway of activation thus bypasses the slow priming step in activation through Ca2+ binding to a preexisting population of TnC-TnI in the primed-closed state. The accessory pathway of activation suggests that the TnC-TnI assembly does not completely deactivate to the closed conformation when regulatory Ca2+ is not bound.
Mesoscopic modeling
Our mesoscopic model of TnC-TnI allostery (Fig. 2 b) recognizes transition rate degeneracy due to nearest-neighbor-limited influence, and it recognizes the kinetic linkages between activation and deactivation stages of the signaling cycle. Transition rate degeneracy arises from the complex nature of the system. Simple systems such as chemical networks—networks of chemical reactions of diffusing molecules—do not exhibit transition rate degeneracy. The model shows, for example, that the elementary transition rate parameters that govern the accessory pathway of activation are the same rate parameters that govern the kinetics of deactivation. These linkages affect both structural and kinetic aspects of the measured interprobe distance relaxations in the two activation measurements, the deactivation measurement, and the Ca2+-titration measurement. Recognizing these linkages enabled recovery of the model parameters from the measurements through a global analysis of the data because the observed experimental relaxation rates jointly depend upon the linked model parameters. Independent empirical fitting of stopped flow experiments ignores the intensity information in the measurements and the inherent kinetic linkages in the system. In the compartmental analysis of kinetic transitions, the most common type of analysis, intensity information is not utilized because 1), analytical expressions for intensity are complicated functions of the transition rates and initial conditions; 2), initial conditions must be known or assumed; and 3), the species-associated intensities, including intermediate species, must be known. The lack of constraint when data are independently fit and empirically fit to sums of exponentials makes drawing biological conclusions problematic. In contrast, global analysis of a diverse set of experiments in terms of a single model facilitates strong conclusions because global analysis is self-constraining—recovered model parameters must account for the observed behavior in all experiments.
Induced-fit opening
Two mechanistic models of TnC-TnI allostery (Fig. 4)—the population-shift-stabilization model and induced-fit model—are consistent with the small Ca2+-induced change in isolated TnC and the large distance change observed upon saturation of TnC-TnI with Ca2+ (Fig. 3). These models provide different interpretations with respect to structure, kinetics, and energetics of the transitions in the model of TnC-TnI allostery (Fig. 2 b). The population-shift-stabilization model interprets the isomerization of TnC as a structural opening event that, in the absence of TnI, is energetically unfavorable and statistically improbable. TnI switching, through TnI-R association with the opening-induced hydrophobic pocket in TnC, stabilizes the otherwise unfavorable transition. The induced-fit model interprets the TnC isomerization as a structurally subtle, but energetically favorable, transition that generates a Ca2+-primed state with a structure that is closed. TnC opening is the TnI-mediated opening of permissive Ca2+-primed TnC. The two models have different kinetic signatures. Of the two, only the induced-fit model allows the rate of TnI-induced activation to exceed the rate of Ca2+-induced activation. The mechanism is diagnosed by an observed rate of TnI-induced activation (305 s−1, Fig. 5 b) that greatly exceeds the slow rate of Ca2+-induced activation (19 s−1, Fig. 5 a).
Theories of allosterism assume that ligand agonists directly stabilize the active state of their receptor (reviewed in (42)). In the population-shift-stabilization model, Ca2+ binding does not directly stabilize the receptor TnC. Instead, TnC is indirectly stabilized by Ca2+ in a process that relies on a free energy drop provided by TnI. In the induced-fit mechanism, Ca2+ binding directly stabilizes the primed-closed conformation of TnC, which we find has a 300-times greater affinity for Ca2+ than the closed conformation. Our finding that the cardiac TnC-TnI assembly switches as an induced-fit process questions the belief that energetics must correlate with structural change, i.e., small energy drops produce little structural change; large energy drops produce appreciable movement. TnC opening, which involves an 8.3 Å interprobe distance change, is, thermodynamically, marginally favorable (ΔG = −1.1 kJ/mol, 15 C). In contrast, the Ca2+-priming step, which produces a subtle 2.2 Å interprobe distance change, is thermodynamically very favorable (ΔG = −6.9 kJ/mol, 15 C). Mechanistically, induced-fit opening appears to involve the replacement of intra-TnC hydrophobic interactions with interprotein TnC-TnI hydrophobic interactions as the TnI-R diffusively creeps deeper into the TnC hydrophobic pocket. TnC opening is coupled to, and limited by, TnI isomerization.
Free energy landscape
The mesoscopic free energy landscape consists of the set of one-dimensional free energy surfaces along the reaction coordinates of all system-state transitions (edges in the Markov network; see Fig. 2 a). System-states (nodes in the Markov network) are regions of local stability (low energy wells) in the free energy landscape. Collectively, the system-states Si and the macroscopic free energies of the system states  define the macroscopic free energy landscape
define the macroscopic free energy landscape 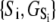 of the system. The free energy landscape of the TnC-TnI assembly (excluding the high energy states (\01)) is shown in Fig. 7 b. The free energy landscape is of fundamental interest because it provides the weighting scheme needed to calculate the macroscopic measure of any observable property of the equilibrated system. Through the Boltzmann equation (Eq. 6), the
of the system. The free energy landscape of the TnC-TnI assembly (excluding the high energy states (\01)) is shown in Fig. 7 b. The free energy landscape is of fundamental interest because it provides the weighting scheme needed to calculate the macroscopic measure of any observable property of the equilibrated system. Through the Boltzmann equation (Eq. 6), the 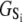 determine the equilibrium probability
determine the equilibrium probability 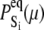 that the system occupies system-state Si under an externally imposed Ca2+ chemical potential μ. The ensemble measurement of any observable
that the system occupies system-state Si under an externally imposed Ca2+ chemical potential μ. The ensemble measurement of any observable 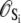 of the equilibrated system is the inner-product of the observable with the equilibrium probability distribution
of the equilibrated system is the inner-product of the observable with the equilibrium probability distribution
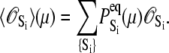 |
(27) |
The 𝒪-based pCa50 = −βμ′/ ln(10) is obtained from the μ′ where
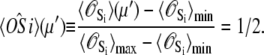 |
(28) |
The FRET distance  (defined in Methods) in a Ca2+ titration experiment is one such system observable
(defined in Methods) in a Ca2+ titration experiment is one such system observable  many others exist. The distance-pCa50 or pd50(5.78) was obtained by solving Eq. 28 for the observable
many others exist. The distance-pCa50 or pd50(5.78) was obtained by solving Eq. 28 for the observable 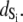 It is generally assumed that the sensitivity to Ca2+ of some physical observable of myofilament regulation (e.g., force, probe fluorescence) is equal to the net affinity of the TnC regulatory site for Ca2+. To test this assumption, we examined the correspondence between the pd50 and the net Ca2+-binding-pCa50 or pK50. The Ca2+-binding status
It is generally assumed that the sensitivity to Ca2+ of some physical observable of myofilament regulation (e.g., force, probe fluorescence) is equal to the net affinity of the TnC regulatory site for Ca2+. To test this assumption, we examined the correspondence between the pd50 and the net Ca2+-binding-pCa50 or pK50. The Ca2+-binding status 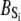 of system-state Si is defined as
of system-state Si is defined as
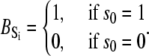 |
(29) |
Here,  was calculated using Eqs. 27–29. Significantly, the traces of
was calculated using Eqs. 27–29. Significantly, the traces of 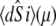 and
and 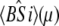 superimpose, and the recovered pd50 and pK50 are identically 5.78 (data not shown). This supports the assumption that the sensitivity to Ca2+ of a system observable is a measure of net Ca2+ affinity for the regulatory site of TnC.
superimpose, and the recovered pd50 and pK50 are identically 5.78 (data not shown). This supports the assumption that the sensitivity to Ca2+ of a system observable is a measure of net Ca2+ affinity for the regulatory site of TnC.
In addition to its quantitative value, the free energy landscape (Fig. 7 b) provides a visual representation of how activation/deactivation occurs. The Boltzmann equation (Eq. 6) dictates that the system will respond to any perturbation by preferentially populating the regions of lowest free energy. In the TnC-TnI assembly, as [Ca2+] is raised, the 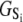 of the Ca2+-unbound system states (0\s1s2) (green plane) rise above the Ca2+-bound system states (1\s1s2) (blue plane), which are stationary. Population density (represented as sphere radius in Fig. 7 b) is greatest for those states with lowest free energy at a given [Ca2+] (pCa). Activity is defined as a change in the probability that TnI, the reporting component of the assembly, is either active (s2 = 1) or inactive (s2 = 0). Visualized in terms of the free energy landscape, activation is rightward movement of density toward the TnI-active states (0\s11) and (1\s11). Deactivation is leftward movement of density away from the TnI-active states. At low [Ca2+], the system is mostly deactivated in (0\00) with very little partially activated species (0\10). At high [Ca2+] a 3:2 mixture of primed-closed (1\s10) and open (1\s11) system-states occurs.
of the Ca2+-unbound system states (0\s1s2) (green plane) rise above the Ca2+-bound system states (1\s1s2) (blue plane), which are stationary. Population density (represented as sphere radius in Fig. 7 b) is greatest for those states with lowest free energy at a given [Ca2+] (pCa). Activity is defined as a change in the probability that TnI, the reporting component of the assembly, is either active (s2 = 1) or inactive (s2 = 0). Visualized in terms of the free energy landscape, activation is rightward movement of density toward the TnI-active states (0\s11) and (1\s11). Deactivation is leftward movement of density away from the TnI-active states. At low [Ca2+], the system is mostly deactivated in (0\00) with very little partially activated species (0\10). At high [Ca2+] a 3:2 mixture of primed-closed (1\s10) and open (1\s11) system-states occurs.
Although the microequilibrium constants 𝒦1 = k1/k−1 = 18.0 and 𝒦3 = k3/k−3 = 0.052 were determined inexactly, we can confirm that their values jointly satisfy the requirement that the work done on the free energy landscape by Ca2+ binding not exceed the input of free energy to the assembly from Ca2+ binding. From the Ca2+ titration measurement, Ca2+ binding provides ΔGin = ln(10)RTpCa50 = 31.9 kJ/mol of free energy into the TnC-TnI assembly (15 C). This free energy is the maximum amount of energy available to change the free energy landscape of the assembly. Kinetic linkages governing the TnI isomerization, (/10) ↔ (/11), dictate that the bound and unbound surfaces have the same ΔG for the TnI isomerization, i.e., G1\11 – G1\10 = G0\11 – G0\10. However, the Ca2+-bound and Ca2+-unbound surfaces of the free energy landscape have different ΔG for the isomerization of TnC, (/00) ↔ (/10). Indeed, without some difference in ΔG between the Ca2+-bound and Ca2+-unbound surfaces, no Ca2+-induced population shift would occur for the protein states (\s1s2). From the estimated 𝒦1 and 𝒦3, the total relative change between the unbound and bound free energy surfaces is ΔGout = −RT ln(𝒦3/𝒦1) = 14.0 kJ/mol. The efficiency of coupling the free energy of ligand binding into a change in the free energy landscape, ε ≡ ΔGout/ΔGin = 0.44. As required, ε ≤ 1.
Thermokinetics of TnC-TnI opening
From temperature-dependent stopped flow kinetics, we have determined the enthalpy ΔH (−33.4 kJ/mol), entropy ΔS (−0.110 kJ/mol/K), and heat capacity change ΔCp (−7.6 kJ/mol/K) of the isolated opening transition in the activation of the cardiac TnC-TnI assembly (Table 2). The measured values are for the opening step in activation, which is distinct from other processes such as Ca2+-binding, Ca2+-priming, and overall TnC-TnI association. Opening is promoted by a favorable decrease in enthalpy that is partially offset by a loss of entropy. Like cardiac TnC, calmodulin is a member of the super-family of bi-lobed Ca2+ binding proteins with two EF-hand domains per lobe. The entropy change for the binding of a peptide of myosin light-chain kinase to calmodulin has been studied by deuterium NMR relaxation (43), where side-chain order parameters provide an upper limit on ΔS (−0.4752 kJ/mol/K). Our measured ΔS (−0.110 kJ/mol/K) for TnI-R-induced TnC opening follows this trend of entropy loss upon complexation. Our measured ΔH and ΔS are opposite those observed for the tension generating step in psoas muscle, which is endothermic and disordering (44,45). Large negative ΔCp have been consistently observed for ligand binding-induced isomerizations of proteins. Examples include ΔCp = −3.5 kJ/mol/K for DNA binding by the transcription factor Oct-1 (46) and ΔCp = −3.1 kJ/mol/K for NAD+ binding to glyceraldehyde-3-phosphate dehydrogenase (47). Large negative ΔCp indicate sequence-specific recognition (48). In most cases, ΔCp are measured as average quantities for coupled equilibria involving combinations of bound/unbound ligand and active/inactive protein. In this context, ΔCp is properly regarded as an apparent heat capacity change 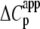 with contributions from the intrinsic ΔCp between the inactive and active protein states and the ligand-induced redistribution of the macrostate population (49). Our measurements have resolved the true ΔCp for the opening transition of the TnC-TnI assembly.
with contributions from the intrinsic ΔCp between the inactive and active protein states and the ligand-induced redistribution of the macrostate population (49). Our measurements have resolved the true ΔCp for the opening transition of the TnC-TnI assembly.
The measured ΔH, ΔS, and ΔCp values can be used to recover the distribution of enthalpy (energy) in the open and primed-closed macrostates. The enthalpy distribution arises from structural fluctuations (i.e., interconverting microstates) within each macrostate. Each macrostate consists of a set of N microstates m1, m2, …, mN, and each microstate has an enthalpy H(mi). We define a set of discrete enthalpy intervals H1, H2, …, H∞ of constant width Δ. We cluster the microstate enthalpies H(mi) into the enthalpy levels Hi; each level contains some number gi microstates. The probability of finding the macrostate in the enthalpy interval Hi is p(Hi) = gi/N. The continuous probability distribution of enthalpy is obtained in the limit, p(H)dH = limΔ→0 p(Hi). Evidently, p(H) is the probability that a macrostate has enthalpy in the interval [H, H + dH) given that H is available (∼e−βH, a decreasing function in H) times the probability that H is available (Ω(H), an increasing function in H). p(H) is therefore a peaked function. The enthalpy distribution p(H) is parameterized by its moments
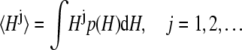 |
Ignoring moments in p(H) greater than 2, p(H) is Gaussian,
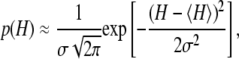 |
(30) |
with mean 〈H〉 = Hobs and variance related to the enthalpy fluctuations δH by σ2 = 〈δH2〉 = 〈H2〉 − 〈H〉2. The variance is related to the heat capacity through
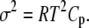 |
(31) |
By introducing the subscript (k) into p(H), 〈H〉, σ, etc., we emphasize that the quantities are properties of the macrostate (k). They are mesoscopic quantities, not macroscopic quantities of the system as a whole. The enthalpy distribution p(k)(H) of macrostate (k) is thus parameterized by H(k) = 〈H〉(k) and Cp(k).
We now show how the measured ΔS for opening is used to resolve the heat capacities, hence the width of the enthalpy distributions, of the open and primed-closed macrostates. The macrostate, a mesoscopic entity, is a sufficiently large collection of microstates that thermodynamic quantities can be appropriately defined for it by statistical thermodynamics (50). As with macroscopic entropy, the mesoscopic entropy S(k) of macrostate (k) is a functional of the probability distribution of enthalpy,
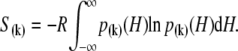 |
For Gaussian-distributed p(k)(H) (Eq. 30) with standard deviation σ(k), we obtain (51)
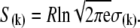 |
(32) |
Quite remarkably, σ(k) is completely determined by S(k). From Eqs. 31 and 32, the entropy change for opening, 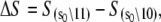 is a simple expression of the heat capacities of the open and primed-closed macrostates,
is a simple expression of the heat capacities of the open and primed-closed macrostates,
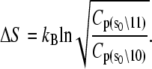 |
(33) |
The specific heat capacities of the open and primed-closed states are
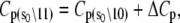 |
(34a) |
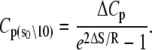 |
(34b) |
Evaluating, we obtain 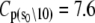 kJ/mol and
kJ/mol and  ∼10−10 kJ/mol. The extremely low value of
∼10−10 kJ/mol. The extremely low value of  is due to the highly negative ΔS, causing e2ΔS/R → 0. The enthalpy distribution of the primed-closed state
is due to the highly negative ΔS, causing e2ΔS/R → 0. The enthalpy distribution of the primed-closed state 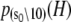 is broad with
is broad with 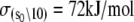 (T = 15 C). Compared to
(T = 15 C). Compared to 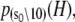 the enthalpy distribution of the open state
the enthalpy distribution of the open state 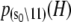 is almost δ-correlated,
is almost δ-correlated, 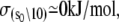 and shifted to lower enthalpy (by −33.4 kJ/mol).
and shifted to lower enthalpy (by −33.4 kJ/mol).
We have obtained, additionally, the enthalpy of activation for opening δ‡ (10.6 kJ/mol) and the entropy-adjusted, or effective, barrier-crossing attempt frequency for opening vadj ≡ ν exp(σ‡/R)(1.8 × 104 s−1), where σ‡ is the entropy of activation. The value νadj is very slow, and the rate of TnC opening is limited by a large loss of entropy σ‡ needed to reach the transition state. We conclude that TnC-TnI opening involves a large transient loss (σ‡) of configurational freedom and a net loss (ΔS) of configurational freedom.
Finally, we note that the third law of thermodynamics demands that Cp be nonnegative (50). From Eq. 34b, we obtain the constraint
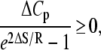 |
(35) |
which is satisfied by our results. This provides a useful check for experimental results.
CONCLUSIONS
Our results indicate the presence of dynamic exchange on two levels: dynamic exchange among macrostates of the cardiac TnC-TnI regulatory complex (the closed, primed-closed, and open states) and dynamic exchange among microstates within each macrostate. A statistical description is necessary to explain the macroscopic (physiologic) behavior of cardiac regulation because activation and deactivation are never complete. The chance that the system occupies an active or inactive macrostate is only more or less probable. One thus speaks of the cardiac regulatory cycle in terms of shifting macrostate populations determined by a macroscopic free energy landscape that is modulated by the cytosolic concentration of Ca2+.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health (grants No. HL052508 and HL80186), the European Union (grant No. MSCF-CT-2004-013119) and the American Heart Association (grant No. 0330170N).
Molecular structural images were rendered using VMD (52).
APPENDIX A
Here we derive expressions that allow an experimental thermokinetic parameterization of the energy landscape of a bi-meta-stable system that reversibly and stochastically jumps between two states, A and B (Fig. S1 in Data S1), according to the kinetic scheme
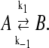 |
(36) |
The reversible transition is of interest not only in single step reactions but also as a component step of multistep reactions in coupled allosteric transitions. An Arrhenius analysis of temperature-dependent kinetic data, where the logarithm of the observed reaction rate is plotted against inverse temperature, is typically limited to the analysis of an irreversible reaction
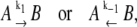 |
(37) |
either because k1 ≫ k−1 or k1 ≪ k−1, or because k1 and k−1 can be resolved through external information (44). We wish to perform an Arrhenius analysis of the reversible first-order process in Eq. 36. A general expression is derived for the dependence of the observed relaxation rate, τ−1 = k1 + k−1, on inverse temperature. The expression applies to both reversible and irreversible reactions.
We assume that both forward and reverse isomerizations in Eq. 36 are governed by the van 't Hoff-Arrhenius law
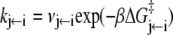 |
(38) |
with effective barrier crossing attempt rate νj←1 from Kramers' reaction rate theory (36,53,54), barrier crossing free energy 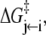 and β = 1/RT. Barrier crossing free energies are defined by
and β = 1/RT. Barrier crossing free energies are defined by
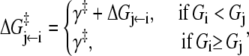 |
(39) |
where γ‡ is the nominal Gibbs free energy of activation. Inserting Eq. 39 into Eq. 38, the forward and reverse kinetic rates are given by
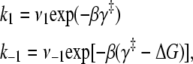 |
(40) |
with forward and backward barrier crossing attempt frequencies ν1 and ν−1. The values ΔG, 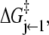 γ‡, k1, and k−1 are shown in Fig. S1 in Data S1. From detailed balance, k−1/k1 = exp(βΔG), and we find that the forward and backward barrier crossing attempt frequencies are identical, ν1 = ν−1 = ν.
γ‡, k1, and k−1 are shown in Fig. S1 in Data S1. From detailed balance, k−1/k1 = exp(βΔG), and we find that the forward and backward barrier crossing attempt frequencies are identical, ν1 = ν−1 = ν.
The observed relaxation rate τ−1 in any perturbation of a system governed by Eq. 36 is the eigenvalue τ−1 = k1 + k−1. Substituting the expressions for k1 and k−1 and rearranging, we obtain τ−1 = ν exp(–βγ‡)[1 + exp(βΔG)]. The change in Gibbs free energy ΔG depends on the change in enthalpy ΔH and the change in entropy ΔS through, ΔG = ΔH – TΔS. Similarly, the change in the nominal activation free energy γ‡ depends on the nominal change in the enthalpy of activation δ‡ and the nominal change in the entropy of activation σ‡ through γ‡ = δ‡ – Tσ‡. To simplify the derivation, we ignore any temperature dependence in ΔH, ΔS, δ‡, and σ‡ over the limited experimental range of temperatures. Making the substitution βγ‡ = βδ‡ – βTσ‡ = βδ‡ − σ‡/R, we obtain
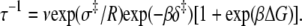 |
(41) |
We define νadj = ν exp(σ‡/R) as the forward entropy-adjusted (effective) barrier-crossing attempt frequency. Taking the logarithm of Eq. 41 and defining Kd = exp(βΔG) = k−1/k1 = x, we obtain the equation for the curve of a reversible reaction in an Arrhenius plot,
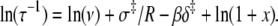 |
Recalling, ∂ ln(1 + x) = (1 + x)−1∂(1 + x), and observing, ∂x/∂β = xΔH, we obtain the desired expression for the slope in an Arrhenius plot from the relaxation rate of a reversible reaction
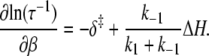 |
(42) |
In the forward irreversible limit (k−1 ≪ k1), we obtain the classical result, ∂ ln(λ)/∂β = – δ‡. In the backward irreversible limit (k−1 ≫ k1), ∂ ln(λ)/β = –δ‡ + ΔH. In a fully reversible reaction, (k−1 = k1), ∂ ln(λ)/∂β = –δ‡ + ΔH/2. In an Arrhenius analysis that ignores reversibility, activation enthalpy is underestimated for endothermic reactions (ΔH > 0), and activation enthalpy is overestimated for exothermic reactions (ΔH < 0).
APPENDIX B
The equilibrium association constants K0, K1, and K2 for Ca2+ binding to the system states (\00), (\10), and (\11) are defined based on two assumptions.
Assumption 1. The free energies of all ligand-unbound species
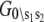 depend linearly on the chemical potential of [Ca2+], μ = RT ln [Ca2+], and the free energy of the protein complex
depend linearly on the chemical potential of [Ca2+], μ = RT ln [Ca2+], and the free energy of the protein complex 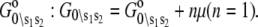
Assumption 2. The free energies of the ligand bound species
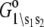 are fixed:
are fixed: 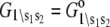 (n = 0).
(n = 0).- For Ca2+ binding to some configuration of TnC-TnI (\s1s2), Eq. 9 gives
where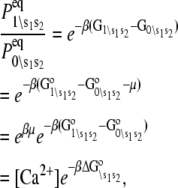
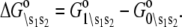 The equilibrium association constant K0 for Ca2+ binding to (\00) is
The equilibrium association constant K0 for Ca2+ binding to (\00) is
and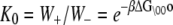
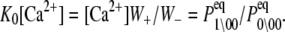
Thus, K0[Ca2+] is the pseudoequilibrium constant that governs Ca2+ binding to fully deactivated TnC-TnI (i.e., the (0\00) → (1\00) transition). K1[Ca2+] and K2[Ca2+] are the pseudoequilibrium constants that govern Ca2+ binding to partially activated (0\10) and fully activated (0\11) TnC-TnI. K1 and K2 are related to K0 by macroscopic detailed balance (Eq. 10): K0W1W−3 = K1W3W−1 and K1W2W−2 = K2W2W−2, which simplifies to K1 = K2.
Editor: Doug Barrick.
References
- 1.Robinson, J. M., W.-J. Dong, J. Xing, and H. C. Cheung. 2004. Switching of troponin I: Ca2+ and myosin-induced activation of heart muscle. J. Mol. Biol. 340:295–305. [DOI] [PubMed] [Google Scholar]
- 2.Gordon, A. M., E. Homsher, and M. Regnier. 2000. Regulation of contraction in striated muscle. Physiol. Rev. 80:853–924. [DOI] [PubMed] [Google Scholar]
- 3.Kobayashi, T., and R. J. Solaro. 2005. Calcium, thin filaments, and the integrative biology of cardiac contractility. Annu. Rev. Physiol. 67:39–67. [DOI] [PubMed] [Google Scholar]
- 4.Tao, T., B. Gong, and P. Leavis. 1990. Calcium-induced movement of troponin-I relative to actin in skeletal muscle thin filaments. Science. 247:1339–1341. [DOI] [PubMed] [Google Scholar]
- 5.Pate, E., K. Franks-Skiba, and R. Cooke. 1998. Depletion of phosphate in active muscle fibers probes actomyosin states within the powerstroke. Biophys. J. 74:369–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Herzberg, O., J. Moult, and M. James. 1986. A model for the Ca2+-induced conformational transition of troponin C. A trigger for muscle contraction. J. Biol. Chem. 261:2638–2644. [PubMed] [Google Scholar]
- 7.Spyracopoulos, L., M. X. Li, S. K. Sia, S. M. Gagne, M. Chandra, R. J. Solaro, and B. D. Sykes. 1997. Calcium-induced structural transition in the regulatory domain of human cardiac troponin C. Biochemistry. 36:12138–12146. [DOI] [PubMed] [Google Scholar]
- 8.Dong, W. J., J. Xing, M. Villain, M. Hellinger, J. M. Robinson, M. Chandra, R. J. Solaro, P. K. Umeda, and H. C. Cheung. 1999. Conformation of the regulatory domain of cardiac muscle troponin C in its complex with cardiac troponin I. J. Biol. Chem. 274:31382–31390. [DOI] [PubMed] [Google Scholar]
- 9.Wyman, J. 1948. Heme proteins. Adv. Protein Chem. 4:407–531. [DOI] [PubMed] [Google Scholar]
- 10.Koshland, D. E. J., G. Nemethy, and D. Filmer. 1966. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 5:365–385. [DOI] [PubMed] [Google Scholar]
- 11.Wyman, J. 1972. On Allosteric Models. Curr. Top. Cell. Regul. 6:209–226. [Google Scholar]
- 12.Weber, G. 1972. Ligand binding and internal equilibria in proteins. Biochemistry. 11:864–878. [DOI] [PubMed] [Google Scholar]
- 13.Kern, D., and E. R. P. Zuiderweg. 2003. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 13:748–757. [DOI] [PubMed] [Google Scholar]
- 14.Hilser, V. J., E. B. Garcia-Moreno, T. G. Oas, G. Kapp, and S. T. Whitten. 2006. A statistical thermodynamic model of the protein ensemble. Chem. Rev. 106:1545–1558. [DOI] [PubMed] [Google Scholar]
- 15.Matoba, Y., and M. Sugiyama. 2003. Atomic resolution structure of prokaryotic phospholipase A2: analysis of internal motion and implication for a catalytic mechanism. Proteins. 51:453–469. [DOI] [PubMed] [Google Scholar]
- 16.Prabhu, N. V., A. L. Lee, A. J. Wand, and K. A. Sharp. 2003. Dynamics and entropy of a calmodulin-peptide complex studied by NMR and molecular dynamics. Biochemistry. 42:562–570. [DOI] [PubMed] [Google Scholar]
- 17.Clegg, R. M. 2006. The history of FRET: from conception through the labors of birth. In Reviews in Fluorescence. C. D. Geedes and J. R. Lakowicz, editors. Springer, Berlin.
- 18.Lakowicz, J. R. 2006. Principles of Fluorescence Spectroscopy, 3rd Ed. Springer, Berlin.
- 19.Cheung, H. C., C. K. Wang, I. Gryczynski, W. Wiczk, G. Laczko, M. L. Johnson, and J. R. Lakowicz. 1991. Distance distributions and anisotropy decays of troponin C and its complex with troponin I. Biochemistry. 30:5238–5247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dong, W.-J., J. Xing, Y. Ouyang, J. An, and H. C. Cheung. 2008. Structural kinetics of cardiac troponin C mutants linked to familial hypertrophic and dilated cardiomyopathy in troponin complexes. J. Biol. Chem. 283:3424–3432. [DOI] [PubMed] [Google Scholar]
- 21.Bernasconi, C. F. 1976. Relaxation Kinetics. Academic Press, New York.
- 22.Beechem, J. M. 1992. Global analysis of biochemical and biophysical data. Methods Enzymol. 210:37–54. [DOI] [PubMed] [Google Scholar]
- 23.Robinson, J. M., W.-J. Dong, and H. C. Cheung. 2003. Can Forster resonance energy transfer measurements uniquely position troponin residues on the actin filament? A case study in multiple-acceptor FRET. J. Mol. Biol. 329:371–380. [DOI] [PubMed] [Google Scholar]
- 24.Dong, W.-J., J. An, J. Xing, and H. C. Cheung. 2006. Structural transition of the inhibitory region of troponin I within the regulated cardiac thin filament. Arch. Biochem. Biophys. 456:135–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dong, W. J., J. M. Robinson, J. Xing, P. K. Umeda, and H. C. Cheung. 2000. An interdomain distance in cardiac troponin C determined by fluorescence spectroscopy. Protein Sci. 9:280–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dong, W.-J., J. M. Robinson, J. Xing, and H. C. Cheung. 2003. Kinetics of conformational transitions in cardiac troponin induced by Ca2+ dissociation determined by Forster resonance energy transfer. J. Biol. Chem. 278:42394–42402. [DOI] [PubMed] [Google Scholar]
- 27.Robinson, J. M., Y. Wang, W. G. L. Kerrick, R. Kawai, and H. C. Cheung. 2002. Activation of striated muscle: nearest-neighbor regulatory-unit and cross-bridge influence on myofilament kinetics. J. Mol. Biol. 322:1065–1088. [DOI] [PubMed] [Google Scholar]
- 28.Monod, J., J. Wyman, and J. P. Changeux. 1965. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 12:88–118. [DOI] [PubMed] [Google Scholar]
- 29.Volkman, B. F., D. Lipson, D. E. Wemmer, and D. Kern. 2001. Two-state allosteric behavior in a single-domain signaling protein. Science. 291:2429–2433. [DOI] [PubMed] [Google Scholar]
- 30.Dong, W. J., C. K. Wang, A. M. Gordon, S. S. Rosenfeld, and H. C. Cheung. 1997. A kinetic model for the binding of Ca2+ to the regulatory site of troponin from cardiac muscle. J. Biol. Chem. 272:19229–19235. [DOI] [PubMed] [Google Scholar]
- 31.McCammon, J., and S. Harvey. 1987. Dynamics of Proteins and Nucleic Acids. Cambridge University Press, Cambridge, UK.
- 32.Fischer, E. 1894. Syntheses in the sugar group II. Ber. Deutsch. Chem. Ges. 27:3189. [Google Scholar]
- 33.Freire, E. 1999. The propagation of binding interactions to remote sites in proteins: analysis of the binding of the monoclonal antibody D1.3 to lysozyme. Proc. Natl. Acad. Sci. USA. 96:10118–10122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schnakenberg, J. 1976. Network theory of microscopic and macroscopic behavior of master equation systems. Rev. Mod. Phys. 48:571–585. [Google Scholar]
- 35.Bar-Yam, Y. 1992. Dynamics of Complex Systems. Addison-Wesley, Reading, MA.
- 36.Hänggi, P., P. Talkner, and M. Borkovec. 1990. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62:251–341. [Google Scholar]
- 37.Berezhkovskii, A., and A. Szabo. 2005. One-dimensional reaction coordinates for diffusive activated rate processes in many dimensions. J. Chem. Phys. 122:014503–014504. [DOI] [PubMed] [Google Scholar]
- 38.Lehrer, S. S. 1994. The regulatory switch of the muscle thin filament: Ca2+ or myosin heads? J. Muscle Res. Cell Motil. 15:232–236. [DOI] [PubMed] [Google Scholar]
- 39.Liao, R., C. K. Wang, and H. C. Cheung. 1994. Coupling of calcium to the interaction of troponin I with troponin C from cardiac muscle. Biochemistry. 33:12729–12734. [DOI] [PubMed] [Google Scholar]
- 40.Takeda, S., A. Yamashita, K. Maeda, and Y. Maeda. 2003. Structure of the core domain of human cardiac troponin in the Ca2+-saturated form. Nature. 424:35–41. [DOI] [PubMed] [Google Scholar]
- 41.Solzin, J., B. Iorga, E. Sierakowski, D. P. Gomez Alcazar, D. F. Ruess, T. Kubacki, S. Zittrich, N. Blaudeck, G. Pfitzer, and R. Stehle. 2007. Kinetic mechanism of the Ca2+-dependent switch-on and switch-off of cardiac troponin in myofibrils. Biophys. J. 93:3917–3931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Luque, I., S. Leavitt, and E. Freire. 2002. The linkage between protein folding and functional cooperativity: two sides of the same coin? Annu. Rev. Biophys. Biomol. Struct. 31:235–256. [DOI] [PubMed] [Google Scholar]
- 43.Lee, A. L., S. A. Kinnear, and A. J. Wand. 2000. Redistribution and loss of side chain entropy upon formation of a calmodulin-peptide complex. Nat. Struct. Biol. 7:72–77. [DOI] [PubMed] [Google Scholar]
- 44.Davis, J. S., and N. D. Epstein. 2007. Mechanism of tension generation in muscle: an analysis of the forward and reverse rate constants. Biophys. J. 92:2865–2874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang, G., and M. Kawai. 2001. Effect of temperature on elementary steps of the cross-bridge cycle in rabbit soleus slow-twitch muscle fibers. J. Physiol. 531:219–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lundback, T., J. F. Chang, K. Phillips, B. Luisi, and J. E. Ladbury. 2000. Characterization of sequence-specific DNA binding by the transcription factor Oct-1. Biochemistry. 39:7570–7579. [DOI] [PubMed] [Google Scholar]
- 47.Niekamp, C. W., J. M. Sturtevant, and S. F. Velick. 1977. Energetics of the cooperative and noncooperative binding of nicotinamide adenine dinucleotide to yeast glyceraldehyde-3-phosphate dehydrogenase at pH 6.5 and pH 8.5. Equilibrium and calorimetric analysis over a range of temperature. Biochemistry. 16:436–445. [DOI] [PubMed] [Google Scholar]
- 48.Prabhu, N. V., and K. A. Sharp. 2005. Heat capacity in proteins. Annu. Rev. Phys. Chem. 56:521–548. [DOI] [PubMed] [Google Scholar]
- 49.Eftink, M. R., A. C. Anusiem, and R. L. Biltonen. 1983. Enthalpy-entropy compensation and heat capacity changes for protein-ligand interactions: general thermodynamic models and data for the binding of nucleotides to ribonuclease A. Biochemistry. 22:3884–3896. [DOI] [PubMed] [Google Scholar]
- 50.Chandler, D. 1987. Sec. 8.3. In Introduction to Modern Statistical Mechanics. Oxford University Press, Oxford, UK.
- 51.Shannon, C. E. 1948. A mathematical theory of communication. Bell Sys. Tech. J. 27:379–423,623–656. [Google Scholar]
- 52.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 53.Kramers, H. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica (Utrecht). 7:284–304. [Google Scholar]
- 54.Langer, J. S. 1968. Theory of nucleation rates. Phys. Rev. Lett. 21:973–976. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.