Estimating the probability for a protein to have a new fold: A statistical computational model

Abstract

Structural genomics aims to solve a large number of protein structures that represent the protein space. Currently an exhaustive solution for all structures seems prohibitively expensive, so the challenge is to define a relatively small set of proteins with new, currently unknown folds. This paper presents a method that assigns each protein with a probability of having an unsolved fold. The method makes extensive use of protomap, a sequence-based classification, and scop, a structure-based classification. According to protomap, the protein space encodes the relationship among proteins as a graph whose vertices correspond to 13,354 clusters of proteins. A representative fold for a cluster with at least one solved protein is determined after superposition of all scop (release 1.37) folds onto protomap clusters. Distances within the protomap graph are computed from each representative fold to the neighboring folds. The distribution of these distances is used to create a statistical model for distances among those folds that are already known and those that have yet to be discovered. The distribution of distances for solved/unsolved proteins is significantly different. This difference makes it possible to use Bayes' rule to derive a statistical estimate that any protein has a yet undetermined fold. Proteins that score the highest probability to represent a new fold constitute the target list for structural determination. Our predicted probabilities for unsolved proteins correlate very well with the proportion of new folds among recently solved structures (new scop 1.39 records) that are disjoint from our original training set.

The number of known protein sequences already exceeds 400,000 and is rapidly growing. Despite recent technological advances in structural determination (1) it is still infeasible to solve experimentally the structure of hundreds of thousands of proteins in the foreseeable future. Therefore, it is necessary to find ways to predict key structural properties of a protein based on its sequence and on data derived from structurally solved proteins. Current attempts to computationally determine a protein's structure based on sequence alone still have a limited success, partly because of the shortage in solved structures that can be used as models. The challenge, then, is to determine a relatively small set of representative proteins the solution of whose structure will enrich our known repertoire of protein folds (2). Techniques such as comparative modeling and fold recognition then will be applied for large-scale structural prediction (3). It generally is accepted that reasonable predictions are possible for proteins that share at least 30% sequence identity with some solved protein (2). The expansion and eventual completion of our archive of three-dimensional (3D) protein templates depend on the development of new methodologies to properly select an expanded (comprehensive) set of target proteins (discussed in refs. 4–8).

Data accumulated from complete genomes has accelerated the development of computational approaches to assign 3D structures in a genomic scale (3, 9–13). On the experimental side, several pilot projects in structural genomics were initiated in recent years. Most of these projects use known structures as models to assign structure to other related proteins of a specific organism (Saccharomyces cerevisiae, Haemophilus influenzae, Pyrobaculum aerophilum, Mycoplasma genitalium, Methanococcus jannaschii, and more). Those proteins, for which no related structure is known, can form a basis for a list of targets likely to have unknown folds (2, 14). Of course, a critical requirement for the selection of targets is a comprehensive and consistent organization of protein sequences. Several databases have been developed that provide exhaustive classification of proteins sequences to families (reviewed in ref. 15).

How many target proteins should be selected in such a process? The answer to this question is closely linked to the (currently unknown) number of protein folds that exist in the entire protein universe (16, 17). Estimates for this number range from 700 to more than 10,000 (18–23). The total number of currently known protein folds is 473 according to the scop 1.39 classification (24, 25) and 635 folds (topologies) according to cath 1.5 (26).

In this study, we address the problem of compiling a list of target proteins. We develop a statistical model that assigns each protein sequence a probability to have a new fold. Consequently, we derive a prioritized list that contains those proteins that are likely to represent new structural folds. Our work is based on a comparative study of sequence- and structure-based classifications of proteins. This study leads to a statistical model according to which we evaluate the probability that a given cluster (and the proteins it contains) corresponds to a new fold. Our predicted probabilities are evaluated against all recently solved structures whose folds were determined past the computations. There are about 100 nonmembranous proteins that achieve the highest probability to have a new fold. A rational selection for 3D determination of those targets is expected to accelerate the pace of discovering new folds.

Methods

Sequence- and Structure-Based Classifications.

A computational-statistical method is developed here that assigns each protein an estimate on how likely it is to represent a new fold. This approach is based on two classifications of proteins: protomap, a sequence-based classification of the protein space (27), and scop, the structure based classification (28). scop is a hierarchical classification of all known protein structural domains. We have used scop release 1.37 [5,741 natural protein entries that were registered at the Protein Data Bank (PDB) database before Oct. 20, 1997]. This release comprises 11,748 records represented by 2,264 domains. The transformation from the number of PDB entries to the number of scop records and scop domains reflects (i) parsing of proteins to their structural domains and (ii) a grouping of entries in scop records that reflects the redundancy within PDB. These 2,264 domains are classified to 834 families, 593 superfamilies, 427 folds, and eight classes. Two more classes (designed proteins and nonprotein) are not considered in this study. Notice that some changes in scop class definition is associated with a recent release (scop 1.48, created Dec. 20, 1999). scop can be accessed at http://scop.mrc-lmb.cam.ac.uk/scop.

protomap is an automatically generated hierarchical and relational classification of all protein sequences in SwissProt. To construct the statistical model in this study, we use the most relaxed level of classification (level e = 10^-0) of protomap version 2.0. This version includes 72,623 protein sequences that are classified to 13,354 clusters, 5,869 of which contain at least two proteins and 1,403 clusters at size 10 and above. protomap version 2.0 can be accessed at http://www.protomap.cs.huji.ac.il.

Local Graphs in protomap.

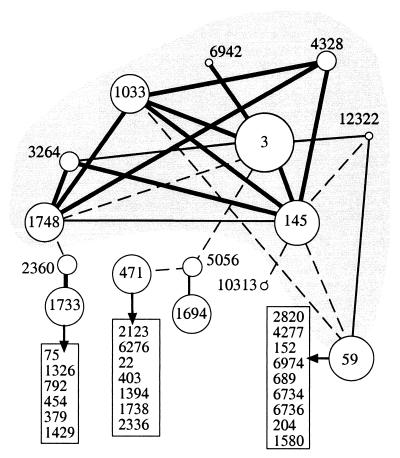
Each cluster in protomap has a weighted list of related clusters. The weights (called quality) reflect relatedness among clusters. The lists of related clusters encode many biologically meaningful relations and form the basis for mapping the protein space. This statement was illustrated for the Ig superfamily (29), the Ras superfamily (30), and more. The notion of the protomap graph and the information that may be extracted from the protomap graph are illustrated by a specific example of the globin family (Fig. 1). The scheme shows a two-dimensional presentation of all clusters related to cluster 3 and their immediate related clusters. Proteins of the globin family are all classified to cluster 3. This cluster consists of 621 proteins representing myoglobins, globins, and hemoglobins throughout the evolutionary tree. Inspection of the map in Fig. 1 indicates that additional globin-related clusters are linked to cluster 3 either directly or indirectly. For example, cluster 4,328 contains proteins of Calyptogena soyoae (deep-sea clam) that are only weakly related to globins of other mollusca. Still, a connection can be traced between these globins and myoglobin of mullusca and insecta (presented in cluster 145) and those of nematoda (cluster 1,748). Another key feature of this graph is that a numerical value (quality) is assigned to pairs of related clusters to quantify their degree of proximity. Indeed, considering the level of proximity (described by the quality score) it is evident that edges connecting clusters of the globin family have higher scores as compared with edges in the periphery. Several low-score connections to cluster 59 (from clusters 145, 1,033, and 12,322) expose the relation to the globin family via the flavohemoproteins (combined with FAD-containing reductase domain). The other low-score edges point to additional, nonrelated local graphs (such clusters are listed in boxes, Fig. 1). This observation suggests that the graph of related clusters can be “clipped” at different thresholds, by eliminating all edges of significance below a given threshold. Each threshold yields a different scheme and thus, the protein universe is partitioned to connected components of varying sizes and graph connectivity. In a protomap graph (at threshold 0.0) 37.7% of the clusters form one connected component. Clipping the graph at thresholds 0.1 and 0.3 reduces the size of the largest connected component to 17.2% and 6.1%, respectively. The 13,354 clusters in protomap have an average 3.7 of related clusters each. However, the distribution of this value is very broad and is correlated with the cluster's size. For example, most singleton clusters (5,545 of 7,485) are isolated and have no related clusters at all.

Figure 1.

A local graph of the globin family. A representation of the protomap graph surrounding cluster 3. The 15 clusters indicated by the circles account for 845 proteins, those that belong to globin family are within the gray area. The sizes of the circles are correlated with number of proteins (in increasing order 1–5, 5–50, 51–200, and >200 proteins in a cluster). Edges in the graph indicating the proximity between any two clusters as measured by the quality score. Quality score at e = 10^-0 ranges from 0.99 to 0.01. Edges with quality >0.1, 0.06–0.1, and 0.01–0.05 are indicated by thick, thin, and dashed lines, respectively. All solved protein structures associated with the globin map (26 domains in cluster 3; 10 domains in cluster 145, and one domain in cluster 1748) belong to the globin fold. Clusters outside the gray area belong to unrelated sub graphs in terms of sequence and structure. See details in text.

Results

The Statistical Model and Scheme of the Procedure.

Our working hypothesis is that proximity (i.e., small distances in the protomap graph) is correlated with similarity among protein features, including 3D structures. This hypothesis should imply that clusters that are proximal in protomap tend to share a similar fold, whereas clusters that are distant tend to have unrelated folds. This general hypothesis has been put to a number of biological tests. Such tests were carried out with respect to several biological features, and in protein structure the following procedure was applied. We have manually compared several of the structure-based maps provided by fssp (31) with protomap clusters. In many instances, structurally related proteins that do not fall into the same protomap cluster do, however, belong to neighboring clusters in the protomap graph (not shown).

To describe the statistical model within which we work some technical terminology is required. A cluster that contains no known structures is said to be empty. Otherwise, a cluster is called occupied. A vacant cluster is said to be new when its (presently undetermined) corresponding fold is absent from scop, and old otherwise. We based our statistical model on the distribution of distances among occupied clusters in the protomap graph. Our goal is to derive an estimate for two probability distributions: (i) The first one consists of distances (within the protomap graph) from old clusters to occupied clusters. We posit that this distribution is a good approximation for the typical distance distribution from a known structural fold to all clusters. (ii) The distribution of distances from new clusters to occupied clusters. This second distribution does the same for yet unsolved folds.

Our original hypothesis implies that the second distribution should be biased (compared with the first one) toward larger distances. These distributions are the basis for evaluating the distances measured from all vacant clusters to occupied clusters. Specifically, Bayes' rule is used to estimate, on the basis of these two distributions, the probability that a given cluster be new. This is done by using the measured distances from this cluster to all neighboring occupied clusters and the estimated number of folds in the protein space. Such probabilities were calculated for every vacant cluster in protomap. Our estimates subsequently were put to a test by comparing our predictions on all newly released protein structures, which were still unavailable at the time of creating the model.

The probabilities of all vacant clusters to have new folds are estimated in a four-step procedure: (i) Positioning each domain with a solved 3D structure (from scop) into its proper protomap cluster. (ii) For each cluster a “representative fold” was determined based on the folds associated with most structural domains in that cluster. (iii) Distances within the protomap graph were computed from each representative fold to the neighboring folds. The distributions of these distances are used to create a statistical model for distances among those folds that are known and those that have yet to be discovered. (iv) Statistical estimation is derived for the probability that any protein has a new, yet undetermined fold.

Proteins that score the highest probability to represent a new fold constitute the list of preferred target proteins for structural determination.

Mapping scop Domains to SwissProt Protein Chains (SP-Chains).

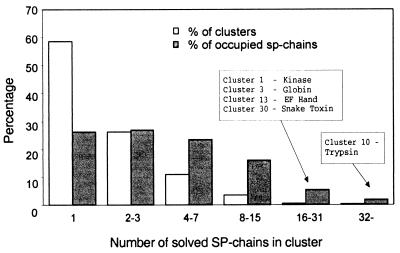
To position the known structures vis-a-vis the protomap graph, the information from the PDB database is matched with that of the SwissProt records (SP-chain). We used the 2,264 representative domains as defined in scop 1.37. Among these, 1,986 domains are successfully associated with SP-chains (the rest do not have a corresponding record in the SwissProt database). The correspondence among structural domains and SP-chains is bidirectional. Of the 72,623 SP-chains, 1,688 are solved. As noted above, a cluster is defined as occupied if it contains at least one solved SP-chain, and as vacant otherwise. Of the 13,354 clusters in protomap, 756 are occupied. The distribution of the number of solved SP-chains in each occupied cluster is shown in Fig. 2. Whereas 59% of the occupied clusters contain only one solved SP-chain (with one or more solved domains), 73% of the solved SP-chains are in clusters with two or more solved SP-chains. An occupied cluster is mapped to a specific fold if it contains an SP-chain that is mapped to that fold.

Figure 2.

Distribution of the number of solved SP-chains in each occupied cluster. Percent of occupied clusters with indicated number of solved SP-chains (empty bar) and the percent of solved SP-chains in each category (filled bar) is shown. The clusters with the largest number of solved SP-chains are indicated along with the cluster's signature.

Assigning Representative Folds to Occupied protomap Clusters.

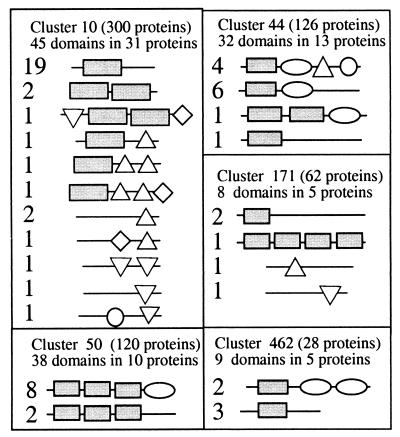
As the above mapping indicates, there is no one-to-one correspondence between clusters and folds. It would clearly be desirable if we could correctly assign a single representative fold to each protomap cluster, although it is not a priori clear whether such a selection can be carried out. This is not just a failure of protomap and scop. Many proteins are multidomains, and an SP-chain may correspond to several domains, which usually have distinct folds. In this view, we define for each occupied cluster the best representative fold as the one most abundant in the cluster. For an occupied cluster with only a single domain, this is, of course, the representative fold of that domain. The same applies to those occupied clusters that have more than one domain, all of which with the same fold. The rest of the occupied clusters include domains of several folds. Several typical examples are illustrated in Fig. 3. Cluster 10 that contains the highest number of domains in one cluster consists of 300 trypsin-like proteases. In this cluster, 45 domains are mapped to 31 solved SP-chains. These domains are associated with five different folds (Fig. 3). Still, in 25 of these 31 solved SP-chains a trypsin-like fold is represented. All other examples in Fig. 3 show clusters that contain several solved SP-chains, mostly from multidomain proteins. The selected representative fold in such cases is the one that occurs in the largest number of solved SP-chains in the cluster. In a small number of cases, this rule was indecisive because two distinct folds scored equally. For example, cluster 86 of the lactate/malate dehydrogenase superfamily contains 30 scop domains that are associated with 15 solved SP-chains, each having exactly two different folds of the N- and C-terminal domain. In such cases, ties were broken arbitrarily.

Figure 3.

Representative clusters with solved multidomains SP-chains. The geometrical symbols represent different folds within each cluster. The numbers indicate the occurrence of a specific fold combination among the solved SP-chain in that cluster. In all of the examples, the representative fold is indicated by a rectangle. Clusters illustrated in the scheme are: cluster 10, trypsin proteases; cluster 44, α and β amylases; cluster 50, pyridine nucleotide-disulphide oxidoreductases; cluster 171, endochitinases; and cluster 462, shiga/ricin ribosomal inactivating toxins.

We turn to discuss the outcome of this selection procedure from the fold's perspective. Of the 411 folds in scop 1.37 that are mapped to solved SP-chains, 329 folds were chosen as clusters' representatives. Of the remaining 82 folds that were never chosen as representatives, most are coupled to a representative fold. Many of these folds that were never chosen as representatives are peptides (class 8 in scop) or very short domains that rarely dominate a cluster.

This selection procedure has worked remarkably well, in that only 80 solved SP-chains are not mapped to the representative fold of their cluster. Even among clusters that contain more than one solved SP-chain, these 80 SP-chains constitute less than 6.5% of the solved SP-chains. This matching suggests that protomap is selective for scop folds. That is, a cluster gathers proteins of the same fold, although not necessarily all proteins of that fold.

Predicting a Protein's Probability to Have a New Fold.

Our statistical estimates are based on an analysis of distances in the protomap graph. Our goal is to predict for each cluster whether it is old or new (i.e., represents an already known or a yet unknown fold, respectively). Our basic premise is this: Distances among pairs of clusters are distributed differently depending on whether or not the clusters represent the same fold, because similar folds tend to be close together in the protomap graphs (e.g., globin-like fold in Fig. 1). We also assume that occupied clusters and their distances from other clusters offer a good sample of these two distributions. Distances are not the only relevant information that can be extracted from the protomap graph. The local density of the graph (number of clusters at given distances) provides additional and less noisy data. After some optimization, the most informative parameter turned out to be the maximal vacant volume around a cluster, the formal definition of which appears below. We thus consider two distributions: (i) distances from old clusters to occupied clusters and (ii) distances from new clusters to occupied clusters. The computational procedures by which we estimate these two distributions are similar: Start from any occupied cluster that we call the origin. Consider all neighboring clusters, then their own neighbors, etc. This procedure is stopped when an occupied cluster is encountered. For the old distribution, any occupied cluster terminates the procedure. In the new distribution, the procedure is halted only upon encountering a cluster whose representative fold differs from the fold representing the origin cluster. Say that the scanning is halted because of an occupied cluster at a distance r from the origin cluster (this parameter r usually will differ in the old/new scanning schemes). We define the maximal vacant volume V as the number of clusters whose distance from the origin is smaller than r. If there are no occupied clusters in the connected component of the origin cluster, then the maximal vacant volume V is defined as empty. This procedure (in both its old and new versions) is carried out with each of the 756 occupied clusters as origins. Based on the information collected from scanning the protomap graph, the distributions of maximal vacant volumes are calculated to derive two probability distributions: D^old[V] and D^new[V].

There is an additional consideration that is necessary here, because the protomap graph can be clipped at different threshold (clipping means eliminating all edges below a certain quality score, as discussed above). The parameter V strongly depends on choice of such a specific threshold. To extract as much information from the protomap graph as possible, we carried out the scanning procedure on the protomap graph clipped at various thresholds. Optimizing the threshold for clipping the graph was based on Kullback-Leiber (KL) divergence (D_KL) as a measure for the difference between the two distributions (D^old and D^new). The D_KL analysis was carried out for thresholds 0.0, 0.1, and 0.3. The KL divergence for threshold 0.1 turned out the highest and thus 0.1 was selected for clipping the protomap graph. At threshold 0.0 (no clipping) D_KL was only slightly lower than at threshold 0.1 but at threshold D_KL 0.3 is significantly lower. In the sequel we consider both the 0.1 and the 0.0 graphs.

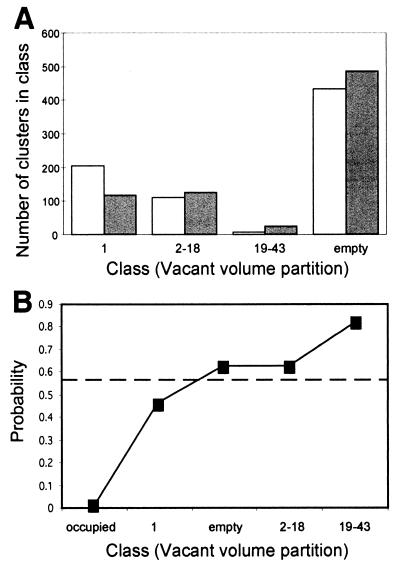
To construct the distributions of D^old[V] and D^new[V] some smoothing is necessary to filter the noise on the parameter V. We have classified V values to three consecutive intervals and the value empty. This partition was again optimized by D_KL analysis. The distributions for D^old and D^new at threshold 0.1 are shown (Fig. 4A). Notice that the two distributions are substantially different, so one can hope for meaningful old/new predictions.

Figure 4.

The base distributions of D^old[V] and D^new[V] for threshold 0.1. (A) Partition of the vacant volumes to classes was performed as detailed in the text. Number of clusters counted in the training set in each class is shown. (B) Probability of having a new fold for various vacant volumes as calculated according to Bayes' rule. The dashed line indicates the a priori probability to be new (see details in text).

We now turn to all protomap clusters that are vacant (12,598 clusters). In the same way described above, we take some cluster X as our origin and proceed from it until the first occupied cluster is encountered. Thus, a vacant volume V is associated with cluster X and we want to find the probability:

P[X is new|V is X's vacant volume]. In other words, given a cluster with a specific vacant volume V, what is its probability to have a new fold?

According to Bayes' rule,

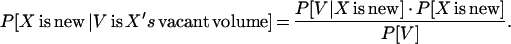We estimate this probability through

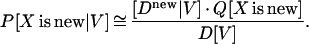P[X is new] is estimated by Q[X is new]. This estimate is defined through the number of known folds (427, according to scop 1.37) and an accepted estimate for the total number of folds, for which a rather conservative estimate of 1,000 is taken (23). That is Q[X is new] = 1 − (total number of known folds)/(total estimated number of folds) = 0.573. The other term in that equation, D[V], is given by the weighted sum over the two empirical distributions (as in Fig. 4A), i.e.,

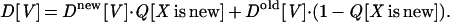Fig. 4B shows the values calculated for the probability that a cluster as a new fold for various vacant volumes (at threshold 0.1). As seen, the probability function increases monotonically with the volume, V. Notice that the correlation between the probability function and V is not a purely mathematical statement, but rather inherent properties of the data. This supports the initial hypothesis that distances in protomap graphs reflect structural relatedness. Unfortunately, for the many clusters to which no vacant volume can be assigned (denoted empty) this analysis provides little information (see Discussion). For these clusters, the probability values slightly exceed the a priori value (0.573).

Evaluation of the Predicted Probability to Have a New Fold.

To evaluate this prediction, a test was carried out that involved the membranous proteins. So far, the structures of only few membranous proteins have been solved (mostly classified in scop class 6). Therefore, clusters of membranous proteins can be expected to be associated with a high probability for being new. This test involved more than 1,000 membranous clusters (representing about 20% of the SP-chains). A cluster is considered membranous if at least one-third of its proteins have multiple membrane spanning regions. Indeed, membranous clusters occur in the highest probability class 6.5 times more often than their overall occurrence (Table 1). Moreover, this ratio varies monotonically throughout the probability range, as would be expected. Although these results support our intuition, we currently are unable to make specific predictions on the number of different folds among membranous proteins. This test was carried out at threshold 0.0 and 0.1 (D^old and D^new were evaluated for each separately). This is reflected in Table 1: Clusters that are assigned to the highest class in threshold 0.0 but lower in threshold 0.1 are joined together (indicated as Add 0.0, Table 1). Otherwise a cluster is assigned the probability of its class in threshold 0.1.

Table 1.

Membranous clusters tests

Classes (V)	P (New)	All clusters, number (%)	Membranous number (%)	Ratio*
Occupied	0.00	756 (5.7)	13 (1.2)	0.2
1	0.46	1,123 (8.4)	45 (4.3)	0.5
Empty	0.62	9,651 (72.3)	639 (61.0)	0.8
2–18	0.63	1,111 (8.3)	91 (8.7)	1.0
Add-0.0	0.76	405 (3.0)	104 (9.9)	3.3
>19	0.82	308 (2.3)	156 (14.9)	6.5
Total		13,354 (100)	1,048 (100)

*Ratio between membranous clusters and all clusters. 

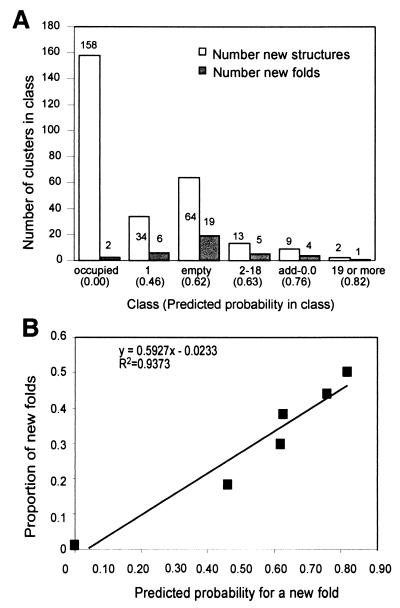
A very significant and encouraging test set has been carried out on data that was not available at the time of creating the model. The original analysis was performed by using scop 1.37 (about 13,000 domains) and re-evaluation was performed against scop 1.39 (about 18,000 domains). scop 1.39 contains 2,092 domains that constitute 404 folds. Following mapping to protomap, we obtained 388 domains and 48 folds that are in scop 1.39 and not in 1.37. All of these structures were allocated as before to protomap clusters and the previously defined probability scores (based on scop 1.37 alone) of these clusters were recorded. Thus, the new structures fall into the six categories into which the probability scores are grouped (as defined in Table 1). Because clusters with high vacant volume have high probability to adopt a new fold (Fig. 4B), we expect that large fraction of these clusters are represented by new folds. That is, the proportion of new clusters out of all clusters would increase with the vacant volume V. Fig. 5 shows the assignment of all scop 1.39 domains to the probability classes (Fig. 5A) and the percentage of (actual) new folds within each category. A strong correlation between the predicted probability of being new and the proportion of new folds among the recently released structures is found. The success of this test strongly suggests that selecting targets from the top probability class will accelerate the discovery of new folds.

Figure 5.

Distribution of new structures from scop 1.39 records according to the probability classes. (A) Number of clusters in a class that were assigned with a new structure (open bar) and with a new fold (filled bar) from scop 1.39. (B) Proportion of new folds out of new structures that were assigned to any class as a function of the predicted probability to be new assigned to these classes. A linear trend line with its r-square value is shown.

List of Selected Targets for Structural Genomics.

The list of targets at the top probability score contains 713 clusters (5.3% of all clusters) that account for 8.2% of the SP-chains. Excluding membranous clusters (as in Table 1) and those with fewer than five SP-chains in each yields our prioritized target list. This list contains 125 clusters. The complete list of target proteins and their properties can be accessed at http://www.cs.huji.ac.il/∼elonp/Targets. A structural genomics project at Argonne National laboratory (Argonne, IL) was initiated to determine as many new folds as possible by x-ray crystallography. Out of our proposed target list, more than 80 proteins were selected and are at different stages of expression, purification, crystallization, and data collection (unpublished data).

Discussion

The discovery of a novel fold may contribute to the understanding of the functional characteristics of entire protein families. Thus, a scheme for discovering the currently missing folds is desirable (31, 32). Although the number of solved structures has been growing exponentially in recent years, the fraction of new folds among them is constantly decreasing (based on the yearly deposit of folds by scop and on records from the PDB). Here we present a systematic statistical-computational approach that can accelerate the pace of discovering new folds (see Fig. 5B). About 5.4% of the SP-chains are assigned a high probability for having new folds, which amounts to 453 nonmembranous clusters. Unfortunately, there are many clusters for which our computational procedure fails to provide any significant information. This is the case with clusters whose connected components are completely vacant. Intuitively, these isolated clusters are distant from any known fold and can hence be expected to provide new structural information. Most of the empty clusters are either singletons or reside in small connected-components (up to two clusters). Our analysis of scop 1.39 records show that new structures that are associated with empty, nonsingleton clusters (at threshold 0.1) give a high yield of new folds. Namely, 13 of the 31 (42%) new structures in this class turned out to be new folds. This is comparable with our highest scoring classes (see Fig. 5B). In this view, we place all such clusters in a list that can be found at http://www.cs.huji.ac.il/∼elonp/Targets.

Our statistical analysis has shown that the protomap graph captures structural information about proteins. This is interesting, because protomap is based solely on sequence information. This shows that a global approach to the sequence space can yield significant structural information. As is the case with constructing any such large-scale statistical model, several key decisions were made based primarily on heuristic arguments: (i) protomap was used at its most relaxed level (e = 10^-0). (ii) A single representative fold was assigned to each occupied cluster. (iii) Vacant surrounding volume was used as our parameter to reflect the distance distribution in protomap. (iv) A specific threshold for clipping the graph was used. (v) A single estimate for the total number of folds was selected. Alternative choices for several of these heuristic decisions were tested, some of which hardly affect the outcome of the analysis. For example, for any estimate for the total number of folds from 700 to 10,000 the relative order of the predicted probabilities assigned to the classes stays the same. Some of the other heuristic decisions were made according to outcome of relevant biological tests (e.g., membranous clusters test, Table 1).

Not all of the proteins that are predicted to have new fold will indeed reveal new folds. About 10% of all folds as defined in scop include superfamilies that often share the same fold as a result of convergent evolution (e.g., triosephosphate isomerase barrel, ferredoxin folds, etc.). Consequently, we expect that some of the target proteins, even if they yield no new fold, do represent new superfamilies that belong to already known folds. In addition, several of the clusters in our target list are neighbors in the same protomap graph. In such instances, it is expected that these different clusters correspond to the same (yet unknown) fold. A point is case is cluster 2,050 that was assigned with the top probability of having a new fold. This cluster resides in a highly connected subgraph with another 18 clusters, all with the highest score as well. This set of clusters is a part of a highly connected local graph of the GCN5 superfamily (not shown). Despite a relatively low sequence identity and diverged biological functions among proteins of those clusters, we predict that the same fold is shared among all proteins in the graph.

Abbreviations

3D

three-dimensional

PDB

Protein Data Bank

SP-chain

SwissProt protein chain

KL

Kullback-Leiber