The Dewetting Transition and The Hydrophobic Effect

Abstract

A molecular-level description of the behavior of water in hydrophobic spaces is presented in terms of the coupled effects of solute size and atomic solute–solvent interactions. For model solutes with surface areas near those of protein contacts, we identify three different regions of solute–water interaction to be associated with three distinctly different structural characteristics of water in the intersolute region: dry, oscillating, and wet. A first orderlike phase transition is confirmed from the wet to dry state bridged by a narrow region with liquid–vapor oscillations in the intersolute region as the strength of the solute–water attractive dispersion interaction decreases. We demonstrate that the recent idea that cavitation in the intersolute region of nanoscopic solutes is preceded by the formation of a vapor layer around an individual solute is not the general case. The appearance of density waves pulled up around and outside of a nanoscopic plate occurs at lower interaction strengths than are required to obtain a wet state between such plates. We further show that chemically reasonable estimates of the interaction strength lead to a microscopically wet state and a hydrophobic interaction characterized by traps and barriers to association and not by vacuum induced collapse.

Introduction

The mechanism of the hydrophobic effect is an issue of fundamental chemical interest. The explanation of the hydrophobic effect between solutes or within a flexible solute is of relevance to a variety of processes. In this paper we identify three different regions of solute–water interaction that are associated with three distinctly different structural characteristics of water in a region between solutes. The three ranges of interaction characterize the fluctuations in water occupancy: dry, oscillating, and wet. It is the chemically relevant interaction strengths inducing these different states that we wish to quantify here.

Although hydrophobicity has long been recognized as one of the main driving forces in the aggregation of biological assemblies in water, the precise role of water in the process is still debated.^1–4 Recent work has sought to unify the phenomenon of macroscopic dewetting to microscopic hydrophobicity.⁵ Early work by Patey and co-workers⁶ showed that for a Lennard-Jones fluid near vapor–liquid coexistence, cavitation can be observed if the fluid is confined between two infinite, hard walls. Since this pioneering investigation, numerous studies have been reported with both finite solute and infinite plate models in water and other solvents.^4,5,7–22 Of particular importance for the current study is the quantification of length scale dependent hydrophobic effects with respect to varying the interactions of water with the solute. Widely different views have emerged from numerous previous studies and there is no consensus¹³ as yet. Some confusion exits over what one might term hydrophobic. Different authors have dealt with different topologies and interactions of the solute.⁹ Categorizing the universality of dewetting in terms of solute size and interaction strength is thus of interest.

The behavior of water in the confined hydrophobic environments, as depicted in many recent theoretical and computational studies^5,6,14–22 can be classified into three main categories. One depicts that a large hydrophobic solute surface produces a thin vapor layer around it because of disruption of the local hydrogen-bond (H-bond) network of liquid water.^5,11,15,16 When two such solutes come close enough to each other, fluctuations in the individual solute–vapor interfaces expel remaining water molecules from the intersolute region leading to a dewetting induced collapse of the solutes.

A quite different perspective on hydrophobicity allows a wet but atomically narrow region containing as little as a single 2-D layer or even a 1-D molecular chain of water with some solutesolvent attraction.^14,18,20,21 This leads to a barrier to the association or dissociation of the solutes when planes are near contact. Water is expelled from the hydrophobic intersolute region only when it is sterically forbidden with a substantial free energetic barrier between the contact and solvent separated states.²¹ Recently it has been demonstrated²³ that for atomic models of water, the transition from the solvent separated to the contact pair state of nanoscopic solutes with dispersion attraction is entropy driven. It is not substantially enthalpy driven as expected from the H-bond energy loss perspective.¹⁶ This is also evident from the analogous nonaqueous system considered by Patey and co-workers,⁶ which demonstrated that even for a Lennard-Jones fluid, which has no H-bonding network, dewetting occurs when confined between two infinite repulsive walls. Pressure can also be a controlling factor.⁷ Thus a simple explanation in terms of an uncompensated loss of hydrogen bonds of water near a solute is not sufficient to describe such behavior.

Apart from these two extreme views, there is also an intermediate picture with the possibility of liquid–vapor oscillations^18,22,24 in a confined hydrophobic environment. Water in the intersolute region or inside a nanopore has been found to go through alternating wet and dry phases in a range of solutesolvent attraction. The intermittent permeation of water in biological pores is well-known experimentally as well.

One of the objectives of the present investigation is to unify the contrasting previous literature results by identifying two governing parameters. Considering a single, ideal geometric arrangement of the solute atoms, here we show, via atomistic molecular dynamics simulation, how the apparently contrasting views of hydrophobicity described above can be reconciled with each other by considering the response of water to variations in solute–water interactions and solute sizes. We trace the origin of the disparate behaviors by analyzing the response of the system to the solute–water attractive dispersion interaction in the case of a range of nonpolar solutes sizes.

Arguments based on the energetic cost of breaking the H-bond network of water for cavitation lead to a proposed^5,16 dewetting mechanism for hydrophobicity and induced association of biomacromolecules. Such a mechanism relies on drying at a single solute–vapor interface as the precursor for the cavitation in the intersolute region. In the present investigation we therefore investigate possible correlation, if any, between drying at a single solute surface and in between two surfaces. The effects of the weak van der Waals attraction combined with finite size scaling on the solvent structure in the vicinity of a solute are characterized in terms of the solution fluctuations leading to drying or wetting.

Models and Methods

The rigid planar solutes used in this study are made up of carbon atoms modeled as Lennard-Jones (LJ) particles with diameter σ_CC = 3.4 Å placed in a graphitic lattice with carbon–carbon bond lengths of 1.4 Å. The carbon–carbon LJ energy parameter ∊_CC is varied from 0.3598 kJ mol^–1, corresponding to the sp² carbon atoms in the biomolecular Amber force field²⁵ to essentially 0. The point at ∊ = 0 is obtained from the Weeks–Chandler–Andersen (WCA) decomposition.²⁶ Water is modeled by the standard SPC/E⁵⁴ 3-site potential. In most of the cases, two solute plates are placed at the middle of a water box at an intersolute separation of 6.8 Å which is the solvent separated minimum in the potential of mean force.²¹ This minimum corresponds to the solvent separated configuration, the stability of which determines the mechanism of hydrophobic association. For demonstration purposes, a single solute carbon atom is also considered.

Ewald molecular dynamics simulations in isothermal–isobaric (NPT) ensemble were used to sample the water configurations. Solute–water interactions, U_sw(r), were represented by the LJ interaction between carbon atoms and the oxygen atoms of water.

$$U_{ij}(r)=4{∊}_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r}\right)}^6\right]$$ (1)

The cross parameters for the carbon–oxygen interactions, ∊_CO and σ_CO, are obtained from ∊_CO = (∊_CC∊_OO)^1/2 and σ_CO = [σ_CC + σ_OO]/2. Further details of the simulation methods have been given elsewhere.²¹ All simulations were run for 1 ns or longer.

Results and Discussions

We use molecular dynamics simulations in the NPT ensemble to avoid potential constant volume artifacts. With that we consider the hydration of nanoscopic, rigid, rectangular graphene plates of several different sizes, namely, (a) solute-I, made up of 28 carbon atoms (with edge to edge van der Waals (vdW) span or diameter of 10 Å), (b) solute-II, made up of 60 carbon atoms (15 Å diameter), (c) solute-III consisting of 180 carbon atoms (24 Å diameter), and (d) a single carbon atom. Given a constant topology for the solute, variation of the solute–water interaction will characterize the effect of attractive potential interactions on the wetting behavior of the nanoscopic hydrophobic materials.

Consider the behavior of water in the intersolute region of the first three systems as shown in Figure 1. In order to follow the wetting-dewetting behavior in the intersolute region, we use a traditional order parameter (and its fluctuations): the average density calculated as the average number of intersolute water molecules 〈n(t)〉 per area, A, of the solute plate, ${\rho }_{\text{av}}^A=\langle n(t)\rangle /A$ as a function of the dispersion interaction between the solute and the solvent.

Figure 1.

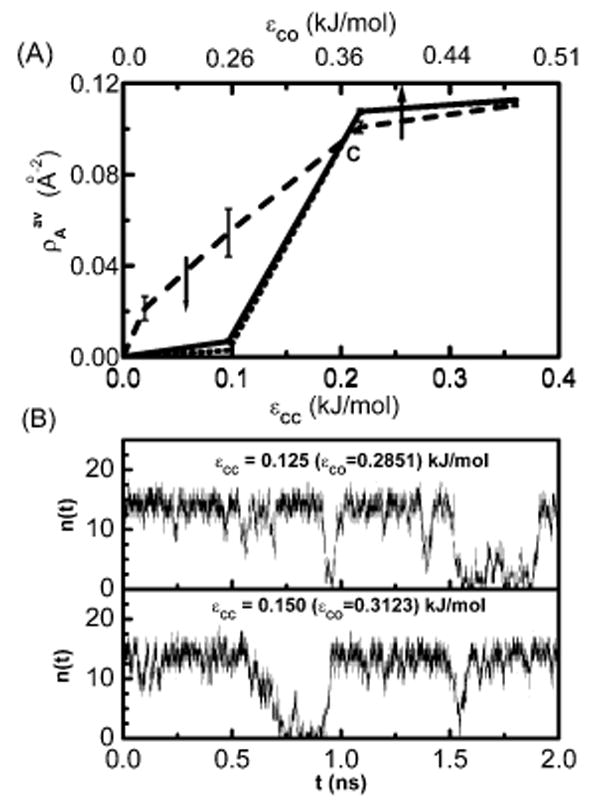
(A) Plot of the average number of water molecules per unit area of the solute plate ${\rho }_{\text{av}}^{\text{A}}$ as a function of ∊_CC (bottom axis) or ∊_CO (top axis) for three different solute sizes. The solute-I with two 28-atom plates is shown by a dashed line, the solute-II (60-atom plates) system is shown by a solid line and the solute-III (180-atom plates) system is shown by a dotted line. (B) Plot of the instantaneous number of confined water molecules n(t) between the two solute-II plates vs time in nanoseconds for two different attraction strengths of the solute atom.

To investigate the effect of the attractive strength of the solute interaction we have varied the carbon–carbon LJ energy parameter ∊_CC from 0.3598 kJ mol^–1, corresponding to the sp² to small values near 0. The extreme case of purely repulsive interaction we denote as ∊ = 0 is obtained through a Weeks–Chandler–Andersen (WCA) decomposition.²⁶ For all other points investigated we use eq 1.

In Figure 1A, we plot ${\rho }_{\text{av}}^A$ as a function of the solute–solute or equivalently, solute–solvent attractive interaction parameter ∊_ij. The LJ interaction parameters for water were unchanged through out all the simulation runs. For the purely repulsive interaction, we have found dewetting in the intersolute region for each plate size considered. For all solute plates considered here, we see that intersolute water density increases monotonically with solute–solvent interaction until it reaches the completely wet state. For the larger solutes, we observe a distinct sigmoidal behavior consistent with a first-order-like vapor–liquid phase transition with the increase in attractive solute–solvent interaction. The larger the plate, the steeper the sigmoidal curve. We decompose this into three regions of solute–solvent interaction with three different zones of adsorption behavior. The average density is nearly zero up to ∊_CC = 0.1 kJ/mol indicating a dry state or vapor phase. We note this range of interaction parameter is smaller than found in typical empirical force fields for protein–hydrocarbon side chains and lipids.²⁵ Water behavior in this zone of solute–solvent interaction is reminiscent of that observed in many earlier studies where either a hard sphere model or a vdW model with a very small attraction for the solute was considered.^{5,6,15,27–31} As mentioned, Patey and co-workers first observed⁶ that in between two, infinite, hard walls even a simple LJ fluid near bulk-phase coexistence can undergo a dewetting transition. Recently a simulation study on the liquid–vapor phase coexistence of water in infinitely long slits or pores has been reported.³² The critical temperature of the vapor–liquid phase diagram was shown to decrease with the increase in the attractive wall–water interaction. These seminal works did not deal with finite-sized spaces or pores, which are relevant to hydrophobic biomacromolecular assembly. Using finite methane plates, however, Koishi et al.¹⁷ found cavitation at an intersolute distance of 11 Å during a particular expansion process, but not in the corresponding contraction process. This hysteresis could be due to equilibration problems since, as noted, in the expansion process there was a preexisting nanobubble and such a system may reside in a metastable state for a relatively long time. The drying at around 7 Å in that study does not show hysteresis. Considering the size parameters used in this study for methane and water LJ potential, it appears that the drying observed at 7 Å is due to steric constriction much as in our earlier study of graphene plates beneath 6.5 Å.²¹ It is important to note that the hydration study of a methane cluster by Ashbaugh et al.²⁰ shows a pronounced wetting at the nanoscopic solute surface. As we shall see below, the present study demonstrates the existence of completely dry, intermittently wet–dry, and completely wet intersolute states for a range of sizes of nanoscopic solutes simply by varying the solute–water attraction.

Moving from ∊ = 0, a purely repulsive interaction, to an increase in solute attraction yields a number density which increases sigmoidally to a value corresponding to a completely wet state and does not change much thereafter. The wet state was observed in many other recent studies, ^18,20,21,33 which considered an atomistic description of solute and solvent with realistic model potentials. Simulations of a one-dimensional chain of water molecules inside a carbon nanotube,^18,19 clusters of a few water molecules inside a nonpolar cavity,³⁴ a monolayer of water between two planar solutes,²¹ and wetting of methane clusters²⁰ fall into this category. Experimental evidence for the existence of water inside weakly polar cavities in protein interiors^35–39also corroborate this picture. Studies on the behavior of water near hydrophobic graphitic materials from recent experimental literature,^40,41 indicate that water may atomically wet a graphite surface, which is macroscopically water shedding. Interpretations of X-ray reflectivity differ.¹¹

In the intermediate region between ∊_CC = 0.1 and 0.2 kJ/mol, the average water density changes sharply. Further analysis of the instantaneous number of water molecules n(t) in the intersolute region as shown in Figure 1B for ∊_CC = 0.125 to 0.150 kJ/mol reveals that the intersolute region oscillates between a wet and a dry state. This behavior resembles that of many recent investigations such as the transitions for water in a carbon nanotube^18,24 with reduced solute–water interaction, capillary evaporation alternating with condensation of water in model pores,²² and an intermittent permeation of cylindrical nanopores by water.^42,43 Partial occupancy is also common for relatively nonpolar cavities on the interior of proteins.

It is interesting to observe (see Figure 1A) that the density curves for all three solutes pass near a common point C when ∊ is varied. Near the origin, we observe that with increasing size of the solute area, dewetting increases, that is, average density decreases as indicated by the downward arrow. This is in accordance with earlier theoretical predictions on hard solutes.^5,28 However, on the other side of the transition (right side of the point C in Figure 1A), we do not observe any microscopic dewetting with the increase in solute sizes. In fact, a closer look reveals that the average water density in this region increases slightly from the smallest solute to larger ones. This apparent increase in the intersolute density with increasing solute sizes is due to a small increase in attractions in the intersolute region which saturates with size for larger solutes.

The transition from a dry to a wet state in the case of medium and large solute plates is fairly sharp and occurs between the ∊_CC values 0.1 and 0.2 kJ/mol for the systems studied. However for the smaller plate this transition is not sharp, and the density grows more gradually. A balance between the loss in energy due to H-bond breaking and the gain in energy due to solutesolvent attractive interaction dictates whether the intersolute region between the two solutes will be wet or not.

In Table 1 we have tabulated solute–solvent interaction energies for all the three solute sizes with two ∊_CC values of 0.1 and 0.2 kJ/mol between which the transition occurs. We have also tabulated the loss in H-bond energies and the average number of water molecules accommodated in the wet state for the three solute sizes. We approximate the lost H-bond energy by considering a loss of around 0.6 H-bonds per water molecule near the solute²¹ and a H-bond energy of 10 kJ/mol per hydrogen bond. We estimate the total energy loss due to H-bond breaking by considering the number of water molecules accommodated in the case of the completely wet state for that particular solute size, that is, $E_{\text{HB}}^{\text{lost}}=N_{\text{wet}}\times 0.6\times 10\text{kJ}/\text{mol}$, where N_wet is the average number of water molecules accommodated in the intersolute region in the completely wet state for a particular plate size. We compare with half the solute–solvent interaction energy to approximately compensate for only two of the four solute surfaces being of interest. In case of a small solute, even for ∊_CC = 0.1 kJ/mol the gain in solute–solvent energy is more than the loss in H-bond energy, and that is why this state is not completely dewetted. In the case of the other two larger solutes, for the dry state (∊_CC = 0.1 kJ/mol) the gain in solute–solvent interaction energy cannot compensate for the loss in H-bond energy, and thus water prefers to stay away from the intersolute region into the bulk. However at ∊_CC = 0.2 kJ/mol the gain in solute–solvent energy is sufficient to compensate for the lost H-bond energy, and thus wetting is seen in these cases.

Table 1.

Interaction Energies Balance (kJ/mol) for Different Solute–Solvent Systems

solute type	〈Nwet〉a	${\text{E}}_{\text{HB}}^{\text{lost}}$	∊CC	Euvb
solute-I	5.8	34.8	0.1	−54.2
			0.2	−96.1
solute-II	15.2	91.2	0.1	−59.8
			0.2	−177.4
solute-III	48.5	291.0	0.1	−171.6
			0.2	−540.1

^aAverage number of intersolute water in the fully wet state.

^bSolute–solvent potential energy/2.

One may argue that the average density or number of water molecules in the intersolute region, being an ensemble (time) averaged quantity, may not be a good order parameter to follow the wetting/dewetting transition near a hydrophobic surface, which is expected to be associated with a substantial fluctuation in the number of water molecules. Calculation of the fluctuation in the number of intersolute water molecules is necessary to validate the observation of a phase transition especially when finite-size scaling plays a role.

Therefore, we have calculated the relative fluctuation in the instantaneous number of confined water molecules n(t) as given by

$${\sigma }^2(n)/n_{\text{av}}=(\langle n{(t)}^2\rangle -{\langle n(t)\rangle }^2)/\langle n(t)\rangle$$ (2)

and plotted the result in Figure 2 as a function of the attractive strength parameter for system II with the absolute fluctuations σ²(n) in the inset. It is important to note that relative fluctuations σ²(n)/n_av (as well as σ²(n)) in the low ∊_CC region (up to 0.1 kJ/mol) as well as in the higher range are quite low, whereas in the intermediate region of ∊_CC = 0.1–0.2 kJ/mol, they are strongly peaked, indicating that water occupancy fluctuation is a good measure of this phase transition.

Figure 2.

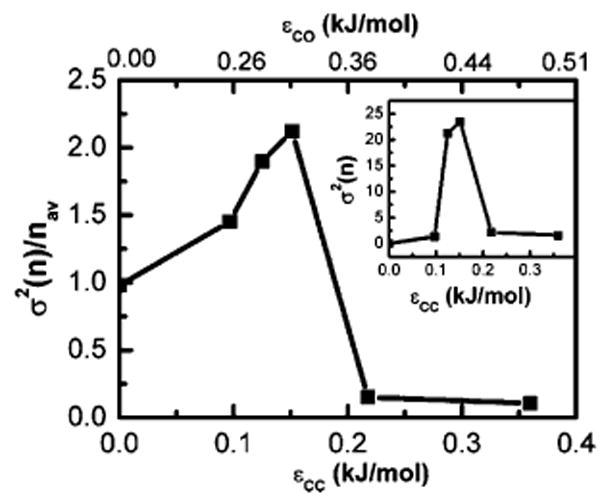
Plot of the relative fluctuation in the number of confined water molecules between the two solutes σ²(n)/n_av for the water–solute-II system as a function of the attractive strength of the solute (∊_CC) (bottom axis) or the solute–solvent (∊_CO) (top axis)

The instantaneous behavior of water occupancy in the confined region also gives information about density fluctuations that change with respect to solute size. To normalize, we plot the instantaneous number of water molecules per unit surface area, ρ_A(t)( = n(t)/A) for values of solute attraction on each side of the transition, that is, at ∊_CC = 0.1 kJ/mol in Figure 3A and at a stronger attraction of ∊_CC = 0.2 kJ/mol in Figure 3B for all of the three solute sizes. In the case of the smallest solute (see top panel of Figure 3A), we see the intermittent emptying and filling of the intersolute region, whereas drying occurs for the other two larger solute sizes (see middle and bottom panels), where almost all the water molecules are pushed out within the first 100 ps and the intersolute region never fills up again on the nanosecond time scale. In the stronger attraction case (Figure 3B), we observe that for each of the three solutes, the instantaneous area densities ρ_A(t) are fluctuating around the average density ${\rho }_{\text{A}}^{\text{av}}$ corresponding to a wet state. Fluctuations in ρ_A(t) decrease with increasing solute sizes leading to slightly increasing average densities with increased solute size. Thus the effect of increasing solute sizes on intersolute dewetting acts in the opposite direction in the region of more attraction to preferentially wet the planes.

Figure 3.

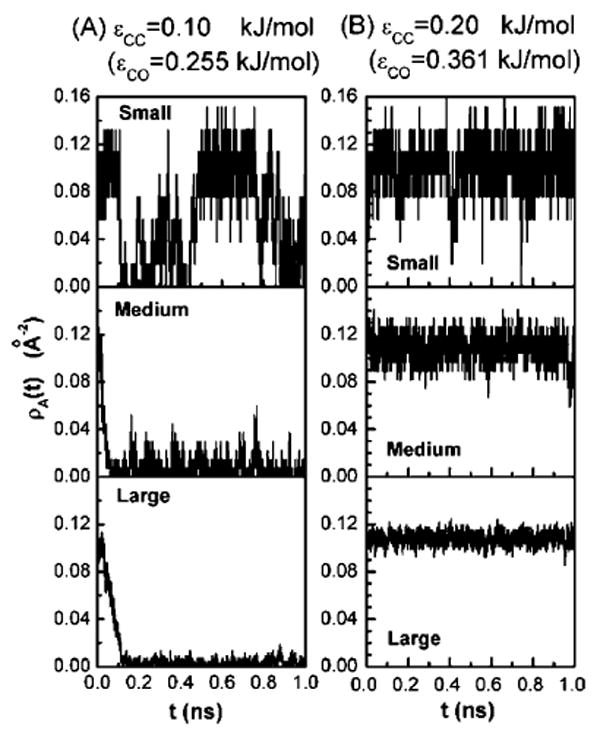
Plot of the instantaneous variation in water density ρ_A(t) in the intersolute region for three solute sizes with solute attraction strengths (A) ∊_CC = 0.1 kJ/mol and (B) ∊_CC = 0.2 kJ/mol.

The effect of solute size on the wetting/dewetting at small ∊ can be rationalized in terms of an effective repulsive potential— the cavity expulsion potential (CEP) that arises between water and the repulsive solute owing to the unbalanced attractive forces in water near a purely repulsive solute as compared to the bulk.⁴⁴ The CEP increases with the increase of the solute size, because of more and more unfavorable interaction with a larger interfacial region.²⁰ However, when an attractive interaction between the solute and the water molecule is present, the stabilizing effect offsets the CEP.²⁰ In the present case, when solute attraction is small (∊_CC is up to 0.1 kJ/mol), with an increase in solute size, an increase in CEP is not counterbalanced by the solute–solvent attractive interaction. Hence we observe increasing dewetting with an increase in solute size. For the case of a higher attractive strength of the solute atom (∊_CC = 0.2 kJ/mol and beyond) the solute–solvent attractive interaction offsets the CEP.

As discussed earlier, it has been proposed⁵ that first a thin vapor layer is formed around a large hydrophobic solute in water and when two such solutes come closer to each other, correlated fluctuations from the individual solute–liquid interfaces causes an intersolute dewetting and explains hydrophobic collapse. One might thus expect a liquid–vapor-like density profile outside of each solute plate whenever the intersolute region between them is dewetted. To test this hypothesis we plot water density profiles in Figure 4A for the largest solute plates considered here for two different solute interactions: the purely repulsive WCA interaction as shown by the solid line and a very weakly attractive interaction with ∊_CC = 0.1 kJ/mol as shown by the dotted line. In both cases the intersolute region is nearly dry. For the WCA repulsive solute, the density profile outside the plate is more like that of a liquid–vapor interface with a slow and featureless growth over a large interfacial region. Yet, in the other case, with a finite solute–water interaction so small that the intersolute region is dewetted, the density of water outside the plate displays the strong oscillations characteristic of liquids near walls and does not appear similar to the structureless liquid–vapor interface. In this case, although no vapor layer has been formed around the individual solute as suggested by the fully wet outside surface of the solute, dewetting in the intersolute region is observed. This demonstrates that drying in the intersolute region does not necessarily proceed via the initial formation of a thin vapor layer around a single nanoscopic solute and is in fact a cooperative phenomena in some cases.

Figure 4.

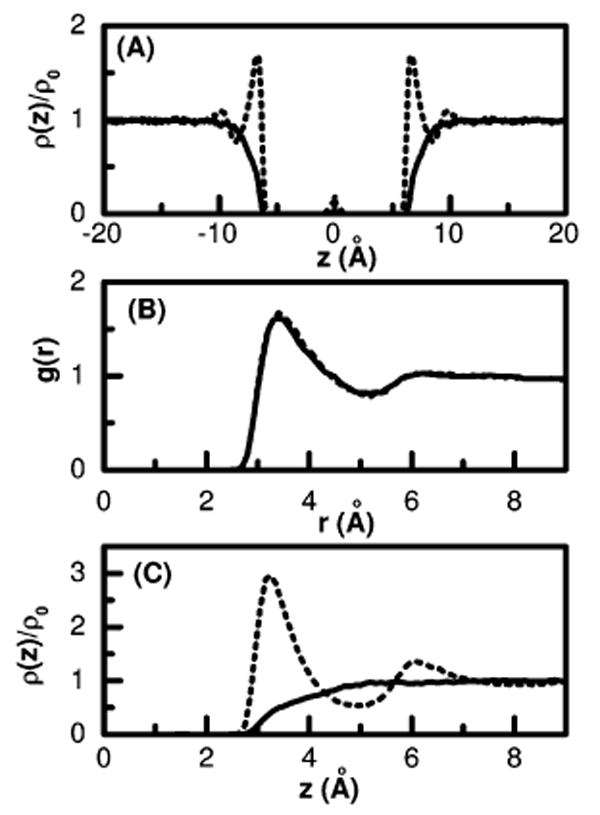
(A) The normalized single particle density ρ(z)/ρ₀ of water oxygen in and around two type III solute plates with an intersolute distance of 10 Å as a function of the distance perpendicular to the solute plates; a purely repulsive WCA potential (solid) and with attraction parameter ∊_CC = 0.1 kJ/mol (dotted). (B) The radial distribution function g(r) of a single carbon atom in water, WCA (solid) and with attraction parameter ∊_CC = 0.3598 kJ/mol (dotted). (C) Same as in Figure 4A but for a single solute plate in water and the dotted line corresponds to a stronger solute attractive interaction taken to be the same as that in Figure 4B.

The coupled effect of solute size and weak attractive solutesolvent interactions on the structure or spatial arrangement of water around a single hydrophobic solute can also be seen in Figure 4. The solute–water radial distribution function for a single solute carbon atom in water is shown in Figure 4B with two different interaction parameters for the solute atom; ∊_CC = 0.3598 kJ/mol corresponding to the AMBER force field of sp² carbon and a purely repulsive interaction as obtained by WCA decomposition of the same LJ potential. It is important to notice that the water correlation hardly changes on going from repulsive to attractive solute–solvent interactions for this atomic solute. Thus the present result (Figure 4B) as well as reported results on small alkane hydration⁴⁵ demonstrate the validity of the vdW picture for water around a small nonpolar solute: harshly varying, purely repulsive interaction determines the overall shape and magnitude of the density distribution (water structure), slowly varying attractions being a small perturbation to the overall structure. In this picture we expect that slowly varying attractive interactions have only a minor effect^26,46 on water structure around a small nonpolar solute. If this assumption was true for water around larger solutes as well, one should not expect that the behavior of water in and around larger nonpolar solutes with purely repulsive interaction would be different from the same with realistic LJ interaction. However water correlations at large length scales, as shown below, significantly depend on the attractive interaction strength of the solute.

To get insight into the effect of solute dispersion interactions on the water structure around a larger solute, we have calculated the singlet density distribution of water perpendicular to a nanoscopic plate with and without dispersion interaction and compared them in Figure 4C. We used the same attraction parameter as that of the solute atoms described in Figure 4B. The density profile in Figure 4C clearly shows that the structure of water near the solute surface is significantly perturbed by the attractive dispersion interaction of the solute. Thus although attractive dispersion interaction has a limited effect on the water structure around a small nonpolar solute, when the solute size is larger and polyatomic, the individually small attractive solute–solvent dispersion interaction per atom may have a significant effect on the solvent structure around the more substantial solute. For the nanoscopic solutes considered here, we observe that addition of the weak attractive dispersion interaction, of the order of a fraction of k_BT, to the usual repulsive core interaction of the solute atoms not only eliminates the vapor interface for realistic estimates of its size,²⁸ but affects a dramatic change in density correlations preceding wetting. The appearance of density waves, pulled-up outside a nanoscopic plate, occur at lower interaction strengths than are required to obtain a wet state between such plates. While density waves are necessary for the wetting transition observed in the intersolute region of nanoscopic solutes as a function of the solute water attractive interaction, their presence is not sufficient. Our results with attractive mean-field atomic models is related to that found using polarizability.¹²

It is important to note here that the intersolute cavitation observed in many theoretical and computational investigations^{5,6,15,27–31} with a repulsive description of the solute interactions cannot capture and thus elucidate the mechanism of the strong long-range attractive forces between macroscopically large plates, as observed in some surface force measurements,^47–50 that extend over several thousands of angstrom in some cases⁴⁹ to a few hundred angstroms in some others.⁵¹ Problems about surface composition and prohibitive computational requirements due to size make it infeasible at present to computationally explore at atomic resolution the length scales and materials relevant to such experimental investigations.

Concluding Remarks

We have demonstrated that the recent idea that cavitation in the intersolute region of nanoscopic solutes, preceded by the formation of a vapor layer around an individual solute, is not a mechanistic description of the hydrophobic effect. We further showed that chemically reasonable estimates of the interaction strength for carbons such as those used in hydrocarbon interactions in biomolecular systems lead to a microscopically wet state and a hydrophobic interaction characterized by significant barriers to association and not by vacuum induced collapse. The fact that the solute–solvent attractive interaction strength correlates with a good order parameter for the drying transition gives a mechanism to relate many previous results. Indeed, by modifying the attractiveness of the constituent solute atoms one can expect to regulate the influx of water in nanopores and nanoslits accordingly. This property could be used to construct environments such as channels and nanosensors where gated water pores may be useful. The identification of the solutewater attraction as a key determinant for the regulation and stability of water in the intersolute region for nanoscopic systems suggests amenable experimental studies. Thus the observations from the present study can be used to tailor new materials with desired wettability and permeability as well as understand environments near protein surfaces.

Although the common idea in liquid structure theory that a slowly varying attractive dispersion interaction has only a minor effect^28,46 on the solvent structure around a solute is true for small solutes, it does not always hold in case of larger solutes and aqueous solutions. The behavior of water near a substantially large hydrophobic surface is determined by the detailed nature and arrangement or topology of the solute atoms dictated by both interactions and geometry.^6,52,53 Hydrophobicity is a term commonly used for describing the inter- and intramolecular association propensity of alkane, alkene, and aromatic side chains in proteins and other biomolecular solutes in aqueous solution. We find that characterizing the nature of the hydrophobic effect at larger length scales with only repulsive interactions, neglecting weak dispersion interactions of the constituent solute atoms with solvents, yields a picture which is incomplete for realistic systems near the nanometer length scale such as proteins and lipid bilayers.