Annotating proteins with generalized functional linkages

Abstract

As genome sequencing outstrips the rate of high-quality, low-throughput biochemical and genetic experimentation, accurate annotation of protein function becomes a bottleneck in the progress of the biomolecular sciences. Most gene products are now annotated by homology, in which an experimentally determined function is applied to a similar sequence. This procedure becomes error-prone between more divergent sequences and can contaminate biomolecular databases. Here, we propose a computational method of assignment of function, termed Generalized Functional Linkages (GFL), that combines nonhomology-based methods with other types of data. Functional linkages describe pairwise relationships between proteins that work together to perform a biological task. GFL provides a Bayesian framework that improves annotation by arbitrating a competition among biological process annotations to best describe the target protein. GFL addresses the unequal strengths of functional linkages among proteins, the quality of existing annotations, and the similarity among them while incorporating available knowledge about the cellular location or individual molecular function of the target protein. We demonstrate GFL with functional linkages defined by an algorithm known as zorch that quantifies connectivity in protein–protein interaction networks. Even when using proteins linked only by indirect or high-throughput interactions, GFL predicts the biological processes of many proteins in Saccharomyces cerevisiae, improving the accuracy of annotation by 20% over majority voting.

Increased automation in gene sequencing and protein structure determination has brought biomolecular sciences to the point at which no function is known for most of the sequences determined and for many of the structures. To fill this void of knowledge, a function is often transferred to the target protein from one that has a similar sequence. This process has difficulties that can lead to errors in annotation (1): function diverges with sequence, it can be difficult to distinguish among paralogs, and proteins with multiple domains present puzzles when the homolog contains only some domains in common with the target.

Here, we describe an alternative approach to protein annotation that describes the function of a protein by the context of its functional linkages–metabolic, signaling, and structural–to other proteins. Functional linkages not only provide evidence of function where no homology to experimentally characterized proteins has been found, it retrieves a complementary type of function that concerns the larger biological role or process of a protein rather than its specific biochemical activity (2). In this view, the function of the target protein is defined by information available on all of the functions of the linked proteins (3–7).

The methods of annotation from functional linkages are less mature than those based on homology. Functional linkages are typically defined by algorithms that use abundant data: genome sequences underlie functional linkages generated by phylogenetic profiles and operon predictions, whereas others use high-throughput experiments such as gene-expression or protein–protein interactions. These methods share the idea that if linked proteins contribute to a larger biological function, the “guilt by association” principle can be applied to transfer annotations from one protein to another (for a review, see ref. 8).

Several issues arise when integrating pairwise functional linkages extracted from high-throughput data. The typical response to noisy data is to use restrictive thresholds, but we work from the principle that we can improve both the accuracy and coverage of annotation if we use all available information while controlling sources of error. We hope to improve the prediction of the target by combining many linked proteins, but to include less reliable links, we must appropriately weigh the contribution of each. Depending on the method defining the functional linkage, some annotations may be more useful than others: e.g., linkages defined by protein interactions may work well to predict functions performed by protein complexes. We should integrate the annotations of the linked proteins in a manner that accounts for their similarity and explicitly address error in annotations and the limitations in our description of protein function. Finally, we need to incorporate other forms of knowledge about the target protein, such as its cellular component (CC) or molecular function (MF) annotations, to provide a unified description of its biological process (BP).

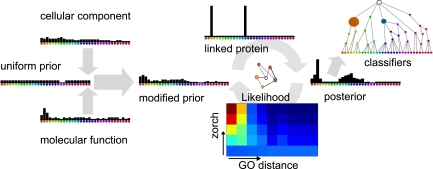
Our method, Generalized Functional Linkages (GFL), deals with these challenges by balancing pairwise functional linkages and additional information about the target through a Bayesian framework (Fig. 1) that treats protein function as distributions over BP of the Gene Ontology (GO) (9). To test GFL, we defined functional linkages by quantifying protein connectivity in the Database of Interacting Proteins (DIP) (10) with zorch (Fig. 2), the result of an algorithm modified from the field of cognitive sciences (11). We show that GFL successfully combines the functional linkages from many linked proteins that are moderately connected to a target protein of interest through indirect (i.e., >1 edge away) and high-throughput interactions, improving upon majority voting while extending annotation through the DIP network to proteins of unknown function.

Fig. 1.

Overview of GFL. GFL integrates prior information with linked proteins to determine whether each hypothesis, or Gene Ontology (GO) biological process (BP) annotation, best describes the target protein. Existing cellular component (CC) or molecular function (MF) annotations of the target, and negative results, modify a uniform prior probability distribution. The likelihood controls the influence of each linked protein over the prior distribution according to the strength of its functional linkage (here measured by zorch) and the confidence in its ‘known’ annotations. The matrix shows the relationship between protein function and functional linkages used by the likelihood: warmer colors denote the increased probability of observing proteins with similar GO biological process annotations when highly connected with zorch. After all linked proteins have contributed, the resulting posterior distribution provides a probabilistic description of the biological process of the target protein. This distribution can be used to link new targets, or can be summarized as naïve Bayes classifiers that group similar GO terms.

Fig. 2.

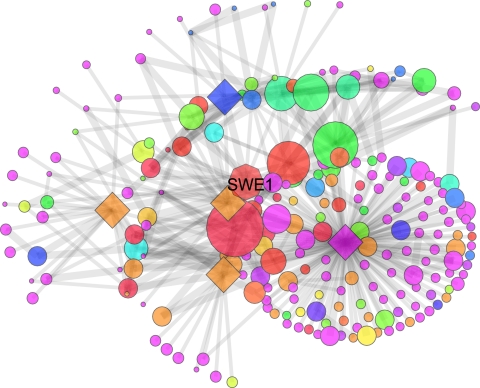
Zorch quantifies connectivity to the target. An initial unit of zorch flowed from the target SWE1 throughout the protein–protein interaction network. Protein interactions identified by reliable small-scale experiments in DIP core (wide edges) allowed more flow than those from high-throughput experiments (narrow edges). Highly connected proteins accumulated more zorch (large nodes). Proteins shown to interact with SWE1 with edges in DIP core were removed to rigorously evaluate GFL annotation (diamonds). Despite the influence of many linked proteins with different functions (blue transport, green cytoskeleton organization, purple other), GFL combined prior information, the MF kinase activity of SWE1, with zorch-linked proteins involved in the cell cycle (red and orange), to successfully predict a correct biological process: regulation of cyclin-dependent protein kinase activity. Voting failed for SWE1.

Results

Defining Functional Linkages by Network Connectivity with Zorch.

A unit of zorch was placed on the target protein and allowed to propagate throughout the protein–protein interaction network of Saccharomyces cerevisiae in DIP, decaying as it traveled over edges. The total amount of zorch that passed through a node quantified the network connectivity to the target. Edge decay rates were optimized separately for protein–protein interactions described by small scale experiments (i.e., those in DIP core) and high-throughput experiments. Links between protein pairs shown to interact by small-scale experiments were removed so that these were not used to predict each other's function.

GFL predicts functions by combining functionally linked proteins by training on protein pairs that have been given a linkage score with an external method: here we used zorch. A GFL likelihood that describes the probability of observing any BP in a protein at various linkage scores, given another BP as a hypothesis for the target protein, was constructed by first counting observations of linked proteins at discretized linkage scores and a GO similarity metric (12). This general relationship between functional linkages and annotation similarity was refined by counting observations between specific BP at various linkage levels. Next, target proteins enter GFL with any existing MF or CC that has already been ascribed. These annotations are converted to a prior distribution over BP by Bayesian processes uninformed by functional linkages. As each linked protein updates the distribution, all BP hypotheses compete through the likelihood to describe the biological process of the target. More strongly linked proteins with more reliable annotations will have more influence over the prior. After the final update, the posterior distribution over most specific BP annotations is the resulting description of function: these probabilities are combined at more general BP or classifiers so that predictions to similar annotations support each other.

Evaluation of GFL.

We predicted the functions of known target proteins with existing BP that are supported by more reliable forms of evidence: direct experimental assay (GO evidence code IDA), traceable author statement (TAS), inferred by curator (IC), inferred by genetic interaction (IGI), or inferred by molecular phenotype (IMP). Although we consider annotations inferred by interacting proteins (IPI) reliable, we did not use these to avoid circularity with zorch. Of 4,012 proteins meeting these requirements, 3,433 were linked by zorch to at least 1 annotated protein, representing the entire set of known proteins we evaluated.

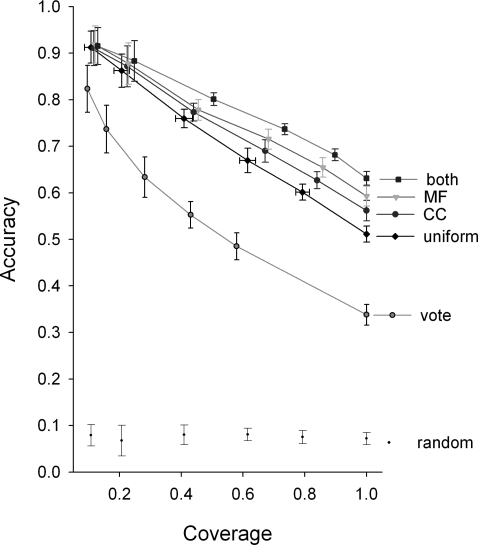
We estimated prediction accuracy with 10-fold cross-validation (Fig. 3), in which we separated known targets into 10 randomly selected test sets. For each set we recalculated all probabilities used by GFL without the benefit of the targets in the set. We then annotated each target, scoring the prediction a success if our single most probable annotation matched at least 1 of the existing target annotations. Although we used the most detailed GO annotations as hypotheses for the BP of a target protein, we combined the resulting probability of the detailed annotations into 206 general annotations, or naïve Bayes classifiers, before judging (13). Accuracy was calculated as the number of correctly annotated targets divided by the total targets attempted. The predicted targets were ranked by the maximum posterior probability of their assigned annotation. As shown in Fig. 3, ranking by the posterior probability reflects the accuracy of the prediction, allowing us to estimate the confidence in our annotations.

Fig. 3.

GFL increases accuracy over voting and improves with informative priors. Predicted targets were ranked according to their maximum posterior probability: those with probability concentrated on fewer annotations were more often correct. A prior inferred using CC, MF, or both, produced more accurate predictions than a uniform prior, especially when predicting more difficult targets. Coverage was measured over the 3,433 proteins with high-quality annotation (excluding those inferred by protein interaction). The mean and standard deviations of predictions were generated by 10-fold cross-validation in which the assayed targets had no influence upon the predictive model; however, gains from priors cannot be considered as cross-validated as MF and CC correlate with BP. Random predictions were generated by shuffling target proteins within the protein interaction network and with uniform priors.

Accuracy Improves with Prior Information.

Incorporating molecular function (MF) or cellular component annotations (CC) of the target as Bayesian priors to GFL improved the accuracy, especially at higher levels of coverage (Fig. 3). MF priors were more helpful than those derived from CC, whereas priors that included both types of annotations produced the most accurate predictions; however, such gains should not be considered the results of cross-validation, because incorporation of the priors adds information that correlates with the BP of the targets. With or without informative priors, GFL performed better than a majority voting method (Methods, Voting), obtaining more than a 20% gain in accuracy as coverage increased to include protein targets that were more difficult to annotate correctly. GFL increased accuracy at least 5-fold over results obtained by randomly shuffling the target proteins within the DIP interaction network.

Predicting Unannotated Proteins.

To estimate the accuracy of predicting yeast proteins without BP, we first grouped them by their GFL posteriors and whether they had other annotations (CC or MF). We then calibrated the accuracy for these groups with the results of 10-fold cross validation [supporting information (SI) Fig. S1], which predicts that GFL annotated 150 of these proteins of unknown function with ≥50% accuracy using DIP and zorch. For known proteins, short lists of 2 or 3 predicted BP fared better with a relaxed evaluation that required that at least 1 of these annotations were correct: the same is expected for the unknown group (Fig. S1). For predictions of annotated proteins, see our web site (www.doe-mbi.ucla.edu/services/GFL).

Accuracy of Different Functional Classes.

Because functional linkages can be defined by different types of data, e.g., protein–protein interactions, gene expression, or genome context, it should be expected that different methods will perform better on proteins involved in some biological processes (13). Functional linkages defined by zorch performed well on processes performed by protein complexes such as the spliceosome and proteasome but less well on cellular respiration or most metabolic pathways (Table S1), likely because these generally rely on fewer stable protein–protein interactions (5). Other well-predicted BP were those involved in the cell cycle, transport, and cytoskeleton, whereas cell wall organization and regulation of translation fared relatively poorly.

Accuracy Improves with More Linked Proteins.

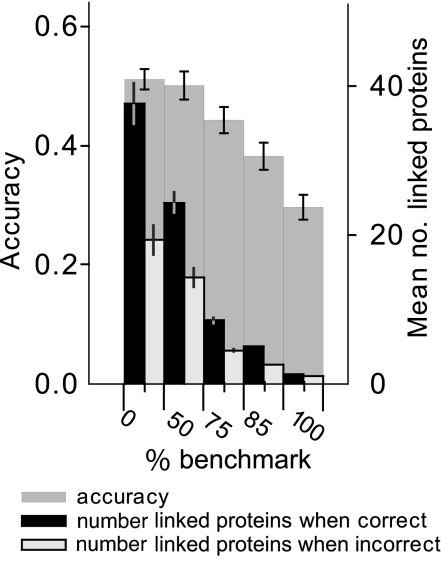
To assay whether GFL could successfully integrate weaker functional linkages, we compared predicting each target using large numbers of linked proteins with using fewer of the best proteins. For each target we removed linked proteins based on the probability that they yield correct annotations when used individually. Best results were obtained by using the full complement of linked proteins (Fig. 4). Reducing the number of proteins to fewer than 10 markedly decreased accuracy, demonstrating that GFL improves annotation by including lower quality functional linkages. Targets that began with more zorch-linked proteins were also more likely to be predicted correctly: the top one-third ranked targets had >50 linked proteins on average.

Fig. 4.

Linking many proteins improves annotation. For each target protein, we found the linked protein with the maximum probablity of successfully predicting the target annotation when used alone. We used the probability of success for this protein (based on its zorch and annotation) as a benchmark to test the effect of integrating many proteins less strongly linked to the target. GFL achieved the greatest accuracy at the lowest stringency threshold, which used all linked proteins (threshold at 0% of benchmark). Independently, targets that were linked by zorch to more proteins were predicted more accurately (black vs. white inner bars). Error bars show 1 standard deviation above and below the mean using a uniform prior.

Estimating the Error Rate in Linked Protein Annotations.

The GO consortium couples their annotations with codes that classify the evidence used to infer them. GFL uses these evidence codes to estimate the uncertainty in the ‘known’ annotations of the linked proteins. We devised an indirect method for making quantitative estimates of reliability. We first selected target proteins with annotations supported by those evidence codes we considered most reliable: those inferred by direct assay and traceable author statement. We then made isolated predictions of the annotations of these gold standard targets using individual linked proteins with annotations supported by each evidence class. We assumed that a prediction failed for 1 of 2 reasons: the annotation of the linked protein was correct, but the inference failed to assign an appropriate function to the target, or the annotation of the linked protein was incorrect; the possibility of both was ignored. A baseline failure rate was estimated by finding the accuracy of predicting a gold standard target annotation with a gold standard linked protein annotation.

We estimated the confidence in each evidence class by dividing by the baseline rate, which provided the following ranking: (best first) molecular phenotype, genetic interaction, sequence similarity, reviewed computational analysis, and expression profile (Table S2). Because we derived functional linkages from a protein interaction network, we expect that this test is biased in favor of annotations inferred from protein–protein interactions. For other classes we made the assumption that the baseline rate was independent of the type of supporting evidence. Using the derived confidence values as input to GFL, rather than treating annotations equally, improved the results slightly but significantly (T test P value 0.001), resulting in the correct annotation of an additional 38 proteins.

Discussion

Examples of Proteins of Unknown Biological Process.

We note a few promising examples among our predictions of yeast proteins (Table S3). Protein YDR387C has not been experimentally characterized, but by sequence similarity had been annotated, at the time of our data collection at SGD, with the MF permease activity, generating a BP prior that favored vitamin transport and biotin biosynthetic process. Although 6 proteins were linked to the target, 5 of these had the lowest level of zorch we accepted. The single highly connected protein was annotated with posttranslational protein targeting to membrane, whereas the 5 weakly linked proteins contained this BP and peptide pheromone export, filamentous growth, cytosol to ER transport, transport, and hexose transport. Recent phylogenetic sequence analysis has shown that YDR387C is a member of the sugar transporter family (14), which supports the second of our ranked posteriors, hexose transport, with 41% of the probability, a prediction that relied on the integration of prior knowledge with weakly linked proteins: neither functional linkages nor an inference from MF reproduced this result individually. The most probable posterior, posttranslational targeting to protein membrane, with 57%, might reflect a passive rather than active role of the target.

Another example, protein YAL027W, lacked both BP and MF, although its green fluorescent fusion protein had been observed in the nucleus (15). Integration of the prior with 25 predictors divided the posterior among G₁/S transition of mitotic cell cycle (63%) and response to DNA damage stimulus (33%). SGD reports that unpublished research suggests that it works with Rad1/Rad10 endonuclease to resolve DNA recombination intermediates. High throughput affinity capture methods identified many protein interactions to YAL027W (16, 17); the 2 that received the highest zorch were Rad1 and Rad10, which also function in microhomology-mediated end joining, a form of DNA repair that is thought to be especially important during G₁ (18).

Priors Incorporate Additional Knowledge.

We tested priors based on the CC and MF of the target protein (Fig. 3). Some BP become more likely with this additional information, because certain biological processes are carried out in defined cellular locations, and biological processes coordinate groups of proteins with specific molecular functions. For example, if the target protein has the MF kinase activity, the 2 most likely BP leaves for fungi become, with a 35-fold increase in probability, peptidyl-histidine phosphorylation and 2-component signal transduction system (phosphorelay); each still accounts for little more than 2 percent of the total prior probability, however, and functional linkages are needed to further reduce the uncertainty (Fig. 2). The prior also provides an opportunity to add other independent knowledge about the target. If the GO “not” qualifier is used, we set the prior probability to zero for that annotation. Individual researchers may have their own unpublished negative results or clues not present in the public databases, and GFL could integrate these through the prior as well.

We Make Several Choices to Use GO Annotations as Bayesian Hypotheses.

The GO consortium provides a system of annotation noteworthy for its detail, use of multiple inheritance, and evidence codes. A protein can be annotated at varying degrees of specificity on the GO hierarchy, but our hypotheses are described by a probability distribution over all BP and one cannot be a more general form of another. Thus, we use only the most specific annotations (i.e., leaves) as hypotheses as the best description of the target protein. If a primary annotation, by which we mean a preexisting annotation of the protein, is general (i.e., not a leaf), we posit that with additional knowledge, it would have been replaced with 1 of its more specific leaves, assuming an appropriate leaf existed in GO. Thus, we treat primary annotations as probability distributions over their leaves, based on the frequency of annotated proteins within fully sequenced fungal organisms. To account for the possibility that no GO leaf exists to describe the protein in more specific detail, either because biology has not yet described the function, or because of choices made in the structure of the ontology, we created an additional leaf that represents a conditional unknown for each primary annotation. These conditional unknowns are given an estimate of the probability that the primary annotation, but none of its existing leaves, is correct. In this manner each primary GO annotation is represented as a set of mutually exclusive hypotheses, and the function of a protein is described as a collection of distributions over these hypotheses, 1 distribution for each primary annotation.

Measuring GO Similarity.

We extended a popular, information-content GO metric to measure the functional similarity between annotated proteins (12). This method considers 2 annotations more similar if their most specific ancestor is found less frequently in an applicable reference set of annotated proteins. To extend the metric of functional similarity to 2 proteins, we used the nearest distance between any of their annotations. Although proteins might be considered more similar if they shared more than 1 similar annotation, much more data would be needed to make such extensive comparisons robust; otherwise, adding dissimilar pairs of annotations to a metric would likely confound the relationship between proteins engaged in at least 1 shared task. We note that our method of representing the uncertainty in primary annotations as distributions over leaves partly addresses the lack of support for multiple inheritance in this GO metric: normally, 2 terms are not considered more similar because they share children. Using the expected similarity between their 2 leaf distributions, however, provides that annotations that share children become more similar.

GO Evidence Codes Yield Confidence in Existing Annotations.

Incorporating the confidence in an annotation allows linked proteins with higher quality annotations to have a greater impact on the prediction, whereas larger expected error dilutes the degree to which the likelihood can favor 1 hypothesis over another. Other Bayesian methods have used confidence in GO evidence codes (19), but we are not aware of another that quantitatively estimates them. Our broad assay reflects the expectation that small-scale laboratory experiments provide the best inferences of protein function (19), but further corroboration of the confidence values (Table S2) with other types of functional linkages is needed. Annotations supported by the GO code “inferred by unreviewed electronic annotation” (IEA) had not been incorporated by the Saccharomyces Genome Database (SGD) (20) at the time of our data collection.

Likelihood Combines High-Dimensional and Uncertain Data.

The likelihood is the probability of the data given the hypothesis; here, the data include the annotations and evidence codes of 1 linked protein and the functional linkage to the target. For each BP hypothesis, we focus the likelihood on the most supportive data: that BP of the linked protein that is expected to be both correct and observed (see Methods). This strategy departs from a typical Bayesian procedure, because it allows uncertainty in the data to translate differentially to each hypothesis. We first use the GO structure to guide a prior count of linked proteins at their nearest BP GO distance, representing the general relationship between the functional linkage and BP similarity, and then add counts of specific pairs of BP. If an annotation is poorly represented, the prior count will dominate the likelihood, and strongly linked proteins will predict similar annotations with a typical “guilt-by association” principle; with more data, the likelihood can accommodate specific relations between BP and the particular functional linkage. Because the general relationship is robust, the balance between performance on known targets and overfitting can be controlled by the size of the prior count. GFL can predict BP not already found in the target organism: here, we emphasize discovery over recall of known functions by creating the prior from all BP annotating any fungal protein.

Posterior Represents Protein Function as a Probability Distribution.

The result of GFL is a distribution over BP expressing the probability that each is the best description of the target. As a distribution, the hypotheses are mutually exclusive, allowing simple combination of probabilities at general classifiers without the typical need for further methodology (21). We can draw multiple annotations from this distribution to describe >1 BP, but the posterior does not guide us on how many to choose. Currently GFL uses a naïve Bayesian process by assuming the linked proteins provide independent data. Breaking this assumption leads to amassing probabilities very close to 1 on a single annotation when many linked proteins with similar annotations are used, limiting the use of the posterior as a guide to the true confidence in our predictions. Fortunately, the ranked order of probabilities reflects the accuracy of the prediction (Fig. 3), so we calibrate our expected outcome accordingly (Fig. S1).

Comparison with Other Methods.

Recently, a landmark collaborative effort to predict mouse gene annotations introduced and evaluated a number of approaches that employ functional linkage or gene association data (22). Our method is substantially different from these in the manner we apply Bayes' theorem to arbitrate competition among all hypotheses and our likelihood's use of the GO graph structure to leverage the relationship between functional linkages and functional similarity. We also introduce the use of MF and CC priors, and in addition, show how uncertainty in existing annotations and incompleteness in the GO can be addressed. Herein we have used only 1 type of functional linkage, but we expect that, like other methods (3, 5–7, 22, 23), GFL will improve using multiple types. We believe that the rigor and flexibility of GFL provides a comprehensive framework that will benefit from data accumulating from high-throughput experiments.

Methods

Zorch.

To quantify network connectivity between one protein and others, we adapted the idea of zorch originally used to describe cognition (11). Although we developed this use of zorch independently, it is similar to the FunctionalFlow algorithm (23), although simpler, because it does not attempt to make functional predictions itself but only defines functional linkages based on network connectivity (24). The algorithm is straightforward: a unit of zorch is placed on the target protein and allowed to propagate throughout the DIP S. cerevisiae protein interaction network, decaying as it travels over edges, so that zorch passing through a node is equivalent to the zorch at the previous node multiplied by a constant (e.g., one-half). Each path is calculated independently so that zorch does not recombine but decreases at each step. Cycles are allowed. After zorch falls below a threshold the path is terminated. The result, a measure of network connectivity between target and other proteins, is the total amount of zorch that passed through each node from all paths. To limit the flow radiating from experimentally “sticky” proteins, zorch passing along high-throughput interactions is further reduced by multiplying by 1/n^r, with r optimized as 0.2 and n as the number of interactions of a protein observed only by high-throughput experiments.

Parameters were optimized by maximizing the area under the receiver-operator characteristic (ROC) curve obtained by using zorch to predict pairs of proteins that shared similar BP. The optimal decay rate for DIP core interactions was 0.5 and 0.3 for high-throughput interactions. Zorch propagation ended after reaching a minimum threshold of 0.25 units, a maximum of 3 steps at these decay rates. The optimal values were stable over all 10 cross-validation sets used during simultaneous evaluation with GFL.

The Prior.

CC and MF priors were inferred through a separate Bayesian process using a uniform prior with any GO “not” qualifier annotations set to zero. The needed likelihoods, the probability of a MF or CC given a BP, were obtained by finding the maximum coannotation counts in any fully sequenced fungus. We allowed a small contribution (up to a count of 2) for combinations of protein annotations not found in a fully sequenced organism. Counts at general annotations were redistributed to their leaves according to the frequency of leaf annotations among fungal proteins. The same counting method was used to construct the GO distance (12). In an attempt to limit unwarranted performance gains, if we found a 1 to 1 correspondence with a MF or CC to BP, we replaced the MF or CC with a more general annotation to provide uncertainty in the BP prior and make evaluation using priors more realistic.

Linked Proteins.

We described the function(s) of a protein as a collection of weighted distributions over BP (SI Text, Materials and Methods). To model uncertainty in existing annotations, each primary (existing) annotation generated a distribution over its leaves according to the counts used to calculate the GO distances. To model error in primary annotation, each distribution was weighted by confidence because of its evidence code. In addition, a uniform distribution was weighted by the probability that all primary BP were incorrect. To model incompleteness in the ontology, each primary annotation generated a conditional unknown annotation with probability estimated, as a first approximation, by the fraction of times both a parent and child Interpro accession mapped (25) to the same GO term. We used a prior count of 1 so that all annotations had some conditional unknown probability.

The Likelihood.

We estimate the likelihood for each hypothesis using the expected maximum normalized likelihood (SI Text, Materials and Methods) based on empirical counts. To describe the general relationship between the linkage score (e.g., zorch) and function, we first counted each linked pair of annotated proteins in S. cerevisiae at their nearest discretized GO distance and linkage score. For each pair of GO annotations, we corrected for the graph structure of GO with the probability of choosing the BP from among all BP at the linkage score and GO distance from the hypothesis. In a second step we estimated the more specific relationship between each individual BP pair and the linkage score by counting observations of the pairwise BP of linked proteins, initializing these sparse counts with a prior count guided by the general relationship found earlier.