Abstract
Some epithelial cells display asymmetry along an axis orthogonal to the apical-basal axis, referred to as planar cell polarity (PCP). A Frizzled-mediated feedback loop coordinates PCP between neighboring cells, and the cadherin Fat transduces a global directional cue that orients PCP with respect to the tissue axes. The feedback loop can propagate polarity across clones of cells that lack the global directional signal, although this polarity propagation is error prone. Here, we show that, in the Drosophila wing, a combination of cell geometry and nonautonomous signaling at clone boundaries determines the correct or incorrect polarity propagation in clones that lack Fat mediated global directional information. Pattern elements, such as veins, and sporadic occurrences of irregular geometry are obstacles to polarity propagation. Hence, in the wild type, broad distribution of the global directional cue combines with a local feedback mechanism to overcome irregularities in cell packing geometry during PCP signaling.
Keywords: cell shape, Fat, Frizzled, feedback, mathematical model
Some epithelial cells, such as cochlear hair cells, or fly wing cells, produce asymmetrical cytoskeletal structures on their apical surfaces that project in an oriented fashion with respect to the tissue in which they reside. Disruptions of PCP in humans have been linked to various diseases, such as a congenital deafness syndromes, neural tube closure defects, respiratory diseases, and polycystic kidneys. The mechanism that controls PCP has been intensively studied in the Drosophila wing, where a flat bilayer of cells makes PCP easy to observe, and powerful genetic tools facilitate analysis (1–3). The PCP signaling network polarizes Drosophila wing cells in a proximal-distal direction with respect to the tissue axes. A group of “core proteins,” including Frizzled [Fz (4)], Dishevelled [Dsh (5, 6)], Prickle [Pk (7)], and Van Gogh [Vang (8, 9)] adopts polarized cortical distributions that underlie PCP (10–13) (Fig. 1 A and B). At the cell-cell boundary, the core proteins comprise a feedback loop that results in enrichment of Fz and Dsh on the distal sides of cells and Vang and Pk on the proximal sides (13, 14). In wing cells, evidence favors the hypothesis that these distributions determine the location of an actin-rich trichome, or hair, which emerges from the distal side of the apical cortical domain and points distally.
Fig. 1.
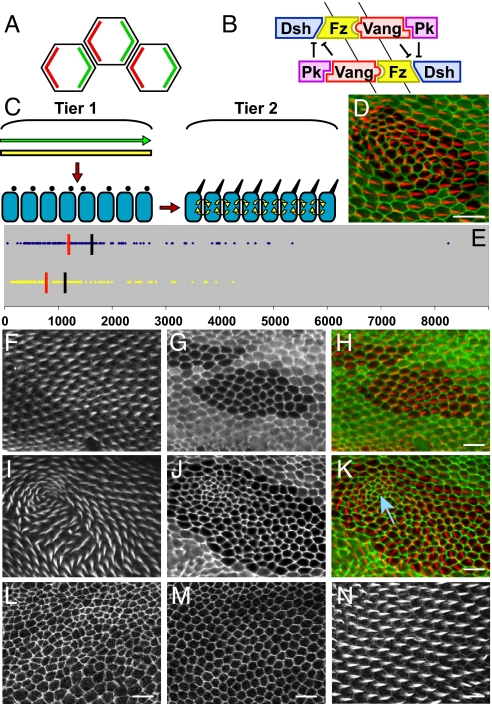
Irregularities in cell geometry are associated with polarity disruption in fat mutant clones. (A) In wildtype, Fz and Dsh segregate to distal cortical domains (green), whereas Vang and Pk segregate to proximal cortical domains (red). (B) Schematic of the feedback loop in which Dsh·Fz·Vang·Pk complexes in opposite orientations antagonize each other. (C) Schematic of 2 tiers of regulation of the PCP signal network in the Drosophila wing. The first tier signaling molecules provide a proximal-distal directional cue across the plane of the epithelium. Yellow bar represents uniform Fat expression, and green arrow represents directional signal transduced by Fat. Black dots represent interpretation of the directional cue; note that not all cells interpret the global signal correctly. The second tier functions as an intercellular feedback mechanism (yellow arrows) to locally propagate and align PCP, thus compensating for errors because of misinterpretation of the global information. (D) In the absence of the global information mediated by Fat, mutant cells (marked by the absence of ubiquitous GFP) show polarity disruption as shown with phalloidin staining for prehairs (red). Note that prehairs emerge from the cell periphery, indicating that cells remain polarized. Cell shapes are outlined by GFP-tagged cell junction marker [line ZCL1792 (34)]. (Scale bar in this and all subsequent figures represents 10 microns.) (E) Size distribution of an unbiased selection of fat clones that show normal (yellow triangles; n = 144) and disrupted (blue diamonds; n = 134) polarity. (Clone size is given in microns2.) The mean (black bars: 1,057 μm2 for normal, 1,569 μm2 for disrupted polarity) and median (red bars: 719 μm2 for normal, 1,260 μm2 for disrupted polarity) of each population is shown. A fat mutant clone that retains wild-type polarity and shows relatively regular cell geometry (F–H). A fat clone that exhibits polarity disruption and noticeable irregularities in cell geometry (I–K). The blue arrow in K marks the nidus of the swirls, which corresponds to the most severe geometry irregularity. (F and I) Phalloidin staining revealing prehairs. (G and J) Ubiquitous GFP marking clone positions. (H and K) Composite images. (L and M) Evolution of cell geometry visualized by E-cadherin::GFP. At 22 h, the apical-cell cortices are disorganized (L) compared to the orderly hexagonal arrays at 33 h (M). (N) Phalloidin staining showing wild-type prehairs in a parallel array. Note that all prehairs emerge from the distal periphery. All wing images are confocal sections. Proximal is to the left and distal is to the right for all images.
Mutations affecting any of the core polarity proteins impair the asymmetric subcellular localization of all known components in the feedback loop. When subcellular asymmetry is lost, the cell does not select an apicolateral cortical domain for prehair growth, and instead a prehair emerges near or at the center of the apical surface (14, 15). An important property of the Fz feedback loop is that it propagates polarity from cell to cell, as distal Fz and Dsh on one cell promote selective accumulation of Vang and Pk on the neighboring cell surface (13). The Fz feedback loop therefore tends to locally align cell polarity (13, 16, 17).
Although the Fz feedback loop polarizes cells with respect to their neighbors, a global directional cue orients this polarization with respect to the tissue axes. The nonclassical cadherin Fat (18) is an essential mediator of the global directional cue [Fig. 1C (17, 19–22)]. Fat exists in a heterotypic complex with the cadherin Dachsous (Ds), and in contrast to the core polarity proteins, Fat and Ds are observed in punctate structures uniformly distributed just apical to the zonula adherens, where the core proteins reside (17, 20). In the fly eye, directional information for PCP resides in the oppositely oriented gradients of Four-jointed (Fj) and Ds, and this information is transduced through Fat by an unknown mechanism (20–25). In the wing, graded expression of Fj and Ds is not essential for PCP, suggesting that redundant sources of directional information exist (21). However, all directional signals appear to require Fat function, because cells lacking fat behave as though they lack global directional cues. In fat mutant clones, the core polarity proteins sort into oppositely oriented Dsh·Fz and Vang·Pk complexes, and prehairs emerge from cell peripheries, indicating that the local Fz feedback loop remains functional (17). The orientation of these complexes is often normal, but sometimes the orientation deviates from wild type. Based on these observations, we proposed that in fat mutant clones, the mutant cells derive polarity information by local propagation from the neighboring wild-type tissue, but the propagation mechanism is imperfect, resulting in varying polarization patterns that are frequently incorrectly oriented with respect to the global tissue axes [Fig. 1D (17)]. We suggested that in wild type, the ability to propagate polarity information compensates for imperfect interpretation of the directional information transduced by Fat, resulting in a robust polarization response.
Here, we ask what impediments challenge the Fz-mediated feedback mechanism to propagate in the correct proximal-distal direction, thereby producing the characteristic phenotypes seen when global signaling is impaired. In this report, we first demonstrate a correlation between irregular cell geometry and polarity disruption. We then demonstrate causality by showing that manipulating cell geometry alters the frequency of polarity defects in fat clones. Finally, by using mathematical modeling, we both reinforce this conclusion, and demonstrate that geometry dependence is a simple consequence of feedback loop function when presented with irregular geometry. Our model predicts the in vivo results much more accurately when a potential nonautonomous effect of Fat-Ds signaling is included (26), suggesting nonautonomous Fat-Ds signaling occurs in the wing. Our results indicate that irregular cell packing is an obstacle to correctly oriented polarity propagation, necessitating a robustly engineered system for reliable PCP readout.
Results
Cell Geometry Impacts Polarity Propagation.
In a large number of fat clones, the polarity patterns vary, even when the clones are generated in similar positions in the wing [(17, 27); data not shown]. Furthermore, smaller clones may or may not induce polarity disruption, whereas larger clones usually do induce disruptions (Fig. 1E) whose patterns are unique. We observed that fat clones of any size that produce polarity defects often show striking irregularities in cell geometry compared with wildtype clones (Fig. 1 F–K).
Concurrent with segregation of Dsh·Fz and Vang·Pk to their respective distal and proximal cortical domains (Fig. 1 A and B), wing epithelial cells significantly change their geometry (28). The final cell divisions are concluding by 22 h after puparium formation (APF) (29) at which time the cell packing is quite irregular (Fig. 1L). By 30 h APF, cells have rearranged their adherens junctions, as visualized with E-Cadherin:GFP, into a relatively regular hexagonal array [Fig. 1M; (28)]. At the same time, PCP signaling is nearly complete. By 32–34 h APF, the prehairs are emerging from the distal periphery of each cell (Fig. 1N). We hypothesize that in the absence of Fat-mediated directional signaling, sporadically occurring failures to resolve cell-packing irregularities cause the Fz feedback loop to propagate polarity in aberrant directions.
To test this hypothesis, we first rigorously assessed whether the occurrence of polarity disruptions correlates with the irregularity of cell geometry within fat clones. Our hypothesis predicts that cell shapes will be more irregular in the population of clones with abnormal polarity. A GFP-tagged marker of cell junctions was incorporated to reveal cell shapes within fat clones. An image analysis tool (see supporting information (SI) Figs. S1 and S2 and SI Appendix) was developed to extract cell-shape information, allowing us to quantify the regularity of cell geometry. Two measures were used to represent the degree of packing regularity. First, we calculated the maximum percentage difference between the area of each cell and its neighbors and averaged this value over all of the cells in the clone (mean of the maximum percentage area difference). Second, we calculated the difference between the largest and smallest internal angle of each cell and averaged this value over all of the cells in the clone (mean of the maximum angle difference; see SI Appendix and Fig. S2). Increasing positive values for these measures express increasing irregularity of cell geometry in the specified cells. We compared 31 fat clones that show polarity disruption to 28 fat clones of similar size that retain wild-type polarity; with each measure, there is a statistically significant difference in the mean irregularity of the cell geometry between fat clones that display polarity defects and those that do not [P = 1.5e-5 (1 tail) for mean of the maximum percentage area difference, and P = 0.027 (1 tail) for mean of the maximum angle difference; Fig. S2]. Therefore, in fat clones the occurrence of polarity defects correlates with less regular cell packing.
Irregular Cell Geometries Cause PCP Defects in fat Clones.
A correlation between irregular cell packing and polarity disruption in fat clones need not imply a causal relationship. Furthermore, the possibilities that cell packing influences polarity, and that polarity influences cell packing might each independently be true. We wished to investigate whether irregular cell packing causes polarity disruptions in the absence of Fat. To do so, we sought ways to manipulate cell geometry and assess potential changes in the polarity phenotypes in fat clones. We and others have observed that fat clones more frequently show polarity disruptions in the region around the crossveins (27). We have also noted that clones are more likely to show aberrant polarity whether they are on or near any vein: Analysis of 111 fat clones on any vein throughout otherwise wild-type wings and 97 fat clones of similar size that are not on veins shows that clones on any vein are much more likely to disrupt polarity than clones not on veins (Table 1). Vein cells are easily recognized because in cross section, their apical surface area is substantially smaller than that of intervein cells (Fig. 2A). Juxtaposition of smaller and larger cells necessitates irregular cellular packing. We could therefore ask whether making cell geometry more regular by removing the crossveins would reduce the frequency with which fat clones in the crossvein region produce polarity disruptions.
Table 1.
Irregular cell geometries cause PCP defect in fat clones
| polarity | abnormal | normal | abnormal | normal |
|---|---|---|---|---|
| on/off veins | on veins | off veins | ||
| number | 67 | 44 | 30 | 67 |
| percent | 60% | 40% | 31% | 69% |
| mean size* | 1018 | 836 | 1095 | 872 |
| aggregate mean* | 946 | 941 | ||
| cv | ft | cv ft | ||
| number | 35 | 29 | 19 | 55 |
| percent | 55% | 45% | 26% | 74% |
| mean size* | 1458 | 788 | 2042 | 938 |
| aggregate mean* | 1234 | 1225 | ||
| PTEN | ft | PTEN ft | ||
| number | 81 | 114 | 29 | 24 |
| percent | 42% | 58% | 55% | 45% |
| mean size* | 886 | 675 | 769 | 730 |
| aggregate mean* | 750 | 751 | ||
*Clone sizes are given in square microns.
Fig. 2.
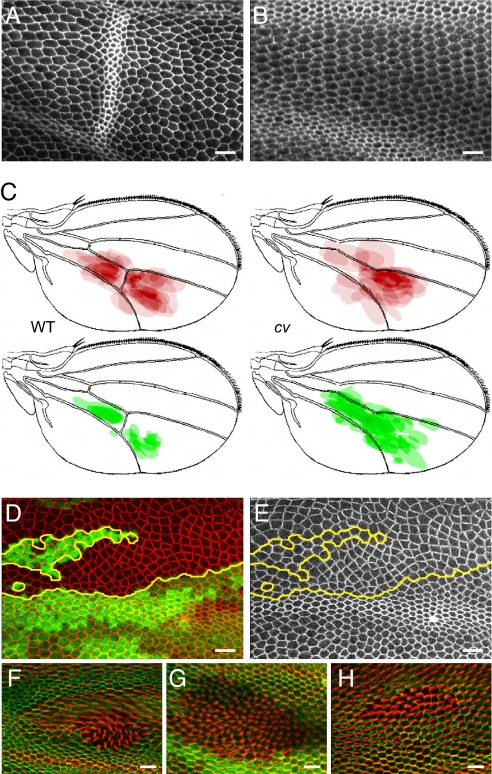
Altering cell geometry affects polarity disruption in fat clones. (A) E-cadherin staining in the region of the posterior crossvein (PCV) in a wild-type pupal wing at 33-h APF. Note that cell–cell packing around the PCV is more irregular compared to intervein regions. (B) Corresponding region of a cv1 wing of similar age, where PCV is absent. In a square region surrounding the crossvein, or its normal position in cv1 mutants, greater irregularity of cell geometry in wildtype compared to cv1 is observed, by using both measures [P = 4.6e-14 (1 tail t test) for mean of the maximum percentage area difference, and P = 3.6e-16 (1 tail t test) for mean of the maximum angle difference]. (C) Composite drawings showing the positions of all fat clones of a defined size range generated near the PCV region in either wild-type (62 clones in 20 wings) or crossveinless background (51 clones in 26 wings). Clones with polarity disruption (red); clones without polarity disruption (green). (D and E) PTEN mutant clones marked with E-cadherin::GFP (red) to display cell geometry; loss of GFP (green) marks clone locations. (F–H) PTEN fat double mutant clones show strong (F), weak (G) or no (H) polarity disruption. PTEN also causes a thickened prehair morphology. Statistically significant greater irregularity of cell geometry in PTEN/fat double mutant clones (n = 16, mean size 771 microns2) compared with fat mutant clones (n = 21, mean size 771 microns2) is observed with both measures of cell geometry [P = 3.2e-5 (1 tail t test) for mean of the maximum percentage area difference, and P = 3.1e-6 (1 tail t test) for mean of the maximum angle difference].
Crossveinless (cv) mutants lack crossveins (Fig. 2B). Cv is a homolog of Twisted gastrulation (Tsg), and like Tsg, Cv regulates the spread of BMPs, that, in the wing are required for crossvein formation (30). It would thus not be expected to directly affect PCP signaling, and indeed, cv mutants display wild-type polarity. We made a large number of fat clones in both wild-type and cv mutant backgrounds, and scored all clones within a defined size range in a region near the posterior crossvein (PCV) for the occurrence of polarity disruption. We found that eliminating the PCV, thereby making cell geometry more regular, caused a large decrease in the frequency of fat clones that produce polarity disruptions (Table 1). Furthermore, the distribution of clones having wild-type or mutant polarity revealed that in a wild-type background, clones with normal polarity are almost never found on the PCV; they show a bimodal distribution proximal and distal to the PCV and mostly between the longitudinal veins. In contrast, in a cv background, clones with normal polarity show a unimodal distribution that spans the region of the PCV (Fig. 2C). We conclude that the PCV is a barrier to the propagation of polarity, and in the absence of the global Fat signal, polarity cannot be faithfully propagated across the PCV; removing the crossvein allows a much higher frequency of correct polarity propagation across the same region of the wing. This result is consistent with the hypothesis that cell packing influences polarity.
Although there is no evidence that cv/BMP signaling directly regulates the Fz feedback loop, we sought to test this possibility by modifying cell geometry in an entirely different way. We observed that cells in PTEN mutant clones display markedly unusual cell geometries (Fig. 2 D and E), yet do not disturb planar polarity (Fig. S3). We therefore compared fat mutant clones to clones of similar size doubly mutant for PTEN and fat. Our hypothesis predicts that these clones would show more polarity disruption than control fat clones. Among the double mutant clones, we observed clones with a range of polarity disruption (Fig. 2 F and G) as well as clones with normal polarity (Fig. 2H). Consistent with the prediction of our hypothesis, we found that the double mutant clones have a higher probability of showing aberrant polarity than do fat single mutant clones (Table 1). Thus, the data argue that irregularities in hexagonal packing disrupt polarity in fat mutant clones. To reject this hypothesis, one would have to argue that both cv/BMP signaling and PTEN signaling both directly modify Fz-dependent polarity propagation, which seems highly unlikely.
Polarity Disruption is a Direct Consequence of Fz Feedback Loop Function on Irregular Cell Geometries.
We wished to provide additional evidence that cell geometry directly affects Fz-dependent polarity propagation. We also wished to determine whether the dependence of correct polarity propagation on cellular packing is a consequence of Fz-dependent feedback loop function, or whether an alternative mechanism of geometry dependence must be invoked. We have recently described a mathematical model of PCP signaling that relies solely on the assembly and interaction of Dsh, Fz, Vang, and Pk, and a global asymmetric input (14). The model captures the characteristic phenotypes resulting from perturbation of the Fz feedback loop. For example, the model recapitulates polarity propagation resulting from the domineering nonautonomy of fz or vang clones, the relative autonomy of dsh clones, and the nearly normal polarization of pk clones. The model also successfully demonstrates the propagation of polarity across cells lacking global directional information in a simulated fat clone. We have modified the model, so that rather than simulating on regular hexagonal cell arrays, we can simulate on irregular arrays representing fields of cells captured by the image analysis tool described above (see SI Appendix and Fig. S1). Because the model does nothing more than simulate the reactions in the Fz feedback loop, and irregular cell geometry is the only variable input, if cell geometry directly impacts the correct orientation of polarity propagation in fat clones, then one should be able to simulate the resulting polarity pattern—normal or perturbed—of fat clones, given their cell geometries. In contrast, if cell packing does not impact feedback loop function, the model should not recapitulate this behavior of fat clones.
To modify the model, we took advantage of the insensitivity of the original model to diffusion rate parameters by replacing the diffusion terms in the original mathematical model by their quasi-steady-state values, thereby reducing the system of governing equations into a series of coupled nonlinear ordinary differential equations. This modification reduces the computational complexity of the mathematical model and facilitates simulations by using irregular cell geometries. A further modification of the model was the inclusion of nonperiodic boundary conditions because cells on one side of an irregularly shaped cell array would not in general align with cells on the opposite side of the array. Instead, we defined a set of free boundary conditions for the cells at the edge of a simulated cell array, in which these cells extrapolate some of their concentration values from neighboring internal cells. A detailed description of the mathematical model can be found in the SI Appendix.
We selected parameters for the modified mathematical model by requiring that the model reproduce the same characteristic PCP phenotypes as the previous model, and simultaneously that it reproduce the normal or disrupted polarity phenotypes of different fat clones. The only variables in the subsequent simulations are cell geometry and the presence or absence of Fat activity in a given cell. We then predicted spatial distributions of Dsh, Fz, Pk, and Vang from a simulation by using the modified mathematical model on a cell grid extracted from a wild-type wing, and found that the predicted hair polarity, based on the final distribution of Dsh, was wild type (see SI Appendix and Fig. S4). By simulating the complete removal of Fat activity from a wing with the same geometry, it is apparent that cell geometry affects the polarity, as can be observed near veins, where cell packing is more irregular (see SI Appendix and Fig. S4 and Table S1). It is important to note that the cell geometry is the only symmetry-breaking input in this experiment.
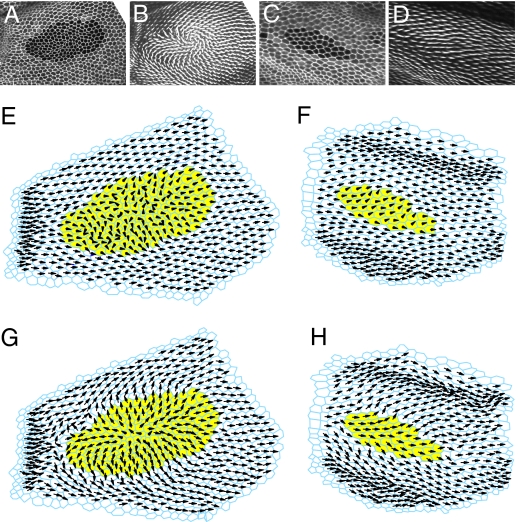
To model fat clones, we began with the observed cell geometry, and removed the directional bias from the fat mutant cells. Fig. 3 A–D show 2 of 4 fat clones used to identify parameters for the modified mathematical model. These clones were chosen to be small enough that they might, with similar probability, disrupt polarity or not. The corresponding simulations correctly exhibit whether the polarity is normal or perturbed, although the precise polarity patterns vary from those seen in vivo (Fig. 3 E and F and Fig. S5).
Fig. 3.
Fitting the mathematical model to simulate fat clone phenotypes. (A–D) Two fat clones used to identify parameters for the model, and (E–H) the corresponding simulations. Clone (GFP) and cell geometry (ZCL1792) markers (A and C) and hair polarity (B and D). Yellow cells in the simulations represent the fat mutant clone cells. Hair polarity, derived from the vector sum of Dsh protein localization is represented with direction indicating the orientation of the hair, and distance from cell centroid indicating the amount of Dsh asymmetry within the cell (E and F). Corresponding simulation results (G and H) after incorporating Fat-Ds nonautonomy.
Although these simulations predict grossly normal versus abnormal polarity, they do not precisely predict the polarity patterns observed. We considered the possibility that nonautonomous Fat-Ds signaling (26) might provide an additional signal that controls the polarity pattern within and around these clones. Inside a fat clone, the only binding partner for Ds expressed in the mutant cells touching the clone boundary is in the neighboring wild-type cells, and indeed, one sees selective recruitment of Ds at these clone boundaries (17). This accumulation of Ds might be expected to perturb Fat distribution in the wild-type cells, thereby altering the global polarity signal in these cells (see SI Appendix and Fig. S6). To test this hypothesis, we allowed both the magnitude and direction of the vector representing the global signal in the wild-type cells touching the mutant clone to be parameters in our simulations, and repeated our parameter identification under this regime. The simulations identified a global signaling vector in these cells that points away from the clone, consistent with an alteration of Fat distribution in the predicted direction in these cells. By using this parameter set, the simulations were markedly improved, showing stronger local alignment between cells, and producing a closer overall match with measured hair orientations (Fig. 3 G and H; see SI Appendix and Fig. S7 for a statistical analysis). Briefly, the difference between mean-measured and mean-simulated hair angles decreases from 42.6 to 34.1°, and the Pearson correlation coefficient increases from 0.905 to 0.957.
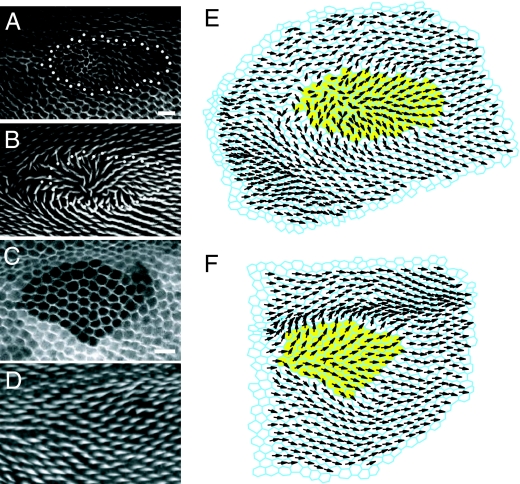
The mathematical model, incorporating Ft-Ds nonautonomy, was then challenged to simulate normal or perturbed phenotypes for four additional small fat clones that were not used in the original parameter identification for the mathematical model. This ensured that the ability of the model to match the polarity phenotypes of fat clones was not merely an artifact of the parameter selection procedure (that is, of overfitting), but rather an expected consequence of the Fz feedback loop when acting in the context of irregular cell geometries. The results show that the Fz feedback loop operating in the presence of irregular geometry can reproduce the normal or perturbed polarity of fat clones that were not used for parameter identification (Fig. 4 A–F; see SI Appendix and Fig. S5). Because in these experiments, the only independent variable is the input cell geometry, the results argue that, operating within a given cell geometry context, the polarity within these clones is strongly dependent on Fz feedback loop function.
Fig. 4.
Prediction of fat clone phenotypes with or without polarity disruption. (A–D) Two fat clones not used to identify parameters for the model and (E and F) the corresponding simulations. Clone (GFP) and cell geometry (ZCL1792) markers (A and C) and hair polarity (B and D). (E and F) Simulations of corresponding clones. Yellow cells represent the fat mutant clone cells. Prehair orientation represented as in Fig. 4. Results incorporate Fat-Ds nonautonomy.
Does Loss of Fat Disturb Cell Geometry?
It appears that fat clones may have more irregular cell geometry than control tissue. To examine this issue, we compared the cell geometry in a large sample of randomly chosen fat clones, with or without polarity disruption, with the cell geometry in corresponding regions of wild-type pupal wings marked with the same cell shape marker. As Fat is a tumor suppressor and its loss leads to over-proliferation (18), we selected clones that have no obvious overgrowth phenotype. We find a significantly larger mean of the maximum percentage area difference in fat clones compared with wild-type cells [P = 0.0019 (1 tail)], indicating that loss of Fat increases cell size variability. However, there is no significant difference in the mean of the maximum angle difference in fat clones compared with wild-type cells. Therefore, loss of fat itself may account, at least in part, for the perturbed cell geometries in clones that produce polarity disruption. The mechanism by which fat clones impair the transition to regular geometry is not known. However, we observe no fat dependent alteration of E-cadherin expression as has been observed in the wing imaginal disk (31), and Crumbs localization and levels appear normal in fat clones (not shown), implying that there is no obvious defect in junctional complex formation. One possible explanation is the excess proliferation that occurs within fat clones, as suggested by previous results (32), and this is consistent with the observation that suppression of hyperproliferation by overexpressing Warts partially suppresses the polarity disruption phenotype (33). fat clones in 18-h APF pupal wings often have higher cell density than surrounding tissue (data not shown). Although this excess of cells within fat clones is most often remedied by 24–30-h APF by poorly understood mechanisms, the excess cell division within the clone, or the subsequent compensation, may impair the transition to regular cell geometry.
Discussion
We previously proposed that PCP signaling consists of a multitiered system [Fig. 1C (3)]. This system design produces robust PCP function, and polarity errors are almost never seen in wild-type animals (17). Here, we identify an obstacle that limits the effectiveness of the Fz-mediated feedback loop alone to propagate polarity. Our data indicate that, in the absence of Fat activity, propagation of polarity across a field of cells requires regular cell packing. The local Fz feedback loop interacts with variable cell geometry to produce the observed, variable, patterning defects when Fat signaling is impaired. A nonautonomous signal mediated by the Fat-Ds system produces a perturbation of the global directional cue in wild-type cells surrounding the clone, and together with cell geometry, determines the polarity pattern in and around fat clones.
If it were not true that cell geometry could alter polarity propagation in the absence of the fat-mediated global directional cue, we would not be able to modify the frequency of polarity defects in fat clones by changing their cell geometry with PTEN or by altering veins. Neither would we be able to replicate the effects of cell geometry on PCP by simulating Fz feedback loop function on regular versus irregular cell grids. Therefore, cell geometry impacts PCP signaling.
Irregular cell geometry appears to be the primary determinant for which fat clones produce polarity defects. Absence of Fat can contribute to the irregular cell packing, although other sources of packing irregularities, such as veins and random errors, can also disrupt cell packing. This is illustrated by the finding that fat clones larger than a few cells but with normal polarity are virtually never observed to intersect the posterior crossvein, which itself produces substantial geometry disruption. Although perturbation of the global directional signal at fat clone borders contributes to the polarity patterns seen in clones, it is not sufficient to disrupt normal polarity, because many fat clones have normal polarity. Local alignment mediated by the Fz-dependent feedback loop is therefore strong enough to overcome these perturbations unless sufficiently irregular cell geometry also exists.
Several previously published observations argue that Fat transduces a directional signal and therefore does not simply affect PCP by modifying cell geometry. For example, Fat overexpression alters polarity in the wing without substantially altering cell geometry (20), and domineering nonautonomy from a Fz overexpression boundary is enhanced inside a fat mutant clone (17). In the eye, Fat srongly influences the competition between prospective R3 and R4 cells. Furthermore, the finding that simulation of fat clones was more accurate when we accounted for nonautonomous perturbation of the asymmetry signal at the clone boundaries than when this feature was omitted from the simulations argues that Fat must bias the directionality of Fz function. How Fat transduces the global directional signal is an important problem that will be the subject of additional investigation. Here, we have addressed the consequences of disabling this system, and find that the ability of the Fz feedback loop to propagate polarity is sensitive to cell geometry irregularities.
A dependence of cell packing regularity on the core PCP proteins, including Pk and Fz, has recently been observed (28). The change from irregular to regular cell packing is mediated by a Rab11- and exocyst-dependent process, and some of the core PCP proteins may modify this process (28). However, the core PCP signaling mechanism is intact in fat mutant clones, so our observed geometry defects in these clones and the consequent polarity disruption cannot result from compromised core PCP protein-dependent trafficking. Accordingly, we observe no abnormality of staining for the junctional adhesion proteins, E-cadherin and Crumbs, in fat clones.
It is also possible that absence of fat may have a direct effect on polarity that in turn affects cell geometry. Because we observe similar irregularities of cell geometry in populations of fat clones before and after the emergence of prehairs (data not shown), we do not believe that mechanical forces of aberrant hair growth cause the cell geometry defects seen in fat clones. We also note that the aberrant polarity caused by domineering nonautonomy near fz and vang mutant clones does not produce geometry defects similar to those characteristic of fat clones with disrupted polarity [Figs. 1, S1, 3, and 4; data not shown (28)]. Whereas our data argue that cell packing affects polarity propagation, we have no evidence for or against the independent possibility that fat dependent polarity defects affect cell geometry.
The inherent design of the PCP signaling network allows for a robust polarization response that depends on the combination of a diffusely distributed global directional cue and a local polarity propagation mechanism. These simple modules collaborate to overcome system disturbances such as irregular cell packing that occur randomly, or in pattern elements such as veins in the wing, and possibly other structures in other regions of the epidermis. Perturbations are ubiquitous during development, and similar principles are likely to be used by other signaling networks that function in various developmental processes.
Methods
Somatic clones were generated by inducing mitotic recombination by using the FLP-FRT method (34). Genotypes were the following: hsFLP; l (2)ftfd FRT40A/ubGFP FRT40A; ZCL1792/+
hsFLP; ftGrV FRT40A/ubGFP FRT40A
cv1/cv1; ftGrV FRT40A/ubGFP FRT40A; hsFLP, Sb/+
hsFLP, dpten1 FRT40A/ubGFP FRT 40A
hsFLP, dpten1 l (2)ftfd FRT40A/ubGFP FRT 40A; ZCL1792/+
Other fly stocks included:
w; DE-cadherin::GFP
cv1/cv1
w; ZCL1792 [ZCL1792 is a fluorescently tagged cell-junction marker (35)]
Pupal wings were prepared and stained according to (10) and viewed by using confocal microscopy.
Supplementary Material
Acknowledgments.
We thank Seth Blair (University of Wisconsin, Madison) for fly stocks and Mike Simon for useful discussions. This work was supported by the National Institutes of Health (NIH) Grants R01GM59823 (J.D.A.) and R01 GM075311 (C.J.T. and J.D.A.); DARPA BioInfoMicro and BioComp, and Stanford's Bio-X IIP (C.J.T. and J.D.A.); PHS Grant CA09302 was awarded by the National Cancer Institute, Department of Health and Human Services (D.M.); and a Burt and Deedee McMurtry Stanford Graduate Fellowship was also awarded (K.A.). Anti-DE-cadherin (Tadashi Uemura) and anti-Crumbs (Elisabeth Knust) were obtained from the Developmental Studies Hybridoma Bank.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0808868105/DCSupplemental.
References
- 1.Adler PN. Planar signaling and morphogenesis in Drosophila. Dev Cell. 2002;2:525–535. doi: 10.1016/s1534-5807(02)00176-4. [DOI] [PubMed] [Google Scholar]
- 2.Klein TJ, Mlodzik M. Planar cell polarization: An emerging model points in the right direction. Annu Rev Cell Dev Biol. 2005;21:155–176. doi: 10.1146/annurev.cellbio.21.012704.132806. [DOI] [PubMed] [Google Scholar]
- 3.Tree DRP, Ma D, Axelrod JD. A three-tiered mechanism for regulation of planar cell polarity. Semin Cell Dev Biol. 2002;13:217–224. doi: 10.1016/s1084-9521(02)00042-3. [DOI] [PubMed] [Google Scholar]
- 4.Vinson CR, Conover S, Adler PN. A Drosophila tissue polarity locus encodes a protein containing seven potential transmembrane domains. Nature. 1989;338:263–264. doi: 10.1038/338263a0. [DOI] [PubMed] [Google Scholar]
- 5.Klingensmith J, Nusse R, Perrimon N. The Drosophila segment polarity gene dishevelled encodes a novel protein required for response to the wingless signal. Gene Dev. 1994;8:118–130. doi: 10.1101/gad.8.1.118. [DOI] [PubMed] [Google Scholar]
- 6.Thiesen H, et al. dishevelled is required during wingless signaling to establish both cell polarity and cell identity. Development. 1994;120:347–360. doi: 10.1242/dev.120.2.347. [DOI] [PubMed] [Google Scholar]
- 7.Gubb D, et al. The balance between isoforms of the prickle LIM domain protein is critical for planar polarity in Drosophila imaginal discs. Gene Dev. 1999;13:2315–2327. doi: 10.1101/gad.13.17.2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Taylor J, Abramova N, Charlton J, Adler PN. Van Gogh: A new Drosophila tissue polarity gene. Genetics. 1998;150:199–210. doi: 10.1093/genetics/150.1.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wolff T, Rubin GM. Strabismus, a novel gene that regulates tissue polarity and cell fate decisions in Drosophila. Development. 1998;125:1149–1159. doi: 10.1242/dev.125.6.1149. [DOI] [PubMed] [Google Scholar]
- 10.Axelrod JD. Unipolar membrane association of Dishevelled mediates Frizzled planar cell polarity signaling. Gene Dev. 2001;15:1182–1187. doi: 10.1101/gad.890501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bastock R, Strutt H, Strutt D. Strabismus is asymmetrically localised and binds to Prickle and Dishevelled during Drosophila planar polarity patterning. Development. 2003;130:3007–3014. doi: 10.1242/dev.00526. [DOI] [PubMed] [Google Scholar]
- 12.Strutt DI. Asymmetric localization of Frizzled and the establishment of cell polarity in the Drosophila wing. Mol Cell. 2001;7:367–375. doi: 10.1016/s1097-2765(01)00184-8. [DOI] [PubMed] [Google Scholar]
- 13.Tree DRP, et al. Prickle mediates feedback amplification to generate asymmetric planar cell polarity signaling. Cell. 2002;109:371–381. doi: 10.1016/s0092-8674(02)00715-8. [DOI] [PubMed] [Google Scholar]
- 14.Amonlirdviman K, et al. Mathematical modeling of planar cell polarity to understand domineering nonautonomy. Science. 2005;307:423–426. doi: 10.1126/science.1105471. [DOI] [PubMed] [Google Scholar]
- 15.Wong LL, Adler PN. Tissue polarity genes of Drosophila regulate the subcellular location for prehair initiation in pupal wing hairs. J Cell Biol. 1993;123:209–221. doi: 10.1083/jcb.123.1.209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Adler PN, Charlton J, Liu J. Mutations in the cadherin superfamily member gene dachsous cause a tissue polarity phenotype by altering frizzled signaling. Development. 1998;125:959–968. doi: 10.1242/dev.125.5.959. [DOI] [PubMed] [Google Scholar]
- 17.Ma D, Yang CH, McNeill H, Simon MA, Axelrod JD. Fidelity in planar cell polarity signalling. Nature. 2003;421:543–547. doi: 10.1038/nature01366. [DOI] [PubMed] [Google Scholar]
- 18.Mahoney PA, et al. The fat tumor suppressor gene in Drosophila encodes a novel member of the cadherin gene superfamily. Cell. 1991;67:853–868. doi: 10.1016/0092-8674(91)90359-7. [DOI] [PubMed] [Google Scholar]
- 19.Casal J, Struhl G, Lawrence P. Developmental compartments and planar polarity in Drosophila. Curr Biol. 2002;12:1189. doi: 10.1016/s0960-9822(02)00974-0. [DOI] [PubMed] [Google Scholar]
- 20.Matakatsu H, Blair SS. Interactions between Fat and Dachsous and the regulation of planar cell polarity in the Drosophila wing. Development. 2004;131:3785–3794. doi: 10.1242/dev.01254. [DOI] [PubMed] [Google Scholar]
- 21.Simon MA. Planar cell polarity in the Drosophila eye is directed by graded four-jointed and Dachsous expression. Development. 2004;131:6175–6184. doi: 10.1242/dev.01550. [DOI] [PubMed] [Google Scholar]
- 22.Yang C, Axelrod JD, Simon MA. Regulation of Frizzled by Fat-like cadherins during planar polarity signaling in the Drosophila compound eye. Cell. 2002;108:675–688. doi: 10.1016/s0092-8674(02)00658-x. [DOI] [PubMed] [Google Scholar]
- 23.Fanto M, et al. The tumor-suppressor and cell adhesion molecule Fat controls planar polarity via physical interactions with Atrophin, a transcriptional corepressor. Development. 2003;130:763–774. doi: 10.1242/dev.00304. [DOI] [PubMed] [Google Scholar]
- 24.Hannus M, Feiguin F, Heisenberg CP, Eaton S. Planar cell polarization requires Widerborst, a B′ regulatory subunit of protein phosphatase 2A. Development. 2002;129:3493–3503. doi: 10.1242/dev.129.14.3493. [DOI] [PubMed] [Google Scholar]
- 25.Lawrence PA, Casal J, Struhl G. Cell interactions and planar polarity in the abdominal epidermis of Drosophila. Development. 2004;131:4651–4664. doi: 10.1242/dev.01351. [DOI] [PubMed] [Google Scholar]
- 26.Casal J, Lawrence PA, Struhl G. Two separate molecular systems, Dachsous/Fat and Starry night/Frizzled, act independently to confer planar cell polarity. Development. 2006;133:4561–4572. doi: 10.1242/dev.02641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Strutt H, Strutt D. Nonautonomous planar polarity patterning in Drosophila: Dishevelled-independent functions of frizzled. Dev Cell. 2002;3:851–863. doi: 10.1016/s1534-5807(02)00363-5. [DOI] [PubMed] [Google Scholar]
- 28.Classen A-K, Anderson KI, Marois E, Eaton S. Hexagonal packing of Drosophila wing epithelial cells by the planar cell polarity pathway. Dev Cell. 2005;9:805–817. doi: 10.1016/j.devcel.2005.10.016. [DOI] [PubMed] [Google Scholar]
- 29.Milan M, Campuzano S, Garcia-Bellido A. Cell cycling and patterned cell proliferation in the Drosophila wing during metamorphosis. Proc Natl Acad Sci USA. 1996;93:11687–11692. doi: 10.1073/pnas.93.21.11687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shimmi O, Ralston A, Blair SS, O'Connor MB. The crossveinless gene encodes a new member of the Twisted gastrulation family of BMP-binding proteins which, with Short gastrulation, promotes BMP signaling in the crossveins of the Drosophila wing. Dev Biol. 2005;282:70–83. doi: 10.1016/j.ydbio.2005.02.029. [DOI] [PubMed] [Google Scholar]
- 31.Jaiswal M, Agrawal N, Sinha P. Fat and Wingless signaling oppositely regulate epithelial cell–cell adhesion and distal wing development in Drosophila. Development. 2006;133:925–935. doi: 10.1242/dev.02243. [DOI] [PubMed] [Google Scholar]
- 32.Garoia F, et al. Cell behaviour of Drosophila fat cadherin mutations in wing development. Mech Dev. 2000;94:95–109. doi: 10.1016/s0925-4773(00)00306-3. [DOI] [PubMed] [Google Scholar]
- 33.Chou TB, Perrimon N. Use of a yeast site-specific recombinase to produce female germline chimeras in Drosophila. Genetics. 1992;131:643–653. doi: 10.1093/genetics/131.3.643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Morin X, Daneman R, Zavortink M, Chia W. A protein trap strategy to detect GFP-tagged proteins expressed from their endogenous loci in Drosophila. Proc Natl Acad Sci USA. 2001;98:15050–15055. doi: 10.1073/pnas.261408198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.