A Spatial Toggle Switch Drives Boundary Formation in Development

Abstract

Herein we introduce a multicellular network motif that performs as a spatial toggle switch and explains how boundary formation can be faithfully accomplished in developmental processes. Importantly, we show that expression and activity patterns of proteins must be simultaneously characterized for a proper understanding and description of the underlying mechanism. Our in silico experiments, in agreement with in vivo results, evaluate different genetic backgrounds and shed light on the dynamics of boundary formation. In addition, we provide an estimation of relevant biological parameters and a robustness analysis.

INTRODUCTION

Biological pattern formation relies on mechanisms that faithfully translate gene expression into positional information for further genetic regulation, cellular proliferation, and tissue differentiation. Thus, the link between the gene expression pattern and the resulting biological structure ultimately implies the existence of a coordinate system readable by cells (1,2). In this regard, morphogen gradients constitute a paradigm for positional signaling, and their establishment and functioning are classical issues in Developmental Biology that continue to prompt modeling of physical interest (3). Morphogens are diffusive molecules secreted by cells. Upon binding with receptors, morphogens trigger gene regulation (4). What genes are regulated and the magnitude of the regulation depends on the on-site concentration of the morphogen. As a result, morphogen gradients provide organisms with a mechanism to confer differential expression levels in spatial domains thus patterning the primordium during embryonic development. Within this framework, segmentation is the simplest patterning process one can envision. One illustrative example is the segmentation of the Drosophila embryo (5,6). At blastoderm stage (single cell), the so-called syncytium becomes patterned into stripes driven by the interactions of morphogen gradients. This pattern establishes the Drosophila body plan at later developmental stages. Many aspects of this process have been characterized including the elucidation of the gene networks that drives patterning, the engineering of artificial synthetic networks to emulate the segmentation process, and the limits to the precision of position determination (7–13). Segmentation-like patterning by means of the morphogen gradient mechanism also occurs at subsequent phases of Drosophila development where a multicellular environment, e.g., the imaginal disks, has been defined already. The imaginal disks are groups of cells that during metamorphosis from larval to adult form produce the cuticular structures of the organism, e.g., the wing (3). During the so-called compartmentalization of the imaginal disks, cell populations (compartments) become characterized and segregated in terms of a differential gene expression, and morphogen gradients are responsible for shaping the compartments and determine the cell fate (3,14,15). Recent progresses in this system include the characterization of the mechanisms of morphogen transport in epithelia, the precision of the positional information, and the quantification of relevant parameters (e.g., morphogen diffusion rates) (16–19).

A common feature in both single and multicellular patterning processes controlled by morphogen gradients is the requirement of a localized source from which morphogens are produced and released. However, a distinctive property of multicellular environments with respect to those in single cells is the existence of a specialized boundary cell population in the former (3,15,20). Boundary cells set up an effective barrier in terms of proliferation, motility, and adhesion that keep cells of different compartments segregated. Moreover, boundaries constitute the axes of the aforementioned coordinate system for the development of the body plan, and it has been suggested that they provide a link between the embryo and the adult by orienting the axes defined by those cellular populations coordinately with the rest of the animal (15). Surprisingly, the all-important question of how compartment boundaries are established has been far less investigated from the point of view of modeling (21,22) than morphogen gradient formation and functioning. Recent developments include an analysis on the stability and robustness of the gene network responsible for the dorsal-ventral (DV) boundary establishment in the Drosophila's wing imaginal disk (23). It is useful to notice that such gene network is conserved among organisms; e.g., the same regulatory network also applies to hindbrain segmentation in terms of rhombomeres during vertebrate development (24).

A powerful approach for understanding the properties and functionalities of genetic regulation is the analysis of reduced functional blocks, namely network motifs (25). In fact, crosstalk of motifs has been proved useful to clarify how spatial and temporal patterning may arise in developmental processes (26). Herein we aim at applying this formalism and obtaining a minimal multicellular network motif to explain how boundary formation can be faithfully accomplished. Much effort has been done to characterize the so-called toggle switch, a circuitry for temporal alternation of gene activities in single-cell processes (27–35). Here we introduce a spatial toggle switch where simultaneous signaling pathways are kept spatially alternated in a multicellular environment. Yet, we must first recall a simple, but nevertheless crucial, biological concept that, as shown below, is relevant for understanding how patterning during the boundary formation process arises: the difference between protein expression and protein activity. Expression simply refers to the synthesis of a protein whereas activity indicates that a protein has triggered subsequent processes. For example, if protein X induces the expression of protein Y, then measuring X concentration obviously indicates the gene X expression levels, but does not specify its activity whatsoever. However, if X is necessary for the expression of Y, then Y is an appropriate reporter of protein X activity (see Theory and Methods). The set of activities of a protein is commonly known as its signaling pathway.

To firmly ground our model on biological facts we start with an abridged description of DV boundary formation in the Drosophila wing imaginal disk (the most profusely characterized case). At third-instar larval stages during Drosophila development, the imaginal disk of the wing is segmented in dorsal and ventral compartments (3). These cell populations enable the construction of the dorsal and ventral parts of the wing blade. The boundary cell population physically separates those regions, operates as a morphogen signaling center, and constitutes the margin of the wing blade in the adult (see Fig. 1). A distinctive feature of boundary cells in such process is a complex crosstalk between two pathways, those of Notch (36) and Wingless (37). More precisely, boundary cells characteristically exhibit the sustained expression and activity of transmembrane receptor Notch, and the expression, but not the activity, of morphogen Wingless (Wg) (38). Those species are respectively responsible for short- and long-range signaling by means of the following mechanism. Notch is expressed by compartments' cells at basal level, and upon intercellular binding with ligands (transmembrane proteins) of neighboring cells (short-ranged signaling), e.g., Delta or Serrate ligands, accomplishes further regulatory tasks, i.e., activities. In particular, Notch induces its own expression as well as the expression of Wg once the expression level of the former surpasses a threshold (39). Porcupine protein then helps Wg molecules to be secreted from cells (40). Once the morphogen is in the extracellular space it diffuses and binds to membrane receptors of cells (Frizzled protein) that transduce its signal (41). This process provides compartments' cells with a long-ranged signaling mechanism. The Wg signal induces expression of Notch ligands, particularly in cells neighboring the boundary, thus closing a positive feedback loop that helps to increase transiently the expression and activity of Notch receptor in boundary cells. However, this positive input to Notch pathway has a side effect: Disheveled (Dsh), a cytoplasmatic mediator of Wg signaling pathway, becomes accumulated and operative if the levels of the morphogen exceed a threshold. This, in turn, represses Notch activity (42). Therefore, as recently demonstrated, for a stable and robust boundary formation, boundary cells must themselves become refractory to Wg signal, namely, they must be blind to its activity (23). Refractoriness is conferred by the transcription factor Cut that is expressed and translocated to the nucleus once Notch expression surpasses another threshold above that of Wg that triggers the expression of the morphogen (43). This complex set of interactions translates into precise patterns of expression and activity summarized as follows (see Fig. 2; see also Fig. 3 in (23)): in boundary cells, Notch expression and activity are operational, whereas Wg expression (respectively, activity) is kept active (respectively, inactive); contrariwise, in neighboring cells adjacent to the boundary Notch expression and activity are inhibited, whereas Wg expression (activity) is inactive (active). These patterns strikingly illustrate that a correct understanding of the crosstalk between signaling pathways requires a multicellular network motif approach that simultaneously characterizes expression and activity. Such double pattern constitutes the final stage of the developmental process we aim to model.

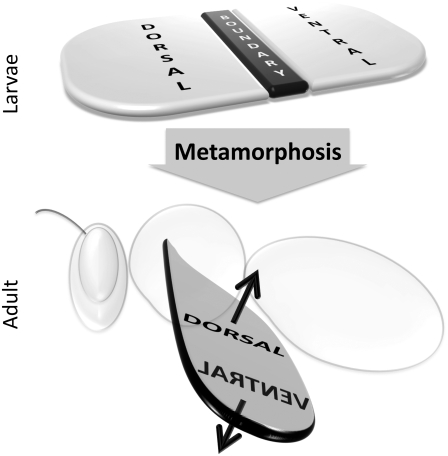
FIGURE 1.

The imaginal disk of the wing (top) elicits the formation of the wing blade of the adult organism (bottom) during metamorphosis. The former is segmented in dorsal and ventral compartments that produce the dorsal and ventral parts of the wing blade. The boundary cell population separates the compartments, serves as a morphogen signaling center, and generates the margin of the wing blade at subsequent developmental stages.

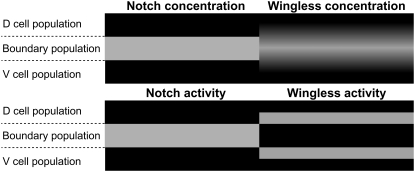
FIGURE 2.

Schematic representation of the concentration (top) and activity (bottom) patterns of Notch (left) and Wg (right) once the DV boundary has been established in the Drosophila wing imaginal disk. In boundary cells, Notch expression and activity are operational, whereas Wg expression (activity) is kept active (inactive); in neighboring cells adjacent to the boundary, Notch expression and activity are inhibited, whereas Wg expression (activity) is inactive (active). This double pattern is the trademark of boundary formation.

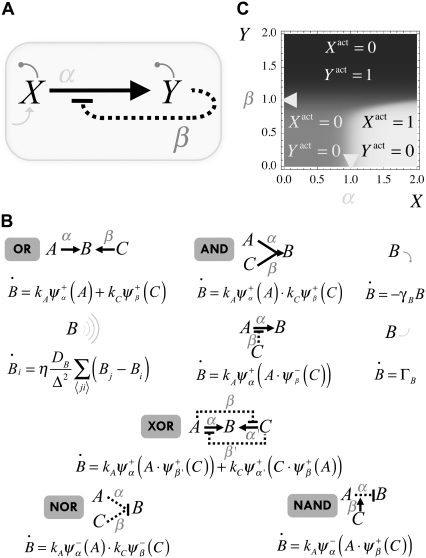
FIGURE 3.

(A) Single-cell protein network: X induces Y expression that in turn represses the activity of X. In addition, X is autonomously expressed and both species degrade. A mathematical representation of this and other networks, including that of Fig. 4, can be obtained by means of the rules shown in panel B. The correspondence between some interactions and logical functions has been also indicated in panel B. (C) Density plot of the relative activity, Δ_XY = X^activity – Y^activity, as a function of the expression levels of X and Y. The value of the cooperativity has been set to n = 10. The location of the thresholds (α = β = 1) is indicated by arrows. Three different regimes of activities are represented as a function of the expression levels: full X/null Y activities (white), null X/full Y activities (black), and null X/null Y activities (gray).

More specifically, we intend to address the following issues:

1. To propose a minimal network motif and a modeling approach that accounts simultaneously for dynamical patterns of expression and activity in boundary formation.

2. To clarify the role played by different interactions in the patterning by means of mutant analysis.

3. To characterize the robustness of the motif in terms of its parameters.

THEORY AND METHODS

Modeling approach: a single-cell example

To illustrate our modeling approach we first consider a simple single-cell problem. We choose it in such a way that is constructed with the two basic types of regulations employed later on in our DV model scheme. This will show the basic rules for defining interactions between proteins, the derivation of the equations that dictate the dynamics of their expressions, and also the characterization of their activities. Later, we extend this formalism to the problem of our interest, boundary formation, by introducing a multicellular description.

Let us consider a protein, X, that is autonomously expressed and degraded. The activity of this protein consists, depending on its expression level, in inducing the expression of another protein, Y, which is also degraded. In turn, the activity of protein Y consists in repressing that of X (see Fig. 3 A), but not X expression itself. In our modeling, we use an effective approach and disregard intermediate species in transcription-translation processes. Thus, X and Y characters in Fig. 3 A account for protein concentrations. By disregarding transcriptional processes and other molecular and cellular details (e.g., phosphorylation events, cell cycle, and divisions), we clearly set the limitations of our modeling.

Positive and negative regulations between proteins are symbolized by means of thick solid (induction) and dotted (repression) lines, respectively. The graphical description is complete by including basal expression levels of X (thin solid arrow) and degradation of both species (thin circle-finished lines). Positive and negative regulatory interactions are modeled by dimensionless functions 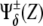that, in terms of the concentration, Z, and a threshold, δ, asymptotically behave as

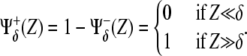In Fig. 3 A the interactions driven by X and Y are identified by symbols α and β that also indicate the threshold values of the regulatory functions. Logical gates providing a binary response (Boolean approach) are the simplest functional form for 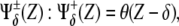θ(·) being the Heaviside step function. More realistically, Hill functions, 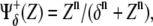have been reported in gene expression experiments for protein regulation, n being the so-called cooperativity exponent (44). We note that in our in silico experiments of the multicellular network we use Hill functions, whereas the Boolean approach is only employed for the analytical treatment of the model (see below).

The graphical representation depicted in Fig. 3 A can be translated into a mathematical model by using the rules illustrated in Fig. 3 B. These rules are general and include interactions that can be relevant in a multicellular motif, e.g., diffusion. Fig. 3 B also describes the correspondence between some interactions and logical functions, e.g., XOR. Importantly, we show the interactions that lead to the universal logical functions NOR and NAND from which all logical functions can be derived (45).

Thus, the dynamical equations for the expression levels of the species in Fig. 3 A become

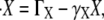(1)

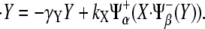(2)

On the other hand, the activity of a species (pathway) can be estimated in a [0,1] scale by averaging all its regulatory interactions toward other species both positive and negative, i.e., thick lines departing from a species. Note that a negative regulation due to a species Z must be taken into account as 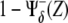when evaluating the pathway of Z, otherwise the larger the Z, the smaller would be the contribution to its pathway. However, this rule does not apply when a negative interaction due to Z is within the argument of the regulatory function due to other species, e.g., when evaluating the pathway of species Z′. In this case, the contribution of the species Z must be simply taken as 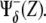Therefore,

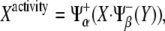(3)

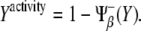(4)

Note that X expression level, Eq. 1, does not depend on Y expression level, whereas X activity, Eq. 3, relies on Y expression level. Contrariwise, Y expression level, Eq. 2, is a function of X expression level while Y activity, Eq. 4, is not. Therefore, this simple scheme perfectly stresses the aforementioned difference between those two concepts. A comprehensive analysis of the simultaneous characterization of activity and expression can be performed by means of the function Δ_XY = X^activity – Y^activity. This function is bounded between the values −1 (full Y pathway activity and complete repression of X pathway) and +1 (converse case). By representing Δ_XY as a function of the levels of X and Y we can shed light on how activity is driven by expression levels and reveal the potentialities of the cell's behavior that are conferred by the network motif. Fig. 3 C shows Δ_XY for the unicellular network motif by means of a density plot: black/white stands for Δ_XY = −1(+1). Three different regions can be distinguished in that plot, representing three characteristic functional regimes of X and Y pathways. All these regimes are indeed accessible by tuning the parameters of the model, i.e., changing the expression levels of X and Y. As shown below, this kind of analysis will be particularly useful for examining the behavior of the multicellular motif we propose for boundary formation.

Boundary formation: multicellular network motif

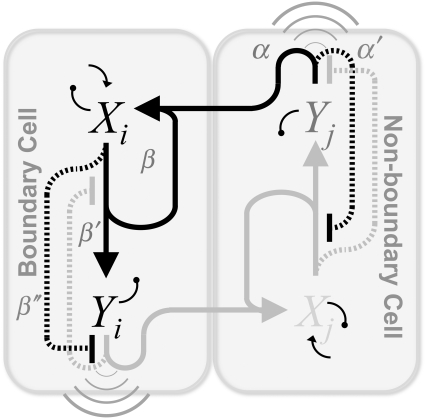
We now apply our formalism to the boundary formation problem and, by including the main interactions that have been described in the literature, we propose a motif and derive its mathematical formulation. This requires a multicellular extension since that problem involves short- and long-ranged interactions between cells: receptor-ligand binding and diffusion of the morphogen, respectively. According to the description provided in the Introduction, two main actors and their pathways drive boundary formation, namely Notch, X, and Wg, Y. Fig. 4 represents a boundary and a neighboring nonboundary cell where the proposed protein network motif for boundary formation is shown. Note that the same circuitry applies to both cells, i.e., they are genetically identical. In this case, we also depict the expected values of the concentration and the activities in the steady state by using different gray intensities for both the interaction lines and the lettering (see Fig. 4 legend). Three main actions, i.e., activities, derive from Notch (irrespectively those are operative or not): the expression of receptors (β line) and Wg (β′), and the repression of the Wg pathway via Cut (β″). On the other hand, Wg induces the expression of ligands (α) and partially inhibits Notch pathway (α′) via Dsh. In addition to the basal expression levels of Notch receptor and the degradation of both species, morphogen diffusion (wavelike symbol) has been also included. Notice that binding between expressed Notch receptors (β) and its ligands (α) in neighboring cells have been taken into account too. As in the case of Fig. 3, in Fig. 4 the symbols α, α′, β, β′, and β″ that identify the interactions also indicate the threshold values of the regulatory functions. According to experimental results (23,38,39,43), β < β′ < β″ and α < α′.

FIGURE 4.

Multicellular protein network leading to boundary formation. The main interactions between species have been included (see text). In the steady state Notch, X, pathway, i.e., lines departing from X, is active in boundary cells (dark) whereas Wg, Y, pathway is nonactive (light). The opposite occurs in neighboring nonboundary cells. This activity pattern (spatial toggle switch) is driven by the concentration pattern of Notch and Wg as indicated by the color intensity of the letters X and Y dark/light corresponds to high/low concentrations. The mathematical representation of this spatially extended motif can be obtained by using the rules shown in Fig. 3 B.

By applying the rules shown in Fig. 3 B, the graphical representation depicted in Fig. 4 can be described in mathematical terms. Thus, the dynamical equations for the concentration levels at a given cell, i, become

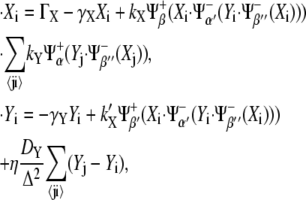(5)

where Δ stands for the lattice spacing (cell size), the sums run over the nearest neighbors j of cell i, and η is a parameter that depends on the lattice geometry: η = 1 (2/3) for a square (hexagonal) lattice.

As for the activities of X and Y, the average of their interactions leads to

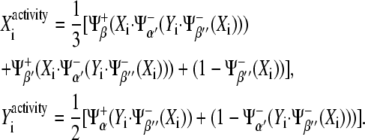(6)

Numerical simulations scheme and model parameters

Numerical simulations are implemented by means of a standard forward time-centered space Euler scheme with temporal step 10⁻³ (in units of degradation rates, see below). The in silico primordium comprises 1500 cells (two-dimensional). As for boundary conditions, we use periodic boundary conditions and check that this choice does not introduce any artifact. As for the initial condition, we choose 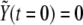for all cells and 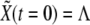(basal levels) for all cells except for two adjacent cells for which 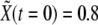(see below definition of dimensionless quantities). The initial configuration mimics the initial condition for boundary formation at early developmental stages of the Drosophila wing primordium, particularly at the DV edge due to the activity of the gene Apterous (46).

Dimensionless concentrations and thresholds (denoted by overtildes throughout the text) are given in units of β″. For the sake of simplicity, in our modeling we assume that γ_X = γ_Y = γ and k_X · k_Y = k′_X = k. In addition, we use dimensionless variables for time and space (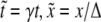) and define the following dimensionless parameters: κ = k/(γβ″); Λ = Γ_X /(γβ″); and D = D_Y/(Δ²γ).

Recent experimental results quantified some of the parameters of our modeling while others helped to constrain their values between some limits (17,23). Thus, guided by those studies we perform the numerical simulations exploring the following parameter space: γ = 10⁻³ s⁻¹; α = β = 4 · 10² molecules/cell; α′ = β′= 6 · 10² molecules/cell; β″ = 10³ molecules/cell; Δ = 2.6 μm; k ∈ [0.5,30] molecules/(cell · s); Γ ∈ [10⁻², 5 · 10⁻¹] molecules/(cell · s); and D_Y ∈[1.4 · 10⁻³, 7 · 10⁻²] μm²/s. This choice fixes the dimensionless values 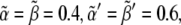κ ∈ [0.5,30], Λ ∈ [0.01,0.5], and D ∈ [0.2,10].

RESULTS

Activity versus expression: spatial toggle switch

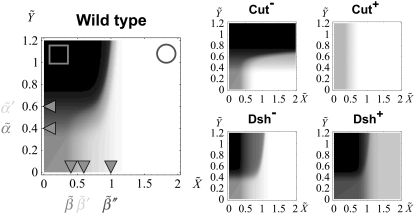
Fig. 5 shows Δ_XY = X^activity – Y^activity for in silico experiments of the wild-type case, the expressions in Eq. 6, and also for other genotypic backgrounds discussed below. Remarkably, a spatial toggle switch, the basic motif of our genetic network for boundary formation, is guaranteed if, and only if, the Δ_XY plot presents distinct zones of Notch and Wg activities as a function of their expression levels, i.e., black and white regions. This indicates that every single cell has the potentiality of switching between different behaviors as the concentration levels of Notch and Wg vary. The boundary cell population advantageously benefits from this potentiality to set the boundary and pattern neighboring regions. According to experimental results (23,38,39,43), boundary cells are characterized by high levels of both Wg (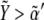) and Notch (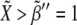): see top-right corner in the Δ_XY graphs of Fig. 5. On the other hand, neighboring nonboundary cells are characterized by high levels of Wg (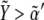) and low levels of Notch (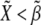): see top-left corner. Threshold values in Fig. 5 are 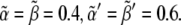Therefore, these studies indicate that the transition between regions of activity must occur as Notch expression levels, 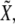vary by keeping high expression levels of Wg (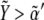). That is indeed the case of the in silico wild-type genotype shown in Fig. 5: moving from the circle region to the square region (that is, changing Notch expression levels) causes a switch in the activity. Note also that such transition is quite sharp. In terms of Δ_XY, this is the graphical signature of the spatial toggle switch leading to boundary formation.

FIGURE 5.

Density plot of the relative activity, Δ_XY, as a function of Notch and Wg levels: black/white indicates full Wg/Notch activity. Left panel stands for the in silico wild-type genotype. The circle and square illustrate the concentration levels in boundary and nonboundary cells respectively (see text). From top to bottom and from left to right, the right panels stand for Cut lack-of-function, Cut overexpression, Dsh lack-of-function, and Dsh overexpression backgrounds, respectively. The locations of the thresholds have been indicated as a guide to the eye; n = 10 in all cases.

Mutant backgrounds

Comparison with different genotypic backgrounds provides useful information on the role played by different regulatory interactions. In practice this supposes to strengthen (overexpression experiments) or weaken (lack-of-function experiments) a branch, or set of branches, departing from X (Notch) or Y (Wg) in Fig. 4, independently of the value of these species. More specifically, overexpression can be mimicked in our model by imposing the corresponding regulatory interaction, either positive or negative, as 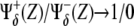independently of the argument Z. By disregarding the value of Z, we assume an autonomous (i.e., nonregulated by the network circuitry) effect of the overexpressed species. Similarly, lack-of-function mutant experiments can be implemented by setting 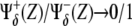as positive/negative regulatory interactions. Proper functioning, i.e., correct patterning, of the network depends on the cooperative effect of the negative interactions between Notch and Wg pathways. Thus, herein we focus our analysis on the role played by Cut (β″) and Dsh (α′). According to the aforementioned graphical signature of the spatial toggle switch, simple visual inspection of Fig. 5 reveals that Cut and Dsh overexpression experiments, and Cut lack-of-function mutants, are not able to induce boundary formation in our modeling since no transition between white and black regions of activity can be obtained varying Notch expression levels, X, while keeping high Wg levels, Y. Interestingly, Dsh lack-of-function mutants do allow for boundary formation, albeit the transition between domains of activity is smoother than in wild-type genotypes. Sharp transitions are related to the robustness and reliability of the switching mechanism (47). Actually, our in silico experiments show that Dsh lack-of-function mutants show boundary formation but ectopic boundaries develop (see Data S1 in the Supplementary Material, and Discussion, below).

Phase diagram and robustness analysis

Plausibility of a biological mechanism lies in its robustness to parameter variation. We address this important issue in the context of boundary formation by estimating a phase diagram in the parameter space (both analytically and numerically) that determines the region where the correct pattern for boundary formation is obtained (see Fig. 2). Such a phase diagram allows us to compute the robustness to parameter variation as discussed below. Our theoretical analysis makes use of a Boolean approach for regulatory interactions. The main result of this analysis is that the model parameters for proper functioning (i.e., correct patterning) of the spatial toggle switch are restricted to the inequalities (see Data S1 for derivation):

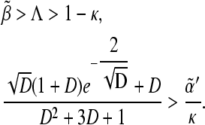(7)

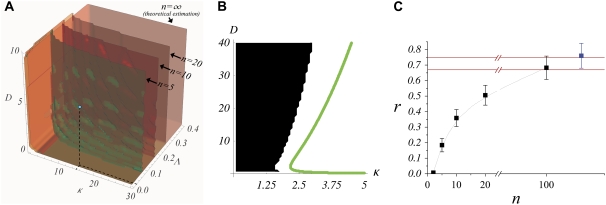
To validate these results in a more general and realistic scenario we perform extensive numerical simulations using Hill regulatory functions with finite cooperativity. Parameter sampling, for a given value of the cooperativity, is implemented by means of ∼2 · 10⁵ numerical simulations, i.e., different parameter sets. For each of them, we check the stability and uniqueness of the boundary. This procedure allows us to construct a numerical phase diagram and compare with the analytical results given by the expressions in Eq. 7. Our simulations explore the aforementioned parameter space (see Theory and Methods). In Fig. 6 A, we compare several numerical phase diagrams (Hill regulatory functions with different values of the cooperativity) with the theoretical estimation (Boolean regulatory functions) given by the expressions in Eq. 7 in the parameter space κ – Λ – D (binding rate, receptor basal expression rate, and Wg diffusion, respectively). The region of parameters for stable and unique boundary formation is defined, depending on the value of n, by the volume confined by the corresponding surface depicted in Fig. 6 A (from back to front, i.e., decreasing Λ; from left to right, i.e., increasing κ; and from bottom to top, i.e., increasing D). The blue dot in Fig. 6 A illustrates a set of parameters that, at least if n ≥ 5, leads to the right patterning since it is located inside the volume previously mentioned. For the sake of clarity, in Fig. 6 B we show a cross section of that volume for which Λ is constant. We point out that by keeping constant D and κ, and surpassing the phase diagram boundary by moderately increasing Λ, (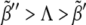) still leads to spatial toggle switching but multiple boundaries develop. If such increasing is excessive (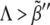), no boundary is produced at all. These results indicate that a combined effect of basal expression levels and the regulatory interactions, especially that of Dsh, are responsible for a stable and unique boundary formation. As expected, when the cooperativity is large, theoretical and numerical computed surfaces become close since Hill functions tend to Heaviside functions. Of the three sections of the phase diagram in Fig. 6 A, the D-κ cross section reveals the most interesting behavior (see Fig. 6 B). In that figure, the green line corresponds to the theoretical estimation whereas the numerical results are shown in black and white (no boundary formation and boundary formation regions, respectively). The value of the cooperativity for numerical simulations in Fig. 6 B is n = 10. As discussed below, such nonmonotonous behavior implies biological consequences.

FIGURE 6.

(A) Phase diagram in the parameter space for boundary formation: numerical simulations and theoretical estimation. As a function of the parameters D, κ, and Λ the different surfaces (depending on the value of n) delimit the region that lead to a correct patterning for boundary formation (see text). The blue dot indicates the parameters used in numerical simulations in Fig. 7. (B) Detail of a D-κ cut of the phase diagram at the blue point highlighted in panel A (Λ = 0.02). (C) Robustness to parameter variation as a function of the cooperativity. Black/blue squares correspond to numerical simulations where Hill/Boolean regulatory functions were respectively used. Red solid lines stand for the bounds calculated analytically as n → ∞ (see Data S1 for calculation).

Finally, robustness to parameter variation, r, can be estimated as the ratio between the volume where toggle switch is obtained within the phase diagram, V_boundary, and the total explored volume, V_total. The inequalities defining the phase diagram allow us to compute analytically this ratio for the Boolean approach: 0.67 < r < 0.75 (see Data S1 for calculation). As shown in Fig. 6 C, our numerical simulation results using Hill functions reveal that cooperativity plays indeed a major role: the larger the n (more tightly regulated interactions), the larger the robustness. Thus, the value of r estimated in the theoretical calculations when using Boolean regulatory interactions sets an upperbound for the robustness of the motif under realistic conditions in terms of n: ∼70%.

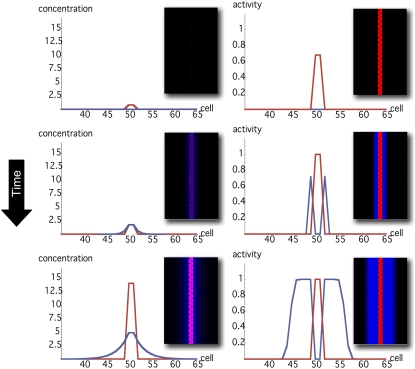
Boundary formation dynamics

An added value of our model is that it reproduces the dynamics that leads to boundary establishment. Fig. 7 shows snapshots of the evolution of both, the concentration and the activities levels of Notch and Wg in one- and two-dimensional numerical simulations (see Movie S1 in the Supplementary Material). The initial configuration mimics the initial condition at the DV edge due to previous developmental modules that seeds the location of the boundary: onset of Notch expression due to Apterous activity. Evolving from such initial condition and numerically integrating the expressions in Eq. 5, the activity and expression patterns of Wg and Notch reach a steady state, the boundary is generated, and the morphogen gradient becomes established. The latter provides positional information to cells in the in silico primordium. Note also that regardless of the fact that Wg expression levels are high in boundary cells, the morphogen activity is null in those cells. This double pattern of concentration and activity in the in silico primordium is in agreement with experimental results as sketched in Fig. 2 (see also Fig. 3 (23)).

FIGURE 7.

Snapshots of both the concentrations (left) and the activities (right) of Notch (red) and Wg (blue) in a typical evolution of the boundary formation process (top, initial condition; bottom, steady state). Main panels/insets show results of in silico experiments in one and two dimensions. The dimensionless parameters for these simulations were κ = 15, D = 6, Λ = 0.02, and n = 10 (blue dot in Fig. 4 A). Threshold values are as indicated in the Theory and Methods section.

DISCUSSION

Let us comment first on our results corresponding to lack-of-function and overexpression mutant backgrounds. These experiments are a crucial technique in Developmental Biology to elucidate the role of different regulatory interactions and indeed constitute a benchmark to test the realism of modeling approaches. In this regard, we notice that our results in terms of activity-expression landscapes are in agreement with in vivo experimental observations showing that:

1. Cut overexpression or lack-of-function experiment lead to boundary suppression (23) (recall that our analysis in terms of expression-activity, Fig. 5, indicates that these mutants are not able to generate a boundary).

2. If Dsh is overexpressed before the DV margin has started to develop, the boundary is frequently lost (42) (our in silico expression-activity profiles also indicate that no boundary is induced in this mutant background).

3. In Dsh lack-of-function mutants, bristles (a phenotypic characteristic of the boundary) may appear off the margin (48). (In Fig. 5 we show that this mutant can potentially lead to boundary formation but the switch between regions of activity is not as sharp as in the in silico wild-type case. This in fact produces ectopic boundaries; see Data S1 for in silico experiments of this genotype.)

Another important way to check the truthfulness of proposed biological mechanisms by means of modeling approaches is the adaptability of biological systems to parameter variation. Here we have addressed this topic by estimating analytically and numerically a phase diagram in the parameter space and also the robustness. As for the analytical results, several points are noteworthy about the expressions in Eq. 7. First, note that only if 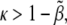can the first inequality be satisfied. Thus, a minimum rate for biochemical signaling, including binding between receptors and ligands is required (49). Second, morphogen diffusion, D, also enforces a limiting rate for biochemical signaling κ > κ_α(D) = 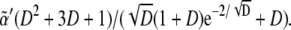As the threshold for Dsh expression, 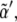decreases, κ_a(D) becomes smaller. In the limit 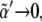then κ_a(D) → 0, thus posing the question of the role and necessity of Dsh interaction for obtaining a spatial toggle switch. Such question has been answered when analyzing the Dsh lack-of-function backgrounds in terms of concentration-activity landscapes: Dsh promotes the robustness and reliability of the switching mechanism (see Data S1). Other consequences can be extracted from the phase diagram. A qualitative result worth stressing is that when varying the cooperativity exponent the region that leads to boundary formation shows a strong dependence on the value of the receptor basal expression: the larger the cooperativity the larger the value of Λ that allows for boundary formation. Note also (see Fig. 6 B) the nonmonotonic behavior of D versus κ for a given value of Λ: the smaller the binding rate, the larger the sensitivity to diffusion since the interval of diffusion values that lead to boundary formation shrinks. These results admit a simple yet enlightening interpretation. Concerning the effect of cooperativity, as the latter increases, interactions are more tightly regulated since they provide a binary (Boolean) response to the regulatory inputs. This allows for higher levels of basal expression rates until binary gates switch. Consequently this extends the parameter region in terms of the basal expression rate still securing proper functioning of the network. On the other hand, when κ is small and consequently Wg expression levels are small too, the role of morphogen diffusion becomes more critical. Tiny diffusion coefficients are unable to propagate the morphogen, whereas very large diffusion rates lead to (effectively) null morphogen concentrations everywhere (see Data S1 for the analytical expression of the morphogen concentration in boundary and nonboundary cells).

In addition, the phase diagram provides a geometrical interpretation of the robustness concept. According to this definition, the robustness is not an absolute observable since it depends on the parameter space that is explored. Our analytical and numerical results cover, based on experimental results, a wide range of biological plausible values and estimate that the robustness of the proposed network motif has an upperbound of ∼70%. We acknowledge that comparison between experimental and simulation results in terms of the robustness parameter as a function of n is not possible. The main reason is the lack of experiments measuring the effective cooperativity of the interactions between Wg and Notch pathways. However, the Wg signaling pathway has been profusely characterized from reception to nuclear translocation of its active form (37). That is also the case of the Notch signaling pathway (36). These studies reveal a large number of intermediates regulating the Wg-Notch pathways interaction. It is easy to see that every intermediate, i.e., species, contributes by increasing the effective cooperativity, thus suggesting a robust mechanism for boundary formation.

Finally, the patterning dynamics explains how morphogen gradient profiles becomes established and indicates that the onset of Notch expression and activity is amplified and stabilized in a nontrivial way since:

1. Boundary and neighboring nonboundary cells are patterned differently in terms of expression and activity thus determining the boundary cell population.

2. Wg and Notch pathways must tightly regulate themselves in combination with basal expression levels to avoid the formation of new boundaries.

3. This dynamics is robust to parameter variation.

In summary, we have proposed a simplified, yet novel and generic, modeling scheme for spatially extended network motifs. We emphasize that full understanding of the underlying mechanisms can only be achieved if both expression and activity patterns are properly characterized simultaneously. With that in mind, herein we have addressed the problem of boundary formation inspired by the corresponding developmental process of DV compartmentalization in the Drosophila wing imaginal disk. However, our approach can be easily applied to other situations where cellular interactions drive the gene activity/expression dynamics. This may open new perspectives toward a better understanding of cellular communication and differentiation processes that are crucial in Developmental Biology.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.