Measuring internal friction of an ultrafast-folding protein

Abstract

Nanosecond laser T-jump was used to measure the viscosity dependence of the folding kinetics of the villin subdomain under conditions where the viscogen has no effect on its equilibrium properties. The dependence of the unfolding/refolding relaxation time on solvent viscosity indicates a major contribution to the dynamics from internal friction. The internal friction increases with increasing temperature, suggesting a shift in the transition state along the reaction coordinate toward the native state with more compact structures, and therefore, a smaller diffusion coefficient due to increased landscape roughness. Fitting the data with an Ising-like model yields a relatively small position dependence for the diffusion coefficient. This finding is consistent with the excellent correlation found between experimental and calculated folding rates based on free energy barrier heights using the same diffusion coefficient for every protein.

Despite the complexity of the protein folding process, the kinetics and mechanisms of folding can be usefully and accurately described by diffusion over barriers on a low-dimensional free-energy surface (1–5). For ultrafast-folding proteins, the barriers are small and the rates may be affected by the variation of the diffusion coefficient along the reaction coordinate. In addition to solvent friction, the diffusion coefficient is determined by internal friction, which reflects the “roughness” of the energy landscape that arises from drag because of intrachain interactions and escape from local minima on the energy surface (1, 4, 6, 7). Both theoretical studies (1, 8) and simulations (4, 9, 10) indicate that the internal friction depends on position along the reaction coordinate, but there have been no experiments that address this important issue in the physics of protein folding. In this work, we obtain a quantitative measure of the contribution of internal friction to the dynamics of folding from experiments on the viscosity dependence of the kinetics for the ultrafast-folding villin subdomain. Fitting the data with an Ising-like theoretical model, moreover, yields information on the position dependence of the diffusion coefficient. Unlike all previous studies of the viscosity dependence of protein-folding kinetics (11–17), we carried out experiments under conditions where there is no effect of the viscogen on the equilibrium thermal unfolding, as was done in a previous study of α-helix and β-hairpin formation (18).

For barriers >∼ 3RT separating folded and unfolded states, Kramers theory (19) predicts that the relaxation rate, 1/τ, is given by:

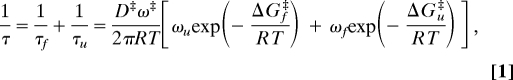where τ is the relaxation time, τ_f and τ_u are the folding and unfolding times, ΔG_f^‡ is the free energy barrier to folding, ΔG_u^‡ is the free energy barrier to unfolding, R is the gas constant, T is the absolute temperature, (ω_u)² is the curvature in the unfolded free energy well, (ω_f)² is the curvature in the folded free energy well, (ω^‡)² is the curvature at the (inverted) barrier top, and D^‡ is the diffusion coefficient at the barrier top, the important dynamical variable. For simple barrier-crossing processes, D^‡ = RT/ζ, where the friction coefficient, ζ, is proportional to the solvent viscosity, η, so a plot of τ vs. η should be linear with zero intercept. The crucial assumption in determining the viscosity dependence is, of course, that the viscogen does not alter the free energy surface, but only changes the observed relaxation rate through its effect on the dynamics of motion on the surface, namely D^‡.

In all but one of the previous protein folding studies a chemical denaturant was used to counter the increase in stability caused by the viscogen and thereby maintain a constant equilibrium population of folded to unfolded molecules (equal to τ_u/τ_f) (11–13, 15–17). The use of denaturant to maintain a constant equilibrium population ratio does not guarantee that the free energy surface, defined by the 5 parameters of Eq. 1 (ΔG_f^‡, ΔG_u^‡, ω_u, ω_f, ω^‡), and, therefore, the kinetics remain unaffected. Moreover, the recent work of Schuler and coworkers shows that chemical denaturant significantly increases the diffusion coefficient for chain motion (20), which had been assumed in previous studies to be influenced only by solvent viscosity. This acceleration of conformational diffusion can have a significant effect on the interpretation of the viscosity dependence of the observed kinetics. In the one study that did not employ denaturant, the stability was unaffected by viscogen over a temperature range of just a few degrees (21), indicating that the viscogen affects the equilibrium enthalpy of folding and therefore alters the free energy barrier height from a change in the activation enthalpy. Thus, there have been no previous studies of protein folding kinetics in which the changes in measured relaxation rates are due exclusively to changes in solvent viscosity, so the reported viscosity dependencies must be viewed as qualitative results.

Results and Discussion

Equilibrium and Kinetic Data.

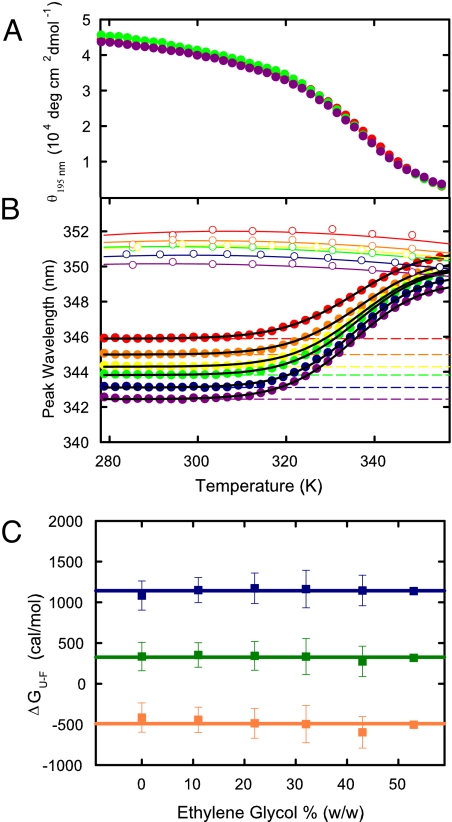
After trying several viscogens, including glycerol and glucose, we found that ethylene glycol increases the solvent viscosity by up to a factor of 3 without altering the thermal unfolding curve of the villin subdomain (Figs. S1 and S2). Fig. 1 shows that the thermal unfolding curves measured by natural circular dichroism are superimposable(Fig. 1A). For thermal unfolding measured by tryptophan fluorescence there is a shift in the peak position of the spectrum upon unfolding, so the effect of the viscogen on stability was determined by fitting the spectral shift data with a 2-state model to obtain an apparent equilibrium constant, K, at each temperature (Fig. 1B). The absence of any effect on K at each ethylene glycol concentration is demonstrated in Fig. 1C, which shows the free energy changes calculated from −RTlnK at each temperature where the kinetics were studied. The largest deviation from the average is 106 cal/mol. This corresponds to a maximum uncertainty (assuming a linear free energy relation) in the relaxation time τ of ±exp(ΔΔG/RT) = ±16%. Most deviations are <30 cal/mol, corresponding to variations in the relaxation time of ±5%. Importantly, none of these small deviations are systematic, indicating that the differences are due to experimental error and not a change in protein stability with ethylene glycol concentration.

Fig. 1.

Equilibrium thermal unfolding measured by natural circular dichroism and tryptophan fluorescence. (A) Ellipticity at 195 nm versus temperature at 0% (red), 32% (green), and 53% (violet) ethylene glycol (wt/wt). (B) Peak wavelength of tryptophan fluorescence versus temperature at 0% (red), 11% (orange), 22% (yellow), 32% (green), 43% (blue), and 53% (violet). In calculating the populations of folded and unfolded states in a 2-state analysis, the peak wavelength of the folded state (dashed lines) was assumed to be independent of temperature, as suggested by the data at temperatures <305 K. The peak wavelength for the unfolded state (upper set of continuous curves through open circle experimental points) was assumed to correspond to that of the peptide fragment: AcWKQQH, after multiplying the measured curves by factors between 0.986 and 0.990 to optimize the fit. The continuous curves through the data are the results of the 2-state fit. (C) Equilibrium free energies at 50 °C (blue), 60 °C (green), and 70 °C (orange) as a function of ethylene glycol concentration. The lines represent the mean value at all ethylene glycol concentrations at each temperature. Error bars are standard deviations from triplicate equilibrium experiments.

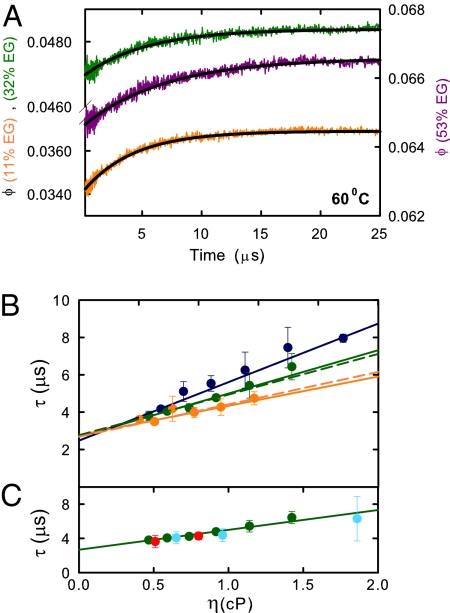
Fig. 2 shows the relaxation times of the villin subdomain as a function of viscosity following temperature jumps to 3 different final temperatures: 50 °C, 60 °C, and 70 °C. In each case, the time course is well fit by a single-exponential function (Fig. 2A). Straight line fits to the data yield non-zero intercepts, indicating that solvent viscosity is not the only source of friction influencing the diffusion coefficient of Eq. 1.

Fig. 2.

Kinetic data. (A) Representative tryptophan quantum yield versus time curves following a 5° temperature jump to 60 °C. The orange curve corresponds to data collected at 11% wt/wt ethylene glycol, the green curve to data collected at 32% wt/wt ethylene glycol, and violet to data collected at 53% wt/wt ethylene glycol. The black lines are single-exponential fits to the data. (B) Relaxation time versus viscosity at 50 °C (blue), 60 °C (green), and 70 °C (orange). The points are the data. The continuous curves are the best fit using Eq. 2 with σ = 0.79 ± 0.07 cP and B = 0.32 ± 0.02 cP/μs at 50 °C, σ = 1.16 ± 0.22 cP and B = 0.43 ± 0.07 cP/μs at 60 °C, and σ = 1.78 ± 0.49 cP and B = 0.64 ± 0.07 cP/μs at 70 °C. The dashed curves are the best fit using Eq. 3 and the Ising-like model after scaling the free energies by a factor of 1.23, with α = 0 ± 0.35 cP, β = 4.0 ± 0.4, corresponding to a 68% interval, Δχ² = 1, Γ (50 °C) = 2.87 ± 0.14 × 10⁸ s⁻¹ cP, Γ (60 °C) = 3.12 ± 0.21 × 10⁸ s⁻¹ cP, and Γ (70 °C) = 4.09 ± 0.31 × 10⁸ s⁻¹ cP. (C) Relaxation time versus viscosity at 60 °C. The green circles are the observed relaxation times in ethylene glycol; the red circles are corrected relaxation times in glucose, and the cyan circles are corrected relaxation rates in glycerol. The numerical values of the viscosities, and the experimentally measured relaxation times and corrected relaxation times are listed in the SI Text.

Because, as we show below (see Quantitative Interpretation of Viscosity-Dependence of Relaxation Time) the barriers are very small, population changes at all positions along the reaction coordinate can influence the thermal unfolding curves, so it is reasonable to assume from the equilibrium data in Fig. 1 that ethylene glycol only influences the kinetics through its effect on the dynamics. Nevertheless, to further ensure that the increase in relaxation time due to adding viscogen results only from increased solvent viscosity, we measured the relaxation times in the presence of 2 different viscogens, glucose and glycerol. The viscosity dependence of the relaxation times is almost identical to that measured with ethylene glycol, demonstrating that it is independent of the viscogen^†. Fig. 2C and Fig. S3 show, moreover, that the rates change only slightly after correcting for the small change in stability using a 2-state model and a linear free energy relation between the folding rate and stability, i.e., 1/τ ≈ K^ν. The exponent (ν = 0.1) was chosen to be consistent with the position of the free energy barrier top obtained from the theoretical model discussed below (Fig. 3A),but data corrected with 0.1 < ν < 0.4 also nearly superimpose on the results for ethylene glycol.

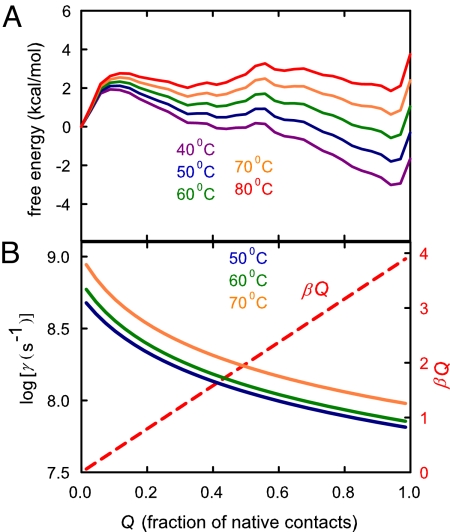
Fig. 3.

Results from the Ising-like model. (A) Free energy versus fraction of native contacts, Q, at 40 °C (violet), 50 °C (blue), 60 °C (green), 70 °C (orange), and 80 °C (red). (B) Dependence of γ for the transition between adjacent values of the reaction coordinate at 50 °C (blue), 60 °C (green), and 70 °C (orange) at the viscosity of water. The red dashed lines shows the dependence of the contribution from internal viscosity, (α + βQ), to γ obtained by fitting the experimental data using the Ising-like model and Eq. 3 with the 1.23 scale factor on the free energies of A.

Qualitative Interpretation of Viscosity Dependence of Relaxation Time.

One possible explanation for the non-zero intercept in the relaxation time versus viscosity plot (Fig. 2B) (equivalent to a fractional power-law viscosity dependence in a rate versus 1/η plot) is a breakdown of Kramers's equation [1] because of barrier crossing that is not slow compared with the solvent relaxation time (23, 24), as suggested for α-helix formation (18). However, both the free energy barrier to folding, estimated by several different methods to be only 1–2 kcal/mol (22), and the near zero activation energy for folding argue against this possibility. A more likely explanation is that the weaker viscosity dependence results from internal friction. Following Ansari et al. (25), we assume that the total friction is the sum of the solvent friction and internal friction, so Eq. 1 becomes:

where B characterizes the free energy surface at the specified temperature, and σ is the contribution from internal friction and has units of viscosity. Fitting the data in Fig. 2B, using Eq. 2, yields values of σ that, in contrast to the solvent viscosity, increase with increasing temperature (σ = 0.8 ± 0.1 cP at 50 °C, 1.2 ± 0.2 cP at 60 °C, and 1.8 ± 0.5 cP at 70 °C).

One interpretation is that the increase in temperature strengthens hydrophobic interactions, resulting in a larger internal friction (26). However, the only previous study of the temperature dependence of protein internal friction that did not vary the denaturant concentration argues against this interpretation. Hagen and coworkers studied the kinetics of binding of methionine, the native ligating residue, to the heme following displacement of carbon monoxide by photodissociation in a compact state of cytochrome c (14). They found that the rate as a function of viscosity is independent of the viscogen used and exhibits a much weaker than a 1/η dependence. Fitting their data with Eq. 2 yields a σ that decreases by ≈3-fold from 50 °C to 70 °C (0.22 cP to 0.08 cP), the temperature range of our experiments.

An alternative explanation of our findings is that the transition state moves closer to the folded state as the temperature is increased, resulting in an increased internal friction associated with more compact structures, as suggested in the lattice simulations of Wang and coworkers (9).

Quantitative Interpretation of Viscosity Dependence of Relaxation Time.

To test this idea quantitatively, we used a simple Ising-like statistical-mechanical model that has been remarkably successful in predicting the relative rates of folding for 2-state proteins (3, 27), and in explaining the lack of denaturant dependence observed for the relaxation rate of the villin subdomain (28). The model is similar to the one that was first successfully used to explain both the equilibrium and kinetic data for α-helix and β-hairpin formation (29–32) and takes advantage of two major developments from experiment, theory, and simulations. The first development is the idea of funneled energy landscapes for describing folding dynamics advanced by Wolynes, Onuchic, and coworkers (1, 5, 33), in which there is a strong bias for interactions that are present in the native structure. This postulate is supported by the empirical finding that relative folding rates for 2-state proteins can be predicted from the contact map of the native structure (34). It is also the important underlying assumption in interpreting the relative effect of site-directed mutations on rate and equilibrium constants in terms of native structure in transition state ensembles [φ value analysis (35)]. The second is the demonstration in simulations of simplified representations of proteins that diffusion on a 1D free energy surface, as in Kramers's theory, using an order parameter, such as the fraction of native contacts for the reaction coordinate (Q), can accurately describe the kinetics (2, 4).

The key assumptions of the Ising-like model are that each residue exists in only 2 conformations—native and nonnative, that structure grows in a small number of continuous stretches of native residues, and that the interaction energy and conformational entropy loss are the same for all contacting residues (see Materials and Methods and refs. 22 and 27 for additional details). Although the model does not explicitly consider nonnative interactions, they are reflected in the diffusion coefficient (the hopping parameter, γ; see below) for motion along the reaction coordinate of the 1D free energy surface.

Fig. 3A shows plots of the free energy versus reaction coordinate, Q, the fraction of native contacts, calculated from the model at temperatures from 40 °C to 80 °C, using parameters that provide the best fit to an extensive set of equilibrium and kinetic data (36). The important prediction of the model is that as the temperature is increased, a barrier at higher Q (= 0.56) becomes more prominent than the barrier at Q = 0.12, so the diffusion coefficient that dominates the dynamics should shift from being close to that of the denatured state to being closer to the native state. A change in position of the barrier can occur because the free energy varies little along the reaction coordinate, so that the temperature changes can introduce qualitative changes in the shape of the profiles. To an excellent approximation, the change in the free-energy difference between 2 positions along Q because of a temperature change, ΔT, is given by ΔT × ΔS, where ΔS is the difference between the average conformational entropy of the microstates at the two values of Q. The difference in the average entropy at Q = 0.12 and Q = 0.56 is 57 cal·mol⁻¹·K⁻¹, which is sufficient to increase the height of the barrier at Q = 0.56 relative to that at Q = 0.12 by ΔΔG = 1.1 kcal/mol with a 20 °C temperature increase, making it an important barrier. Because the structures are more compact at the Q = 0.56 barrier the contribution from internal friction to the diffusion coefficient will be larger than for the Q = 0.12 barrier top, and we would therefore expect a decreased viscosity dependence for the relaxation rate as the temperature is increased.

To calculate the effect of viscosity on the kinetics predicted by the Ising-like model, the relaxation rate at each temperature was calculated from the rate matrix for hopping along the discretized reaction coordinate. A linear free energy relation was assumed for transitions between adjacent values of Q, i.e., k_{Q,Q + 1} = γ (K_{Q,Q + 1})^1/2, where K_{Q,Q + 1} is the ratio of populations at adjacent values of Q, and the hopping parameter γ [which is proportional to the diffusion coefficient (37)] sets the absolute rate. The viscosity dependence of γ is assumed to be given by the simplest possible empirical extension of Eq. 2, i.e.:

where Γ(T) is a temperature-dependent but Q-independent empirical constant, η(T) is the solvent viscosity, and the quantity (α + βQ), which for simplicity is assumed to be temperature-independent, measures the contribution of the internal viscosity of the protein at each value of Q.

An initially puzzling result is that even with the flexibility of the 3 adjustable parameters of Eq. 3, it is not possible to reproduce the increase in the experimentally determined σ with increasing temperature (see SI Text). A more detailed analysis shows that although the free energy profiles generated by the model exhibit a shift in the major barrier (Fig. 3A) that might be expected to explain the temperature dependence of σ, the kinetics calculated from these profiles do not fulfill this simple expectation. The measured relaxation rates not only depend on the barrier heights and diffusion coefficient at the thermodynamic barrier top, but are also significantly influenced by the detailed shape of the free energy surface (i.e., the curvatures as in Eq. 1). This is most easily discussed in terms of mean first-passage times, described in detail in SI Text, which show that the lack of a temperature dependence of σ obtained from the free energy profiles results from the fact that the barrier at Q = 0.12 is too small to control the relaxation times for the folding transition under any experimental conditions, even at 40 °C where it is by far the largest barrier to folding.

Because the failure of the model to generate a temperature-dependent σ results from low barriers, and models which only include native interactions are known to yield barriers that are too low (38), we altered the model in two ways to increase the barrier heights. In the first, the 3 body terms were included in the model following Plotkin and coworkers (38), and new contact energies and conformational entropies were obtained by refitting the excess heat capacity data (22). The result was an increase in the Q = 0.12 free energy barrier but a profile (data not shown) in which there is no shift in the major barrier and consequently no temperature dependence to σ. The second, purely empirical, method was to simply scale the free energies to raise the barriers, i.e., multiply the free energies at each value of Q by the same factor. A least-squares minimization resulted in an excellent fit to the data (Fig. 2B) with a scale factor of only 1.23, with α = 0 ± 0.35 cP and β = 4.0 ± 0.4 cP. The values of both α and β are physically reasonable, namely that the contribution from internal viscosity is negligible or small for the fully unfolded protein (Q = 0), and 4.0 ± 0.4 cP for the fully folded protein (Q = 1), the same as found for the conformational relaxation of folded myoglobin (σ = 4.1 ± 1.3 cP) (25).

Fig. 3B shows that γ decreases ≈10-fold or less over the entire range of Q at all 3 temperatures, which span the midpoint temperature of the unfolding transition (T_f = 63 °C). The relatively small position dependence of γ is consistent with the finding of an excellent correlation between observed and calculated folding rates for 2-state proteins with the same value of γ for all proteins (3, 27) despite large differences in the position of the transition state as measured by the relative sensitivity of the folding rate and equilibrium constant to denaturant concentration (i.e., m_f^‡/m_eq) (see SI Text).

Comparisons of Experiments and Simulations.

It may be possible to gain insight into the relative contributions to the internal friction by comparing results of simulations with experiments on the viscosity dependence of folding kinetics. Zagrovic and Pande (39) carried out Langevin simulations of the viscosity dependence of the folding time of the 20-residue Trp cage studied by Qiu and Hagen (15). Fitting the calculated folding time versus viscosity in the range of 0.1–1.0 cP with Eq. 2 yields σ = 0.05 ± 0.03, compared with the value of σ = 0.28 ± 0.06 cP from the experiments of Qiu and Hagen (Figs. S4 and S5). There are, however, caveats to the results of both the experiments and the simulations. In the experiments, increasing denaturant concentration was used to counter the increase in stability upon adding glucose to increase the viscosity. As mentioned in the introduction, the denaturant could alter both the free energy barrier height and shape of the surface (see Eq. 1) and increase chain diffusion at the transition state, as Schuler and coworkers found for an unfolded protein (20). The effect on chain diffusion would result in an erroneously higher value of σ. In the simulations the collision frequency of the solvent with protein atoms was kept constant, independent of whether or not the protein atoms are exposed to solvent, rather than scaling the friction coefficient for solvent accessibility, as suggested by Pastor and Karplus (40). Consequently, the contribution from solvent friction is very likely to be overestimated, and, therefore, σ calculated from the simulations should be considered as a lower limit.

A possible clue to the relative contributions to internal friction comes by comparing these Langevin simulations for the Trp cage to those of Best and Hummer for a bead model of a 47-residue 3-helix bundle at very low solvent friction, in which the only attractive interactions are between residues that are in contact in the native folded structure (4). Fitting their folding time versus viscosity in the range of 0.01–0.2 cP with Eq. 2 yields a negligible internal friction (σ = −0.015 ± 0.012 cP) compared with the friction from water (Fig. S6). The lack of nonnative interactions might be responsible for the slightly lower σ compared with the result from the Trp cage simulation.

Conclusion

In this study, we have shown that experimental studies on the viscosity dependence of protein folding kinetics provide a totally new and different kind of test for both theoretical models and molecular simulations. Although the position dependence of the diffusion coefficient is more important for determining rates for ultrafast-folding proteins than for slow folding proteins, it is difficult to derive this information from experimental data because the diffusion coefficient at positions other than at the top of the largest barrier influence the kinetics. In proteins with high barriers only the diffusion coefficient at the barrier top contributes to the kinetics (Eq. 1), so it should be possible to obtain more definitive experimental information on the position dependence of the diffusion coefficient. One approach would be to investigate the viscosity dependence of the kinetics for proteins that exhibit a large shift in the position of the transition state with mutations or changing solvent conditions, if the position of the free energy barrier top can be reliably determined (5, 41). Another approach might be to carry out single molecule pulling experiments as a function of force and viscosity, which can potentially yield transition state position and free energy barrier heights (42, 43).

Materials and Methods

Materials.

The 35-residue villin subdomain (LSDED FKAVF GMTRS AFANL PLWKQ QHLKK EKGLF) was obtained from California Peptide Research. The fragment AcWKQQH used to determine the effect of temperature on the unfolded state tryptophan fluorescence, synthesized by standard solid-phase fluorenylmethoxycarbonyl chemistry on an Applied Biosystems peptide synthesizer AB433A, and purified by HPLC. Solutions were buffered with 20 mM sodium acetate at pH = 4.9. Ethylene glycol (>99% purity; Sigma) was added to obtain the following final concentrations: 11, 22, 32, 43, and 53% wt/wt. Viscosities of ethylene glycol (44), glycerol (45), and glucose (46) were obtained from the literature.

Equilibrium Measurements.

Tryptophan fluorescence at 300–450 nm was measured with a Spex Fluorolog spectrofluorimeter, using 20 μM protein samples excited at 284 nm with minimal exposure of sample to the excitation light to avoid photodamage. Natural circular dichroism was measured with a Jasco 720 spectropolarimeter at a protein concentration of 200 μM with 0.01 cm pathlength cuvette. The observed fluorescence emission peak wavelength, λ_max,obs, as a function of temperature was fitted to the following equations for a 2-state system

where λ_max,f is the peak wavelength of the folded state assumed to be independent of temperature, as suggested by the data <32 °C (Fig. 1B), λ_max,u is the temperature-dependent peak wavelength for the unfolded state and was obtained from the product aλ_max,fragment, where λ_max,fragment was obtained from a polynomial fit to the wavelength peak of the tryptophan emission of the peptide fragment (open circles in Fig. 1 of the text), K is the unfolding equilibrium constant defined as the unfolded/folded population ratio, ΔH is the enthalpy change upon unfolding, R is the gas constant, T is the absolute temperature and T_f is the temperature where K = 1. The parameters λ_f, a, ΔH, and T_f were calculated from a least-squares fit of the data to Eq. 4 and 5. The thermal unfolding curve at each viscogen concentration was measured in 3 separate experiments. The unfolding curves of villin in glucose and glycerol are shown in the SI Text.

Kinetic Measurements.

Kinetic measurements were carried out on solutions containing 200 μM protein or N-acetyl tryptophanamide (NATA) at various ethylene glycol concentrations using a nanosecond-laser temperature-jump instrument described in ref. 47. Briefly, temperature jumps of 4–7 °C to a final temperature of 50, 60, or 70 °C were generated by Raman shifting pulses of a Nd:YAG fundamental at 1,064 to 1,560 nm, using ²H₂ gas. The temperature-jump was recalibrated each time the solution conditions were altered. A frequency-doubled Kr laser with an output at 284 nm was used to excite tryptophan fluorescence. In each experiment, 4–8 traces of 512 laser shots were collected. Rate constants and amplitudes were calculated by a least-squares fit of the data to a sum of exponentials and baseline from an NATA trace. Each experiment (ethylene glycol concentration and temperature) was performed at least 3 times.

Absolute quantum yields were calculated by integrating the emission spectra from 300 nm to 450 nm and scaling to NATA as a reference assuming a quantum yield of 0.14 at 293 K. Refractive-index measurements required for the calculation of quantum yield were taken as a function of temperature and ethylene glycol concentration using an ABBE refractometer (American Optical) and attached water bath.

Calculation of Viscosity Dependence of Unfolding/Refolding Relaxation Rate Using Muñoz–Eaton–Henry Ising-Like Model.

To greatly reduce the number of possible configurations, the double sequence approximation was used, in which no more than 2 continuous stretches of native residues (n) are allowed in each molecule (e.g., … cnnncccnnnccc …). The free energy and thermodynamic weight of a stretch of native residues of length j beginning at residue i are, respectively,

where q_ij is the number of native interresidue contacts, ε is the energy of an interresidue contact and Δs_conf is the entropy cost of fixing a residue in its native conformation. Only residues that are in contact in the native structure are considered and are defined by a separation between alpha carbons of ≤0.8 nm in the native structure (PDB entry 1YRF) (48). In this double sequence, approximation contacts can occur if all residues in the sequence between the contacting residues are in a native conformation. Contacts are also allowed between native segments connected by a disordered loop. The entropy loss associated with forming a loop was calculated from the interresidue distance distribution between 2 contacting native segments for a worm-like chain of persistence length 0.6 nm and is described in detail elsewhere (22). The total number of microstates for the villin subdomain is 92,696. The only adjustable thermodynamic parameters are the contact energy ε (equal to 0.628 kcal·mol⁻¹) and the conformational entropy loss Δs_conf (equal to −3.70 cal·deg⁻¹·mol⁻¹), which are the same for every contact and residue, respectively, and were taken from the fit to equilibrium and kinetic data in ref. 36.

The relaxation rate was obtained by solving the rate equations for hopping along the free-energy surface in Fig. 3A between adjacent values of the reaction coordinate Q, the fraction of native contacts, using a linear free energy relation:

where P_eq is the relative population at the final temperature (the initial condition utilizes the population at the temperature before the jump) and γ is a function of Q and T, given by Eq. 3.

The predicted experimental fluorescence signal was computed from the resulting time-dependent populations assuming 2 values for the quantum yield—the quantum yield of a peptide fragment if the W24-H27 contact is not formed, and a second quantum yield corresponding to microstates in which this contact is present (22). The time course of the calculated fluorescence can be accurately described by a single exponential. The calculated relaxation rates were compared with the measured rates, and the parameters of Eq. 3, α, β, and Γ were adjusted to minimize the squared differences between the calculated and observed relaxation rates.

Additional information, including Fig. S7–S9 and Table S1, can be found in the SI Text.