Permutation-Based Adjustments for the Significance of Partial Regression Coefficients in Microarray Data Analysis

Abstract

The aim of this paper is to generalize permutation methods for multiple testing adjustment of significant partial regression coefficients in a linear regression model used for microarray data. Using a permutation method outlined by Anderson and Legendre [1999] and the permutation P-value adjustment from Simon et al. [2004], the significance of disease related gene expression will be determined and adjusted after accounting for the effects of covariates, which are not restricted to be categorical. We apply these methods to a microarray dataset containing confounders and illustrate the comparisons between the permutation-based adjustments and the normal theory adjustments. The application of a linear model is emphasized for data containing confounders and the permutation-based approaches are shown to be better suited for microarray data.

INTRODUCTION

Permutation-based multiple comparison adjustments are among the most common methods for adjustment of significance of gene expression between classes. [Dudoit et al., 2003; Ge et al., 2003; Korn et al., 2004; Simon et al., 2004; Westfall and Young, 1993; Yang and Speed, 2003]. A t test or a simple ANOVA is applied to each of a large number of genes and the adjusted significance is calculated using the joint distribution of P-values where the class designation for each subject is randomly permuted several thousand times under the global null hypothesis. Westfall and Young [1993] suggest several variations of this approach including bootstrap as well as permutation resampling and a generalization to linear regression with several independent variables. Their regression extension involves resampling residuals from the full model, and controls only family-wise error rates (FWER). Simon et al. [2004] and Korn et al. [2004] generalized the approach to control the number and proportion of false discoveries, a more practical goal for analysis of microarray data, but did not retain Westfall and Young’s [1993] generalization to linear regression. We wish to fill some gaps by discussing permutation procedures generalized both to multiple linear regression and to the control of the number and proportion of false discoveries using recent results by Anderson and Legendre [1999]. In particular, we will entertain permuting residuals from reduced models as proposed by Freedman and Lane [1983].

We are unaware of any comparable permutation approach of the P-value adjustments in the microarray literature if we wish to generalize to a linear regression with several independent variables. Pollard and Van der Laan [2003] contrast permutation and bootstrap resampling to address multiple testing for gene expression data, but do not extend to the problem of testing partial regression coefficients. Shannon et al. [2002] apply permutation analysis to microarray to assess the significance of Mantel statistics which can be used to test partial regression coefficients in a linear regression but do not address the multiple comparisons problem.

This paper was prompted by recent high-throughput gene expression studies of psychiatric illness utilizing postmortem brain tissues. Expression changes between a nonmentally ill brain and a bipolar or schizophrenic brain are relatively small, often below two-fold. These alterations could be masked by the effects of brain pH, a parameter that has been shown to have the greatest influence on postmortem brain gene expression patterns [Li et al., 2004; Tomita et al., 2004; Iwamoto et al., 2005; Mexal et al., 2006]. In addition to brain pH, cigarette smoking may also contribute a significant amount of noise to microarray studies of psychiatric illness. A recent microarray study has shown that there are considerable differences in gene expression between postmortem brains of smokers and non-smokers [Mexal et al., 2005]. Because approximately 80% of schizophrenia patients smoke, changes due to the effects of smoking could easily be interpreted as alterations associated with the disease state. Therefore, in order to accurately capture the differential expression between mentally ill and control brains, it is imperative to account for the effects of brain pH and smoking, as well as other possible confounding variables.

BRB array tools [Simon and Lam, 2003] is a commonly used software package in the analysis of the large datasets generated by microarray studies. Currently, this program is capable of analyzing differences between classes while stratifying for one additional categorical covariate or a two-way ANOVA without an interaction term. The SAS procedure MULTEST [SAS Institute, Inc.: Cary, NC, 2004] that also calculates P-value adjustments for several multiple testing procedures has similar limitations. By using the proposed method in this paper, one is able to apply the same types of tests that are included in BRB array tools but is not restricted to a simple ANOVA to model the gene expression data.

The method is proposed as a generalization to class comparison between groups of arrays. It allows the use of a model with several independent variables, none of which are restricted to be categorical, and can include interaction terms. In other words, it is possible to test the effects of a continuous factor of interest on gene expression and perform the permutation-based multiple testing adjustments used in BRB array tools. The goal of this experiment is to identify those genes that have significant partial regression coefficients for the variables of interest in a multiple regression model. This includes but is not limited to the important special case of identifying those genes that are differentially expressed between groups of interest.

With consideration of this special case, a statistical test is performed to determine the significance of the difference between the groups and the genes are then ranked. Once this ranking has been established the next step is to determine a cutoff point, and create a list of genes that are differentially expressed for the factor of interest. This cutoff point can be determined several ways. The first is to use a cutoff value in which all of the genes with P-values below a certain threshold are included in the list. Several alternative approaches make multiple testing adjustments to the P-values and then apply the threshold to determine the list of genes [Yang and Speed, 2003; Simon et al., 2004]. The permutation adjustments resample the data without replacement to approximate the distribution of P-values for all the tests. This distribution is then used to adjust the raw P-values. Among these, the permutation approaches discussed by Simon et al. [2004] are particularly appealing because of their ability to control the FWER, numbers of false discoveries, and proportions of false discoveries in which the correlations and distributional characteristics are incorporated into the adjustments [Westfall and Young, 1993]. This makes the approach appropriate for microarray data because of the correlations between genes and also new test statistics for which distributions have yet to be determined. The statistical properties for the adjustments, which control the numbers of false discoveries and proportions of false discoveries, are explored in Korn et al. [2004].

Other well-known multiple testing adjustments applied to microarray data are the Bonferroni correction and Benjamini and Hochberg’s [1995] false discovery rate (FDR). The Bonferroni correction is aimed at controlling the FWER by dividing the desired α level by the number of tests performed. This approach is the most conservative of the P-value adjustments and rarely do any of the expression changes reach significance, because the number of tests being performed is usually in the thousands. Instead, Benjamini and Hochberg’s [1995] method controls the expected proportion of falsely rejected hypothesis or the FDR. This is a step-up adjustment, which in practice usually requires the assumption of independence between the test statistics.

Suppose we are interested in finding which genes are differentially expressed between groups but we also want to correct for the effect of other factors. The permutation method for a simple one-way ANOVA is straightforward, but when we generalize to a regression model with several independent variables, how does one use permutation to adjust the significance of only one of the regression coefficients?

METHODS

PERMUTATION METHOD OF ADJUSTMENT FOR MULTIPLE TESTING

We will generalize the permutation approach of Simon et al. [2004] and Korn et al. [2004] for the multiple testing adjustments for P-values when looking at a large number of genes. This approach has been used when comparing expression between two groups but to our knowledge it has not yet been applied to a more general multiple regression model, particularly when subsets of the regression coefficients are to be tested. Consider an ANOVA model for testing the significance of differences in gene expression between several groups. Simon et al. [2004] and Korn et al. [2004], randomly permute the group labels several thousand times to obtain an approximate distribution of the P-values for the test that there is no difference in gene expression between any of the groups. The P-values can be adjusted based on several criteria for multiple testing. The following are the permutation-based adjustments that are often used when doing a simple comparison of expression between two groups.

$$\mathrm{adj}P­{\mathrm{value}}_j=\frac{1+(\#\mathrm{permutations}\mathrm{where}q\le p_j)}{1+(\#\mathrm{permutations})},$$ (1)

where p_j is the jth P-value for the observed data and q is the P-value calculated for each permutation. The permutation based adjustments suggested by Simon et al. [2004] and Korn et al. [2004] may be implemented by replacing q in (1) as indicated below.

If the P-value is to be adjusted for no false positives, (1) is equivalent to Westfall and Young’s [1993] adjustment to control the classical FWER at an α level:

• q = p₍₁₎ where p₍₁₎ is the smallest P-value for each permutation.

If the P-value is to be adjusted so that no more than U false positives are included:

• adj P-value_j = 0 for the first U ranked genes

• q = p_(u+1), where p_(u+1) is the (u+1)th smallest P-value for each permutation.

If the P-value is to be adjusted to keep the false discovery proportion (FDP) < γ with confidence 1−α, where the test is rejected for all genes for which adj P-value < α:

• If | rγ | > | (r−1)γ | then P-value = 0

• q = p_(|rγ|+1) where r is the rank of gene j.

The notation | x | indicates the greatest integer ≤ x and p_(|rγ|+1)is the (| rγ | + 1)th smallest P-value for each permutation.

adj P-value_j = max(1st through jth ranked P-values).

Note, the expected value of the FDP is Benjamini and Hochberg’s [1995] FDR and it is the only adjustment which requires the tests to be sorted in rank order.

Most biologists are prepared to accept that some errors will occur and are therefore less likely to want to control the FWER [Allison et al., 2006]. The choice of the P-value adjustment and its level of control is chosen by the investigator to best reflect their willingness to accept false positives.

Next, we modify the permutation-based multiple testing adjustment approach of Simon et al. [2004] and Korn et al. [2004] in a simple ANOVA by introducing a more general permutation method advocated by Anderson and Legendre [1999] for testing the significance of partial regression coefficients, in which we can handle multiple and continuous covariates.

FREEDMAN AND LANE METHOD FOR TESTING PARTIAL REGRESSION COEFFICIENTS

Consider a partitioned linear regression model with two sets of independent variables.

$$\mathrm{y}=\mathrm{\alpha }+{\mathrm{\beta }}_1{\mathit{x}}_1+{\mathrm{\beta }}_2{\mathrm{x}}_2+\mathrm{\epsilon },$$ (2)

where y is a n × 1 matrix, the α and βs are fixed and unknown constants and the elements of ε are identically distributed random variables with mean zero. We wish to test the significance of β₁(i.e., β₁ = 0) while correcting for x₂, in other words, given x₂ there is no further relationship between y and x₁. In the microarray setting this model would be fit separately for each gene, thereby requiring an additional subscript.

The test statistic for the significance of the partial regression vector, β₁, is the partial F statistic, which can be calculated using a reduced model which excludes the effect of main interest

$$\mathrm{y}={\mathrm{\alpha }}_{\mathit{R}}+{\mathrm{\beta }}_{\mathit{R}\mathit{2}}{\mathrm{x}}_{\mathit{2}}+{\mathrm{\epsilon }}_{\mathit{R}}$$ (3)

$$F=({\mathrm{RSS}}_{\mathrm{full}}-{\mathrm{RSS}}_{\mathrm{reduced}})/(k{\mathrm{EMS}}_{\mathrm{full}}),$$ (4)

where RSS_full is the regression sum of squares from the full model (2), RSS_reduced is the regression sum of squares from the reduced model (3), k is the number of regression coefficients in the vector β₁, and EMS_full is the error mean square from the full model.

Several methods have been proposed for extending permutation analysis to the problem of testing partial regression coefficients. These methods include permutation of raw data values [Manly, 1997], permutation of residuals under the reduced model [Freedman and Lane, 1983; Kennedy, 1995], and permutation of residuals under the full model [Ter Braak, 1992; Westfall and Young, 1993]. Anderson and Legendre [1999] tested the properties of some of these different methods using simulation studies. The Freedman and Lane [1983] reduced model had the most consistent and reliable results, including stable type I error levels, when tested under the effects of sample size, collinearity between regression coefficients, size of the covariable’s parameter, the distribution of the random error and the presence of an outlier. Hence, in this paper, we shall only consider the Freedman and Lane [1983] approach of permuting the residuals from the reduced model. In our applications, all permutations will be made under the null hypothesis that β₁ = 0 globally for all genes. Permuting the residuals from the reduced model preserves the covariances between y and x₂, x₁ and x₂, and among the x₁ variables if there are more than one.

After performing the regression model in (2) and the test statistic for the partial regression coefficient is obtained using equation (4), the residuals from (3) are then randomly permuted between subjects, after which new ys are calculated using the following:

$$\mathrm{y}\ast ={\widehat{\mathrm{\alpha }}}_{\mathit{R}}+{\widehat{\mathrm{\beta }}}_{\mathit{R}\mathit{2}}{\mathrm{x}}_2+{\mathrm{\epsilon }}_R^{\ast }$$ (5)

where α̂_R and β̂_R2 are the least squares estimators of α_R and β_R2 determined for the observed permutation of the reduced model, and ${\mathrm{\epsilon }}_{\mathit{R}}^{\ast }$ is a randomly permuted residual determined for the observed permutation of the reduced model.

Regress the new y*s on equation (2) to obtain estimates and partial F statistics for the β*s.

$$\mathrm{y}\ast ={\mathrm{\alpha }}^{\ast }+{\mathrm{\beta }}_1^{\ast }{\mathrm{x}}_1+{\mathrm{\beta }}_2^{\ast }{\mathrm{x}}_2+{\mathrm{\epsilon }}^{\ast }.$$ (6)

The permutation P-value for β̂₁ is calculated as the number of F statistics associated with ${\widehat{\mathrm{\beta }}}_1^{\ast }$, which are greater than or equal to the F_ref (the F statistic calculated for β̂₁ from the observed permutation) divided by the number of permutations performed.

APPLICATION

The Department of Psychiatry at the University of Colorado Health Sciences Center (UCHSC) provided expression data for 5,190 genes from oligonucleotide arrays on postmortem hippocampal brain tissue from 34 subjects (17 subjects with schizophrenia and 17 control subjects). Additional information was also collected for each subject including mental illness diagnosis, smoking status, brain pH, agonal state, age, and gender. The details of the collection and preprocessing of this data can be found in Mexal et al. [2005]. We will use this dataset to demonstrate the proposed method’s ability to determine which genes are differentially expressed after adjusting for a covariate and for multiple testing.

Previous studies have indicated that the effects of smoking status and brain pH on gene expression are important confounders to consider in this type of study [Li et al., 2004; Tomita et al., 2004; Iwamoto et al., 2005; Mexal et al., 2005, 2006]. Therefore, to accurately capture the differential expression between the groups of interest (i.e., schizophrenics and controls), it is imperative to account for these effects. This can be seen from the results displayed in Table I in which a separate list of ranked genes is obtained depending on whether or not the model determining the significance of disease status accounts for smoking status and pH. After looking at the corresponding genes for the top 10 ranked probesets for each model, it appears that the genes listed have different functions. The model that does not include smoking and pH as covariates includes genes that are mostly related to the ribosomal structure. Once smoking and pH are included in the linear model the top ranked genes are more related to nucleotide binding. Multiple testing adjustments are not commonly used with this type of experiment due to the fact that the highly conservative adjustments do not leave any significant results. It is of interest to apply the less conservative permutation-based methods to this dataset to determine if this problem can be alleviated. Currently, the significance of the disease status using the model that accounts for these other factors can only be adjusted using normal theory analysis of covariance, and Simon et al.’s [2004] permutation-adjusted P-values as of yet could not be obtained.

TABLE I.

Top 10 ranked genes for models which do and do not account for covariates

			P-value rank (unadjusted P-value)
Affymetrix Hu95Av2 probe set	Gene	Gene ontology molecular function(s)	Accounting for smoking status and pH	Not accounting for smoking status and pH	Accounting for smoking status, pH, age and gender	Accounting for smoking status, pH and random covariate
1495_at	Latent transforming growth factor β binding protein 1	Calcium ion binding/growth factor binding/transforming growth factor β receptor activity/protein binding	1 (0.0007)	20 (0.008)	6 (0.0003)	1 (0.0001)
41863_at	Hypothetical protein LOC138046	Nucleotide binding/RNA binding	2 (0.0007)	28 (0.009)	2 (0.0001)	4 (0.0002)
327_f_at	Ribosomal protein S20	RNA binding/structural constituent of ribosome	3 (0.0007)	35 (0.010)	4 (0.0002)	2 (0.0001)
41666_at	Heat shock 70kDa protein 12A	ATP binding/nucleotide binding	4 (0.0007)	350 (0.064)	10 (0.0004)	3 (0.0001)
32838_at	Myosin, heavy polypeptide 10, non-muscle	Actin binding /ATP binding/ calmodulin binding/ motor activity/nucleotide binding	5 (0.0007)	7 (0.004)	5 (0.0002)	6 (0.0003)
41474_at	Kinesin heavy chain member 2	ATP binding/microtubule motor activity/motor activity/ nucleotide binding	6 (0.0007)	543 (0.094)	17 (0.0009)	8 (0.0004)
39173_at	Fibrillarin	Protein binding/RNA binding	7 (0.001)	107 (0.027)	18 (0.0009)	7 (0.0003)
37508_f_at	Formin binding protein 3	Protein binding	8 (0.001)	17 (0.007)	28 (0.0015)	10 (0.0005)
39549_at	Neuronal PAS domain protein 2	DNA binding/signal transducer activity/transcription factor activity/transcription regulator activity	9 (0.002)	31 (0.008)	22 (0.0013)	5 (0.0002)
39338_at	S100 calcium binding protein A10	Calcium ion binding	10 (0.002)	14 (0.005)	11 (0.0004)	20 (0.001)

The expression data were analyzed using a linear model in which disease status (ds), smoking status (sm) and pH were independent variables.

$$\mathrm{y}=\mathrm{\alpha }+{\mathrm{\beta }}_1\mathrm{ds}+{\mathrm{\beta }}_2\mathrm{sm}+{\mathrm{\beta }}_3\mathrm{pH}+\mathrm{\epsilon },$$ (7)

where ds and sm are vectors of indicator variables and pH is a vector of continuous values.

The main comparison of interest is the difference in gene expression between the two disease diagnosis groups or whether β₁ = 0 adjusting for smoking status and pH as covariates while using the Freedman and Lane [1983] method outlined previously.

The reduced model is therefore:

$$\mathrm{y}={\mathrm{\alpha }}_{\mathit{R}}+{\mathrm{\beta }}_{\mathit{R}\mathit{2}}\mathrm{sm}+{\mathrm{\beta }}_{\mathit{R}\mathit{3}}\mathrm{pH}+{\mathrm{\epsilon }}_R.$$ (8)

The least squares estimates of the parameters were obtained and the residuals from the reduced model were randomly permuted. The P-values were calculated for each of the 5,190 genes, and were adjusted by Bonferroni and FDR [Benjamini and Hochberg, 1995], using SAS proc MULTTEST [SAS Institute, Inc.: Cary, NC, 2004] and the three methods from Simon et al. [2004] and Korn et al. [2004] outlined earlier, using 1,500 permutations and where U = 5 and γ = .30. The proposed method was applied to the dataset using a program written in SAS IML [SAS Institute, Inc.: Cary, NC, 2004]. Requests for a copy of the program can be obtained from the corresponding author.

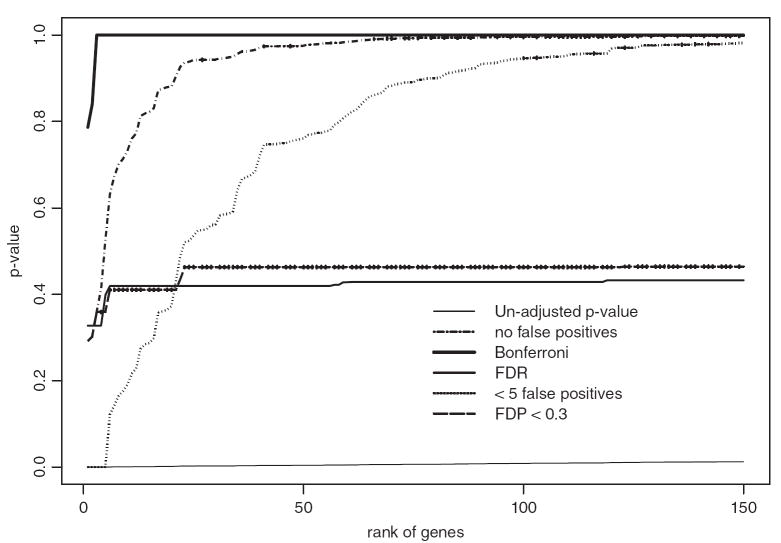
Using a 5% significance level there are 515 rejections using raw P-values for the model testing genes which are differentially expressed between disease groups after accounting for the effects of smoking status and pH of the samples. The raw P-values for the first 150 ranked genes are displayed in Figure 1. This figure also includes both permutation-based multiple testing adjustments and the common adjustments, Bonferroni and FDR [Benjamini and Hochberg, 1995]. The Bonferroni approach is the most conservative, whereas the permutation-based adjustment for no false positives is less so because it capitalizes on the correlation that exists between genes. However, this difference in conservativeness decreases with increasing rank of the gene. The permutation approach controlling the actual number of false discoveries to be less than five and even more so the permutation approach controlling FDP to be less than 0.3 also capitalize on the correlation between genes, and their adjustments are flexible in that the number or proportion of false positives may vary. These methods are therefore less conservative and hence likely more useful to medical investigators. The FDR approach of Benjamini and Hochberg [1995] yielded adjusted P-values that were initially more conservative than the permutation-based counterparts, but then more liberal. However, the FDR approach controls only the expected number rather than the actual number or proportion of false discoveries and under the naive assumption that genes express independently. Korn et al. [2004] showed through simulation that when correlations between the genes increase, the control of the expected rather than actual number or proportion of false discoveries can “give a false sense of security.” That is, the FDR approach leads incorrectly to smaller P-values when correlations are present.

Fig. 1.

Raw and multiple testing adjusted P-values for testing the partial regression coefficient associated with schizophrenia after correcting for the effects of smoking status and pH.

This permutation method allows for the correction of continuous covariates as in the above example and also the ability to test the significance of a continuous variable such as pH. Setting the number or proportion of false discoveries allows the control of the actual rather than expected false discoveries and the adjustments can be made as stringent or accommodating as is deemed appropriate.

DISCUSSION

We have proposed a merging of two previously published methods, the Freedman and Lane [1983] permutation method as discussed by Anderson and Legendre [1999] for assessing significance of partial regression coefficients and the Simon et al. [2004] permutation-based multiple testing adjustments. The merging of these two approaches allows one to apply the multiple testing adjustments to a more general linear regression model and to test association with continuous variables.

This method was applied to a schizophrenia microarray dataset and used to find permutation-based multiple testing adjusted P-values for the test of association for disease status after accounting for smoking status and pH, which in previous studies of schizophrenia have been determined to be nonignorable confounders. The permutation approach to P-value adjustment is not subjected to the same assumptions as adjustment under parametric theory and is actually better suited for microarray data, in that it is capable of reducing conservatism by capitalizing on the correlation between genes. The Bonferroni and the FDR [Benjamini and Hochberg, 1995] corrections that ignore or assume no correlation are more conservative and falsely generous, respectively, compared with the corresponding permutation-based adjustments. Although the permutation P-value adjustments still did not yield significant results at the given adjustment levels, we have successfully shown that the permutation-based adjustments are more appropriate and have extended the adjustments to include partial coefficients in a regression model.

The application of a linear regression model to microarray data requires caution. The factors are considered additive and in the case of continuous covariates linearly related to gene expression. The modeling assumptions need to be validated just as they would for univariate data. Some standard needs to be adopted as to when these assumptions are considered met for a substantial portion of the genes of interest, because some genes will not meet these assumptions merely by chance. The selection of variables to be included in the model as covariates is of consequence to the end results. Ideally, covariates are determined a priori based on clinical relevance or findings from previous studies as was the case for smoking status and pH. In a situation where there is no prior information available, a variable selection procedure might be useful.

At the suggestion of a referee, age and gender were added as covariates. In addition, a random covariate was generated by random uniform numbers between 0 and 1. The results from the inclusion of these additional covariates are listed in the last two columns of Table I. As expected, the addition of the random covariate did not drastically change the ranking of the genes. Although the inclusion of age and gender did disarrange the ranks, all of the original top 10 ranked genes remain significantly differentially expressed between disease groups. It is interesting to note that pH and smoking status were individually significant (p<0.05) for 41.1 and 7.3%, respectively, of the 5,190 genes. Age and gender were significant only for 12.4 and 4.7% of the genes, respectively.

Due to the permutation of residuals, the interpretation is related to, but differs slightly from the concept of randomization tests. The fundamental randomization test restricts inference to include only those subjects in the dataset and is best based on the assumption of the physical act of randomization [Kempthorne, 1955]. The reference set for the basic randomization test consists of considering the permuted raw data as other possible realizations under replication of the original experiment. Freedman and Lane’s [1983] approach permutes observed residuals and therefore extends the reference set to conceptual observations that were not observed. This results in a permutation test that has an asymptotically exact significance level. The application of this permutation method implies that each permuted dataset is equally likely under the null hypothesis or that we are assuming the exchangeability of the residuals [Freedman and Lane, 1983]. Freedman and Lane [1983] emphasize two conditions for their permutation method: (1) the data should not have extreme outliers and (2) x₁ and x₂ should not be highly collinear.

The permutation approach does not work well with extremely small sample sizes, because enough subjects are needed in each group to be able to calculate sufficient permutations. Without a sufficient number of permutations it is impossible to obtain permutation P-values below a specified level, e.g. with a sample of three subjects, the total number of permutations is 3! (factorial) or 6, and the smallest possible P-value is .14. Discussion of sample size is always difficult, and is particularly complex with a large number of genes. If there were but one gene, we could evoke rough rules of thumb for regression analysis such as that of Harrell [2001], “a sample size of 10p, where p is the number of predictors, is required in order for the regression model to be reliable”, or better yet, we could employ a formal power analysis for our single test. Extending these concepts to situations where there are large numbers of genes, each fitted with a regression model, is beyond the scope of this paper, but certainly a useful area for further research. One approach might be to generalize the method proposed by Dobbin and Simon [2005].

Several other possible test statistics [Chen et al., 2005; Yang and Speed, 2003] and analysis methods [Tusher et al., 2001] have been developed for microarray data, and could be easily incorporated because this approach does not rely on distributional assumptions.