Global temperature responses to current emissions from the transport sectors

Abstract

Transport affects climate directly and indirectly through mechanisms that cause both warming and cooling of climate, and the effects operate on very different timescales. We calculate climate responses in terms of global mean temperature and find large differences between the transport sectors with respect to the size and mix of short- and long-lived effects, and even the sign of the temperature response. For year 2000 emissions, road transport has the largest effect on global mean temperature. After 20 and 100 years the response in net temperature is 7 and 6 times higher, respectively, than for aviation. Aviation and shipping have strong but quite uncertain short-lived warming and cooling effects, respectively, that dominate during the first decades after the emissions. For shipping the net cooling during the first 4 decades is due to emissions of SO₂ and NOx. On a longer timescale, the current emissions from shipping cause net warming due to the persistence of the CO₂ perturbation. If emissions stay constant at 2000 levels, the warming effect from road transport will continue to increase and will be almost 4 times larger than that of aviation by the end of the century.

Transportation of passengers and goods leads to emissions that affect climate in a variety of ways. The emissions consist of long-lived greenhouse gases (LLGHG; mainly CO₂), short-lived chemically active gases (NOx, CO, and VOCs) that indirectly lead to changes in greenhouse gases (mainly CH₄ and O₃), and emissions of short-lived aerosols and aerosol precursors (black carbon, organic carbon, and SO₂). Emissions from aviation also cause changes in stratospheric water vapor, contrails, and cirrus cloud coverage. In addition to very different timescales of the effects, the climate forcings are both negative and positive, thereby contributing to both warming and cooling. Thus, comparing the total climate effects of the different transportation modes raises many difficult issues, some of which are scientific in nature, and some of which touch on value-related issues that go beyond what science alone can answer. The primary cause of the difficulties is the fact that the lifetimes/adjustment times of the various components span from hours to centuries, which raises 2 main questions: First, how does one compare climate impacts that occur across different timescales? For example, how should the effects of emissions of black carbon aerosols that cause a large but relatively short-term warming be compared with the effects of CO₂, which persists centuries after the time of emission? Second, short lifetimes mean that the climate effects of some emissions can be very dependent on their location. This is particularly true for transport emissions, which show large regional variations and operate in quite separate compartments of the atmosphere.

In this article we address the first question by focusing on the impact of current global emissions (with the current geographical emission patterns). One way to assess the future climatic effects of current emissions (as 1-year pulses, see Materials and Methods for details) is by integrating radiative forcing (RF) over a chosen time horizon (giving the unit Wm⁻² yr), which is the approach taken when Global Warming Potentials (GWPs) are used as weights for comparing emissions (e.g., refs. 1–3). The integrated RF concept is constructed to include effects occurring between the time of the emission and the chosen time horizon, and it puts equal weight on all years along the path up to the horizon. Recently, Fuglestvedt et al. (4) used a global 3D chemical transport model to calculate the change in RF resulting from emissions from road traffic, shipping, rail, and aviation. Corresponding values for aviation were presented by Sausen et al. (5) and partly applied in ref. 4 to perform a consistent and comprehensive comparison of the future climatic effects of current emissions from each transportation mode. Fuglestvedt et al. (4) used the approach of future integrated RF over different time horizons reflecting short-term and long-term perspectives on climate change (20, 100, and 500 years), which has been the standard approach [i.e., as in the definition of the GWP concept (6) for LLGHG]. GWPs, or RFs that can readily be used to calculate GWPs, have been calculated in several studies for short-lived components (e.g., refs. 7–12) either for current global emissions or for emissions from specific sectors or regions.

One of the main criticisms of the application of GWPs is that the impacts of 2 equal GWP-weighted emissions are equal only in terms of integrated RF over the chosen time horizon and not in terms of actual temperature change along the path or at the end of the time horizon (13–16). Furthermore, the application of integrated RF may overestimate the effect of short-lived species if the goal of climate policies is to limit long-term temperature increase (17). Alternative approaches include choosing the change in global mean temperature for a selected year as an indicator (18, 19). This would reduce the contribution from short-lived components compared with using the integrated RF concept, when the thermal inertia of the system is taken into account.

To facilitate comparison in terms of temperature change, the global temperature change potential (GTP) as an alternative emission metric was proposed (18). The absolute GTP_i (i.e., AGTP_i) gives the temperature change at a chosen time in response to a unit pulse emission of gas i. The ratio between the AGTP_i and the corresponding absolute global temperature potential for the reference gas CO₂ gives the GTP for gas i. Using the GTP, 2 equal GTP-weighted emissions would give the same temperature change at the end of the specified time horizon but not along the path. The GTP concept is further discussed in ref. 19, and a modified version has been applied to emissions of black carbon aerosols (20).

Previous studies of the climate impacts of transportation have used RF for a chosen year (e.g., refs. 5 and 21–23) or integrated RF up to a chosen time horizon (4, 24), but this work goes 1 step further in comparing emissions from the main transport sectors (road transport, aviation, shipping, and rail) by using the change in global mean temperature as function of time as the climate impact indicator. This allows us to study the temporal behavior of the response, which is controlled by the adjustment times of the various components and the heat uptake and vertical transport of energy in the ocean. To gain insight into the importance of the various components, the temperature response is given per component in addition to total net temperature response for each sector. Looking at temperature response instead of integrated RF represents a step further down the cause–effect chain (i.e., from emissions to impacts), and thus introduces more uncertainty, but on the other hand it does increase the relevance. Using change in global mean temperature as the indicator of climate impact may give information that is easier to understand in a policy-making context than the somewhat abstract concept of integrated RF.

When comparing the relative climate impact of the different transport sectors, a natural point of comparison is efficiency—that is, how much is transported per unit impact on climate. Comparing efficiencies requires that climate impacts by transport work are normalized across transport sectors. This first requires distinguishing between passenger transport and freight transport, which allows normalization in terms of both passenger-km and tonne-km. There are then several alternative approaches to evaluating the climate impacts of the various transport sectors, and the relative preferability of each of these alternatives depends entirely on the type of question being asked. For this reason, we view this line of inquiry as beyond the scope of this article. Here our main concern is quantifying each sector's contribution to climate change and the resulting temperature response. Nevertheless, it is important to keep in mind that transport volumes vary considerably between the sectors. For example, data (ref. 25 and www.airlines.org/economics/traffic/World+Airline+Traffic.htm) indicate that transport volume in terms of passenger-km for road transport is 5–10 times greater than for aviation on a global scale.

We use the emissions and global and annual mean RF numbers by component and transport mode as presented in ref. 4 as input to a simple 2-box analytical climate model [see supporting information (SI) Appendix]. This facilitates a comparison of the current emissions from the transportation sectors in terms of contribution to global temperature change over time consistent with the use of GTP as the metric to compare climate impacts. We include all of the major components of the emissions from transportation in the tank-to-wheel cycle (i.e., neglecting the smaller fraction from well-to-tank emissions). Vehicle emissions that are not related to combustion of the fuel (e.g., emissions through leakages of HFC used in air conditioning and refrigeration) are not included. The analysis includes CO₂, ozone and methane (both of which change as a result of emissions of NOx, CO, and VOCs), black carbon aerosols, primary organic carbon aerosols, and sulfate aerosols. For aviation, changes in stratospheric water vapor, contrails, and cirrus cloud coverage are also included. Direct emissions of CH₄ and N₂O and the resulting RFs were included in ref. 4, but, because the calculated RFs are negligible, these emissions are not included in this study.

This study does not consider impacts of emission scenarios. However, the results presented for temperature responses of pulse emissions can be used by convolution of emissions as a function of time to make simple estimates of the impact of emission scenarios for the various transport sectors (see below).

Results

The components emitted initiate very different temperature responses with respect to temporal behavior, and the responses can be categorized in 3 groups: (i) the short-lived species (BC, OC, sulfate, and the short-lived part of the ozone response) have adjustment times of <1 year, and for these species the climate model gives a maximum temperature response after 1 year declining to 10% within 13 years. (ii) The loss rate of methane is enhanced by OH radicals produced by NOx emissions during the first year, leading to reduced methane concentrations. The negative methane perturbation and a corresponding ozone (primary mode) perturbation (26) have an atmospheric adjustment time of 12 years (24), and thus the temperature response is delayed (maximum after 8 years, and reduced to 10% of the maximum after 45 years). (iii) CO₂ is the only significant gas that shows persistence on a century scale.

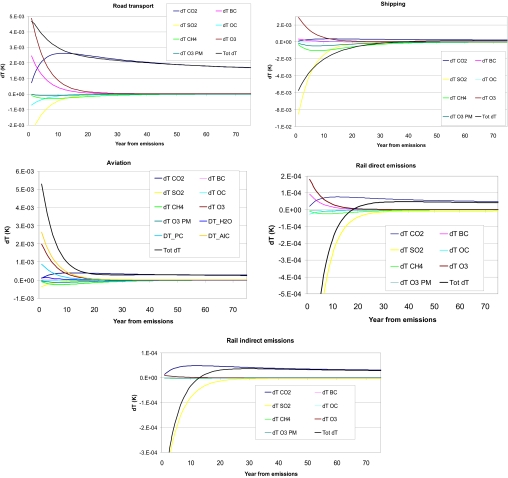
Fig. 1 shows, for the injection of 1 year's worth of emissions by each transport subsector, the time development in the global mean temperature change response for the 10 components individually and the total net effect of the sectors.

Fig. 1.

Global mean temperature (Kelvin) change after 1 year of emissions from the major transportation modes given per component and for the total net effect. AIC, aviation-induced cirrus; PC, persistent contrails; O₃ PM, primary mode ozone. Note that the first data points represent the responses 12 months after the emissions perturbations.

For all transport subsectors the response is dominated by the impact of short-lived components during the first years. However, because of very different mixes of short-lived components, the subsectors show very different temporal behavior in total net effect. For road transport and aviation, the short-lived components (dominated by ozone and BC for road transport and by ozone, contrails, and cirrus clouds for aviation) contribute to positive peaks in the warming initially. For shipping and rail (both direct emissions and indirect emissions through electricity production) the initial response is dominated by the strong cooling from sulfate aerosols. For shipping there is also a substantial cooling on decadal timescales through significant reductions in methane and ozone (primary mode; O₃ PM). This particular feature for shipping is caused by the fact that the large engines on ships have an efficient combustion at high temperatures, thereby emitting large quantities of NOx and relatively little CO and VOCs (4). Because of the initial and intermediate cooling effects, we find that 1 year of emissions from the current global shipping fleet will cause a net cooling for the coming 4 decades. A recent study (23) indicates that the RF due to indirect cloud effects (both first and second indirect effects) after SO₂ emissions from shipping may be substantially higher than the values used in ref. 4, which included only the first indirect effect. Using results for sulfate from ref. 23 would extend the cooling period even longer. In the uncertainty analysis below, this calculation defines the lower bound for the uncertainty in the temperature change for shipping. Using the estimate from ref. 23, we find that 1 year of current shipping emissions could cause a global cooling effect for a period of 55 years. For the other subsectors, road transport, aviation, and rail, the temperature responses are completely dominated by the impact of CO₂ on timescales of >2 decades after the emissions.

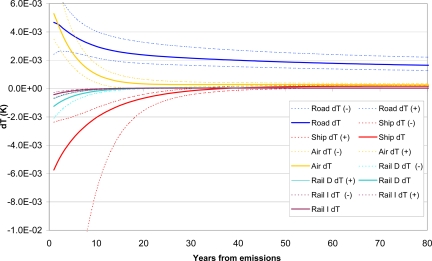
Whereas Fig. 1 gives a detailed overview of the contributions from the various forcing components, Fig. 2 shows the total net temperature change for all of the transport modes, including uncertainty ranges at the 1-sigma level (i.e., there is a 67% probability that the true value is within the given range). Road transport clearly dominates, primarily because of much higher fuel consumption in this sector (6–7 times higher CO₂ emissions than shipping and aviation) and also because the cooling effects from road transport emissions are relatively minor.

Fig. 2.

Global net temperature effect (Kelvin) per sector as function of time after one year of emissions, including uncertainties at the 1-sigma level.

There are several factors that contribute to considerable uncertainties in the estimates presented. The analysis includes uncertainties in emissions, in concentration–RF estimates, and in the RF–temperature relation (the climate response). The uncertainties in the 2 first factors are adopted from ref. 4, except for the negative RF from sulfate from shipping where the uncertainty range has been extended to include the new results from ref. 23. For the snow/albedo effect of BC aerosols that was not included in ref. 4, it is assumed that the relative uncertainty is equal to that for the direct BC forcing. The uncertainty in the climate sensitivity is adopted from ref. 24 based on the discussion there on the uncertainty in the transient climate response (TCR). It should be noted that the uncertainty in the TCR is considerably less toward high climate sensitivities than the more commonly used equilibrium climate response. In this work we have used a slightly skewed uncertainty of −19% and +33% for the climate response.

There are indications that the climate efficacy* may be somewhat different for different forcing mechanisms (24). Except for black carbon aerosols deposited on snow and ice, we have assumed that the efficacy is equal to 1 for all forcing mechanisms considered here. For BC deposited on snow/ice, we have assumed an efficacy of 1.7 (29).

Discussion

The results presented above very clearly illustrate some key issues that must eventually be answered by policy makers when it comes to how impacts of short-lived components should be compared with those of the LLGHGs. Because of the broad mix of gases emitted, this is a significant challenge also in the comparison of climate impacts of transport sectors. If one is mainly concerned about climate change toward the end of this century, then the emphasis should be put on limiting the emissions of the LLGHGs (CO₂ in the case of transportation). If, on the other hand, one is more concerned about the rapid rate at which climate seems to be changing at present, and that there may be a risk of the system reaching some kind of a “tipping point” (e.g., ref. 30) in the next few decades, then logically more emphasis should be put on the short-lived species.

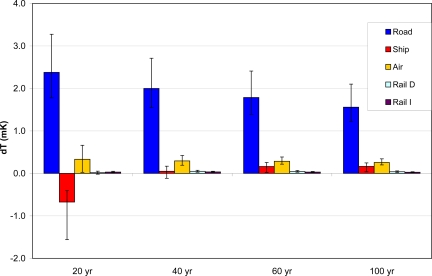
Fig. 3 shows a comparison of the transport sectors in terms of net warming for 4 chosen time horizons after 1 year's (i.e., year 2000) emissions. In line with the results in ref. 4 this work shows that for year 2000 emissions road transport is clearly the dominating sector, with aviation as the second largest contributor. For time horizons of 20 and 100 years, the net warming from road transport is 7 and 6 times larger, respectively, than the net warming from aviation. This is approximately the same ratio as the ratio between the CO₂ emissions from these sectors; thus, in these cases, it is mainly CO₂ that controls the climate response on timescales beyond 10 years. Another striking feature is that the net warming of shipping changes sign from negative for a time horizon of 20 years to positive for the other horizons used here (see also Fig. 1B). The 2 rail sectors seem small, but added together they become on the order of 15–30% of the effect of the aviation sector for time horizons between 20 and 100 years.

Fig. 3.

Contribution from a 1-year pulse of current emissions to net future temperature change (millikelvin) for each transport mode for 4 future times (20, 40, 60, and 100 years), including uncertainties at the 1-sigma level.

The results in Fig. 3 show how the relative importance of the different transport sectors changes depending on the time perspective. It is, of course, not possible to determine 1 single time horizon that is “correct.” The choice of time horizon will reflect how different people evaluate future changes (e.g., corresponding to the choice of discount rate in economic evaluations (see, e.g., refs. 16 and 31). However, in some cases one can implicitly give an indication of what should be the preferred time horizon based on policy decisions. If, as the European Union has decided, the goal of climate policy is to ensure that climate change does not exceed 2°C of warming above preindustrial levels, and a reasonable scenario will reach this limit in ≈40 years, then a time horizon of this length may be adequate. Given this time perspective, aviation, total rail, and shipping cause warming that is, respectively, 15%, 4%, and 2% of the warming from road transport.

The main purpose of this article is to discuss the temperature effects of 1 year of current emissions. However, the results also provide a simple tool for assessing how different future emission scenarios may affect global temperatures. For those components that do not interact with other components of the emissions chemically (i.e., all components other than NOx, CO, and NMVOCs^†), the temperature responses given in Fig. 1 can be normalized by the global emission rate to obtain an absolute GTP [AGTP(t), i.e., warming at time t per unit mass emission at t = 0]. The AGTP is a function of time since the emission took place and will be different for different transport modes (i.e., the AGTP for SO₂ from road is different from for shipping because of the differences in the environment where the emissions take place; see above and ref. 4). If one makes the assumption that the global patterns of emissions do not change and that there are no significant nonlinear interactions between the individual components of the emissions, then the impact of future emission scenarios from transportation can be assessed.

If future emissions from 1 transport sector is given by E_s(i,t_e) where i denotes component, s denotes sector, and t_e is the time of emissions, then the global mean temperature change at any future time t can be estimated through convolution by the following:

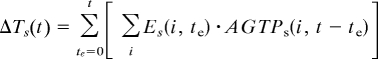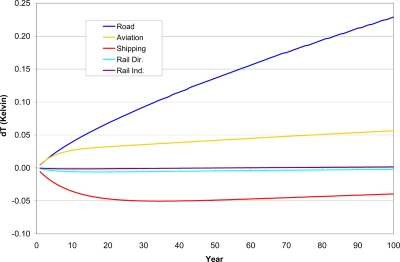
To illustrate how the timescales of the response are affected by assuming continuous emissions and the application of the AGTP(t), we have performed a comparison using the simplest possible future “scenario” of just keeping emissions constant at year 2000 levels. Fig. 4 shows the future global temperature change resulting from the 5 transport subsectors as a function of time. With these sustained emissions, the impact of shipping is a net cooling throughout the century due to the continuous strong cooling from sulfate aerosols and the negative methane perturbation. After ≈35 years the increasing warming due to accumulation of CO₂ becomes strong enough to slowly reverse the cooling temperature trend from shipping so that the magnitude of the net cooling slowly decreases. For road traffic and aviation the difference in the rate of net temperature increase after the first decade is almost equal to the difference in the CO₂ emissions from these modes. In other words, CO₂ is the driving force of the warming from these 2 sectors. During the first decade, the large RF from contrails, cirrus, and ozone from aviation causes a rapid warming. Over the course of the century the warming from road transport grows, however, to become ≈4 times larger than the warming from aviation.

Fig. 4.

Future temperature change (Kelvin) due to transportation with constant 2000 emissions.

Conclusions

Transport affects climate directly and indirectly through mechanisms that cause both warming and cooling of climate and operate on very different timescales. By applying knowledge about the various forcing mechanisms from detailed studies, we have calculated responses in global mean temperature resulting from current emissions from the main transport subsectors (road transport, aviation, shipping, and rail). The emissions from these sectors represent a broad mix of components with respect to strength, temporal behavior, and sign of climate effect.

This work goes 1 step beyond using the integrated forcing concept (e.g., refs. 4 and 24), and we calculate the responses to 1-year emission pulses in terms of global mean temperature development. This approach gives a much better picture of the temporal behavior of the various components and of the net effect of all of these emissions on global temperature. This is important given the large differences between the sectors with respect to the mix of short-lived and long-lived components and the sign of the forcing. We also demonstrate how our results for pulse emissions can be used to give an estimate of global mean temperature changes due to future emissions. In line with the results of Fuglestvedt et al. (4), this work shows that for current emissions (i.e., year 2000) road transport has the largest effect on global mean temperature, regardless of the chosen time horizon. Aviation has some strong but short-lived warming effects that dominate during the first decade after emission. Shipping, on the other hand, causes a net cooling during the first 4 decades mainly due to SO₂, NOx (via methane), and OC. On a longer timescale, however, the current emissions from shipping cause net warming because of the persistence of the CO₂ perturbation. However, one should keep in mind that the components causing cooling can affect other parameters than the global mean temperature, e.g., the hydrological cycle and wind patterns (32), and that they have indirect effects through acidification and fertilization of the ocean (33).

The discussion above shows that the comparison and ranking of the transport sectors and the various forcing agents depend strongly on the temporal perspective chosen. There is, of course, no single correct time horizon for such an analysis. However, if a climate target has been chosen (e.g., like the European Union target to stay below 2°C) then this provides an indication of an appropriate time horizon. If we are on the path to reaching this limit within the next, say, 40 years, then this time span may be a relevant time horizon for policymaking. In this time perspective, aviation, total rail, and shipping cause warming that is, respectively, 15%, 4%, and 2% of the warming from road transport. As the target year approaches, then the time horizon has to be reduced and the ranking of the sectors will change accordingly, giving more emphasis to the short-lived components.

In terms of global mean temperature change, our calculations show that aviation gives largest warming from the short-lived components (i.e., induced cirrus, contrails, and changes in ozone) whereas shipping shows the largest cooling effect from the short-lived components. In contrast, road transport shows the smallest relative effect of short-lived forcing agents.

The results also show that, in a very short-term perspective, road and aviation give temperature responses of similar magnitudes—due to the strong effects of short-lived warming components. In a long-term perspective, the effect of 1 year of current emissions for road transport is a warming that is ≈7 times larger than aviation (because of the dominating effect of CO₂). If, however, sustained constant emissions are assumed instead of pulses, then this ratio is reduced to 4. Thus, the short-lived gases have a stronger effect when emissions are sustained, but still the temperature change after 100 years is dominated by CO₂.

Materials and Methods

The emissions and RF estimates for all components are taken from ref. 4, in which the global and annual mean RF for the short-lived species is calculated with a 3D model. Thus the RFs are representative for the global annual average RF for 1 year of current emissions. For OC, only the direct effect is included; for BC, the direct and snow/albedo effect is included [but not the semidirect effect (34)]; whereas for sulfate we include the cloud albedo indirect effect (first indirect effect), with a higher sensitivity for emissions from shipping due to the location of the emissions (4).

The global temperature response is calculated by using a simple climate model to calculate the future temperature change. In the original article outlining the GTP concept (18), a 1-box analytical model accounting for only the mixed layer of the ocean was used. As discussed in refs. 19 and 20, the more long-term response of the climate system through perturbations of the deep ocean should also be taken into account. This can be achieved by applying any kind of climate model that includes the large thermal inertia of the deep ocean. However, for practical purposes in the context of emission metrics where the model must be computationally efficient and easy to understand for users, 2 alternatives have been proposed: a pulse–response relationship for the climate system (20), or an analytical 2-box model (35). The latter method has also been applied in coupled analysis of economic consequences of climate mitigation policies with a temperature constraint (36). To calculate future temperature changes we apply a 2-box analytical model similar to the model used in ref. 35, but with parameters tuned so that the response of the model represents the response of an idealized GCM experiment (N. Stuber, personal communication). With this 2-box model the temperature response of the short-lived components (e.g., sulfate or BC) is down to 1% of the response at the end of the first year after 30 years. The 2-box model is linear in RF so that temperature responses of the RF of the individual components of the emissions can be added together. The details of the model and the parameters used are given in SI Appendix.

In the climate model the RF is implemented as pulses decaying corresponding to the atmospheric residence time of each component. For the short-lived species the initial RF value is calculated so that the integrated RF over the first year is equal to the annual mean RF from ref. 4. The structure of the 2-box model with a coupled atmosphere/mixed layer of the ocean as the upper box means that a RF causing a change in the net heat flux to the atmosphere will mix the heat instantaneously within the mixed layer of the ocean (above the pycnocline). Because we are using a constant annual averaged depth of the mixed layer in our calculations, the setup effectively represents the climate response to 1 year of emissions causing a RF perturbation that lasts for ≈1 year for the short-lived components.