Kinesin's cover-neck bundle folds forward to generate force

Abstract

Each step of the kinesin motor involves a force-generating molecular rearrangement. Although significant progress has been made in elucidating the broad features of the kinesin mechanochemical cycle, molecular details of the force generation mechanism remain a mystery. Recent molecular dynamics simulations have suggested a mechanism in which the forward drive is produced when the N-terminal cover strand forms a β-sheet with the neck linker to yield the cover-neck bundle. We tested this proposal by comparing optical trapping motility measurements of cover strand mutants with the wild-type. Motility data, as well as kinetic analyses, revealed impairment of the force-generating capacity accompanied by a greater load dependence in the mechanochemical cycle. In particular, a mutant with the cover strand deleted functioned only marginally, despite the fact that the cover strand, the N-terminal “dangling end,” unlike the neck linker and nucleotide-binding pocket, is not involved with any previously considered energy transduction pathway. Furthermore, a constant assisting load, likely in lieu of a power stroke, was shown to rescue forward motility in the cover strand deletion mutant. Our results support a stepping mechanism driven by dynamic cover-neck bundle formation. They also suggest a strategy to generate motors with altered mechanical characteristics by targeting the force-generating element.

Translocating motors, such as kinesins and certain myosins, form a distinct class of proteins that “walk” along biofilament tracks to perform a wide range of vital cellular processes (1). A fundamental, yet poorly understood aspect of these motors is the energy transduction mechanism that converts the chemical energy of ATP binding, hydrolysis, and product release into mechanical work. Kinesins and myosins appear to have a common nucleotide sensor (2, 3) yet have evolved different energy conversion mechanisms to achieve a variety of motile properties. In myosin, a series of structural changes leading to the rotation of its lever arm have been identified (4), but the details of the force generation have yet to be established.

Likewise, the force generation mechanism of kinesin (herein, we mainly consider Kinesin- 1) is not known. Until recently, the only mechanical element considered was the neck linker (NL), which connects the N-terminal motor head to the α-helical stalk. This ≈12-residue segment is disordered and flexible in the absence of ATP and “docks” when ATP binds to the motor head (5). Mutations in the NL impair the motility while preserving ATPase activity and microtubule (MT) binding (6, 7). However, a mechanism for its contribution to force generation is not available, and, in lieu of this, affinity-driven zippering of the NL to the motor head has been assumed. Unlike the structurally well-defined lever arm of myosin, the NL is short and flexible when detached. Furthermore, it interacts only weakly with the motor head (8), drawing further question to whether the NL alone is capable of generating the necessary forces to bias the forward motion of the trailing head.

To address the question of force generation in kinesin, we have recently carried out a series of molecular dynamics simulations and structural analyses, which suggest that an additional element is involved in the stepping mechanism. It is the motor head's N-terminal cover strand (CS) (8). In a MT-bound, nucleotide-free leading head, the CS is separated from the rearward-pointing, “undocked” NL. In this state, the α4-helix (corresponding to myosin's relay helix) prevents α6 from forming an extra helical turn at the N-terminal base of the NL, which renders the NL out-of-register with the CS (Fig. 1A). When ATP binds to the motor head, conformational changes in the switch II cluster lead to retraction of α4 (9, 10), the subsequent formation of the α6 extra helical turn, followed by shortening of the NL. This places the CS and NL in-register to form a 2-stranded β-sheet, which we refer to as the “cover-neck bundle” (CNB) (Fig. 1B). The CNB was shown by simulations to possess a forward conformational bias and generate forces consistent with previous 2D force-clamp motility measurements (11). Specifically, a force map capturing the conformational bias of the CNB, generated through a new “tug-of-war” sampling method (12), was shown to be directed toward the motor head binding pocket and to be transversely anisotropic, helping to explain the asymmetric response of kinesin in 2D force clamp experiments (11). In contrast, the NL alone was shown to exhibit little forward bias and generate much smaller forces, in accord with the fact that its role as a force-generating element continues to be under debate (13). The simulations thus suggested a force generation mechanism triggered by this dynamic disorder-to-order transition (i.e., formation of the CNB from the NL and CS).

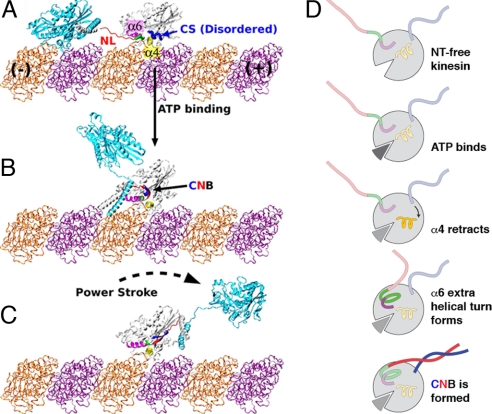
Fig. 1.

Model for kinesin's power stroke. (A) Before ATP binding, the NL (red) and N-terminal CS (blue, thick S-shaped tube) of the leading motor head are rendered out-of-register by the unwound portion (green, thick tube) of α6 (magenta). (B) ATP binding results in retraction of α4 (yellow), allowing the extra helical turn of α6 to form and bringing the NL and CS into a favorable position to form a β-sheet, known as the CNB. (C) The CNB possesses the forward bias to deliver a power stroke and propel the trailing head forward. After this action, the new leading head searches for its next MT binding site in a poststroke confined space, and the C-terminal half of the NL latches onto the motor head, achieving its final, “docked” position. Kinesin dimers were constructed by using PDB PDB (with CNB) and PDB 1BG2 (without CNB). The neck coiled-coil stalk was extended based on PDB 3KIN. (D) Diagram model highlighting the major molecular events that lead to CNB formation and a power stroke.

If CNB formation initiates the kinesin power stroke, specific disruption of this local interaction should interfere with the ability of the molecule to exert force and move forward. To test this hypothesis, we designed 2 CS mutants, one that renders the CS more flexible by mutation of 2 residues to glycines, and the other one lacking the CS. Single-molecule motility measurements with use of an optical trap revealed that the CS mutants indeed generate less force than the wild-type (WT), and, as a result, display a variety of altered motile properties, such as processivity and load-dependent kinetic substeps. Taken together, our data suggest that the CS, which is separate from the conserved motor head core, is a key element in the force generation machinery of kinesin (5, 13). Force generation by a disorder-to-order transition also suggests that static crystal structures may have to be supplemented with simulations to elucidate the dynamical features of motor proteins.

Results

Design of Cover Strand Mutants.

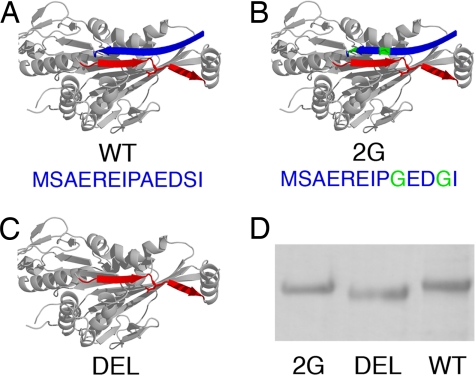
For mutagenesis, we used Drosophila kinesin, for which there is a well-studied recombinant form (14) and which is highly homologous to the kinesins studied previously (8) (Fig. 2 A–D). The CS of Drosophila kinesin is 13 residues long and a sequence comparison (8) indicated that CNB formation is achieved primarily through residues 9–13 (AEDSI), although a zipper-like interaction might also engage residues 1–8 into β-sheet formation (8). Therefore, we generated a relatively conservative mutant 2G (A9G and S12G) and a second, more severe mutant DEL that lacks the entire CS (i.e., residues 1–13 were deleted) (Fig. 2 B and C).

Fig. 2.

Kinesin mutant design. (A) WT: full CS (blue ribbon). (B) 2G: CS with mutated residues in green. (C) DEL: CS is absent. The NL is in red and the structure is based on PDB 2KIN, modified to incorporate the Drosophila CS (SwissProt ID P17210). (D) SDS/PAGE gel, confirming DEL's smaller molecular weight compared with WT and 2G.

Kinesin Motility with Load.

We mechanically probed the force-generating capacities of both mutants, along with the WT, with classical single-molecule motility experiments by using a custom-built optical trap apparatus with nanometer-level spatial resolution (15). Motility was retained in all constructs. WT walking records were normal, in that motors running at maximum velocity were slowed by the increasing optical force until near stall where the characteristic 8-nm steps are easily resolved (Fig. 3A). Although mutant 2G behaved qualitatively similar to WT, DEL motors were drastically crippled: relatively small backward loads (0.5–2 pN) caused motor stalling and stunted processivity, resulting from backward motions and/or slippage from MTs (Fig. 3B). Nonetheless, all 3 kinesins walked in stepwise fashion, as confirmed by the processive walking records measured at limiting ATP levels (4.2 μM ATP) (see supporting information (SI) Fig. S1).

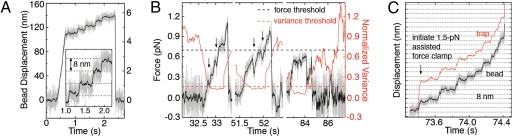
Fig. 3.

WT and DEL kinesin motility with load. (A) Representative stalling event for WT, which walks with 8-nm steps away from the trap center until stall (F_s ≈ 6 pN). (B) Representative walking events for DEL, taken from a single trace, displaying the significantly impaired processivity and load-bearing capacity against low opposing forces. Events include many instances of backward motion (arrows) and trajectories below the 0.7 pN force threshold (black dashed line) that is used for counting stalling events. For instance, in the rightmost event, the maximum force was only ≈0.6 pN, despite observing a drop in the running variance of the bead position (red trace) that is characteristic of MT binding and kinesin motility. The variance threshold (red dashed line) was 3 times below the standard deviation of the normalized variance. (C) Representative walking event for DEL with a constant 1.5-pN, assisted load, which resulted in forward stepwise motion, typical of WT kinesins that possess the ability to produce a power stroke. The trap position (red trace) is maintained at a constant offset from the bead position (black trace) by an automated feedback control system.

For a more quantitative comparison, we determined stall forces (F_s) and force–velocity (F–V) behaviors for the 3 motors. The mean stall force of mutant 2G was 61% of WT, whereas that of the more drastic mutant DEL was at most 27% of WT (Fig. 4A, Table 1). DEL motors repeatedly bound and released, sometimes taking no or only a few steps, before reaching the 0.7-pN force threshold, one of several stalling criteria (16) for detection of stalling events. This made it difficult to build the full stall force distribution for mutant DEL. A running variance of bead displacement for 4 different DEL traces (Fig. 3B) showed that, of events in which the variance dropped 2 or 3 times below standard deviation (a characteristic drop in bead fluctuations accompanying MT binding), only 30–60% of DEL events surpassed the force threshold compared with 100% of WT and 2G.

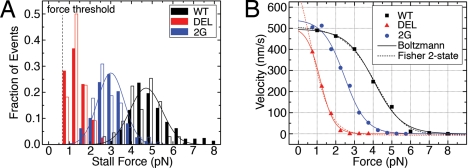
Fig. 4.

Measured mechanical characteristics of kinesin mutants. (A) Stall force histograms at 1 mM ATP (solid bars, saturating [ATP]) and 4.2 μM ATP (open bars, limiting [ATP]). Solid lines: Gaussian fits for WT and 2G at 1 mM ATP. DEL histogram was not fit because of the unknown number of stalls below the minimum detection force threshold (mean stall forces given in Table 1). (B) Global F–V curves generated from stalling event records at saturating [ATP]. Solid lines: Fits using the Boltzmann model (Eq. 1). Dotted: Fits using the Fisher-Kolomeisky 2-state kinetic model (19), which further support the biasing of the reaction coordinate toward a single state, likely by nullifying the power stroke (Table 1). For a complete list of parameter results, see SI Text and Table S1.

Table 1.

Summary of motility and load-dependent kinetic parameters measured at saturating [ATP]

Kinesin	Load						No load
	Stall force,*Fs (pN)	Blotzmann			Fisher 2-state		v(0)*, nm/s	L*, μm
		vmax,† nm/s	A†	δ,† nm	d0, nm	d1, nm
WT	4.96 ± 0.05	493.7 ± 26.4	0.0043 ± 0.0050	5.53 ± 1.04	4.4	3.8	581.1 ± 38.8	1.104 ± 0.215
2G	3.02 ± 0.03	535.2 ± 27.8	0.0137 ± 0.0101	7.15 ± 1.10	1.1	7.1	608.2 ± 22.5	1.740 ± 0.209
DEL	1.37 ± 0.04‡	482.1 ± 33.5	0.0357 ± 0.0202	11.28 ± 1.24	0.4	7.8	254.8 ± 27.2	0.342 ± 0.088

Number of measurements: n_loaded = 373, 487, 117; n_unloaded = 34, 75, 32 (WT, 2G, DEL).

*Mean ± SEM.

^†Mean ± 95% confidence interval.

^‡Potentially biased toward a higher mean value on account of the unknown number of stalling events below the minimum detection threshold of 0.7 pN.

The effect on force production by CS mutation was also manifested in the F–V curves (Fig. 4B). A minimal kinetic model capturing the F–V relationship for many mechanoenzymes is the Boltzmann relation for the velocity, v(F), as a function of the force, F, with a single load-dependent step (11, 17, 18):

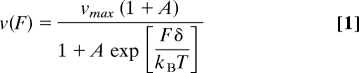where v_max is the unloaded velocity given by v_max = Δ/(τ₁ + τ₂), Δ = 8.2 nm, τ₁ and τ₂ are the times associated with load-independent (biochemical) and load-dependent (mechanical) transitions at zero load, respectively, A is the ratio τ₂/τ₁, δ is the effective distance over which the force acts, k_B is Boltzmann's constant, and T is temperature. In fits using this model (Fig. 4B, solid lines), v_max was relatively unaltered, whereas both A and δ increased for the mutants (Table 1). Thus, an increase in A with load suggests that τ₂ increases, i.e., the kinetics of the load-dependent mechanical transition is being affected by disrupting proper CNB formation. The increase of the “characteristic distance” δ from WT to 2G to DEL suggests that a larger fraction of the step distance is load-dependent. For WT, δ is smaller than the physical step size of 8.2 nm, as found previously (11), whereas for DEL, a larger value of δ indicates that the applied external load has a more significant influence over the molecule's mechanical step. In the absence of the CNB that generates a power stroke and holds the unbound head in the poststroke leading position (Fig. 1C), thermal fluctuations may be the main driving force for the motor head motion.

It has been suggested that >1 load-dependent step occurs in the kinesin cycle (11). Consequently, we also applied a model proposed by Fisher and Kolomeisky (19) that partitions the reaction coordinate into 2 states with spacings d₀ and d₁, such that d₀ + d₁ = 8.2 nm (Fig. 4B). Although the reaction coordinate was divided nearly equally for WT, it was skewed in 2G and more severely in DEL toward the second state (Table 1). Consistent with a division of the reaction coordinate into a power stroke (i) leading to a diffusive search (ii) by the unbound, new leading head (13), the fit implies a larger contribution from ii. Although larger datasets, preferably involving force-clamped measurements (11), would yield more adequate and detailed kinetic modeling, the simple models reveal the impaired motility characteristics of the mutants specifically designed to generate less force.

Stall force results were found to be consistent over a wide range of conditions, in that stall force histograms at 4.2 μM ATP overlaid predictably onto the respective histograms at saturating ATP and showed the same progression with CS mutations (Fig. 4A). Furthermore, the force dependence of the F–V curves on the CS mutations at limiting ATP levels shows a trend similar to the case of saturating ATP, suggesting that the load dependence occurs mainly on or after ATP binding (see Fig. S2).

With deletion of the CS nullifying the folding transition necessary for a power stroke, we hypothesized that external assisting loads would help to recover some of the forward bias of mutant DEL and bring approximately normal, processive motion. We tested this in a preliminary experiment, in which we implemented an optical force clamp by feedback control of the trapping laser and subjected DEL motors to constant assisting forces at saturating ATP conditions. With the aid of a 1.5-pN forward load, walking records restored much of the character of WT kinesin, i.e., forward processive motion in 8-nm steps (Fig. 3C). Although further force clamp experiments are necessary, the present results indicate that DEL lacks the forward bias generated by a power stroke, which can be compensated for by an external assisting force.

Kinesin Motility Without Load.

The unloaded velocity, v(0), and processive run length, L, of mutant 2G were at least those of WT (Table 1), suggesting that its ATPase machinery was unaffected by mutation of the CS, which is structurally separate from the highly conserved catalytic core. Interestingly, we observed slightly enhanced unloaded velocity and run length for 2G. Even though the faster unloaded velocity was not statistically significant, this enhancement was similarly observed and even more pronounced in initial velocities at 4.2 μM ATP (see Fig. S2). Presumably, this is due to the increased flexibility of its CS, which may reduce the time for CNB formation. In 2G, the decreased time associated with load-independent transitions (τ₁) may offset the increase in time for load-dependent transitions (τ₂; due to the diminished force generation), ultimately resulting in a slightly higher v_max. Furthermore, a more flexible CS may allow the molecule to enter its power stroke more quickly, thus reducing the time in a single-headed bound state and increasing processivity. In a sense, 2G can be regarded as being in a “high-gear” state, in which it can generate less force but is faster.

By contrast, DEL had severely lower processivity (4-fold reduction), as foreshadowed by the abundant releasing and backward events observed under load, and, as a result, it was difficult to estimate unloaded velocity (Table 1). Compared with the extrapolated value from F–V curves (487.4 nm/s, Fig. 4B), the unloaded velocity by direct bead tracking (254.8 nm/s) was significantly lower, in contrast to WT or 2G, whose velocities from the 2 measurements were comparable. Also note that with a 1.5-pN constant assisting force, where we have increased position resolution, DEL appears to step similarly to WT. The nonzero unloaded velocity of DEL, although ill-defined because of short run lengths, may correspond to a pure thermal diffusion with rectification by binding to the MT. During its mechanochemical cycle, when both heads are bound to the MT, ATP binding to the leading head would still be limited by strain on its rearward-pointing NL (20). Alternatively, ADP release from the trailing head may be suppressed by the forward-pointing conformation of the NL (21). One or both of these effects could contribute to maintaining the motor head coordination and forward directionality of DEL, although the reduced pulling force from the leading head weakens the strain-induced regulation and makes detachment of the trailing head more difficult. Furthermore, when the trailing head detaches, there is no active machinery to bring it forward (Fig. 1 B and C), and its search for the next MT binding site will be largely driven by thermal fluctuations. Because this is expected to be much slower than the forward motion of the unbound head via a power stroke, the MT-bound head may undergo ATP hydrolysis and detach before the unbound head finishes its diffusive search, resulting in a short run length. Thus, mutations in 2G and DEL have opposite effects on processivity.

Concluding Discussion

The cover-neck bundle (CNB) action proposed for kinesin involves force generation by the folding of a domain (i.e., a disorder-to-order transition), rather than by conformational changes of well-defined domains. This new, dynamic energy transduction pathway was identified by simulations based on the available structures (8). To test the model, mutants of the CS, which forms the CNB with the NL, were generated and shown to be deficient in their force generation capacities. The altered kinetics of CNB formation in the 2G mutant led to increased processivity, whereas deletion of the CS resulted in motility that was stunted and likely driven in large part by thermal fluctuations without a power stroke. In the latter, processive forward motility was rescued by applying a small assisting load.

The force generation mechanism by CNB formation explains why changes in the NL, despite being clearly associated with kinesin's stepping motion (5, 22), alone do not appear sufficient to generate force (7, 13). A previous study using electron paramagnetic resonance (EPR) suggests that NL docking is weakly favorable, with only a 3 kJ/mol free-energy loss associated with the event (7). However, this measurement was made on unloaded kinesin monomers, for which the undocked NL would assume a relaxed, likely forward-pointing conformation. However, when a kinesin dimer walks on a MT, the power stroke in the leading head begins from a rearward-pointing NL state and proceeds against load. Because the conformational ensemble of the undocked NL is different, the 3 kJ/mol free energy of NL docking may not be applicable to the case of a dimer under load. Furthermore, the EPR measurement compares ADP with AMP-PNP states, as a proxy for the transition between nucleotide-free and AMP-PNP states. Because the NL may exist in an ADP state that is partially bound (see figure 4d in ref. 5), the EPR measurements may include transitions between weak and strong NL bound states. Furthermore, without load, CNB formation is simply a short β-sheet-folding process. In analogy with β-hairpin formation, the associated free-energy change is expected to be low (8), consistent with the result of (7). Yet the CNB picture permits the possibility of a larger free-energy change when loads are applied. For a clearer picture of how force is generated, a more detailed study on thermodynamics of CNB formation under load is necessary.

When the NL docks to the motor head from the rearward-pointing state, according to our structural modeling, its end translates by ≈7.5 nm along the MT axis. Of the motion over this distance, ≈5.1 nm is caused by the power stroke carried out by the β9 half of the NL, and a latch mechanism in its C-terminal half is thought to carry out the rest of the docking event (8). Because the NL of the stepping motor head makes a reverse transition from a forward- to rearward-pointing state, the distance covered by the NL motion in both heads (7.5 × 2 nm) is close to the total 16-nm distance of travel by the stepping head. The small gain in axial distance caused by the ≤20° motor head rotation on ATP binding (23) may cover the remaining distance during a stepping event. However, rotation of the motor head on ATP binding is not likely to affect the proposed force generation mechanism. A recent cryo-EM study showed that the conformation of the nucleotide-free motor head bound to the MT virtually mirrors the X-ray structure of an isolated head, except for the nucleotide switch region (24). On ATP binding, the head rotates so that the NL binding pocket moves further away from the MT; hence, there is no obvious rearrangement induced by interaction with the MT that might enable a zipper-like binding of β9 without assistance of the CS. Although the 2-part mechanism of power stroke followed by latching (8) explains the NL docking action in the MT-bound head, it is yet unclear how the forward- to backward-pointing transition of the NL in the moving head occurs.

A sequence comparison shows that the CNB-forming part of the CS is conserved among Kinesin-1, 3, and 5 (8). The minus-end-directed, C-terminal ncd motor also possesses a 36-residue N-terminal cover domain, which is invisible (hence, flexible) in available crystal structures (25). As in Kinesin-1, the cover domain is in close proximity to the N-terminal neck of ncd, which suggests that a dynamic interaction between the cover and the neck domains could be a common feature across many kinesin families. More generally, approximately half of single-domain proteins in the Protein Data Bank have contacting N- and C-terminal elements (26). Furthermore, it has been recently suggested that proteins with N and C termini forming a β-sheet domain may possess a “chameleon” behavior in which the terminal segments switch between different secondary structures to assist with proper folding (27). The disorder-to-order transition of the CS and the NL would be an adaptation of this type of behavior to force generation in kinesin motor domains. Identifying and characterizing the force generation elements of motors other than kinesin would aid in understanding how they function.

Materials and Methods

Plasmid Preparation.

Kinesin mutants were designed from an existing expression plasmid for a recombinant truncated derivative of kinesin, which includes the N-terminal 401 aa of Drosophila melanogaster kinesin heavy chain (DmK401), followed by a biotin carboxyl carrier protein (BCCP) and a His₆ tag (gift of J. Gelles, Brandeis University) (14). To create the 2G mutant, we mutated the gene sequences for residues 9 and 12 by using the QuikChange Multi Site-Directed Mutagenesis Kit (Stratagene) with a single oligonucleotide primer containing the desired mutations (5′-CGAGAGATTCCCGGCGAGGACGGCATCAAAGTGG-3′). We created the DEL mutant by cassette mutagenesis of the original expression plasmid, specifically by taking advantage of the unique restriction sites flanking residues 1–13 (XbaI11 and NgoM IV). First, we constructed a 133-bp mutant gene insert, possessing the 2 restriction sites, from 6 overlapping oligonucleotide primers: (i) 5′-CCACAACGGTTTCCCTCTAGAAATAATTTTG-3′; (ii) 5′-CTCCTTCTTAAAGTTAAACAAAATTATTTCTAGAGG-3′; (iii) 5′-CTTTAAGAAGGAGATATACATATGATCAAAGTGGTCTGCCG-3′; (iv) 5′-CTGTCGTTCAGCGGTCGGAATCGGCAGACCACTTTG-3′; (v) 5′-CGCTGAACGACAGCGAAGAGAAGGCCGGCTCC-3′; (vi) 5′-ACTTGACCACGAACTTGGAGCCGGCCTTC-3′. The original plasmid and the mutant gene insert were digested with XbaI and NgoM IV and subsequently ligated together, and the resulting plasmid was transformed into One Shot TOP10 Chemically Competent Cells (Invitrogen). The final expression plasmids carrying the WT, 2G, and DEL genes were confirmed by sequencing of the entire protein-reading frames.

Protein Preparation.

BL21(DE3)pLysS Escherichia coli cells (Invitrogen) were transformed with the 3 plasmids to create expression strains. Protein expression and purification followed from previously described methods (28, 29). Briefly, midlog cultures in TB medium, supplemented with 24 mg/L biotin, were induced with 1 mM isopropyl-β-d-thiogalactopyranoside (IPTG) and subsequently brought from 37 °C to room temperature. After 3 h, 0.2 mM rifampicin was added, and the cultures were grown overnight. Harvested cell pellets were resuspended in lysis buffer (20 mM imidazole, pH 7, 4 mM MgCl₂, 2 mM PMSF, 2 μg/ml pepstatin A, 20 μg/ml TPCK, 20 μg/ml TAME, 2 μg/ml leupeptin, 20 μg/ml soybean trypsin inhibitor, 10 mM β-mercaptoethanol) and lysed via 3 freeze–thaw cycles. The lysates were incubated with 1 mg/ml RNase A (Sigma, type II-A) and 0.5 mg/ml DNase I (Sigma, grade II) for 30 min at 4 °C and then clarified by centrifugation (21,800 × g, 20 min, 4 °C) followed by ultracentrifugation (180,000 × g, 30 min, 4 °C). The clarified lysate was purified by using liquid chromatography by binding to Ni-NTA resin (Qiagen, Ni-NTA Superflow) and eluting with 70–100 mM imidazole. The collected fractions were pooled, concentrated in a Vivaspin 15 spin column (Vivascience, 30,000 MWCO), and stored at −80 °C in storage buffer (50 mM imidazole, pH 7, 100 mM NaCl₂, 1 mM MgCl₂, 20 μM ATP, 0.1 mM EDTA, 5% sucrose).

Extensive characterization of the protein products was carried out. Kinesin proteins were well-expressed (final concentrations typically exceeded 1 mg/ml), pure (according to SDS/PAGE gels), and healthy (large dilutions of ≥300,000-fold were required to drive motility assays to the single-molecule limit). Finally, to ensure that proper protein translation had taken place, the protein sequences of the 3 kinesins were confirmed by standard Edman degradation N-terminal sequencing with 2 separate automated systems: Procise and ABI 494 Protein Sequencers (Applied Biosystems).

Single-Molecule Motility Assay.

Dilutions of kinesin corresponding to the single-molecule limit were incubated with 0.44-μm diameter streptavidin-coated polystyrene microspheres (Spherotech Inc.) for 1 h at 4 °C in assay buffer (80 mM Pipes, pH 6.9, 4 mM MgCl₂, 50 mM potassium acetate, 1 mM EGTA, 0.1 mM DTT, 20 μM Taxol, 1 mg/ml casein, 1 mM ATP) to allow binding. MTs, polymerized from tubulin (Cytoskeleton), were diluted and stabilized in PemTax buffer (80 mM Pipes, pH 6.9, 4 mM MgCl₂, 1 mM EGTA, 20 μM Taxol) and then immobilized on poly(l-lysine)-coated etched coverslips. After a series of washes with PemTax and assay buffers, kinesin-loaded beads were introduced to the 10-μl flow cells.

Motility Measurements with Load.

Freely diffusing beads carrying kinesin motors were optically trapped with an infrared laser and positioned atop fixed MT filaments. Displacements from the trap center of motile beads were recorded at 2 kHz, antialias-filtered at a Nyquist frequency of 1 kHz, as kinesin motors processively walked against the increasing optical force until stall. Beads from each motility record were position-calibrated (30) and stiffness-calibrated by the positional variance method (31). Trap stiffness ranges were 0.040–0.060 pN/nm, 0.025–0.045 pN/nm, and 0.010–0.025 pN/nm for WT, 2G, and DEL, respectively.

Data analysis was performed with custom software written in MATLAB (Mathworks). Raw motility records were transformed to displacement and force transients, filtered with a boxcar window of 25 ms, and parsed into stalling events that met stalling criteria (16): stall force ≥0.7 pN, stall plateau time ≥0.1 s, stall velocity ≤50 nm/s, snapback velocity ≥500 nm/s, and a snapback to baseline. Stall forces were extracted from each stalling event and compiled into histograms. Force–velocity (F–V) curves for each stalling event were constructed by dividing motility data into 15-ms (1 mM ATP records) and 175-ms (4.2 μM ATP records) windows, in which the force trace was averaged and the velocity was obtained from linear fits to the corresponding bead displacement trajectory. Curves from each motility record (i.e., per kinesin molecule) were pooled into global F–V curves by averaging into 1-pN force bins for WT and 0.5-pN force bins for mutants.

Motility measurements were found to be reproducible. A second preparation of Mutant 2G, for instance, yielded ≤6% deviation in mean stall force: 3.09 ± 0.04 pN (mean ± SEM, n = 286) vs. 2.92 ± 0.05 pN (n = 201).

Optical Force Clamp.

An optical force clamp was implemented by following previously described methods (30). A constant force was applied to kinesin-loaded, motile beads by maintaining the center of the trapping beam at a constant, specified displacement. Custom software written in Labview 6.1 (National Instruments) was used to control the trap position via acousto-optic deflectors (IntraAction). First, freely diffusing beads were trapped and position- and stiffness-calibrated. Beads were then steered atop MTs, and the trap center was placed at the edge of the detection zone. Bead position data were sampled at 5 kHz, antialias-filtered at 2 kHz, and the trap position was updated at 500 Hz to maintain a constant displacement from the bead center. The force clamp feedback was triggered manually, based on visual inspection of the drop in bead positional variance accompanying motility, and stopped when beads reached the outer edge of the detection zone.

Motility Measurements Without Load.

Single kinesin molecules were attached to 0.8-μm streptavidin-coated beads (Spherotech Inc.). The optical trap was operated at ≤0.05 pN/nm. The KG filter (CVI Laser, CGKG-5-1.00-3) before the CCD camera (Dage-MTI, CCD-100) was partially removed so that the laser was visible on the camera. An unloaded velocity event was captured by trapping a bead, starting video recording at 30 frames per second, positioning the bead above a MT, releasing the trap at the first sign of motility, and continuing recording until the bead detached from the MT and diffused away. Movies were clipped to start at the first frame after shutting the trap off and to end with the last frame where the bead was attached to the MT. Bead position was calculated by using a centroid method to map out the traveled paths. A second-order polynomial was fit to the paths to quantify run lengths. Because of the speed of video capture and operator speed, short run events were difficult to capture, as was typically the case for DEL.