Abstract
Although a single binary functional complex between cytochrome P450 and cytochrome P450 reductase (CPR) has been generally accepted in the literature, this simple model failed to explain experimentally observed catalytic activity of recombinant P450 2E1 in dependence on the total concentration of added CPR-K56Q mutant. Our rejection of the simplest 1:1 binding model was based on two independent lines of experimental evidence. First, under the assumption of the 1:1 binding model, separate analyses of titration curves obtained while varying either P450 or CPR concentrations individually produced contradictory results. Second, an asymmetric Job plot suggested the existence of higher order molecular complexes. To identify the most probable complexation mechanism, we generated a comprehensive data set where the concentrations of both P450 and P450 were varied simultaneously, rather than one at a time. The resulting two-dimensional data were globally fit to 32 candidate mechanistic models, involving the formation of binary, ternary, and quaternary P450:CPR complexes, in the absence or presence or P450 and CPR homodimers. Of the 32 candidate models (mechanisms), two models were approximately equally successful in explaining our experimental data. The first plausible model involves the binary complex P450•CPR, the quaternary complex (P450)2• (CPR)2, and the homodimer (P450)2. The second plausible model additionally involves a weakly bound ternary complex (P450)2•CPR. Importantly, only the binary complex P450•CPR seems catalytically active in either of the two most probable mechanisms.
Protein-ligand and protein-protein interactions are fundamental to biological processes such as signal transduction, chemical transformations, and electron transport. An understanding of the role of these processes in biological function requires the identification of the detailed interaction mechanisms. These details provide a framework in which to understand how the process of molecular recognition maintains proper homeostasis, or leads to deleterious conditions. In this study, we characterize the details of protein-protein interactions involving cytochrome P4501 (P450) and the cytochrome P450 reductase (CPR). Traditional experimental protocols and data-analytic methods applied to this two-component system failed to provide a clear answer regarding the binding stoichiometry. We describe an alternative data-analytic approach applicable to any multi-component system. The method is based on a general numerical analysis of simultaneous biochemical equilibria, without any restriction on the number of component molecular species or the number of complexes they form (1). Our results indicate the involvement of the quaternary complex (P450)2•(CPR)2, in addition to possible involvement of the ternary complex (P450)2•CPR, the ternary complex P450•(CPR)2, or both ternary complexes.
Microsomal P450 enzymes are major catalysts in the oxidative transformation of a structurally diverse class of compounds including steroids, fatty acids, hormones, antibiotics, and a wide variety of artificially produced chemicals (xenobiotics), such as drugs, food additives, and environmental contaminants (2). P450s convert lipid-soluble molecules to more water-soluble forms and in effect, modulate transport and other chemical properties. To accommodate a wide array of compounds, typical P450 enzymes have evolved low specificity and activity toward substrates, making interpreting and predicting their catalytic properties difficult. Localized to the endoplasmic reticulum, the membrane-bound P450 is best considered to be an aggregate of multiple distinct P450s associating with redox partners, the obligatory cytochrome P450 reductase (CPR) and in some cases cytochrome b5 (cyt b5) (reviewed in (3)). The resulting protein-protein interactions ultimately define activity for P450s.
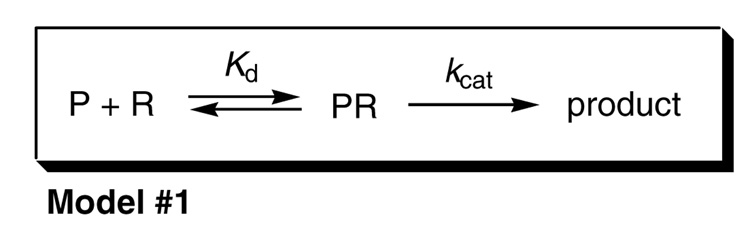
Understanding the biological impact of P450 activity requires knowledge of the identity of the P450 functional complex and the mechanism modulating its formation. Because the estimated molar ratio for P450 and CPR in membranes is approximately 20:1 (4) to 40:1 (5), one of the first models of the functional P450 complex was a rigid cluster of multiple P450 molecules surrounding a single CPR molecule (4). However, rotational diffusion studies (6, 7), cross-linking efforts (8, 9), and catalytic studies with solubilized P450 and CPR (10–12) later favored a more dynamic mass action model whereby monomeric P450 and CPR were in equilibrium with a functional binary complex, as shown in Scheme 1. Predictions from this mechanism have influenced both the design and interpretation of studies elucidating the biological impact of P450 activity.
Scheme 1.
The formation and catalytic activity of the simplest (binary) functional complex between P450 and CPRa.
aP = P450; R = CPR.
P450 2E1 activity is highly dependent on the composition of the functional complex. P450 2E1 plays a central role in the metabolism of a large number of small molecular weight compounds (molecular weight < 100), such as aliphatic, aromatic, and halogenated hydrocarbons, many of which are solvents and industrial monomers, and some of which are suspected to cause cancer (13). Although the most notable P450 2E1 substrate is ethanol, p-nitrophenol (pNP) is regarded as a typical model substrate (14). The ability to transform these compounds to products depends on the coupling of electron-transfer processes between P450 2E1 and redox partners, CPR and cyt b5 (14). The mechanism by which the functional complex(es) form for these prospective partners remains to be resolved. Unlike other P450s, cyt b5 can even support certain reactions in the absence of CPR (15), further underscoring the complexity of the role of protein-protein interactions in P450 2E1 function. Poor coupling efficiency for P450 2E1 reactions leads to decreased transformation of organic substrates to products and the formation of reactive oxygen species, a precursor to oxidative stress. The biological significance of P450 2E1-induced oxidative stress has been implicated in alcohol-induced liver damage and roles in diabetes, obesity, fasting, cancer, and nonalcoholic steatohepatitis (reviewed in (16)).
Due to the significance of protein-protein interactions in P450 2E1 activity, our goal in this study was to observe the effect of varied total concentrations of both proteins (P450 2E1 and CPR) on the overall catalytic activity of P450 2E1 toward the model substrate pNP. Because CPR is prone to degradation by contaminating proteases, we employed a proteolytically-resistant form of reductase, CPR-K56Q, which eliminated a known site of cleavage (17, 18). Initially, we employed the strategy of Miwa et al. (12) and performed a series of catalytic titrations for P450 2E1 and CPR-K56Q under conditions of excess titrant. Nevertheless, the choice of titrant yielded contradictory parameters for a binary complex mechanism, and a Job plot at 400 nM indicated the presence of a higher order complex.
To reconcile these results, we eliminated titrant bias by expanding the experimental conditions and fit the data to models incorporating multiple complexes. For these experiments, both CPR and P450 were varied simultaneously and neither protein was in very large excess. Based on reports by others (19, 20), we proposed P450 2E1 and CPR-K56Q could form binary, ternary, and quaternary complexes in the absence or presence of P450 and CPR homodimers. Due to evidence for the binary functional complex, we required all models to include P450•CPR. For simplicity, we also assumed all complexes including both P450 and CPR to be catalytically active. The resulting 32 complexation models were used to perform global regression analysis of all pooled experimental data. Model discrimination analysis was performed on the basis of the second-order Akaike Information Criterion, which properly takes into account the fact that various fitting models contain a different number of adjustable model parameters. The approach enabled the ability to identify the most probable complexes present in the P450 2E1–CPR system.
EXPERIMENTAL PROCEDURES
Materials
Components of the NADPH regenerating system (NADP+, glucose 6-phosphate, torula yeast glucose 6-phosphate dehydrogenase) for catalytic assays were purchased from Sigma-Aldrich, as were dilauroyl-L-α-phosphatidylcholine, p-nitrophenol, p-nitrocatechol, 2-nitroresorcinol, bovine erythrocyte superoxide dismutase, and catalase were obtained from Sigma-Aldrich. HPLC grade acetonitrile, trifluoroacetic acid, and other basic chemicals were purchased from Fisher Scientific (Houston, TX). Rabbit P450 2E1 and CPR-K56Q were expressed in Escherichia coli and purified to homogeneity using modifications of published protocols (18, 21).
Enzyme assays
Initial reaction rates of P450 2E1 mediated oxidation of p-nitrophenol to p-nitrocatechol were determined by a high-throughput HPLC method developed in our laboratory (18). In brief, a 96 well 0.5 mL V–bottom assay block (Corning Inc, NY) was used to reconstitute CPR-K56Q mediated P450 2E1 activity at appropriate protein concentrations. The reaction contained also 50 mM potassium phosphate pH 7.4, 20 µM dilauroyl-α-L-phosphatidylcholine (DLPC), 250 µM pNP, 2 U/µL catalase, 0.04 µg/µL superoxide dismutase, and an NADPH regenerating system (2 µU/µL glucose 6-phosphate dehydrogenase, 10 mM glucose 6-phosphate, 2 mM MgCl2, 500 µM NADP+). Superoxide dismutase and catalase were added to the reaction to scavenge reactive oxygen species (O2•− and H2O2), because these products of uncoupled catalytic complex(es) may inactivate P450 2E1, which would complicate the analyses of the data. Reactions were prepared in sets of eight to correspond to the eight wells for each column of the microplate. The strategy facilitated large scale, simultaneous manipulation of samples with a multi-channel pipettor. Following the addition of all components except NADP+, the reactions in the assay block were incubated at 37 °C for 5 min. The reactions were initiated upon addition of NADP+. At three time points, an aliquot was taken from the reaction, quenched with acetonitrile, and further analyzed by HPLC as described (18).
Catalytic titrations
For a two-component system whereby only one functional complex forms, catalytic titrations are a commonly used method for obtaining apparent dissociation constants based on the observed reaction rate. The application of the approach has been discussed in detail elsewhere for the P450 system (22). For these studies, the concentration of one component was held constant (at concentrations equal to 15, 30 and 60 nM) while the second component served as a titrant varied at the following concentrations: 7.5, 15, 30, 60, 100, 200, 300, and 400 nM. The rates (v) for pNP oxidation under those conditions were measured, plotted as a function of the variable component concentration, and fit to Eqn (1) using GraphPad Prism (SanDiego, CA) to yield the maximal rate (Vmax) and the apparent dissociation constant, Kd. In Eqn (1), [P] is the total or analytic concentration of P450 and [R] is the total or analytic concentration of CPR.
| (1) |
Because the reaction rate according to Eqn (1) presumably derives from a single 1:1 complex, we determined the apparent turnover number (kcat) from a series of catalytic titrations at concentrations of the constant component held at 15, 30, and 60 nM. The concentration of the putative binary complex is directly proportional to Vmax, according to Eqn (2).
| (2) |
At Vmax the system is saturated such that the concentration of the binary complex is defined by the concentration of the limiting component. We constructed linear plots Vmax vs. the total concentration of the fixed component, and fit the data to a straight line through origin using GraphPad Prism (San Diego, CA), to determine the kcat value for the presumed binary functional complex.
Mathematical models for P450-CPR interactions
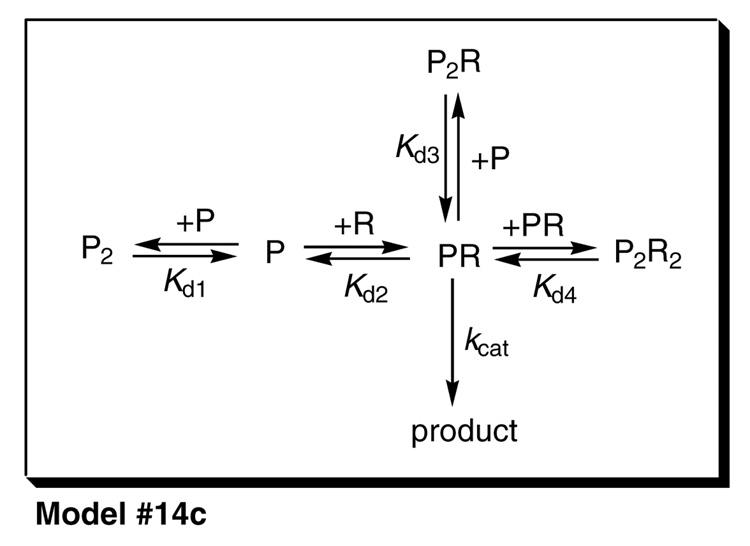
The mathematical models for the catalytic activity of the reconstituted P450 enzyme were represented as systems of simultaneous nonlinear algebraic equations for the mass balances of the component molecular species, according to a formalism described earlier (1). For example, for the Mechanism #14c shown in Scheme 2, the system of nonlinear equations is (3a,b), where the subscript "tot" means total or analytical concentration, and otherwise square brackets symbolize the concentrations at equilibrium:
| (3a) |
| (3b) |
After substituting for the equilibrium concentrations of molecular complexes in terms of equilibrium constants (see Scheme 2), we obtain for Mechanism 14c two nonlinear algebraic equations (4a,b) for two unknowns, [P]eq and [R]eq:
| (4a) |
| (4b) |
Scheme 2.
The most plausible mechanism for the formation and the catalytic activity of functional complexes between P450 and CPRa.
aP = P450; R = CPR.
Similar systems of simultaneous nonlinear algebraic equations were automatically derived by the data-fitting software package DynaFit (23) from a symbolic input shown in the Supplementary Material. Each system of nonlinear equations, corresponding to the given mechanism, was iteratively solved within DynaFit by using a modification of the algorithm equil by I and Nancollas (24) based on the multi-dimensional Newton-Raphson method. Subsequently, the equilibrium concentrations of the molecular complexes are computed from the definition of the corresponding dissociation constants. For example, for Model #14c we obtain Eqn (5a–d):
| (5a) |
| (5b) |
| (5c) |
| (5d) |
Finally, the observed catalytic activity is modeled as the sum total of the catalytic activities of all reactive molecular complexes. In Model #14c in Scheme 2, there is only one catalytically active complex. Therefore, the Eqn (6) below contains only a single term:
| (6) |
Rate equations similar to Eqn (6) were automatically derived by DynaFit (23) for all 32 models (mechanism) in Table 2 and for additional mechanisms shown in Table 3.
Table 2.
Complete list of binding models considered in this study. Symbol "A" means that the given molecular complex is present and catalytically active. Symbol "N" means that the given complex is present but not catalytically active. Models #17 through #32 (not shown) are exactly identical to Models #1 through #16, except for the fact that the reductase dimer (R2) is also present.
| Model No. | PR | P2R | PR2 | P2R2 | P2 |
|---|---|---|---|---|---|
| 1 | A | ||||
| 2 | A | A | |||
| 3 | A | A | |||
| 4 | A | A | A | ||
| 5 | A | A | |||
| 6 | A | A | A | ||
| 7 | A | A | A | ||
| 8 | A | A | A | A | N |
| 9 | A | N | |||
| 10 | A | A | N | ||
| 11 | A | A | N | ||
| 12 | A | A | A | N | |
| 13 | A | A | N | ||
| 14 | A | A | A | N | |
| 15 | A | A | A | N | |
| 16 | A | A | A | A | N |
Table 3.
First round of discrimination between candidate mechanisms by global analysis. For explanation of symbols "A" and "N", see Table 1. SSrel – relative sum of squares; ΔAICc – increase in the second order Akaike Information Criterion, Eqn (7), relative to the best model (ΔAICc = 0); w – Akaike weight, Eqn (8). Only models resulting in Akaide weight w > 0.10 (10% probability) are shown. For further explanation see text.
| Model No. | PR | P2R | PR2 | P2R2 | P2 | R2 | SSrel | ΔAICc | w > 0.10 |
|---|---|---|---|---|---|---|---|---|---|
| 13 | A | A | N | 1.094 | 0.0 | 0.259 | |||
| 14 | A | A | A | N | 1.069 | 1.6 | 0.116 | ||
| 15 | A | A | A | N | 1.064 | 1.0 | 0.160 | ||
| 32 | A | A | A | A | N | N | 1.000 | 0.1 | 0.248 |
Regression analysis
Each mathematical model, for example Eqn (6) for Mechanism 14c, was fit to the available experimental data by using two different methods. First, a global nonlinear least-squares minimization technique, based on the Differential Evolution (DE) algorithm (25) was used to approximately locate the global least-squares minimum in the multidimensional parameter space. The DE algorithm is mathematically guaranteed to find the best possible nonlinear fit within a prescribed range of model parameters, regardless of the initial estimates. Our constraints for all model parameters (equilibrium constants and turnover numbers) spanned twelve orders of magnitude. Secondly, the approximate solution obtained by DE was further refined by the usual Levenberg-Marquardt nonlinear regression algorithm implemented in DynaFit (23).
Model discrimination analysis
The residual sum of squares for each candidate fitting model (see Mechanism 1 through 4 in Scheme 1), SSQ, was used to compute the second-order Akaike Information Criterion AICc, according to Eqn (7) (26). In Eqn (7), nP is the number of adjustable model parameters (e.g., equilibrium constants and turnover numbers appearing in the given model) and nD is the number of data points.
| (7) |
To assess the plausibility of different candidate models, we used the heuristic criteria proposed by Burnham and Anderson (27). First, we ranked all models in order of increasing value of AICc. We then considered a candidate model as implausible if the difference between the AICc value for this particular model and the AICc value for the "best" model (characterized by the lowest AICc value) was larger then 10. An additional measure of model adequacy was the Akaike weight defined by Eqn (8) (26), where ΔAICc(i) is the difference between the AICc value for the ith model being compared and the lowest AICc value seen among all N candidate models.
| (8) |
RESULTS
Catalytic titrations at excess of titrant
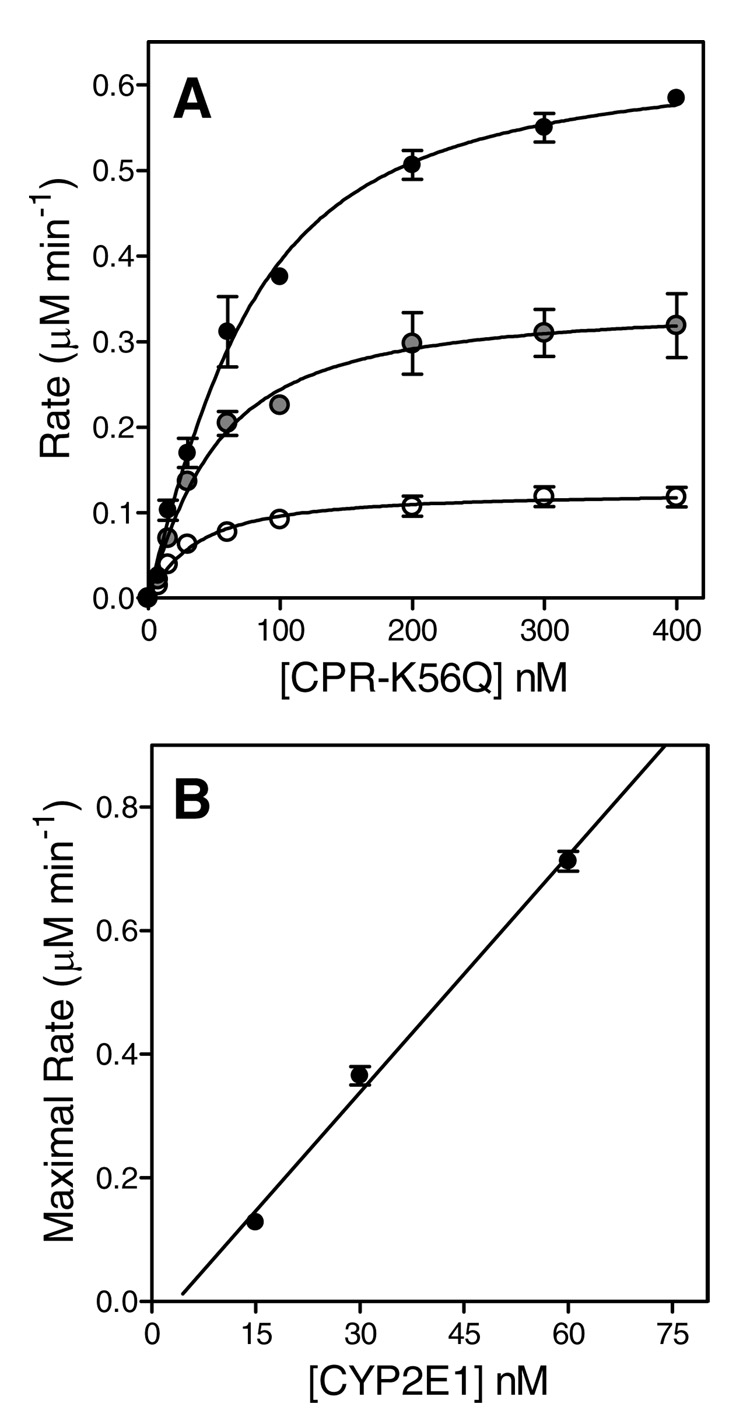
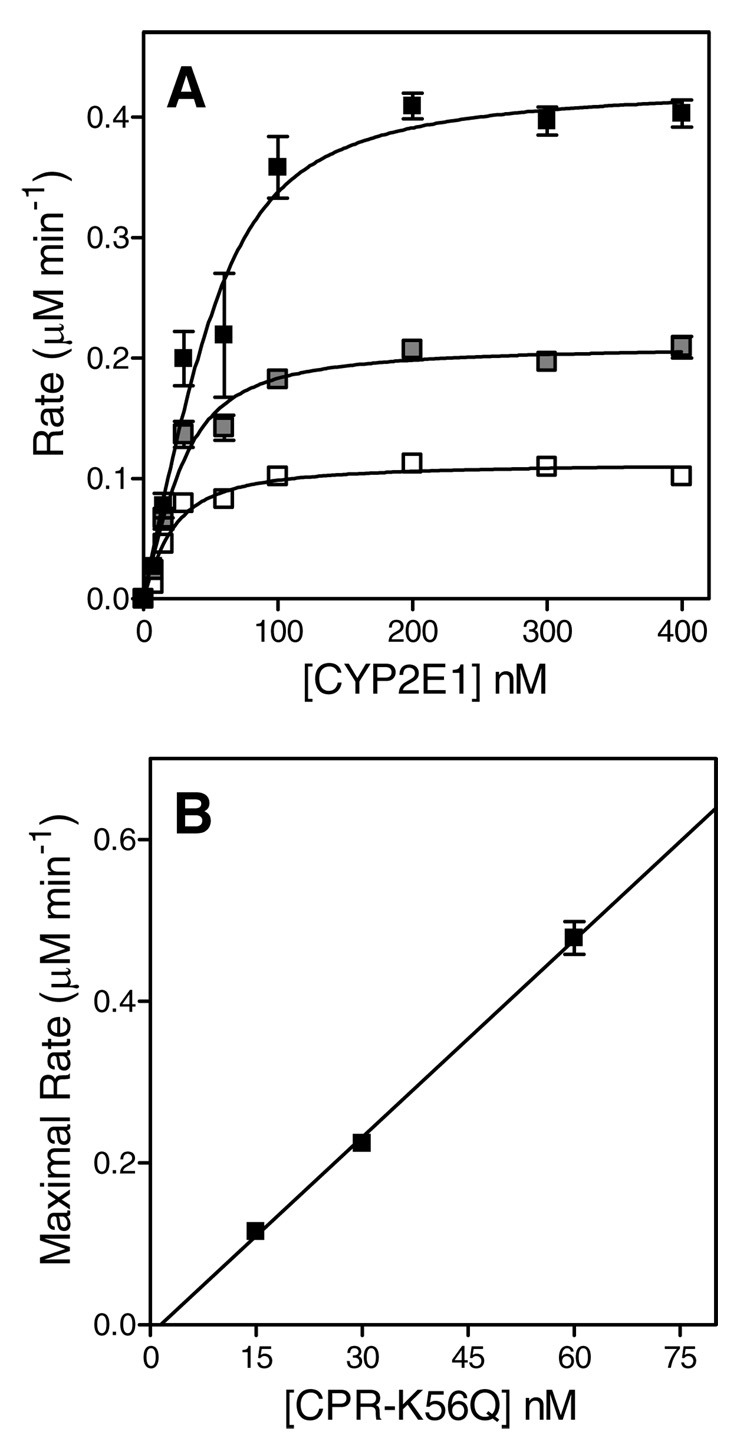
Similar to the approach adopted by Miwa et al. (12) for P450 2B1, we performed and analyzed a series of catalytic titrations to determine the apparent Kd for the putative binary complex, and assess the relationship between the binary complex concentration and the maximal rate of substrate turnover. In one set of experiments, we titrated 15, 30, and 60 nM P450 2E1 with increasing concentrations of CPR-K56Q to near-saturation at 400 nM and measured the observed reaction rate for pNP oxidation, as shown in Figure 1, Panel A. Unlike the original study (12), we additionally conducted a complementary set of experiments, whereby we held the concentration of CPR-K56Q constant and varied P450 2E1 (Figure 2, Panel A). Initially, we analyzed each titration curve independently as described by others (12). These data were fit individually to Eqn (1) to determine the apparent dissociation constants (Kd) and maximal rates (Vmax). The average of the Kd values for each set of titrations where either CPR-K56Q or P450 2E1 served as titrant are shown in Table 1. The binary complex mechanism predicts a linear correlation between Vmax and the P450 2E1•CPR-K56Q concentration, with slope equal to the turnover number, kcat (Eqn 2). Under near-saturating concentration of the varied component, the concentration for the putative binary complex is equal to the concentration of the constant component, based on the one-to-one correspondence between these equilibrium components in the mechanism (Scheme 1). Thus, we plotted the Vmax as a function of P450 2E1 concentration for titrations with CPR-K56Q and vice versa for the titrations with P450 2E1 (Figure 1 and Figure 2, Panel B). Both data sets were fit to a straight line forced through the origin, to determine the respective turnover numbers in Table 1. To improve the precision of data analysis, we fit all three data sets globally to the binary complex mechanism shown in Scheme 1 using DynaFit (23) and compared the resulting Kd and Vmax values from the respective methods. Although the resulting parameters were similar to those obtained by the traditional analysis of the data, there was at least a 2-fold drop in the formal standard error for the respective model parameters while using global analysis of the data (Table 1).
FIGURE 1.
Catalytic titrations using CPR-K56Q as the titrant. (A) Reaction rates were plotted as a function of CPR-K56Q concentration. The reported values reflect the results from average of 2–4 experiments including the standard deviation of the mean. The concentration of P450 2E1 in each titration was 15, 30, and 60 nM, as indicated by the white to black filling of the respective circles. The fitted line reflects the fit of each data set to a binding quadratic equation (Equation 1). (B) The maximal rates from each titration were plotted as a function of the concentration of the limiting complex partner, P450 2E1, and then fit to a linear regression to determine kcat.
FIGURE 2.
Catalytic titrations using P450 2E1 as the titrant. (A) Reaction rates were plotted as a function of P450 2E1 concentration. The reported values reflect the results from average of 2–4 experiments including the standard deviation of the mean. The concentration of CPR-K56Q in each titration was 15, 30, and 60 nM, as indicated by the white to black filling of the respective squares. The fitted line reflects the fit of each data set to a binding quadratic equation (Equation 1). (B) The maximal rates from each titration were plotted as a function of the concentration of the limiting complex partner, CPR-K56Q, and then fit to a linear regression to determine kcat.
Table 1.
Determination of binary complex parameters using either CPR-K56Q or P450 2E1 as the titrant.
| Method of analysis | CPR-K56Q as the titrant | P450 2E1 as the titrant | ||
|---|---|---|---|---|
| Kd (nM) | kcat (min−1) | Kd (nM) | kcat (min−1) | |
| Independenta | 30 ± 10 | 9.7 ± 1.2 | 12 ± 5 | 7.9 ± 0.2 |
| Globalb | 36 ± 3 | 10.7 ± 0.3 | 15.6 ± 1.4 | 7.2 ± 0.2 |
Kd values were determined by averaging the results from the fit of each titration curve to the respective binding quadratic equation (Equation 1). The turnover numbers, kcat, were derived from slope of the linear regression between Vmax and the concentration of limiting complex partner as shown in Figure 1 and Figure 2, Panel B.
Parameters reflect the global fit of all three titration curves to a binary complex mechanism using the software DynaFit (23). The input data for this analysis is included in Supplemental Information.
In both cases (independent or global analysis, see Table 1), the relationship between the observed reaction rates and the titrant concentrations conformed to the predictions based on assuming the simplest binary complex mechanism, but yielded significantly different results depending on which component was held constant in the experiment and which component was varied. Regardless of the method of analysis, the titration of P450 2E1 with CPR-K56Q seemingly resulted in the formation of a functional complex, which displayed an approximate 2.5-fold lower affinity but ~50 % higher activity than that predicted when P450 2E1 served as the titrant. Taken together, our results contradicted the predictions of the binary complex mechanism, because merely exchanging the constant component and the variable component in catalytic titrations seemed to produce fundamentally different properties for the putative 1:1 functional complex between P450 2E1 and CPR-K56Q.
Job plot at 400 nM total protein concentration
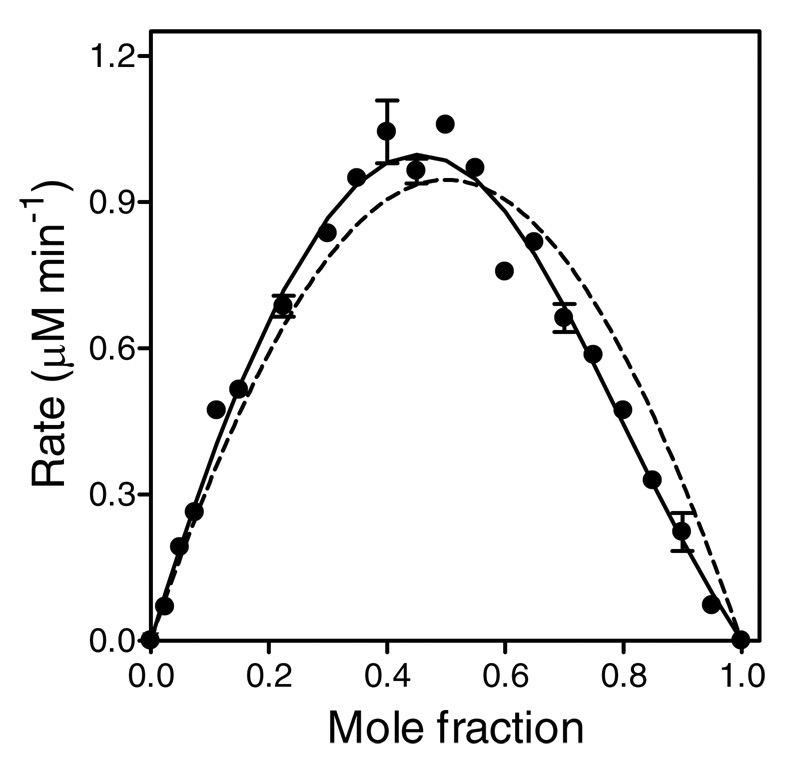
To determine the stoichiometry for the P450 2E1 and CPR-K56Q complex(es), we performed a Job titration (28) at 400 nM total protein (P450 plus reductase), as described for P450 2B1 (12). The data were fit to a binary complex mechanism (Figure 3, dashed curve). If the reductase-cytochrome binding were strictly 1:1, the theoretically predicted maximum on the Job plot would be located at the center, at mole fraction xP450 = 0.5. Instead, the experimentally observed maximum is shifted toward xP450 < 0.5, indicating other than 1:1 molar ratio in at least one molecular complex being formed. These results unambiguously establish that a higher-order molecular complex is present.
FIGURE 3.
Job plot at a total protein concentration of 400 nM. The mole fraction (x) is defined by [P450 2E1]/([P450 2E1] + [CPR-K56Q]). Reaction rates were measured while CPR-K56Q and P450 2E1 concentrations were varied such that the total protein concentration remained 400 nM. These data were fit to two different models using DynaFit (23) The dashed curve represents the best least-squares fit to the binary complex model (Scheme 1). The solid represents the fit to a model possessing a binary (P450•CPR) and ternary (P450•CPR2) complex.
Global analysis of potential complexation mechanisms
To explain these observations, we developed a novel approach to identify the complexation mechanism for P450 2E1 and CPR-K56Q. As a first step, we generated a comprehensive data set to avoid bias from the choice of titrant (vide infra). Our comprehensive data set consisted of both components (P450 and CPR) being varied simultaneously over a wide range of concentration, rather than being varied one at a time (as in catalytic titrations), or being varied such that the sum total of protein concentrations remain constant (as in the Job plot). We then globally fit these data to a variety of potential binding mechanisms and statistically analyzed the quality of the fits, to select the most probable model.
Similar to the approach adopted by Hazai et al. (20), we proposed that P450 2E1 and CPR-K56Q could form binary (P450•CPR), ternary (P4502•CPR and P450•CPR2), and quaternary (P4502•CPR2) complexes in the absence or presence or P450 and CPR homodimers. Due to experimental support for the binary complex, we required the presence of the P450•CPR complex in all model mechanisms. To further limit the number of possible models, we assumed all complexes containing at least one P450 and one CPR molecule, respectively, were catalytically active. Altogether, there were 32 possible combinations of these complexes (Table 2). We did not consider alternate pathways to generate these complexes, because the equilibrium conditions for the system enabled only the ability to identify complexes, not the path through which they formed (29). The detailed description of the 32 reaction mechanisms is shown in the Supplemental Information.
After fitting the data to all 32 possible binding mechanisms, we generated a corresponding Akaike Information Criterion (AICc) to describe statistically the quality of the respective fits. The models were ranked according to the difference in Akaike weights relative to the most probable model. To evaluate the plausibility of models, we employed the significance rules outlined by Burnham and Anderson ((26), p.70). Low AICc values indicated comparatively high support for the given model. More specifically, there was substantial support for the given model when the ΔAICc was between 0 and 2. Values between 4 and 7 signify considerably less support for the model, while a ΔAICc of 10 or greater indicated essentially no support for the given model.
Identification of plausible complexation models
In the first round of model discrimination analysis we compared 32 possible complexation models (mechanism) shown in Table 2, while assuming all molecular complexes except the (P450)2 and (CPR)2 homodimers are catalytically active. Of these 32 possible models for complexation, only four (Model #13, #14, #15, and #32) were associated with Akaike weights greater than 0.10 (corresponding to 10% statistical probability of the given model being correct). Numerical results for the four preferred models are summarized in Table 3. Model #32, involving all possible molecular complexes being formed simultaneously, produced an extremely large uncertainty of all model parameters (equilibrium constants and turnover numbers) and was excluded from further consideration. The three remaining preferred models shown in Table 3 (Model #13, #14, and #15) all include the binary complex P450•CPR and the quaternary complex (P450)2•(CPR)2. Model #14 additionally includes the ternary complex (P450)2•CPR, whereas Model #15 includes the ternary complex P450•(CPR)2.
While examining the best-fit parameters for Models #13 through #15 (data not shown), we noted that all turnover numbers associated with molecular complexes other than the binary complex P450•CPR were extremely small, numerically approaching zero. This observation suggested that we perform a second round of model discrimination analysis, summarized in Table 4. Here we have modified Models #13 through #15 such that all complexes appearing in each given mechanism, except the binary complex P450•CPR, were progressively rendered catalytically inactive. The results of model discrimination analysis (Table 4) show that in fact nominally the most plausible mechanism is represented by Model #14c, in which only the binary complex P450•CPR is catalytically active, but not the ternary complex (P450)2•CPR or the quaternary complex (P450)2•(CPR)2, both of which are also formed. A close second in order of plausibility is Model #13a, which is identical to Model #14c except for the fact that the ternary complex (P450)2•CPR is not formed at all.
Table 4.
Second round of discrimination between candidate mechanisms by global analysis. For explanation of symbols "A" and "N", see Table 1. SSrel – relative sum of squares; ΔAICc – increase in the second order Akaike Information Criterion, Eqn (7), relative to the best model (ΔAICc = 0); w – Akaike weight, Eqn (8). The Akaide weight is listed only for those models where w > 0.10 (10% probability). For further explanation see text.
| Model No. | PR | P2R | PR2 | P2R2 | P2 | SSrel | ΔAICc | w > 0.10 |
|---|---|---|---|---|---|---|---|---|
| 13 | A | A | N | 1.029 | 3.40 | |||
| 13a | A | N | N | 1.028 | 1.10 | 0.183 | ||
| 14 | A | A | A | N | 1.004 | 4.80 | ||
| 14a | A | A | N | N | 1.003 | 2.40 | ||
| 14b | A | N | A | N | 1.003 | 2.40 | ||
| 14c | A | N | N | N | 1.002 | 0.00 | 0.318 | |
| 15 | A | A | A | N | 1.001 | 4.40 | ||
| 15a | A | A | N | N | 1.000 | 2.00 | 0.118 | |
| 15b | A | N | A | N | 1.043 | 7.40 | ||
| 15c | A | N | N | N | 1.028 | 3.30 |
Confidence intervals for model parameters
Nonsymmetrical confidence intervals for all model parameters, at the 90% probability level, were computed by using the profile-t method of Bates & Watts (30). The results are summarized for nominally the most plausible Model #14c in Table 5.
Table 5.
Optimized parameters for most plausible Model #14c (see Table 4 and Scheme 2 for model description). The limiting values were computed at 90% confidence level, by using the profile-t method of Bates & Watts (30).
| Reaction | Parameter | Best-fit value | Std. Error | Lower limit | Upper limit |
|---|---|---|---|---|---|
| 2P ⇔ P2 | Kd1, µM | 0.038 | ± 0.052 | 0.0013 | 0.28 |
| P + R ⇔ PR | Kd2, µM | 0.021 | ± 0.011 | 0.0044 | 0.041 |
| PR + P ⇔ P2R | Kd3, µM | 0.37 | ± 0.12 | 0.19 | 1.9 |
| 2PR ⇔ P2R2 | Kd4, µM | 0.041 | ± 0.019 | 0.0036 | 0.070 |
| PR → product | kcat, min−1 | 10.6 | ± 0.6 | 9.7 | 11.9 |
DISCUSSION
In this study, traditional approaches failed to explain the observed catalytic activity of P450 2E1, in dependence on the total concentration of added CPR-K56Q. Thus, we developed a novel approach to studying protein-protein interactions that revealed P450 2E1 and CPR-K56Q form multiple complexes rather than the expected single binary P450•CPR complex.
For the titrations with either CPR-K56Q or P450 2E1 as the titrant, the reaction rates and the titrant concentration seemingly followed the simplest 1:1 binding isotherm (Figure 1 and Figure 2, Panel A). The maximal rates from each of the titration curves were linearly dependent on the concentration of the limiting complex partner, regardless of the choice of titrant (Figure 1 and Figure 2, Panel B). The low dissociation constant for the binary complex in each set of experiments is reasonable based on similar reported values for titrations by other P450 systems (12, 22, 31, 32). Each data set viewed independently would support the contention that only a single functional complex forms between CPR-K56Q and P450 2E1. However, depending on which component was varied and which was held constant, the two subsets of the experimental data were mutually contradictory. With CPR-K56Q used as the titrant, the apparent Kd 2.5-fold higher and the apparent kcat was approximately 50 % higher, compared to the data obtained with P450 2E1 as the titrant (Table 1). Thus, a reliance on simple titrations to study protein-protein interactions has led to contradictory conclusions.
To shed light on the inconsistencies resulting from the postulated 1:1 binding model, we generated a traditional Job plot (28, 33) to determine a possible presence of higher order complexes, characterized by stoichiometries other than 1:1. For this study, catalytic activity was measured as a function of the mole fraction for each complex partner at a constant total molar concentration of protein. The exclusive presence of a 1:1 binary complex between P450 2E1 and CPR-K56Q should yield a symmetrical parabola with a maximum at mole fraction (χ) exactly identical to 0.5, where the concentrations of P450 and CPR are the same. For P450 2E1 and CPR-K56Q, we found the maximum rate to be located clearly at χ< 0.5 (Figure 3), indicating that a higher molecular order complex was in fact present. The simultaneous presence of a binary complex cannot be ruled out. For example, a binary complex could serve as an intermediate to forming a higher order complex.
Although the first reported Job plot for a P450 system was symmetrical (12), subsequent publications (34, 35) for the P450 2B1 system included asymmetrical curves, whereby the maxima for the reaction rates were less than a mole fraction of 0.5 as we observed for P450 2E1. The unexpected Job plot for P450 2B1 was independent of the type (34, 35) or concentration (34) of lipid present. Whereas the authors suggested the unexpected results were due to detergent contamination or protein aggregation, we interpret their results as early evidence of the actual molecular order of the P450 complex. Coupled with our findings for P450 2E1, these results for P450 2B1 suggest higher molecular order functional complexes may be more common mechanism determining activities for P450s. Nevertheless, the strategy of relying on simple catalytic titrations, where one component concentration is held constant and the other varied, or a single Job plot to determine the mechanism of complexation is obviously not sufficient.
Despite the general acceptance of the binary complex mechanism, there is accumulating evidence in support of alternative functional complexes. The temperature dependence for P450 reduction by CPR provided early support for the presence of mobile and immobile populations of P450s. Based on the properties of reduction and known excess of P450s relative to CPR (4), the authors favored a functional complex in which 8 to 12 P450 molecules associated with an individual CPR molecule, which was in equilibrium with a mobile P450 population. The use of detergents to modulate protein-protein interactions provided the first direct evidence for higher order functional complexes. Based on sedimentation and gel filtration studies, P450 1A2 (36) and 2B4 (37) formed pentamers that associated with CPR for optimal activity (P4505•CPR). CPR also formed dimers and other higher ordered complexes; however, low amounts of detergent dispersed the complexes indicating CPR homo-oligomers were less stable than those for the P450s.
More recently, the binary complex model failed to explain activity from mixed P450 systems whereby two different P450s were co-expressed or reconstituted with CPR. Rather than simple competition as expected for a single binary functional complex, different P450 isoforms decreased, increased, or did not alter respective P450 activities (reviewed in (38)). To explain these observations, Backes et al. (19) proposed several alternate mechanisms including the traditional binary complex mechanism and compared the simulations of these mechanisms to correlate changes in protein concentration to activity. The most likely mechanism incorporated the generation of two functional complexes; each of the respective P450s associated with CPR to form a ternary (P4502•CPR) complex, whose catalytic properties were distinct from an intermediary binary (P450•CPR) complex. Building on previous efforts, another proposal incorporated more elaborate complexation mechanisms (20) incorporating binary, ternary, and quaternary (P4502•CPR2) complexes formed from monomeric and dimeric P450s and CPR. The authors based the formation of these complexes on (a) the crystallization of some P450s and CPR as dimers and (b) the known self-association of P450 and CPR whereby the dimer is the simplest homo-oligomer.
Similar to the approach adopted by Hazai et al. (20), we proposed that multiple functional complexes were possible under our reaction conditions. Specifically, varying the concentrations of P450 2E1 and CPR-K56Q could result in the formation of binary (P450•CPR), ternary (P450)2•CPR and P450•(CPR2), and quaternary (P4502•CPR2) complexes in the absence or presence or P450 and CPR homodimers. Unlike the authors of the original study, we wanted to explore all possible combinations of complexes that could exist and discriminate between the corresponding models to identify the most likely one for the P450 2E1 system. Due to the experimental evidence for the binary complex, we required all models to possess the P450•CPR complex. To further simplify this effort, we assumed all active complexes contained at least one P450 and one CPR molecule, respectively. We did not consider the alternate pathways to generate complexes. Like in other studies (19, 39), our system was at equilibrium and therefore (29) we could not even in principle determine the path through which these complexes were generated. Our equilibrium binding studies could only reveal which complexes were most likely to be present under reaction conditions. A more in depth understanding of the complexation would require further study. Altogether, there were 32 possible combinations of these complexes (Table 2).
An investigation of the possible complexation mechanisms required a suitable data set describing the system of interest. Rather than the choice of titrant causing the conflicting results with the initial sets of catalytic titrations, the conditions of the experiments likely introduced bias in the analysis. Titrations were unidirectional in that the titrant was added to excess with respect to the limiting complex partner, rather than any of the conditions in between these extremes. Our initial titrations and Job plot were limited subsets of data for the system, and thus limited the ability to assess the role of protein-protein interactions in regulating P450 activity. Similarly, reliance on the titration format and small data sets may explain why groups were not able to actually fit data from mixed P450 systems to possible complexation mechanisms (19, 32, 39, 40).
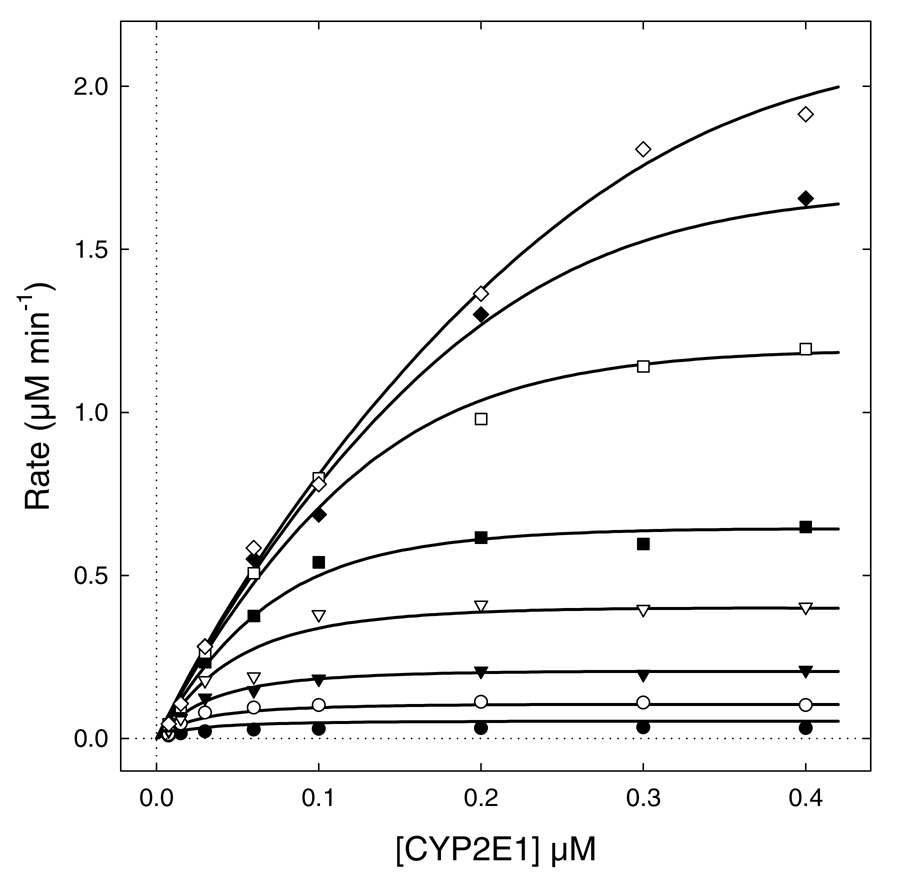
As discussed by Beechem (41), global analysis of multi-dimensional data, for example, where multiple component concentrations are simultaneously varied and the entire superset is analyzed as a whole, is always more informative about the underlying biochemical mechanism, in comparison with trying to analyze individual subsets of data separately. For this study, we generated a two-dimensional data set where both P450 and CPR were simultaneously varied over a wide range of concentrations. In contrast, our preliminary experiments shown in Figure 1 and Figure 2 only covered a narrow range of concentrations for either of the fixed components (P450 in Figure 1 or CPR in Figure 2). The experimental data we have collected are shown in Figure 4. These respective data sets provided an opportunity to determine which approach yielded most useful information about the P450 2E1 system.
FIGURE 4.
The pooled experimental data and the best-fit model (smooth curves) for Model #14c defined in Table 3 and Scheme 2. P450 2E1 was varied from 7.5 nM to 400 nM. CPR concentrations were as follows: 7.5 nM (filled circles); 15 nM (filled circles); 30 nM (filled triangles); 60 nM (open triangles); 100 nM (filled squares); 200 nM (open squares); 300 nM (filled diamonds); 400 nM (open diamonds). The best-fit model is represented by the system of simultaneous nonlinear algebraic Eqns (3–6), automatically derived and numerically solved by the software package DynaFit (23).
While previous efforts (19, 20) simulated a limited number of proposed mechanisms, we fit our experimental data for the P450 2E1 system to 32 distinct models. Our ability to globally analyze the resulting data marked a significant step forward in understanding protein-protein interactions. The fit of each model provided values for parameters for models and corresponding confidence limits. From these fits, we also generated a corresponding second-order Akaike Information Criterion (AICc, (26)) to describe statistically the quality of the respective fits. Based on the differences between AICc for the proposed models (ΔAICc), we were able to identify a group of probable models for the P450 2E1 system. The results of this first round of model discrimination are summarized in Table 3.
Out of the 32 models examined, only four produced Akaike weight w (Eqn 8) higher than 0.10 (Table 3). This corresponds to the statistical probability higher than 10 % that the given theoretical model could represent the "true" binding mechanism. Model #32 (last row in Table 3) was excluded from further consideration because it produced extremely high uncertainty in all adjustable model parameters (data not shown). This is not surprising, because Model #32 encompasses all possible molecular interactions we allowed, with the simultaneous formation of six different P450–CPR complexes (four of which were presumed to be catalytically active), including the two homodimers. This degree of mechanistic complexity cannot be captured in our kinetic data. Therefore, we focused our attention on the three remaining mechanisms, Models #13, #14, and #15 (see Table 3).
Models #13 through #15 are quite similar, in that they all involve the formation of the binary complex P450•CPR and the quaternary complex (P450)2•(CPR)2. The difference between the three mechanisms is a possible presence of either the ternary complex (P450)2•CPR (Model #14) or the ternary complex P450•(CPR)2 (Model #15). We consider the similarity within this small family of plausible binding mechanisms encouraging – a good evidence for the applicability of the Akaike Information Criterion in model discrimination (26). It would have been harder to understand if widely dissimilar mechanisms turned out equally plausible by AICc.
The best-fit values of the turnover numbers for the various complexes appearing in Models #13 through #15 followed a consistent pattern, in that the numerical values of kcat for all complexes, except the binary complex P450•CPR, were at least three orders of magnitude lower when compared to the kcat for P450•CPR. We interpreted this result to mean that although the quaternary complex (P450)2•(CPR)2 is quite clearly formed, it is likely not to be catalytically active. The same applies to the homodimer (P450)2 and to the ternary complexes (P450)2•CPR (Model #14) or P450•(CPR)2 (Model #15). Therefore, in the next round of model discrimination analysis we rendered various P450–CPR complexes catalytically inactive, by assigning to them zero turnover number in the corresponding mathematical models. This generated eight candidate models (mechanisms) summarized in Table 4, along with the numerical results of model discrimination.
Nominally the most plausible model in Table 4 is represented by Model #13b, shown in greater detail in Scheme 2. According to this mechanism, P450 forms a homodimer and additionally three different molecular complexes with CPR, namely, the catalytically active 1:1 complex P450•CPR and two catalytically inactive complexes, (P450)2•(CPR)2 and (P450)2•CPR. The nonsymmetrical confidence intervals (30) for all model parameters (equilibrium constants and turnover numbers) are listed in Table 5. The overall stability of the ternary complex (P450)2•CPR, as measured by the dissociation constant Kd3 in Scheme 2, is significantly lower in comparison with the stability of both the binary complex (Kd2) and the quaternary complex (Kd4).
It is important to point out that, on the basis of equilibrium binding studies, we cannot unambiguously determine the pathway(s), by which the quaternary complex is formed, and in this sense the mechanism shown in Scheme 2 is only one of two possible pathways. In principle, the quaternary complex (P450)2•(CPR)2 could also be formed from the ternary complex (P450)2•CPR by associating an additional CPR molecule. However, this would imply that the association of the second molecule of CPR to the ternary complex (P450)2•CPR would have to be accompanied by strong positive cooperativity, given the relative values of Kd3 < Kd4. For this reason we favor the mechanism shown in Scheme 2, according to which the quaternary complex is shown by dimerization of the heterodimer P450•CPR.
Concluding remarks
Although we initially assumed recombinant CPR-K56Q and P450 2E1 formed a single functional complex, our study revealed that P450 2E1 catalytic activity derives from the presence of multiple complexes, which co-exist under reaction conditions. The formation of these complexes resulted in an overall negative cooperative effect, whereby higher P450 concentrations suppressed activity. This effect may provide a toxicological advantage for the metabolism of P450 2E1 substrates when toxic products are generated. Through these efforts, we identified inherent shortcomings of traditional approaches to studying protein-protein interactions. To better understand the P450 system, we are the first to eliminate bias from reaction conditions and globally analyze data to identify the most probable complexes present in the system. Knowledge of these complexes provide an important foundation for further studies to confirm the presence of the complexes and explore the role of their formation and contribution to overall enzymatic activity. The utility of our approach applies to any two-component system such as protein-ligand and protein-protein interactions, which provide the foundation for many biological processes.
Supplementary Material
The file includes the scripts (input data) for the DynaFit (23) software and the resulting output files. This information is available free of charge via the Internet at http://pubs.acs.org.
ACKNOWLEDGEMENTS
We are thankful for helpful comments from a reviewer of the manuscript.
This work was supported by National Institutes of Health NCRR COBRE Grant 1 P20 RR015569-06.
Footnotes
The abbreviations used are: P450, cytochrome P450; CPR, cytochrome P450 reductase; CPR-K56Q, cytochrome P450 reductase with Lys56Gln substitution; pNP, p-nitrophenol; pNC, p-nitrocatechol; NADP+, nicotinamide adenosine dinucleotide phosphate (oxidized); AIC, Akaike Information Criterion.
REFERENCES
- 1.Kuzmic P. A generalized matrix formalism for steady state enzyme kinetics: Application to 17beta-HSD. Mol. Cell. Endocrinol. 2006;248:172–181. doi: 10.1016/j.mce.2005.10.012. [DOI] [PubMed] [Google Scholar]
- 2.Porter TD, Coon MJ. Cytochrome P-450: multiplicity of isoforms, substrates, and catalytic and regulatory mechanisms. J. Biol. Chem. 1991;266:13469–13472. [PubMed] [Google Scholar]
- 3.Hlavica P, Schulze J, Lewis DF. Functional interaction of cytochrome P450 with its redox partners: a critical assessment and update of the topology of predicted contact regions. Inorg. Biochem. 2003;96:279–297. doi: 10.1016/s0162-0134(03)00152-1. [DOI] [PubMed] [Google Scholar]
- 4.Estabrook R, Franklin MR, Cohen B, Shigamatzu A, Hildebrandt AG. Biochemical and genetic factors influencing drug metabolism. Influence of hepatic microsomal mixed function oxidation reactions on cellular metabolic control. Metabolism. 1971;20:187–199. doi: 10.1016/0026-0495(71)90091-6. [DOI] [PubMed] [Google Scholar]
- 5.Watanabe J, Asaka Y, Fujimoto S, Kanamura S. Densities of NADPH-ferrihemoprotein reductase and cytochrome P-450 molecules in the endoplasmic reticulum membrane of rat hepatocytes. J. Histochem. Cytochem. 1993;42:43–49. doi: 10.1177/41.1.8417111. [DOI] [PubMed] [Google Scholar]
- 6.Gut J, Richter C, Cherry RJ, Winterhalter KH, Kawato S. Rotation of cytochrome P-450: complex formation of cytochrome P-450 with NADPH-cytochrome P-450 reductase in liposomes demonstrated by combining protein rotation with antibody-induced cross-linking. J. Biol. Chem. 1983;258:8588–8594. [PubMed] [Google Scholar]
- 7.Schwarz D, Pirrwitz J, Ruckpaul K. Rotational diffusion of cytochrome P-450 in the microsomal membrane - evidence for a clusterlike organization from saturation transfer electron paramagnetic resonance spectroscopy. Arch. Biochem. Biophys. 1982;216:322–328. doi: 10.1016/0003-9861(82)90217-x. [DOI] [PubMed] [Google Scholar]
- 8.Tamburini PP, MacFarquhar S, Schenkman JB. Evidence of binary complex formations between cytochrome P-450, cytochrome b5, and NADPH-cytochrome P-450 reductase of hepatic microsomes. Biochem. Biophys. Res. Commun. 1986;134:519–526. doi: 10.1016/s0006-291x(86)80451-x. [DOI] [PubMed] [Google Scholar]
- 9.Nisimoto Y, Otsuka-Murakami H. Cytochrome b5, cytochrome c, and cytochrome P-450 interactions with NADPH-cytochrome P-450 reductase in phospholipid vesicles. Biochemistry. 1988;27:5869–5876. doi: 10.1021/bi00416a008. [DOI] [PubMed] [Google Scholar]
- 10.Yang CS, Strickhart FS. Interactions between solubilized cytochrome P-450 and hepatic microsomes. J. Biol. Chem. 1975;250:7968–7972. [PubMed] [Google Scholar]
- 11.Yang CS, Strickhart FS, Kicha LP. Interaction between NADPH-cytochrome P-450 reductase and hepatic microsomes. Biochim. Biophys. Acta. 1978;509:326–337. doi: 10.1016/0005-2736(78)90051-2. [DOI] [PubMed] [Google Scholar]
- 12.Miwa GT, West SB, Huang MT, Lu AY. Studies on the association of cytochrome P-450 and NADPH-cytochrome c reductase during catalysis in a reconstituted hydroxylating system. J. Biol. Chem. 1979;254:5695–5700. [PubMed] [Google Scholar]
- 13.Guengerich FP, Kim DH, Iwasaki M. Role of human cytochrome P-450 IIE1 in the oxidation of many low molecular weight cancer suspects. Chem. Res. Toxicol. 1991;4:168–179. doi: 10.1021/tx00020a008. [DOI] [PubMed] [Google Scholar]
- 14.Ronis M, Lindros KO, Ingelman-Sundberg M. In: Cytochromes P450 - metabolic and toxicological aspects. Ioannides C, editor. Boca Raton, FL: CRC Press; 1996. pp. 211–239. [Google Scholar]
- 15.Yamazaki H, Nakano M, Gillam EMJ, Guengerich FP, Shimada T. Requirements for cytochrome b5 in the oxidation of 7-ethoxycoumarin, chlorzoxazone, aniline, and N-nitrosodimethylamine by recombinant cytochrome P450 2E1 and by human liver microsomes. Biochem. Pharmacol. 1996;52:301–309. doi: 10.1016/0006-2952(96)00208-0. [DOI] [PubMed] [Google Scholar]
- 16.Lewis DF, Bird MG, Parke DV. Molecular modelling of CYP2E1 enzymes from rat, mouse and man: an explanation for species differences in butadiene metabolism and potential carcinogenicity, and rationalization of CYP2E substrate specificity. Toxicology. 1997;118:93–113. doi: 10.1016/s0300-483x(96)03583-4. [DOI] [PubMed] [Google Scholar]
- 17.Bonina TA, Gilep AA, Estabrook RW, Usanov SA. Engineering of proteolytically stable NADPH-cytochrome P450 reductase. Biochemistry (Moscow) 2005;70:357–365. doi: 10.1007/s10541-005-0122-3. [DOI] [PubMed] [Google Scholar]
- 18.Collom SL, Jamakhandi AP, Tackett AJ, Radominska-Pandya A, Miller GP. CYP2E1 active site residues in substrate recognition sequence 5 identified by photoaffinity labeling and homology modeling. Arch. Biochem. Biophys. 2007;459:59–69. doi: 10.1016/j.abb.2006.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Backes WL, Batie CJ, Cawley GF. Interactions among P450 enzymes when combined in reconstituted systems: formation of a 2B4-1A2 complex with a high affinity for NADPH-cytochrome P450 reductase. Biochemistry. 1998;37:12852–12859. doi: 10.1021/bi980674a. [DOI] [PubMed] [Google Scholar]
- 20.Hazai E, Bikadi Z, Simonyi M, Kupfer D. Association of cytochrome P450 enzymes is a determining factor in their catalytic activity. J. Comput. Aided Mol. Design. 2005;19:271–285. doi: 10.1007/s10822-005-4995-4. [DOI] [PubMed] [Google Scholar]
- 21.Cheng D, Kelley RW, Cawley GF, Backes WL. High-level expression of recombinant rabbit cytochrome P450 2E1 in Escherichia coli C41 and its purification. Prot. Express. Purif. 2004;33:66–71. doi: 10.1016/j.pep.2003.08.009. [DOI] [PubMed] [Google Scholar]
- 22.Bridges A, Gruenke L, Chang Y-T, Vakser IA, Loew G, Waskell L. Identification of the binding site on cytochrome P450 2B4 for cytochrome b5 and cytochrome P450 reductase. J. Biol. Chem. 1998;273:17036–17049. doi: 10.1074/jbc.273.27.17036. [DOI] [PubMed] [Google Scholar]
- 23.Kuzmic P. Program DYNAFIT for the analysis of enzyme kinetic data: Application to HIV proteinase. Anal. Biochem. 1996;237:260–273. doi: 10.1006/abio.1996.0238. [DOI] [PubMed] [Google Scholar]
- 24.I T-P, Nancollas GH. EQUIL -- A general computational method for the calculation of solution equilibria. Anal. Chem. 1972;44:1940–1950. [Google Scholar]
- 25.Price KV, Storm RM, Lampinen JA. Differential Evolution - A Practical Approach to Global Optimization. Berlin - Heidelberg: Springer Verlag; 2005. [Google Scholar]
- 26.Burnham KB, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. 2nd ed. New York: Springer-Verlag; 2002. [Google Scholar]
- 27.Burnham KP, Anderson DR. Model Selection and Multimodel Inference - A Practical Information-Theoretic Approach. 2nd Edition ed. New York: Springer; 2004. [Google Scholar]
- 28.Job P. Recherches sur la formation de complexes mineraux en solution, et sur leur stabilityé. Ann. Chim. (Paris) 1928;9:113–203. [Google Scholar]
- 29.Denbigh K. The Principles of Chemical Equilibrium. Cambridge: Cambridge University Press; 1964. [Google Scholar]
- 30.Bates DM, Watts DG. Nonlinear Regression Analysis and its Applications. New York: Wiley; 1988. [Google Scholar]
- 31.Kaminsky LS, Lee JJ, Guengerich FP. Abstracts, Fourth International Symposium on Comparative Biochemistry. Belgium: Beerse; 1985. p. 43. [Google Scholar]
- 32.Kelley RW, Reed JR, Backes WL. Effects of ionic strength on the functional interactions between CYP2B4 and CYP1A2. Biochemistry. 2005;44:2632–2641. doi: 10.1021/bi0477900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huang CY. Determination of binding stoichiometry by the continuous variation method: the Job plot. Methods Enzymol. 1982;87:509–525. doi: 10.1016/s0076-6879(82)87029-8. [DOI] [PubMed] [Google Scholar]
- 34.Miwa GT, Lu AYH. Studies on the stimulation of cytochrome P-450-dependent monooxygenase activity by dilauroylphosphatidylcholine. Arch. Biochem. Biophys. 1981;211:454–458. doi: 10.1016/0003-9861(81)90477-x. [DOI] [PubMed] [Google Scholar]
- 35.Miwa GT, Lu AYH. The association of cytochrome P-450 and NADPH-cytochrome P-450 reductase in phospholipid membranes. Arch. Biochem. Biophys. 1984;234:161–166. doi: 10.1016/0003-9861(84)90337-0. [DOI] [PubMed] [Google Scholar]
- 36.Sevrukova IF, Kanaeva IP, Koen YM, Samenkova NF, Bachmanova GI, Archakov AI. Catalytic activity of cytochrome P4501A2 in reconstituted system with Emulgen 913. Arch. Biochem. Biophys. 1994;311:133–143. doi: 10.1006/abbi.1994.1218. [DOI] [PubMed] [Google Scholar]
- 37.Dean WL, Gray RD. Relationship between state of aggregation and catalytic activity for cytochrome P-450LM2 and NADPH-cytochrome P-450 reductase. J. Biol. Chem. 1982;257:14679–14685. [PubMed] [Google Scholar]
- 38.Backes WL, Kelley RW. Organization of multiple cytochrome P450s with NADPH-cytochrome P450 reductase in membranes. Pharmacol. Therapeut. 2003;98:221–233. doi: 10.1016/s0163-7258(03)00031-7. [DOI] [PubMed] [Google Scholar]
- 39.Hazai E, Kupfer D. Interactions between Cyp2C9 and Cyp2C19 in reconstituted binary systems influence their catalytic activity: Possible rationale for the inability of Cyp2C19 to catalyze methoxychlor demethylation in human liver microsomes. Drug Metab. Dispos. 2005;33:157–164. doi: 10.1124/dmd.104.001578. [DOI] [PubMed] [Google Scholar]
- 40.Davydov DR, Petushkova NA, Bobrovnikova EV, Knyushko TV, Dansette P. Association of cytochromes P450 1A2 and 2B4: are the interactions between different P450 species involved in the control of the monooxygenase activity and coupling? Adv. Exp. Med. Biol. 2001;500:335–338. doi: 10.1007/978-1-4615-0667-6_53. [DOI] [PubMed] [Google Scholar]
- 41.Beechem JM. Global analysis of biochemical and biophysical data. Meth. Enzymol. 1992;210:37–54. doi: 10.1016/0076-6879(92)10004-w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The file includes the scripts (input data) for the DynaFit (23) software and the resulting output files. This information is available free of charge via the Internet at http://pubs.acs.org.