Abstract
Because it increases relatedness between interacting individuals, population viscosity has been proposed to favour the evolution of altruistic helping. However, because it increases local competition between relatives, population viscosity may also act as a brake for the evolution of helping behaviours. In simple models, the kin selected fecundity benefits of helping are exactly cancelled out by the cost of increased competition between relatives when helping occurs after dispersal. This result has lead to the widespread view, especially among people working with social organisms, that special conditions are required for the evolution of altruism. Here, we re-examine this result by constructing a simple population genetic model where we analyse whether the evolution of a sterile worker caste (i.e. an extreme case of altruism) can be selected for by limited dispersal. We show that a sterile worker caste can be selected for even under the simplest life-cycle assumptions. This has relevant consequences for our understanding of the evolution of altruism in social organisms, as many social insects are characterized by limited dispersal and significant genetic population structure.
Keywords: altruism, sterile workers, Hamilton's rule, population viscosity, inclusive fitness, dispersal
1. Introduction
Family-based group structure and high relatedness are recognized as key factors allowing the emergence of altruistic behaviours in social animals such as ants, bees and cooperative breeding birds and mammals (Bourke & Franks 1995; Emlen 1997). Hamilton (1971) also proposed that limited dispersal of individuals from the natal group (population viscosity) would increase the relatedness between interacting individuals, and so would be a factor favouring the evolution of altruistic helping. But genetically-related neighbours also more strongly compete for the same local resources, which could at least partially offset the fecundity benefits to neighbours. Analysing a situation where adult individuals help their group neighbours after dispersal and where relatedness depends on group size and migration rates, Taylor (1992a,b) showed that the kin selected fecundity benefits arising as a result of limited dispersal are exactly cancelled out by the cost of increased competition between relatives. Taylor's results has lead to the widespread view that limited dispersal (population viscosity) cannot favour the evolution of altruism when helping occurs after dispersal (e.g. Queller 1992; Taylor 1992a; Chapuisat et al. 1997; Mittledorf & Wilson 2000; West et al. 2002, 2006; Yamamura et al. 2004; Trontti et al. 2005). However, it has also been emphasized (Rousset 2004, pp. 112–115) that a helping trait can qualify as altruistic in Taylor's model once it is defined from its effect on fitness (i.e. expected number of adult offspring produced by an adult) as Hamilton (1964, 1970) did. Rousset's (2004) analysis suggests that, contrary to the current view, extreme cases of reproductive altruism might evolve in viscous populations when helping occurs after dispersal, even without considering life-cycle conditions (e.g. overlapping generations, empty breeding spots, kin recognition, budding dispersal, selective extinction, selective emigration, long-lasting niche construction effects) that are known to promote the evolution of altruism.
The aim of this paper is to determine whether specialized worker sterile caste can be selected for when workers help after dispersal under conditions of high kin competition. To do this we construct a simple population genetic model, where we analyse whether a specialized worker sterile caste can evolve when helping occurs after dispersal. We investigate the direction of selection on worker caste under haploid, diploid and haplo-diploid genetic systems; under maternal and offspring control of the trait; and under infinite island and isolation by distance population structures. Our results show that under all these settings, the evolution of sterile workers can easily evolve under minimal life-cycle conditions. This illustrates that limited dispersal is a potent force favouring the evolution of sterile workers in a situation that was previously unrecognized.
2. Model
(a) Life cycle
We consider a population consisting of an infinite number of colonies connected by random migration (isolation by distance is considered in appendix A). We assume that each colony has a finite number N of breeding spots, each of which is occupied by a single queen and a variable number of sterile individuals (the workers) that conduct all the tasks necessary to raise the brood. Under this population setting, we consider that a single locus with additive gene action controls the expression of a helping behaviour and that two alleles segregate at this locus: a mutant allele and a resident (wild-type) allele. A focal adult queen bearing a copy of the mutant helping allele (or two copies in the case of diploidy) produces an additional amount of workers (i.e. maternal control of the trait) at a cost C (relative to a queen bearing the resident allele) in terms of the number of reproductive individuals (new queens and males) produced. We assume colony productivity to be an increasing function of the number of workers relative to the number of larvae in a colony (worker-to-larvae ratio), and that the additional workers produced by a focal queen bearing the mutant allele (relative to those produced by a queen bearing the resident allele) increase colony productivity by B. This formulations of the cost (C) and the benefit (B) also applies to the origin of the worker caste as well, in which case adult individuals bearing two copies of the resident (wild-type) allele do not produce any workers at all. We investigate the direction of selection on the helping allele under haploid, diploid and haplo-diploid genetic systems (here males are haploid as in Hymenoptera), and under maternal and offspring control of the trait.
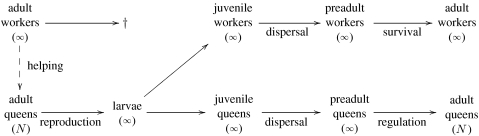
The sequence of life-history events is as follows (figure 1). (i) Each adult individual (queen) produces, with the help of workers, a very large number of broods that can develop into queens, males or workers (the later being completely sterile). (ii) These offspring disperse independently of each other with probability m to a new colony. All mother queens as well as workers of the previous generation die. (iii) The males compete for mating and every new queen mates once. All males die. (iv) Density-dependent competition occurs among queens for access to the N breeding spots per colony. All new workers (same generation as the queens) survive and then help to raise the brood in their colony.
Figure 1.
Life cycle. For simplicity, we considered only a haploid representation.
In this model, the density-dependent competition occurring among queens for the N breeding spots can be interpreted as being competition for space. This interpretation does not preclude density-dependent competition occurring among queens or workers for resources. But we assume that enough queens are produced to fill all the breeding spots in the population, in which case competition for resources between members of a colony does not affect the dynamics of helping under our life-cycle assumptions.
Under these assumptions, the change over one iteration of the life cycle in the frequency p of a mutant helping allele, whose phenotypic effect on fitness deviates only slightly from that of a resident allele (weak selection), can be written as , where S is frequency independent (Rousset 2004, pp. 108–109 and pp. 206–207). Accordingly, the coefficient of selection S determines the direction of selection on the helping trait at all allele frequencies under weak selection and fits Hamilton's definition of the inclusive fitness effect (Hamilton 1964, 1970), which is a relatedness-weighted sum of the expected effects of all actors in the population on the fitness of a focal individual bearing the mutant allele. In order to evaluate the inclusive fitness effect, we adopt the gene-centred point of view of the direct fitness method (e.g. Taylor & Frank 1996; Frank 1998; Rousset & Billiard 2000; Rousset 2004), concentrating on a copy of the mutant allele residing in a focal adult (e.g. Rousset 2004, pp. 138–140). We then evaluate the effect of all actors expressing the helping allele in a colony on the fitness of the focal individual (including the effect of the focal individual on itself). This approach allows us to consider both a parental and offspring control of the helping allele. As our model is very close to that of Taylor (1992a), we structured its development in a similar way to facilitate comparisons.
(b) Haploid reproduction
Under haploid reproduction, stage 3 of the life cycle is absent and offspring are genetically identical to their mother. By producing workers, a focal queen decreases the number of her reproductive offspring (new queens) by C. This is the direct fitness cost of helping. Producing workers instead of queens also reduces the amount of local competition between juvenile queens, so that helping has an indirect effect on the fitness of a focal queen. The additional number of focal queen's juveniles that find a local breeding spot as a result of her producing workers is given by C(1−m)2/N, where (1−m)2 is the probability that an offspring of the focal queen competes against another offspring produced in the focal colony and C/N is the decrease in average colony productivity caused by the action of the focal queen. The total decrease in local competition depends on the total number of queens in the focal colony carrying the mutant helping allele. The net indirect fitness benefit is then given by C(1−m)2 weighted by , where Q is the probability that two distinct adults sampled randomly from the same colony carry homologous genes identical by descent (probability of identity evaluated after dispersal).
The increment in the number of juveniles produced by the focal queen as a result of the additional workers produced by queens of the parental generation carrying the mutation depends on the relative benefit B of helping, weighted by the probability that a worker remains philopatric and the probability that a queen from the parental generation carries the same helping allele as the focal queen. This weight is equal to the probability Q that two adults sampled from the same colony carry homologous genes identical by descent, which produces a benefit of BQ. Since workers help unconditionally every queen on the focal patch, helping also increases local competition. The number of juvenile queens of the focal queen, which are displaced as a consequence of the increased competition is given by (1−m)2BQ. The overall accounting is provided in table 1.
Table 1.
Inclusive fitness change: asexual.
| offspring number | weight |
|---|---|
| −C | 1 |
| C(1−m)2 | QR |
| B(1−(1−m)2) | Q |
In order to ascertain whether the mutant helping allele will invade the population, we need to calculate the explicit value of the relatedness coefficient Q. At equilibrium, we have
| (2.1) |
because with probability (1−m)2, two different adult individuals randomly sampled from the same colony are philopatric, in which case they descend with probability 1/N from the same mother (e.g. Taylor 1992a; Frank 1998; Rousset 2004). From this equation, and the definition of QR we have . Using this result and summing up all the elements of the first column in table 1, weighted by the corresponding elements of the right column, allows us to write the inclusive fitness effect as
| (2.2) |
The mutant allele is selected for when S>0, i.e. when , which, upon insertion of equation (2.1) and simplification, gives
| (2.3) |
This inequality indicates that worker production is selected for provided that the cost-to-benefit ratio is lower than the probability that a worker and a queen descend from the same mother (i.e. with probability (1−m)2 two individuals originate from the same group, in which case they descend from the same mother with probability 1/N). Hence, helping is favoured because workers eventually help individuals from the same parental gene lineage.
Equation (2.3) reveals that sterile workers (whose production results in a decreased number of new queens produced by the focal queen) can be selected for even when helping occurs after dispersal. The difference between our model and Taylor's (1992a) original model, where the benefits cancel out, is that the benefit B of helping in our life history is conferred to receptors (queens) only after dispersal by the workers produced by a focal queen (as opposed of being conferred directly by the focal adult itself in Taylor's model). By contrast, adults carrying the mutant helping allele in Taylor's model simultaneously help neighbours and bear the cost of helping (in that respect they differ from the workers), hence resulting in greater competition for the focal adult's own offspring than in our model. Accordingly, in Taylor's model, the focal adult looses more offspring through kin competition by expressing the mutant helping allele. The additional number of offspring lost by a focal adult when it directly helps its neighbours, instead of its descendants doing so in the next generation is B(1−m)2/N (see Taylor (1992a), eqn (1) and Rousset (2004), eqn (7.13)), which is equivalent to the left hand side of equation (2.3).
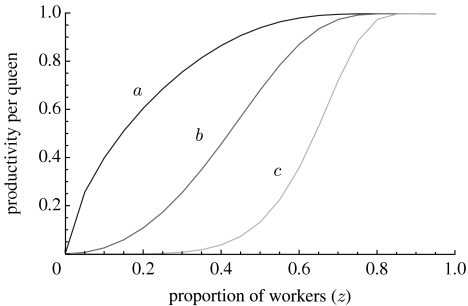
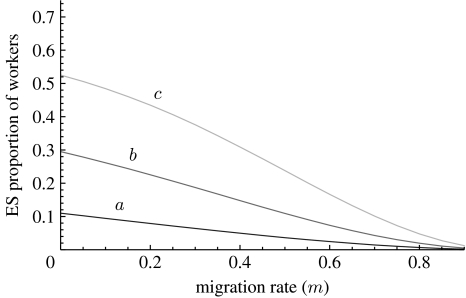
The tension between the cost C and the benefit B in equation (2.3) leads to a candidate evolutionarily stable (ES; Maynard-Smith 1982) proportion of worker phenotypes, which equalizes both sides of equation (2.3) when the worker phenotype is modelled explicitly (e.g. Taylor & Frank 1996; Frank 1998; Rousset 2004). If we denote by z, the probability that a larva develops into a worker, the relative productivity cost for the focal queen is given by C=1/(1−z) and the relative increment in colony productivity is , where the prime denotes a derivative and b(z) is a saturating production function (see Lehmann (2007), equations (A 1)–(A 7) for a derivation). The ES trait value ultimately depends on the shape of the production function b(z), an example of which is presented in figure 2. Figure 3 reveals that the ES probability of becoming a worker increases with decreased migration rate between colonies (i.e. higher population viscosity) and a slower saturation of worker number on group productivity.
Figure 2.
Productivity function of a queen graphed as a function of the proportion z of workers in a colony. The parameter y (varying between 0 and 1) and ν (varying between 0 and ∞) shape the production function from concave to sigmoidal. As y and ν increase, a higher proportion of workers is needed to achieve a given productivity. In the graph, the values of the parameters are set to y=0.1 for all lines, ν=0.7 for line a, ν=2 for line b and ν=5 for line c.
Figure 3.
Candidate ES probability z of developing the worker phenotype as a function of the migration rate m (population viscosity) with the number of queens per colony being set to N=5. The three curves correspond to the productivity functions depicted in figure 2 with the same label.
(c) Sexual reproduction
Evaluating the inclusive fitness effect under sexual reproduction is more difficult because both sexes have to be considered as well as the caste controlling the phenotype of offspring (i.e. maternal versus offspring control). In order to investigate these cases, we follow Taylor (1992a) and measure fitness in units of mated females. That is, we have to consider the expected number of adult mated females produced, through sons and daughters, by mated males and females carrying the mutation. If we denote by s the proportion of males to females (male-to-female colony sex ratio) produced by a female, each male expects 1/s mates; so every female produces the same number of mated females through sons and daughters, and the value of s does not affect the evolution of the helping allele (Taylor 1992a). For simplicity, we also assume that workers can be either males or females both in the diploid and haplo-diploid genetic systems. This assumption allows us to consider the diploid and haplo-diploid case simultaneously, under both parental and offspring control, and avoids us to derive four different models (note, assuming that only females can develop into workers affects the result in a quantitative but not in a qualitative manner).
In order to evaluate the inclusive fitness effect under sexual reproduction, we can use the fitness components already evaluated for the haploid model (left hand side of table 1), but must take into account that the focal helping allele can reside in an adult male or queen, and that it affects the fitness of these adults through the production of sons and queens. Hence, we need to weight the fitness components through each reproductive male and female by the probabilities tij that a gene randomly taken in an individual of sex i descends from an individual of sex j. This is tij=1/2 for all i and j in a diploid system while under haplo-diploidy the values are tff=1/2, tfm=1/2, tmf=1 and tmm=0. Since the frequency of transmission of a gene in the population through the different sexes differ under haplo-diploid genetics, we also need to weight the fitness components by the reproductive value νi of an individual of sex i (e.g. Taylor 1990, 1992a; Frank 1998; Rousset 2004). For a diploid system, νm=1/2 and νf=1/2, while for a haplo-diploid system νm=1/3 and νf=2/3. Finally, we will need to evaluate the probabilities of identity between homologous genes sampled within and between various categories of actors separately for maternal or offspring control of the trait.
(i) Maternal control
Under maternal control of the trait, only genes in adult females control the development of a larva into a worker or a reproductive individual. We thus need to consider the probability of identity of genes within females, and denote by Qi the probability of identity between two homologous genes randomly sampled with replacement from the same individual of sex i (i.e. coancestry with self). We also need the probability Qij of identity between a gene sampled in an adult of sex i and another homologous gene randomly sampled from a distinct adult of sex j (i.e. identity evaluated after dispersal). Finally, we need , which stands for the probability of identity between two genes sampled with replacement from same-sex individuals at the adult stage. The values of these probabilities for diploid and haplo-diploid genetic systems were obtained using the recursions presented in Taylor (1988; see appendix A), which allow us to calculate explicitly the weights of the various changes in fitness resulting from the expression of the helping allele under maternal control, and which are summarized in table 2.
Table 2.
Inclusive fitness change: sexual maternal control.
| offspring number | weight | |
|---|---|---|
| through daughters | −C | |
| C(1−m)2 | ||
| B(1−(1−m)2) | ||
| through sons | −C | |
| C(1−m)2 | ||
| B(1−(1−m)2) |
Summing up all the elements of this table and inserting the equilibrium values for the probabilities of identity (see appendix A) allows us to calculate the inclusive fitness effect under maternal control by following the same line of arguments as for the haploid case. For both, diploid and haplo-diploid reproduction, we find (see the electronic supplementary material) that the helping allele can invade the population when
| (2.4) |
This invasion condition is identical to the one for the haploid model (equation (2.3)). That the direction of selection on the helping allele is the same under haploid, diploid and haplo-diploid systems under maternal control parallels the results of Taylor (1992a).
(ii) Offspring control
Under offspring control of the worker caste, it is the genes in the larvae of a focal queen that control its own development into a worker or a reproductive individual. In this case, we also need to consider probabilities of identity by descent between juveniles, and denote by , the probability of identity between pairs of genes sampled in two juvenile individuals (i.e. the identity is evaluated before dispersal). Finally, we need the probability x=1/(1+s) that a worker helping a queen is a female. With this and standard inclusive fitness arguments (e.g. Taylor 1988; Rousset 2004, pp. 138–140), we find the expression of the helping allele results in the fitness changes given in table 3.
Table 3.
Inclusive fitness change: sexual offspring control.
| offspring number | weight | |
|---|---|---|
| through daughters | −C | |
| C(1−m)2 | ||
| B(1−(1−m)2) | ||
| B(1−(1−m)2) | ||
| through sons | −C | |
| C(1−m)2 | ||
| B(1−(1−m)2) | ||
| B(1−(1−m)2) |
By summing up all the elements in table 3, and inserting the equilibrium values of the probabilities of identity (see appendix A), we find (see the electronic supplementary material) that the direction of selection on the helping allele is again the same in the diploid and haplo-diploid systems
| (2.5) |
That is, the benefits of helping are exactly halved when compared with the case of maternal control (see equation (2.4)), but the worker caste may still be selected for. The decrease in selective pressure on the trait stems from the actor (i.e. the offspring) sacrificing itself under offspring control (relatedness to the receptor is one), while under maternal control the actor (i.e. the queen) sacrifices some of its offspring (relatedness to the receptor is less than one).
3. Discussion
In Taylor's (1992a,b) model, the indirect fecundity benefits of helping are exactly cancelled out by the increase in kin competition. This is a pivotal result for the evolution of helping behaviours in viscous populations because it provides a null model for comparative analyses and identification of life-cycle conditions promoting or inhibiting the evolution of helping in subdivided populations. For instance, previous work showed that costly helping can evolve when it results in group size expansion by reducing group extinction rates, or by increasing individual productivity through the effect of helping on several demographical variables (e.g. Eshel 1972; Aoki 1982; Taylor 1992a; van Baalen & Rand 1998; Le Galliard et al. 2003; Lehmann et al. 2006; Grafen 2007a; Lions & van Baalen 2007). Similarly, the possibility of kin recognition, punishment of defectors within groups, long-lasting niche construction effects, different modes of dispersal and competition between groups, different life histories such as overlapping generations and non-Poisson progeny distribution can also promote the evolution of costly helping (e.g. Rogers 1990; Taylor & Irwin 2000; Axelrod et al. 2004; Bowles & Gintis 2004; Gardner & West 2006; Jansen & van Baalen 2006; Grafen 2007b; Lehmann 2007; Rousset & Roze 2007; van Veelen & Hopfensitz 2007; Wakano 2007).
Taylor's findings also spread the view, especially among people working with social organisms, that special conditions are required to favour the evolution altruism when it is expressed after dispersal. Rousset's (2004, pp. 112–115) re-interpretation of Taylor's result showed that helping can qualify as altruistic in Taylor's model once it is defined from its effect on fitness (i.e. expected number of adult offspring produced by an adult). This result suggests that reproductive altruism could evolve even under the most minimalistic life-cycle assumptions in viscous populations. Here, we have put this idea to the test and found that, in a perfectly reasonable alternative biological scenario to Taylor's original model, a specialized worker sterile caste readily evolves without having to incorporate special life-cycle assumptions known to promote the evolution of altruism.
The conditions that have been derived here for a mutant altruistic allele to invade a population of residents (equations (2.3)–(2.5)) give the generic selective pressure on the probability that a larva becomes a sterile worker. For instance, for the haploid model, equation (2.3) can be applied to the origin of the worker caste, where the mutant allele induces a larva to become a worker only with a small probability while a larva bearing the resident allele always becomes a queen (weak selection). But this invasion condition (equation (2.3)) can also be applied to any mutant allele inducing a larva to increment by a small amount its probability to become a worker relative to that of a larva bearing a resident allele, and thus allows us to characterize the ES proportion of workers in the population. The ES proportion of sterile workers increases with decreased migration rate between colonies (i.e. higher population viscosity) and a slower saturation of worker number on group productivity (figure 3). The ES proportion of sterile workers increases with decreased migration rate between colonies (i.e. higher population viscosity) and a slower saturation of worker number on group productivity (figure 3). This finding holds for both parental and offspring control of the trait, although the selective pressure on altruism is halved under offspring control (compare equations (2.4) and (2.5)). The fact that these two types of control of the trait lead to different selection pressure on altruism also suggest that there can be genetic conflicts over who is in control of worker production within insect colonies, a topic that remains an empirically open question (Ratnieks & Wenseleers 2008).
Two assumptions about the population structure of our model are worth discussing. The first is that we assumed equal dispersal rates among males, queens and workers. This assumption was made because it allows us to investigate the evolution of the trait under both diploid and haplo-diploid genetic systems without adding too much complexity in the model. Under natural conditions, female and male dispersal rates are likely to differ, but such differences only have a quantitative effect on the dynamics of helping (results not shown). The second assumption is that of the infinite island model of dispersal, where individuals disperse randomly to new colonies. Haploid models with isolation by distance (presented in appendix A) reveal that the benefit B in the selective pressure on helping is weighted by the probability that a randomly sampled interacting worker and queen from the same colony descend from the same mother (see equation (A 10)). This is qualitatively exactly the same result as obtained for the infinite island model (see equation (2.3)). However, under isolation by distance this probability is increased relative to the infinite island model, because individuals from the same focal colony are likely to disperse to a same colony in the vicinity of the focal colony. Thereby, a migrant worker is likely to help a migrant queen stemming from the same natal colony. For instance, when migration occurs only to the nearest neighbour groups in a one-dimensional habitat (stepping-stone model of dispersal), the probability that two interacting individuals in a group descend from the same mother is (1−m)2+m2/2, instead of (1−m)2, with the consequence that the selective pressure on worker production increases markedly. Interestingly, this differs from other life-history conditions (e.g. overlapping generations) known to promote the evolution of costly helping (Taylor & Irwin 2000; Irwin & Taylor 2001; Ohtsuki et al. 2006; Grafen 2007b), because it was usually found that introducing isolation by distance in this case (Lehmann et al. 2007) does not significantly affect the selective pressure on helping among group members.
In conclusion, our theoretical analysis reveals that a specialized worker sterile caste can be selected for by population viscosity in a situation that was previously unrecognized. Our life-history model is very simple and similar to the life cycle of many ant species containing multiple queens per nest (e.g. Bourke & Franks 1995; Keller 1995). This has direct consequences for our understanding of the social behaviour of these organisms. For example, the social organization of some ants has been seen as a potential problem for kin selection theory because queens disperse between neighbouring colonies, hence resulting in almost no genetic differentiation at a local scale. However, the local dispersal of reproductive individuals typically results in significant population viscosity (Pamilo 1983; Sundstrom 1993; Herbers & Grieco 1995; Chapuisat et al. 1997; Ross et al. 1997, 1999; Pedersen & Boomsma 1999), which, as illustrated by our analyses, may select for the maintenance of reproductive altruism. Similarly, the occurrence of limited dispersal in many social organisms (e.g. Balloux & Lugon-Moulin 2002; Pope et al. 2006), and the ensuing viscosity, may help to reconcile theory and empirical studies showing that altruistic helping is relatively common in nature.
Acknowledgments
We thank Michel Chapuisat, Steve Frank, David Queller and François Rousset for their useful comments on previous versions of this manuscript. L.K. and L.L. were both supported by several grants from the Swiss NSF.
Appendix A.
(a) Probabilities of identity by descent
We computed the probabilities of identity between pairs of homologous genes sampled within and between individuals as is usually carried out for the infinite island model of dispersal (e.g. Taylor 1988; Frank 1998; Perrin & Mazalov 2000; Rousset 2004). All the results given in this appendix can directly be obtained from Taylor (1988), but since our notations differ from his, we still present the recurrence equations for the probabilities of identity.
(i) Diploid genetics
The probability of identity between two genes randomly sampled in two juveniles (right after reproduction) of sex i and j can be expressed as a function of the identities Qij between adults (after dispersal) by noting that with probability 1/4 the two genes are from maternal origin, with probability 1/4 they are both of paternal origin and with probability 1/2 one gene is of maternal origin and the other is of paternal origin. Because individuals are diploid, the probabilities of identity between any pair of juveniles are the same, irrespective of their sexes. Thereby, at equilibrium
| (A1) |
where Pf is the probability that two randomly sampled juveniles descend from the same female and Pm is the probability that two juveniles descend from the same male. With our life-cycle assumptions, we have Pf=Pm=1/N and Qf=Qm=(1+F)/2, where F is the inbreeding coefficient (i.e. probability of identity between the maternally and paternally inherited genes within an individual). The coefficient of inbreeding is equal to the genetic identity between the parents of an individual, which, at equilibrium, gives F=Qfm. When the dispersal rate is the same for each sex, the probabilities of identity between two genes sampled in two adults will be identical, irrespective of their sexes. Hence, and Qij is related to according to the equation
| (A2) |
The equilibrium value of Qij is then obtained by inserting equation (A 1) into equation (A 2) and solving for Qij (see the electronic supplementary material).
(ii) Haplo-diploid genetics
Under haplo-diploidy with haploid males and diploid females, the probability of identity between two genes randomly sampled in two juveniles (after reproduction) expressed as a function of the identities between adults (after dispersal) is, at equilibrium,
| (A3) |
where we used Qm=1, and, as for the diploid case, we have Pf=Pm=1/N with our life-cycle assumptions. As for the diploid case, we also have at equilibrium Qf=(1+F)/2 with F=Qfm and Qij is given by equation (A 2) with the given by equation (A 3).
(b) Isolation by distance
Here, we present a haploid version or our model, which takes isolation by distance into account in the same manner as in previous inclusive fitness models (Taylor 1992b; Gandon & Rousset 1999; Rousset & Billiard 2000; Irwin & Taylor 2001; Rousset 2004; Lehmann et al. 2007). We assume that the population consists of a finite discrete space: a circular lattice in one dimension and a torus in two dimensions where each node of the lattice consists of a colony of size N (e.g. Maruyama 1970; Malécot 1975; Nagylaki 1983; Taylor 1992b; Epperson 1999; Rousset 2004).
The life cycle is the same as the one presented in the main text, the only difference being the dispersal stage. Instead of juveniles dispersing randomly, each juvenile is now assumed to disperse with probability mj to a deme at distance j from its natal deme. ‘Distances’ in the population are denoted by a vector j, which refers to a coordinate (single or pair) of a deme relative to the position of a focal deme, so that j=0≡(0, 0) stands for the deme of a focal individual in two dimensions (i.e. focal deme). The dispersal distribution is assumed to be symmetric and identical for all individuals in all colonies (isotropic dispersal).
As in the infinite island model of dispersal, a focal queen decreases the number of her juvenile queens that will enter into competition for breeding spots by C. But queens from different colonies are likely to be related, and by producing workers instead of queens, a queen in a colony neighbouring the focal colony and bearing the mutant allele decreases the intensity of competition faced by the offspring of the focal queen. This increases indirectly the fitness of the focal queen. The additional number of a focal queen's juveniles that find a breeding spot when one queen bearing the mutant allele in colony j produces additional workers is given by , where is the probability that a focal queen's juveniles compete with offspring produced in deme j (with probability mi an offspring of the focal queen disperses at distance i, in which case it enters in competition with offspring produced in deme j with probability mi−j). By summing over all colonies and all individuals within colonies, the indirect fitness benefit stemming from the reduction in competition is given by , where is the probability that two individuals, sampled with replacement from two colonies at distance j, carry homologous genes identical by descent. As in the infinite island model of dispersal, the increment in the number of juveniles produced by the focal queen stemming from the additional number of workers produced by queens of the parental generation carrying the mutation depends on the relative benefit B of helping, weighted by the probability Q0 that two distinct adult individuals sampled without replacement from the same colony carry homologous genes identical by descent (Q0 corresponds here to Q used in the main text). Workers from different colonies are also likely to be related, and by helping queens, workers bearing the mutant allele in a colony neighbouring the focal colony increase the intensity of competition faced by the offspring of the focal queen. This is likely to indirectly decrease the fitness of the focal queen. The total number of focal queen's juveniles that are displaced as a consequence of this increment in competition is , where Qj is the probability that two individuals sampled without replacement from two colonies at distance j carry homologous genes identical by descent. Since sampling individuals with or without replacement matters only when individuals are sampled from the same deme, we have
| (A4) |
Collecting all components, the inclusive fitness effect under isolation by distance is given by
| (A5) |
In order to simplify the sum in the first parentheses of equation (A 5), we use the classical equilibrium relation (e.g. Malécot 1975; Nagylaki 1976; Taylor 1992b; Epperson 1999; Gandon & Rousset 1999; Rousset & Billiard 2000; Rousset 2004)
| (A6) |
which is written here, for simplicity, without the term taking mutation into account. In order to simplify the second parentheses of equation (A 5), we first note that on substitution of equation (A 4) (by writing ) into equation (A 6), we have
| (A7) |
which can be used to simplify the term in the second parentheses of equation (A 5) to
| (A8) |
With this, we obtain that the inclusive fitness effect simplifies to
| (A9) |
The helping allele spreads when S>0, i.e. when
| (A10) |
where the sum of the squared dispersal probabilities over all distances can be interpreted as the probability that a randomly sampled worker and a queen from the same colony descend from the same mother. Since m0=(1−m) and mi=0 for i≠0 in the infinite island model, we recover equation (2.3) of the main text in that case.
Supplementary Material
SuppMat_Worker
References
- Aoki K. A condition for group selection to prevail over counteracting individual selection. Evolution. 1982;36:832–842. doi: 10.1111/j.1558-5646.1982.tb05449.x. doi:10.2307/2407896 [DOI] [PubMed] [Google Scholar]
- Axelrod R, Hammond R.A, Grafen A. Altruism via kin-selection strategies that rely on arbitrary tags with which they coevolve. Evolution. 2004;58:1833–1838. doi: 10.1111/j.0014-3820.2004.tb00465.x. doi:10.1111/j.0014-3820.2004.tb00465.x [DOI] [PubMed] [Google Scholar]
- Balloux F, Lugon-Moulin N. The estimation of population differentiation with microsatellite markers. Mol. Ecol. 2002;11:155–165. doi: 10.1046/j.0962-1083.2001.01436.x. doi:10.1046/j.0962-1083.2001.01436.x [DOI] [PubMed] [Google Scholar]
- Bourke A, Franks N. Princetion University Press; Princeton, NJ: 1995. Social evolution in ants. [Google Scholar]
- Bowles S, Gintis H. The evolution of strong reciprocity: cooperation in heterogeneous populations. Theor. Popul. Biol. 2004;65:17–28. doi: 10.1016/j.tpb.2003.07.001. doi:10.1016/j.tpb.2003.07.001 [DOI] [PubMed] [Google Scholar]
- Chapuisat M, Goudet J, Keller L. Microsatellites reveal high population viscosity and limited dispersal in the ant Formica paralugubris. Evolution. 1997;51:475–482. doi: 10.1111/j.1558-5646.1997.tb02435.x. doi:10.2307/2411120 [DOI] [PubMed] [Google Scholar]
- Emlen S.T. Predicting family dynamics in social vertebrates. In: Krebs J.R, Davies N, editors. Behavioural ecology. An evolutionary approach. Blackwell; Oxford, UK: 1997. pp. 228–253. [Google Scholar]
- Epperson B.K. Gene genealogies in geographically structured populations. Genetics. 1999;152:797–806. doi: 10.1093/genetics/152.2.797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eshel I. On the neighbor effect and the evolution of altruistic traits. Theor. Popul. Biol. 1972;11:258–277. doi: 10.1016/0040-5809(72)90003-2. doi:10.1016/0040-5809(72)90003-2 [DOI] [PubMed] [Google Scholar]
- Frank S.A. Princeton University Press; Princeton, NJ: 1998. Foundations of social evolution. [Google Scholar]
- Gandon S, Rousset F. Evolution of stepping-stone dispersal rates. Proc. R. Soc. B. 1999;226:2507–2513. doi: 10.1098/rspb.1999.0953. doi:10.1098/rspb.1999.0953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner A, West S.A. Demography, altruism, and the benefits of budding. J. Evol. Biol. 2006;19:1707–1716. doi: 10.1111/j.1420-9101.2006.01104.x. doi:10.1111/j.1420-9101.2006.01104.x [DOI] [PubMed] [Google Scholar]
- Grafen A. Detecting kin selection at work using inclusive fitness. Proc. R. Soc. B. 2007a;274:713–719. doi: 10.1098/rspb.2006.0140. doi:10.1098/rspb.2006.0140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafen A. An inclusive fitness analysis of a network model of Ohtsuki et al. J. Evol. Biol. 2007b;20:2278–2283. doi: 10.1111/j.1420-9101.2007.01413.x. doi:10.1111/j.1420-9101.2007.01413.x [DOI] [PubMed] [Google Scholar]
- Hamilton W.D. The genetical evolution of social behaviour, I. J. Theor. Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. doi:10.1016/0022-5193(64)90038-4 [DOI] [PubMed] [Google Scholar]
- Hamilton W.D. Selfish and spiteful behavior in an evolutionary model. Nature. 1970;228:1218–1220. doi: 10.1038/2281218a0. doi:10.1038/2281218a0 [DOI] [PubMed] [Google Scholar]
- Hamilton W.D. Selection of selfish and altruistic behaviour in some extreme models. In: Eisenberg J, Dillon W, editors. Man and beast: comparative social behavior. Smithsonian Institutions Press; Washington, DC: 1971. pp. 59–91. [Google Scholar]
- Herbers J.M, Grieco S. Population structure of Leptothorax ambiguus, a facultatively polygynous, polydomous ant species. J. Evol. Biol. 1995;7:581–598. doi:10.1046/j.1420-9101.1994.7050581.x [Google Scholar]
- Irwin A.J, Taylor P.D. Evolution of altruism in stepping-stone populations with overlapping generations. Theor. Popul. Biol. 2001;60:315–325. doi: 10.1006/tpbi.2001.1533. doi:10.1006/tpbi.2001.1533 [DOI] [PubMed] [Google Scholar]
- Jansen V.A.A, van Baalen M. Altruism through beard chromodynamics. Nature. 2006;440:663–666. doi: 10.1038/nature04387. doi:10.1038/nature04387 [DOI] [PubMed] [Google Scholar]
- Keller L. Social life: the paradox of multiple-queen colonies. Trends Ecol. Evol. 1995;10:355–360. doi: 10.1016/s0169-5347(00)89133-8. doi:10.1016/S0169-5347(00)89133-8 [DOI] [PubMed] [Google Scholar]
- Le Galliard J.-F, Ferrière R, Dieckmann U. The adaptive dynamics of altruism in spatially heterogeneous populations. Evolution. 2003;57:1–17. doi: 10.1111/j.0014-3820.2003.tb00211.x. doi:10.1111/j.0014-3820.2003.tb00211.x [DOI] [PubMed] [Google Scholar]
- Lehmann L. The adaptive dynamics of niche constructing traits in spatially subdivided populations: evolving posthumous extended phenotypes. Evolution. 2007;62:549–566. doi: 10.1111/j.1558-5646.2007.00291.x. doi:10.1111/j.1558-5646.2007.00291.x [DOI] [PubMed] [Google Scholar]
- Lehmann L, Perrin N, Rousset F. Population demography and the evolution of helping behaviors. Evolution. 2006;60:1137–1151. doi:10.1554/05-655.1 [PubMed] [Google Scholar]
- Lehmann L, Keller L, Sumpter D. The evolution of helping and harming on graphs: the return of the inclusive fitness effect. J. Evol. Biol. 2007;20:2284–2295. doi: 10.1111/j.1420-9101.2007.01414.x. doi:10.1111/j.1420-9101.2007.01414.x [DOI] [PubMed] [Google Scholar]
- Lions S, van Baalen M. Self-structuring in spatial evolutionary ecology. Ecol. Lett. 2007;11:277–295. doi: 10.1111/j.1461-0248.2007.01132.x. doi:10.1111/j.1461-0248.2007.01132.x [DOI] [PubMed] [Google Scholar]
- Malécot G. Heterozygosity and relationship in regularly subdivided populations. Theor. Popul. Biol. 1975;8:212–241. doi: 10.1016/0040-5809(75)90033-7. doi:10.1016/0040-5809(75)90033-7 [DOI] [PubMed] [Google Scholar]
- Maruyama T. Effective number of alleles in a subdivided population. Theor. Popul. Biol. 1970;1:273–306. doi: 10.1016/0040-5809(70)90047-x. doi:10.1016/0040-5809(70)90047-X [DOI] [PubMed] [Google Scholar]
- Maynard-Smith J. Cambridge University Press; Cambridge, UK: 1982. Evolution and the theory of games. [Google Scholar]
- Mittledorf J, Wilson D. Population viscosity and the evolution of altruism. J. Theor. Biol. 2000;204:481–496. doi: 10.1006/jtbi.2000.2007. doi:10.1006/jtbi.2000.2007 [DOI] [PubMed] [Google Scholar]
- Nagylaki T. The decay of genetic variability in geographically structured populations. Theor. Popul. Biol. 1976;10:70–82. doi: 10.1016/0040-5809(76)90006-x. doi:10.1016/0040-5809(76)90006-X [DOI] [PubMed] [Google Scholar]
- Nagylaki T. The robustness of neutral models of geographical variation. Theor. Popul. Biol. 1983;24:268–294. doi:10.1016/0040-5809(83)90029-1 [Google Scholar]
- Ohtsuki H, Hauert C, Lieberman E, Nowak M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006;441:502–505. doi: 10.1038/nature04605. doi:10.1038/nature04605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pamilo P. Genetic differentiation within subdivided populations of Formica ants. Evolution. 1983;37:1010–1022. doi: 10.1111/j.1558-5646.1983.tb05629.x. doi:10.2307/2408415 [DOI] [PubMed] [Google Scholar]
- Pedersen J.S, Boomsma J.J. Effect of habitat saturation on the number and turnover of queens in the polygynous ant, Myrmica sulcinodis. J. Evol. Biol. 1999;12:903–917. doi:10.1046/j.1420-9101.1999.00109.x [Google Scholar]
- Perrin N, Mazalov V. Local competition, inbreeding and the evolution of sex-biased dispersal. Am. Nat. 2000;155:116–127. doi: 10.1086/303296. doi:10.1086/303296 [DOI] [PubMed] [Google Scholar]
- Pope L, Domingo-Roura X, Erven K, Burke T. Isolation by distance and gene flow in the Eurasian badger (Meles meles) at both a local and broad scale. Mol. Ecol. 2006;15:371–386. doi: 10.1111/j.1365-294X.2005.02815.x. doi:10.1111/j.1365-294X.2005.02815.x [DOI] [PubMed] [Google Scholar]
- Queller D.C. Does population viscosity promote kin selection. Trends Ecol. Evol. 1992;7:322–324. doi: 10.1016/0169-5347(92)90120-Z. doi:10.1016/0169-5347(92)90120-Z [DOI] [PubMed] [Google Scholar]
- Ratnieks F.L.W, Wenseleers T. Altruism in insect societies and beyond: voluntary or enforced? Trends Ecol. Evol. 2008;1:45–52. doi: 10.1016/j.tree.2007.09.013. doi:10.1016/j.tree.2007.09.013 [DOI] [PubMed] [Google Scholar]
- Rogers A.R. Group selection by selective emigration: the effects of migration and kin structure. Am. Nat. 1990;135:398–413. doi:10.1086/285053 [Google Scholar]
- Ross K.G, Krieger M, Shoemaker D.D, Vargo E.L, Keller L. Hierarchical analysis of genetic structure in native fire ant populations: results from three classes of molecular markers. Genetics. 1997;147:643–655. doi: 10.1093/genetics/147.2.643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross K, Shoemaker D, Krieger M, DeHeer C, Keller L. Assessing genetic structure with multiple classes of molecular markers: a case study involving the introduced fire ant Solenopsis invicta. Mol. Biol. Evol. 1999;16:525–543. doi: 10.1093/oxfordjournals.molbev.a026134. [DOI] [PubMed] [Google Scholar]
- Rousset F. Princeton University Press; Princeton, NJ: 2004. Genetic structure and selection in subdivided populations. [Google Scholar]
- Rousset F, Billiard S. A theoretical basis for measures of kin selection in subdivided populations: finite populations and localized dispersal. J. Evol. Biol. 2000;13:814–825. doi:10.1046/j.1420-9101.2000.00219.x [Google Scholar]
- Rousset F, Roze D. Constraints on the origin and maintenance of genetic kin recognition. Evolution. 2007;61:2320–2330. doi: 10.1111/j.1558-5646.2007.00191.x. doi:10.1111/j.1558-5646.2007.00191.x [DOI] [PubMed] [Google Scholar]
- Sundstrom L. Genetic population structure and sociogenetic organisation in Formica truncorum (Hymenoptera; Formicidae) Behav. Ecol. Sociobiol. 1993;33:345–354. doi:10.1007/BF00172934 [Google Scholar]
- Taylor P.D. An inclusive fitness model for dispersal of offspring. J. Theor. Biol. 1988;130:363–378. doi:10.1016/S0022-5193(88)80035-3 [Google Scholar]
- Taylor P.D. Allele-frequency change in a class-structured population. Am. Nat. 1990;135:95–106. doi:10.1086/285034 [Google Scholar]
- Taylor P.D. Altruism in viscous populations: an inclusive fitness model. Evol. Ecol. 1992a;6:352–356. doi:10.1007/BF02270971 [Google Scholar]
- Taylor P.D. Inclusive fitness in a homogeneous environment. Proc. R. Soc. B. 1992b;240:299–302. doi:10.1098/rspb.1992.0118 [Google Scholar]
- Taylor P.D, Frank S.A. How to make a kin selection model. J. Theor. Biol. 1996;180:27–37. doi: 10.1006/jtbi.1996.0075. doi:10.1006/jtbi.1996.0075 [DOI] [PubMed] [Google Scholar]
- Taylor P.D, Irwin A.J. Overlapping generations can promote altruistic behavior. Evolution. 2000;54:1135–1141. doi: 10.1111/j.0014-3820.2000.tb00549.x. doi:10.1554/0014-3820(2000)054[1135:OGCPAB]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Trontti K, Aron S, Sundström L. Inbreeding and kinship in the ant Plagiolepis pygmaea. Mol. Ecol. 2005;14:748–766. doi: 10.1111/j.1365-294X.2005.02529.x. doi:10.1111/j.1365-294X.2005.02529.x [DOI] [PubMed] [Google Scholar]
- van Baalen M, Rand A. The unit of selection in viscous populations and the evolution of altruism. J. Theor. Biol. 1998;193:631–648. doi: 10.1006/jtbi.1998.0730. doi:10.1006/jtbi.1998.0730 [DOI] [PubMed] [Google Scholar]
- van Veelen M, Hopfensitz A. In love and war: altruism, norm formation, and two different types of group selection. J. Theor. Biol. 2007;249:667–680. doi: 10.1016/j.jtbi.2007.09.007. doi:10.1016/j.jtbi.2007.09.007 [DOI] [PubMed] [Google Scholar]
- Wakano, J. Y. 2007 Evolution of cooperation in spatial public goods games with common resource dynamics. J. Theor. Biol 247, 616–622. (doi:10.1016/j.jtbi.2007.04.008) [DOI] [PubMed]
- West S.A, Pen I, Griffin A.S. Cooperation and competition between relatives. Science. 2002;296:72–75. doi: 10.1126/science.1065507. doi:10.1126/science.1065507 [DOI] [PubMed] [Google Scholar]
- West S.A, Gardner A, Shuker D.M, Reynolds T, Burton-Chellow M, Sykes E.M, Guinnee M.A, Griffin A.S. Cooperation and the scale of competition in humans. Curr. Biol. 2006;16:1103–1106. doi: 10.1016/j.cub.2006.03.069. doi:10.1016/j.cub.2006.03.069 [DOI] [PubMed] [Google Scholar]
- Yamamura N, Higashi M, Behera N, Wakano J.Y. Evolution of mutualism through spatial effects. J. Theor. Biol. 2004;226:421–428. doi: 10.1016/j.jtbi.2003.09.016. doi:10.1016/j.jtbi.2003.09.016 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
SuppMat_Worker