Memory traces in dynamical systems

Abstract

To perform nontrivial, real-time computations on a sensory input stream, biological systems must retain a short-term memory trace of their recent inputs. It has been proposed that generic high-dimensional dynamical systems could retain a memory trace for past inputs in their current state. This raises important questions about the fundamental limits of such memory traces and the properties required of dynamical systems to achieve these limits. We address these issues by applying Fisher information theory to dynamical systems driven by time-dependent signals corrupted by noise. We introduce the Fisher Memory Curve (FMC) as a measure of the signal-to-noise ratio (SNR) embedded in the dynamical state relative to the input SNR. The integrated FMC indicates the total memory capacity. We apply this theory to linear neuronal networks and show that the capacity of networks with normal connectivity matrices is exactly 1 and that of any network of N neurons is, at most, N. A nonnormal network achieving this bound is subject to stringent design constraints: It must have a hidden feedforward architecture that superlinearly amplifies its input for a time of order N, and the input connectivity must optimally match this architecture. The memory capacity of networks subject to saturating nonlinearities is further limited, and cannot exceed $\sqrt{N}$. This limit can be realized by feedforward structures with divergent fan out that distributes the signal across neurons, thereby avoiding saturation. We illustrate the generality of the theory by showing that memory in fluid systems can be sustained by transient nonnormal amplification due to convective instability or the onset of turbulence.

Critical cognitive phenomena such as planning and decision-making rely on the ability of the brain to hold information in short-term memory. It is thought that the neural substrate for such memory can arise from persistent patterns of neural activity, or attractors, that are stabilized through reverberating positive feedback, either at the single-cell (1) or network (2, 3) level. However, such simple attractor mechanisms are incapable of remembering sequences of past inputs.

More recent proposals (4–6) have suggested that an arbitrary recurrent network could store information about recent input sequences in its transient dynamics, even if the network does not have information-bearing attractor states. Downstream readout networks can then be trained to instantaneously extract relevant functions of the past input stream to guide future actions. A useful analogy (4) is the surface of a liquid. Even though this surface has no attractors, save the trivial one in which it is flat, transient ripples on the surface can nevertheless encode information about past objects that were thrown in.

This proposal raises a host of important theoretical questions. Are there any fundamental limits on the lifetimes of such transient memory traces? How do these limits depend on the size of the network? If fundamental limits exist, what types of networks are required to achieve them? How does the memory depend on the network topology, and are special topologies required for good performance? To what extent do these traces degrade in the presence of noise? Previous analytical work has addressed some of these questions under restricted assumptions about input statistics and network architectures (7). To answer these questions in a more general setting, we use Fisher information to construct a measure of memory traces in networks and other dynamical systems. Traditionally, Fisher information has been applied in theoretical neuroscience to quantify the accuracy of population coding of static stimuli (see, e.g., ref. 8). Here, we extend this theory by combining Fisher information with dynamics.

The Fisher Memory Matrix in a Neuronal Network

We study a discrete time network dynamics given by

Here a scalar, time-dependent signal s(n) drives a recurrent network of N neurons (Fig. 1B). x(n) ∈ ℛ^N is the network state at time n, f(·) is a general sigmoidal function, W is an N × N recurrent connectivity matrix, and v is a vector of feedforward connections from the signal into the network. We keep v time independent to focus on how purely temporal information in the signal is distributed in the N spatial degrees of freedom of the network state x(n). The norm ‖v‖ sets the scale of the network input, and we will choose it to be 1. The term z(n) ∈ ℛ^N denotes a zero mean Gaussian white noise with covariance 〈z_i(k₁)z_j(k₂)〉 = εδ_k1,k2δ_i,j.

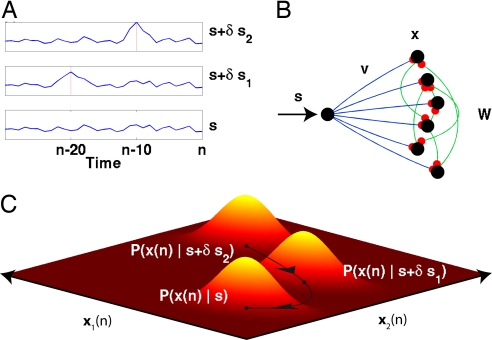
Fig. 1.

Conversion of temporal to spatial information. (A) Three scalar signals: a base signal, s(k), and 2 more signals obtained by perturbing s by the addition of an identical pulse centered at time n − 10 and n − 20. (B) Each of these signals is fed to a recurrent network W through a feedforward connectivity v. (C) At time n, the temporal structure of each signal is encoded in the spatial distribution of the network state x(n), here shown in 2 dimensions. A stronger memory trace for the recent input perturbation δs₂, relative to the remote perturbation δs₁, is reflected by the larger difference between P(x(n)∣s + δs₂) and P(x(n)∣s) relative to that between P(x(n)∣s + δs₁) and P(x(n)∣s). As both perturbations recede into the past, both memory traces decay, and the 3 distributions become identical.

We build upon the theory of Fisher information to construct useful measures of the efficiency with which the network state x(n) encodes the history of the signal. Because of the noise in the system, a given past signal history {s(n − k)∣k ≥ 0}induces a conditional probability distribution P(x(n)∣s) on the network's current state. Here, we think of this history {s(n − k)∣k ≥ 0}as a temporal vector s whose kth component s_k is s(n − k). The Fisher memory matrix (FMM) between the present state x(n) and the past signal is then defined as

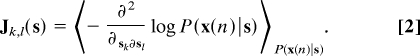This matrix captures [see supporting information (SI) Appendix] how much the conditional distribution P(x(n∣s) changes when the signal history s changes (Fig. 1). Specifically, if one were to perturb the signal slightly from s to s + δs, the Kullback Leibler divergence between the 2 induced distributions P(x(n∣s) and P(x(n)∣s + δs) would be approximated by (½)δs^TJ(s)δs (SI Appendix). Thus the FMM (Eq. 2) measures memory through the ability of the past signal to perturb the network's present state. In this work, we will focus on the diagonal elements of the FMM. Each diagonal element J(k) ≡ J_k,k is the Fisher information that x(n) retains about a pulse entering the network at k time steps in the past. Thus, the diagonal captures the decay of the memory trace of a past input, and so we call J(k) the Fisher memory curve (FMC).

For a general nonlinear system, the FMC depends on the signal itself and is hard to analyze. In this article, we focus on linear dynamics where the transfer function in Eq. 1 is defined by f(x) = x. Because the noise is Gaussian, the conditional distribution P(x(n)∣s) is also Gaussian, with a mean that is linearly dependent on the signal δx(n)/δs(n − k) = W^kv, and a noise covariance matrix C_n = ε Σ_k=0^∞W^kW^kT, which is independent of the signal. Hence, the FMC is independent of signal history and takes the form

We focus on two related features of Eq. 3: the form of its dependence on the time lag k and the total area under the FMC, denoted by J_tot. An important parameter is the SNR in the input vector vs(n) + z(n) at a single time n, which is $\frac{1}{\epsilon }$. Because J(k) depends on this input SNR only through the multiplicative factor $\frac{1}{\epsilon }$, we will henceforth express J(k) in units of $\frac{1}{\epsilon }$. In these units, J(k) is the fraction of the input SNR remaining in the system k time steps after an input pulse, and J_tot is the total SNR in the system state x(n) about the entire past signal history, relative to the SNR of the instantaneous input.

FMCs for Normal Networks

In the following, we uncover a fundamental dichotomy in the memory properties of two different classes of networks: normal and nonnormal. We first focus on the class of normal networks, defined as having a normal connectivity matrix W. A matrix W is normal if it has an orthogonal basis of eigenvectors or equivalently commutes with its transpose. For normal networks, the relationship between the connectivity and the FMC simplifies considerably. Denoting the eigenvalues of W by λ_i, the FMC reduces to

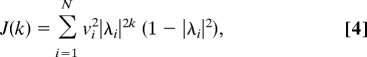where v_i is the projection of the input connectivity vector v on the ith eigenmode. Thus, for normal matrices, the orthogonal eigenvectors do not yield any essential contribution to memory performance.

First we note that summing Eq. 4 over k yields the important sum rule for normal networks,

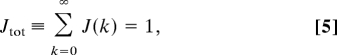which is independent of the network connectivity W and v. This sum rule implies that normal networks cannot change the total SNR relative to that embedded in the instantaneous input but can only redistribute it across time. Whereas in the input vector, the SNR $\frac{1}{\epsilon }$ is concentrated fully in the immediate signal s(n), in the network state x(n), the dynamics has spread this information across time. This implies a tradeoff in memory performance for normal networks; if one attempts to optimize W or v to remember inputs occurring in the recent past, then one will necessarily take a performance loss in the ability to remember inputs occurring in the remote past and vice versa. The way different networks balance this tradeoff is reflected in the form of the time dependence of their FMC.

The reduction of the FMC to eigenvalues allows us to understand its asymptotics. For large k, the decay of the FMC in Eq. 4 is determined by the distribution of magnitudes of the largest eigenvalues. Dynamic stability requires that the largest eigenvalue magnitude, denoted by $\sqrt{\alpha }$, is less than 1. If α is a finite distance from 1, then the FMC for large k is dominated by this single eigenvalue, and it decays exponentially as J(k) ∝ α^k. However, if α is close to 1, then the multiplicity of long time scales associated with the large eigenvalues at the border of instability induces a power-law decay of the FMC. Specifically, if the density of eigenvalue magnitudes ρ(r) near the edge of the spectrum behaves as ρ(r) ∝ ($\sqrt{\alpha }$ − r)^ν, then for large k and α close to 1, the FMC decays algebraically (see SI Appendix) as

Note that because ν > −1, the integral of Eq. 6 remains finite, consistent with the sum rule (Eq. 5).

Examples of Normal Networks

An important class of normal matrices includes translation invariant lattices, i.e., circulant matrices. In the 1D case, W is of the form W_ij = d_(i−j) mod N, where d is any vector, and the eigenvectors of W are the Fourier modes. The signal enters at a single neuron so that v_k = δ_k,0 and couples to all of the modes with a uniform strength 1/$\sqrt{N}$. An important special case is the delay ring (Fig. 2A), with d_k = $\sqrt{\alpha }$δ_k,1. Its FMC is J(k) = α^k(1 − α). For any value of α, the FMC always displays exponential rather than power-law decay. This occurs because the eigenvalues of W all lie on a circle of radius $\sqrt{\alpha }$. Thus ρ(r) = δ(r − $\sqrt{\alpha }$), and there is no continuous spectrum near the boundary of instability. Instead, there is only 1 time constant governed by α. Extensions of the delay ring are the ensemble of orthogonal networks (studied in ref. 7). These are normal networks in which W is a rotation matrix.

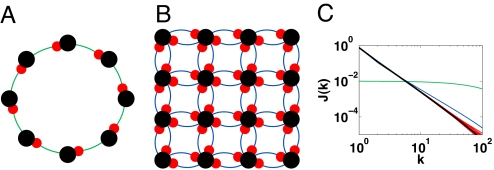
Fig. 2.

Normal networks. (A) A delay ring. (B) A 2D symmetric invariant lattice (periodic boundary conditions not shown). (C) The FMC for the delay ring (green, α = 0.99, N = 1,000), the 2D Lattice (blue, α = 0.99, N = 1,024), and 10 random symmetric matrices (red, α = 0.99, N = 1,000). The black trace is the analytic prediction of a mean field theory for the FMC of random symmetric matrices, derived in SI Appendix.

Another class of normal networks consists of networks with symmetric connectivity matrices. An example is a symmetric d-dimensional lattice (a 2D example is shown in Fig. 2B). Near the edge of the eigenvalue spectrum ρ(r) ∝ ($\sqrt{\alpha }$ − r)^(d−2)/2. Hence, for α → 1, FMC exhibits a power-law decay with exponent −(d + 2)/2 (Fig. 2C). Finally, we consider large random symmetric networks defined by matrix elements W_ij = W_ji that are chosen independently from a zero mean Gaussian distribution with variance α/4N. The eigenvalues of W are distributed on the real axis r according to Wigner's semicircular law, which, near the edge, behaves as ρ(r) ∝ ($\sqrt{\alpha }$ − r)^1/2. Hence, Eq. 6 predicts a power-law decay of the FMC for α → 1, with exponent −5/2 as verified in Fig. 2C.

Preferred Input Patterns in Nonnormal Networks

For nonnormal networks, J_tot depends not only on the network connectivity W but also on the feedforward connectivity v. To investigate the sensitivity to v, we note from Eq. 3 that, in general, J_tot can be expressed as

where we have introduced the spatial FMM

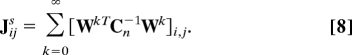This matrix, J^s, and the temporal FMM J in Eq. 2, can be unified into a general space–time framework (see SI Appendix). J^s measures the information in the network's spatial degrees of freedom x_i(n) about the entire signal history. The total information in all N degrees of freedom is Tr J^s = N, independent of W. Because J^s is positive definite with trace N, Eq. 7 yields a fundamental bound on the total area under the FMC of any network W and unit input vector v:

If W is normal, then J_i,j^s = δ_i,_j, implying that all directions in space provide the same amount of total temporal information, and so J_tot is independent of the spatial structure v of the input, consistent with the sum rule (Eq. 5). However, if W is nonnormal, J^s has nontrivial spatial structure, reflecting an inherent anisotropy in state space induced by the connectivity matrix W. There will be preferred directions in state space, corresponding to the large principal components of J^s, that contain a large amount of information about the total history, whereas other directions will perform relatively poorly. The choice of v that maximizes J_tot is the eigenvector of largest eigenvalue of J^s.

The spatial anisotropy of nonnormal networks is demonstrated by evaluating the FMC for random asymmetric networks, where each matrix element W_ij is chosen independently from a zero mean Gaussian with variance α/N. If the feedforward connectivity v is chosen to be a random vector, the distribution of J_tot (Fig. 3A, blue) is centered around 1 as expected, because the trace of J^s equals N. However, if v is chosen as the maximal principal component of J^s, the resultant J_tot is approximately 4 times as large (Fig. 3A, red).

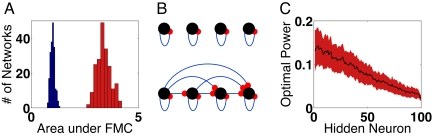
Fig. 3.

Matching input connectivity to nonnormal architectures. (A) Histogram of J_tot for 200 random Gaussian matrices with N = 100, and α = 0.99, for random (blue) and optimized (red) input weights v. (B) (Upper) Every normal matrix can be diagonalized by a unitary matrix, and so its memory properties are equivalent to a set of N disconnected neurons each exerting positive feedback on itself. (Lower) A nonnormal matrix can only be converted to an upper triangular matrix through a unitary transformation and thus has a hidden feedforward architecture. (C) For the same 200 matrices in B, the mean (black) and standard deviation (red) of the magnitude of the components of the optimal input vector v, in the Schur basis, ordered according to the hidden feedforward structure.

Additional insight into the structure of the preferred v comes from the Schur decomposition of W. Whereas every normal matrix is unitarily equivalent to a diagonal matrix (Fig. 3B Upper), every nonnormal matrix is unitarily equivalent to an upper triangular matrix (Fig. 3B Lower). On this basis, it may, in general, be preferable to distribute the signal near the beginning of the network to counterbalance the noise propagation along the network. We have tested this hypothesis by plotting the magnitude of the components of the optimal input vector for the random asymmetric networks in their Schur basis. As Fig. 3C shows, the optimal choice of feedforward weights v does indeed exploit the hidden feedforward structure by coupling the signal more strongly to its source than to its sink.

Transient Amplification and Extensive Memory

Comparing Eqs. 5 and 9 motivates defining networks with extensive memory as networks in which J_tot is proportional to N for large N. With this definition, normal networks do not have extensive memory. Furthermore, as indicated in Fig. 3A, despite the enhanced performance of generic asymmetric networks, their total memory remains O(1), prompting the question whether in fact there exist nonnormal networks with extensive memory. Surprisingly, such networks do exist.

A particularly simple example is the delay line shown in Fig. 4A Upper). In this example, the only nonzero matrix elements are W_i+1,i = $\sqrt{\alpha }$ for i = 1…N − 1. The FMC depends on how the signal enters the delay line. The optimal choice is to place the signal at the source, so that v_i = δ_i,1. Then the FMC takes the form J(k) = α^k(1 − α)/(1 − α^k+1), k = 0…N − 1, and 0 otherwise. For values of α <1, J decays exponentially as α^k and J_tot ≈ 1 (Fig. 4B, blue). However, for α > 1, J saturates to a finite value, 1 − $\frac{1}{\alpha }$ for large k < N, so that J_tot ≈ N (1 − $\frac{1}{\alpha }$) (Fig. 4B, red).

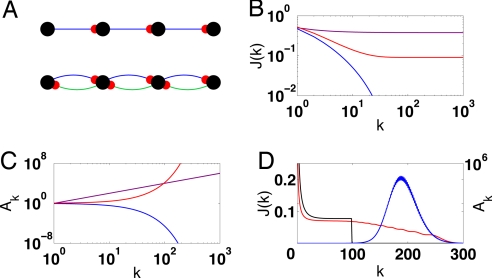
Fig. 4.

Memory from transient amplification. (A) Delay line architecture (Upper) and a delay line with feedback (Lower). (B) The FMC for 3 delay lines of length N = 10³ whose corresponding signal amplification profiles are shown in the same color in C. The red curves correspond to exponential amplification (A_k = α^k, α = 1.1), whereas the blue curves correspond to exponential decay (A_k = α^k, α = 0.9). The magenta curves correspond to power law amplification in an inhomogeneous delay line (A_k = k²). (D) The signal amplification profile (blue) and corresponding FMC (red) for a delay line with feedback of length n = 100 in the transient amplification regime $\sqrt{\alpha }$ and $\sqrt{\beta }$ = 0.2. The black curve shows the FMC of a delay line of length N with the same signal amplification profile up to time N − 1.

The delay line with extensive memory is an example of a dynamical system with strong transient amplification. Network amplification can be characterized by the behavior of A_k ≡ ‖W^kv‖² for k ≥ 0. Whereas in normal systems, A_k is montonically decreasing for all v, in nonnormal networks, A_k may initially increase before decaying to zero for large k (9). In the case of Fig. 4C (red), A_k = α^k increases exponentially, and this amplification lasts for a time of order N. It is important to note that, in such a system, not only the signal but also the noise is exponentially amplified as it propagates along the chain. Introducing the signal at the beginning of the chain guarantees that the signal and noise are amplified equally, resulting in the saturation of J(k) (Fig. 4B).

It is not necessary to have purely feedforward connectivity to have large transient amplification and extensive memory. As an example, we consider a delay line with feedback (Fig. 4A Lower). In addition to the feedforward connections, $\sqrt{\alpha }$, there are feedback connections, W_i,_i+1 = $\sqrt{\beta }$, for i = 1…N − 1. We consider a scenario in which $\sqrt{\alpha }$ < 1, so that in the absence of the feedback, inputs would decay exponentially. If the feedback is in the range 1 − $\sqrt{\alpha }$ < $\sqrt{\beta }$ < 1/(4$\sqrt{\alpha }$), then the system exhibits transient exponential amplification while maintaining global stability (9). Fig. 4D shows an example of the amplification and the extensive FMC in this regime. One advantage of the feedback is that the amplification as well as the tail of the FMC lasts longer than N, which cannot be achieved in a delay line of length N without feedback (Fig. 4D, black curve).

Transient exponential amplification, as in the above examples, is not a necessary condition for extensive memory. Consider, for example, a delay line with inhomogeneous weights, W_i+1,i = $\sqrt{\alpha }$ for i = 1…N − 1, where A_k = Π_p=1^kα_p for 0 < k < N and A₀ = 1. The FMC equals

From Eq. 10, it is evident that J_delay saturates to a finite value at large k as long as A_k increases superlinearly in k, i.e., A_k > O(k), as shown in Fig. 4 B and C (magenta). If this superlinear amplification lasts a time of order N, then J_tot will be extensive. The above results raise the question whether superlinear transient amplification lasting for a time of order N is a necessary prerequisite for extensive memory in general nonnormal networks with feedback. Interestingly, we have proven (see SI Appendix) that this is, indeed, a necessary condition for a general network. Specifically, we have shown that for any network with a given sequence of signal amplification A_m, 0 ≤ m ≤ k, the FMC up to time k cannot be larger than that of a delay line of length k + 1, with input vector v_i = δ_i,1, that possesses the same set of amplification factors, i.e.,W_i+1,i = $\sqrt{A_i/A_i-1}$ for i = 1…k. Thus for any network,

where J_delay(m) is given by Eq. 10. We have further shown (see SI Appendix) that, remarkably, in the space of networks with a given signal amplification profile, the only networks that saturate the bound Eq. 11 are those that are unitarily equivalent to the corresponding delay line, with the signal placed at the source. Thus the delay line is essentially the unique network that achieves the minimal possible noise amplification for a given amount of signal amplification. Therefore, the strong inequality (Eq. 11) reveals that, in general architectures, noise undergoes stronger amplification than it otherwise would in the corresponding delay line. However, the length of the delay line necessary to realize amplification up to k time steps is exactly k + 1, so that for k > N, the number of neurons in the corresponding delay line is larger than that of the actual network with feedback, as noted in the example of Fig. 4D.

Consequences of Finite Dynamic Range

The networks discussed above achieve extensive memory performance through transient superlinear amplification that lasts for O(N) time steps. However, such amplification may not be biophysically feasible for neurons that operate in a limited dynamic range, due, for example, to saturating nonlinearities. This raises the question, what are the limits of memory capacity for networks with saturating neurons? To address this question, we assume that the network architecture is such that all neurons have finite dynamic range, i.e., 〈x_i(n)〉² < R for i = 1, …, N. We show (see SI Appendix) that in this case,

This bound implies that such a network cannot achieve an area under the FMC that is larger than O($\sqrt{N}$) and, in particular, cannot achieve extensive memory.

Can a network of neurons with finite dynamic range achieve the O($\sqrt{N}$) limit? To do so, a network must distribute the signal among many neurons so that as the distributed signal is amplified, the local input to any individual neuron does not grow. An example of such a network is the divergent fan-out architecture shown in Fig. 5A. It consists of L layers where the number of neurons N_k in layer k grows with k. The signal enters the first layer and, for simplicity, the connections between neurons in layer k to those in k + 1 are all equal to $\sqrt{\gamma k}$. We show in SI Appendix that if N_k grows linearly in k, and $\sqrt{\gamma k}$ decreases inversely with k, then as the overall signal propagates through the layers, it is amplified linearly, whereas single-neuron activities neither grow nor decay. Memory traces in such a network last a time proportional to the depth L, but because the number of neurons N is O(L²), in terms of neurons, the area under the FMC is O($\sqrt{N}$, which is the limit.

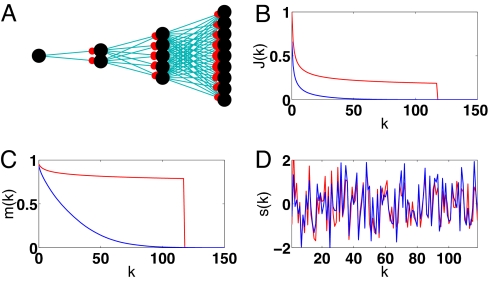
Fig. 5.

Memory in fan-out vs. generic architectures. (A) A feedforward, fan-out architecture, or divergent chain. (B) The FMC of the divergent chain (red) and a random Gaussian network (blue) of comparable size. (C) The reconstruction performance of the divergent chain (red) and Gaussian network (blue). m(k) is defined to be the average correlation between the actual past input s(n − k) and an optimal estimate of this input, constructed from the current network state x(n) (7); see also SI Appendix. (D) An example of the actual input sequence (red) and its optimal linear reconstruction (blue) from the final state of a nonlinear divergent chain.

A comparison between the performance of the fan-out architecture and a random Gaussian network of the same size, N ≈ 7,000, is shown in Fig. 5 B and C. The first network consists of n = 7,021 neurons organized in a divergent chain of length L = 118 with the number of neurons at each layer growing as N_k = k and the connection strengths are $\sqrt{\gamma k}=\frac{1}{k}$. The Gaussian network consists of 7,000 neurons with a Gaussian connectivity matrix; the square magnitude of its maximal eigenvalue is α = 0.95. Fig. 5B shows the marked difference between the FMC of the two systems. The enhanced FMC of the chain translates into a better reconstruction of the signal (see Discussion). To demonstrate this relation, we have computed for the two systems the correlation coefficients between a white noise input with SNR $\frac{1}{\epsilon }$ = 20 and the estimated signal using an optimal readout of the network state. In the case of the divergent chain the optimal estimate of the signal s(n − k) is the summed activity of the neurons at layer k + 1. Fig. 5C shows the vastly improved signal reconstruction of the divergent chain.

Finally, to test the robustness of the fan-out architecture to saturation, we have simulated the dynamics of Eq. 1 with a saturating nonlinear transfer function f(x) = tanh(x) (see SI Appendix). As before, the input is white noise with SNR of 20. A sample of the signal and its reconstruction from the layers' activity is shown in Fig. 5D. The correlation coefficient of the 2 traces, roughly 0.8, is in accord with the theoretical prediction of the linear system, Fig. 5C. Thus, the fan-out architecture achieves impressive memory capacity by distributed amplification of the signal across neurons without a significant amplification of the input to individual neurons.

Nonnormal Amplification and Memory in Fluid Dynamics

To illustrate the generality of the connection between transient, nonnormal amplification and memory performance, we consider an example from fluid mechanics. Indeed, nonnormal dynamics is thought to play an important role in various fluid mechanical transitions, including the transition from certain laminar flows to turbulence (10). Here, we focus on a particular type of local instability known as a convective instability (11) that plays a role in describing fluid flow perturbations around wakes, mixing and boundary layers, and jets. For example, the fluid flow just behind the wake of an object, or in the vicinity of a mixing layer where two fluids at different velocities meet, is especially sensitive to perturbations, which transiently amplify but then decay away as they are convected away from the object or along the mixing layer as the two velocities equalize.

Following refs. 9 and 11, we model these situations phenomenologically through the time evolution of a 1D flow perturbation u(x,t) obeying the linear evolution operator

This describes rightward drift plus diffusion in the presence of a quadratic feedback potential (Fig. 6A) driven by a 1D signal s(t) and zero mean, unit variance additive white Gaussian noise in time and space, η(x, t). Perturbations in the region ∣x∣ ≤ $\frac{1}{2}$ receive positive feedback and are exponentially amplified. However, the system is still globally stable, because these perturbations convect downstream and enter a region of exponential decay for x > $\frac{1}{2}$. The time spent by any perturbation in the amplification region is O(1/h), and thus the total transient amplification will be O(e^1/h). Thus, for small h, significant nonnormal amplification occurs.

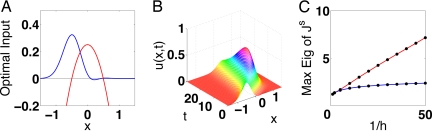
Fig. 6.

Memory through convective instability. (A) The optimal input profile (blue) and quadratic potential (red). (B) The rightward time evolution and transient amplification of this input (h = 0.1). (C) Optimal memory in the presence (red) and absence (blue) of the convective instability.

Although the sum rule (Eq. 5) holds also for continuous time (see SI Appendix) and discrete space, there is no analogous bound (Eq. 9) for continuous space because the number of degrees of freedom is infinite. Nevertheless, for a given system, J_tot is finite and is bounded by the amplification time, or equivalently by the effective number of amplified degrees of freedom, which, in our case, is O(1/h).

The optimal way for the signal to enter the network, i.e., the first principal eigenvector of J^s, is shown in Fig. 6A. This optimal input profile v(x) is a wave packet poised to travel through the convective instability (Fig. 6B). Fig. 6C (red) shows that the optimal memory performance, or maximal eigenvalue of J^s, scales linearly with 1/h. Thus, consistent with the results above, the maximal area under the FMC is proportional to the time over which inputs are superlinearly amplified. For comparison, we have computed the value of the optimal J_tot in the case of a fluid dynamics that contains only diffusion and drift, the first 2 terms of the right-hand side of Eq. 13 but not the amplifying potential. In this case, J_tot is low for all values of h (Fig. 6C, blue).

Discussion

In this work, we focused on the diagonal part of the FMM (Eq. 2. In networks that are unitarily equivalent to simple delay lines (e.g., Fig. 4A Upper and Fig. 5A), this matrix is diagonal. However, in general, the off-diagonal elements are not all zero. Their value reflects the interference between two signals injected into the system at two different times, and their analysis provides an interesting probe into the topology of (partially directed) loops in the system, which give rise to such interference (see SI Appendix).

It is interesting to note the relation between the FMC J(k) and the more conventional memory function m(k) defined through the correlation between an optimal estimate of the past signal ŝ(n − k) based on the network state x(n) and the original signal s(n − k) (see Fig. 5C). Even in the linear version of Eq. 1 studied here, m(k) depends on the full FMM. Furthermore, it depends in a complex manner on the signal statistics (see SI Appendix), whereas Fisher information is local in signal space and in the present case is, in fact, independent of the signal except for an overall factor of the input SNR. Both features render signal reconstruction a much more complex measure to study analytically. Nevertheless, it is important to note that the FMC measures the SNR embedded in the network state, relative to the input SNR $\frac{1}{\epsilon }$. Hence, for small-input SNR, high Fisher memory is crucial for accurate signal reconstruction. On the other hand, when $\frac{1}{\epsilon }$ is sufficiently large, m(k) may be close to 1 even for low Fisher information (see SI Appendix).

Our results indicate that generic recurrent neuronal networks are poorly suited for the storage of long-lived memory traces, contrary to previous proposals (4–6). In systems with substantial noise, only networks with strong and long-lasting signal amplification can potentially sustain such traces. However, signal amplification necessarily comes at the expense of noise amplification, which could corrupt memory traces. To avoid this, long-lived memory maintenance at high SNR further requires that the input connectivity pattern be matched to the architecture of the amplifying network. By analyzing the dynamical propagation of signal and noise through arbitrary recurrent networks, we have shown (see SI Appendix), remarkably, that for a given amount of signal amplification, no recurrent network can achieve less noise amplification (i.e., higher SNR) than a delay line possessing the same signal-amplification profile, with the input entering at its source. However, a recurrent network, unlike a delay line, can amplify signals four times larger than its network size (see Fig. 4D).

Although most of our analysis was limited to linear systems, we have shown that systems with a divergent fan out architecture (see Fig. 5A) can achieve signal amplification in a distributed manner and thereby exhibit long-lived memory traces that last a time O($\sqrt{N}$), even in the presence of saturating nonlinearities. Indeed, this duration of memory trace is the maximum possible for any network operating within a limited dynamic range (see SI Appendix). We further note that it is not necessary for a network to manifestly have a connectivity as in Fig. 5A to achieve this limit. We have tested numerically the memory properties of networks with saturating nonlinearites whose connectivity arises from random orthogonal rotations of the divergent fan-out architecture. Such networks appear to have unstructured connectivity, and the underlying feedforward architecture is hidden. Nevertheless, these networks have memory traces that last a time O($\sqrt{N}$) (S.G. and H.S., unpublished work).

Given the poor memory performance of generic networks, our work suggests that neuronal networks in the prefrontal cortex or hippocampus specialized for working memory tasks involving temporal sequences may posses hidden, divergent feedforward connectivities. Other potential systems for testing our theory are neuronal networks in the auditory cortex specialized for speech processing or networks in the avian brain specialized for song learning and recognition.

The principles we have discovered hold for general dynamical systems, as illustrated in the example from fluid dynamics. In light of the results of Fig. 6, it is not surprising that reconstruction of acoustic signals injected into the surface of water in a laminar state, attempted in ref. 12, fared poorly. Our theory suggests that performance could be substantially improved if, for example, the signal were injected behind the wake of a fluid flowing around an object, or in the vicinity of a mixing layer, or even into laminar flows at high Reynolds numbers just below the onset of turbulence.

In this work, we have applied the framework of Fisher information to memory traces embedded in the activity of neurons, usually identified as short-term memory. However, the same framework can be applied to study the storage of spatiotemporal sequences through synaptic plasticity, i.e., long-term memory (S.G. and H.S., unpublished work). More generally, memory of past events is a ubiquitous feature of biological systems, and they all face the problem of noise accumulation, decaying signals, and interference. In revealing fundamental limits on the lifetimes of memory traces in the presence of these various effects, and in uncovering general dynamical design principles required to achieve these limits, our theory provides a useful framework for studying the efficiency of dynamical processes underlying robust memory maintenance in biological systems.