Incipient criticality in ecological communities

Abstract

In ecology, there have been attempts to establish links between the relative species abundance (RSA), the fraction of species in a community with a given abundance, and a power-law form of the species area relationship (SAR), the dependence of species richness on sampling area. However the SAR and other patterns in ecology often do not exhibit power-law behavior over an appreciable range of scales. This raises the question whether a scaling framework can be applied when the system under analysis does not exhibit power-law behavior. Here, we derive a general finite-size scaling framework applicable to such systems that can be used to identify incipient critical behavior and links the scale dependence of the RSA and the SAR. We confirm the generality of our theory by using data from a serpentine grassland plot, which exhibits a power-law SAR, and the Barro Colorado Island plot in Panama, whose SAR shows deviations from power-law behavior at every scale. Our results demonstrate that scaling provides a model-independent framework for analyzing and unifying ecological data and that, despite the absence of power laws, ecosystems are poised in the vicinity of a critical point.

Scaling in critical phenomena (1–9) is a powerful model-independent framework that allows one to analyze finite-size effects. Scaling behavior is associated with the occurrence of power laws and the scaling framework allows one to link seemingly unrelated exponents characterizing power-law behaviors. Scaling relationships (10–12) have also been derived in contexts not directly related to critical phenomena, such as river networks and agglomerization phenomena, exhibiting power-law behaviors.

Ecosystems are finite-size systems characterized by a wide range of size scales and diverse empirical ecological relationships, which are often treated as being independent of each other. Key patterns include diversity characterized by the relative species–abundance distribution and the species–area relationship (13). Although there have been attempts to construct mechanistic models (14) for understanding these patterns, our focus is on the development of a model-independent theoretical framework to understand how the observed patterns depend on the size, A, of the sampled area. We demonstrate that ecosystems exhibit a nontrivial scaling collapse plot; the relative species abundance (RSA) patterns at different scales can be overlaid on top of each other by the judicious choice of the correct “scaling variables.” We show that this scaling approach yields a model-independent framework for analyzing ecological data and for linking different ecological relationships (15–18).

Consider a sampled area, A, of an ecosystem composed of S(A) species, each associated with a distinct abundance (or number of individuals), n_i ≥ 1, i = 1,2, … S(A). The RSA, P(n|A)dn, is the probability that a species picked, at random, has an abundance between n and n + dn. One may equivalently study the cumulative probability distribution defined by C(n|A) = ∫_n^∞ P(t|A)dt. The normalization condition for P is given by

for any A. For mathematical convenience, we approximate the sum over the discrete distribution P(n|A) with an integral. This assumption, valid for large n, is not restrictive and our results are robust and do not depend on this approximation.

In principle, for different system sizes, say A₁ and A₂, the corresponding relative species abundance distributions (RSAs), P(n|A₁) and P(n|A₂), could be quite different functions of n. However, when the system being studied has an underlying organization, the P(n|A)s for different values of A may be related to each other. The goal of finite-size scaling is to assess whether such a relationship exists and exploit it to derive links between seemingly distinct quantities.

The first step required in applying finite-size scaling techniques to the analysis of RSAs is obtaining a measure of the characteristic scale of the abundance per species for a system of size A, which we denote by f(A). One would expect that f(A) diverges as A tends to infinity. The simplest scenario is one in which f(A) is the average value of n given by

Note that 〈n〉_A = N(A)/S(A), where N(A) and S(A) are the number of individuals and the number of species in the area A, respectively. S(A) is known in ecology as the “species–area relationship” (SAR). Thus, Eq. 2 effectively links together two different patterns in ecology, the RSA and SAR; this link will be further exploited and clarified in the following.

More generally, one may define several measures of the characteristic scale through the ratio of appropriate moments of P(n|A) (note that these measures all have the same units):

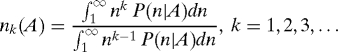The average value of n, 〈n〉_A is equal to n₁(A). There are two extreme cases that one may encounter. In the first, on varying A, all the n_ks are proportional to each other and there is just one characteristic abundance scale proportional to n₁(A). The second corresponds to the situation in which the n_ks exhibit distinct dependencies on A resulting in a plethora of characteristic abundance scales such that the finite-size scaling framework cannot be implemented in a simple manner. An intermediate scenario, which might apply to skewed RSAs, is one in which the n_ks with k > 1 are all proportional to each other and scale as

where Δ is an exponent that is >1 [see supporting information (SI) Appendix for details and derivation]. In the trivial case of all the n_ks being proportional to each other, Δ = 1. Such behavior is expected in noninteracting, unconstrained random situations such as randomly distributed individuals. We show instead that ecological communities lie in a distinct class characterized by Δ = 1, but with logarithmic corrections in the relationship between the n_ks and n₁ for k > 1. These nontrivial corrections likely arise from interactions between individuals in the system. Unlike the conventional critical case (Δ > 1), one has incipient criticality, characterized by the presence of scaling relationships (see below) in the absence of pure power-law behavior. Such logarithmic corrections also arise in conventional critical phenomena at the “upper-critical dimension” (5) in which the behavior of the system is marginally sensitive to the presence of fluctuations.

To deduce the characteristic abundance scale f(A) and the exponent Δ from empirical data, we outline a simple finite-size scaling approach. We make the scaling postulate that the n dependence of P(n|A) can be captured by a “dimensionless” scaling variable n/f(A), i.e., P(n|A) ∼ F(n/f(A)), where F is a suitable function that decays to zero rapidly when n is much larger than its characteristic value, f(A), a condition that is satisfied because there are few, if any, species whose abundance is much greater than this characteristic value. The function F is multiplied by a suitable factor, g(A), to ensure that P is normalized. Our scaling hypothesis is thus:

Whether or not the data satisfy the scaling hypothesis, Eq. 4, can be determined by plotting P(n|A)/g(A) versus x = n/f(A) for a range of areas and assessing whether the data collapse (8) onto a single curve, F(x). The key simplicity underlying such a scaling hypothesis is that the scale-dependent RSA is no longer an arbitrary function of the two variables n and A, but is postulated to satisfy a much simpler scaling form embodied in Eq. 4. In critical phenomena (1–6, 8, 9), in coarsening dynamics (7), and in other contexts in which power laws are observed (10–12, 18–20), the two functions f and g are power laws of A. Here, we do not impose such restrictions.

Results

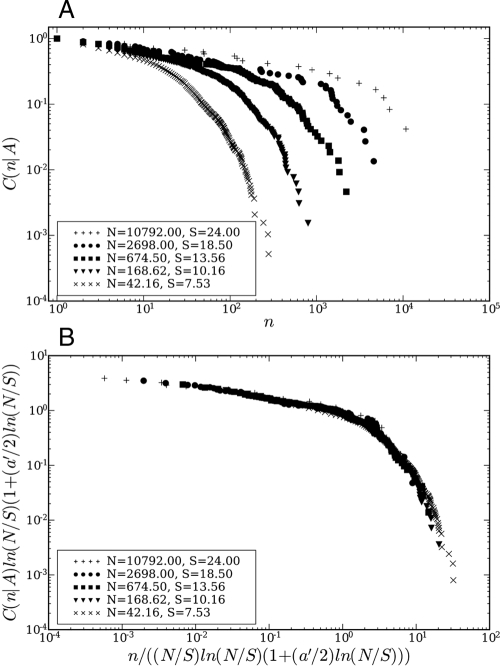
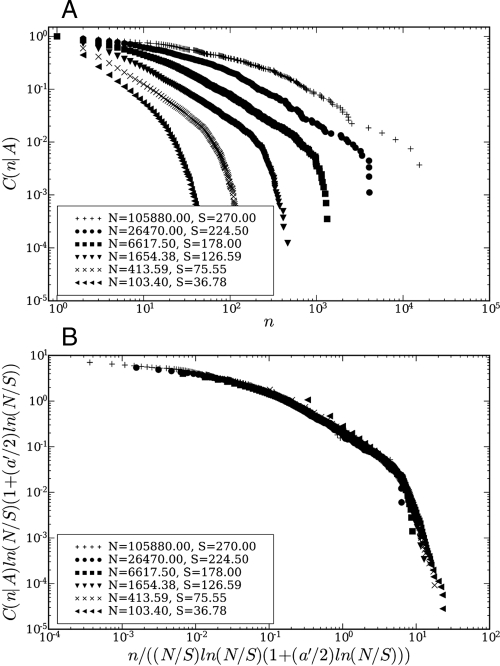
We analyzed two different sets of ecological data, one from a serpentine grassland characterized by an approximate power-law SAR (21) and the other from the Barro Colorado Island (BCI) forest in Panama (22, 23) for which the SAR shows deviations from power-law behavior at all scales (24–27). The best fit is indeed obtained with Δ = 1 with nontrivial logarithmic corrections. The scaling collapse is carried out with one adjustable parameter a′ (see Materials and Methods): for various values of A, one plots $ln{〈n〉}_A(1+\frac{a\text{'}}{2}ln{〈n〉}_A)C(n|A)$ versus n/f(A) and assesses the quality of the collapse. For the ranges of A and n values shown, Fig. 1B shows a collapse plot (28) for the serpentine grassland plot with a′; = -0.12±0.01. The scaling collapse provides a unification of the SAR and the RSA measured at different scales, in the sense that the scaling of the RSA at different scales is determined by the SAR through the term 〈n〉_A in Eqs. 14 and 15. Likewise, Fig. 2B depicts the collapse plot for the BCI data with a choice of a′ = 0.06±0.01. The error estimates are obtained by performing a set of collapse plots, each time excluding a single RSA curve, and calculating the variance of the distribution of the resulting a′ values.

Fig. 1.

Collapse plot for serpentine grassland data. (A) Plot of the cumulative RSA C(n|A) = ∫_n^∞ P(t|A)dt for a serpentine grassland plot for different areas. The average number of individuals N and the average number of species S are indicated. (B) Scaling collapse plot of the cumulative RSA curves for the serpentine grassland plot. The axes are rescaled according to Eq. 15 and the parameter a′ has been chosen to be -0.12.

Fig. 2.

Collapse plot for BCI data. (A) Plot of the cumulative RSA C(n|A) = ∫_n^∞ P(t|A)dt for the BCI plot for different areas. The average number of individuals N and the average number of species S are indicated. (B) Scaling collapse plot of the cumulative RSA curves for the BCI plot. The axes are rescaled according to Eq. 15 and the parameter a′ has been chosen to be 0.06.

In the best fit case, Δ = 1, one predicts to lowest order that

and thus

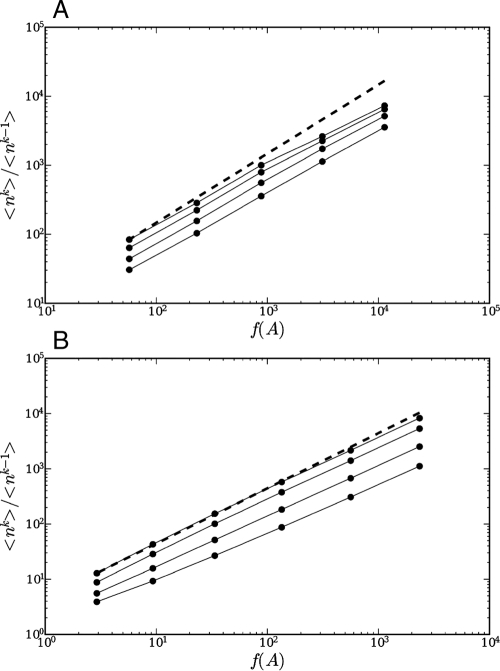
with f(A) defined in Eq. 12. Fig. 3 confirms the approximate validity of the above prediction in the limit of large enough A. The agreement is better for the BCI forest than for the serpentine grassland because of its larger size and especially because the serpentine grassland is species poor (only 24 species instead of ∼300 in BCI).

Fig. 3.

Moment ratio. Plot of the moment ratio n_k = 〈n^k〉/〈n^k-1〉 vs. f(A), k = 1.3,1.6,2, and 2.4 for different values of the area for the serpentine grasslands (A) plot and the BCI plot (B). The dashed line is a power law with exponent 1.

Discussion

Despite their differences, both the BCI forest and the serpentine grassland are characterized by Δ = 1 with nontrivial logarithmic corrections. In critical phenomena, when two distinct systems are characterized by the same set of critical exponents, they are said to belong to the same “universality class.” For example, the liquid–vapor critical point is in the same universality class as the onset of ordering of a binary alloy such as brass. One obtains the same set of critical exponents for those systems, even though they are quite distinct at the atomic scale. What is remarkable in critical phenomena is that, despite the immense variety of systems, there are just a few universality classes that depend only on essential features, such as the spatial dimensionality and the symmetry of the ordering. We find that, despite their apparent differences, the well-known Fisher log series (29), the BCI forest, and the serpentine grassland have an underlying deep commonality and lie in the same universality class.

In physics, as a system approaches criticality, the correlations between different parts of the system extend over increasingly large distances, and when the system is precisely at the critical point, the correlations are limited only by the size of the system considered. These correlations effectively “organize” the system, and are manifested in the scaling hypothesis. An open issue is to understand the key factors underlying the emergence of nontrivial scaling, through the interdependencies of the components of an ecosystem.

A physical system in the vicinity of a critical point is different from an ecosystem in several respects: (i) there is a lack of knowledge of the Hamiltonian governing the dynamics of the ecosystem; (ii) in an ecosystem, there are no obvious dials similar to the temperature, pressure, and magnetic field in condensed matter physics to tune the system to or away from criticality; (iii) as a consequence, there is no measure of how far from criticality an ecosystem is; and (iv) the scaling in an ecosystem involves quantities such as the number of species instead of standard thermodynamic variables such as temperature, pressure, and magnetic field, whose scaling is known from the singular behavior of physical quantities as the critical point is approached. It has been standard practice in ecology to fit the RSA to models derived based on simple biological assumptions. Such a procedure could only work as long as the underlying assumptions are valid. Here, instead, we consider the RSA at different scales and show that they can be linked with each other and with the SAR. Our work suggests that ecosystems are in a state of incipient criticality—they satisfy scaling relationships even in the absence of power-law behavior (30, 31). This observation opens the attractive possibility of using the generalized scaling hypothesis as a model-independent means of linking ecological relationships beyond the species abundance relationship and the SAR to include allometric relationships such as individual metabolic rate–mass scaling and the community mass spectrum (32, 33)

Material and Methods

1Consider the behavior of the scaling function F(x) with x = n/f(A). For large arguments, as noted previously, F(x) necessarily decays to zero. When x is vanishingly small, i.e., for n much smaller than its characteristic value, we characterize the behavior of F(x) by

In the SI Appendix we show that the exponent Δ is the same as that introduced earlier in Eq. 3. Note that the behavior of F(x) for intermediate values of x is not required for our analysis (see SI Appendix).

One may derive expressions for g(A) and f(A) by imposing the normalization condition (Eq. 1) and by using the definition of 〈n〉_A (Eq. 2). We find that there are 3 distinct cases depending on the value of Δ (plus one important borderline case, see below. The derivations are presented as in SI Appendix):

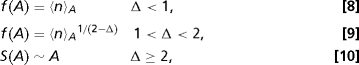with f and g remaining unspecified in the last case. In the first case, g(A) ∼ f(A)⁻¹. For both the second and third cases, g(A) ∼ f(A)^−Δ.

The borderline case Δ = 1, which separates two distinct scaling regimes (Eqs. 8 and 9 is associated with logarithmic corrections and deserves special attention. Examples of this case include the classic Fisher log series (29), which has been invoked to describe the RSA of a metacommunity (14, 34); and a simple form of the species–abundance distribution equation 1 of ref. 35 arising from symmetric density dependence. To identify logarithmic corrections, we postulate that Δ − 1 ≡ a with vanishingly small a. One then obtains from Eq. 7:

yielding

where a′ is a constant proportional to a (see SI Appendix) and

Finite-size scaling works by postulating a scaling relation, Eq. 4, whose validity can be assessed by a procedure called “data collapse” (8). To smooth the data so as to better judge the quality of the collapse, we will use the cumulative probability distribution. Eq. 4 can be used to show that when Δ ≠ 1:

while when Δ = 1 with logarithmic corrections,

Let us assume that we know the cumulative probability distribution C(n|A) and 〈n〉_A for several values of the system size A. A stringent test of the scaling hypothesis is the collapse procedure carried out with either the exponent Δ or the parameter a′ as the only free parameter: for various values of A, one would plot $\frac{C(n|A)}{f(A)g(A)}$ versus $\frac{n}{f(A)}$ or $ln{〈n〉}_A(1+\frac{a\text{'}}{2}ln{〈n〉}_A)C(n|A)$ versus n/f(A) and assess the quality of the collapse or the extent to which the data fall on to a single curve (28). One would strictly expect data collapse to occur in the scaling regime when n and A tend to ∞ but with the ratio n/f(A) remaining finite.