Enhancement of sensitivity gain and frequency tuning by coupling of active hair bundles

Abstract

The vertebrate inner ear possesses an active process that provides nonlinear amplification of mechanical stimuli. A candidate for this process is active hair bundle mechanics observed, for instance, for hair cells of the bullfrog's sacculus. Hair bundles in various inner ear organs are coupled by overlying membranes. Using a stochastic description of active hair bundle dynamics, we study the consequences of an elastic coupling on the properties of amplification. We report that collective effects in arrays of hair bundles can enhance the amplification gain and the sharpness of frequency tuning as compared with the performance of an isolated hair bundle. We also discuss the transient response elicited by the sudden onset of a periodic stimulus and its relation to temporal integration curves. Simulations of systems with a gradient of intrinsic frequencies show an enhanced amplification gain while preserving a frequency gradient, provided the coupling strength is similar to the hair bundle stiffness. We relate our findings to the situation in the bullfrog's sacculus and the mammalian cochlea.

The extraordinary ability of the vertebrate ear to detect sound stimuli over many orders of magnitude in sound amplitude relies on active processes. The key features of the auditory amplifier are (i) the amplification of weak stimuli, (ii) a compressive nonlinearity for stronger stimuli, (iii) frequency selectivity, and (iv) the generation of spontaneous emissions (1–3). All these properties could be understood as the consequence of nonlinear dynamic oscillators that operate in the ear (4–7). There is clear evidence for nonlinear amplification to occur in all vertebrates (3) and even some insects (8). However, the specific molecular and cellular mechanisms underlying the amplifiers in different species are still under debate.

Mechano-sensitive hair cells play a key role in the amplification. Two mechanisms have been suggested. First, outer hair cell electromotility, which involves cell body contractions (9), could be an important element of the amplifier in the mammalian cochlea (10–12). Second, the hair bundle, which is the mechano-sensitive organelle at the apical surface of the hair cell, could generate forces and movements that contribute to amplification (13–15).

Electromotility is absent in nonmammalian vertebrates, which nevertheless display exquisite signal detection with all signatures of the auditory amplifier (3). It has been shown in turtles and frogs that hair bundles are able to generate noisy spontaneous oscillations (13, 16–19). Furthermore, mechanical stimulation of individual hair bundles of the frog revealed a frequency selective response (13), a compressive nonlinearity (20), and a high sensitivity at weak stimuli (20). This suggests that the hair bundles themselves are an essential part of the nonlinear amplifier (21). However, the properties of an individual hair bundle are not sufficient to account quantitatively for the properties of the auditory amplifier. For example, an important characteristics of the amplifier is the amplification gain, defined as the ratio of sensitivity for weak and strong stimulation. The amplification gain measured in the mammalian cochlea is ≈1,000 (22), whereas for a single hair bundle of the bullfrog a value of only ≈10 was observed (20). The amplification gain of a hair bundle is largely limited by random influences, such as thermal fluctuations, channel clatter, and stochastic variations occurring at the scale of the hair bundle (23).

This raises the question what mechanisms underlie the discrepancy between single hair bundle properties and those of the auditory amplifier. In mammals, outer hair cell electromotility could enhance amplification by hair bundles. Another mechanism to increase signal amplification is the cooperative response of groups of coupled hair bundles. In most hearing organs, hair bundles are mechanically coupled via an overlying membranous structure as sketched in Fig. 1A. For example, the outer hair cells of the mammalian cochlea are directly linked via their hair bundles to the tectorial membrane, which is an elastic polymer network (24). Otolithic membranes can also provide an elastic coupling of hair bundles as for instance in the bullfrog's sacculus (25).

Fig. 1.

Coupled hair bundles. (A) Schematic view of a group of hair cells (HC), stereociliary bundles are elastically coupled via an overlying gelatinous membrane (side view). (B) Representation of coupled hair bundles (top view). Hair bundles are arranged on a square lattice with spacing d. Each hair bundle is labeled according to its position (i,j) on the lattice where i = 1,…,N, j = 1,…,M and N·M is the total number of hair bundles. Solid lines represent elastic springs. The excitatory direction of the hair bundles is the positive X direction.

Here, we study the consequences of elastic coupling of hair bundles for their amplification properties. Although our model does not describe an entire hearing organ it characterizes groups of hair bundles as active subunits that are key elements of the auditory amplifier. Specifically, we investigate the properties of groups of hair bundles that are coupled mechanically by elastic springs, excluding from our description inertial elements, such as cochlear fluids or otolithic masses. We discuss properties of spontaneous oscillations and of the nonlinear amplification in response to mechanical stimulation of coupled hair bundles as a function of the coupling strength. Individual hair bundles in the group are described by a simple stochastic model (23, 26) that takes into account random fluctuations and can capture the noise-limited amplification gain of a single hair bundle. Because this example is best studied, we choose parameters that correspond to hair bundles observed in the sacculus of the bullfrog. The same model, however with different parameters, could also be used to describe hair bundles in the cochlea (26).

Physical Description of Coupled Hair Bundles.

We discuss a regular arrangement of hair bundles that are mechanically coupled by elastic elements to their neighbors. In our model, hair bundles are arranged on a square lattice with spacing d (see Fig. 1B). They are labeled (i,j) according to their position on the lattice where i = 1,…, N and j = 1,…, M. Each hair bundle is described by two variables X^i,j and X_a^i,j, characterizing the stereociliary deflection and the state of adaptation motors, respectively. We consider hair bundles that are all oriented with their excitatory direction in the positive X direction and X^i,j are the deflections along this direction. In the following, we ignore deflections in the Y direction^†. A given hair bundle at site (i,j) is coupled via linear springs to the neighboring hair bundles at sites (i + k,j + l) with k,l = −1,0,1, including diagonal connections.

Boundary conditions are introduced via the boundary sites (k,k′) where at least 1 of these indices is 0, N + 1 or M + 1 (see gray boxes in Fig. 1B). We focus on open boundary conditions for which no elastic connections exist to the boundary sites. In the case of fixed boundaries these connections exist and X_k,k′ 0 for all boundary sites. Periodic boundary conditions can be defined in a standard way^‡.

We will consider both spontaneous activity of coupled hair bundles and the response to a periodic stimulus force F_ext(t) = F cos(2πf_s t). In the latter case, all hair bundles are stimulated by the same periodic force F_ext(t) = d²σ_ext(t). This corresponds to the situation where a collection of hair bundles is mechanically stimulated by a periodic shear stress σ_ext(t) applied homogeneously via the overlying elastic membrane.

The equations governing the dynamics of a system of coupled hair bundles read

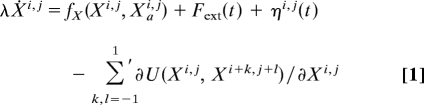where the prime in the first equation indicates that the sum excludes boundary sites for open boundary conditions. The potential corresponding to the elastic forces with spring constant K is given by^§

The force generated by active and passive elements within a given hair bundle is given by

The pivotal stiffness and the gating stiffness of each hair bundle are denoted by K_SP and K_GS, respectively. The open probability of the mechano-sensitive ion channels is given by P_o(X, X_a) = [1 + Aexp(−K_GS D(X − X_a)/(N_ek_BT))]⁻¹, where N_e is the number of transduction elements within each hair bundle, the displacement D is associated with channel gating, k_BT is the thermal energy, and A = exp[(ΔG + K_GS D²/2N_e)/k_BT ]. Eq. 2 describes the force-velocity relation of the adaptation motors. The force

is the difference of the force f_m = K_GS(X − X_a − DP_o) exerted on the motors and the force f_a = F_max(1 − SP_o) generated by the motors at stall. If all channels are closed, the latter is maximal f_a = F_max. Calcium influx through open channels inhibits motor activity; the strength of calcium inhibition is characterized by the parameter S.

The hair bundle is subject to various sources of fluctuations. Brownian motion of the surrounding fluid and channel clatter, i.e., the stochastic opening and closing of ion channels, lead to noise in the position variable X. The variable X_a is influenced by motor noise stemming from stochastic activity of adaptation motor proteins. Stochastic forces are represented by the independent Gaussian white noises η^i,j(t) and η_a^i,j(t) with correlations 〈η^i,j(t)η^i,j(0)〉 = 2k_BTλδ(t), 〈η_a^i,j(t)η_a^i,j(0)〉 = 2k_BT_aλ_aδ(t), where T_a is an effective temperature.

Results

We perform numerical simulations of Eqs. 1 and 2 for varying system size, coupling strength, and driving parameters. First we consider homogeneous systems with N = M, using a single set of parameters (see Table 1) and study spontaneous and driven movements, and transient responses. Finally, we discuss effects of heterogeneities.

Table 1.

List of parameters and their values used in our simulations

Parameter	Definition	Value
λ	Friction of hair bundle	2.8 μN·s·m−1
λa	Friction of adaptation motors	10 μN·s·m−1
Ne	Number of adaptation motors	50
KGS	Combined gating-spring stiffness	0.75 mN·m−1
KSP	Hair bundle pivot stiffness	0.6 mN·m−1
T	Temperature	300 K
ΔG	Ion channel energy	10 kBT
D	Gating-spring elongation	60.9 nm
Fmax	Maximal motor force	50.24 pN
S	Feedback strength	0.65
Ta	Effective temperature	1.5 T
d	Lattice spacing	50 μm

Spontaneous Noisy Oscillations and Synchronization.

In the absence of coupling, external force, and noise, hair bundles show spontaneous relaxation oscillations. If fluctuations due to Browninan motion, channel clatter, and stochastic binding and unbinding of motor proteins are taken into account these turn into noisy oscillations characterized by a broad peak in the power spectrum S(f). The latter is defined by S(f) = lim_{T → ∞}〈|X̃|²〉/T where X̃(f) = ʃ₀^TdtX(t)e^2πift is the Fourier transform of a hair bundle's deflection and 〈.…〉 denotes the average over a stationary ensemble. For the parameters chosen, the spectral properties closely match those observed for a hair bundle from the sacculus of the bullfrog (23).

To reveal the effect of coupling on an N × N array of hair bundles, we varied the spring constant K and the system size, and determined the power spectrum of the central hair bundle's displacement^¶. Power spectra for increasing coupling strength K, shown in Fig. 2A for a 9 × 9 array, demonstrate a sharpening of the spectral peak. This is further quantified in Fig. 2 B and D in terms of the height S(f₀) of the spectral peak at its characteristic frequency f₀, and its quality factor Q = f₀/|f₂ − f₁| where the halfwidth |f₂ − f₁| is defined by S(f₁) = S(f₂) = S(f₀)/2.

Fig. 2.

Spectral statistics of spontaneous oscillations in a group of hair bundles coupled with strength K. (A) power spectra of the central hair bundle for various K as given in the legend. (B) Height of the spectral peak S(f₀). (C) Correlation coefficient between the central hair bundle and its neighbors to the right for different K as indicated in A. (D) Quality of oscillations of the central hair bundle for different system sizes vs. K. System sizes in A and C are 9 × 9 and as indicated in B and D. The dashed lines in B and D mark the passive stiffness K_SP of an individual hair bundle.

The height and quality dependence on K reveal three regimes: weak (low plateau), intermediate (steep slope), and strong coupling (high plateau). In the latter two regimes, the height and quality of the spectral peak depend on the system size—the respective plateau at large K is growing with N. We note that the frequency f₀ varies only mildly with increasing coupling strength (≈10%; data not shown) resulting in a shallow maximum of the quality factor vs. K.

Coupling also introduces synchrony among the different hair bundles that can be characterized by cross-correlation coefficients. Specifically, we show in Fig. 2C the cross-correlation coefficients between the central hair bundle and its neighbors to the right for a 9 × 9 array. Cross-correlations increase with increasing K and for sufficiently strong coupling (see the data for K = 1 mN·m⁻¹) all hair bundles in the array are synchronized; the correlation coefficient between any two hair bundles in this case is close to 1 (data not shown).

Nonlinear Amplification and Frequency Tuning.

The main task of hair bundles is the transduction and amplification of sound signals that are in the simplest case pure harmonics. In this section, we study how the linear and the nonlinear response of the system of coupled hair bundles depends on coupling parameters. If all hair bundles in a given system are simultaneously driven by a periodic stimulus F_ext(t) = F cos(2π f_s t), the central hair bundle responds after a transient with a periodic mean motion of the same frequency. This response contains in general higher harmonics of the driving frequency and reads 〈X(t)〉 = A₁ cos(2π f_s t − φ₁) + A₂ cos(4π f_s t − φ₂) +..., where the dots indicate further harmonics and φ_i is the phase shift of the ith Fourier mode. The sensitivity is defined as the absolute value |χ(f_s,F)| of the nonlinear response function of the first Fourier mode χ = (A₁/F)e^iφ₁. The sensitivity has units of a compliance. It describes the elicited output amplitude per unit driving force. We discuss the sensitivity as a function of the coupling strength, of the driving frequency for weak periodic driving, and as a function of the forcing amplitude. In the latter case, the sensitivity saturates for both very weak and very strong stimuli. The ratio of these two limiting values for a driving at the characteristic frequency f_s = f₀ defines the gain

because of the nonlinearities in the hair bundle dynamics.

The sensitivity as a function of coupling strength for a weak driving at f_s = f₀ is displayed in Fig. 3A. The resulting behavior resembles the one of the spectral peak height discussed above. At weak coupling the sensitivity changes little with increasing coupling or system size and is close to the value of a single hair bundle (23). Beyond a certain critical coupling K > 0.1 mN·m⁻¹, the sensitivity sharply increases and saturates at a size-dependent level.

Fig. 3.

Sensitivity of coupled hair bundles for periodic forcing. (A and B) Linear response (sensitivity at weak forcing) of the central hair bundle for various system sizes as indicated. Forcing amplitudes are F = 0.1 pN for 1 × 1, F = 0.05 pN for 3 × 3, 4 × 4, F = 0.025 pN for 6 × 6, F = 0.01 pN for 9 × 9. (A) Linear response to a stimulus tuned to the frequency of spontaneous oscillations (f_s = f₀) vs. coupling strength K. (B) Linear response vs. frequency detuning f_s − f₀. (Inset) Same data with maxima normalized to 1. (C) Nonlinear response as represented by the sensitivity vs. forcing amplitude F. (D) Amplification gain as a function of the total number of hair bundles (boundary conditions as indicated). In B and C, the coupling strength K is chosen such that the quality of spontaneous oscillations is maximal (K = 0.45 mN·m⁻¹ for 3 × 3 and 4 × 4, K = 0.32 mN·m⁻¹ for 6 × 6, K = 0.28 mN·m⁻¹ for 9 × 9). The dashed line in C indicates a power law for comparison. The dashed line in A marks the passive stiffness K_SP of an individual hair bundle.

To characterize the best possible performance, in the following we tune the coupling such that the sensitivity is at or close to its high-coupling limit. Specifically, we choose the coupling that maximizes the quality of the spontaneous activity. We have checked that the exact value of the coupling is immaterial as long as we are in the strong-coupling regime discussed above.

The sensitivity for weak stimuli (linear response) is shown in Fig. 3B as a function of the frequency mismatch f_s − f₀. Close to the spontaneous frequency (f_s ≈ f₀), the sensitivity attains its maximum, which increases and sharpens strongly for increasing N. For large frequency mismatch the sensitivity is independent of N. The nonlinear response to periodic forcing can be characterized by the dependence of the sensitivity on the forcing amplitude F (see Fig. 3C). A clear nonlinearity can be seen already for a single hair bundle (23). At small driving amplitude, the linear response regime manifests itself by a plateau. At higher values of F, the sensitivity decreases approximately like a power law |χ| ∼ F^−α. Remarkably, by increasing the system size we increase considerably the range of forcing amplitudes for which a power law applies. For a 9 × 9 array, the sensitivity exhibits a power-law behavior with α ≈ 0.88 over at least two orders of magnitude. Note that the value of α is larger than the one characterizing the nonlinearity for a single hair bundle (α ≈ 0.66). The larger value of α implies an even stronger nonlinear compression.

We also find that the gain increases almost linearly with the number of hair bundles (see Fig. 3D) and attains a value of ≈400 for a 9 × 9 array. To verify that this result is not solely due to the kind of boundary conditions chosen we repeated the simulations for periodic and fixed boundary conditions. The resulting gain (see Fig. 3D) demonstrates that even in the rather pessimistic setting with fixed boundaries an enhancement effect (although reduced compared with the case with open boundary conditions) survives. Interestingly, the curve for periodic boundary conditions differs only marginally from the main result for open boundary conditions.

Transient Responses.

So far, we have discussed the nonlinear amplification of coupled hair bundles for long stimulation times. However, after a periodic stimulus is switched on it takes a certain time until this full response is reached (see Fig. 4A). This limits the time resolution of the system regarded as a detector. We now discuss the characteristic relaxation time τ of a group of hair bundles for a periodic stimulus with frequency f_s = f₀. In general, τ depends on the force amplitude F and the system size. If the stimulus is switched on at t = 0 the mean response for t > 0 is well described by

The relaxation time τ(F) obtained by a fit of this expression to simulation data is displayed in Fig. 4B as a function of stimulus amplitude F. At small amplitude, the relaxation time is largest and is given by τ ≈ Q/(π f₀), i.e., by the inverse half-width of the spectral peak in the absence of a stimulus (shown by solid lines in Fig. 4B). A 9 × 9 system relaxes at weak stimulus after ≈100 stimulus cycles whereas a single hair bundle already relaxes after one cycle. Remarkably, the relaxation time decreases for stronger stimuli as a power law τ ∼ F^−β with β ≈ 1.17, which occurs in the same range of stimulus amplitudes as does the power law of the sensitivity (Fig. 3C). Therefore, as the stimulus amplitude is increased, sensitivity is reduced but the response becomes faster. We note that the relaxation time saturates for strong forcing at a value corresponding to the relaxation time of the passive system (τ_∞ ≈ (K_GS + K_SP)/λ), which is smaller than 1/f₀.

Fig. 4.

Transient response to periodic forcing applied for times t ≥ 0 to a system of coupled hair bundles initially in steady state. (A) Time-dependent mean response of the central hair bundle (black line) for a 3 × 3 array (F = 0.065 pN, averaged over 263,000 realizations). Envelope (red line) resulting from a fit according to Eq. 2. After time t_th, the average response reaches a detection threshold X* (dashed line). (B) Relaxation time τ determined from fits as shown in A in units of periods f_s⁻¹ vs. forcing amplitude F for various systems as indicated. For a weak forcing, τ ≈ Q/(πf₀) (horizontal lines); for intermediate values of the forcing amplitude, τ ∼ F^−1.17 (dashed line). (C) Minimal force F* needed to reach a given threshold X* after a given number t_thf₀ of stimulus cycles. For large systems, F* ∼ t_th^−0.78 (dashed line).

For a sound detector an important property is the minimal force amplitude F* required for the mean response to reach a detection threshold X* within a given time t_th (see Fig. 4A). Put differently, F* is the threshold force of the system for a given time resolution t_th and detection threshold X*. Using Eq. 7 we find that the relation between F* and t_th is given by

This relation is displayed in Fig. 4C using our simulation data for arrays of different sizes and a threshold amplitude of X* = 1 nm (15). For increasing detection window t_th, the threshold amplitude F* decreases until a minimal threshold force X*/|χ(F = 0)| is reached. For large systems, we obtain a power law dependence F* ∼ t_th^{1/(α − β − 1)}, which is indicated in Fig. 4C as a dashed line. For increasing system size, cooperativity of hair bundles leads to a reduction of the minimal threshold force X*/|χ(F = 0)|; this requires increasingly large stimulus durations t_th. Note, however, that for a force amplitude of F = 10⁻² pN, which is in the sensitive linear response regime, only ≈20 stimulus cycles (t_th = 20 f₀⁻¹) are required to reach the detection threshold of X* = 1 nm.

Heterogeneities.

So far, we have considered systems of N × N identical hair bundles. However, in vertebrate hearing organs neighboring hair cells can differ in their characteristic frequencies. In addition, hair cells are arranged in various geometries. For instance, in the cochlea outer hair cells occur in three rows and exhibit a frequency gradient along the basilar membrane.

To verify that the effects discussed above are not solely due to the specific setup chosen, we have also investigated systems of N × M coupled hair bundles with different values of N and M, and random and graded frequency profiles with up to 20% frequency variability. In general, if the coupling is sufficiently strong, we recover all of the effects found in homogeneous quadratic systems (synchronization, enhanced frequency tuning, and enhanced gain).

In the following, we discuss the specific case of N = 3 and M = 27 with a linear gradient of the intrinsic frequencies of individual hair bundles along the Y axis. The intrinsic frequency of an individual hair bundle depends on the pivotal stiffness K_SP in an almost linear fashion (see Fig. 5A Inset). By varying K_SP between 0.5 mN·m⁻¹ and 0.7 mN·m⁻¹, we tune the spontaneous oscillations to frequencies varying ≈20%. In Fig. 5, we show the statistics of spontaneous and driven activity of the central hair bundle of a system of coupled hair bundles for different ranges of intrinsic frequencies. These frequency ranges are introduced by a linear gradient of pivotal stiffness^‖ with a range ΔK_SP.

Fig. 5.

The effect of a linear gradient of intrinsic frequencies in a system of 3 × 27 coupled hair bundles with open boundary conditions. Four different frequency gradients are generated by a linear variation of pivotal stiffness over different ranges ΔK_SP as indicated in D. (A) Frequency gradient along the Y axis characterized by the range of frequencies Δ f₀ of spontaneous hair bundle movements relative to the frequency of the central hair bundle f̄₀ as a function of coupling strength K. (B) Sensitivity |χ| in linear response of the central hair bundle vs. coupling strength K for stimulus frequency f_s = f̄₀ and stimulus amplitude F = 0.01 pN. (C) Quality Q̄ of spontaneous oscillations of the central hair bundle vs. coupling strength K. The dashed lines in A–C indicate the passive stiffness K̄_SP of the central hair bundles. (D) Sensitivity vs. F for K = K̄_SP = 0.6 mN ·m⁻¹ and f_s = f̄₀. A–D, the pivotal stiffness of the central hair bundle is K̄_SP = 0.6 mN ·m⁻¹.

Fig. 5A shows the frequency range Δ f₀ relative to the frequency of the central hair bundle f̄₀ of the spontaneous activity^††. The relative frequency range depends on coupling strength K. In the absence of coupling (K = 0), Δ f₀ equals the intrinsic frequency range of the system. The examples shown correspond to relative intrinsic frequency ranges of 0% (green), 2% (red), 9% (blue) and 18% (yellow). In the limit of large coupling (K ≫ K_SP), Δ f₀ vanishes and all hair bundles are synchronized. For K ≲K̄_SP, the frequency range is reduced but a significant frequency gradient remains. The maximal sensitivity |χ| and the quality Q̄ of the central hair bundle are displayed in Fig. 5 B and C, respectively, as functions of K. For both quantities, deviations from the homogeneous case (green lines) occur predominantly for K ≈ K̄_SP. If K differs by less than an order of magnitude from K̄_SP, amplification and frequency tuning are significantly enhanced, while at the same time frequency gradients can be preserved. The sensitivity as a function of driving amplitude is shown in Fig. 5D for coupling strength K = K̄_SP. At this coupling strength sensitivity is significantly enhanced by coupling while there still exists a range Δf₀ of frequencies of the spontaneous activity in heterogeneous systems. All cases shown exhibit a strong compressive nonlinearity and amplification gain. Increasing the intrinsic frequency range from 0% to 18%, the amplification gain is reduced from ≈300 to ≈100.

Discussion

Using a theoretical description, we have numerically studied the properties of hair bundles that are mechanically coupled to their neighbors. We have shown that this local coupling has a significant impact already on small groups of hair bundles. Upon periodic stimulation, coupled hair bundles exhibit compared with single hair bundles (i) a substantially enhanced amplification gain; (ii) a more pronounced compressive nonlinearity, extending over a larger range of amplitudes; and (iii) a sharper frequency discrimination. Groups of synchronized hair bundles generate enhanced responses and almost attain the extraordinary features observed for the cochlear amplifier of mammals with G ≈ 1,000 (22). In comparison, we found for a sufficiently large coupling strength K a pronounced nonlinearity in the response to periodic stimulation with an amplification gain of ≈400 for a 9 × 9 system.

The substantial enhancement of the amplification coincides with a pronounced synchronization of hair bundles. Both effects suddenly appear for increasing coupling strength at values of approximately the passive stiffness of the single bundle and persist for stronger coupling (K ≳ K_SP). In the strong coupling regime, all hair bundles become synchronized (see Fig. 2C), suggesting that the group of hair bundles behaves effectively like one oscillator, but with a reduced noise intensity. In this case, the movements of the central hair bundle are well-described by the average movement of the group, which is subject to an average noise. Because the sources of noise in different hair bundles are uncorrelated, the noise intensities k_BTλ and k_BT_aλ_a are reduced by the total number of hair bundles N². To test this idea, we have performed simulations of a single hair bundle with artificially lowered noise intensities, dividing the original noise intensities by N² = 81. We find a compressive nonlinear response with a gain of ≈400 (data not shown), very similar to a coupled 9 × 9 system. This suggests that the increased sensitivity observed in arrays of coupled hair bundles is a consequence of noise reduction due to coupling.

In addition to the long-time behavior, we also observe strong effects of hair bundle coupling on the transient response to periodic stimulation. The minimal amplitude F* of a stimulus to reach a detection threshold after a finite time t_th can obey a power law (see Fig. 4C). In many hearing organs, temporal integration curves have been measured (28, 27) revealing nonlinear relationships between threshold and duration; often, power laws close to F* ∼ t_th^−3/8 are reported (27) (assuming that F is proportional to stimulus pressure). As shown above, coupling of hair bundles naturally generates power laws, but with an exponent closer to −3/4 than to −3/8.

The properties of hair bundles coupled via the tectorial or otolithic membranes can be related to features of the auditory amplifier of different species. Our results for many hair bundles of the same intrinsic frequency apply, for example, to the echo-response region of some bats. There many hair cells, specialized to the same frequency, generate extremely sharply tuned threshold responses. The observed sharpness of tuning corresponds to a quality of the detector Q ≈ 500 (29, 30). This can be related to the quality of spontaneous activity of a homogeneous 9 × 9 system for which we find Q ≈ 160. Therefore, the sharp tuning observed in the echo-response region in bats could result from the mechanical coupling of large groups of hair bundles that operate at the same frequency.

Although in special cases, as just discussed, many hair cells of the same frequency can exist nearby, in most hearing organs neighboring hair cells are tuned to different frequencies. To study the effects of frequency variability on the amplification gain we have studied systems of coupled hair bundles with a linear frequency gradient. Motivated by the arrangement of outer hair cells in the cochlea, we have chosen a geometry of 3 × 27 coupled hair bundles. For sufficiently strong coupling, we recover the amplification gain of homogeneous systems of the same number of hair bundles. In this case, the frequency gradient is drastically reduced because of synchronization effects. Our analysis shows that there is characteristic range of coupling strengths K approximately K ≈ K_SP where amplification is significantly enhanced while at the same time frequency variability is preserved. For smaller K values, synchronization is lost, whereas, for larger K values, frequency variability is lost.

In our work, we have studied the effect of coupling on hair bundle dynamics as a function of coupling strength K. Values of K in different hearing organs can be estimated from the elastic properties of otolithic or tectorial membranes. In the otolithic membrane of the bullfrog, direct mechanical measurements show that the membrane constitutes an elastic medium and local stresses lead to displacements that decay exponentially with a characteristic length ℓ, which depends on direction in the sacculus (31). Such a decay with ℓ ≈ d(K/K_SP)^1/2, where d is the spacing between hair cells, also occurs in our model (data not shown). Using d ≈ 50 μm, ℓ ≈ 150 μm (31), and K_SP = 1 mN·m⁻¹ (including contributions from subotolithic filaments; see ref. 31) results in K ≈ 9 mN·m⁻¹. Alternatively, we can estimate the coupling strength based on the Young's modulus E of the membrane overlying the hair bundles as K ≈ Ed. For the otolithic membrane of the bullfrog's sacculus E ≈ 6.6 kPa has been suggested (31, 32), leading with d = 50 μm to an estimate of K ≈ 330 mN·m⁻¹. Both estimates of K correspond to the strong coupling regime and lead to complete synchronization and reduction of frequency heterogeneities in our simulations. Note that these estimates do not take into account the 3 dimensional shape of the otolithic membrane that exhibits large cavities inside which hair bundle tips are attached (25). This specific geometry and a potentially soft coupling of the hair bundle to the otolithic membrane could reduce K, thus permitting different frequencies to coexist. Furthermore, inertial effects introduced by otolithic masses that we have neglected in our simulations might also influence synchronization in the system.

In the mammalian cochlea the Young's modulus of the tectorial membrane has been estimated and exhibits a gradient of tectorial stiffness (33–37). Values reported range from E = 0.3 kPa at the apex to 3 kPa at the base in gerbil (37) and from E = 24 kPa at the apex to 224 kPa at the base in mouse (36). With d = 10 μm the values observed in gerbil correspond to a range K = 3−30 mN·m⁻¹. As discussed above, to benefit from hair bundle coupling, while retaining a frequency profile, the coupling strength provided by the tectorial membrane should be within an order of magnitude of the hair bundle stiffness. Hair bundle stiffness does indeed vary along the cochlea. In guinea pig values of K_SP of outer hair cells ranging from ≈0.5 mN·m⁻¹ at the apex to ≈40 mN·m⁻¹ at the base, have been reported (38). This suggests that the tectorial membrane stiffness is tuned to the local hair bundle stiffness following a similar gradient (37), ensuring that the local coupling strength K is adjusted to the local hair bundle stiffness K_SP. Our work shows that such an adjustment of coupling permits a significant enhancement of amplification via coupling while preserving at the same time gradual frequency changes.