Multilocus LD Measure and Tagging SNP Selection with Generalized Mutual Information

Abstract

Linkage disequilibrium (LD) plays a central role in fine mapping of disease genes and, more recently, in characterizing haplotype blocks. Classical LD measures, such as D′ and r², are frequently used to quantify relationship between two loci. A pairwise “distance” matrix among a set of loci can be constructed using such a measure, and based upon which a number of haplotype block detection and tagging single nucleotide polymorphism (SNP) selection algorithms have been devised. Although successful in many applications, the pairwise nature of these measures does not provide a direct characterization of joint linkage disequilibrium among multiple loci. Consequently, applications based on them may lead to loss of important information. In this paper we propose a multilocus LD measure based on generalized mutual information, which is also known as relative entropy or Kullback-Leibler distance. In essence, this measure seeks to quantify the distance between the observed haplotype distribution and the expected distribution assuming linkage equilibrium. We can show that this measure is approximately equal to r² in the special case with two loci. Based on this multilocus LD measure and an entropy measure that characterizes haplotype diversity, we propose a class of stepwise tagging SNP selection algorithms. This represents a unified approach for SNP selection in that it takes into account of both the haplotype diversity and linkage disequilibrium objectives. Applications to both simulated and real data demonstrate the utility of the proposed methods for handling a large number of SNPs. The results indicate that multilocus LD patterns can be captured well, and informative and nonredundant SNPs can be selected effectively from a large set of loci.

Introduction

It has been suggested in recent years that patterns of linkage disequilibrium (LD) vary across the human genome, leading to the concept of haplotype blocks (high LD regions), with its main characteristic being reduced haplotype diversity within each block. For a block containing n single nucleotide polymorphisms (SNPs), the number of observed haplotypes with greater than 5% frequencies is typically much smaller than the 2ⁿ potential haplotypes (Gabriel et al. 2002). SNPs are not only instrumental in the definition of haplotype blocks, but they also play important roles in genetic studies as they are highly abundant and some may even be functional variants themselves (which makes them ideal markers for candidate gene association studies). Thus, it is an important, although highly challenging, task to select a minimal subset of SNPs that represent haplotype diversity in the blocks in an optimum way. One indirect approach of SNP selection is via studying local patterns of LD, which are thought to contain information about evolutionary history of SNPs. A great deal of research have been carried out that seek to characterize LD patterns, and to use them for haplotype block identification and SNP selection (e.g., Abecasis et al. 2001; Daly et al. 2001; Reich et al. 2001; Gabriel et al. 2002, Clark et al. 2003; McVean et al. 2004; Schaid 2004; Rinaldo et al. 2005).

Classical pairwise LD measures, such as D′ and r², are commonly used in LD characterization, block detection, and SNP tagging studies, including those referenced above. Despite the popularity of these measures, their pairwise fashion does not provide a direct measure of joint LD among multiple loci. Moreover, D′ may be biased for small to moderate sample sizes (Terwilliger et al. 2002), and it may not be sensitive enough to distinguish between different degrees of LD either (Nothnagel et al. 2002). Other new pairwise LD measures have also been proposed (Morton et al. 2001; Pritchard and Przeworski 2001). While those measures have their own merits, they have the same disadvantage as the classical ones in that they do not provide a single direct measure of LD for multiple loci jointly.

Measures of gametic disequilibrium for three and four loci were discussed in Weir (1996). A couple of general multilocus LD measures were proposed in recent years. In Sabatti and Risch (2002), a multilocus LD measure was developed, but this measure is haplotype specific and thus it is not clear whether or how it can be used for SNP selection. Nothnagel et al. (2002) proposed an entropy based multilocus LD measure, ε. It is defined as follows. For a chromosomal segment containing n SNPs, let p_j be the frequency of the major allele of the jth SNP, j = 1, middot; middot; middot;, n. Suppose that there are m observed haplotypes with frequencies q_i, i = 1, ···, m, then the entropy of this haplotype distribution is defined as $H={\sum }_{i=1}^m{q}_i{log}_2(q_i)$. Under the assumption of linkage equilibrium, the frequency of any haplotype k can be calculated using the formula $q_k^E={\prod }_{j=1}^n{p}_j^{I_k^j}{(1-p_j)}^{1-I_k^j}$, where $I_k^j$ is 1 if the allele on haplotype k at the jth SNP is the major allele, otherwise it is 0. The corresponding entropy is then $H_E={\sum }_{k=1}^{2^n}{q}_k^E{log}_2(q_k^E)$. The authors then defined a normalized entropy,

$$\epsilon =\frac{H_E-H}{H_E},$$

as a multilocus LD measure. Note that 0 ≤ ε < 1, and larger ε is interpreted as indicating a greater degree of LD. This measure is useful for detecting genomic regions with low LD, and it can be based upon to find haplotype blocks, as proposed by the authors, and as in Rinaldo et al. (2005).

Despite its potential usefulness, this LD measure has several drawbacks. First, the upper bound of 1.0 can never be reached (which can be viewed as a sub-measure), and thus its performance in the special case with two loci cannot be directly compared with classical pairwise LD measures. Second, for a block in which all SNPs are in complete LD, ε’s outcome is dependent on the number of SNPs it considered. This is rather undesirable for haplotype block detection as it may fail to recognize blocks containing a small number of SNPs. Third, it is not computationally efficient when it is applied to selecting SNPs in a haplotype block with a large number of loci. With current computing power, the number of SNPs that ε can handle is limited to about 10 with the accompanying software by Nothnagel et al. (2002). As we will show later, the first two issues can be easily resolved by a modified ε measure. However, the last issue about the computational intensity remains.

In an association study of a candidate region, it is usually too costly to genotype all SNPs within the region, as the number of SNPs can be very large given their abundant nature. On the other hand, genotyping only an appropriately selected subset may not lead to much, if any, reduction in information. This is due to limited diversity within haplotype blocks, which renders information in some of the SNPs redundant. Thus, the challenge is to select a minimal subset that retains most of the information provided by the full set. This should reduce genotyping cost without sacrificing the ability to assess disease association in the region. Note that the term “information” is used in a loose sense here, as it may mean different measures from different perspectives, as discussed below.

SNP selection is usually either based on pairwise LD measures (leading to tagging SNPs, or tagSNPs) or on estimated haplotype frequencies from genotype data (leading to haplotype tagSNPs, or htSNPs). In this paper, no distinction between tagSNP or htSNP is made; they are all referred to as tagging SNPs. There is currently no consensus on optimization criteria, or what the benchmark should be to compare the relative performances of tagging SNPs selected by different methods/criteria. Discussion on these issues can be found in Weale et al. (2003) and references therein. Briefly, one of the broad criterion for measuring informativeness of a selected subset is the proportion of “haplotype diversity” being explained. Another broad criterion is based on how well the frequencies of the other SNPs (those not being tagged) can be predicted, an “association” (or LD) criterion.

Regardless of which selection criterion or which measure of informative is being used, most of the methods in the literature select tagging SNPs using an all-possible-subset approach. That is, all possible subsets of a given size are considered, and the one that optimizing the chosen criterion is retained as the best subset of that size. This is a fine strategy if the number of SNPs in the full set is not too big. However, the number of all possible subsets simply becomes too large to be practical for large haplotype blocks; there are more than 300,000,000 subsets of size 16 to comb through with a full set of 31 SNPs, for instance.

In this article, we propose a novel multilocus LD measure with generalized mutual information. Our measure overcomes the drawbacks of ε discussed above. In particular, the measure is more computational efficient so that it can handle any number of SNPs, and its value is 1.0 when the SNPs within a haplotype block are completely dependent, regardless of the number of loci. It is also approximately equal to r² for the special case with two loci when there is strong LD. Based on this multilocus LD measure and an entropy measure that characterizes haplotype diversity, we propose a stepwise tagging SNP selection algorithm. This represents a unified approach for SNP selection in that it takes into account of both the haplotype diversity and linkage disequilibrium objectives. Applications to both simulated and real data demonstrate the utility of the proposed methods for handling a large number of SNPs. The results indicate that multilocus LD patterns can be captured well, and informative and nonredundant SNPs can be selected effectively from a large set of loci.

Methods

A Multilocus LD Measure

Information theory provides a natural way to quantify relevant information. Here we propose a multilocus linkage disequilibrium measure through extending the mutual information theory to measuring multivariate statistical dependency. This measure uses the Kullback-Leibler (K-L) distance to quantify the difference between the observed distribution of haplotype and the expected distribution under linkage equilibrium (LE; independence of SNPs). Suppose that there are n SNPs under consideration, with m observed haplotypes. Let X be the random variable of haplotype, and let X_j be the random variable of alleles at SNP j, j = 1, middot; middot; middot;, n. Thus X takes the values of x_i = (x_i1, x_i2, middot; middot; middot;, x_in), i = 1, middot; middot; middot;, m, where x_ij is the allele on haplotype i at locus j. Furthermore, let p and p_j be the probability distribution of X and X_j, j = 1, middot; middot; middot;, n, respectively. Our LD measure is defined as follows:

$$E=\sum _{i=1}^{m}p({\mathbf{x}}_i){log}_2\frac{p({\mathbf{x}}_i)}{{\prod }_{j=1}^n{p}_j(x_{ij})}.$$ (1)

The definition in equation (1) is referred to as relative entropy, or K-L distance, a basic measure in information theory (Cover and Thomas 1991). In our particular setting here, the relative entropy measures the distance between two distributions, p and $q={\prod }_{j=1}^n{p}_j$, defined on the same sampling space of haplotypes over the n loci.

The properties of K-L distance ensure that the quantity defined in (1) is nonnegative and is zero if and only if the SNP variables are independent. Larger value of E is taken to indicate greater degree of LD. This measure is also bounded above. The upper bound can be found in terms of the entropies H_pj (X_j) of the distributions p_j of individual SNP variables X_j (to be proved in Appendix A):

$$E\le \sum _{j=1}^{n}H({\mathbf{X}}_j)-\underset{j}{max}H({\mathbf{X}}_j)=E_{max}.$$ (2)

Note that the subscript p_j is dropped from H_pj (X_j) in the above inequality, and it will continue to be omitted hereafter where no ambiguity can occur. The upper bound in the inequality is attainable, which occurs when all the loci are in complete LD. Thus, a normalized LD measure is defined as

$$ER=ER({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_n)=\frac{E}{E_{max}}=\frac{{\sum }_{i=1}^{m}p({\mathbf{x}}_i){log}_2\frac{p({\mathbf{x}}_i)}{{\prod }_{j=1}^n{p}_j(x_{ij})}}{{\sum }_{j=1}^{n}H({\mathbf{X}}_j)-{max}_{j}H({\mathbf{X}}_j)}.$$ (3)

The properties of equation (3) as discussed above as well as additional ones, to be proved in Appendix B, are summarized as follows:

1. 0 ≤ ER ≤ 1, with the lower and upper bounds being attained when the SNPs are in complete LE and LD, respectively.

2. For two loci, this LD measure reduces to mutual information between the two SNPs, and it is approximately equal to the classical LD measure r² under certain conditions to be detailed in the appendix.

Criteria and Algorithms for Selecting Tag SNPs

The relationship between joint entropy (or total information; H(X_j, X_k)) and individual entropies (H(X_j) and H (X_k)) of two loci (X_j, X_k) can be expressed as follows:

$$H({\mathbf{X}}_j,{\mathbf{X}}_k)=H({\mathbf{X}}_j)+H({\mathbf{X}}_k)-I({\mathbf{X}}_j;{\mathbf{X}}_k),$$

where I(X_j; X_k) is the mutual information between the two loci. It is easily seen that mutual information I and total information H are complementary to one another, in that their sum is equal to the sum of marginal entropies. However, they are not equivalent to one another since their sum is not a constant; it is dependent on the entropies of individual SNPs.

Extending the concept to multiple loci, we can regard our LD measure as the generalization of mutual information. More specifically, let S be a subset of the full set of SNPs under consideration, then

$$H(S)=\sum _{{\mathbf{X}}_j\in S}H({\mathbf{X}}_j)-E(S),$$

where H(S) is the joint entropy of all SNPs in S, and can be viewed as a measure of haplotype diversity. On the other hand, E(S), as defined before, is our LD measure prior to normalization. Since H(S) is maximized when S = X = {X₁, ···, X_n}, the full set of SNPs, we can define a normalized haplotype diversity measure as

$$HD(S)=\frac{H(S)}{H(\mathbf{X})}.$$

By construction, the two measures, HD and ER, belong to the broad categories of selection criteria based on diversity and association, respectively, according to the classification of Weale et al (2003). Although one can select tagging SNPs by optimizing one of the two criteria, it may be advantageous to devise a class of criteria that combine the two objectives, with either one as a special case. The idea is to find a subset of SNP, S*, that compromises between the objective of maximizing HD and that of minimizing ER. This is motivated by the fact that there is currently no consensus as to which criterion is the best for evaluating the performance of a set of tag SNPs (Weale et al. 2003). Specifically, we maximize the following criterion among the subsets of the same size:

$$\omega (S;\lambda )=(1-\lambda )HD(S)+\lambda (1-ER(S)),$$

where λ (0 ≤ λ ≤ 1) is a pre-determined constant that weighs the relative importance of the two objectives.

With the above proposed criterion ω, both exhaustive search and stepwise selection algorithms can be implemented. For a dataset with a large number of SNPs, a stepwise algorithm will be more computationally efficient, although both types of searching schemes are implemented in our tagSNPfinder software package. In the following, we discuss a forward selection algorithm. The algorithm will stop when either HD(S) ≥ δ₁ or ER(S) ≥ δ₂. We recommend setting δ₁ ≥ 0.9 to capture most (a large proportion) of haplotype diversity. Determining a suitable threshold δ₂ is less straightforward, as it should depend on the amount of LD in the full set of SNPs. From our experience, a stopping rule based on HD only seems to performed well, therefore, for any weighting scheme λ < 1, we recommend setting δ₂ = 1. In the special case in which only ER is used for SNP selection (i.e., λ = 1), we suggest setting δ₂ to be in the range of 0.5 – 0.7 to have an adequate number of SNPs selected. One can further restrict the maximum number of SNPs, N, to be selected, if desired, perhaps due to budgetary consideration. This option was utilized in one of our comparative studies to be described below.

Forward Selection Algorithm FSA(λ)

1. Set predetermined constants δ₁, δ₂, and λ (and the maximum number of tagging SNPs, N, if so desired).

2. Choose the first SNP X_j that maximizes HD(X_j). Then set t = 1 and S^t = {X_j}.

3. Let j = argmax_k{ω({S^t, X_k};, λ), X_k ∈ X–_S^t}, where X–_S^t contains the remaining SNPs not in the selected set S^t already. Set S* = {S^t, X_j}. If HD(S*) ≥ δ₁, or ER(S*) ≥ δ₂ (or t + 1 = N if N is specified), then the algorithm is terminated and S* is the selected set of tagging SNPs. Otherwise, increase t by 1 and set S^t = S*, then go back to step 3.

Clearly the selection algorithm described above is in a forward fashion. Backward selection and stepwise selection algorithms have also been similarly devised. The backward selection algorithm eliminates SNPs one by one, while a stepwise algorithm selects SNPs in a back and forth fashion in which only one SNP is removed or added sequentially. The program implementing all these algorithms can be downloaded freely from our website.

Results

In this section, we first examined the performance of our LD measure, ER, on two sets of data. We compared the results with those obtained using the ε measure of Nothnagel et al. (2002), and a modified measure of ε that will reach the upper limit of one under complete LD. These results were also compared to those given by the classical LD measure r² for the special cases with two loci, demonstrating the similarity between ER and r² empirically. Then we evaluated the proposed SNP selection algorithm and conpared it with four other methods in the literature using two real datasets with 20- and 50-SNPs, respectively. Further comparative studies were performed on simulated data based on various coalescent models.

Comparisons of multilocus LD measures

Our first dataset depicts 10 loci in complete linkage disequilibrium among them, with the frequencies of haplotypes 1111111111 and 2222222222 set to be 0.9 and 0.1, respectively. For this full set of data with 10 loci, ER gave a value of 1.0, correctly reflecting the nature of complete LD. However, ε yielded a LD measure of 0.9, a value hard to be interpret. More serious problems were seen when one further evaluated ε with various window sizes. With a window of size 2 (i.e., considering every two consecutive loci), ε gave a value of merely 0.5. Since 0.5 is much smaller than 0.9, it might lead to the interpretation that the degree of LD for the two-locus case is less than that for the 10-locus situation, when in fact both cases contain loci in complete LD. ER, on the other hand, still yielded a value of 1.0 to signify complete LD of the two loci involved. Note that the pairwise measure r² also led to a value of 1.0. Both ER and ε were also calculated for window sizes of 3–5, and their results, together with those from sizes 2 and 10, are given in table 1. As can be seen from the table, ER always produced a value of 1.0 regardless of the number of loci. However, the value of ε was dependent on the number of loci considered, even when there was complete LD in each case. Since ε gives smaller value for fewer number of loci, small haplotype blocks may be missed when the measure is used for block identification. A modified measure, defined as ${\epsilon }^{\prime }=\frac{n}{n-1}\epsilon$, where n is the number of loci considered, can easily overcome this problem, as it now gives a value of 1.0 regardless of the window size (Table 1).

Table 1.

Outcomes from four LD measures with various number of loci (window sizes). Note that for r², only pairwise LD value is available.

No. Loci	ER	ε	ε′	r2
2	1.0	0.50	1.0	1.0
3	1.0	0.67	1.0	-
4	1.0	0.75	1.0	-
5	1.0	0.80	1.0	-
10	1.0	0.90	1.0	-

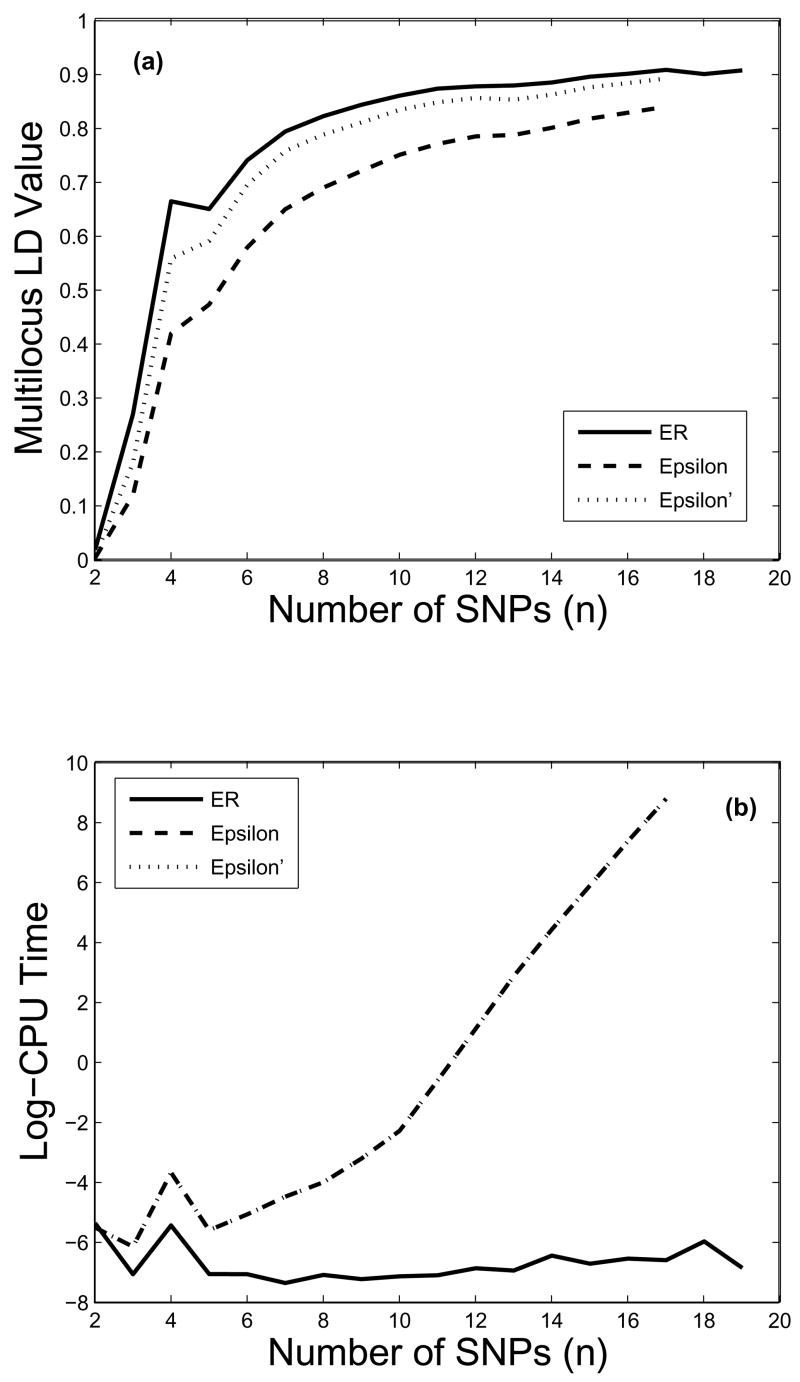
Our second dataset, consisting of 19 SNPs in the gene CYP19, is from Table 3 in Stram et al. (2003), which was used there for a different purpose. There were a total of 12 observed haplotypes, with five having frequencies above 5% (.36, .32, .12, .10, .05), while the remaining seven haplotypes all having frequencies at or less than one percent. We used ER, ε and ε′ to examine multilocus patters of the data. Specifically, we calculated LD for the first n loci, n = 2, middot; middot; middot;, 19, if a measure can be computed. In figure 1(a), each multilocus LD value is plotted above the number of loci over which the LD is computed, whereas the log-CPU time is plotted in figure 1(b) in the same fashion. All computations were carried out on a Pentium 4, 3.2Ghz computer with 1GB of memory, running on Red Hat Enterprise Linux 4. Several features of these two plots are apparent yet noteworthy. First, ε is consistently below ER due to its sub-measure nature, whereas ε′, the modified measure, is much closer to ER. Second, the computational time needed for ER is rather constant regardless of the number of loci (for the entire range from 2–19 loci) being evaluated, while that for both ε and ε′ grows exponentially (i.e., log-CPU time is linear, at least for large number of loci). This difference is dramatic, but not surprising: the number of haplotypes needed to be considered in computing ER is at most 12 (the number of observed haplotypes in the data), regardless of the number of loci, n, whereas that involved in the calculation of ε (or ε′) is 2ⁿ. Due to the computational intensity, Nothnagel et al.’s software package in fact limits the number of loci to be nine. With our own Matlab version, we could manage up to 17, which took more than 2 hours to compute, whereas ER required only 0.001 second for the same number of loci. We estimated the computational time for ε to be around 18 hours with an additional locus, and days for two more loci, due to the nature of exponential growth, and thus they were not attempted. This computational intensity limits the usefulness of ε (or ε′) for evaluating LD in large haplotype blocks.

Figure 1.

Comparison of multilocus LD measures for the first n SNPs, n = 2, ···, 19: (a) LD values, and (b) Logarithm of CPU times in seconds. Note that for ε and ε′, due to the computational intensity, the LD values and CPU times were evaluated only to up 17 loci.

Selection of tagging SNPs

20-SNP dataset

We first considered a 20-SNP dataset downloaded from www-rcf.usc.edu/~stram. This dataset contains the derived haplotypes and the associated frequencies based on the first 20 loci of the 51-SNP genotype data posted at http://www-gene.cimr.cam.ac.uk/clayton. There are a total of 31 haplotypes, with five having frequencies above 5% (0.31, 0.24, 0.09, 0.07, and 0.06). We analyzed this dataset using our forward selection algorithm with several values of the weight parameter: λ ∈ {0, 0.3, 0.5, 0.8, 1}. For each λ < 1, FSA(λ) was stopped when either threshole δ₁ = 0.9 or δ₂ = 1 was exceeded. This effectively inactivated the role of ER in the number of SNPs selected, as discussed in the Methods section. On the other hand, for λ = 1, since the set of SNPs selected was dependent on ER only, we required δ₂ = 0.6 to have an adequate number of SNPs selected, as HD would not play a role in this case.

For comparison purpose, we also analyzed the same data using four other existing methods in the literature. They are: the coefficient of determination measure, $R_h^2$, of Stram et al. (2003); the H-clust method of Rinaldo et al. (2005), and the proportion of diversity explained (PDE; P_i) and the Haplotype $r^2(\text{RSQ};r_{[\mathit{hap}]}^2)$ measures given in Table 1 of Weale et al. (2003). The programs used for these four measures were all downloaded, respectively, from each of the authors’ websites. To facilitate these comparisons, we limited the maximum number of tagging SNPs to be up to N = 10, as the programs downloaded (except H-clust) can handle only a small number due to the all-possible-subset implementations of their algorithms. More specifically, for each of the algorithm considered in the comparison, we selected N sets of tag SNPs, each of size N, for N from 1 to 10. To compare the performances of the tag SNP sets of the same size selected from the different algorithms, we evaluated them using both the PDE and the RSQ criteria, which represent the general broad categories of diversity and association, respectively, as discussed in Weale (2003).

Table 2 shows the results with FSA(λ), λ ∈ {0, 0.3, 0.5, 0.8, 1} For each value of the weight parameter, λ, we report the SNP selected at each iteration and the corresponding HD (for λ < 1) or ER (for λ = 1) value for the set of tag SNPs selected thus far. Also shown in the table are the RSQ and PDE values of the selected subsets after each iteration. For the case with λ= 0.5, which gives equal weights to the two optimization objectives, the stopping rule HD(S) ≥ 0.9 was achieved at iteration 10. The results show that the selected subset gives satisfactory performance evaluated under the RSQ and the PDE criteria, as both have reached a high threshold value of 0.95. The results for the other λ (< 1) values are very similar. For each of these cases, the stopping rule was reached after 10 iterations, and the RSQ and PDE values of the selected subsets all reached the high threshold value of 0.95. In fact, although the orders in which the SNPs were selected were all different among the settings, the final sets of selected tag SNPs for the various λ values were all the same. The reason for different SNP selection orders with different λ values is due to the different emphasis on the relative importance of the two objectives, but it is heartening to see that the different weights all led to the same final selected set. For the setting with λ = 1, 10 iterations were also needed before the stopping rule ER(S) ≥ 0.6 was reached. However, the selected set included a SNP that was not in the common set of SNPs selected with the other λ values, and the corresponding RSQ and PDE values were slightly lower than the rest.

Table 2.

Outputs of FSA(λ) with various weight parameter values^a for the 20-SNP dataset.

	FSA(0)				FSA(.3)				FSA(.5)
Iter	SNP	HD	RSQ	PDE	SNP	HD	RSQ	PDE	SNP	HD	RSQ	PDE
1	11	.304	.021	.498	11	.304	.021	.498	11	.304	.021	.498
2	1	.480	.112	.583	16	.469	.089	.581	17	.403	.029	.553
3	13	.581	.117	.723	13	.570	.089	.674	7	.469	.112	.583
4	17	.663	.123	.805	17	.657	.157	.854	13	.570	.290	.714
5	16	.737	.181	.896	7	.706	.642	.939	16	.706	.642	.939
6	18	.794	.452	.948	20	.769	.773	.967	20	.769	.773	.967
7	5	.828	.452	.948	1	.822	.773	.978	18	.796	.867	.967
8	20	.857	.452	.948	18	.849	.931	.980	1	.849	.931	.980
9	7	.884	.947	.981	5	.884	.947	.981	5	.884	.947	.981
10	19	.909	.959	.987	19	.909	.959	.987	19	.909	.959	.987
	FSA(.8)				FSA(1.0)
Iter	SNP	HD	RSQ	PDE	SNP	HD	RSQ	PDE
1	11	.304	.021	.498	11	.013	.021	.498
2	7	.372	.046	.540	7	.072	.046	.540
3	17	.469	.112	.583	17	.092	.112	.583
4	3	.570	.290	.714	13	.155	.290	.714
5	16	.706	.642	.939	16	.223	.642	.939
6	18	.748	.754	.947	18	.334	.754	.947
7	20	.796	.867	.967	20	.425	.867	.967
8	1	.849	.931	.980	1	.520	.931	.980
9	5	.884	.947	.981	14	.595	.931	.980
10	19	.909	.959	.987	5	.648	.947	.981

^aFor λ < 1, the stopping rule was only based on the HD values.

For λ = 1, on the other hand, only the ER criterion was used, and thus no HD values were available.

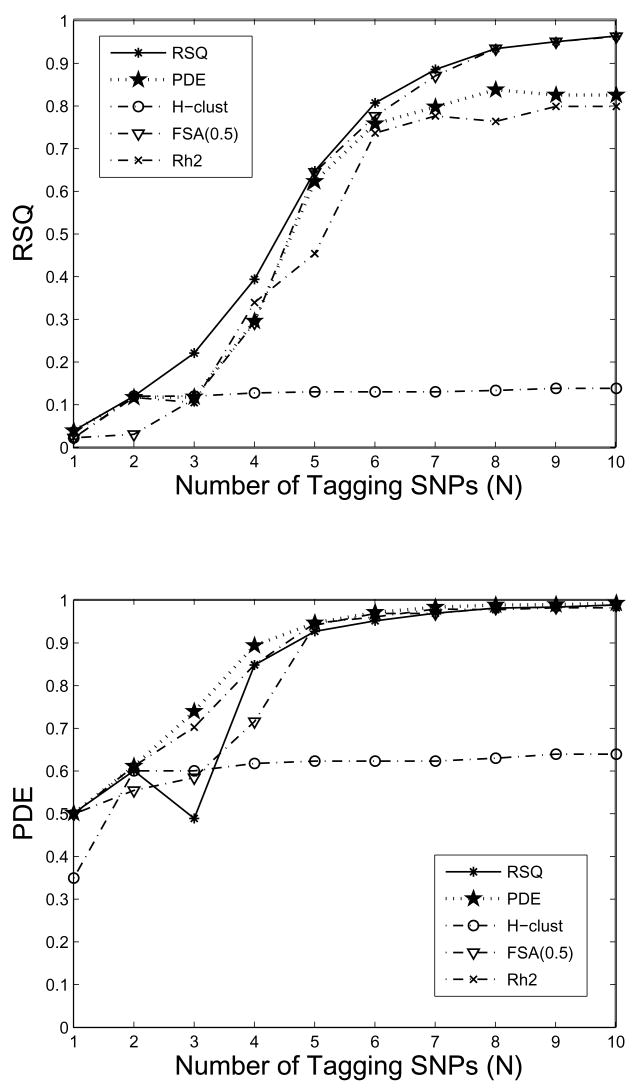
Figure 2(a) plots the RSQ values for the subsets selected based on RSQ, PDE, FSA(0.5), H-clust, and $R_h^2$, for each N from 1 to 10. Note that the RSQ values for the subsets selected under RSQ constitute the gold standard (upper limits). As can be seen from the figure, the RSQ value (0.959) for the 10 SNPs selected under FSA(0.5) matches up almost exactly with that (0.960) from RSQ, the gold standard. In fact, nine of the 10 selected SNPs from the two FSA algorithms are in common with those selected under RSQ. For smaller subset sizes (before our selection criteria were reached), there are greater discrepancies, but our selected subsets with at least five SNPs still almost achieve the optimal values. On the other hand, the RSQ value for the 10 SNPs selected under PDE is considerably lower than the gold standard, explaining only about 80% of the variability. For the 10 SNPs selected under $R_h^2$, the corresponding RSQ value is yet lower than that achieved by PDE. We are surprised by the performance of H-clust evaluated with the RSQ criterion, which might be explained by the amount of missing genotype data present in the dataset. Figure 2(b) shows the results when PDE is treated as the gold standard. Our results show that all algorithms (except H-clust) performed well (all close to the optimum) for subsets containing at least five SNPs. There are much improvements for the H-clust tag SNP sets evaluated under PDE than under RSQ, but their PDE values are still much lower than the rest, which is again hypothesized to be (at least partially) due to the missing genotypes.

Figure 2.

Evaluations of tagging SNP sets of size N, N = 1, ···, 10, selected from the 20-SNP dataset with FSA(0.5), H-clust, $R_h^2$, RSQ, and PDE; (a): evaluated under the RSQ criterion; (b): evaluated under the PDE criterion.

51-SNP dataset

We have also analyzed the full data with 51 SNPs using FSA(λ) for the same set of λ values considered for the 20-SNP dataset. The results (not shown, but are available as Supplementary Information) support our finding from the smaller dataset that the selected tag SNP sets for all λ values in the mid-range perform satisfactorily with both the PDE and the RSQ criteria. Furthermore, there is a large degree of consistencies across the SNP sets selected, with most of the SNPs being common across the sets.

Six simulated datasets

Six datasets, downloaded from http://www.biostat.umn.edu/~nali/software/data/hotspot60.tar.bz2, were used to further evaluate the performance of our SNP selection method under various models and to compare with other methods. Specifically, each of the six datasets represents a different coalescent model, with the incorporation of a single recombination hotspot. More detailed descriptions of the models can be found in Hudson (2002) and Li and Stephens (2003), and in the footnote of table 3 in the current paper. For each dataset, there are 60 haplotypes, arising from approximately 50 SNPs, with the exact number given in table 3 (column #SNP). Note that these SNPs are not necessarily within a single haplotype block. Both FSA(0.5) and H-clust were applied to each of the six datasets to select tag SNPs. We first selected tag SNPs using H-clust by setting the threshold to correspond to the pairwise r² value of 0.95 (Rinaldo et al. 2005). Based on the number of SNPs in the above selected set, we then used FSA(0.5) to select its SNP set of the same size. Since there were no missing genotypes in these simulated data, we were also interested in exploring our hypothesis that the performance of H-clust in the 20-SNP real dataset was affected by the missing genotypes. We note that the other three algorithms used for analyzing the 20-SNP data, RSQ, PDE, and $R_h^2$, could not be used for comparisons here as the numbers of SNPs in the datasets were too large to be amenable with the programs downloaded from the authors’ websites.

Table 3.

Comparisons between FSA and H-clust for their performances on six simulated datasets based on various coalescent models^a.

			RSQ		PDE
Model	#SNP	N	FSA(0.5)	H-clust	FSA(0.5)	H-clust
Standard	45	11	0.976	0.944	0.949	0.864
Common(f > 0.1)	34	11	1.000	1.000	1.000	1.000
Island(mixed)	49	12	0.986	0.960	0.983	0.898
Island(single)	53	11	0.992	0.982	0.989	0.932
Expansion(t=500)	59	11	0.804	0.439	0.881	0.475
Expansion(t=5000)	51	11	0.876	0.924	0.915	0.898

^aThe six coalescent models under which the datasets were simulated are as follows.

Standard: constant-size random mating population; Common: same random mating model as the previous one, but only retaining SNPs having minor allele frequency f > 0.1; Island(mixed): two-island model with migration rate of 1.0 per generation (an equal number of haplotypes was sampled from each island); Island(single): same island model as the previous one but with all samples coming from the same island; Expansion(t=500): exponentially expanding population with fast expansion starting 500 generations ago; Expansion(t=5000): exponentially expanding population with slow expansion starting 5000 generations ago.

The selected SNP sets of the two algorithms evaluated under the RSQ and the PDE criteria, for each of the six datasets, are given in table 3. The numbers of tag SNPs selected were all 11 or 12 (column N), with both FSA(0.5) and H-clust performed similarly for five of the datasets, although FSA(0.5) achieved higher values of the criteria in most cases. However, in the dataset “Expansion(t=500)”, compared to H-clust, FSA(0.5) captured almost twice as much as the variability, evaluated under both of the criteria. In summary, FSA(0.5) performed reasonably well for the datasets simulated from various coalescent models. In the only case in which both the RSQ and the PDE criteria were below 90%, it actually outperformed H-clust the most. Overall, the results seem to be consistent with our hypothesized effect of missing data on H-clust, as it performed quite well for five out of the six datasets without missing genotypes. It would be of interest in a future study to investigate the underlying causes for the diminishing performance of the algorithms (especially the H-clust algorithm) on the dataset simulated under the “Expansion(t=500)” model.

Discussion

In this paper, information theory is employed to study linkage disequilibrium and to select tagging SNPs in haplotype blocks. Specifically, we propose a multilocus LD measure based on relative entropy, which is a quantity between 0 and 1, with 0 corresponding to linkage equilibrium while 1 signaling complete linkage disequilibrium. Furthermore, a larger value of the measure indicates greater distance between the true (observed) haplotype distribution and the expected haplotype distribution under linkage equilibrium, signifying greater degree of linkage disequilibrium.

We compared and contrasted the properties and performances of our proposed measure ER with those from two other LD measures, ε and r², and a modified measure of ε, ε′. We showed, both analytically and empirically, that in the special case with two loci, ER matches up well with r². The multilocus LD measure ε, on the other hand, is demonstrated clearly to be lacking some of the desirable properties. The measure being dependent on the number of loci considered rather than just on the degree of LD among the loci is a major defect. However, as we have also shown, a slight modification of ε can lead to a measure that effectively eliminates these problems.

The improved properties of ε′ notwithstanding, ER is computationally more efficient than ε or ε′. By expressing the relative entropy as shown in equation (1), which makes use of the convention that 0 log 0 = 0 (see Appendix A), the formula can deal with as many loci as needed. This is because, in practice, the number of observed haplotypes (especially if the loci are within a haplotype block) is much smaller than the number of all possible haplotypes 2ⁿ. On the other hand, both ε and ε′ consider all 2ⁿ haplotypes, severely limiting their computational feasibility.

Note that since our “true” and “expected” haplotype distributions are estimated from the observed data, our LD measure is thus only an estimate, whose accuracy is dependent on the amount of data available. It should also be noted that haplotypes are usually not observable in most studies; they (and their frequencies) are in fact estimated from genotype data. Hence, another level of uncertainly is added. It would be important to investigate the statistical properties of the estimate from the observed data, although this is not within the scope of the current paper.

As a second major focus, we also propose an information-based measure for selecting tag SNPs. Combining two broad criteria discussed in the literature for SNP selection, namely, haplotype diversity and association, we seek to devise a unified approach that takes both criteria into account. This offers a greater degree of flexibility, as this approach presents a class of optimization criteria, including the haplotype diversity and association criteria as two special cases. More importantly, it is hoped that more information is being utilized by combining both objectives. Knowledge of a scientific investigator can be incorporated through the specification of the weighting parameter. The threshold values for terminating the selection process can also be set by the investigator to reflect the degree of tolerance for the amount of information loss. In particular, one may set δ₂ = 1 if there is a great deal of uncertainly about a suitable level of LD before termination, as we have done for all the analyses performed in the current paper with λ < 1. This amounts to relying completely on the more easily managed index of haplotype diversity for terminating the selection process, although note that LD still plays an important role in which SNPs are being selected unless the weighting parameter λ is set to be 0.

Our limited experiments with the forward selection algorithm for various weights indicate that taking both haplotype diversity and linkage disequilibrium into account seems to yield more satisfactory results than observing either one alone. By satisfactory results, we mean the final selected tagging SNPs attaining near optimal values under two different evaluation criteria in the literature. Since a consensus on what should be the best criterion for evaluating a set of SNPs selected is lacking, our algorithm's ability to compromise between two different objectives, yet still achieving near optimal results in either one, seems to be quite a desirable one. This is a strength unmatched by some other selection methods, as we note that the tagging SNPs selected under the proportion of diversity explained criterion is far from reaching the optimal value set by the haplotype R-square criterion. Furthermore, despite different selection orders of SNPs with different weights, the final tagging sets show a large degree of consistencies as long as the parameters are in the mid range. Not only that the sizes of the sets are similar, but most of the SNPs selected are also common across the sets. Based on these results, we would recommend against setting λ = 0 or λ = 1 (i.e., based solely on the haplotype diversity or the association criteria), or a value close to one of the two extremes.

Extensive evaluations of the proposed SNP selection method and comparisons with four other methods in the literature seem to demonstrate the value of our algorithm, as it outperformed the others in most cases. However, we note that the comparison with H-clust in the 20-SNP dataset might not be completely fair, as H-clust is based on SNP genotypes, some of which were missing in the data. Furthermore, as with other heuristic methods, such as those based on principal component analysis (Meng et al. 2003; Horn and Camp 2004; Lin and Altman 2004), H-clust was not designed to optimize either of the two broad categories of criteria, and thus the performances of the selected SNP sets are harder to evaluate under our framework.

In addition to the flexibility and the potential efficiency that our proposed selection method may offer, another major advantage of the proposed approach is its computational feasibility. The stepwise fashion of the proposed algorithms can handle a much larger number of loci (such as our 51-SNP dataset or the six simulated datasets) than any all-possible-subset algorithm, the type of approach adopted by most of the current tag SNP selection methods. Although we note that this is not an inherent problem, as most other tagging SNP selection algorithms can easily be implemented in a stepwise fashion. As mentioned before, in addition to the forward selection algorithm, backward selection as well as forward and backward stepwise algorithms have also been implemented in our software. Although satisfactory results for all datasets explored were achieved using the forward selection algorithm, it is possible that a backward or a stepwise selection one may yield better results with other data. Regardless of which of the four types of algorithms are used, their greedy nature may lead to suboptimal selected sets, although optimum/near optimum subsets have been selected in the cases that we have investigated. Thus, we have also implemented the all-possible-subset selection option in our software, which may be used when the number of SNPs in the full set is small, say less than 25.

Electronic-Database Information

The URL for the software package tagSNPfinder and supplementary information is: http://www.stat.ohio-state.edu/~statgen/PAPERS/tagSNPfinder.html

Appendix A: Proof of inequality (2)

Note that the definition of relative entropy in (1) is equivalent to

$$\sum _{x_1}\cdots \sum _{x_n}p(x_1,\cdots ,x_n){log}_2\frac{p(x_1,\cdots ,x_n)}{{\prod }_{j=1}^n{p}_j(x_j)},$$ (A1)

where x_j denotes the allele of the jth SNP. This expression is simplified to the definition in (1) by noting the convention that 0 log₂ 0 = 0. This simplification leads to computational efficiency, as most of the 2ⁿ terms under the summations are zero and thus do not need to be considered in the computation. However, the definition in (A1) lends itself easily to proving the following two facts:

$$\begin{array}{l}E({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_n)=\sum _{j=1}^{n}H({\mathbf{X}}_j)-H({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_n),\\ H({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_n)\ge H({\mathbf{X}}_j)\text{for}\text{any}j,1\le j\le n,\end{array}$$

where H(X₁, ···, X_n) is the joint entropy of the n SNP variables under the haplotype distribution p. From these facts, it is then easily seen that

$$E({\mathbf{X}}_1,\cdots ,{\mathbf{X}}_n)\le \sum _{j=1}^{n}H({\mathbf{X}}_j)-\underset{j}{max}H({\mathbf{X}}_j).$$

Appendix B: Proof of properties of equation (3)

1. From the properties of K–L distance and the definition of ER, it is obvious that 0 ≤ ER ≤ 1. The lower bound 0 is obtained when $p(x_1,\cdots ,x_n)={\prod }_{j=1}^n{p}_j(x_j)$, which is the necessary and sufficient condition for LE. On the other hand, under complete LD, there are only two haplotypes with nonzero probabilities, and they are the same as the allele frequency at each locus. Thus, H(X₁, ···, X_n) = H(X_j), 1 ≤ j ≤ n, and consequently, H(X₁, ···, X_n) =max_j H(X_j).

2. For two loci X_j and X_k, E(X_j, X_k) = H(X_j)+ H(X_k) − H(X_j, X_k), which is usually referred to as mutual information, I(X_j; X_k), between the two variables. This relationship (among individual entropies, joint entropy, and mutual information) is illustrated in figure 1. Let us denote by j and k the alleles of the two loci, both of which take values in {1, 2}. Furthermore, let p_jk, p_j. and p._k denote respectively the probability of haplotype jk, alleles j and k, j, k =1, 2. Then

$$E({\mathbf{X}}_j,{\mathbf{X}}_k)=\sum _{j,k=1}^2{p}_{jk}{log}_2\frac{p_{jk}}{p_{j.}{p}_{.k}}.$$

Let D_jk = p_jk − p_j.p._k, j, k = 1, 2. Applying Taylor series expansion, we have

$$\begin{array}{l}E=\sum _{j,k=1}^2(p_{j.}{p}_{.k}+D_{jk}){log}_2\left(1+\frac{D_{jk}}{p_{j.}{p}_{.k}}\right)\\ =\frac{1}{ln2}\sum _{j,k=1}^2(p_{j.}{p}_{.k}+D_{jk})\left(\frac{D_{jk}}{p_{j.}{p}_{.k}}-\frac{1}{2}{\left(\frac{D_{jk}}{p_{j.}{p}_{.k}}\right)}^2+\sum _{s=3}^{\infty }\frac{{(-1)}^{s+1}}{s!}{\left(\frac{D_{jk}}{p_{j.}{p}_{.k}}\right)}^s\right)\\ =\frac{1}{2ln2}{r}^2+\sum _{j=1}^2\sum _{k=1}^2\sum _{s=2}^{\infty }{C}_s{\left(\frac{D_{jk}}{p_{j.}{p}_{.k}}\right)}^s{D}_{jk}\end{array}$$

where the coefficients are

$$C_2=-\frac{1}{3ln2},\text{and}{C}_s={(-1)}^{s+1}\frac{s}{(s+1)!ln2},s\ge 3.$$

When |D_jk/p_j.p._k| ≤ 1 for all j, k = 1, 2, the second term of the above formula (triple sums) is much smaller compared to the first term, and thus $E\approx \frac{1}{2ln2}{r}^2$. This condition is met when there is evidence of LD with the haplotype composed of the two minor alleles being absent. Since both ER and r² are 1 under complete LD, we have

$$1=\frac{E}{E_{max}}\approx \frac{r^2}{(2ln2)(E_{max})}=\frac{1}{(2ln2)(E_{max})},$$

thus E_max ≈ 1/2 ln 2. Consequently, ER ≈ r² under the conditions discussed above. Note that this is a sufficient condition, although it may not be necessary for the two measures to yield similar values.