Predicting Random Effects with an Expanded Finite Population Mixed Model

Abstract

Prediction of random effects is an important problem with expanding applications. In the simplest context, the problem corresponds to prediction of the latent value (the mean) of a realized cluster selected via two-stage sampling. Recently, Stanek and Singer (JASA, 2004) developed best linear unbiased predictors (BLUP) under a finite population mixed model that outperform BLUPs from mixed models and superpopulation models. Their setup, however, does not allow for unequally sized clusters. To overcome this drawback, we consider an expanded finite population mixed model based on a larger set of random variables that span a higher dimensional space than those typically applied to such problems. We show that BLUPs for linear combinations of the realized cluster means derived under such a model have considerably smaller mean squared error (MSE) than those obtained from mixed models, superpopulation models, and finite population mixed models. We motivate our general approach by an example developed for two-stage cluster sampling and show that it faithfully captures the stochastic aspects of sampling in the problem. We also consider simulation studies to illustrate the increased accuracy of the BLUP obtained under the expanded finite population mixed model.

1. INTRODUCTION

Optimal estimation of average costs for hospitals that typically vary in size is an important practical problem because of the impact in health care economics, and patient choice of hospital care (see http://www.healthgrades.com, for example). In many cases, this is based on information obtained from patients (units) in hospitals (clusters) realized under a two-stage sampling scheme.

The best linear unbiased predictor (BLUP) developed under a mixed model is often offered as a solution to this problem (Searle et al. 1992). Although the mixed model accounts for unequal numbers of units in sample clusters, it does not use often available information about their sizes. The superpopulation model of Scott and Smith (1969) is an alternative that incorporates this information. Both models can be plausibly used to represent the problem of interest, but neither is formally linked to the finite population from which the two-stage sample is drawn as is the finite population mixed model recently proposed by Stanek and Singer (2004)¹ for situations where clusters are of equal size. Under this model, predictors have smaller mean squared error (MSE) than the competitors, even when the variance components are replaced by estimates as indicated in San Martino, Singer and Stanek (2007). We extend the approach Stanek and Singer (2004) by developing predictors under a new expanded finite population mixed model that outperforms the competitors both in equal and unequal size two-stage cluster sampling problems.

Suppose our interest is in the average cost of appendectomies (the latent value) for each of three hospitals in the past year (Table 1), and that such costs are known (without error) for some patients in two of the hospitals. When the data are obtained from a stratified simple random sample of appendectomy patients, with hospitals as strata, the best linear unbiased estimate is the average cost for the available patients in each hospital (i.e., $2000 for Central, and $1800 for Mercy).

Table 1.

Population of hospital’s appendectomy patients in the past year and observed data

Hospital (s)	Ms	Mean	Variance	Patient* (t)
s=1 (County)	2	μ1	${\sigma }_1^2$	y11	y12
s=2 (Central)	4	μ2	${\sigma }_2^2$	y21	y22	y23	y24
				$2100 (Jane Blake)		$1400 (Sam Evans)	$2500 (Hong Yao)
s=3 (Mercy)	2	μ3	${\sigma }_3^2$	y31	y32	y33
				$1700 (Mary Slokum)	$1900 (Juan Marcus)

^*Names are fictitious

Now assume that a simple random sample of appendectomy patients is selected from each of a simple random sample of hospitals (Table 2) according to a two-stage sampling scheme. We refer to a sample hospital as a primary sampling unit (PSU) to distinguish it from a specific hospital, and to a sample patient as a secondary sampling unit (SSU) to distinguish it from a specific patient. Under the usual mixed model, the sample appendectomy cost for SSU j in PSU i is

$$Y_{ij}=\mu +B_i+E_{ij}$$ (1)

where μ is the overall mean, B_i is the random effect for PSU i, and E_ij is a random variable corresponding to the deviation of the response of SSU j from the latent value of PSU i, namely T_i = μ + B_i The random variables B_i and E_ij are usually considered independent with null expected values, and variances given by σ² and ${\sigma }_i^2,$ respectively. Model (1) is an example of the general linear mixed model

$$\mathbf{Y}=\mathbf{X}\mathbf{\alpha }+\mathbf{Z}\mathbf{B}+\mathbf{E}$$ (2)

where, for the sample in Table 2, $\mathbf{X}={\mathbf{1}}_r,\mathbf{Z}=\underset{i=\mathbf{1}}{\overset{n}{\oplus }}{\mathbf{1}}_{m_i},\mathbf{\alpha }=\mu ,$ and B = (B₁,…,B_n)′ with $\mathbf{\Gamma }={\sigma }^2{\mathbf{I}}_n,\mathbf{\sum }=\underset{i=1}{\overset{n}{\oplus }}{\sigma }_i^2{\mathbf{I}}_{m_i},$ and var (Y) = Ω = ZΓZ′ + ∑ with 1_a denoting an a×1 vector with all elements equal to one, I_a representing an a×a identity matrix, and $\underset{i=1}{\overset{n}{\oplus }}{\mathbf{A}}_i$ indicating a block diagonal matrix with blocks given by A_i (Graybill 1983). This model has a long history (see for example Harville 1978, Laird and Ware 1982) and is the main topic in several recent texts such as Brown and Prescott (1999), Verbeke and Molenberghs (2000), McCulloch and Searle (2001), Byrk and Raudenbush (2002), Diggle et al (2002), Singer and Willett (2003), Demidenko (2004), Littell et al (2006), and Jiang (2007). Under (1), the BLUP of the latent value for PSU i is

$${\widehat{P}}_i=\widehat{\mu }+k_i\left({\overline{Y}}_i-\widehat{\mu }\right)$$ (3)

where $\widehat{\mu }={\displaystyle \sum _{i=1}^n\left(w_i/{\displaystyle \sum _{i=1}^n{w}_i}\right){\overline{Y}}_i}$ is a weighted sample mean with $w_i=1/\left({\sigma }^2+{\sigma }_i^2/m_i\right),{\overline{Y}}_i=\frac{1}{m_i}{\displaystyle \sum _{j=1}^{m_i}{Y}_{ij},\text{and}}{k}_i=\frac{{\sigma }^2}{{\sigma }^2+{\sigma }_i^2/m_i}$ (Goldberger 1962; Henderson 1984, McLean, Sanders and Stroup 1991; Robinson 1991). The predictor ${\widehat{P}}_i$ is a linear function of Y (i.e., ${\widehat{P}}_i=\mathbf{L}\prime \mathbf{Y}$), is unbiased (i.e. $E\left({\widehat{P}}_i-T_i\right)=0$), and has minimum MSE. Using the realized random variables represented in Table 1, and assuming that σ = 100, σ₁ = 300 and σ₂ = 50 it follows that μ̂ = $1844, k₁ = 0.25, k₂ = 0.89, and the predictor of the latent value for the realized hospital corresponding to i = 1 (i.e., Central) is ${\widehat{P}}_1=\$1883,$ while the predictor of the latent value for i = 2 (i.e., Mercy) is ${\widehat{P}}_2=\$1805.$

Table 2.

Notation for common mixed model (sample) and superpopulation model (sample and remainder)

	Sample Hospital PSU (i)	Sample Size mi	Latent Value μ + Bi	Sample Patient SSU (j)
				j=1	j=2	j=3	j=4
	i=1	3	μ + B1	Y11	Y12	Y13
	i=2=n	2	μ + B2	Y21	Y22
	i=1 (Central)						Y14
	i=2 (Mercy)					Y23
	i=3=N (County)			Y31	Y32

The estimate of a realized hospital’s latent value derived from the stratified model or the corresponding predictor obtained from the mixed model do not use additional information, such as the number of hospitals in the population, or the number of appendectomy patients in each hospital, even though such additional information may be available (as illustrated in the remainder in Table 2). The combined sample and remainder represents a superpopulation that is constructed by first (conceptually) selecting a finite population (presumably from some larger population in time or space), and then selecting a two-stage sample from it. Scott and Smith (1969) show that the latent value for a hospital in the superpopulation, $T_i={\displaystyle \sum _{j=1}^{M_i}{Y}_{ij}/M_i},$ is predicted by

$${\widehat{P}}_i=f_i{\overline{Y}}_i+(1-f_i)\left[\widehat{\mu }+k_i\left({\overline{Y}}_i-\widehat{\mu }\right)\right],$$ (4)

where f_i = m_i/M_i. Using the data in Table 1, the resulting predictor for i = 1 (i.e., Central) is ${\widehat{P}}_1=\$1971,$ and for i = 2 (i.e. Mercy) is ${\widehat{P}}_2=\$1802.$

The superpopulation model does not clearly separate the labeled clusters (as in Table 1) from random variables that represent a sample of clusters (i.e., note how Central Hospital is uniquely associated with i = 1 in Table 2). This separation is clear when the two-stage sampling process is represented with indicator random variables in the finite population mixed model developed by Stanek and Singer (2004). The resulting predictor (limited to equal size clusters and equal size cluster sample sizes) is

$${\widehat{P}}_i=f{\overline{Y}}_i+(1-f)\left[\overline{Y}+k\left({\overline{Y}}_i-\overline{Y}\right)\right]$$ (5)

where $\overline{Y}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\overline{Y}}_i},f=\frac{m}{M},k=\frac{{\sigma }^{*2}}{{\sigma }^{*2}+{\sigma }_e^2/m},{\sigma }^{*2}={\sigma }^2-\frac{{\sigma }_e^2}{M}\text{and}{\sigma }_e^2=\frac{1}{N}{\displaystyle \sum _{s=1}^N{\sigma }_s^2.}$ With equal size clusters, the predictor specified by (4) differs from (5) since variance components have different definitions. Theoretically, the expected MSE of (5) is less than the expected MSE for (4) or (3) as shown by Stanek and Singer (2004), while the empirical version of (5), formed by replacing variance components with their sample estimates, in general outperforms the empirical versions of the other predictors, as summarized by San Martino, Singer and Stanek (2007). However, (5) cannot be used for data like those in Table 1 and Table 2 since cluster and sample sizes differ.

When clusters are of equal size, the finite population mixed model can be used to represent the remaining random variables (as in Table 2) without the need to identify the realized clusters for sample PSUs. When clusters differ in size, we do not know how many SSUs remain since we do not know the size of the realized PSU. Other problems occur with the representation in Table 2, as for example, the impossibility that the PSU i = 1 be County Hospital (Table 2), even though the first stage sampling is assumed to be simple random sampling, or the apparent random nature of the second stage sample size, PSU size, and SSU variance due to the first stage sampling.

We extend the expanded model used by Stanek, Singer, and Lencina (2004) for simple random sampling to two-stage unbalanced sampling to overcome these problems. The expanded model simultaneously retains the cluster identity and the PSU position, and for each PSU, distinguishes the relevant contribution of both sampled SSUs, and non-sampled SSUs to a target random variable such as a PSU mean. For such purposes, we first define an expanded set of random variables, and subsequently show that a lower dimensional (collapsed) set can adequately represent the problem without loss of information. Following the steps in Stanek and Singer (2004), we specify the expanded finite population mixed model in Section 2, derive the corresponding BLUP along with its theoretical expected MSE in Section 3, and compare the proposed predictor to others via simulation studies in Section 4, and conclude with discussion in Section 5.

2. AN EXPANDED MIXED MODEL FOR A FINITE CLUSTERED POPULATION

Let a finite population be defined (as in Table 1) by a listing of units, labeled by t = 1,…, M_s, in each cluster, labeled by s = 1,…,N, where the non-stochastic potentially observable response for unit t in cluster s is given by y_st. The finite population mean and variance for cluster s are respectively defined as ${\mu }_s=\frac{1}{M_s}{\displaystyle \sum _{t=1}^{M_s}{y}_{st}}\text{and}\left(\frac{M_s-1}{M_s}\right){\sigma }_s^2=\frac{1}{M_s}{\displaystyle \sum _{t=1}^{M_s}{(y_{st}-{\mu }_s)}^2}.$ Similarly, the population mean, and between cluster variance are respectively defined as $\mu =\frac{1}{N}{\displaystyle \sum _{s=1}^N{\mu }_s}\text{and}\left(\frac{N-1}{N}\right){\sigma }^2=\frac{1}{N}{\displaystyle \sum _{s=1}^N{({\mu }_s-\mu )}^2}.$ We represent the potentially observable response for unit t in cluster s as y_st = μ + β_s + ε_st where β_s = (μ_s − μ) is the deviation of the mean for cluster s from the overall mean, and ε_st = (y_st − μ_s) is the deviation of the response for unit t (in cluster s) from the mean for cluster s. Letting $\mathbf{y}=\left({\mathbf{y}}_1^{\prime }{\mathbf{y}}_1^{\prime }\dots {\mathbf{y}}_N^{\prime }\right)$ where y_s = (y_s1 y_s2 … y_sMs)′, the reparameterized finite population can be summarized as

$$\mathbf{y}=\mathbf{X}\mu +\mathbf{Z}\mathbf{\beta }+\mathbf{\epsilon }$$ (6)

where $\mathbf{X}={\mathbf{1}}_{\mathbb{N}},\underset{\mathbb{N}\times N}{\mathbf{Z}}=\underset{s=1}{\overset{N}{\oplus }}{\mathbf{1}}_{M_s},\mathbb{N}={\displaystyle \sum _{s=1}^N{M}_s},\mathbf{\beta }=({\beta }_1{\beta }_2\mathrm{\dots }{\beta }_N)\prime ,$ and ε is defined similarly to y. None of the terms in (6) are random variables.

2.1. The Expanded Set of Random Variables

We define a vector of random variables to represent equally likely two-stage random permutations of the population (i.e., with probability $\frac{1}{N!{\displaystyle \prod _{s=1}^N{M}_s!}},$ as in Cochran 1977). Without loss of generality, we assume that the sample clusters are in the first n positions in a permutation of clusters and that the sample units in cluster s correspond to the units in the first m_s positions in a permutation of that cluster’s units. The ordering of the random variables is important, since any realization can be re-ordered to exactly match the finite population values.

We use indicator random variables to relate the response for unit t in cluster s, namely, y_st, to the response for SSU j in PSU i. To do so, we let $U_{jt}^{(s)}$ be an indicator random variable that takes on a value of one when SSU j in cluster s is unit t, and zero otherwise, so that the response for SSU j in cluster s may be expressed as ${\tilde{Y}}_{sj}={\displaystyle \sum _{t=1}^{M_s}{U}_{jt}^{(s)}{y}_{st}.}$ We include a fixed non-stochastic weight w_sj for SSU j in cluster s, and define the weighted response as ${\tilde{Y}}_{wsj}=w_{sj}{\tilde{Y}}_{sj}$ so that the sum, ${\displaystyle \sum _{j=1}^{M_s}{\tilde{Y}}_{wsj},}$ will correspond to a cluster total when w_sj = 1 for all j = 1,…,M_s, or to a cluster mean when $w_{sj}=\frac{1}{M_s}$ for all j = 1,…,M_s, for example. Letting ${\mathbf{U}}_j^{(s)}=\left(U_{j1}^{(s)}{U}_{j2}^{(s)}\mathrm{\dots }{U}_{j{M}_s}^{(s)}\right)\prime ,$ it follows that ${\tilde{Y}}_{wsj}=w_{sj}{\mathbf{y}}_s^{\prime }{\mathbf{U}}_j^{(s)}.$ The vector ${\tilde{\mathbf{Y}}}_{ws}=\left({\tilde{Y}}_{ws1}{\tilde{Y}}_{ws2}\mathrm{\dots }{\tilde{Y}}_{ws{M}_s}\right)\prime$ represents a permutation of weighted responses for the SSUs in cluster s.

We also let U_is be an indicator random variable that takes on a value of one when PSU i is cluster s, and a value of zero otherwise. If all clusters were equal in size, we could represent a permutation of SSUs for PSU i by ${\displaystyle \sum _{s=1}^N{U}_{is}{\tilde{\mathbf{Y}}}_{ws}}.$ When cluster sizes differ, this sum is not defined, since the dimensions of the vectors composing it cannot all be equal. We solve this problem by expanding the set of random variables associated to PSU i into the ℕ×1 vector ${\overleftrightarrow{\mathbf{Y}}}_{wi}=\left(\left(U_{is}{\tilde{\mathbf{Y}}}_{ws}\right)\right)=\left(U_{i1}{\tilde{\mathbf{Y}}}_{w1}^{\prime }{U}_{i2}{\tilde{\mathbf{Y}}}_{w2}^{\prime }\mathrm{\dots }{U}_{iN}{\tilde{\mathbf{Y}}}_{wN}^{\prime }\right)\prime$ so that a two-stage random permutation of the population is then represented by the Nℕ × 1 vector, ${\overleftrightarrow{\mathbf{Y}}}_w=\left(\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)\right)=\left({\overleftrightarrow{\mathbf{Y}}}_{w1}^{\prime }{\overleftrightarrow{\mathbf{Y}}}_{w2}^{\prime }\mathrm{\dots }{\overleftrightarrow{\mathbf{Y}}}_{wN}^{\prime }\right)\prime ,$ where the j^th element of ${\overleftrightarrow{\mathbf{Y}}}_w$ that corresponds to U_is is $U_{is}{\tilde{Y}}_{wsj}.$

2.2 The Expanded Finite Population Mixed Model

We construct a mixed model for the expanded response vector ${\overleftrightarrow{\mathbf{Y}}}_w$ next. Indexing expectation with respect to permutations of clusters with the subscript ξ₁ and expectation with respect to permutations of units in a cluster with the subscript ξ₂, and for PSU i, we let

$${\overleftrightarrow{\mathbf{Y}}}_{wi}=E_{{\xi }_1{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)+\left[E_{{\xi }_2|{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)-E_{{\xi }_1{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)\right]+{\overleftrightarrow{\mathbf{E}}}_{wi}$$

where $E_{{\xi }_1{\xi }_2}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)=\frac{1}{N}\left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s\right)\mathbf{\mu },E_{{\xi }_2|{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)=\left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s{\mu }_s\right){\mathbf{U}}_i,{\overleftrightarrow{\mathbf{E}}}_{wi}={\overleftrightarrow{\mathbf{Y}}}_{wi}-E_{{\xi }_1|{\xi }_2}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)$, ${\mathbf{w}}_s=\left(\left(w_{sj}\right)\right)=\left(w_{s1}{w}_{s2}\mathrm{\dots }{w}_{s{M}_s}\right)\prime ,\mathbf{\mu }=\left(\left({\mu }_s\right)\right)=\left({\mu }_1{\mu }_2\mathrm{\dots }{\mu }_N\right)\prime$, ${\mathbf{U}}_i=\left(\left(U_{is}\right)\right)=\left(U_{i1}{U}_{i2}\mathrm{\dots }{U}_{iN}\right)\prime \text{and}{\overleftrightarrow{\mathbf{E}}}_{wi}$ denotes the deviation of response from the expected response within a PSU. The fixed effects are given by μ, the vector of cluster means, while the random effects correspond to $E_{{\xi }_2|{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right)-E_{{\xi }_1{\xi }_1}\left({\overleftrightarrow{\mathbf{Y}}}_{wi}\right).$ In the finite population mixed model of Stanek and Singer (2004), the random effect for PSU i was defined as ${\displaystyle \sum _{s=1}^N{U}_{is}{\beta }_s}={\displaystyle \sum _{s=1}^N\left(U_{is}{\mu }_s-U_{is}{\displaystyle \sum _{s*=1}^N\frac{1}{N}{\mu }_{s*}}\right),}$ with the random variables U_is explicitly linking the clusters to PSU i. In the finite expanded mixed model, random effects are defined for SSU j in PSU i as $w_{sj}{\mu }_s\left(U_{is}-E_{{\xi }_1}\left(U_{is}\right)\right).$ For example, when $w_{sj}=\frac{1}{M_s}$ for all j = 1,…,M_s (corresponding to the PSU mean), it follows that ${\displaystyle \sum _{j=1}^{M_s}{w}_{sj}{\mu }_s}\left(U_{is}-E_{{\xi }_1}\left(U_{is}\right)\right)=U_{is}{\mu }_s-\frac{1}{N}{\mu }_s.$ For both models, the expected value of the random effects (with respect to ξ₁) is zero. We combine the fixed and random effects to define the expanded finite population mixed model as

$${\overleftrightarrow{\mathbf{Y}}}_w=\left[\frac{1}{N}{\mathbf{1}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s\right)\right]\mathbf{\mu }+\left[{\mathbf{I}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s{\mu }_s\right)\right]vec\left(\mathbf{U}-E_{{\xi }_1}\left(\mathbf{U}\right)\right)+{\overleftrightarrow{\mathbf{E}}}_w$$ (7)

where U = (U₁ U₂ … U_N). The covariance matrix of the random effects is

$${\text{var}}_{{\xi }_1{\xi }_2}\left(\left[{\mathbf{I}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s{\mu }_s\right)\right]vec\left(\mathbf{U}-E_{{\xi }_1}\left(\mathbf{U}\right)\right)\right)=\frac{1}{N-1}{\mathbf{P}}_N\otimes \left[\left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s{\mu }_s\right){\mathbf{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}{\mathbf{w}}_s{\mu }_s\right)\right]$$

while the covariance matrix of ${\overleftrightarrow{\mathbf{E}}}_w$ is

$${\text{var}}_{{\xi }_1{\xi }_2}\left({\overleftrightarrow{\mathbf{E}}}_w\right)={\mathbf{I}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}\left[\frac{{\sigma }_s^2}{N}\left(\underset{j=1}{\overset{M_s}{\oplus }}{w}_{sj}\right){\mathbf{P}}_{M_s}\left(\underset{j=1}{\overset{M_s}{\oplus }}{w}_{sj}\right)\right]\right),$$

where ${\mathbf{P}}_a={\mathbf{I}}_a-\frac{1}{a}{\mathbf{J}}_a$ and J_a denotes an a × a matrix with all elements equal to one.

2.3. Defining Target Quantities

Model (7) is an expanded version of a finite population mixed model that retains the identity of clusters, while accounting for a two-stage random permutation. Our interest is to predict target linear combinations defined by $T=\mathbf{g}\prime {\overleftrightarrow{\mathbf{Y}}}_w,$ where g is non-stochastic. For simplicity, we limit discussion to the case

$$\mathbf{g}\prime =\mathbf{c}\prime \otimes {\mathbf{1}}_{\mathbb{N}}^{\prime }$$ (8)

where c is an N × 1 vector of constants. In particular, we focus on the setting where c = e_i, i.e., an N × 1 vector with all elements equal to zero, except for element i which has the value of one. The principal interest lies in the setting where i≤n, i.e., in the clusters realized in the sample. When $w_{sj}=\frac{1}{M_s}$ for all s = 1,…,N, j = 1,…,M_s, the target, $T={\displaystyle \sum _{s=1}^N{U}_{is}}\left({\displaystyle \sum _{j=1}^{M_s}{w}_{sj}{\tilde{Y}}_{sj}}\right)$ is the mean of PSU i; when w_sj = 1 for all s = 1,…,N, j = 1, …,M_s, the target, $T={\displaystyle \sum _{s=1}^N{U}_{is}}\left({\displaystyle \sum _{j=1}^{M_s}{w}_{sj}{\tilde{Y}}_{sj}}\right)$ is the total of PSU i. Note that in both cases, the target is a random variable.

3. PREDICTING A PSU MEAN IN THE EXPANDED FINITE POPULATION MIXED MODEL

To obtain the BLUP, we adopt the basic strategy employed by Scott and Smith (1969), Royall (1976), Bolfarine and Zacks (1992), Valliant et al. (2000), and Stanek and Singer (2004), among others. We assume that the elements in the sample portion of ${\overleftrightarrow{Y}}_w$ will be observed, and express the target T as the sum of two parts, one which is a function of the sample, and the other, a function of the remaining random variables. Then, requiring the predictor to be a linear function of the sample random variables and to be unbiased, we obtain coefficients that minimize the MSE. While in theory, an optimal predictor can be obtained via this recipe, in practice, the high dimensionality of the expanded random vectors may result in singularities that lead to multiple solutions as discussed in Stanek, Singer, and Lencina (2004). For this reason, we explore projections of the expanded random variables into lower dimensional spaces that retain the necessary information for an optimal solution.

3.1. Partial Collapsing of the Expanded Finite Population Mixed Model Random Variables

Following Rao and Bellhouse (1978), we provide a way of determining whether the optimal linear unbiased predictor of a target random variable, $T=\mathbf{g}\prime {\overleftrightarrow{\mathbf{Y}}}_w$ can be obtained as the optimal linear unbiased predictor of $T={\mathbf{g}}_p^{\prime }{\overleftrightarrow{\mathbf{Y}}}_{wp}$ based on a vector of collapsed random variables that spans a lower dimensional space defined by ${\overleftrightarrow{\mathbf{Y}}}_{wp}=\overleftrightarrow{\mathbf{C}}\prime {\overleftrightarrow{\mathbf{Y}}}_w,\text{where}\overleftrightarrow{\mathbf{C}}$ is a matrix of dimension Nℕ × c with c < Nℕ. We take $\overleftrightarrow{\mathbf{C}}\prime =\left(\frac{\underset{i=1}{\overset{N}{\oplus }}}{\underset{i=1}{\overset{N}{\oplus }}}\frac{\underset{s=1}{\overset{N}{\oplus }}}{\underset{s=1}{\overset{N}{\oplus }}}\frac{\left({\mathbf{1}}_{m_s}^{\prime }|{\mathbf{0}}_{M_s-m_s}^{\prime }\right)}{\left({\mathbf{0}}_{m_s}^{\prime }|{\mathbf{1}}_{M_s-m_s}^{\prime }\right)}\right)\text{and}{\mathbf{g}}_P^{\prime }=\mathbf{g}\prime \left[\overleftrightarrow{\mathbf{C}}{\left(\overleftrightarrow{\mathbf{C}}\prime \overleftrightarrow{\mathbf{C}}\right)}^{-1}\right],$ so that the effect of collapsing is the generation of sums of the SSUs for the sample and for the remainder in each cluster for each PSU, thus reducing the number of random variables from Nℕ to 2N². Since ${\overleftrightarrow{\mathbf{Y}}}_w=\left[\overleftrightarrow{\mathbf{C}}{\left(\overleftrightarrow{\mathbf{C}}\prime \overleftrightarrow{\mathbf{C}}\right)}^{-1}\right]{\overleftrightarrow{\mathbf{Y}}}_{wp}+{\mathbf{P}}_{\overleftrightarrow{\mathbf{C}}}{\overleftrightarrow{\mathbf{Y}}}_w,\text{where}{\mathbf{P}}_{\overleftrightarrow{\mathbf{C}}}={\mathbf{I}}_{N\mathbb{N}}-\overleftrightarrow{\mathbf{C}}{\left(\overleftrightarrow{\mathbf{C}}\prime \overleftrightarrow{\mathbf{C}}\right)}^{-1}\overleftrightarrow{\mathbf{C}}\prime ,$ we can write $\mathbf{g}\prime {\overleftrightarrow{\mathbf{Y}}}_w=\mathbf{g}\prime \left[\overleftrightarrow{\mathbf{C}}{\left(\overleftrightarrow{\mathbf{C}}\prime \overleftrightarrow{\mathbf{C}}\right)}^{-1}\right]{\overleftrightarrow{\mathbf{Y}}}_{wp}+\mathbf{g}\prime {\mathbf{P}}_{\overleftrightarrow{\mathbf{C}}}{\overleftrightarrow{\mathbf{Y}}}_w.$ Using (8), it follows that ${\mathbf{g}}_p^{\prime }={\mathbf{1}}_2^{\prime }\otimes \left[\mathbf{c}\prime \otimes {\mathbf{1}}_N^{\prime }\right],\mathbf{g}\prime {\mathbf{P}}_{\overleftrightarrow{\mathbf{C}}}{\overleftrightarrow{\mathbf{Y}}}_w=0\text{and}T={\mathbf{g}}_p^{\prime }{\overleftrightarrow{\mathbf{Y}}}_{wp}.\text{Let}{\widehat{\mathbf{L}}}_p$ represent an nN × 1. vector of constants, and ${\overleftrightarrow{\mathbf{Y}}}_{wI}$ be the first nN random variables (corresponding to the sample) in ${\overleftrightarrow{\mathbf{Y}}}_{wP}.$ Then letting ${\widehat{T}}_p={\widehat{\mathbf{L}}}_p^{\prime }{\overleftrightarrow{\mathbf{Y}}}_{wI}$ be the optimal linear unbiased predictor of T based on ${\overleftrightarrow{\mathbf{Y}}}_{wI}\text{and}{\widehat{B}}_P$ be a linear unbiased predictor of $\mathbf{g}\prime {\mathbf{P}}_{\overleftrightarrow{\mathbf{C}}}{\overleftrightarrow{\mathbf{Y}}}_w=0$ it follows from Rao and Bellhouse (1978, Theorem 1.1) that ${\widehat{T}}_p$ will be optimal for $T=\mathbf{g}\prime {\overleftrightarrow{\mathbf{Y}}}_w$ if and only if $E_{{\xi }_1{\xi }_2}\left[\left({\widehat{T}}_p-T\right){\widehat{B}}_p\right]=0.$ Expressing $E_{{\xi }_1{\xi }_2}\left[\left({\widehat{T}}_p-T\right){\widehat{B}}_p\right]$ as a function of $E_{{\xi }_1{\xi }_2}\left({\overleftrightarrow{Y}}_w{\overleftrightarrow{Y}}_w^{\prime }\right),$ and simplifying terms, it follows that $E_{{\xi }_1{\xi }_2}\left[\left({\widehat{T}}_p-T\right){\widehat{B}}_p\right]=0$ when w_sj = w_s for all j = 1,…,M_s (see details at http://www.umass.edu/cluster/). This implies that we can obtain the optimal predictor using the partially collapsed random variables as long as within each cluster, the weights are equal for all SSUs.

Having this in mind, we assume that w_sj = w_s for all j = 1,…,M_s and develop the BLUP of $T=\mathbf{g}\prime {\overleftrightarrow{\mathbf{Y}}}_{wp}$ based on the 2N² collapsed random variables contained in ${\overleftrightarrow{\mathbf{Y}}}_{wp}$. The first N² of them are of the form $U_{is}{w}_s{m}_s{\overline{Y}}_{sI},$ while the remaining N² are of the form. $U_{is}{w}_s\left(M_s-m_s\right){\overline{Y}}_{sII},\text{where}{\overline{Y}}_{sI}=\frac{1}{m_s}{\displaystyle \sum _{j=1}^{m_s}{\tilde{Y}}_{sj}}\text{and}{\overline{Y}}_{sII}=\frac{1}{M_s-m_s}{\displaystyle \sum _{j=m_s+1}^{M_s}{\tilde{Y}}_{sj}}.$

3.2. Predicting Linear Combinations of PSU Latent Values Using the Expanded Finite Population Mixed Model

We partition ${\overleftrightarrow{Y}}_{wp},$ into the first nN random variables corresponding to the sample, ${\overleftrightarrow{Y}}_{wI},$ and the N(N − n) remaining random variables, ${\overleftrightarrow{Y}}_{wII},$ and write the target as $T={\mathbf{g}}_I^{\prime }{\overleftrightarrow{Y}}_{wI}+{\mathbf{g}}_{II}^{\prime }{\overleftrightarrow{Y}}_{wII},\text{where}{\mathbf{g}}_I^{\prime }=c_I^{\prime }\otimes 1_N^{\prime }\text{and}{\mathbf{g}}_{II}^{\prime }=\left(c_{II}^{\prime }\otimes 1_N^{\prime }|c\prime \otimes 1_N^{\prime }\right).$ Explicitly, the partitioned expanded finite population mixed model is

$$\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)=\left(\begin{array}{c}{\mathbf{X}}_I\hfill \\ {\mathbf{X}}_{II}\hfill \end{array}\right)\mathbf{\mu }+\left[E_{{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)-E_{{\xi }_1{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)\right]+\left(\begin{array}{c}{\overleftrightarrow{\mathbf{E}}}_{WI}\hfill \\ {\overleftrightarrow{\mathbf{E}}}_{WII}\hfill \end{array}\right).$$ (9)

Requiring the predictor of T to be a linear function of ${\overleftrightarrow{Y}}_{wI},$ to be unbiased, and to have minimum MSE, the BLUP of T in (9) is

$${\widehat{T}}_p={\displaystyle \sum _{i=1}^n{c}_i\left(\widehat{Y}-\overline{\widehat{Y}}\right)+\overline{c}\frac{N}{n}\left({\displaystyle \sum _{s=1}^N{I}_s\left(M_s{w}_s{\overline{Y}}_{sI}\right)}\right)+{\overline{c}}_{II}\frac{N-n}{n}\left({\displaystyle \sum _{s=1}^N{I}_s\left(M_s{f}_s{w}_s{\overline{Y}}_{sI}\right)}\right)}$$ (10)

where ${\widehat{Y}}_i={\displaystyle \sum _{s=1}^N{U}_{is}{M}_s{w}_s{k}_s^{*}{\overline{Y}}_{sI},\overline{\widehat{Y}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Y}}_i,}}{k}_s^{*}=k_s-\frac{k_s}{d_s}\frac{1}{N}{\displaystyle \sum _{s^{*}=1}^N\left(\frac{1-k_{s^{*}}}{1-\overline{k}}\right)d_{s^{*}},d_s=M_s{w}_s{\mu }_s,k_s=\frac{f_s^2{d}_s^2}{f_s^2{d}_s^2+\left(N-1\right){\nu }_{se}^2}}$ (see a: http://www.umass.edu/cluster/ for details), $\overline{k}=\frac{1}{N}{\displaystyle \sum _{s=1}^N{k}_s},{\overline{c}}_{II}=\frac{1}{N-n}{\displaystyle \sum _{i=n+1}^N{c}_i},\overline{c}=\frac{1}{N}{\displaystyle \sum _{i-1}^N{c}_i}\text{and}{I}_s={\displaystyle \sum _{i=1}^n{U}_{is}}$ is an indicator ‘inclusion’ random variable for cluster s in the sample (see derivation in Appendix A). An expression for the MSE of the predictor can be developed directly using expressions for the variance, and simplifies to

$$\begin{array}{cc}{\mathrm{var}}_{{\xi }_1{\xi }_2}\left({\widehat{T}}_p-T\right)\hfill & =\left({\displaystyle \sum _{i=1}^N{\left(c_i-{\overline{c}}_I\right)}^2}\right)\left({\sigma }_{kd}^2-2{\sigma }_{kd,d}+\frac{1}{N}{\displaystyle \sum _{s=1}^N\frac{k_s^{*2}{v}_{se}^2}{f_s^2}}\right)+\frac{{\left(N\overline{c}\right)}^2}{n}\left(\frac{1}{N}{\displaystyle \sum _{s=1}^N\frac{v_{se}^2}{f_s^2}}\right)\hfill \\ \hfill & +\left[{\displaystyle \sum _{i=1}^N{c}_i^2}+\frac{N\overline{c}}{n}(N\overline{c}-2n{\overline{c}}_I)\right]{\sigma }_d^2\hfill \end{array}$$

where ${\overline{c}}_I=\frac{1}{n}{\displaystyle \sum _{i=1}^n{c}_i},{\mu }_d=\frac{1}{N}{\displaystyle \sum _{s=1}^N{d}_s},{\mu }_{kd}=\frac{1}{N}{\displaystyle \sum _{s=1}^N{k}_s^{*}{d}_s},{\sigma }_{kd}^2=\frac{1}{N-1}{\displaystyle \sum _{s=1}^N{(k_s^{*}{d}_s-{\mu }_{kd})}^2}$, ${\sigma }_d^2=\frac{1}{N-1}{\displaystyle \sum _{s=1}^N{(d_s-{\mu }_d)}^2\text{and}{\sigma }_{kd,d}=\frac{1}{N-1}{\displaystyle \sum _{s=1}^N(k_s^{*}{d}_s-{\mu }_{kd})}(d_s-{\mu }_d)}$ (see b. http://www.umass.edu/cluster/ for details).

When predicting a PSU mean, i.e., using $w_s=\frac{1}{M_s},$ (10) simplifies to ${\widehat{T}}_p=\overline{Y}+\left({\widehat{Y}}_i-\overline{\widehat{Y}}\right)$ if i ≤ n and to ${\widehat{T}}_p=\overline{Y}$ when i > n, where ${\overline{Y}}_i={\displaystyle \sum _{s=1}^N{U}_{is}{\overline{Y}}_{sI}}.$ The MSE for a sample PSU mean predictor (when i ≤ n) simplifies to

$$\begin{array}{cc}{\text{var}}_{{\xi }_1{\xi }_2}\left({\widehat{T}}_p-T\right)\hfill & =\left(\frac{n-1}{n}\right)\frac{1}{N-1}{\displaystyle \sum _{s=1}^N\left[{\left(\left(k_s^{*}-1\right){\mu }_s-\frac{1}{N}{\displaystyle \sum _{s=1}^N\left(k_s^{*}-1\right){\mu }_s}\right)}^2\right]},\hfill \\ \hfill & +\frac{1}{nN}{\displaystyle \sum _{s=1}^N\left[1+\left(n-1\right)k_s^{*2}\right]\left(1-f_s\right)\frac{{\sigma }_s^2}{m_s}}\hfill \end{array}$$

(see c. http://www.umass.edu/cluster/ for details) while the MSE for a PSU not in the sample is given by

$${\mathrm{var}}_{{\xi }_1{\xi }_2}\left({\widehat{T}}_p-T\right)=\left(\frac{n=1}{n}\right){\sigma }^2+\frac{1}{nN}{\displaystyle \sum _{s=1}^N\left(1-f_s\right)\frac{{\sigma }_s^2}{m_s}.}$$

4. COMPARISON OF PREDICTORS

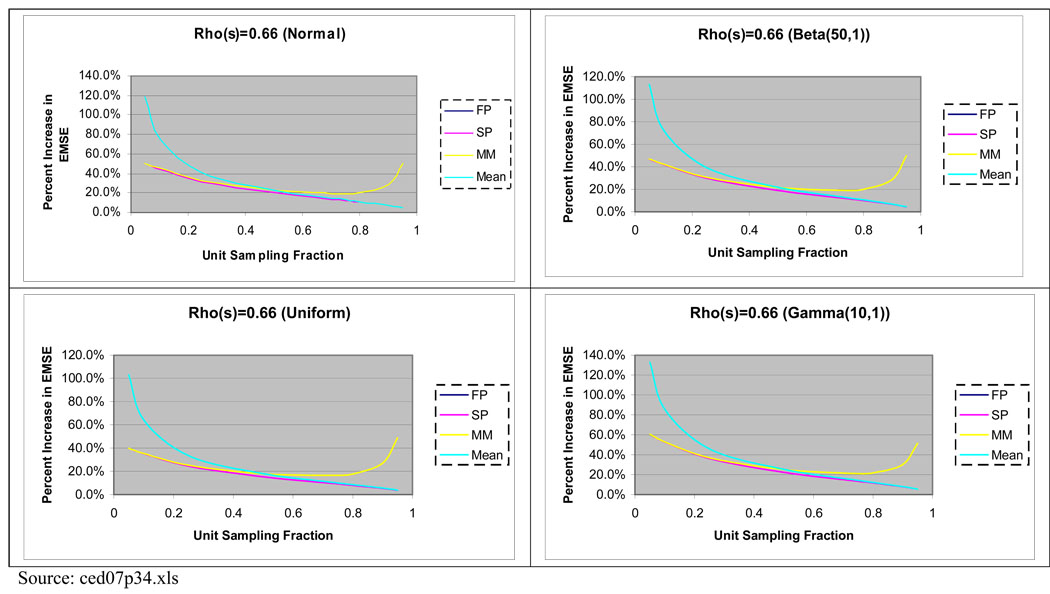
We compare the MSE of (10) to that of the simple mean, and of predictors (3) and (4). When clusters are of equal size, have homogeneous unit variances, and sample sizes are equal, the MSE for each predictor can be explicitly calculated. In this setting, we also compare the results with the MSE for predictor (5). For the sample mean, $MSE\left({\overline{Y}}_i\right)-\frac{1}{N}{\displaystyle \sum _{s=1}^N\left(1-f_s\right)\frac{{\sigma }_s^2}{m_s},}$ while for (5), $MSE\left({\widehat{T}}_{RP}\right)=\left(1-f\right)\left[\frac{{\sigma }_e^2}{nm}+\left(\frac{n-1}{n}\right)\left(1-k\right){\sigma }^2\right].$ The MSE for predictors (3) and (4) are given by $MSE\left({\widehat{T}}_{RP}\right)+\left(\frac{n-1}{nk}\right)\left({\sigma }^2-\frac{{\sigma }_e^2}{M}\right){\left(c-\left[f+\left(1-f\right)k\right]\right)}^2\text{with}c=\frac{m{\sigma }^2}{m{\sigma }^2+{\sigma }_e^2}$ for (3) and $c=f+\frac{\left(1-f\right)m{\sigma }^2}{m{\sigma }^2+{\sigma }_e^2}$ for (4) as shown in Stanek and Singer (2004). Although we have explicit expressions for the MSE of these predictors, the difference between them is a complicated function of the population parameters. Since shrinkage constants for the expanded predictor depend on the cluster latent values, we compare the MSE relative to the expanded finite population mixed model predictor in four settings with different values of the unit intra-class correlation coefficient, ${\rho }_s=\frac{{\sigma }^2}{{\sigma }^2+{\sigma }_s^2}.$ In each setting, the cluster latent values are set equal to evenly spaced quantiles from some specified distribution. The results, expressed as percent increase in MSE relative to the MSE of (10) are presented in Figure 1, and illustrate that in all settings considered, using (10) results in a substantial reduction in MSE (over 40% when f < 0.2). This is true even for (5), illustrating that a smaller MSE can be achieved for the BLUP derived under the expanded finite population mixed model as compared to the BLUP obtained under the finite population mixed model of Stanek and Singer (2004). There were little differences in the MSE comparisons with different distributions of the cluster latent values. The results illustrate that predictor (3) has larger MSE relative to the other predictors when f > 0.5. The MSE for predictors (4) and (5) are similar, and differ more from the MSE of (10) when f is small.

Figure 1.

Percent increase in MSE for the Finite Population Mixed Model (FP), Superpopulation Model (SP), Mixed Model (MM), and Sample Mean (Mean) Predictors Relative to Finite Expanded Mixed Model Predictor of a Realized PSU Mean where N = 100, n = 30, and M = 20 for all clusters. Equal Size Clusters and Equal Unit Sampling Fractions per Cluster

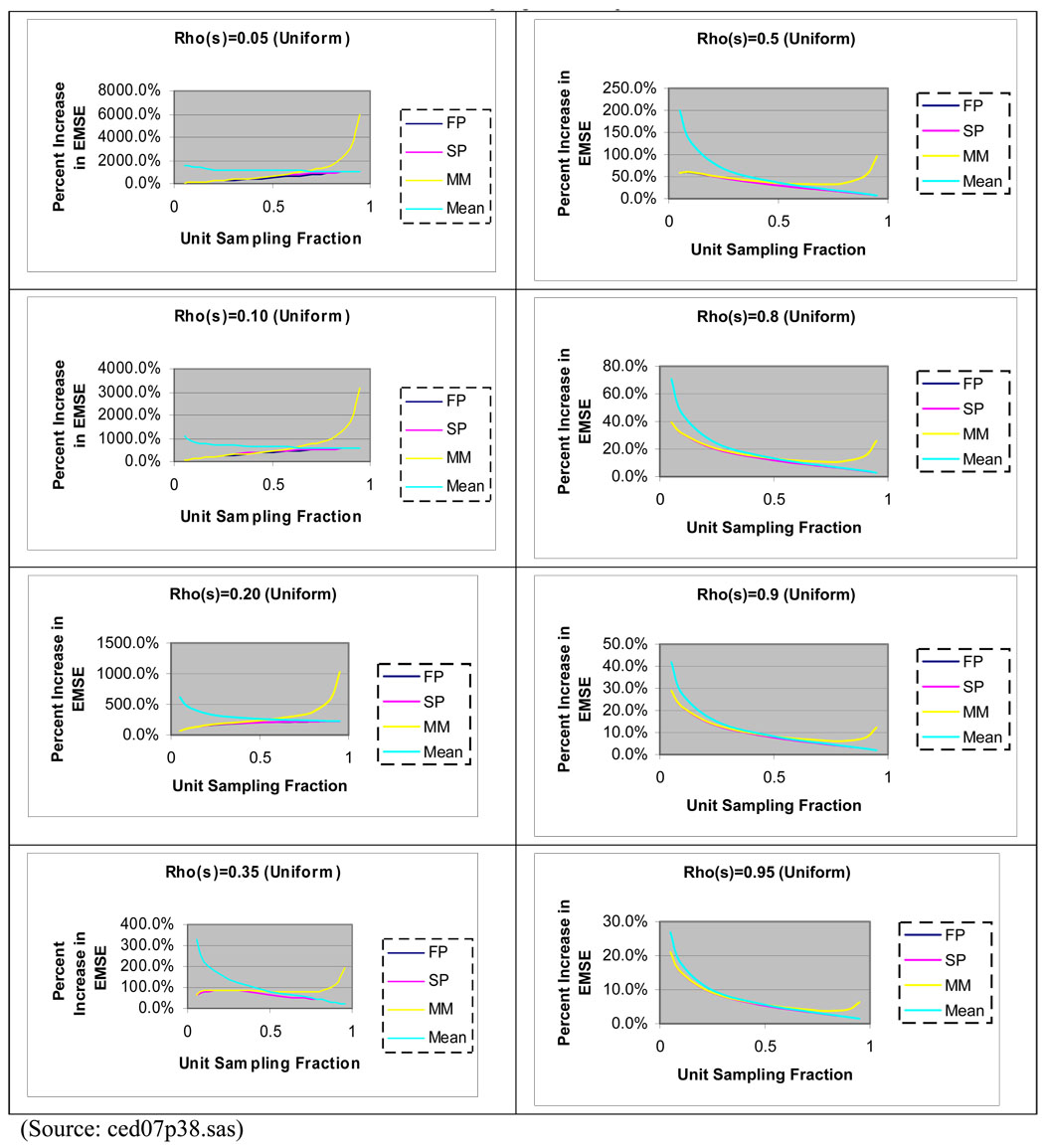
Figure 2 summarizes increases in MSE for different intra-class correlation coefficients; quantiles of a uniform distribution were used to determine cluster latent values and unit parameters. The results illustrate that for low intra-class correlation coefficients, the relative increase in MSE can be dramatic. Once again, for low sampling fractions, similar patterns in MSE are evident for (3), (4) and (5).

Figure 2.

Percent increase in MSE for the Finite Population Mixed Model (FP), Superpopulation Model (SP), Mixed Model (MM), and Sample Mean (Mean) Predictors Relative to Finite Expanded Mixed Model Predictor of a Realized PSU Mean by Unit Intra-class Correlation and Unit Sampling Fraction where N = 100, n = 30, and M = 20 for all clusters. Equal Size Clusters and Equal Unit Sampling Fractions per Cluster

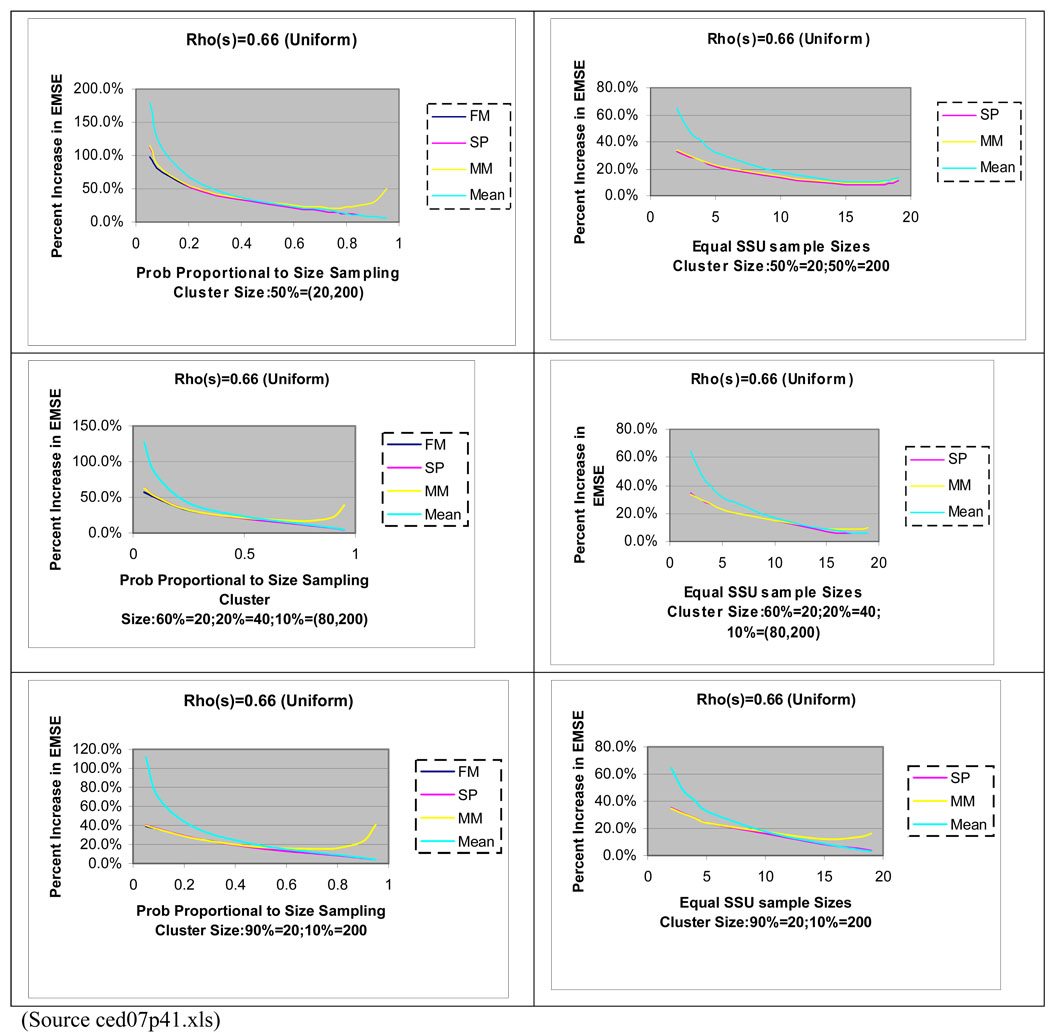
In Figure 3, we compare predictors of the sample mean, for (3) and (4) in two settings where cluster sizes differ. Predictor (5) is not applicable in such settings. These results are based on simulation studies (with 5000 trials each) that repeat a two-stage sampling process from a finite population. The MSE is estimated by the average squared difference between the predictor and the latent PSU value in each case. In the left column, cluster sizes differ by 10-fold, with sample sizes for clusters proportional to the cluster size. The results illustrate the performance of the predictors for different sampling fractions. The right column in Figure 3 compares the MSE of predictors when the sample size per cluster is constant.

Figure 3.

Percent increase in MSE for the Finite Population Mixed Model (FP), Superpopulation Model (SP), Mixed Model (MM), and Sample Mean (Mean) Predictors Relative to Finite Expanded Mixed Model Predictor of a Realized PSU Mean with Probability Proportional to Size SSU sampling and for Equal SSU size sampling for different Cluster Sizes where N = 100, n = 30, and M = 20 for all clusters.

5. DISCUSSION

The expanded finite population mixed model uses a larger set of 2N² random variables than the ℕ random variables typically used in superpopulation models or in the finite population mixed model of Stanek and Singer (2004). These random variables are fewer than the ℕ₂ random variables resulting from an expansion that retains the identity of units and SSUs, and even fewer than the very general representation of the model used by Godambe (1955). We show that this intermediate set of random variables allows a clear representation of a two-stage sample, while accounting for details on different cluster and sample sizes. Other approaches do not appear to connect the potentially observable data to the random variables in the stochastic model. Since more than one finite population mixed model can be used, we have shown how they can be compared by considering them in a hierarchy, and identifying whether the additional set of orthogonal random variables adds to the information about the target quantity. Further reductions in the number of random variables from the expanded finite population mixed model were considered (Appendix B), each of which lead to loss of information.

It is valuable to note that these results depend on selection of the target quantity. For example, if there is interest in the relationship between two variables among units (in a cluster), the collapsed expanded set of 2N² random variables is not likely to be sufficient.

The BLUP obtained under the new model offers substantial gains over previous predictors. These gains are likely mitigated by the need to estimate shrinkage constants for use in practical setups. Simulation studies comparing the performance of the empirical predictors (3), (4), and (5) in the equal cluster size/sample size settings indicate some loss in efficiency, but with a similar ordering of MSE (San Martino, Singer, and Stanek 2007). Limited simulation studies have been conducted using the expanded model predictor and have indicated that there is a greater loss in the MSE of (10) relative to the other predictors. Iterative estimation procedures may be possible, and are currently being investigated. This area requires more study.

APPENDIX A

Consider the partitioned expanded finite population mixed model in (9) where ${\mathbf{X}}_i=\left[\frac{1}{N}{\mathbf{1}}_n\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{w}_s{m}_s\right)\right]\text{and}{\mathbf{X}}_{II}=\left(\frac{\frac{1}{N}{\mathbf{1}}_{N-n}\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{w}_s{m}_s\right)}{\frac{1}{N}{\mathbf{1}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{w}_s(M_s-m_s)\right)}\right),$ and the random effects are given by $\left[E_{{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)-E_{{\xi }_1{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)\right]=\left[\begin{array}{c}{\mathbf{I}}_n\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right)vec\left({\mathbf{U}}_I-E_{{\xi }_1}({\mathbf{U}}_I)\right)\hfill \\ \frac{{\mathbf{I}}_{N-n}\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right)vec\left({\mathbf{U}}_{II}-E_{{\xi }_1}({\mathbf{U}}_{II})\right)}{{\mathbf{I}}_N\otimes \left(\underset{s=1}{\overset{N}{\oplus }}(1-f_s)d_s\right)vec\left[\mathbf{U}-E_{{\xi }_1}(\mathbf{U})\right]}\hfill \end{array}\right],$ with $\left(\begin{array}{c}{\overleftrightarrow{\mathbf{E}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{E}}}_{WII}\hfill \end{array}\right)=\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{WI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{WII}\hfill \end{array}\right)-E_{{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{WI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{WII}\hfill \end{array}\right),$ and U = (U_I U_II), U_I = ((U_i)) = (U₁ U₂ … U_n) and U_II = ((U_i)) = (U_n+1 U_n+2 … U_N). The corresponding covariance matrix is given by

$$\begin{array}{ll}\text{var}\left({\overleftrightarrow{\mathbf{Y}}}_{wp}\right)\hfill & =\frac{1}{N-1}\left(\frac{{\mathbf{P}}_N\otimes \left[\left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right){\mathbf{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right)\right]{\mathrm{P}}_N\otimes \left[\left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right){\mathrm{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}(1-f_s)d_s\right)\right]}{{\mathrm{P}}_N\otimes \left[\left(\underset{s=1}{\overset{N}{\oplus }}(1-f_s)d_s\right){\mathrm{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}{f}_s{d}_s\right)\right]{\mathbf{P}}_N\otimes \left[\left(\underset{s=1}{\overset{N}{\oplus }}(1-f_s)d_s\right){\mathbf{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}(1-f_s)d_s\right)\right]}\right)\hfill \\ \hfill & +\left(\frac{{\mathbf{I}}_N-{\mathbf{I}}_N}{-{\mathbf{I}}_N{\mathbf{I}}_N}\right)\otimes \left(\underset{s=1}{\overset{N}{\oplus }}{v}_{se}^2\right)\hfill \end{array}$$

(see a. http://www.umass.edu/cluster/ for details) which we partition as ${var}_{{\xi }_1{\xi }_2}\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right)=\left(\begin{array}{cc}{\mathbf{V}}_I\hfill & {\mathbf{V}}_{I,II}\hfill \\ {\mathbf{V}}_{I,II}^{\prime }\hfill & {\mathbf{V}}_{II}\hfill \end{array}\right),$ where $V_{se}^2=f_s\left(1-f_s\right)\frac{M_s{w}_s^2{\sigma }_s^2}{N}$ (see b. http://www.umass.edu/cluster/ for details). Letting L be a vector of constants, it follows that $\mathbf{L}\prime {\overleftrightarrow{\mathbf{Y}}}_{wI}-T=(\mathbf{L}\prime -{\mathbf{g}}_I^{\prime }-{\mathbf{g}}_{II}^{\prime })\left(\begin{array}{c}{\overleftrightarrow{\mathbf{Y}}}_{wI}\hfill \\ {\overleftrightarrow{\mathbf{Y}}}_{wII}\hfill \end{array}\right),$ and the unbiased constraint is given by $(\mathbf{L}\prime -{\mathbf{g}}_I^{\prime }){\mathbf{X}}_I-{\mathbf{g}}_{II}^{\prime }{\mathbf{X}}_{II}=0.$ Using Lagrange multipliers, we minimize ${var}_{{\xi }_1{\xi }_2}\left(\mathbf{L}\prime {\overleftrightarrow{\mathbf{Y}}}_{wI}-T\right)$ while accounting for the unbiased constraint results and obtain the familiar solution

$$\widehat{\mathbf{L}}={\mathbf{g}}_I+\left[{\mathbf{V}}_I^{-1}-{\mathbf{V}}_I^{-1}{\mathbf{X}}_I{\left({\mathbf{X}}_I^{\prime }{\mathbf{V}}_I^{-1}{\mathbf{X}}_I\right)}^{-1}{\mathbf{X}}_I^{\prime }{\mathbf{V}}_I^{-1}\right]{\mathbf{V}}_{I,II}{\mathbf{g}}_{II}+{\mathbf{V}}_I^{-1}{\mathbf{X}}_I{\left({\mathbf{X}}_{\mathbf{I}}^{\prime }{\mathbf{V}}_I^{-1}{\mathbf{X}}_I\right)}^{-1}{\mathbf{X}}_{II}^{\prime }{\mathbf{g}}_{II}.$$

This result simplifies to

$$\widehat{\mathbf{L}}=\left({\mathbf{P}}_n{\mathbf{c}}_I\otimes \left[\underset{s=1}{\overset{N}{\oplus }}\frac{k_s^{*}}{f_s}\right]{\mathbf{1}}_N\right)+\frac{N}{n}\overline{c}\left[{\mathbf{1}}_n\otimes \left(\underset{s=1}{\overset{N}{\oplus }}\frac{1}{f_s}\right){\mathbf{1}}_N\right]+\frac{N-n}{n}{\overline{c}}_{II}\left({\mathbf{1}}_n\otimes {\mathbf{1}}_N\right)$$

(see c. http://www.umass.edu/cluster/ for details) where $k_s^{*}=k_s-\frac{k_s}{d_s}\frac{1}{N}{\displaystyle \sum _{s^{*}=1}^N\left(\frac{1-k_{s^{*}}}{1-\overline{k}}\right)d_{s^{*}},}{k}_s=\frac{f_s^2{d}_s^2}{f_s^2{d}_s^2+\left(N-1\right)v_{se}^2}$ (see d. http://www.umass.edu/cluster/ for details), $\overline{k}=\frac{1}{N}{\displaystyle \sum _{s=1}^N{k}_s},{\overline{c}}_{II}=\frac{1}{N-n}{\displaystyle \sum _{i=n+1}^N{c}_i}\text{and}\overline{c}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{c}_i}.$ The predictor ${\widehat{T}}_p=\widehat{\mathbf{L}}\prime {\overleftrightarrow{\mathbf{Y}}}_{wI}$ can then be expressed as as (10) (see e. http://www.umass.edu/cluster/ for details).

APPENDIX B

We discuss whether several other plausible reductions in the dimension of the set of expanded random variables (given by Nℕ), including a reduction to the set of 2N random variables used by Stanek and Singer (2004), may be considered without loss of information. First, it is natural to consider whether it is sufficient to predict $T={\mathbf{g}}_p^{\prime }{\overleftrightarrow{\mathbf{Y}}}_{wp}$ using the 2N collapsed random variables defined by ${\mathbf{Y}}_w={\mathbf{C}}^{*}\prime {\overleftrightarrow{\mathbf{Y}}}_{wp}.$ This set of random variables is similar to that used by Stanek and Singer (2004) for a population with equal size clusters and equal size samples per cluster with no response error. Since ${\mathbf{g}}^{*}\prime ={\mathbf{g}}_p^{\prime }\left[{\mathbf{C}}^{*}{\left({\mathbf{C}}^{*}\prime {\mathbf{C}}^{*}\right)}^{-1}\right]={\mathbf{1}}_2^{\prime }\otimes \mathbf{c}\prime ,\text{the target}T={\mathbf{g}}^{*}\prime {\overleftrightarrow{\mathbf{Y}}}_w$ defines a linear combination of PSU means.

First, let T̂ = L̂′Y_wI where L^ represents an n × 1. vector of constants, and Y_wI represents the first n random variables (corresponding to the sample) in Y_w. In this case, the bias E_ξ1ξ2(L̂′Y_WI − T) = (L̂′1_n)m_s − (c′1_N)(M_s − m_s) is zero only if sampling of clusters is conducted with probability proportional to size (PPS) (see a. http://www.umass.edu/cluster/).

Now assume a PPS sampling scheme, and notice that since ${\mathbf{g}}_p^{\prime }\left({\mathbf{P}}_{{\mathbf{C}}^{*}}{\overleftrightarrow{\mathbf{Y}}}_{wp}\right)=0$, we may write $T={\mathbf{g}}^{*}\prime {\mathbf{Y}}_w+{\mathbf{g}}_P^{\prime }\left({\mathbf{P}}_{{\mathbf{C}}^{*}}{\overleftrightarrow{\mathbf{Y}}}_{wp}\right).$ Letting $\widehat{B}=\widehat{\mathbf{b}}\prime (I_n\otimes P_n){\overleftrightarrow{Y}}_{wI}$ be a linear unbiased predictor of ${\mathbf{g}}_p^{\prime }\left({\mathbf{P}}_{{\mathbf{C}}^{*}}{\overleftrightarrow{\mathbf{Y}}}_{wp}\right)$ based on the sample part of ${\mathbf{P}}_{{\mathbf{C}}^{*}}{\overleftrightarrow{\mathbf{Y}}}_{wp}\text{given by}({\mathbf{I}}_n\otimes {\mathbf{P}}_N){\overleftrightarrow{\mathbf{Y}}}_{wI},$ the predictor T̂ will be optimal if and only if E_ξ1ξ2[(T̂ − T)B̂] = 0. Simplifying this expectation, we find

$$\begin{array}{ll}{E}_{{\xi }_1{\xi }_2}\left[\left(\widehat{T}-T\right)\widehat{B}\right]\hfill & =\left[f\left(f\widehat{\mathbf{L}}\prime -{\mathbf{c}}_I^{\prime }\right)\otimes {\mathbf{1}}_N^{\prime }\right]\left[{\mathbf{I}}_n\otimes \left(\frac{1}{N-1}\left(\underset{s=1}{\overset{N}{\oplus }}{d}_s\right){\mathbf{P}}_N\left(\underset{s=1}{\overset{N}{\oplus }}{d}_s\right){\mathbf{P}}_N\right)\right]\widehat{\mathbf{b}}\hfill \\ \hfill & +[\frac{f(1-f)}{N}(\widehat{\mathbf{L}}\prime +{\mathbf{c}}_I^{\prime })\otimes [{\mathbf{1}}_N^{\prime }(\underset{s=1}{\overset{N}{\oplus }}{M}_s{w}_s^2{\sigma }_s^2){\mathbf{P}}_N]]\widehat{\mathbf{b}}\hfill \end{array}$$

where $d_s=M_s{w}_s{\mu }_s,\mathbf{c}=({\mathbf{c}}_I^{\prime }{\mathbf{c}}_{II}^{\prime })\prime ,$ c_I is an n × 1. vector and f denotes the common sampling fraction (see b. http://www.umass.edu/cluster/). This expression is not equal to zero, even when the population consists of equal size clusters with homogeneous variances, and equal size samples are taken from sample clusters. By Theorem 1.1 in Rao and Bellhouse (1978), this result implies that some efficiency is lost in prediction when collapsing ${\overleftrightarrow{Y}}_{wp}$ to Y_w. The predictor based on ${\overleftrightarrow{Y}}_{wp}$ will have smaller MSE than the predictor based on Y_w, even in the settings considered by Stanek and Singer (2004) with no response error when clusters are of equal size, and equal size samples are selected.