High Resolution Approach to the Native State Ensemble Kinetics and Thermodynamics

Abstract

Many biologically interesting functions such as allosteric switching or protein-ligand binding are determined by the kinetics and mechanisms of transitions between various conformational substates of the native basin of globular proteins. To advance our understanding of these processes, we constructed a two-dimensional free energy surface (FES) of the native basin of a small globular protein, Trp-cage. The corresponding order parameters were defined using two native substructures of Trp-cage. These calculations were based on extensive explicit water all-atom molecular dynamics simulations. Using the obtained two-dimensional FES, we studied the transition kinetics between two Trp-cage conformations, finding that switching process shows a borderline behavior between diffusive and weakly-activated dynamics. The transition is well-characterized kinetically as a biexponential process. We also introduced a new one-dimensional reaction coordinate for the conformational transition, finding reasonable qualitative agreement with the two-dimensional kinetics results. We investigated the distribution of all the 38 native nuclear magnetic resonance structures on the obtained FES, analyzing interactions that stabilize specific low-energy conformations. Finally, we constructed a FES for the same system but with simple dielectric model of water instead of explicit water, finding that the results were surprisingly similar in a small region centered on the native conformations. The dissimilarities between the explicit and implicit model on the larger-scale point to the important role of water in mediating interactions between amino acid residues.

INTRODUCTION

The native state of a typical globular protein is not a single static conformation but possesses rich intrinsic dynamics. In many cases, these dynamics are essential for protein function. Examples include enzymatic catalysis (1), allosteric switching (1–3), protein-ligand binding (Mb-CO) (4), the change of antibody-ligand binding during maturation process (5), and photorhodopsin photocycle at low temperature (6). The main objective of this article is to advance our understanding of the kinetics of conformational switching in the native basin of a globular protein. In particular, we address the question of whether native dynamics are activated, showing normal Arrhenius temperature dependence, or diffusive, similar to those of ordinary fluids. After reviewing the underlying energy landscape theory and reaction coordinates used in protein folding, we show a novel way to study the kinetics of protein conformational transitions by carrying out a Brownian dynamics simulation on our two-dimensional free energy surface (FES) with two collective coordinates defined by the initial and final conformations.

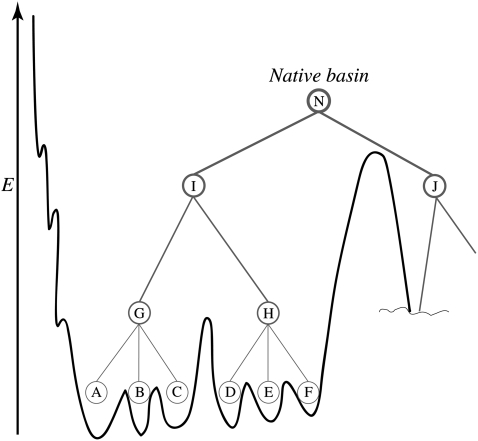
A successful statistical mechanical approach to understanding protein folding is based on the concept of there being a funneled effective energy landscape (7–13). The native state is thought to be a set of deep minima, in which the residual frustration between subtly different structural conformations leads to a rugged topography (7,8,11–13). Residual entropy plays a similar role in spin glasses (7,11–14). A protein at room temperature explores multiple conformations with different thermodynamically favorable contacts engendering this frustration (14,15). These native structural substates seem to be hierarchically organized into a tree with some ultrametric character that, in principle, can be mapped onto the funnel (Fig. 1). Kinetics of transitions between the substates is also hierarchical with timescales dictated by the details of the distribution of energy barriers (7,13,16–20).

FIGURE 1.

A sketch of a hierarchical organization of native substates at the bottom of the energy funnel is shown. Native state on this schematic picture consists of two substates I and J interchanging on some timescale. On shorter timescales and higher resolution in energy, each one of them also splits into substates. The substate I splits into G and H, which split further into yet another level of substates and corresponding microbasins.

By energy, we mean the energy of contacts. That, strictly speaking, is not an energy in the thermodynamic sense, because it includes the solvent coordinates in an implicit way. For example, hydrophobic interactions, though substantially entropic in origin, may be viewed as an energetic attraction between apolar residues. Even this effective energy of a protein conformation is still a function of hundreds or thousands of protein degrees of freedom (13). Often physical considerations permit phase space reduction through integration leaving only a few degrees of freedom that define then some very low-dimensional FES. Therefore, to avoid confusion (and also for historical reasons) the former representation of the landscape (funnel picture) is phrased in terms of energy, and the latter (low-dimensional FES)—in terms of free energy. The quantity and nature of the remaining coordinates determines the resolution of the FES. In particular, one may choose these so that the hierarchical organization of the substates and transitions will still be manifest. For instance, we may still see this hierarchy in nontrivial multiple timescale non-Arrhenius dynamics with an abundance of traps and barriers on the surface. Once the surface is constructed, studying the features of complicated protein dynamics consumes considerably less effort and permits a concentration on the kinetics of conformational switching. This technique can also be used to shed light on many interesting phenomena such as protein quakes (21).

In this work, we constructed a FES, in two dimensions, for the native state of Trp-cage, a 20-residue protein that folds in 4 μs (22,23). There are 38 nuclear magnetic resonance (NMR) structures recorded for this protein in PDB code (1L2Y) (24). Using the constructed surface, we studied the transition between two NMR conformations, numbered 1 and 37, the most dissimilar of all 38 structures.

Among the plethora of possible order parameters in polymer physics and protein folding in particular, only those with a sufficiently high structural resolution can serve our purposes. One way to achieve such a high resolution is to define a coordinate with respect to a particular conformation A. A widely used coordinate is the root-mean-square distance (RMSD) between the corresponding atoms (usually, of the backbone, C_α). Another possible order parameter has evolved from spin-glass energy landscape theories and is a generalization of what is called the “overlap parameter” (25). In case of polymer chains, the latter is a fraction of contacts that the two conformations have in common (26). This parameter is often called Q, and may be defined as

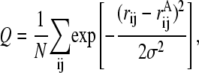(1)

where r_ij values are the distances between i^th and j^th atom in the conformation of interest, 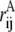is the same for the conformation A with respect to which the Q value is defined (usually, it is the native state), and normalization factor N is equal to number of pairs of atoms whose positions are defining the conformation (27). The similarity index Q changes from 1 (for the conformation A itself) to 0 (when there is no resemblance to A). Indeed, the Gaussian in Eq. 1 suppresses the contribution of a pair of atoms if the distance between these atoms (r_ij) is very different from that in conformation A (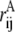). If one replaces the Gaussian with a rectangular peak and, in addition, only includes pairs of proximal atoms (r_ij ≲ 5 Å), Q will turn into a fraction of shared contacts (fraction of native contacts when A is the native state).

Though RMSD might seem more familiar and natural, in some cases Q is preferable. If one imagines, for example, two conformations having two α-helices, that are close in one of them and apart in the other one, then RMSD between them will be very large, suggesting no structural similarity, while Q will still show the similarities of individual helices. Another nice feature of Q is that σ in its definition allows one to control the resolution of the order parameter, and one may tweak the notion of conformational similarity according to the particular questions under consideration. Yet another approach would be to use the fraction of shared dihedral angles of the backbone. Like Q, this parameter has shown considerable correlation with the strata of the folding funnel (28) when defined with respect to the native structure. Along with the native structure RMSD and fraction of native contacts or hydrogen bonds, the radius of gyration has also been used as a coordinate, since it is also correlated with folding. However, this measure lacks resolution inside the native basin, which is the focus of our work, as further elaborated below.

Q is a good coordinate for protein folding because the funnel makes it possible to stipulate that motions in directions transverse to Q will usually be fast, and therefore the motion along Q (folding) is nearly adiabatic (29). A one-dimensional profile is then quite appropriate. However, if there were dynamical variables weakly correlated with Q but evolving on similar timescales, the information yielded by a one-dimensional profile would be of very limited usefulness. In particular, studying the dynamics of allosteric switching may require higher dimensional order parameter space, which allows the possibility to see multiple transition paths separately, rather than integrated into an averaged one. A number of studies constructing 2D FESs have been reported in the context of protein folding (19,30,31).

A natural choice of two dynamical variables having sufficient structural precision to provide a surface that allows the examination of the transition between two states 1 and 37 would be Q₁ and Q₃₇, that is, the similarities to states 1 and 37, respectively. Although Trp-cage is not an allosteric protein it nevertheless serves as a good test case for a general method that we develop here. In these coordinates the whole phase space is represented by a square {0 ≤ Q₁ ≤ 1; 0 ≤ Q₃₇ ≤ 1} (Fig. 2). The Q₁ = Q₃₇ diagonal of this square can be paralleled to a Q-axis in one-dimensional free energy profile of protein folding. With our technique, we pick two extremely close points on the one-dimensional free energy profile, near the folded state (Q = 1), that correspond to models 1 and 37, and pull them apart, unfurling the profile to a surface on a square and greatly increasing the resolution in the vicinity of reference states 1 and 37. On the (Q, R_g)-plot, these two points would nearly coalesce, but we zoom in to the region between and around them, leaving the unfolded state unresolved. All the unfolded structures are found close to the origin of the square.

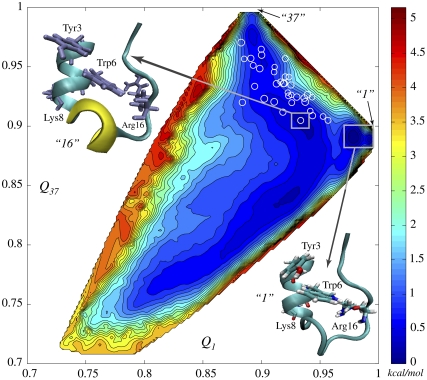
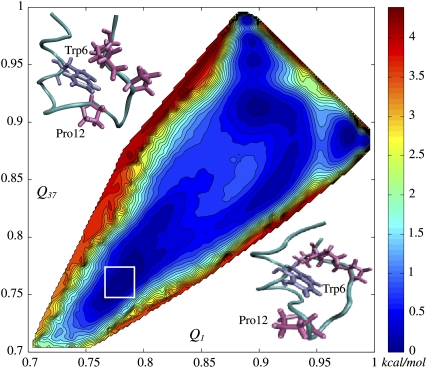
FIGURE 2.

Two-dimensional free energy surface (2D-FES) of Trp-cage native basin as a function of collective coordinates Q₁ and Q₃₇, indicating corresponding similarities to NMR models 1 and 37, was obtained using WHAM in 914 simulation windows (see Methods and Data S1). An all-atom MD simulation of 1.2 ns in duration was carried out in each window. Open circles, marking FES, represent the 38 NMR structures in the Q₁ and Q₃₇ coordinates. Spacing between contour lines is 0.22 kcal/mol (0.37 kT). White rectangles mark the deepest and the second deepest basins corresponding to model 1 (lower right corner) and model 16 (upper left corner), respectively. The difference of ∼0.6 kT in free energy is created by rotation of Tyr-3, cation-π interaction between Arg-16 and Trp-6 and disappearance of 3-10 α-helix.

We obtained the FES through extensive (>1 μs) all-atom explicit water simulations in CHARMM force field (32) using the two-dimensional weighted histogram analysis method (WHAM) (33). Subsequently, we ran damped Brownian dynamics starting from the basin of model 37, looking for the first passage time to the basin of model 1. Analysis of trajectories, first passage time (FPT) distributions, and temperature dependence of switching kinetics suggests a nearly free-diffusional flow, with shallow traps weakly modulating transition dynamics. Approximately half of the trajectories undergo partial unfolding down to Q ≈ 0.8 and visit a number of local traps. We explored a one-dimensional order parameter for describing the kinetics of this transition. Brownian dynamics on this one-dimensional free energy profile yields FPT distributions qualitatively similar to those obtained from the two-dimensional calculations.

We mapped the other 36 NMR structures onto the surface. This is an initial step in ranking them by free energies and organizing into an hierarchy. Having identified two deepest basins we compared structurally the corresponding conformations, highlighting stabilizing contacts and interactions. We also found that entropy and energy surfaces are much more rugged with steeper and higher rises and falls than that of free energy, which we attributed to fast solvent degrees of freedom. Lastly, we repeated the FES calculation with a simple dielectric solvent model (DSM), obtaining surprisingly similar results for the highly native part of the surface. Comparing the differences, however, showed the importance of water in stabilizing the folded state.

METHODS

The Q values among 38 NMR structures were calculated using Biochemical Algorithm Library (i.e., BALL) (34). All MD simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (i.e., LAMMPS) package (35) with the CHARMM27 protein-lipid force field (32). In DSM, the system with dielectric constant 80 was heated up to 282 K and equilibrated for 800 ps using targeted MD to maintain the NMR structures. In the explicit solvent model, the protein was solvated with 2275 TIP3P water molecules and the counterions, 5Na⁺ and 6Cl⁻, in a 50 × 50 × 50 ų water box. The SHAKE algorithm was used to restrain the hydrogen bonds. Minimization was performed in two steps. First we minimized energy of water with protein fixed for 10,000 steps with a conjugate gradient method. Then, using the NAMD suite (36), we minimized the energy of the whole system for an additional 10,000 steps. Using the charm2lammps Perl script, the initial input file was generated for LAMMP, and subsequently, a NVT simulation was carried out for 12 ps, followed by an NPT simulation for 60 ps with targeted MD. In the final production phase, 1.2-ns-long simulations were carried out for each of the 914 WHAM windows. In subsequent analysis, the first 200 ps were discarded. The trajectories were recorded every three picoseconds in each window.

The following two-dimensional umbrella potential was used: 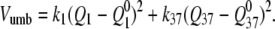The spring constants and simulation time in each window were chosen on the basis of good overlap between neighboring windows. In other words, for each window, the rate of going to the areas covered by neighboring windows multiplied by the simulation time for a window should be considerably greater than unity. It turned out that the spring constants satisfying this criterion were in the range of from 11.2 kcal/mol per Ų to 72.8 kcal/mol per Ų.

Brownian dynamics was carried out using Heun's method for the difference scheme (37). FES was interpolated in MATLAB (The MathWorks, Natick, MA). Gradients were calculated from four nearest points in two dimensions. Forty-thousand trajectories were used to obtain each FPT-distribution.

The equation of one-dimensional collective coordinate ξ is

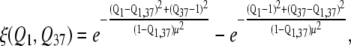(2)

where Q_1,37 is Q between structures 1 and 37 according to Eq. 1 and μ is a parameter that controls structural resolution. This function, shown in Supplementary Material, Fig. S9 in Data S1, corresponds to placing negative and positive Gaussian peaks on top of conformations 1 and 37 in the (Q₁, Q₃₇) square. Then, elevation of the resulting surface, ξ(Q₁, Q₃₇), serves as an order parameter (Fig. S9 in Data S1). The latter has an important feature (as opposed, for example, to ΔQ = Q₁ – Q₃₇ as an order parameter) that the endpoints of the ξ interval describe as compact regions near structures 1 and 37.

RESULTS AND DISCUSSION

Since the configurations of side chains play a key role inside a native basin (Fig. S7 in Data S1), we included side-chain carbons atoms (78 atoms total that include C_α, C_β, C_γ, C_δ, C_ε, and C_z) in the definition Eq. 1 of Q. Fig. 2 shows the computed two-dimensional free energy surface (FES) for the native state of Trp-cage peptide in terms of two similarity indices, Q₁ and Q₃₇. These two conformations (1 and 37) were chosen on the basis of being the most structurally dissimilar among the 38 NMR structures: they belong to different classes (structural basins) according to the hierarchical clustering (38) and have the smallest Q between them. Model 1 corresponds to (Q₁ = 1.0, Q₃₇ = 0.889) and model 37 corresponds to (Q₁ = 0.889, Q₃₇ = 1.0). All the different models of Trp-cage reside within the rectangle of 0.88 < Q₁ < 1.0 and 0.889 < Q₃₇ < 1.0. The deepest microbasin on the whole FES is that of model 1 followed by model 16 as the next deepest.

Stabilizing structural features

A representative structure from the microbasin of model 1 is shown in lower-right corner of Fig. 2 (this structure is almost identical to NMR model 1). Comparing this structure to model 16, which is the second lowest in free energy, reveals structural features that stabilize model 1:

1. The 3-10 helix is not present in model 1, which is quite consistent with previous result by Zhou (39).

2. Arg-16 is shifted toward Trp-6. This hints at the presence of a typical cation-π interaction between Arg and Trp, which are the likeliest amino acid residues to be involved in such an interaction (40). The disappearance of 3-10 helix (residues 11–14) may result from the side-chain movement of Arg-16, which is adjacent to the helix and likely contributes to its stability.

3. Tyr-3 is rotated in model 1, which is favorable for intramolecular interaction between Tyr-3 and Trp-6. Thus, the main factors that lower model 1's free energy are the energetic contribution from the interaction between Trp-6 and Arg-16, the intramolecular interaction due to a ring rotation of Tyr-3, and the increase of entropy due to the loss of the 3-10 helix structure. The backbone RMSD between model 1 and model 16 is ∼0.8 Å.

Transitions between microbasins

Protein dynamics have been thoroughly analyzed in many prior works (41–43), often using very diverse viewpoints on the nature of dynamical transitions. Some techniques, such as normal mode analysis, treat proteins as solids possessing vibrations and phonons (44–46). Another viewpoint is to imagine activated hopping between different conformations separated by energy barriers (17,47). This can be paralleled to the dynamics of a supercooled liquid. Yet another possibility is that the motion is similar to flow of a normal liquid such that the system spends most of the time in saddle points rather than in minima of the energy landscape. There have been indications that activated, or even glassy-dynamics, are more relevant to proteins, at least at low temperatures (7,9,15). In this work we investigate more deeply the nature of protein dynamics at room temperature. Knowing the dynamical regime is important when studying fluorescence intermittency (48) or allosteric regulation (1). For this purpose we considered the transition between two reference conformations, 1 and 37. If the dynamics are activated they should be dominated by a few or one pathway between the reference states. Another issue we address in this section is the determination of the ruggedness of the surface and the degree in which local traps influence transition dynamics. The influence of traps should be considerable in the activated regime and small in the diffusional flow regime.

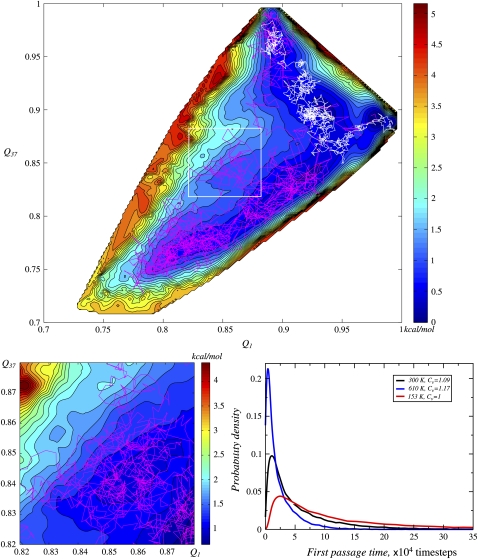
To describe conformational transitions, we ran multiple two-dimensional Brownian dynamics simulations on the computed FES (29), starting from the basin of model 1 (Q₁ = 0.97 and Q₃₇ = 0.895) (see Methods). Two trajectories are shown in Fig. 3 top. Distribution of first passage times (FPT) for transitions from model 1 basin to that of model 37 is given in Fig. 3 bottom right (black line). Our analysis of trajectories suggested a lack of dominant pathway. Indeed, even the trajectories picked from around maximum of the FPT distribution (a typical trajectory is shown in white in Fig. 3 top) linger in different basins, despite other similarities. The trajectories taken from the shoulder of the FPT distribution (an example is shown in magenta in Fig. 3 top) differ completely. It turned out that almost one-half of the trajectories fall into the shoulder of the FPT distribution (Fig. 3 bottom right). The observed multiplicity of transition pathways may be engendered either by trapping in different local traps (and the abundance of traps on the rugged surface causing the large width of the FPT distribution), or by the thermal noise if it is large enough to easily overcome the barriers (free diffusion). Fig. 3 bottom left shows a magnified part of the surface depicting a microbasin. Even though the trajectory might seem as freely moving, it noticeably lingers in this microbasin. We find that there is almost no trapping as such, although the influence of fine features of the surface is conspicuous. This observation, along with the temperature dependence of mean FPTs discussed below, directly suggests that protein conformational dynamics at room temperature shows a borderline behavior between nearly diffusive (as in a normal liquid) and weakly activated (as in a weakly supercooled liquid).

FIGURE 3.

Brownian dynamics of the transition between states corresponding to NMR structures numbered 1 and 37. (top) Two sample trajectories: one (white) is from the peak of FPT distribution in panel bottom right, and the other one (magenta) is from the shoulder. (bottom left) Part of the surface with trajectory shown in higher resolution revealing finer features of the surface and their influence on the trajectory. (bottom right) First passage time (FPT) distributions for conformational transition between 1 and 37. FPTs were computed at two additional temperatures to obtain the corresponding coefficients of variation, to provide reference for categorizing the nature of the dynamical regime at room temperature.

To further support this conclusion, we performed analogous calculations on the same surface, but at several different temperatures, comparing the corresponding FPT distributions. In reality, the FES itself would change with temperature, and therefore, these calculations do not yield direct information on the behavior of Trp-cage at those temperatures: their sole purpose is to provide reference points for identifying the character of the dynamical regime. Higher temperatures promote the role of freely diffusive motions, while lower temperatures promote trapping. The FPT-distributions computed at 153 K, 282 K, and 600 K are given in Fig. 3 bottom right. The FPT distribution variance grows, as temperature drops, but relative variance, or coefficient of variation, decreases. The latter is a measure of distribution width; when C_v < 1, the distribution is considered low-variance, and when C_v > 1, the distribution is considered high-variance. Thus, the number of effective pathways drops with decreasing temperature, and at low temperatures a dominant pathway emerges (C_v = 0.27 at 51 K). We observe at 282 K (C_v = 1.09) a crossover between the low-variance and high-variance regime.

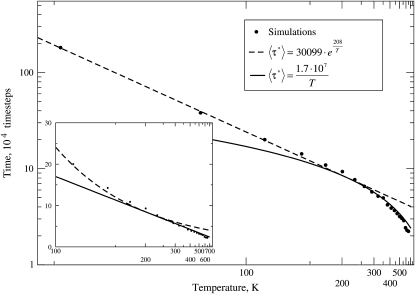
The Arrhenius plot for the mean FPT (〈τ*〉), which is shown in Fig. 4, provides an alternative way to analyze protein conformational dynamics. At low temperatures, we observe normal Arrhenius behavior with 〈τ*〉 ∼ exp(E_A/kT). At high temperatures, dependence becomes characteristic of the diffusive regime (for diffusion in confined space), with 〈τ*〉 ∼ D⁻¹ ∼ T⁻¹. Dashed and solid curves are the fits to these functions, respectively. Room temperature behavior is near the crossover between these two regimes, with activation energy of ∼0.7 kT, corresponding to weak local trapping.

FIGURE 4.

Arrhenius plot shows the dependence of the mean FPT with temperature for the conformational transition from 37 to 1 on fixed FES (computed at 282 K), where the FES is temperature-independent. The inset zooms into higher temperature region using a semireciprocal plot. Two regimes are clearly seen: exponential at low temperatures, and linear at high temperatures. The near room temperature (282 K) result is near the crossover.

This provides another view on the problem of single- and multiexponential behavior that has been discussed in the context of both regular (with a barrier) and downhill protein folding (49,50). If P(τ*) denotes a FPT-distribution, or probability density that the transition time is τ*, then 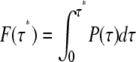is the distribution function, or the probability that the transition has occurred within time τ*. The survival curve, 1 – F(τ*), is then the probability that transition has not yet occurred after time τ*. Though this curve can be fitted by a single exponential, especially at long timescales (where such behavior might be expected, for example, for diffusion in a confined phase space), it turns out that much better fit is achieved by a double exponential (Fig. S8 in Data S1). This is reminiscent of the dynamical behaviors discussed in the context of barrierless, or downhill protein folding where the shorter timescale is called the “speed limit” (49,51).

Summarizing this section, the dynamics of switching between two conformations shows features of both flow (as in a normal liquid) and weakly activated dynamics (as in a weakly supercooled liquid). Also, the transition kinetics shows biexponential dynamical behavior.

One-dimensional reaction coordinate

Next, we investigate whether kinetics of conformational switching between 1 and 37 can be adequately described using a one-dimensional free energy profile, instead of the 2D FES described above. To address this question, we developed an order parameter which smoothly connects the transition endpoints, structures 1 and 37, by placing a positive Gaussian on top of basin 1 and a negative Gaussian on top of basin 37 (P. I. Zhuravlev, S. Wu, M. Rubinstein, and G. A. Papoian, unpublished). Then, elevation of the resulting surface, ξ(Q₁, Q₃₇), serves as an order parameter (Fig. S9 in Data S1). The latter has an important feature that the endpoints of the ξ interval describe compact regions near structures 1 and 37. We obtained the corresponding one-dimensional free energy profile by integrating

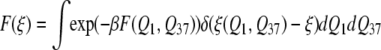and ran subsequent one-dimensional Brownian dynamics simulations. The resulting FPT-distribution was characterized with C_v = 0.91 because of increased contribution of the trap in the middle, which includes partially unfolded states. The change, however, is not very large and still is near the crossover between activated and diffusional flow regimes. Furthermore, using this new variable, one may directly calculate a one-dimensional free energy profile instead of computing 2D FES. This requires much less computational time and may be useful, especially when one is more interested in thermodynamical questions, such as finding the free energy difference between states 1 and 37. More details on free energy calculations using this collective coordinate will be published elsewhere (P. I. Zhuravlev, S. Wu, M. Rubinstein, and G. A. Papoian, unpublished).

Explicit solvent model and dielectric solvent model

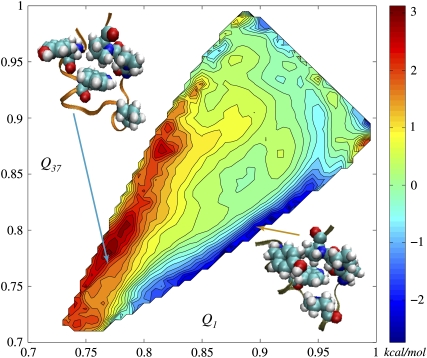
We repeated the 2D FES calculations for a system where explicit water molecules were removed, and, instead, ɛ = 80 was used for all electrostatic terms in the Hamiltonian. The FES from this simple dielectric solvent model (DSM) is given in Fig. 5. It is more symmetric along the diagonal than in case of explicit water. DSM surface has a basin in the region where both Qs are ∼0.75, while that of explicit solvent model does not; this suggests that water molecules prevent the tendency for partial unfolding. This point is also bolstered by the presence of barriers of ∼kT height scattered in the region of Qs between 0.8 and 0.9 on the explicit solvent surface and absent on the DSM surface. The presence of the basin in lower-left corner of DSM 2D FES is also a result of the lack of hydrophobic effect, which leads to opening of hydrophobic cores composed of Trp-6, Pro-12, Pro-17, Pro-18, and Pro-19 (53); the structures there (open box in Fig. 5) correspond to a loop structure L found in a work by Juraszek and Bolhuis (53) as one of the intermediates during Trp-cage folding. In the upper part, near the basins of 1 and 37, surface features are well preserved even though dielectric solvent model is extremely simplistic. The difference between the explicit solvent FES and the DSM FES given in Fig. 6 demonstrates this more clearly. As Qs decrease, more differences appear between explicit and DSM FESs, highlighting the role of the hydrophobic effect, which is completely absent in the DSM simulations. The 2D FES differences are asymmetric with respect to the diagonal line, indicating that the hydrophobic effect favors structures on one part of the surface. To explore this suggestion, we picked several structures from different sides of the diagonal line, (Q₁ = 0.90, Q₃₇ = 0.81) and (Q₁ = 0.77, Q₃₇ = 0.76), and calculated the solvent-accessible surface areas (SASAs) for each residue (see Data S1). The SASAs of the hydrophobic core for the first region turned out to be ∼10% smaller, which provides further support that the asymmetric shape of the FES is also hydrophobic in origin. It is an interesting question whether reasonable corrections for the differences between explicit and DSM FES could be provided by introducing a simple hydrophobic term into the DSM Hamiltonian. It will also be interesting to use a Generalized Born model to treat electrostatics instead of DSM. One might anticipate that a free energy surface calculated using a GBSA Hamiltonian (31) will be more similar to the explicit solvent result.

FIGURE 5.

FES was computed for the dielectric solvent model (see text). Two of the partially unfolded structures from the open square are shown in the corners. The lower basin is absent in the explicit solvent FES. On the other hand, a number of barriers have disappeared in the DSM FES. The vicinities of the reference points 1 and 37 are very similar between explicit and DSM FESs.

FIGURE 6.

The difference between explicit solvent FES and DSM FES. In the Qs ≲ 0.95 region, it mainly represents the hydrophobic effect. The structures in the corners are taken from the hydrophobically favorable and unfavorable regions. The hydrophobic core is shown in van der Waals spheres, so that its opening is visually noticeable.

Finally, we consider physical motivation for the treatment of the hydrophobic effect as an effective energetic term in implicit solvent models. The entropic and energetic landscapes in our explicit water simulations are both very rugged, which we attribute to the solvent degrees of freedom (Fig. S10 in Data S1). However, the protein chain itself is not influenced much by this solvent energy ruggedness, because of the timescale separation between fast motions of the solvent and slower motions of the chain. Instead, the protein chain moves mostly adiabatically in the averaged solvent field, where the resulting free energy ruggedness is ∼10 times smaller. Therefore, treating hydrophobic interactions as though they are energetic has reasonable physical grounds.

CONCLUSION

Two-dimensional FESs are a powerful tool in studying kinetics and thermodynamics of the native state ensemble. With proper choice of dynamical variables one may control the resolution in various regions of the phase space. For investigation of allosteric switching kinetics between two states, similarities to each of these states (generalized fraction of shared contacts) serve as useful collective order parameters. In this work we computed a two-dimensional free energy surface for Trp-cage. We mapped all 38 NMR structures onto the surface, ranking them in free energies and identifying most thermodynamically stable conformations. We pointed out the main interactions that enhance the stability of the deepest basins. Using the computed 2D FES, we studied the kinetics of transition between two Trp-cage native substates reported by a NMR study. We found that the native dynamics of Trp-cage is borderline between diffusional dynamics and weakly activated dynamics. At room temperature and higher, the corresponding survival curve is best fitted by a double exponential. Transition dynamics become clearly activated at lower temperatures, and diffusional at higher temperatures. We constructed a new one-dimensional collective coordinate to describe kinetics and thermodynamics of the native state, with promising results.

To explore the role of the solvent, we also computed 2D FES for the same system but with static dielectric medium instead of water. The explicit and DSM free energy surfaces were quite similar in the vicinity of reference conformations, where resolution of our technique is the highest. However, when protein conformations become somewhat less native, systematic differences between explicit and DSM models point to the role of the hydrophobic effect. Computing energy and entropy contributions separately showed the major role played by water and the necessity for calculation of the free energy as a whole, the latter being a result of cancellation of very large terms. Our method may facilitate rigorous construction of coarse-grained force fields based on free energies. It will be interesting to apply the technique introduced in this work to conformational transitions in larger proteins.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.