PREDICTED EFFECTS OF LOCAL CONFORMATIONAL COUPLING AND EXTERNAL RESTRAINTS ON THE TORSIONAL PROPERTIES OF SINGLE DNA MOLECULES

Abstract

A newly developed, coarse-grained treatment of the low-frequency normal modes of DNA has been adapted to study the torsional properties of fully extended, double-helical molecules. Each base pair is approximated in this scheme as a rigid body, and molecular structure is described in terms of the relative position and orientation of successive base pairs. The torsional modulus C is computed from the lowest-frequency normal twisting mode using expressions valid for a homogeneous, naturally straight elastic rod. Fluctuations of local dimeric structure, including the coupled variation of conformational parameters, are based on the observed arrangements of neighboring base pairs in high-resolution structures. Chain ends are restrained by an elastic energy term. The calculations show how the end-to-end constraints placed on a naturally straight DNA molecule, in combination with the natural conformational features of the double helix, can account for the substantially larger torsional moduli determined with state-of-the-art, single-molecule experiments compared to values extracted from solution measurements and/or incorporated into theories to account for the force-extension properties of single molecules. The computed normal-mode frequencies and torsional moduli increase substantially if base pairs are inclined with respect to the double-helical axis and the deformations of selected conformational variables follow known interdependent patterns. The changes are greatest if the fluctuations in dimeric twisting are coupled with parameters that directly alter the end-to-end displacement. Imposed restraints that mimic the end-to-end conditions of single-molecule experiments then impede the twisting of base pairs and increase the torsional modulus. The natural inclination of base pairs concomitantly softens the Young’s modulus, i.e., ease of duplex stretching. The analysis of naturally curved DNA points to a drop in the torsional modulus upon imposed extension of the double-helical molecule.

1. Introduction

The mechanical properties of DNA play a key role in its biological processing, determining how the long, thin double-helical molecule responds to the binding of proteins and functions in confined spaces within a cell. Tools developed over the past decade to manipulate single molecules have provided unprecedented opportunities to probe the mechanical properties of DNA. The responses of individual molecules to these probes are typically interpreted in terms of the elastic moduli of an ideal polymer that is naturally straight, subject to isotropic bending, and able to undergo independent bending, torsional, and stretching motions.

Although the bending properties of single DNA molecules are consistent with those reported in solution studies [2, 3, 11, 19, 40], values of the torsional modulus, i.e., the global twisting constant C, derived from single-molecule studies of DNA under tension [6] have only added fuel to the long-standing debate over the magnitude of C. The torsional modulus of a DNA monitored by so-called rotor-bead tracking measurements [6] (4.1±0.3 × 10^-19 erg-cm) substantially exceeds the values deduced from many solution experiments [1, 20, 21, 23, 34, 43]. The DNA in the single-molecule experiment is held at both ends, extended to its full contour length, and over- or undertwisted. The nicking of one of the strands allows a twisting motion that relieves the imposed tension. The motion of the rotating bead, which is attached to the unnicked strand in the vicinity of the cutting site, reflects both the imposed tension and the twisting properties of the DNA.

The torsional modulus extracted from the rotor-bead tracking experiment is roughly comparable to the values of C deduced from the distributions of topoisomers of short (237-254 bp), covalently closed DNA duplexes [39] and attributed in the literature to bending strain that restricts the twisting of small, circular molecules [20]. The stretching of a single DNA molecule to full extension may also impose constraints that affect the ease of twisting. On the other hand, the cyclic forms of even smaller, nucleosome-positioning fragments of DNA appear to be more easily twisted than generic, mixed-sequence DNA, with lower values of C in the simulated fit of an ideal polymer model to experimental data [10]. More realistic modeling of the DNA, however, shows that a number of well-known features of double-helical structure, notably the coupling of local conformational variables, can account for the apparent discrepancies in twist deformability in the small rings [12]. Such factors may also contribute to the torsional stiffness of DNA found with rotor-bead tracking experiments.

The ideal models conventionally used in the interpretation of DNA mechanical properties ignore the coupling between modes of deformation observed in high-resolution structures [17, 38]. For example, the protein-induced winding and unwinding of the double helix is generally accompanied by the shearing of base pairs and preferential bending into the minor or major groove. The conformational rearrangement of the familiar, 10-fold B-DNA double helix [46] to the compacted, 11-fold A-DNA structure [14] makes use of this mechanism, narrowing the major groove and opening a channel through the center of the duplex during the course of the structural transition [7, 27, 44].

Normal-mode analysis is a convenient modeling tool for relating the local chemical structure of a molecule to its collective global motions. The mechanical properties of polymeric DNA, including the torsional modulus, are easily computed from the normal-mode frequencies of linear chains of a few hundred base pairs [30]. The effects of known structural features on the dynamics of such molecules can be determined with a new, coarse-grained treatment of the normal modes [30, 31, 32, 33]. Each base pair is approximated in this scheme as a rigid body, and molecular structure is described in terms of the relative positions and orientations of successive pairs.

This article focuses on the subtle relationship between the natural coupling of local conformational variables and the torsional properties of DNA gleaned from the normal-mode analysis of representative, fully extended double-helical molecules. We first summarize the DNA model and computational approach. We then examine both naturally straight and naturally curved duplexes, considering the influence of local conformational features and imposed external restraints on the dominant, lowest-frequency twisting modes. We dissect the effects of individual twisting modes on the computed torsional modulus and present our findings in the context of the micromanipulation of single linear molecules. The computations illustrate a convenient way to bridge the gap between the macromolecular properties and the local conformational features of double-helical DNA.

2. Methods

Normal-mode analysis is a well-established computational method that has been applied to many protein and nucleic acid molecules [5, 9, 15, 18, 22, 24, 25, 29]. Thus, we omit a detailed description of the computational methodology and describe the new features that are used in the present work.

2.1. Independent variables

Usually the positions (x, y, z coordinates) of atoms or groups of atoms in a molecule are used as independent variables to describe the three-dimensional deformations associated with its normal modes. Because manipulations of M × M matrices (where M is the number of variables) are involved in the calculation, the size of the molecule that can be studied is limited by the available computational space. A popular alternative solution is to use the torsion angles of the molecule as independent variables, keeping the bond lengths and bond angles fixed [15, 24, 36]. This method, which is more complicated than normal-mode analysis in Cartesian space, appreciably extends the limitation on molecular size.

The approach used here allows us to treat even larger molecular systems by using a yet simpler representation of three-dimensional structure. We reduce double-helical DNA to the set of constituent base pairs, treating each base pair and the attached sugars and 5′-phosphates as a rigid body. We monitor the spatial configuration of the duplex in terms of the relative positions and orientations of adjacent residues, using six rigid-body variables θ_m(m = 1, . . . , 6) termed, respectively, Tilt, Roll, Twist, Shift, Slide, and Rise [13]. The first three parameters are angular variables and the last three are translational variables.

2.2. Energy function

The potential energy E consists of two parts, the internal DNA deformation energy E_I and the external (restraint) energy E_R,

$$E=E_I+E_R.$$ (1)

Internal energy

The internal energy is a sum of dimeric contributions ε_i,i+1 reflecting the spatial arrangements of consecutive (i, i + 1) base pairs,

$$E_I=\sum _{i=1}^{N-1}{\epsilon }_{i,i+1}.$$ (2)

Here N is the number of base pairs in the linear DNA molecule and ε_i,i+1 is described by an elastic expression of the form

$${\epsilon }_{i,i+1}=\frac{1}{2}\sum _{m=1}^6\sum _{n=1}^6{f}_{mn}({\theta }_m-{\theta }_m^o)({\theta }_n-{\theta }_n^o),$$ (3)

where θ_m is the instantaneous value and ${\theta }_m^o$ the equilibrium value, or rest state, of each base-pair step parameter. The force constants f_mn and the equilibrium rest state, described by the ${\theta }_m^o$, are given as input. In principle, one could use different force constants and equilibrium values at each base-pair step. For simplicity in the present analysis, we use a homopolymeric model of DNA with identical force constants and equilibrium values at every base-pair step.

At first we study intrinsically straight DNA, in which we consider two sets of equilibrium values of the base-pair step parameters: one set, listed in the legend to Table 3.1, corresponds to a generic, mixed-sequence DNA base-pair step and the other, written out in Table A.1, to an ideal, naturally straight B-DNA equilibrium rest state. The rest state of the generic dimer is derived from the mean values of the step parameters adopted by the 16 common base-pair steps in high-resolution crystal structures [38]. The ideal B-DNA model is based on the canonical fiber-diffraction structure [8].

Table 3.1. Effect of local conformational coupling on the lowest-frequency normal twisting mode of a 100 bp generic DNA homopolymer^*.

Coupled variables	${\nu }_1^0$† (cm-1)	${\nu }_1^{\mathrm{eq}}$† (cm-1)	ΔC§ (%)
	0.186	0.186
Tilt-Roll	0.186	0.186	0.0
Tilt-Twist	0.185	0.185	-0.5
Tilt-Shift	0.186	0.186	0.0
Tilt-Slide	0.186	0.186	0.0
Tilt-Rise	0.186	0.186	0.0
Roll-Twist	0.192	0.193	8.6
Roll-Shift	0.186	0.186	0.0
Roll-Slide	0.186	0.186	0.0
Roll-Rise	0.186	0.186	0.1
Twist-Shift	0.185	0.185	-0.6
Twist-Slide	0.185	0.186	0.0
Twist-Rise	0.182	0.193	8.2
Shift-Slide	0.186	0.186	0.0
Shift-Rise	0.186	0.186	0.0
Slide-Rise	0.186	0.186	0.0
Roll-Twist,Twist-Rise	0.188	0.210	28.3
Twist-Slide,Twist-Rise	0.181	0.199	14.7
Roll-Twist,Twist-Slide	0.194	0.198	13.6
Roll-Twist,Twist-Slide,Twist-Rise	0.184	0.214	33.1

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,2.8°,33.8°,0\mathrm{Å},-0.20\mathrm{Å},3.33\mathrm{Å})$.

^†Frequencies of DNA chains subject to the following global constraints: ${\nu }_1^0$, unrestrained chain ends; ${\nu }_1^{eq}$, ends restrained to equilibrium length.

^§Change in torsional modulus of the restrained duplex subject to given conformational coupling compared to that (C = 1.98 × 10^-19 erg-cm) of the unrestrained, generic molecule with independent fluctuations of base-pair step parameters.

We also study intrinsically curved DNA molecules, which are modeled by position-dependent values of the equilibrium step parameters ${\theta }_m^o$ [32]. Here the DNA is bent smoothly via the sinusoidal variation of Tilt and Roll $({\theta }_1^0,{\theta }_2^0)$ into a circle of n_B base pairs, with the bending angles at the mth base-pair step taking the following values, in degrees, if n_B is a multiple of 10:

$$\begin{array}{c}\hfill {\theta }_1^0\left(m\right)=(360∕n_B)\cos ((m-0.5)2\pi ∕10),\hfill \\ \hfill {\theta }_2^0\left(m\right)=(360∕n_B)\cos ((m-0.5)2\pi ∕10+\pi ∕2).\hfill \end{array}$$ (4)

The inverse dependence of the amplitudes of ${\theta }_1^0\left(m\right)$ and ${\theta }_2^0\left(m\right)$ on n_B in this expression means that the intrinsic curvature κ⁰ of the DNA is proportional to the amplitude of local conformational change, i.e., κ⁰ = (2π/3.4n_B). The remaining step parameters are assigned the same equilibrium values as B DNA, i.e., ${\theta }_3^0=36°$, $({\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0,0,3.4\mathrm{Å})$, so that the ideal, naturally straight duplex corresponds to the case when n_B is infinite.

The force-constant matrix F, the elements of which are the f_mn (see (3)), is the inverse of the covariance matrix D, with elements d_mn corresponding to the pairwise covariance 〈Δθ_mΔθ_n〉 of base-pair step parameters [15, 38], i.e.,

$$\begin{array}{c}\hfill \mathbf{F}=k_{B}T{\mathbf{D}}^{-1},\hfill \\ \hfill d_{mn}=\langle \Delta {\theta }_m\Delta {\theta }_n\rangle =\langle {\theta }_m{\theta }_n\rangle -\langle {\theta }_m\rangle \langle {\theta }_n\rangle .\hfill \end{array}$$ (5)

Here k_B is the Boltzmann constant, T the absolute temperature, 〈θ_m〉 the mean value of a given base-pair step parameter, and 〈θ_mθ_n〉 the mean product of parameters.

As a starting point, we consider a DNA that is subject to ideal elastic fluctuations, neglecting cross terms in the covariance matrix. We set the diagonal terms to the squares of the dispersion of generic base-pair step parameters in crystallographic data [38]: ${\langle \Delta {\theta }_1^2\rangle }^{1∕2}=3.1°$; ${\langle \Delta {\theta }_2^2\rangle }^{1∕2}=4.8°$; ${\langle \Delta {\theta }_3^2\rangle }^{1∕2}=4.7°$; ${\langle \Delta {\theta }_4^4\rangle }^{1∕2}=0.61\mathrm{Å}$; ${\langle \Delta {\theta }_5^4\rangle }^{1∕2}=0.62\mathrm{Å}$; ${\langle \Delta {\theta }_6^4\rangle }^{1∕2}=0.22\mathrm{Å}$. Inversion of this matrix is straight-forward, yielding a diagonal force-constant matrix F with nonzero elements $f_{mm}=k_{B}T∕\langle \Delta {\theta }_m^2\rangle$ and thereby describing a chain that (i) bends preferentially (via Roll) into the major and minor grooves, (ii) undergoes a somewhat broader range of bending than twisting, and (iii), if the base pairs are inclined with respect to the helical axis, tends to stretch or contract via the shearing of base-pair steps. For later use, we define a constant k₀ that is inversely proportional to the observed fluctuations in Rise:

$$k_0=k_{B}T∕\langle \Delta {\theta }_6^2\rangle .$$ (6)

To test the influence of the coupling of local conformational variables on the torsional modulus, we examine the effect, on the normal modes, of nonzero terms in the force-constant matrix. We estimate the magnitude of the covariance 〈Δθ_mΔθ_n〉 of an arbitrary pair of step parameters from the observed dispersion, i.e., $\mid \langle \Delta {\theta }_m\Delta {\theta }_n\rangle \mid \approx (1∕2){\left(\langle \Delta {\theta }_m^2\rangle \langle \Delta {\theta }_n^2\rangle \right)}^{1∕2}$, and base the sign of the correlation on the trends in known DNA structures [38]. At first, we consider only a pair of off-diagonal elements, i.e., 〈Δθ_mΔθ_n〉 = 〈Δθ_nΔθ_m〉 ≠ 0, but later allow two or three pairs of off-diagonal elements in the internal energy function.

Restraint energy

For the external (restraint) energy, we assume a very simple form,

$$E_R=\frac{k}{2(N-1)}{(r-r^0)}^2,$$ (7)

where k is a spring constant, N the number of base pairs in the DNA, r the instantaneous end-to-end distance, and r⁰ the desired end-to-end distance. We equate the end-to-end distance to the magnitude of the vector connecting the origins of the base pairs at either end of the molecule, placing the origins and coordinate frames on the base pairs according to standard guidelines [37]. In the case of naturally straight DNA, we first set r⁰ to the end-to-end distance of the molecule in its equilibrium rest state. Thus, the restraint does not impose any extension or compression on the naturally straight double helix. Later, we set r⁰ to values larger than the end-to-end distance of the equilibrium rest state in order to study the effects of stretching and/or to straighten naturally curved DNA.

2.3. Torsional modulus

The torsional modulus C is calculated by substituting the computed normal-mode frequencies in the classical expression for the twisting normal modes of an ideal elastic rod [42], C = (2Lν_n)²I_M/n²; i.e., C is proportional to the square of the normal-mode twisting frequency. Here ν_n is the computed normal-mode frequency of the nth twisting mode, L is the contour length of DNA, and I_M is the moment of inertia per unit length around the twisting axis. The latter axis is assumed to coincide with the helical axis, a straight line determined such that the radial displacement of the backbone atoms (here the P atoms) from the line are similar to one another; i.e., the atoms lie near the surface of a cylinder, the axis of which is the helical axis. The moment of inertia per unit length is given by $I_M=\Sigma m_a{r}_a^2∕L$, where m_a and r_a are, respectively, the mass and the radial displacement of the ath atom and the summation is taken over all atoms in the DNA. The helical axis of an ideal, naturally straight DNA determined in this way runs through the origins of the base-pair planes, validating the approach. See the literature [29] for details.

3. Results

3.1. Effects of end-to-end restraint on large-scale twisting motions

We start with a 100 bp DNA homopolymer with the generic equilibrium structure (defined in section 2) at every base-pair step. We first study an ideal duplex with independent fluctuations of local conformational variables. We obtain the force-constant matrix by inverting a covariance matrix without any cross terms. We subsequently examine a series of molecules subject to local conformational coupling by introducing a pair of nonzero cross terms, one at a time, in the covariance matrix and determining the force-constant matrix. The force-constant matrix is used in the normal-mode calculation, and the frequency ${\nu }_1^{\mathrm{eq}}$ of the dominant global twisting mode, which is listed in Table 3.1, is obtained. Here and in all cases below the temperature is set at 298 K.

The spring constant of the restraint energy k in (7) is set equal to k₀, defined by (6). That is, the restraint energy is comparable to the interaction associated with the fluctuations of Rise, i.e., the van der Waals’ separation of base-pair planes, at a single dimer step. We later study the effect of the magnitude of the spring constant k on the observed frequency of the twisting mode.

As a reference, the normal-mode twisting frequencies ${\nu }_1^0$, which are obtained from calculations without restraint on the end-to-end distance, are listed in the second column of Table 3.1. The increase of the torsional modulus ΔC that results from the end-to-end restraint and selected internal energy function is reported in the last column of the table. Only the lowest-frequency twisting modes are reported in Table 3.1, as well as in Table 3.2. The twisting constants are calculated from these frequencies. This practice assumes that the twisting motion of DNA in the single-molecule experiment, which is modeled by the present calculation, is similar to the lowest-frequency twisting mode. In principle, the torsional modulus might differ from the values in Tables 3.1-3.2 if higher-frequency twisting modes were included in the calculations. We explore this issue after focusing attention on the lowest-frequency twisting modes (see below).

Table 3.2. Effect of local conformational coupling on the lowest-frequency normal twisting mode of a 100 bp slightly perturbed, ideal DNA homopolymer^*.

Coupled variables	${\nu }_1^0$† (cm-1)	${\nu }_1^{\mathrm{eq}}$† (cm-1)	ΔC§ (%)
	0.186	0.186
Tilt-Roll	0.186	0.186	0.0
Tilt-Twist	0.186	0.186	-0.5
Tilt-Shift	0.186	0.186	0.0
Tilt-Slide	0.186	0.186	0.0
Tilt-Rise	0.186	0.186	0.0
Roll-Twist	0.199	0.200	15.5
Roll-Shift	0.186	0.186	0.0
Roll-Slide	0.186	0.186	0.0
Roll-Rise	0.186	0.186	0.1
Twist-Shift	0.186	0.186	0.3
Twist-Slide	0.185	0.187	0.8
Twist-Rise	0.182	0.193	7.9
Shift-Slide	0.186	0.186	0.0
Shift-Rise	0.186	0.186	0.0
Slide-Rise	0.186	0.186	0.0
Roll-Twist,Twist-Rise	0.194	0.217	35.5
Twist-Slide,Twist-Rise	0.181	0.202	17.8
Roll-Twist,Twist-Slide	0.200	0.206	22.4
Roll-Twist,Twist-Slide,Twist-Rise	0.187	0.225	46.5

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,5°,36°,0\mathrm{Å},0\mathrm{Å},3.4\mathrm{Å})$.

^†Frequencies of DNA chains subject to the same global constraints as in Table 3.1.

^§Change in torsional modulus of the restrained duplex subject to given conformational coupling compared to that (C = 2.03 × 10^-19 erg-cm) of the unrestrained molecule with independent fluctuations of base-pair step parameters. See legend to Table 3.1.

According to the data in Table 3.1, the largest change in twisting frequency due to the end-to-end restraint occurs when the Roll-Twist or Twist-Rise conformational correlation, found in known structures of DNA [38], is included in the potential energy function, i.e., f₂₃ > 0 or f₃₆ < 0, with Twist increasing with the decrease of Roll or the increase of Rise and vice versa. We also report normal-mode calculations that consider two or three pairwise coupling terms. The frequency increases even more when two or three parameters are coupled than when only one pairwise interaction is considered. The frequency change and increase in torsional modulus are especially large if Twist-Rise coupling is included in combination with Roll-Twist and/or Twist-Slide interactions in the internal energy.

Interestingly, if no restraint is imposed on the DNA (second column in Table 3.1), the twisting frequency of the DNA with Twist-Rise coupling is smaller than that of the DNA without any coupling, in contrast to the results for the DNA with end restraints (third column in Table 3.1). The twisting frequency of the unrestrained duplex with Roll-Twist coupling, however, is higher than that obtained without coupling.

3.2. Influence of base-pair inclination

The same series of normal-mode calculations was carried out for an ideal, naturally straight B-DNA duplex with base pairs aligned perpendicular to the helical axis in the equilibrium rest state (data reported in Table A.1 in the appendix). Only when Twist-Rise (f₃₆ < 0) interactions are considered is there any frequency change due to the end-to-end restraint. The addition of other local coupling terms has very little effect on the global twisting motions.

Comparison of the twisting modes of generic vs. ideal DNA suggests that the small inclination of base pairs, stemming from the slight intrinsic roll of neighboring base-pair planes in the generic homopolymer, i.e., ${\theta }_2^0=2.8°$, has a large effect on the observed frequency changes and the associated torsional constants found when the chain ends are restrained. To check this idea, we carried out further calculations on a slightly modified B-DNA polymer with ${\theta }_2^0=5°$ and all other step parameters set to standard ideal values. As seen from Table 3.2, the inclination of base pairs that accompanies the change in dimer-step geometry increases the twisting frequency and associated torsional modulus if Roll-Twist (f₂₃ > 0) or Twist-Rise (f₃₆ < 0) coupling is considered in combination with one or two other local couplings in the internal energy.

The effect of Roll-Twist coupling on C is unique to DNA with inclined base pairs. That is, the torsional modulus also increases in an ideal DNA model that is subject to end-to-end restraints and Twist-Rise coupling. Unlike the ideal DNA, where the global helical axis passes through the base-pair origins and coincides with normals of the base-pair planes, none of the local coordinate axes run parallel to the global axis if the base pairs are inclined by slight intrinsic Roll. Because of this unique orientation, only fluctuations in local Twist contribute to the global twisting motions of ideal DNA (if no coupling is considered); i.e., bending fluctuations via Tilt and Roll simply change the displacement of atoms with respect to the global helical axis. By contrast, the fluctuations of all three angular variables—Tilt, Roll, and Twist—have components that add to the twisting motions around the global axis of a DNA with inclined base pairs. Moreover, if the base pairs are inclined via positive Roll $({\theta }_2^0>0)$, the bending components associated with Roll add constructively to those from Twist, enhancing the global motions. The introduction of the negative Roll-Twist coupling, found in high-resolution DNA structures, cancels this effect and reduces the torsional motions of the DNA as a whole. The torsional modulus increases accordingly. If the base pairs are inclined via negative Roll $({\theta }_2^0<0)$ or subjected to positive Roll-Twist coupling, both of which are counter to experimental findings, the twisting constant decreases (data not shown).

3.3. Variation of imposed end-to-end restraint

The computed variation in C of naturally straight DNA, shown in Figure 1, is highly dependent on the choice of the relative spring constant (k/k₀) in the restraint energy. The variation of k mimics the effect of imposed external force on the torsional modulus. Here the equilibrium values of the base-pair step parameters are set to the generic crystallographic values, and three coupling interactions (f₂₃, f₃₅, f₃₆)—Roll-Twist, Twist-Slide, and Twist-Rise—are considered in the internal energy function. The torsional modulus, which is about 1.9 × 10^-19 erg-cm when there is no restraint on the ends of the homopolymer, increases with increase in k/k₀. The increase in C is sharpest in the range of values where the spring constant is near k₀ and levels off at higher imposed forces to a limiting value of 3.4 × 10^-19 erg-cm.

Fig. 1.

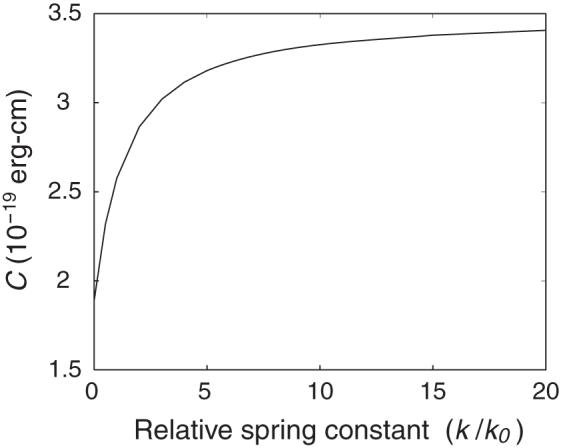
Dependence of the torsional modulus of a generic, naturally straight DNA homopolymer on the relative spring constant k/k₀ used to restrain the chain ends at the equilibrium end-to-end distance. Here k₀ is the force constant, defined by (6), which keeps neighboring base pairs at their van der Waals’ separation distance $({\theta }_6^0=3.4\mathrm{Å})$. Three coupling interactions (f₂₃, f₂₅, f₃₆)—Roll-Twist, Twist-Slide, and Twist-Rise—are incorporated into the internal energy function.

3.4. Effects of higher-order twisting modes on global properties

To this point, we have considered only the lowest-frequency twisting mode, i.e., ν₁, in the estimation of C. As mentioned above, the torsional modulus may also reflect higher-frequency twisting modes. We therefore now turn to the changes of higher-frequency twisting modes that arise from end-to-end distance restraints on the generic homopolymer. These frequencies are obtained in the same calculation used to generate the data in Table 3.1.

Comparison of the frequencies with and without restraint on chain ends shows that restraint has no effect on the frequencies of the second lowest twisting mode, i.e., ν₂ (Table A.2 in the appendix). The different response reflects the fluctuations of base-pair step parameters responsible for the global motion as outlined below.

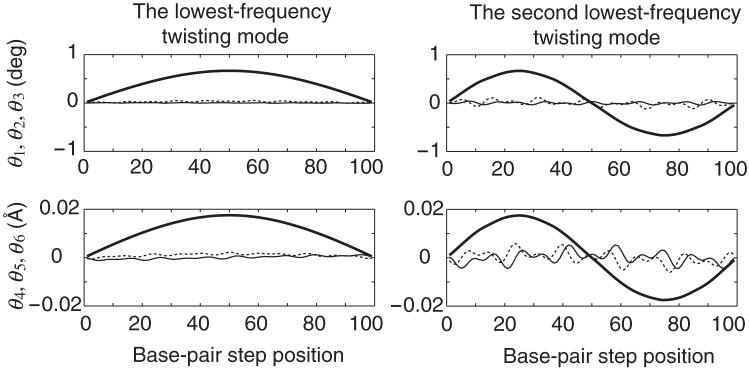
Figure 2 depicts the sequential fluctuations of base-pair step parameters in the lowest-frequency and the second lowest-frequency twisting modes at the moment when the potential energy of the generic DNA homopolymer is raised by k_BT/2; the fluctuations of all parameters are reversed a half cycle later of the mode. Angular parameters (θ₁, θ₂, θ₃)—Tilt (thin solid line), Roll (dashed line), Twist (thick solid line)—are shown in the top half of the figure and translational parameters (θ₄, θ₅, θ₆)—Shift (thin solid line), Slide (dashed line), Rise (thick solid line)—in the lower half. The step parameters associated with the lowest-frequency twisting mode are plotted on the left and those of the second lowest-frequency mode on the right. In both cases Twist-Rise coupling is considered in the internal energy function, i.e., f₃₆ < 0, but no end-to-end restraint is imposed.

Fig. 2.

Sequential fluctuations of base-pair step parameters in the lowest-frequency (left) and second lowest-frequency (right) twisting modes of the unrestrained generic homopolymer at the moment when the potential energy is raised by k_BT/2; the fluctuations of all parameters are reversed a half cycle later of the mode. Angular parameters (θ₁, θ₂, θ₃)—Tilt (thin solid line), Roll (dashed line), Twist (thick solid line)—are shown in the upper figures and translational parameters (θ₄, θ₅, θ₆)—Shift (thin solid line), Slide (dashed line), Rise (thick solid line)—in the lower figures. Base-pair step parameters are set at the equilibrium values listed in Table 3.1. The internal energy function includes a Twist-Rise coupling term, i.e., f₃₆ < 0.

The fluctuations of local dimeric Twist Δθ₃, which underlie the global twisting modes, and the fluctuations of Rise Δθ₆, which are correlated with the changes of Twist, dominate the polymeric motions. The asymmetry/symmetry of these data (Figure 2) shows that the end-to-end distance changes more in the lowest-frequency twisting mode than in the second-lowest mode. The fluctuations in Rise, which are the major determinant of polymer end-to-end extension, are additive in the lowest-frequency twisting mode but cancel one another in the second lowest-frequency twisting mode. Indeed, the increase of the end-to-end distance due to the fluctuations of all step parameters in Figure 2 is 1.13 Å for the lowest-frequency twisting mode but only 0.01 Å for the second-lowest mode. Thus, the effect of the end-to-end distance restraint is very small in the second-lowest mode, accounting for the aforementioned insensitivity of the torsional modulus to that mode. Similar reasoning accounts for cases when other local conformational correlations, such as Roll-Twist coupling, are included in the internal energy.

As expected from the trends in Figure 2, the fluctuations in Rise that accompany the third lowest-frequency twisting mode show two points of inflection along the chain contour and thus do not completely cancel one another. The introduction of an end-to-end distance restraint accordingly changes the frequency of this and other higher-order “odd” twisting modes. The changes in frequency, however, are much smaller than those in the lowest-frequency twisting mode and thus are not considered further.

3.5. Effects of stretching

In this section we introduce constraints that stretch DNA and study the effect of imposed extension on the normal-mode twisting frequencies of an intrinsically straight duplex. We consider the same two sets of equilibrium rest states as above, i.e., a generic, mixed-sequence DNA base-pair step and an ideal B-DNA step. The desired end-to-end distance r⁰ in (7) is set to a value 10% longer than the end-to-end distance in the restraint-free (equilibrium) state, and the spring constant k is set to k₀ (see (6)). Only the results for generic DNA are presented in Table 3.3. Corresponding data for the ideal homopolymer are collected in Table A.3 in the appendix.

Table 3.3. Effect of stretching on the lowest-frequency normal twisting mode and elastic modulus of a 100 bp generic DNA homopolymer^*.

Coupled variables	r (Å)	(r - req)/req (%)	Y/Y0†	${\nu }_1^{\mathrm{str}}$ (cm-1)	C (10-19 erg-cm)
	344.0	5.2	0.89	0.187	2.09
Tilt-Roll	343.9	5.2	0.89	0.187	2.09
Tilt-Twist	344.0	5.2	0.89	0.188	2.12
Tilt-Shift	344.0	5.2	0.89	0.187	2.09
Tilt-Slide	344.0	5.2	0.89	0.187	2.09
Tilt-Rise	343.8	5.2	0.91	0.187	2.09
Roll-Twist	344.0	5.2	0.89	0.197	2.32
Roll-Shift	344.0	5.2	0.89	0.187	2.09
Roll-Slide	344.1	5.3	0.88	0.187	2.09
Roll-Rise	345.0	5.5	0.78	0.188	2.10
Twist-Shift	344.0	5.2	0.89	0.186	2.07
Twist-Slide	344.0	5.2	0.89	0.184	2.04
Twist-Rise	344.0	5.2	0.88	0.195	2.28
Shift-Slide	343.9	5.2	0.90	0.187	2.09
Shift-Rise	344.4	5.4	0.84	0.186	2.09
Slide-Rise	343.2	5.0	0.98	0.185	2.08
Roll-Twist,Twist-Rise	344.0	5.2	0.89	0.211	2.67
Twist-Slide,Twist-Rise	344.0	5.2	0.89	0.197	2.32
Roll-Twist,Twist-Slide	344.0	5.2	0.89	0.212	2.69
Roll-Twist,Twist-Slide,Twist-Rise	344.0	5.2	0.88	0.224	3.01

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,2.8°,33.8°,0\mathrm{Å},-0.2\mathrm{Å},3.33\mathrm{Å})$.

^†Young’s modulus, Y, of the restrained duplex with designated conformational properties compared to that, Y₀, of the free, ideal DNA duplex without coupling.

The end-to-end distances r of the energy-minimized, stretched molecules are listed in Table 3.3, along with the increase, (r - r^eq)/r^eq, in end-to-end extension of these states compared to the free, equilibrium rest structure, for the same set of energy functions considered in Table 3.1. The generic duplex is slightly longer than ideal DNA upon optimization, with respective (r - r^eq)/r^eq values of ∼ 5.2% vs. ∼ 5%. This change in end-to-end extension, although quite small, translates into a fairly large difference in the overall stretching constant, or Young’s modulus Y, of the DNA. The relative changes in Y, calculated from the increased ratios of end-to-end distances associated with the different internal energetic treatments of the generic chain, are also listed in Table 3.3. The data, expressed as the ratio Y/Y₀ of the Young’s modulus of a given duplex compared to that of the unrestrained, ideal molecule free of energetic coupling, shows that the Young’s modulus of generic DNA is about 10% smaller than that of the reference duplex but as much as 20% smaller when local bending via Roll is coupled with Rise, i.e., f₂₆ > 0. This finding is consistent with the elastic constants extracted previously from the normal modes of linear DNA molecules [30]; i.e., the stretching constant is lower for a DNA with base-pair planes inclined with respect to the helical axis than for a duplex with bases perpendicular to the helical axis. By contrast, the coupling of local parameters has essentially no effect on the Young’s modulus of the ideal duplex upon extension (see values of Y/Y₀ in Table A.3.)

Comparison of the lowest twisting frequencies ${\nu }_1^{\mathrm{str}}$ of the overstretched molecules, listed in the fifth column of Table 3.3, with the twisting frequencies ${\nu }_1^{\mathrm{eq}}$ reported with r⁰ set to the end-to-end distance of the rest state reveals further differences in ideal vs. generic DNA. In the case of ideal DNA, the frequency changes are close to zero for many of the energetic treatments (Tables A.1 vs. A.3 in the appendix), but for generic DNA, the frequency changes are nonzero in all cases (Tables 3.1 vs. 3.3). The different responses of the two models to imposed stretching reflect the local conformational variables that contribute to chain extension. Ideal DNA is stretched exclusively through the increase of Rise, i.e., increased van der Waals’ separation of base-pair planes, whereas the extension of generic DNA involves changes of other step parameters, e.g., Roll, which control the inclination of the base pairs with respect to the helical axis and thereby allow for polymeric extension via the lateral shearing of base-pair planes, i.e., global extension via conformationally preferred routes involving Slide and/or Shift. The global twisting motions of ideal DNA are accordingly less sensitive to stretching than those of the generic duplex.

The change in the lowest-frequency twisting mode of an overextended duplex, compared to that of a duplex with r⁰ set to the equilibrium end-to-end distance, is small when only one conformational correlation is introduced in the internal energy (see corresponding entries in Tables 3.1 and 3.3). Even the largest change in frequency, which is observed when Roll-Twist (f₂₃ > 0) coupling is considered, is no more than 2% for either generic or ideal DNA. The changes are greater if two or three conformational correlations are considered, e.g., ∼ 7% when both Roll-Twist and Twist-Slide coupling are included. The frequencies of the overstretched duplex, however, are quite large compared to those $\left({\nu }_1^0\right)$ of restraint-free DNA, particularly when all three common conformational correlations (f₂₃, f₃₅, f₃₆)—Roll-Twist, Twist-Slide, and Twist-Rise—are considered. The computed increase in C for the DNA with such features is roughly 1.5 times that of the unrestrained generic molecule free of conformational coupling.

Interestingly, some types of conformational coupling decrease the twisting frequency when the DNA is stretched. For example, the twisting frequency of both generic and ideal DNA duplexes subject to Twist-Slide (f₂₅ < 0) correlations is ∼ 1% lower when it is stretched than when the ends are held at the end-to-end extension of the equilibrium state (third column of Table 3.1/A.1 vs. fifth column Table 3.3/A.3).

3.6. Effects of intrinsic curvature

We now turn to the twisting properties of intrinsically curved DNA molecules, which form a minicircle, or O-ring, containing n_B base pairs in the equilibrium rest state (see (4)). In order to compare the torsional features of curved DNA with those of naturally straight DNA, we extend the curved duplex by putting a distance restraint on both ends of the molecule and subsequently stretching the duplex.

Normal-mode analyses were carried out on a series of 100 bp molecules with different degrees of intrinsic curvature and end-to-end distances determined by the assumed value of n_B in the equilibrium rest state. At first, we present the results for naturally curved DNA molecules subject to typical, B-like elastic deformations, i.e., the ranges of dispersion listed in section 2. We later examine curved DNA molecules that are subject to conformational coupling with selected elements of the force-constant matrix assigned nonzero values.

Figure 3 illustrates the uptake of bending along the contour of an extended, naturally curved duplex. The 100 bp fragment under consideration, with n_B = 200, would form a semicircle in the absence of the external restraint force. Here the DNA is extended slightly beyond its equilibrium contour length L such that the extension ratio Q = r/L is 1.05. Interestingly, the forced extension of the duplex does not fully suppress dimeric bending. The angular parameters Tilt and Roll (θ₁, θ₂) exhibit sinusoidal patterns in the central part of the optimized molecular structure, with maxima or minima occurring at 10 bp intervals in both θ₁ and θ₂. The pattern is reminiscent of the variation of step parameters in the equilibrium rest state, expressed by (4) and also plotted in Figure 3 (for the same value of n_B). The amplitudes of the two bending components of the stretched duplex are roughly comparable to one another but only a fraction of that of the naturally curved rest state. The degree of bending in the central part of the stretched molecule is proportional to the degree of local bending anisotropy; i.e., Tilt and Roll are uniformly zero if the base-pair steps are subject to isotropic bending (f₁₁ = f₂₂) and exhibit sinusoidal-like variations of increasing amplitude with increase in f₁₁/f₂₂. The relative phasing of angular variables also differs in the extended form compared to the rest state. The maxima in θ₂ precede the maxima in θ₁ by 2-3 bp in the rest state but lag 2-3 bp behind those in θ₁ in the extended duplex. This 4-6 bp difference in phase has a dramatic effect on the global structure. Whereas the changes in Tilt and Roll cooperatively contribute to the intrinsic bending of the rest state, the local bending from the two angles is compensatory in the stretched duplex. In other words, the variation of θ₁ bends the stretched DNA in one direction, and that of θ₂ in the opposite direction, leading to a straightened, “zigzag” global structure.

Fig. 3.

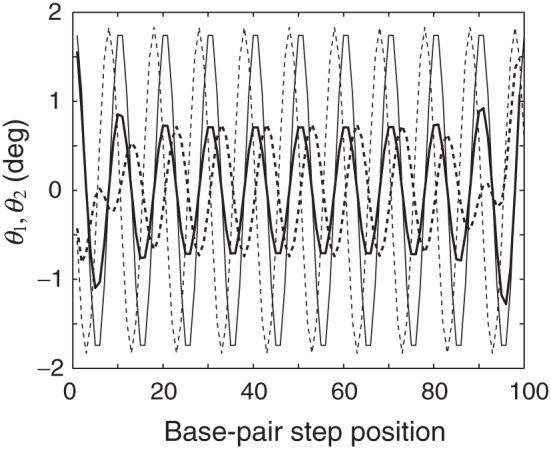
Sequential variations of dimeric bending angles Tilt and Roll (θ₁, θ₂) along the contour of a 100 bp intrinsically curved DNA that is fully extended (thick solid and dashed lines, respectively) and in the equilibrium rest state (thin solid and dashed lines, respectively). The DNA would form a semicircle in the absence of fluctuations and external restraints. The model is subject to ideal elastic deformations without coupling of local step parameters.

The analysis of other curved molecules shows that the variation of (θ₁, θ₂) over the central part of the extended duplex is independent of the value of Q over the range of extension considered here (1 ≤ Q ≤ 1.05). The amplitude of dimeric bending in the center of the duplex is roughly proportional to the assumed degree of curvature, i.e., n_B^-1. That is, the values of (θ₁, θ₂) are constant in the intrinsically straight DNA, when stretched, and vary with increasing amplitude as the degree of curvature is increased, i.e., decrease in n_B.

Figure 4 reports the global bending, as a function of the degree of stretching Q, of a series of 100 bp, naturally curved DNA molecules. Here, as above, the double helix is subject to B-DNA-like elastic deformations with no coupling of step parameters. The bend angle Γ is defined, over the central part of each extended duplex, by the vectors connecting the origins of base pairs 10, 50, and 91. This definition excludes the extremes in Tilt and Roll that occur at the ends of the stretched duplex (Figure 3) and, as explained below, is closely related to the global twisting frequency. As expected, the value of Γ is lower in chains of lesser curvature and decreases as the DNA is stretched.

Fig. 4.

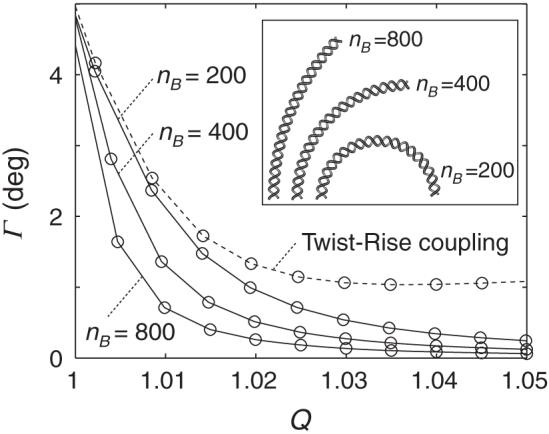
Global bend angle Γ plotted against the extension ratio Q for a series of 100 bp naturally curved DNA molecules. The bending angles for chains subject to ideal elastic deformations are denoted by open circles connected by solid lines, and those for DNA with Twist-Rise (f₃₆ < 0) correlations by open circles connected by a dashed line. Intrinsic curvature is labeled in terms of the number of base pairs n_B required to form a closed circular structure. Relative curvature of the DNA is illustrated by the molecular images in the inset. The model with Twist-Rise coupling would form a semicircle in the absence of fluctuations and external restraints, i.e., n_B = 200.

Figure 5 presents the lowest twisting frequencies ${\nu }_1^{\mathrm{str}}$ found upon stretching the above series of curved molecules. We identify the twisting modes by visualizing each normal mode and observing the global motion. The variation of frequency with Q is irregular for all chains at small degrees of extension but approaches a limiting value as Q becomes larger. The twisting frequency is lower, at the same degree of extension, for more highly curved molecules if the DNA is stretched to the extent that the global bend angle is close to zero.

Fig. 5.

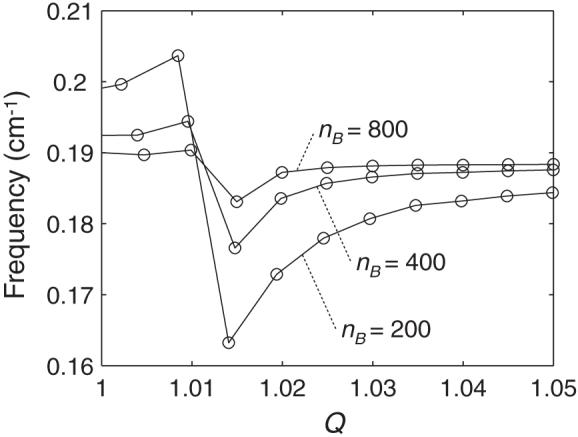
Twisting frequencies plotted against the extension ratio Q for the ideal, naturally curved DNA molecules described in Fig. 4.

The results in Figures 4-5 suggest a correlation between the twisting frequencies and the global bending of DNA. That is, ${\nu }_1^{\mathrm{str}}$ approaches a characteristic limiting value as Γ approaches zero. We rationalize this behavior as follows. At low levels of extension when the DNA as a whole is appreciably bent, global bending motions mix with the overall torsional motions, giving rise to the irregular pattern of twisting frequencies. As the DNA is stretched and the bend angle becomes smaller, the contribution of the bending motions becomes smaller and the twisting modes become “pure.” Because the twisting frequencies are not appreciably affected by stretching (Tables 3.1 vs. 3.3), ${\nu }_1^{\mathrm{str}}$ approaches a constant value as the DNA is stretched.

3.7. Coupling effects in curved DNA

Table 3.4 compares the effects of conformational coupling on the twisting frequencies ${\nu }_1^{\mathrm{str}}$ of an overstretched DNA molecule with intrinsic curvature vs. those of an ideal, naturally straight duplex of the same chain length under identical conditions. Here the curvature of the former molecule is chosen such that the 100 bp fragment forms a semicircle in its rest state, i.e., n_B = 200, and the extension ratio Q is set to a value in the range where the twisting frequency of the naturally curved duplex is fairly pure and close to its limiting value, i.e., Q = 1.05.

Table 3.4. Effect of intrinsic curvature on the twisting properties and global bending of a stretched, 100 bp ideal DNA homopolymer^*.

Coupled variables	${\nu }_1^{\mathrm{str}}$ (cm-1)		Γ (deg)	C§ (10-19 erg-cm)
	nB = ∞	nB = 200
	0.189	0.184	0.25	2.06
Tilt-Roll	0.189	0.184	0.26	2.06
Tilt-Twist	0.190	0.185	0.24	2.08
Tilt-Shift	0.189	0.185	0.22	2.06
Tilt-Slide	0.189	0.185	0.22	2.06
Tilt-Rise	0.189	0.185	0.24	2.06
Roll-Twist	0.191	0.186	0.25	2.12
Roll-Shift	0.189	0.184	0.22	2.06
Roll-Slide	0.189	0.185	0.22	2.07
Roll-Rise	0.190	0.185	0.20	2.06
Twist-Shift	0.187	0.183	0.25	2.03
Twist-Slide	0.187	0.182	0.24	2.01
Twist-Rise	0.197	0.190	1.08	2.20
Shift-Slide	0.189	0.184	0.24	2.06
Shift-Rise	0.188	0.184	0.25	2.06
Slide-Rise	0.188	0.184	0.34	2.06
Roll-Twist,Twist-Rise	0.202	0.194	1.05	2.30
Twist-Slide,Twist-Rise	0.197	0.190	1.05	2.20
Roll-Twist,Twist-Slide	0.205	0.201	0.25	2.44
Roll-Twist,Twist-Slide,Twist-Rise	0.212	0.202	1.06	2.49

^*Intrinsic bending parameters $({\theta }_1^0,{\theta }_2^0)$ defined by (4); $({\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(36°,0\mathrm{Å},0\mathrm{Å},3.4\mathrm{Å})$.

^§Torsional modulus of overstretched, intrinsically curved chain.

As evident from Table 3.4, ${\nu }_1^{\mathrm{str}}$ decreases with the introduction of intrinsic curvature. The drop in frequency is roughly the same for all cases other than those that consider Twist-Rise coupling (f₃₆ < 0). The larger drop in frequency in the latter instances is linked to the larger values of the global bend angle Γ, listed in the fourth column of the table. As shown above, bending motions mix with the twisting modes when Γ is larger. We accordingly attribute the marked decrease in the twisting frequencies to this bending. The computed torsional moduli of the overstretched, naturally curved molecule, reported in the last column of Table 3.4, are about 5% lower than those of the naturally straight, duplex at the same degree of extension.

Figure 4 also includes the bend angles Γ found at different degrees of extension when the same curved DNA, i.e., n_B = 200, is subject to Twist-Rise coupling. If the step parameters are uncoupled, the angle approaches zero with increase in Q, but if Twist and Rise are coupled, Γ levels off to a nonzero value. The intrinsic curvature considered here is planar; i.e., all of the DNA molecules adopt a planar equilibrium rest state. If the step parameters are uncoupled, the DNA remains planar as it is stretched or straightened. By contrast, if Twist and Rise are coupled, the DNA exhibits out-of-plane distortions such that the axis of the double helix follows an approximately superhelical pathway. The global bend angle accordingly approaches a nonzero value as the DNA is stretched.

The superhelical pathway of the stretched duplex stems from the Twist-Rise correlation. The straightening and extension of naturally curved DNA inevitably involve the increase of Rise, which, in turn, changes Twist when f₃₆ is nonzero. The variation in local twisting directs the DNA out of the plane of the equilibrium rest state, generating a superhelical configuration. Thus, naturally curved DNA molecules subject to Twist-Rise coupling deform out of the plane when stretched.

4. Summary and discussion

The ease of twisting successive base pairs contributes to the “melting” that accompanies the biological processing of DNA, e.g., strand separation during transcription or replication. The concomitant anchoring of the double helix to an underlying nuclear scaffold couples these local structural changes with the folding of the molecule as a whole and vice versa. Accurate values of the torsional modulus accordingly underlie reliable prediction of both genetic and topological properties of DNA.

The present calculations show how end-to-end constraints placed on a DNA molecule, in combination with the natural conformational features of the double helix, can account for discrepancies in the torsional moduli determined with state-of-the-art, single-molecule experiments [6] compared to values extracted from various solution measurements [1, 20, 21, 23, 34, 43] and/or incorporated into theories to account for the force-extension properties of single molecules [4, 35, 41, 45]. Although the torsional moduli determined here for naturally straight, mixed-sequence DNA molecules with no constraints on the separation of chain ends are substantially lower than values extracted from solution studies (C ≈ 2.0 × 10^-19 vs. 2.0 - 4.8 × 10^-19 erg-cm), the computed elastic constants increase substantially if base pairs are inclined with respect to the double helical axis and the deformations of selected conformational variables follow known interdependent patterns. The effects are particularly striking for the generic homopolymer, with an equilibrium rest state based upon the observed arrangements of neighboring base pairs in high-resolution crystal structures. The base pairs of the generic model are both inclined and displaced with respect to the helical axis; i.e., the equilibrium Roll $\left({\theta }_2^0\right)$ and Slide $\left({\theta }_5^0\right)$ are nonzero.

The introduction of restraints on DNA ends has no effect on the dominant twisting frequencies and the computed torsional moduli of mixed-sequence chains subject to ideal elastic behavior (compare the entries in the top rows of Tables 3.1, 3.2, and A.1). The fluctuations in twisting are independent of other types of conformational variation in these models. The computed normal-mode frequencies and torsional moduli, however, vary if the fluctuations in dimeric twisting are coupled with parameters that directly alter the end-to-end displacement. Constraints on the end-to-end distance thereby impede the twisting of base pairs and increase the torsional modulus. For example, the value of C increases by 8-15% compared to that of unrestrained DNA with independent torsional fluctuations when the duplex is restrained to full equilibrium extension and subject to Roll-Twist or Twist-Rise coupling of the type seen in high-resolution structures, i.e., cases with nonzero values of f₂₃ or f₃₆ in Tables 3.1, 3.2, and A.1. The effect is even greater if the base pairs are naturally inclined with respect to the helical axis and Twist is also coupled with Slide. If these local conformational features vary in concert, even very small intrinsic inclination of base-pair planes brings about a fairly large change in the global twisting modulus.

The computed torsional modulus of a fully extended, generic DNA molecule subject to Roll-Twist, Twist-Slide, and Twist-Rise correlations is 2.6 × 10^-19 erg-cm and that of a slightly (∼5%) overextended molecule of the same type is 3.0 × 10^-19 erg-cm. The small difference in the computed torsional moduli of fully extended vs. slightly over-extended DNA is consistent with the similar values of C found by Bryant et al. in single-molecule studies performed under two different extension forces (15 and 45pN) [6]. Moreover, the computed modulus drops by only ∼7% if the extension is reduced to one-third (from ∼5% to ∼1.7%), corresponding to the same one-third reduction of the extension force introduced experimentally. The inclination of base pairs allows for fluctuations in polymeric extension via the lateral shearing (Slide) of base-pair planes as well as the vertical separation (Rise) and bending (Roll) of adjacent residues. The 131-152% increase in C in the restrained duplex, compared to the unrestrained polymer free of conformational coupling (Tables 3.1 vs. 3.3), is of the same magnitude as the increase in the torsional modulus found in single-molecule vs. solution experiments. The magnitude of the computed modulus also depends on the degree of base-pair inclination (Tables 3.2 vs. A.1) and the size of the restraint energy, roughly doubling in value with a 20-fold increase the spring constant (Figure 1). The twisting rigidity of spatially constrained A DNA is accordingly expected to be substantially higher than that of B DNA, because of the larger (∼15-20°) natural inclination of base-pair planes in the A-type duplex [28]. Similar effects are anticipated in double-helical A RNA and DNA · RNA hybrids, which also adopt an A-type helical structure. The Young’s moduli of these complexes are further expected to show the compensatory “softening,” i.e., Y/Y₀ < 0, found here (Table 3.3/A.3) upon extension of the generic DNA duplex.

The preceding conclusions rest upon our ability to estimate the torsional modulus of DNA from the normal modes of polymeric fragments and to relate the normal modes to the local conformational properties of the double-helical structure. The end-to-end distance remains unchanged in the second lowest and other “even” frequency twisting modes, and the frequencies of these modes are accordingly insensitive to end-to-end distance restraints (Figure 2, Table A.2). The contributions of higher-order “odd” twisting modes to the end-to-end distance are much smaller than those of the lowest-frequency twisting mode. Thus, the twisting motion of DNA monitored by single-molecule experiments, where a very large twisting modulus is obtained, may resemble the motions of the lowest-frequency twisting normal mode described here. Furthermore, as a result of this similarity, the experimentally observed twisting motions of DNA will be strongly coupled with other motions, such as global bending and stretching, in which the end-to-end distance of the DNA changes. Indeed, new single-molecule studies [16, 26] show that DNA twisting and stretching are coupled at the macromolecular level in the same sense as the high-resolution structural information used in the present computations. That is, when stretched, the double helix overwinds, and when compressed, it unwinds.

Our determination of the torsional modulus of DNA rests upon the classical treatment of a homogeneous, naturally straight elastic rod [42], precluding extraction of the global twisting moduli of naturally curved duplexes free of end-to-end restraints. The lowest twisting frequency of curved DNA, nevertheless, exceeds that of the overextended form under these conditions and up to the point where the molecule is roughly fully extended (Figure 5). The frequency drops when the DNA is overstretched and effectively straightened (see Figures 3-4 for details of straightening). The torsional modulus of the naturally curved molecule, which can be determined under such conditions, falls short of that of naturally straight DNA (Figure 5, Table 3.4). The twisting modulus of the curved molecule presumably exceeds that of the naturally straight duplex prior to forced straightening. Whereas naturally straight DNA rotates “freely” about its global helical axis when covalently closed, the natural DNA O-ring, i.e., a curved molecule closed into a ring of length n_B, resists turning inside out [31, 32, 33]. The higher twisting frequencies of the unrestrained and partially extended fragments of curved DNA studied here may be related to these torsional properties. Single-molecule studies of naturally curved DNA molecules may therefore sense the computed drop in the torsional modulus upon imposed extension.

Appendix

Table A.1.

Effect of local conformational coupling on the lowest-frequency normal twisting mode of a 100 bp ideal DNA homopolymer^*

Coupled variables	${\nu }_1^0$† (cm-1)	${\nu }_1^{\mathrm{eq}}$† (cm-1)	ΔC§ (%)
	0.189	0.189
Tilt-Roll	0.189	0.189	0.0
Tilt-Twist	0.188	0.188	-0.5
Tilt-Shift	0.189	0.189	0.0
Tilt-Slide	0.189	0.189	0.0
Tilt-Rise	0.189	0.189	0.0
Roll-Twist	0.187	0.187	-1.3
Roll-Shift	0.189	0.189	0.0
Roll-Slide	0.189	0.189	0.0
Roll-Rise	0.189	0.189	0.0
Twist-Shift	0.188	0.188	-0.5
Twist-Slide	0.188	0.188	-0.4
Twist-Rise	0.185	0.197	9.1
Shift-Slide	0.189	0.189	0.0
Shift-Rise	0.189	0.189	0.0
Slide-Rise	0.189	0.189	0.0
Roll-Twist, Twist-Rise	0.187	0.199	11.5
Twist-Slide, Twist-Rise	0.186	0.199	11.0
Roll-Twist, Twist-Slide	0.191	0.191	2.1
Roll-Twist, Twist-Slide, Twist-Rise	0.185	0.197	8.9

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,0°,36°,0\mathrm{Å},0\mathrm{Å},3.4\mathrm{Å})$.

^†Frequencies of DNA chains subject to the same global constraints as in Table 3.1.

^§Change in torsional modulus of the restrained duplex subject to given conformational coupling compared to that (C = 2.05 × 10^-19 erg-cm) of the unrestrained, ideal molecule with independent fluctuations of base-pair step parameters. See legend to Table 3.1.

Table A.2.

Effect of local conformational coupling on the second lowest-frequency normal twisting mode of a 100 bp generic DNA homopolymer^*

Coupled variables	${\nu }_2^0$ (cm-1)	${\nu }_2^{\mathrm{eq}}$ (cm-1)
	0.370	0.370
Tilt-Roll	0.371	0.371
Tilt-Twist	0.370	0.370
Tilt-Shift	0.371	0.371
Tilt-Slide	0.371	0.371
Tilt-Rise	0.370	0.370
Roll-Twist	0.384	0.384
Roll-Shift	0.370	0.370
Roll-Slide	0.371	0.371
Roll-Rise	0.370	0.370
Twist-Shift	0.369	0.369
Twist-Slide	0.368	0.368
Twist-Rise	0.363	0.363
Shift-Slide	0.370	0.370
Shift-Rise	0.370	0.370
Slide-Rise	0.370	0.370
Roll-Twist, Twist-Rise	0.373	0.373
Twist-Slide, Twist-Rise	0.361	0.361
Roll-Twist, Twist-Slide	0.386	0.386
Roll-Twist, Twist-Slide, Twist-Rise	0.363	0.363

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,-2.8°,33.8°,0\mathrm{Å},-0.2\mathrm{Å},3.33\mathrm{Å})$.

Table A.3.

Effect of stretching on the lowest-frequency normal twisting mode and elastic modulus of a 100 bp ideal DNA homopolymer^*

Coupled variables	r (Å)	(r - req)/req (%)	Y/Y0†	${\nu }_1^{\mathrm{str}}$ (cm-1)	C (10-19 erg-cm)
	353.4	5.0	1.00	0.189	2.15
Tilt-Roll	353.4	5.0	1.00	0.189	2.15
Tilt-Twist	353.4	5.0	1.00	0.190	2.17
Tilt-Shift	353.4	5.0	1.00	0.189	2.15
Tilt-Slide	353.4	5.0	1.00	0.189	2.15
Tilt-Rise	353.3	5.0	1.02	0.189	2.15
Roll-Twist	353.4	5.0	1.00	0.191	2.19
Roll-Shift	353.4	5.0	1.00	0.189	2.15
Roll-Slide	353.4	5.0	1.00	0.189	2.15
Roll-Rise	353.1	4.9	1.04	0.190	2.15
Twist-Shift	353.4	5.0	1.00	0.187	2.12
Twist-Slide	353.4	5.0	1.00	0.187	2.10
Twist-Rise	353.5	5.0	1.00	0.197	2.35
Shift-Slide	353.4	5.0	1.00	0.189	2.15
Shift-Rise	353.6	5.1	0.98	0.188	2.15
Slide-Rise	353.7	5.1	0.97	0.188	2.15
Roll-Twist, Twist-Rise	353.4	5.0	1.00	0.202	2.47
Twist-Slide, Twist-Rise	353.4	5.0	1.00	0.197	2.35
Roll-Twist, Twist-Slide	353.4	5.0	1.00	0.205	2.53
Roll-Twist, Twist-Slide, Twist-Rise	353.4	5.0	1.00	0.212	2.72

^*Dimeric rest state: $({\theta }_1^0,{\theta }_2^0,{\theta }_3^0,{\theta }_4^0,{\theta }_5^0,{\theta }_6^0)=(0°,0°,36°,0\mathrm{Å},0\mathrm{Å},3.4\mathrm{Å})$.

^§Young’s modulus, Y , of the restrained duplex with designated conformational properties compared to that, Y₀, of the free, ideal DNA duplex without coupling.