Abstract
Dynamic assessment (DA) involves helping students learn a task and indexing responsiveness to that instruction as a measure of learning potential. The purpose of this study was to explore the utility of a DA of algebraic learning in predicting 3rd graders’ development of mathematics problem solving. In the fall, 122 3rd-grade students were assessed on language, nonverbal reasoning, attentive behavior, calculations, word-problem skill, and DA. On the basis of random assignment, students received 16 weeks of validated instruction on word problems or received 16 weeks of conventional instruction on word problems. Then, students were assessed on word-problem measures proximal and distal to instruction. Structural equation measurement models showed that DA measured a distinct dimension of pretreatment ability and that proximal and distal word-problem measures were needed to account for outcome. Structural equation modeling showed that instruction (conventional vs. validated) was sufficient to account for math word-problem outcome proximal to instruction; by contrast, language, pretreatment math skill, and DA were needed to forecast learning on word-problem outcomes more distal to instruction. Findings are discussed in terms of responsiveness-to-intervention models for preventing and identifying learning disabilities.
A major purpose of educational assessment is to forecast academic achievement. The goal is early identification of students who are at risk for poor learning outcomes so that intervention can be initiated before the development of severe academic deficits, which can be intractable and can create life-long difficulty in and out of school (e.g., Rivera-Batiz, 1992). The predominant approach for forecasting academic achievement is traditional testing with a general measure of intelligence (e.g., Raven Progressive Matrices [Raven, 1960]) or a test of specific ability or skill presumed to underlie future academic performance (e.g., phonological processing for development of word-reading performance or calculations skill for development of mathematics word-problem performance). In these conventional testing situations, examinees respond without examiner assistance, and a body of work demonstrates that assessments of intelligence or precursor abilities/skills capture varying amounts of variance in forecasting academic development. For example, a measure of quantity discrimination, when used as a screener near the beginning of first grade, accounts for 25% to 63% of the variance in end-of-year math outcomes depending on the study (e.g., Chard et al. 2005; Clarke & Shinn, 2004; Lembke & Foegen, 2006).
Because these conventional assessments are imperfect predictors of academic learning (e.g., Sternberg, 1996), they have long been the target of scrutiny and criticism (e.g., Tzuriel & Haywood, 1992). A major concern is that these “static” estimates of performance reveal only two states: unaided success or failure. By contrast, as Vygotsky (e.g., 1934/1962) proposed, children may function somewhere between these states: unable to perform a task independently but able to succeed with assistance. This has implications for discriminating students at the lower end of the distribution. For example, when two children earn the same low score on a calculations test, they may not have the same potential to develop word-problem skill. One may succeed in solving word problems given only minimal assistance. This would suggest that the initially low performance on the static assessment stems from inadequate learning opportunity in the child’s present environment, but indicating good learning potential with competent instruction in the future. The other child may struggle to learn word problems even when provided highly explicit instruction (revealing the need for special intervention).
So the question arises: If the goal is to forecast learning potential, why not assess the student’s capacity to learn, rather than assessing what the student presently knows? This alternative form of assessment, whereby students’ learning potential is measured, is known as dynamic assessment (DA). DA has been the focus of discussions and research for more than 75 years (e.g., Kern, 1930; Penrose, 1934; Rey, 1934, as cited in Grigorenko & Sternberg, 1998). In the present study, we considered the contribution of a DA in forecasting students’ development of word-problem competence across third grade. In this introduction, we present a framework for considering prior DA work related to the present study. Then we clarify how the present study builds on and extends this literature.
Prior Work on DA as A Predictor of Academic Development
DA involves structuring a learning task; providing feedback or instruction to help the student learn the task; and indexing responsiveness to the assisted learning phase as a measure of learning potential. Research on DA varies as a function of the structure and design of the DA and in terms of the methodological features of the studies.
In terms of structure and design, DAs vary along three dimensions (see Campione, 1989): index, style of interaction, and the nature of the skills assessed. Index refers to the way in which DAs quantify responsiveness to the assisted phase of learning. This is the measure of learning potential. The first strategy for indexing performance is to characterize the amount of change from an unassisted pretest to an unassisted posttest (with the assisted learning phase intervening between the pre- and posttest) or by scoring students’ unaided performance following the assisted phase of assessment (e.g., Ferrara, Brown, & Campione, 1986). The second approach for indexing performance is to quantify the amount of scaffolding required during the assisted phase of assessment to reach criterion performance (e.g., Murray et al., 2000; Spector, 1992). These alternative methods for indexing DA performance serve the same purpose: to predict whether students require extra attention in order to learn adequately. Researchers who use change from unassisted pre- to posttest or use unaided performance following the assisted phase of assessment typically contrast normal learners against special populations of learners (e.g., students with mental retardation) to examine whether the assisted learning experience produces differential learning outcomes as a function of having a diagnosis associated with inadequate learning (e.g., mental retardation). This suggests that low DA scores (improvement as a function of assisted learning or unaided performance score following assisted learning) serve to predict poor outcomes in other learning situations, indicating that extra instructional support is required to produce adequate learning. In a related way, when research shows that amount of scaffolding predicts learning outcomes outside of DA, this provides evidence that low DA scores (amount of scaffolding needed to reach criterion performance during the assisted learning phase) serve to predict poor outcomes in other learning situations, indicating that extra instructional support is required to produce adequate learning.
The second dimension along which DA varies is the style of interaction. Some DAs (e.g., Ferrara et al., 1986) are standardized, where the tester administers a fixed series of prompts; success with early prompts reflects the need for minimal adult intervention to perform/learn the task, whereas success on later prompts reflects the need for more extensive adult help to perform/learn the task. By contrast, other DAs (e.g., Tzuriel & Feuerstein, 1992) are individualized, where the tester addresses the student’s specific obstacles as revealed by that student’s responses.
The third dimension along which DA varies is the nature of the skills assessed. Early work (e.g., Budoff, 1967; Feuerstein, 1979) tended to focus on domain-general skills associated with cognitive ability. In more recent work, tasks tend to be more academically grounded (e.g., Bransford et al., 1987; Campione, 1989; Campione & Brown, 1987; Spector, 1992).
In terms of research questions and methodological features, some DA studies focus on the amount of learning that accrues on the DA task as a function of student characteristics or the structure of DA (e.g., Tzuriel & Feuerstein, 1992). This approach dominated DA research in the 1970s, 1980s, and 1990s. Alternatively, studies consider DA’s contribution in explaining academic performance outside the DA. This second class of studies can be categorized further in terms of two major methodological features. The first is whether studies account for competing predictors of outcome (including static assessments) while considering DA’s contribution in predicting academic performance. The second methodological feature is whether academic performance (the outcome) is assessed concurrently with DA (the predictor) or at a later time.
Compared to studies that do not control for competing predictors of outcome, studies that exert such control impose a more stringent falsifiability criterion for considering the value of DA. In terms of the timing of the academic outcome, studies that measure academic performance at a later time enhance external validity, given that the purpose of DA is to forecast future academic achievement. After all, if we were interested in present academic performance, the parsimonious approach would be to measure present achievement directly, not via DA. However, it is also possible that forecasting later academic performance creates variance for DA to capture because the relation between learning potential as indexed via DA and upcoming learning in response to instruction may be stronger than the relation between static assessments (which may be determined by culture, socioeconomics, and previous learning opportunity) and upcoming learning. This empirical issue is, of course, central to questions about DA’s utility as a measure of learning potential. For these reasons, in the present study, we examined the contribution of DA in explaining academic performance while accounting for competing predictors of outcome.
To contextualize the present study, we therefore restricted attention in our overview of prior work to the subset of investigations that also explored DA’s contribution in predicting academic performance while controlling for competing predictors. We did, however, consider studies that predicted concurrent as well as future academic performance. We also included DAs of varying structure and design. That is, if a study predicted academic outcome while accounting for competing predictors of outcome, we included it regardless of whether the outcome was measured concurrently or in the future, regardless of the way in which DA performance was quantified, regardless of the style of the DA interaction, and regardless of nature of the DA skills assessed. (For a comprehensive DA review, inclusive of all structures and designs as well as all research questions and methodological features, see Grigorenko & Sternberg, 1998).
Using our inclusion criteria, we identified three relevant studies.1 In the first study, Speece et al. (l990) measured first-grade students’ learning potential with a DA task involving a domain-general skill associated with overall cognitive ability: solving matrices that were borrowed from intelligence tests. Using a standardized style of interaction, the researchers indexed learning potential via the number of prompts required during the assisted phase of assessment. Speece et al. assessed the contribution of DA over verbal IQ, pre-DA matrices performance, and language ability for indicating performance on concurrently administered tests of reading and math achievement. Although statistically significant, DA accounted for less than 2% of the variance in concurrent math performance.
Also predicting concurrent academic performance and using a standardized form of DA, Swanson and Howard (2005) extended the work of Speece et al. (1990) by centering DA on cognitive abilities presumed to underlie reading and math performance: phonological working memory (i.e., rhyming tasks that required recall of acoustically similar words) and semantic working memory (i.e., digit/sentence tasks that required recall of numerical information embedded in short sentences). Four standardized hints were available to DA testers, who selected hints that corresponded to students’ errors, choosing the least obvious, relevant hint. Three DA scores were generated: gain score (highest score obtained with assistance); maintenance score (stability of the highest level obtained with assistance probing after assistance was removed); and probe score (number of hints to achieve highest level). The sample comprised students classified as poor readers, skilled readers, reading disabled, or math and reading disabled, with the age of participants averaging 10 to 12 years. To predict concurrent performance on the Wide Range Achievement Test-Reading and Arithmetic subtests, the DA scores for phonological working memory were combined into a factor score; the same was done for DA semantic working memory. The competing predictors were verbal IQ and pre-DA working memory, which were entered first into multiple regression analyses. In predicting reading, pre-DA semantic working memory, verbal IQ and semantic DA provided unique variance; the unique contribution of the semantic DA factor was 6%. In predicting arithmetic, pre-DA phonological working memory, verbal IQ, and semantic DA provided unique variance; the unique contribution of the semantic DA factor was 25%.
So whereas Speece et al. (1990) found more limited support for DA’s added value as related to math performance when DA addressed a domain-general task associated with cognitive ability, Swanson and Howard’s (2005) work, which centered DA on cognitive abilities presumed to underlie reading and math performance, was more encouraging. Neither study, however, assessed students’ academic performance at a later time. Given that DA’s purpose is to forecast future academic achievement, delaying outcome assessment seems important for external validity. In addition, delaying outcome assessment may create variance for DA to capture, as already discussed.
We identified only one study that centered DA on cognitive abilities presumed to underlie reading and math performance (as done by Swanson & Howard, 2005) and, in contrast to Speece et al. (1990) and Swanson and Howard, delayed the assessment of academic achievement to later in the school year. Spector (1997) administered a standardized DA of phonemic awareness, indexing number of prompts to achieve criterion performance, in November of kindergarten, and then assessed word-level reading skill in May of kindergarten. DA substantially enhanced predictive validity beyond initial verbal ability and beyond initial, static phonological awareness performance in predicting end-of-kindergarten word-reading skill, explaining an additional 21% variance. In fact, November DA was the only significant predictor of May word-reading skill. These results provide promising evidence that DA may enhance the prediction of student learning.
We also considered one additional investigation, even though it did not meet our inclusion criteria (in that it considered DA’s relation to post-DA performance on items that mirrored the DA tasks). This study nonetheless helped inform the present study because of its statistical methods. With 84 preschool children, Day et al. (1997) created DAs that focused on domain-general skills associated with cognitive abilities: similarities and block design tasks. The style of interaction was individualized (i.e., the tester addressed the specific obstacles revealed by the student’s responses), and learning potential was indexed by trials to criterion performance. For block design, for example, children were taught a 4-step strategy, which the experimenter initially modeled using a 4-block problem. If the child failed to solve another 4-block problem correctly, more guidance was provided on a 3-block problem. Assistance was provided whenever a child failed to solve a problem correctly until he/she solved three consecutive 4-block problems without assistance. A transfer task that varied the block design was also presented, with analogous support to learn, and the researchers assessed pre-DA and post-DA similarities and block design performance. Pre-DA performance was considered a competing predictor; post-DA performance was the outcome.
We were interested in Day et al.’s (1997) use of structural equation modeling to test competing measurement and structural models. The measurement model that retained DA as a construct separate from pre-DA and post-DA provided better fit of the data. Thus, DA appeared to tap a construct separate from pre-DA performance, even on analogous tasks. In predicting post-DA scores, Day et al. contrasted four structural models and thereby showed that DA was a viable and necessary predictor of post-DA performance. Of course, academic (or pre-academic) performance or learning, which is the relevant outcome to consider when assessing DA’s value in predicting achievement, was not considered. Accordingly, Day et al. concluded, “We do not know how dynamic measures related to everyday or school learning or how schooling might affect the relationships among the same measures in children older than those who participated in the present study…. Finally, the primary advantage of dynamic measures may lie in how well they predict the ease with which children acquire new information (i.e., training responsiveness) rather than in how well they predict post-training independent performance” (p. 367).
Purpose of the Present Study
As reflected in Day et al.’s (1997) concluding comments, additional work on DA is necessary, especially in light of Spector’s (1997) promising findings. In the present study, the academic outcome was third-grade skill with word problems. Our DA extended the framework for considering type of DA task by employing actual math content that was not a precursor or foundational skill for solving word problems: three basic algebra skills. The question was whether a student’s potential to learn algebra at the beginning of third grade forecasted their development of word-problem competence over the course of third grade. We note that although linguistic content is absent from the algebra skills assessed on the DA, algebra does require understanding of the relations among quantities, as is the case for solving word problems. Hence, a potentially important connection does exist between algebraic learning, as assessed on the DA task, and word-problem learning, as addressed in the 16-week treatment conditions (validated vs. conventional word-problems instruction).
We selected basic algebra skills as our DA content for the following reasons. First, we could safely assume that these skills were unfamiliar to third graders, i.e., the skills had not been introduced in school to students by the beginning of third grade and was not familiar from everyday life experiences. Second, the algebra skills were of sufficient difficulty that most third graders would not be able to solve the problems without assistance but could learn the skills with varying amounts of teaching. Third and relatedly, at the beginning of third grade, students should have mastered the simple calculation skills that we incorporated within the three algebra items. Fourth, we could delineate rules underlying the algebra skills, rules that could be used to construct clear explanations within a graduated sequence of prompts. Fifth, the graduated sequences of prompts for the three skills could be constructed in an analogous hierarchy, thereby promoting equal interval scaling of the DA scoring system. Sixth, the three skills were increasingly difficult (as established in pilot work) and later skills appeared to build on earlier skills; therefore, we hoped that transfer across the three algebra skills might facilitate better DA scores. Seventh, as noted, although linguistic content is absent from the algebra skills, algebra does require understanding of the relations among quantities, as is the case for solving word problems.
In the present study, we controlled for other variables that might be important in predicting outcome. First, we controlled for pretreatment performance on salient cognitive predictors of word-problem skill (language ability, attentive behavior, and nonverbal reasoning). Second, we controlled for students’ pretreatment skill with calculations and word problems. Third, we extended prior work by also controlling for the nature of classroom instruction. Toward that end, on the basis of random assignment, students received conventional mathematical problem-solving instruction or research-validated schema-broadening instruction (e.g., Fuchs et al., in press), and we treated treatment condition as a competing predictor variable (see Method section for a description of these treatment conditions). Two other features of the present study are noteworthy. We examined word-problem outcome as a function of whether the word-problem measures could be considered near versus far transfer from instruction (i.e., the flexibility required to apply the content of the math word-problems curriculum). Also, we relied on structural equation modeling, as did Day et al. (1997), to assess DA’s added value. In the remaining section of this introduction, we briefly explain the basis for selecting language ability, attentive behavior, and nonverbal reasoning as the cognitive predictors of word-problem skill.
Prior work examining cognitive processes that underlie skill with word problems has recurrently identified three important dimensions: attentive behavior, nonverbal reasoning, and language ability. In studies involving attentive behavior, most work has focused on the inhibition of irrelevant stimuli, with mixed results. Passolunghi and colleagues ran a series of studies suggesting the importance of inhibition. For example, comparing good and poor problem solvers, Passolunghi, Cornoldi, and De Liberto (l999) found comparable storage capacity, with inefficiencies of inhibition (i.e., poor problem solvers remembered less relevant but more irrelevant information in math problems). In addition, Fuchs et al. (2005) and Fuchs et al. (2006) studied the role of attention more broadly and, in separate studies, found that a teacher rating scale of attentive behavior predicted the development of skill with word problems at first and third grades.
Nonverbal problem solving, or the ability to complete patterns presented visually, has also been identified as a unique predictor in the development of skill with word problems across first grade (Fuchs et al., 2005), a finding corroborated by Agness and McLone (1987). This is not surprising because word problems, where the problem narrative poses a question entailing relationships between numbers, appear to require conceptual representations, and the finding has been replicated as a unique predictor of concurrent word-problem skill at third grade (Fuchs et al., 2006).
Language ability also is important to consider given the obvious need to process linguistic information when building a problem representation of a word problem. Jordan, Levine, and Huttenlocher (1995) documented the importance of language ability when they showed that kindergarten and first-grade language-impaired children performed significantly lower than nonimpaired peers on word problems. Fuchs, Fuchs, Stuebing, Fletcher, Hamlett, and Lambert (in press) examined concurrent performance on nine cognitive dimensions with multiple measures of calculations skill and word-problem skill on a sample of 917 third graders representatively sampled from 89 classes. Students were classified as having difficulty with calculations, word problems, both domains, or neither domain. Multivariate profile analysis on the nine cognitive dimensions showed that specific calculations difficulty was associated with strength in language whereas difficulty with word problems was associated with deficient language. We also note that language ability and nonverbal reasoning comprise two major dimensions in some prominent assessments of intelligence.
Because these cognitive dimensions are established predictors of word-problem skill, they represent worthy competitors against DA for capturing variance in word-problem outcomes. In addition, these cognitive dimensions, while differing from DA in their demands, connect in transparent ways to word-problem skill or to learning in the general education context. Language, while not reflected in our algebra DA, is clearly involved in word problems, which are communicated via narratives. Nonverbal problem solving asks students to complete matrices presented visually, involving classification and analogy. Although this has no direct connection to our algebra DA, it is linked to word-problem skill, which requires students to connect novel problems with the word-problem types for which they know solutions. Evidence suggests this occurs via classification and analogy (e.g., Cooper & Sweller, 1987). Attentive behavior asks teachers to judge students’ ability to attend to detail, sustain attention, listen, follow directions, organize tasks, keep track of things, ignore extraneous stimuli, and remember daily activities. These ratings, which teachers formulate on the basis of observations of students in their classrooms, seem better connected to learning word problems in general education settings than in one-to-one testing situations like DA, where the tester can redirect and control inattentive behavior more effectively. Finally, we note that language and nonverbal reasoning are two major dimensions of general intelligence, which traditionally has been used to predict academic achievement (in fact, in the present study, the Vocabulary and Matrix Reasoning measures used to index language ability and nonverbal problem solving, respectively, constitute the 2-subtest Wechsler Abbreviated Scale of Intelligence). For this additional reason, these constructs represent worthy competitors with DA in forecasting responsiveness to classroom word-problem instruction.
Method
Participants
With the exception of the DA, the data described in this paper were collected as part of a prospective 4-year study assessing the effects of mathematical problem-solving instruction and examining the developmental course and cognitive predictors of mathematical problem solving. The data in the present article were collected with a subset of students in the fourth-year cohort of the larger study at the first and second assessment waves (at fall and spring of third grade). We sampled students from the 30 participating classrooms in nine schools (five Title 1 and three non-Title 1). Classrooms had been randomly assigned to treatment conditions (conventional vs. validated schema-broadening instruction) within schools. There were two to six students per class.2
We sampled students for the present study from the cohort’s 510 students with parental consent. The sampling process was designed to yield a representative sample. That is, from these 510 students, we randomly sampled 150 for participation, blocking within instructional condition (conventional math problem-solving instruction vs. schema-broadening math problem-solving instruction), within classroom, and within three strata: (a) 25% of students with scores 1 SD below the mean of the entire distribution on the Test of Computational Fluency see Measures; (b) 50% of students with scores within 1 SD of the mean of the entire distribution on the Test of Computational Fluency; and (c) 25% of students with scores 1 SD above the mean of the entire distribution on the Test of Computational Fluency). Of these 150 students, we have complete data for the variables reported in the present study on 122 children. The 122 included students were comparable to the remaining students on the study variables, with varying sample sizes depending on where missing data occurred. See Table 1 for descriptive information on performance variables for the sample of 122 children. Of these students, 67 (54.9%) were male, and 80 (67.0%) received subsidized lunch. Ethnicity was distributed as: 57 (47.5%) African American, 53 (43.4%) European American, 10 (8.3%) Hispanic, and 3 (2.5%) other. Two students (1.7%) were English language learners.
Table 1.
Performance for Total Sample and by Treatment Condition
| Condition
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total Sample
|
Conventional
|
SBI
|
||||||||||
| Raw Score
|
Standard Score
|
Raw Score
|
Standard Score
|
Raw Score
|
Standard Score
|
|||||||
| Variable | X | (SD) | X | (SD) | X | (SD) | X | (SD) | X | (SD) | X | (SD) |
| Descriptive | ||||||||||||
| WASI IQ | NA | 96.10 | (12.55) | NA | 96.60 | (13.28) | NA | 95.58 | (11.83) | |||
| TCAP Reading | NA | 54.74 | (14.55) | NA | 53.81 | (14.67) | NA | 55.61 | (14.51) | |||
| TCAP Math | NA | 60.70 | (17.90) | NA | 59.48 | (18.18) | NA | 61.87 | (17.71) | |||
| WJ-Applied Prob. | 30.04 | (4.15) | 106.97 | (12.58) | 29.90 | (4.58) | 106.52 | (12.90) | 30.18 | (3.68) | 107.43 | (12.33) |
| WRMT-WID | 56.66 | (11.51) | 100.94 | (11.20) | 55.84 | (12.44) | 100.42 | (12.19) | 57.50 | (10.49) | 101.14 | (10.14) |
| Peretreatment Performance | ||||||||||||
| Grammatic Closure | 19.67 | (5.84) | 86.43 | (10.47) | 19.06 | (6.43) | 85.56 | (10.91) | 20.30 | (5.14) | 87.33 | (10.02) |
| Listening Comp. | 21.64 | (3.92) | 98.88 | (17.47) | 21.93 | (4.11) | 99.32 | (16.44) | 21.35 | (3.59) | 98.44 | (18.06) |
| Vocabulary | 26.39 | (5.82) | 45.11 | (9.19) | 26.26 | (6.26) | 44.98 | (9.94) | 26.52 | (5.38) | 45.23 | (8.42) |
| Matrix Reasoning | 16.08 | (5.95) | 49.65 | (10.22) | 16.35 | (5.90) | 50.15 | (10.14) | 15.80 | (6.03) | 49.13 | (10.36) |
| SWAN 1–3 | 12.61 | (3.89) | NA | 12.42 | (4.04) | NA | 12.80 | (3.66) | NA | |||
| SWAN 4–6 | 12.70 | (4.17) | NA | 13.07 | (4.47) | NA | 12.33 | (3.74) | NA | |||
| SWAN 7–9 | 12.70 | (4.06) | NA | 12.98 | (4.47) | NA | 12.42 | (3.52) | NA | |||
| DA1 | 5.25 | (1.53) | NA | 5.29 | (1.69) | NA | 5.20 | (1.36) | NA | |||
| DA2 | 3.34 | (1.81) | NA | 3.23 | (1.94) | NA | 3.45 | (1.68) | NA | |||
| DA3 | 1.39 | (1.99) | NA | 1.35 | (1.91) | NA | 1.42 | (2.06) | NA | |||
| Add Facts | 12.25 | (4.84) | NA | 12.64 | (5.20) | NA | 11.85 | (4.45) | NA | |||
| Subtract Facts | 7.84 | (5.19) | NA | 8.36 | (5.27) | NA | 7.32 | (5.09) | NA | |||
| Mixed Alg. | 23.30 | (10.23) | NA | 22.82 | (10.93) | NA | 23.58 | (9.48) | NA | |||
| Algorithmic Word Problems | 8.80 | (5.45) | NA | 8.21 | (5.32) | NA | 9.39 | (5.41) | NA | |||
| Outcomes | ||||||||||||
| Real-World Word Prob. | 24.38 | (13.96) | NA | 21.65 | (12.97) | NA | 27.21 | (14.49) | NA | |||
| Iowa | 15.74 | (4.36) | 188.05 | (20.60) | 15.44 | (4.24) | 186.61 | (19.97) | 16.05 | (4.50) | 189.53 | (21.31) |
| WJ-Applied Prob. | 32.39 | (4.32) | 106.97 | (12.58) | 32.19 | (4.64) | 106.52 | (12.90) | 32.60 | (4.19) | 107.43 | (12.33) |
| Algorithmic Word Prob. | 23.94 | (12.27) | NA | 15.69 | (9.04) | NA | 15.69 | (9.04) | NA | |||
| Complex Word Prob. | 27.05 | (16.86) | NA | 16.26 | (10.52) | NA | 38.20 | (14.81) | NA | |||
On the basis of random assignment, 61 students received conventional math problem-solving (as determined by their core math program and teachers) and 61 received schema-broadening math problem-solving instruction that has been validated (i.e., five large-scale randomized control trials, published in peer-reviewed journals, have documented the efficacy of the intervention at third grade with similar populations of students; Fuchs et al., 2003a; 2003b; 2004a, 2004b; in press). In Table 1, we show performance variables by instructional condition. Of the 61 students in conventional math problem-solving instruction, 32 (52.5%) were male, and 39 (63.9%) received subsidized lunch. Ethnicity was distributed as: 32 (52.5%) African American, 25 (41.o%) European American, and 5 (8.2%) Hispanic. Two students (3.2%) were English language learners. Of the 61 students in validated, schema-broadening math problem-solving instruction, 35 (57.4%) were male, and 41 (67.2%) received subsidized lunch. Ethnicity was distributed as: 25 (41.1%) African American, 28 (45.9%) European American, 5 (8.2%) Hispanic, and 3 (4.9%) other. None was an English language learner.
Procedure
We describe the subset of measures relevant to this research report. In October, the DA was administered individually in one 30–45 min session. In September and October, we administered measures of language and nonverbal reasoning (Woodcock Diagnostic Reading Battery [WDRB] – Listening Comprehension, Test of Language Development – Primary [TOLD] Grammatic Closure, Wechsler Abbreviated Scale of Intelligence [WASI] Vocabulary, and WASI Matrix Reasoning) and math performance (Woodcock-Johnson [WJ] III Applied Problems) individually in two 45-min sessions. In October, we administered the Test of Algorithmic Word Problems in one 30-min large-group session, and we administered three tests of calculations skill (Addition Fact Fluency, Subtraction Fact Fluency, and Test of Mixed Algorithms) in one 60-min large-group session. We also obtained scores on the previous spring’s state assessment (Tennessee Comprehensive Assessment Program; CTB/McGraw-Hill, 2003) from teachers.
In March, five tests of word-problem skill were administered (Algorithmic Word Problems, Complex Word Problems, Real-World Problem Solving, and WJ III Applied Problems). The first four were administered in two sessions in large groups. WJ III Applied Problems was administered individually in one session. We categorized the word-problem measures in terms of transfer distance (i.e., the distance from the types of word problems addressed during instruction and the degree of flexibility required in applying the word problems taught during instruction). Algorithmic Word Problems and Complex Word Problems were deemed near transfer. Real-World Problem Solving, WJ III Applied Problems, and the Iowa Test of Basic Skills: Problem Solving and Data Interpretation were considered far transfer. (We elaborate on transfer distance for each measure in the measures section.)
Group and individual testing was conducted by trained university examiners, each of whom had demonstrated 100% accuracy during mock administrations. All individual sessions were audiotaped, and 19.9% of tapes, distributed equally across testers, were selected randomly for accuracy checks by an independent scorer. Agreement was between 98.7 and 99.9%. In October, classroom teachers completed the SWAN Rating Scale, the measure of attentive behavior, on each student.
Measures of Cognitive, DA, and Calculations Pretreatment Performance
Language
We used three measures of language skill to create a latent variable representing language. TOLD Grammatic Closure (Newcomer & Hammill, 1988) measures the ability to recognize, understand, and use English morphological forms. The examiner reads 30 sentences, one at a time; each sentence has a missing word. As per the test developers, for 8 year olds, reliability is .88; the correlation with Illinois Test of Psycholinguistic Ability Grammatic Closure is .88. Coefficient alpha on the representative sample was .76. The WDRB Listening Comprehension (Woodcock, 1997) measures the ability to understand sentences or passages. Students supply words missing from the end of each sentence or passage. The test begins with simple verbal analogies and associations and progresses to comprehension involving the ability to discern implications. Testing is discontinued after six consecutive errors. The score is the number of correct responses. As per the test developers, reliability is .80 at ages 5–18; the correlation with WJ-R is .73. Coefficient alpha on the representative sample was .81. WASI Vocabulary (Wechsler, 1999) measures expressive vocabulary, verbal knowledge, and foundation of information. The first four items present pictures; the student identifies the object in the picture. For remaining items, the tester says a word that the student defines. Testing is discontinued after five consecutive errors. As reported by Zhu (1999), split-half reliability is .86–.87 at ages 6–7; the correlation with WISC-III Full Scale IQ is .72. Coefficient alpha on the representative sample was .78.
Nonverbal problem reasoning
WASI Matrix Reasoning (Wechsler, 1999) measures nonverbal reasoning, with pattern completion, classification, analogy, and serial reasoning. Examinees look at a matrix from which a section is missing and complete it. Testing is discontinued after 4 errors on 5 consecutive items or 4 consecutive errors. As per the test developer, reliability is .94 for 8 year olds; the correlation with WISC-III Full Scale IQ is .66. Coefficient alpha on the representative sample was .76.
Attentive behavior
The SWAN inattentive subscale is a 9-item teacher rating scale. Items from the Diagnostic and Statistical Manual of Mental Disorders-IV (APA, l994) criteria for Attention-Deficit/Hyperactivity Disorder are included. Items are rated on a 1 to 7 scale. We grouped items into triads (1–3, 4–6, 7–9) to form three observed attentive behavior variables for use in the structural equation modeling. The SWAN has been shown to correlate well with other dimensional assessments of behavior related to inattention (www.adhd.net). Coefficient alpha in this study was .92 for items 1–3, .94 for items 4–6, and .94 for items 7–9.
DA
The DA addresses three algebra skills assumed to be novel because they have not been taught in school and because they do not routinely occur in children’s extra-school experiences. The three algebra skills are: (a) finding the missing variable in the first or second position in addition equations (e.g., x+5=11 or 6+x=10); (b) finding x in multiplication equations (e.g., 3x=9); and (c) finding the missing variable in equations with two missing variables, but with one variable then defined (e.g., x+2=y−1; y=9). We refer to these three skills, respectively, as DA Skill A, DA Skill B, and DA Skill C.
Mastery of each DA skill is assessed before instructional scaffolding occurs, and mastery testing recurs after each level of instructional scaffolding is completed. The mastery test comprises six items representing the skill targeted for mastery, with mastery defined as at least 5 items correct. The items on the test are never used for instruction but parallel instructional items; each time the 6-item test is readministered for a given skill, a different form is used, although some items recur across forms. If, after 5 sec, the student has not written anything and does not appear to be working, the tester asks, “Can you try this?”; if after another 15 sec, the student still has not written anything and does not appear to be working, the tester asks, “Are you still working or are you stuck?” If the student responds that he/she is stuck, the tester initiates the first (or next) level of instructional scaffolding. If the students responds that he/she is still working but another 30 sec pass without the student writing anything or working, the tester then initiates the first (or next) level of instructional scaffolding. If the student masters the skill (i.e., at least 5 items are answered correctly), the tester administers a generalization problem (i.e., for Skill A: 3+6+x=11; for Skill B: 14=7x; for Skill C: 3+x=y+y; y=2) and moves to the next DA Skill. If the student does not master the skill (i.e., fewer than 5 items are answered correctly), the tester provides the first (or next) level of instructional scaffolding, or support, which is followed by the 6-item test. The levels of instructional scaffolding gradually increase instructional explicitness and concreteness. If a student fails to answer at least five correctly after the tester provides all five scaffolding levels for a given skill, the DA is terminated.
Scores range from 0–21, where 0 is the worst score (i.e., student never masters any of the three skills) and 21 is the best score (i.e., student masters each of the three skills on the pretest and gets every bonus problem correct). So, for each skill, there is a maximum of seven points, awarded as follows: student masters skill on pretest = 6 points; student masters skill after Scaffolding Level 1 = 5 points; student masters skill after Scaffolding Level 2 = 4 points; student masters skill after Scaffolding Level 3 = 3 points; student masters skill after Scaffolding Level 4 = 2 points; student masters skill after Scaffolding Level 5 = 1 point; student never shows mastery = 0 points. In addition, if the student gets the generalization problem correct, one point is added, for the maximum score of 7 points for that DA Skill.
To promote equal interval scaling, scaffolding levels for each of the three skills are structured in analogously. Scaffolding levels, which range from incidental to explicit, are provided in Appendix I for DA Skill A. For this information on DA Skills B and C, contact the first author. Correlations with the previous year’s math composite score on the state assessment (CTB/McGraw-Hill, 2003) were .57 for DA Skill A, .60 for DA Skill B, and .41 for DA Skill C.
Calculations
Three measures were used to create a latent variable representing calculation skill. Addition Fact Fluency (Fuchs, Hamlett, & Powell, 2003) comprises 25 addition fact problems with answers from 0 to 12 and with addends from 0 to 9. Problems are presented horizontally on one page. Students have 1 min to write answers. Percentage of agreement, on 20% of protocols by two independent scorers, was 99.9. Coefficient alpha for this sample was .92; criterion validity with the previous spring’s TerraNova (CTB/McGraw-Hill, 2003) Total Math score was .53 for the 1139 students on whom we had TerraNova scores. Subtraction Fact Fluency (Fuchs et al., 2003) comprises 25 subtraction fact problems with answers from 0 to 12 and with minuends/subtrahends from 0–18. Problems are presented horizontally on one page. Students have 1 min to write answers. Percentage of agreement, on 20% of protocols by two independent scorers, was 98.7. Coefficient alpha for this sample was .93, and criterion validity with the previous spring’s TerraNova (CTB/McGraw-Hill) Total Math score was .51 (n = 1139). The Test of Mixed Algorithms (Fuchs, Hamlett, & Fuchs, 1990) is a 1-page test with 25 items that sample the typical second-grade computation curriculum, including adding and subtracting number combinations and procedural computation. Students have 3 min to complete as many answers as possible. Staff entered responses into a computerized scoring program on an item-by-item basis, with 15% of tests re-entered by an independent scorer. Data-entry agreement was 99.7. Coefficient alpha for this sample was .94, and criterion validity with the previous spring’s TerraNova (CTB/McGraw-Hill) Total Math score was .60 (n = 1139).
Measures of Word-Problem Skill
We measured pretreatment word-problem skill using Algorithmic Word Problems. We measured posttreatment word-problem outcomes using Algorithmic Word Problems, Complex Word Problems, Real-Word Problem Solving, WJ-III Applied Problems, and Iowa Test of Basic Skills: Problem Solving and Data Interpretation.
Four independent judges classified the five word-problem outcome measures in terms of transfer distance from the instruction provided in schema-broadening math problem-solving instruction (i.e., the flexibility required to apply the content of the math word-problems curriculum) into two classes: near transfer versus far transfer. Agreement was 100%. We describe the word-problem outcomes in terms of near-transfer measures (all novel problems but structured similarly to problems used for instruction) versus far-transfer measures (all novel problems, not structured similarly to problems used for instruction). Schema-broadening instruction (SBI) focused on four word-problem types, chosen from the district curriculum to ensure that conventional math problem-solving instruction students had instruction relevant to the study. The four problem types were “shopping list” problems (e.g., Joe needs supplies for the science project. He needs 2 batteries, 3 wires, and 1 board. Batteries cost $4 each, wires cost $2 each, and boards cost $6 each. How much money does he need to buy supplies?), “half” problems (e.g., Marcy will buy 14 baseball cards. She’ll give her brother half the cards. How many cards will Marcy have?), step-up function or “buying bags” problems (e.g., Jose needs 32 party hats for his party. Party Hats come in bags of 4. How many bags of party hats does Jose need?), and 2-step “pictograph” problems (e.g., Mary keeps track of the number of chores she does on this chart [pictograph is shown with label: each picture stands for 3 chores]. She also took her grandmother to the market 3 times last week. How many chores has Mary done?). In addition, SBI was designed to broaden schemas, with each problem varying the cover story and one of the four transfer features, which change a problem without altering its type or solution: a problem with unfamiliar vocabulary, posing an additional question, incorporating irrelevant information, or combining problem types.
Near-transfer word problems
Algorithmic Word Problems (Fuchs et al., 2003) comprises 10 word problems each of which requires 1 to 4 steps. The measure samples the four problem types the correspond to SBI and that are incorporated within conventional classroom instruction: shopping list, half, buying bags, and pictograph problems. The tester reads each item aloud while students follow along on their own copies of the problems; the tester progresses to the next problem when all but 1–2 students have their pencils down, indicating they are finished. Students can ask for re-reading(s) as needed. The maximum score is 44. We used two alternate forms; the problems in both forms required the same operations, incorporated the same numbers, and presented text with the same number/length of words. In half the classes in each treatment condition, we used Form A at pretest and Form B at posttest; in the other half, forms were reversed. For the representative sample, Cronbach’s alpha was .85, and criterion validity with the previous spring’s TerraNova (CTB/McGraw-Hill, l997) Total Math score was .58 for the 844 students on whom we had TerraNova scores. Interscorer agreement, computed on 20% of protocols by two independent scorers, was .984.
Complex Word Problems (Fuchs et al., 2003) comprises nine problems representing the same four problem types within more complex contexts, which incorporate the four transfer features explicitly taught within SBI: (a) adding multiple quantities of items with different prices, with information presented in bulleted format and with a selection response format; (b) adding multiple quantities of items with different prices, also asking for money left at the end; (c) a step-up function problem with irrelevant information; (d) a step-up function that requires students to compare the prices of two packaging options; (e) a half problem using the words share equally instead of half; (f) a pictograph/adding problem asking for money left at the end; (g) a pictograph/adding problem comparing two quantities; (h) a problem with irrelevant information that combined multiple quantities with different prices and pictograph/adding; and (i) a problem with irrelevant information that combined multiple quantities with different prices and a step-up function. The tester reads each item aloud while students follow along on their own copies of the problems; the tester progresses to the next item when all but 1–2 students have their pencils down, indicating they are finished. Students can ask for re-reading(s) as needed. The maximum score is 79. For the representative sample, Cronbach’s alpha was .88, and criterion validity with the previous spring’s TerraNova Total Math Score was .55 for the 844 students on whom we had TerraNova scores. Interscorer agreement, computed on 20% of protocols by two independent, “blind” scorers, was .983.
Far-transfer word problems
Real-World Problem Solving simultaneously assesses transfer of all four problem types and all four transfer features addressed in SBI. Also, to decrease association between the task and classroom or tutoring SBI, far transfer was formatted to look like a commercial test (printed with a formal cover, on green paper, with photographs and graphics interspersed throughout the test booklet). Two assessments were constructed as alternate forms: Although the context of the problem situations differed, the structure of the problem situation and the questions were identical, and the problem solutions and reading demands were equivalent.
Performance was scored according to a rubric with four dimensions: conceptual underpinnings, computational applications, problem-solving strategies, and communicative value. The original rubric (Kansas Board of Education, l991) scored responses on a 6-point scale. To enhance reliability, we awarded points on a finer basis (e.g., the problem-solving strategies score included points for finding relevant information, accumulating to a total, showing all computation, working the answer in distinct multiple parts, labeling at least half of the multiple parts, and labeling work with monetary and operation signs). Across the four questions and four scoring dimensions, the maximum score is 72. On this sample, Cronbach’s alpha was .91 at pretest; .94 at posttest; concurrent validity with WJ-III Applied Problems (Woodcock et al., 2001) was .47 at pretest; .61 at posttest. Interscorer agreement, computed on 20% of protocols by two independent “blind” scorers, was .987 at pretest; .949 at posttest. Given the deleterious effects of student unfamiliarity with performance assessments (Fuchs, Fuchs, Karns, Hamlett, Dutka, & Katzaroff, 2000), research assistants delivered a 45-min “test-wiseness” lesson before pre- and posttesting in all conditions. (The mean score across immediate, near, and far transfer correlated .62 with WJ-III Applied Problems (Woodcock et al., 2001) at pretest; .57 at posttest.)
WJ-III Applied Problems (Woodcock et al., 2001) measures skill in analyzing and solving practical math problems with 60 items. The tester orally presents items involving counting, telling time or temperature, and problem solving. The word problems addressed a range of problem types, none of which was directly addressed within SBI. Testing is discontinued after six consecutive errors. The score is the number of correct items. As reported by McGrew and Woodcock (2001), 1-year test-retest reliability is .85; the ratio of true score variance to observed variance is .88–.91. Coefficient alpha on this sample was .85.
Iowa Test of Basic Skills: Problem Solving and Data Interpretation
With Iowa Test of Basic Skills: Problem Solving and Data Interpretation (Hoover, Dunbar, & Frisbie, 2001), students solve 24 word problems and use data presented in tables and graphs to solve word problems. The problems on this test were related only marginally to the content of SBI. Five problems included pictographs embedded within problem types not addressed in SBI. One problem incorporated irrelevant information, again embedded in a problem type not addressed in SBI. For grades 1–5, KR20 is .83–.87. In this study, coefficient alpha was .86.
Instruction
On the basis of random assignment, students received conventional math problem-solving or validated SBI. We describe these conditions briefly. For additional information, see Fuchs et al. (in press). The problem types were already described under Measures.
Conventional instruction
To guide instruction relevant to the four problem types, conventional instruction relied primarily on Houghton Mifflin Math (Greenes et al., 2007). Instruction addressed one problem type at a time (as did SBI) and focused on the concepts underlying the problem type. In addition, a prescribed set of problem-solution rules was taught, with explicit steps for arriving at solutions to the problems presented in the narrative. There was no attempt to broaden students’ schemas for these problem types to address transfer. However, in comparison to the classroom SBI, classroom control group instruction provided more practice in applying problem-solution rules and provided greater emphasis on computational requirements. Conventional instruction was explicit and relied on worked examples, guided group practice, independent work with checking, and homework. In addition, conventional instruction (as well as SBI) incorporated a 3-week researcher-designed and delivered general problem-solving strategies unit.
General problem-solving strategies instruction (conventional instruction and SBI)
Conventional instruction and SBI students received a researcher-designed 3-week (2 lessons per week) instructional unit on general math problem-solving strategies, which was conceptually unrelated to SBI. It addressed making sure answers make sense; lining up numbers from text to perform math operations; checking computation; and labeling work with words, monetary signs, and mathematical symbols. These six lessons, each lasting 30–40 min, relied on worked examples with explicit instruction, dyadic practice, independent work with checking, and homework, for a total of 210 min. For a manual with general problem-solving strategies, contact the first author.
SBI
For an SBI manual, contact the first author. SBI students received the 3-week general math problem-solving unit as well as four researcher-designed 3-week SBI units. Each SBI unit comprised six sessions. Also, two cumulative review sessions were delivered the week after winter break. In each unit, Sessions 1 and 5 lasted about 40 min; the others lasted about 30 min. This totaled 200 min per unit and 856 min across the units (including the two cumulative review sessions). Each 3-week unit addressed one of the four problem types: shopping list, buying bag, half, and pictograph.
Within each unit, the sequence of lessons was as follows. In Sessions 1–4, problem-solution instruction was delivered, using problems that varied only cover stories. A poster listing the steps of the solution method was displayed in the classroom. In Session 1, teachers addressed the underlying concepts and structural features for the problem type, presented a worked example and, as they referred to the poster, explained how each step of the solution method had been applied in the example. Students responded frequently to questions. After reviewing the concepts and presenting several worked examples in this way, teachers shared partially worked examples while students applied the solution steps. Students then completed 1–4 problems in dyads, where stronger students helped weaker students solve problems and check work with answer keys. Sessions 2–4 were structured similarly, with a greater proportion of time spent on partially worked examples and dyadic practice. Also, at the end of Sessions 2–4, students completed one problem independently; the teacher checked work against an answer key; and students graphed scores.
Sessions 5–6 were designed to broaden schemas, with each problem varying the cover story and one of the four transfer features addressed in SBI. Teachers first taught the meaning of the word transfer. Then, they taught the four transfer features, which change a problem without altering its type or solution: A familiar problem type, for which a solution is known, can use unfamiliar vocabulary, can pose an additional question, can incorporate irrelevant information, can combine problem types. A poster, “Transfer: Ways Problems Change,” was displayed. In Session 5, teachers explained the poster, illustrating each transfer feature with a worked example. They gradually moved to partially worked examples. Then, students worked in pairs to apply the solution method to problems that varied transfer features. In Session 6, teachers reviewed the four transfer features using similar procedures, except students spent more time working in dyads and then completed a problem independently, scored work against a key, and graphed scores.
Delivery
Each research assistant, all full-time research employees or graduate students in the College of Education, had responsibility for students in both conditions. All sessions were scripted to ensure consistency of information; however, to permit natural teaching styles, scripts were studied, not read. To ensure comparable mathematics instructional time across conditions, SBI sessions occurred within the confines of the mathematics instructional block. At the end of the study, classroom teachers reported the number of minutes per week they spent on math, including time on SBI, and the amount of instructional time for conventional versus SBI students was comparable and similar.
Treatment fidelity
Prior to the first delivery of each session, research assistants agreed on the essential information in the script and made a checklist of points. Each session was audiotaped. At the study’s end, two research assistants independently listened to tapes while completing the checklist to identify the percentage of points addressed. We sampled tapes so that, within conditions, research assistants and lesson types were sampled equitably. In conventional instruction, 1–2 tapes were sampled per class (for Unit 1); in SBI, 6–7 tapes were sampled per class (distributed equally across Units 1–5). Intercoder agreement, calculated on 20% of the sampled tapes, was 97.2%. The mean percentage of points addressed was 98.34 (SD = 3.16) for conventional instruction and 95.82 (SD = 2.46) for SBI.
Data Analysis and Results
Descriptive Data
Data analysis progressed in two stages. First, the measurement models for pretreatment and posttreatment measures were estimated using confirmatory factor analysis. Second, various relational models were tested using structural equation modeling. Prior to model estimation, the data were pre-analyzed to identify outliers and estimate departures from univariate and multivariate normality. Univariate plots revealed no significant outliers (plus or minus three standard deviations from the mean of the sample on that variable). PRELIS 8.7 (Jöreskog & Sörbom, 2004) was used to explore univariate and multivariate normality. In the case of univariate normality, PRELIS provides separate estimates of skew and kurtosis for each variable with accompanying p-values. Several variables exhibited significant skew (Complex Word Problems, Subtraction Fact Fluency, and DA Skill A) and kurtosis (Real-Word Problem Solving and Subtraction Fact Fluency). Mardia’s statistic for multivariate normality revealed significant multivariate nonnormality for skew (z = 2.361, p = 0.018) but not for kurtosis (z = 0.787, p = 0.431). To examine the extent to which nonnormality affects the chi-square fit statistic, models were constructed using maximum likelihood versus a scaled chi-square estimated with robust standard errors using the method developed by Satorra and Bentler (1994) as suggested by West, Finch, and Curran (1995). A scaling correction factor was calculated representing the standard chi-square divided by the scaled chi-square. Scaling correction factors ranged from 0.97 to 1.05 across models suggesting little difference between the standard and scaled chi-square values. Thus, we concluded that multivariate nonnormailty had little effect on the estimated chi-square in this study. For the remainder of the paper, we report results from models estimated with LISREL 8.7 (Jöreskog & Sörbom, 2004) using a maximum likelihood estimation on the sample of subjects with complete data. There is growing evidence to suggest that maximum likelihood-based fit indices outperform other estimation procedures and perform reasonably well with small sample sizes even when distributions are less-than optimal (see Hu & Bentler, 1998).
In Table 1, we show means and standard deviations to describe the sample on pretreatment performance variables and on the math outcome variables. We provide this for the total sample and by instructional condition. In Table 2, we show correlations among the pretreatment performance and the math outcome study variables for the total sample. We note that all observed (manifest) variables were transformed to z-scores prior to structural equation modeling. Also in Table 2, we also show correlations between treatment condition (validated SBI vs. conventional) and the math outcome study variables (we do not provide the correlations between treatment condition and pretreatment performance variables because treatment was randomized).
Table 2.
Correlations among Study Variablesa
| Correlations
|
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pre
|
Post
|
|||||||||||||||||||
| Language
|
Attention
|
Dynamic Assessment
|
Calculations
|
Word Problems
|
Word Problems-FT
|
Word Problems-NT
|
||||||||||||||
| Variable | Treatb | GC | LC | V | MR | S13 | S56 | S79 | DA1 | DA2 | DA3 | A | S | M | AL1 | RW | I | AP | AL2 | |
| Pretreatment Performance | ||||||||||||||||||||
| Language | ||||||||||||||||||||
| Grammatic Closure (GC) | --c | |||||||||||||||||||
| Listening Comp. (LC) | -- | 59 | ||||||||||||||||||
| Vocabulary (V) | -- | 55 | 57 | |||||||||||||||||
| Nonverbal Reasoning | ||||||||||||||||||||
| Matrix Reasoning (MR) | -- | 17 | 24 | 23 | ||||||||||||||||
| Attention | ||||||||||||||||||||
| SWAN 1–3 (S13) | -- | 36 | 33 | 42 | 21 | |||||||||||||||
| SWAN 4–6 (S46) | -- | 36 | 30 | 38 | 19 | 93 | ||||||||||||||
| SWAN 7–9 (S79 | -- | 34 | 29 | 37 | 10 | 90 | 93 | |||||||||||||
| Dynamic Assessment | ||||||||||||||||||||
| DA1 | -- | 30 | 30 | 29 | 50 | 36 | 33 | 29 | ||||||||||||
| DA2 | -- | 36 | 37 | 35 | 44 | 43 | 43 | 37 | 58 | |||||||||||
| DA3 | -- | 20 | 27 | 33 | 29 | 20 | 15 | 07 | 28 | 35 | ||||||||||
| Calculations | ||||||||||||||||||||
| Add Facts (A) | -- | 14 | 17 | 25 | 29 | 41 | 43 | 37 | 46 | 37 | 17 | |||||||||
| Subtract Facts (S) | -- | 18 | 17 | 25 | 28 | 39 | 42 | 35 | 39 | 42 | 28 | 73 | ||||||||
| Mixed Algorithms (M) | -- | 17 | 17 | 20 | 24 | 43 | 47 | 40 | 40 | 47 | 24 | 62 | 64 | |||||||
| Word Problems | ||||||||||||||||||||
| Algorithmic Word Problems (AL1) | -- | 36 | 39 | 34 | 35 | 43 | 41 | 34 | 42 | 51 | 25 | 34 | 37 | 32 | ||||||
| Outcomes | ||||||||||||||||||||
| Word Problems-Far Transfer (FT) | ||||||||||||||||||||
| Real-World Word Problems (RW) | 20 | 38 | 45 | 48 | 41 | 53 | 50 | 42 | 41 | 58 | 34 | 40 | 43 | 44 | 67 | |||||
| Iowa (I) | 07 | 44 | 50 | 44 | 38 | 50 | 46 | 42 | 48 | 52 | 36 | 34 | 42 | 36 | 64 | 66 | ||||
| WJ Applied Problems (AP) | 05 | 39 | 45 | 46 | 46 | 45 | 49 | 42 | 60 | 68 | 36 | 52 | 52 | 57 | 61 | 66 | 67 | |||
| Word Problems-Near Transfer (NT) | ||||||||||||||||||||
| Algorithmic Word Problems (AL2) | 69 | 23 | 26 | 19 | 14 | 33 | 36 | 32 | 24 | 30 | 09 | 22 | 17 | 31 | 43 | 49 | 40 | 39 | ||
| Complex Word Problems (C) | 65 | 25 | 26 | 22 | 11 | 37 | 37 | 33 | 23 | 29 | 07 | 24 | 15 | 28 | 45 | 54 | 41 | 39 | 82 | |
Add decimal to each number (e.g., 59 is .59).
Treat is treatment condition, where 1=conventional instruction on word problems and 2=validated SBI on word problems.
The correlation between treatment condition and the dimensions of pretreatment performance were set to zero, given random assignment to treatment.
Pretreatment Measurement Model: Is DA a Distinct Dimension of Pretreatment Ability?
Our pretreatment measurement model included six dimensions of pretreatment performance. The first latent variable, language ability, comprised TOLD Grammatic Closure, WDRB Listening Comprehension, and WASI Vocabulary. The second dimension, attentive behavior, included three clusters of items from the SWAN (items 1–3, items 4–6, and items 7–9). The third latent variable, DA, comprised DA Skill A, DA Skill B, and DA Skill C. The fourth latent variable, calculations skill, incorporated Addition Fact Fluency, Subtraction Fact Fluency, and Test of Mixed Algorithms. The fifth latent variable, a single manifest variable, WASI Matrix Reasoning, was used to measure nonverbal reasoning. Within structural equation modeling, the default is to set the error variance to zero for manifest variables. Instead of using the default, we accounted for measurement error in nonverbal reasoning using the alpha coefficient for the present sample (r = .94) to specify the error variance. A reliability of .94 is equivalent to an error variance of 0.06 times the variance of nonverbal reasoning, which in this case was 1.0 (for details, see MacCallum, 1995). The final latent variable, Algorithmic Word Problems, was also a single manifest variable. It was used to measure pretreatment word-problem skill. To account for measurement error in word-problem skill, we used the alpha coefficient for the present sample (r = .84) to specify the error variance of 0.16.
See Table 3 for correlations among the pretreatment measurement model latent traits. All observed variables loaded substantially and reliably onto their respective factors (standardized coefficients: .44 to .98, ps < .001). Because this base measurement model included the greatest number of estimated parameters (compared to the competing measurement models), it provided the best characterization of the data and served as a basis for comparing the competing, more parsimonious models. Chi-square goodness-of-fit statistic plus four different fit indices (representing Type 1–3 fit and absolute-fix indices) are provided. Jaccard and Wan (1996) and Kline (1998) suggest use of multiple fit indices to reflect diverse criteria. Hu and Bentler (1998) recommend with maximum likelihood estimation methods that standardized root-mean-square residual (SRMR, absolute fit) be reported and supplemented with normed fit index (NFI, Type 1 fit), nonnormed fit index (NNFI, Type 2 fit), and comparative fit index (CFI Type 3 fit). In evaluating a model, adequate fit is indicated by a nonsignificant chi-square test; NFI, NNFI, and CFI exceeding .95; and a SRMR of less than .08 (see Hu & Bentler). The base 6-factor measurement model accounted well for the data structure, X2 (64, N=122) = 58.31, p = .6771; NFI = .965; NNFI = 1.000; CFI = 1.000; and SRMR = 0.0389 (see Pretreatment Measurement Model 1 in Table 4 and Figure 1).
Table 3.
Latent Trait Correlations
| Pretreatment | L | NVR | A | DA | WP |
|---|---|---|---|---|---|
| Language (L) | |||||
| Nonverbal Reasoning (NVR) | .31 | ||||
| Attention (A) | .48 | .18 | |||
| Dynamic Assessment (DA) | .60 | .64 | .50 | ||
| Calculations (C) | .31 | .33 | .52 | .67 | |
| Word Problems (WP) | .52 | .40 | .45 | .68 | .46 |
| Posttreatment | NT | ||||
| Near Transfer (NT) | |||||
| Far Transfer (FT) | .49 | ||||
Table 4.
Fit indices and Model Comparisons for the Competing Measurement Models
| Model | df | χ2 | p | NFI | NNFI | CFI | SRMR | Δχ2 Model 1 |
|---|---|---|---|---|---|---|---|---|
| Pretreatment Measurement Models | ||||||||
| Six-Factor Model | ||||||||
| 1. L, A, DA, C, NVR, WP | 64 | 58.31 | .6771 | .965 | 1.000 | 1.000 | .0389 | |
| Five-Factor Models | ||||||||
| 2. A, C, NVR, WP, L+DA | 69 | 145.88 | .0000 | .927 | .995 | .965 | .0783 | 87.49* |
| 3. L, C, NVR, WP, A+DA | 69 | 199.78 | .0000 | .897 | .912 | .933 | .1325 | 91.47* |
| 4. L, A, NVR, WP, C+DA | 69 | 147.54 | .0000 | .926 | .952 | .964 | .0739 | 89.23* |
| 5. L, A, C, WP, NVR+DA | 69 | 155.82 | .0000 | .917 | .946 | .954 | .1803 | 97.51* |
| 6. L, A, C, NVR, WP+DA | 69 | 137.19 | .0000 | .931 | .960 | .970 | .0686 | 78.88* |
| One-Factor Model | ||||||||
| 7. General Factor | 77 | 634.07 | .0000 | .745 | .731 | .775 | .1753 | 575.76* |
| Posttest Measurement Models | ||||||||
| Two-Factor Models | ||||||||
| 1. Near Transfer, Far Transfer | 4 | 6.67 | .1541 | .981 | .982 | .993 | .0323 | |
| 2. Simple, Complex | 4 | 92.61 | .0000 | .729 | .472 | .736 | .1456 | 84.94* |
| One-Factor Model | ||||||||
| 3. General Math Factor | 5 | 83.41 | .0000 | .686 | .384 | .692 | .1423 | 76.74* |
Note. N = 122. For pretreatment models, L = language factor; A = attention factor; DA = dynamic assessment factor; C = calculation factor; NVR = nonverbal reasoning factor; S = story problem factor. NFI = norm fit index; NNFI = nonnormed fit index; CFI = comparative fit index; SRMR = standardized root-mean-square residual.
p < .001.
Figure 1.
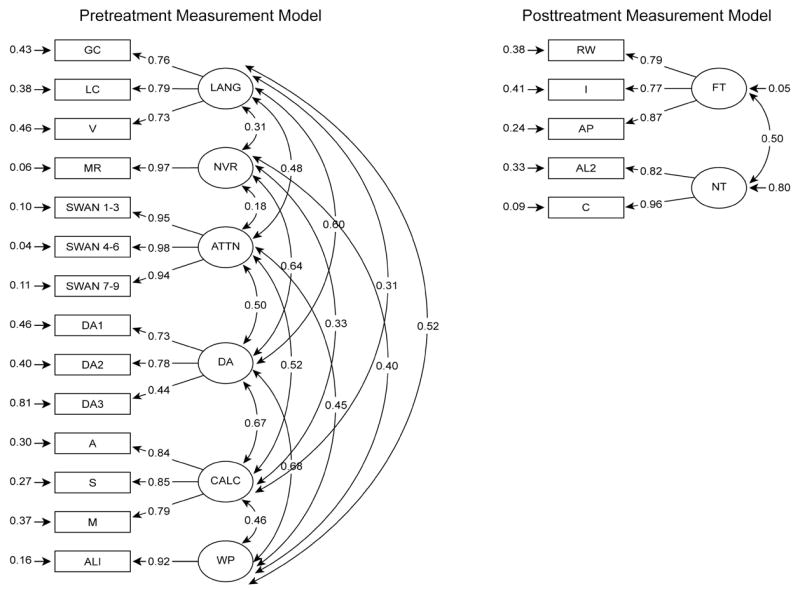
Pretreatment and posttest measurement models. Panel one shows the base pretreatment measurement model, which incorporated each of the six dimensions of pretreatment ability measured in September and October: language ability, attentive behavior, nonverbal reasoning, calculations skill, word-problem skill, and DA. Panel 2 shows the two dimensions of posttreatment word-problem outcome measured in March: near-transfer word problems (Algorithmic Word Problems and Complex Word Problems) and far-transfer word problems (Real-World Problem Solving, the Iowa, and WJ Applied Problems).
To assess the distinctiveness of DA as a pretreatment performance dimension, we compared this base measurement model against five more parsimonious, 5-factor measurement models. The utility of one model to explain data can be compared statistically against the utility of other models in which it is nested by using a chi-square difference tests (i.e., ΔX2). The base model always yields the best fit because it includes the most estimated parameters and is therefore the least restrictive model. However, in the interest of parsimony, a more restrictive nested model that fails to yield a significantly worse fit is accepted as superior.
In each of the five competing 5-factor measurement models, we merged DA with one other dimension of pretreatment performance. So, for example Pretreatment Measurement Model 2 (see Table 4) included a separate attentive behavior factor, a separate calculations skill factor, a separate nonverbal reasoning factor, pretreatment word-problem skill, and a factor in which indices of language and DA loaded together (on a single factor). In Pretreatment Measurement Models 3, 4, 5, and 6 (see Table 4), DA was combined with one of the other pretreatment performance dimensions. Finally, we assessed a most parsimonious model, in which all indices were loaded onto one single factor (see Pretreatment Measurement Model 7 in Table 4). Each of these modified, more parsimonious measurement models yielded a significantly worse fit of the data compared to the base measurement model, as reflected in the significant ΔX2 values in Table 4. We therefore concluded that DA measured a distinct dimension of pretreatment ability, and we incorporated all six dimensions of pretreatment ability into our structural model to predict word-problem outcome.
Posttreatment Measurement Model: Are Near- and Far-Transfer Distinct Dimensions of Posttreatment Mathematics Word-Problem Skill?
Our posttreatment measurement model included two dimensions of posttreatment word-problem skill. The first latent variable, near-transfer word problems, comprised Algorithmic Word Problems and Complex Word Problems. The second dimension, far-transfer word problems, included Real-World Word Problems, the Iowa, and WJ Applied Problems. See Table 3 for correlations among the posttrreatment measurement model latent traits. All observed variables loaded substantially and reliably onto their respective factors (standardized coefficients: .69 to .89, ps < .001). The 2-factor solution (near-transfer and far-transfer) accounted well for the data structure, X2 (4, N=122) = 6.57, p = .154; NFI = .981; NNFI = .983; CFI = .993; and SRMR = 0.0323 (see Posttreatment Measurement Model 1 in Table 4).
We contrasted this base measurement model with an alternative 2-factor model comprising a simple word-problem latent variable (the Iowa and Algorithmic Word Problems) and a complex word-problem latent variable (comprised of Complex Word Problem, Real-World Word Problems, and WJ Applied Problems). The same four independent judges who had classified near versus far transfer re-classified the measures in terms of simple versus complex. This alternative represented a theoretically different means to represent the factor structure of the word-problem outcome measures. This model fit substantially worse than the base model, X2 (4, N=122) = 92.61, p = .0000; NFI = .729; NNFI = .472; CFI = .736; and SRMR = 0.1456. (A chi-square difference score could not be used because these models are not nested.). The 2-factor near- and far-transfer model included more estimated parameters than the competing measurement model; therefore, it provided the better characterization of the data and served as a basis for comparing the competing, more parsimonious model.
We then assessed whether both dimensions (near- vs. far-transfer) of posttreatment word-problem skill were necessary, by comparing this base measurement model against a more parsimonious, 1-factor measurement model, which yielded a significantly worse fit of the data as reflected in the significant ΔX2 value for Posttreatment Measurement Model 2 in Table 4. We therefore concluded that both dimensions of posttreatment word-problem skill (near- and far-transfer) were necessary, and we incorporated both dimensions into our structural model.
Structural Model: Assessing the Predictors of Word-Problem Outcome Skill
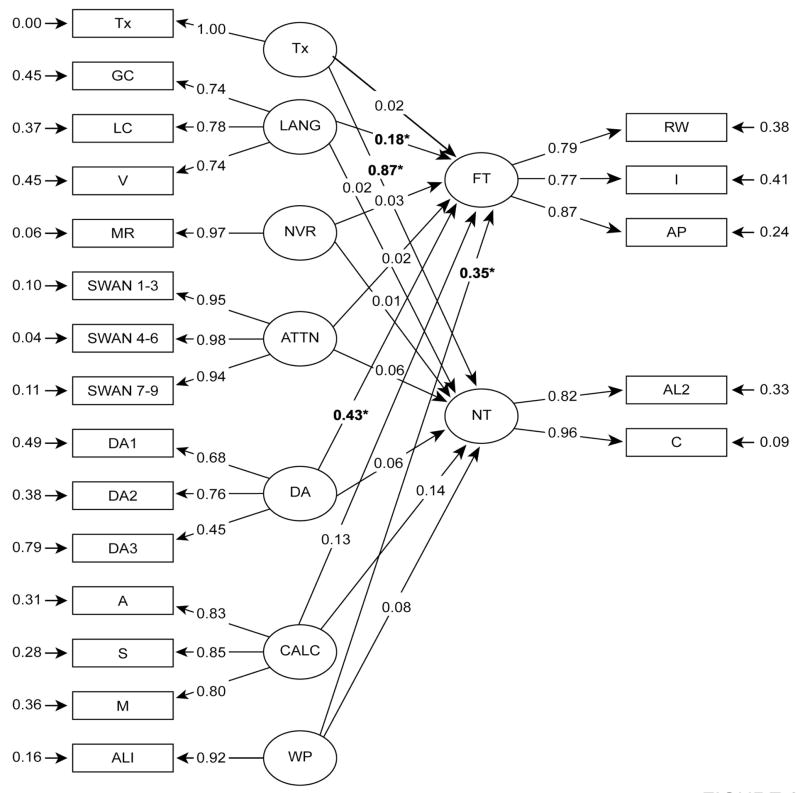
Because few studies of this type have been conducted, we took an exploratory approach to model building. We first assessed the least parsimonious structural model. In this base model, each of the six dimensions of pretreatment performance (measured in September and October) plus treatment was included as a predictor of near-transfer word-problem skill and of far-transfer word-problem outcome (measured in March) (see Table 5 and Figure 2, Full Model). In this model (and in all subsequent nested structural models), we set the correlation between treatment and the dimensions of pretreatment performance to zero, given random assignment to treatment. (The other dimensions of pretreatment performance were allowed to correlate freely.) As shown in Table 5, the model provided a good fit with the data (X2 [143, N=122) = 169.61, p = .0637; NFI = .950; NNFI = .986; CFI = .989; and SRMR = 0.0758). Treatment was the only significant predictor of near transfer. DA, pretreatment word-problem skill, and language were significant predictors of far transfer.
Table 5.
Fit indices and Model Comparisons for the Competing Structural Models
| Model | df | χ2 | p | NFI | NNFI | CFI | SRMR | Δχ2 Model 1 |
|---|---|---|---|---|---|---|---|---|
| 1. Full Model | 143 | 169.61 | .0637 | .950 | .986 | .989 | .0758 | |
| 2. Cognitive Model | 149 | 235.10 | .0000 | .932 | .965 | .977 | .0873 | 65.49* |
| 3. Math Model | 151 | 210.16 | .0011 | .940 | .976 | .981 | .0818 | 40.55* |
| 4. DA Model | 153 | 190.91 | .0203 | .945 | .984 | .987 | .0783 | 21.30* |
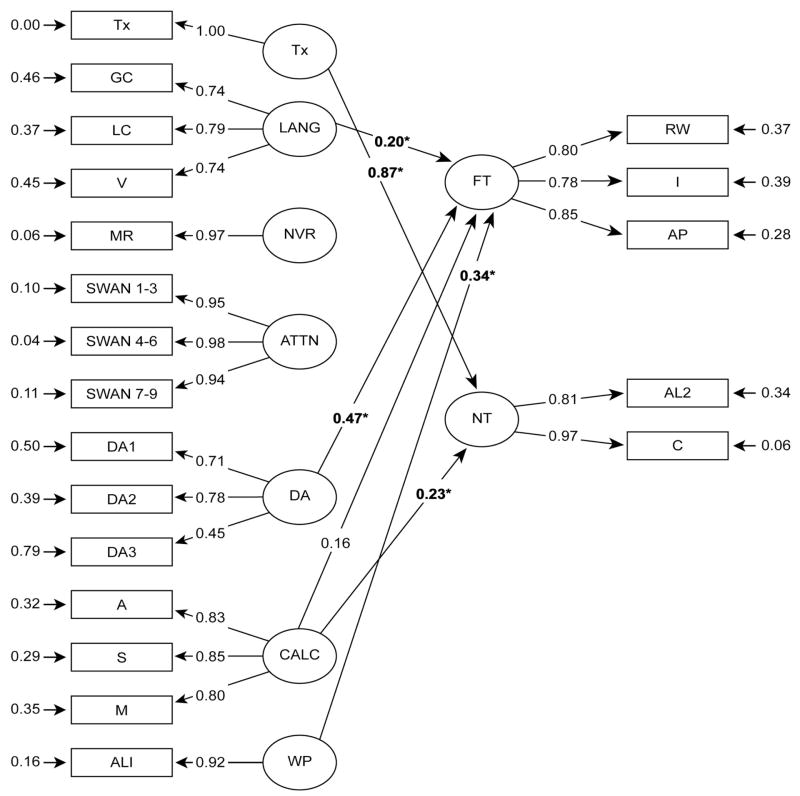
| 5. Trimmed Full Model | 151 | 174.84 | .0895 | .949 | .998 | .991 | .0859 | 5.23 |
Note. N = 122. DA = dynamic assessment factor; NFI = norm fit index; NNFI = nonnormed fit index; CFI = comparative fit index; SRMR = standardized root-mean-square residual.
p < .001.
Figure 2.
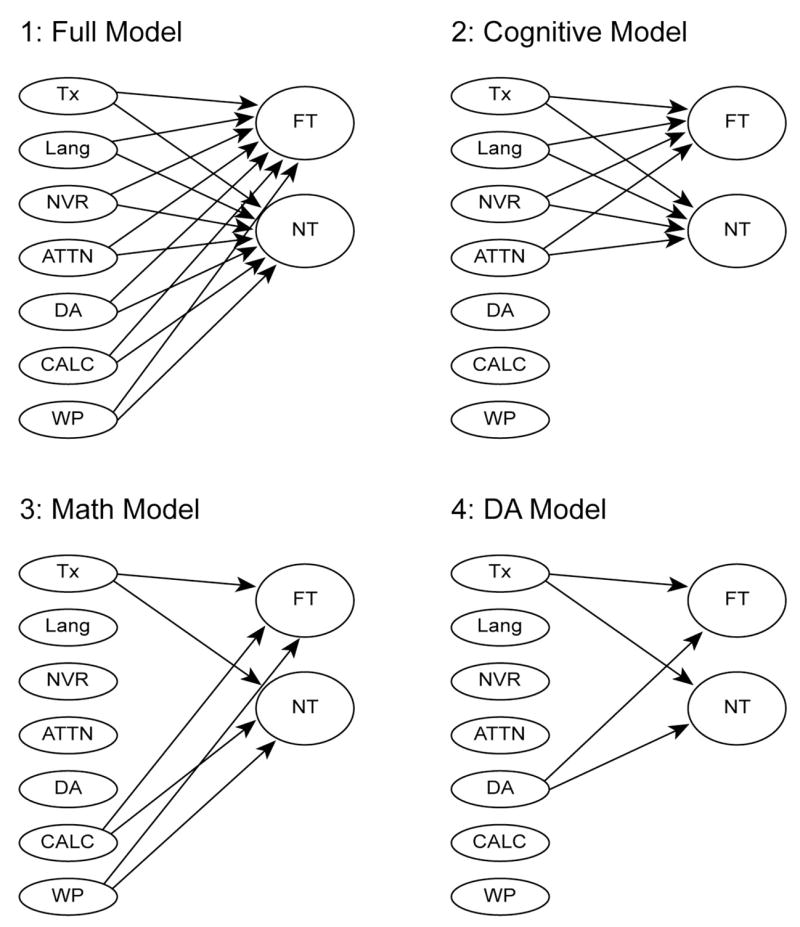
Four structural models predicting pretreatment performance (measured in September and October) plus treatment to posttreatment near- and far-transfer outcomes (measured in March). The Full (base) Model is the least parsimonious structural, in which each of the six dimensions of pretreatment performance plus treatment was included as a predictor of outcomes. Each of the subsequent (nested) models is more parsimonious. In the Cognitive Model, pretreatment cognitive dimensions and treatment were examined as the sole predictors of outcomes. In the Math Model, pretreatment calculations and word-problem skill and treatment were considered as the sole predictors of outcomes. In the DA Model, pretreatment DA and treatment were examined as the sole predictors of outcomes.
We then contrasted three alternative, more parsimonious structural models. In each of these models, treatment was retained as a predictor of outcome. In Models 2 and 3, we considered whether DA was in fact necessary to forecast word-problem outcomes or whether other dimensions of pretreatment ability function well without the inclusion of DA. Alternatively, it is possible that DA, in combination with treatment, is sufficient to account for the data structure in predicting word-problem outcomes, without including pretreatment cognitive abilities or pretreatment math skills. This was assessed in Model 4.
Specifically, in Model 2, the pretreatment cognitive dimensions and treatment were examined as the sole pretreatment predictors of outcome (see Cognitive Model in Table 5 and Figure 2). Given prior work establishing language (Fuchs et al., 2008; Jordan et al., 1995, nonverbal reasoning Fuchs et al., 2005; 2006; Agness & McLone (1987), and attentive behavior (Fuchs et al., 2005; 2006; Passolunghi et al., 1999) as predictors of word-problem skill, we deemed it possible that the cognitive predictors and treatment alone would suffice in accounting for outcomes. If this Cognitive Model did not produce a significantly worse fit of the data structure compared to the base model, then assessing pretreatment foundational math skills and DA would be unnecessary, thereby providing a more parsimonious procedure for predicting outcome and undermining the importance of DA.
In Model 3, pretreatment math skills (on calculations and word problems) and treatment were considered as the sole predictors of near-and far-transfer (see Math Model in Table 5 and Figure 2). Given the transparent nature of the relation of pretreatment calculations skill and pretreatment word-problem skill to the word-problem outcomes, as well as prior work showing the pretreatment skill is often the best predictor of learning, we deemed it possible that these foundational math skills, along with treatment, would be sufficient to account for word-problem outcomes. Again, if this Math Model did not produce a significantly worse fit of the data structure compared to the base model, then assessing the pretreatment cognitive abilities and DA would be unnecessary, consequently providing a more parsimonious approach for predicting outcome and undermining the importance of DA.
By contrast, in Model 4, we examined whether DA (along with treatment) might be sufficient to forecast near- and far-transfer word-problem outcome (see DA Model in Table 5 and Figure 2). As with the previous models, if the DA Model did not produce a significantly worse fit of the data structure compared to the base model, then assessing pretreatment cognitive abilities and pretreatment foundational skills would be unnecessary, hence providing a more parsimonious procedure for predicting outcome. This would demonstrate DA’s power as a predictor of outcome even further than the base model, in which DA is one of three significant predictors of far-transfer outcome.
As shown in Table 5, each of these four nested, contrasting models produced a significantly worse fit of the data, suggesting that the full model is the best representation of the data structure. Figure 3 shows the full model with all coefficients specified (bolded, asterisked coefficients are p < .001).
Figure 3.
The full SEM with all coefficients specified (asterisked coefficients are p < .001).
Then, in the interest of reducing the parameter-to-sample-size ratio, we ran a trimmed model, deleting paths with standardized coefficients of less than .10. This trimmed model also provided a good fit with the data (see Figure 4 and last line of Table 5). Because there was no appreciable change in fit when moving from the full to the trimmed model, the simpler model is preferred. The coefficients in the full and trimmed models were highly similar, except that the path from calculations skill to near-transfer word problems increased from .14 to a significant .23 in the trimmed model.
Figure 4.
The trimmed SEM with asterisked coefficients p < .001.
Discussion
We extended prior work on DA in several ways. First, earlier studies formulated DA tasks to address general cognitive abilities (e.g., Day et al., 1997; Speece et al., 1990) or a cognitive ability specifically linked to performance in the academic domain (e.g., Spector, 1997; Swanson & Howard, 2005). In the present study, by contrast, we centered DA on students’ potential to learn algebra, which is neither a general cognitive ability nor a precursor to third-grade word-problem skill. In fact, skill with algebra is not even considered foundational to third-grade word-problem skill and instead represents novel academic content within the same broad academic area (mathematics). The potential advantage of using a DA task with novel academic content, such as algebra at third grade, is that it increases the probability that students’ DA performance is attributable to their potential to learn new content rather than to existing ability to perform the DA task. In fact, among the 122 participants, only two students exhibited mastery on all three DA skills prior to the introduction of scaffolded instruction (another two exhibited mastery on two of the three skills prior to scaffolded instruction, and another 34 exhibited mastery on one of the three skills prior to scaffolded instruction). The remaining 84 students failed to exhibit mastery on any of the skills prior to scaffolded instruction. At the same time, it is important that the novel academic content connects in some important ways to the predicted learning outcome. In designing this study’s DA as a method of forecasting development of word-problem skill, we hypothesized a connection between algebraic cognition and word-problem skill because (a) although linguistic content is absent from algebra, algebra does require understanding of relations among quantities, as is the case for solving word problems, and (b) some research (e.g., Fuchs, Seethaler, Powell, Fuchs, Hamlett, & Fletcher, 2008) shows that algebra can be used to develop students’ word-problem skill, even in the primary grades.
In addition, we extended prior DA work in terms of the scope of the variables we considered as competitors to DA in predicting outcome. That is, we incorporated the nature of treatment into the prediction model, even as we simultaneously included static cognitive abilities as well as foundational math skill (on calculations as well as word problems) to predict outcomes that were proximal to as well as distal from the instruction students received in school. Our pretreatment measurement modeling supported DA as representing a dimension of pretreatment ability distinct from existing language ability, nonverbal reasoning, attentive behavior, and math skill. This finding echoes the work of Day et al. (1997) conducted with preschoolers, who found that the measurement model that retained DA as a construct separate from pre-DA provided better fit of the data. Together, Day et al.’s and our pretreatment measurement modeling indicates that DA may represent an aspect of students’ learning potential that is distinct from conventional static measures. This makes sense because static assessment quantifies already-developed abilities that are influenced by environmental factors such as educational opportunity in school, parental support, and test-taking skills (Grigorenko & Sternberg, 1998), whereas DA measures a student’s potential to learn. In this way, findings provide support for Vygotsky’s (1978) concept of the zone of proximal development, or the distance between a child’s realized developmental level as assessed by independent performance and that child’s potential development as assessed via supported performance, as a distinct cognitive characteristic.
Importantly, however, our work also extends Day et al.’s (1997) investigation as well as other seminal DA studies that examine DA’s utility as a predictor of academic performance (e.g., Speece et al., 1990; Swanson & Howard, 2005) by assessing whether DA is a viable predictor of future (rather than concurrent) learning. It also extends Spector’s (1997) prediction of kindergarteners’ future reading performance by considering how instruction affects relations among static and dynamic measures in forecasting school learning. In terms of whether DA is a viable predictor of future learning, our results provide support. We contrasted a full model of predictors, which included treatment plus six dimensions of pretreatment performance (language ability, nonverbal reasoning, attentive behavior, DA, calculations skill, and word-problem skill), against models that isolated static cognitive abilities (language ability, nonverbal reasoning, and attentive behavior), that isolated DA, and that isolated math skill (on calculations and word problems). None of these contrasting, more parsimonious models fit the data as well as the full model. Therefore, although DA (along with treatment) was insufficient, it was necessary in accounting for the data structure. This finding suggests that DA may serve an important role in predicting students’ future learning. It also indicates that forecasting later academic performance creates variance for DA to capture. This may occur because upcoming learning may relate better with learning potential as indexed via DA than with static assessments that are determined in part by culture, socioeconomics, and previous learning opportunity. More specifically, these findings support a possible connection between algebraic cognition and word-problem skill, a possibility that should be pursued in future work, and indicate that novel academic content may provide a productive avenue for designing DAs in other academic domains.
With respect to how instruction affects relations among static and dynamic measures in forecasting actual school learning, our measurement models showed that two latent variables of outcome, near- and far-transfer, were necessary to account for the structure of students’ posttreatment word-problem skill, and both dimensions of outcome were important for understanding how instruction affects the relations among static and dynamic measures in forecasting learning. Although all items on all five outcome measures were novel and none had been used for instruction, only treatment and pretreatment calculations skill accounted for learning on the latent outcome variable more closely aligned with treatment. By contrast, to forecast learning on word-problem measures more distally related to treatment, DA as well as pretreatment language ability and pretreatment word-problem skill were necessary.
That treatment forecasted near- but not far-transfer word-problem outcome is not surprising because randomized control trials (e.g., Fuchs et al., 2003; Fuchs, Fuchs, Craddock, Hollenbeck, Hamlett, & Schatschneider, 2007) have, while demonstrating the efficacy of the validated word-problem treatment used in the present study, revealed stronger effect sizes for near-transfer word-problem outcome measures (e.g., 1.73–1.90.; Fuchs et al., in press) than for far-transfer word-problem outcome measures (e.g., 0.36; Fuchs et al., in press). It is possible that with more comprehensive treatments that more fully address more generalized performance, the value of DA (as well as language ability and pretreatment word-problem skill) in predicting outcome would decrease, as the value of the treatment increases. However, effecting transfer to distal problems represents a formidable challenge in the area of math problem solving (Bransford & Schwartz, l999; Cooper & Sweller, l987; Mayer, Quilici, & Moreno, l999). Moreover, we note that the validated intervention employed in the present study is theoretically rooted in schema theory that addresses transfer (e.g., Chi, Feltovich, & Glaser, 1981; Gick & Holyoake, 1980; Mayer, 1992; Quilici & Mayer, 1996) and has been shown to accomplish transfer more effectively than conventional math problem-solving instruction (Fuchs et al., 2003). In addition, it is impossible to address all novel problem types within any given instructional program. Thus, the prediction of distal transfer, as reflected in the kinds of complex, real-world problem solving and high-stakes assessments used as distal measures in the present study, is important.
Results are relevant to the present education reform known as responsiveness-to-instruction (RTI). RTI is embedded in a multi-level prevention system, borrowed from the public health system. In a multi-level prevention system, general education constitutes primary prevention. Students who do not respond to this universal, core program enter secondary prevention. In most research, this involves one or more rounds of small-group tutoring using a validated tutoring protocol. Students who do not respond to this more intensive secondary prevention program are understood to have demonstrated “unexpected failure” to validated instruction (to which most students respond). On this basis, unresponsive students are deemed appropriate for more intensive and individualized forms of instruction at the tertiary prevention level. In this way, RTI has two complimentary purposes: (a) to identify at-risk students early and offer them intervention to prevent the onset of severe and often intractable deficits and (b) to identify students who are unresponsive to standard, validated instruction and who therefore require individualized instruction. In most RTI systems, these chronically unresponsive students are considered to have a learning disability (LD). In fact, the 2004 reauthorization of the Individuals with Disabilities Education Improvement Act (P.L. 108–446) encourages RTI for LD identification as an alternative to the traditional identification procedure, which requires documentation of a discrepancy between IQ and school achievement and often delays identification until the intermediate grades (Vaughn & Fuchs, 2003).
Within RTI models, responsiveness to secondary prevention is considered the “test” for differentiating between two explanations for low achievement: inadequate instruction versus disability. If a child responds poorly to instruction that benefits most students, then this eliminates instructional quality as an explanation of poor learning and instead suggests disability. Although earlier identification/treatment of LD represents a potential advantage of RTI, conducting secondary preventive tutoring requires at least 10 weeks and, in some models, as many as 30 weeks. Present findings suggest that DA might serve an important function in predicting responsiveness to intervention, by forecasting distal, critical aspects of learning that are not highly relevant to the student’s proximal instructional needs. For example, within RTI reading models at first grade, secondary prevention focuses predominantly on the development of word-level skills and fluency because some work (e.g., Fuchs & Fuchs, 2005; Fuchs, Fuchs, Kazdan, & Allen, 1999) suggests that instruction to develop comprehension strategies when students are still struggling to identify words accurately and fluently may detract from reading development. Nonetheless, studies (Catts & Hogan, 2002; Compton, Fuchs, Fuchs, Elleman, & Gilbert, submitted; Leach, Scarborough, & Rescorla, 2003; Lipka, Lesaux, & Siegel, 2006) show that a small but significant portion of the population experiences late-emerging reading disability, whereby their word-level and fluency skills develop typically, but serious comprehension deficits become evident at third or fourth grade. Yet, research has not reliably identified early predictors of late-emerging reading disability (Compton et al., submitted). It is possible that DA might be used in first grade to forecast development of late-emerging reading disability. This would help teachers design appropriate instruction for this subset of students early on. In a different way, DA might be used productively within an RTI framework to help identify students who will ultimately, 10–30 weeks later, prove unresponsiveness to secondary prevention. If earlier identification, via DA, were possible, then more intensive and individualized forms of instruction could be introduced sooner, without children experiencing 10–30 weeks of additional failure.
Before closing, we note the small parameter-to-sample-size ratio in this study. Use of maximum likelihood estimation with small samples size has a tendency to produce χ2 estimates that are too large. Thus, the decision for accepting or rejecting a particular model may vary as a function of sample size. In addition, sample size affects power in a predictable way, with smaller samples sizes having less power to detect differences between competing models using the χ2 statistic. Although our sample size was smaller than desirable, we did succeed in detecting significant differences using the Δχ2 statistic across competing models. In addition, our reported Type 2 and Type 3 fit indices reflected adequate fit for our final measurement and structural models. These indices have been shown to be substantially less biased by sample size (Hu & Bentler, 1998). Therefore, we have some confidence that even with our sample size, the final models represent a good estimation of the relations among measures. Moreover, we ran a trimmed model, deleting paths with standardized coefficients of less than .10, which provided a similarly good fit with the data.
Nevertheless, the parameter-to-sample-size ratio remains a limitation of the present study, and future DA research employing structural equation modeling should incorporate larger samples. With this caution in mind, we conclude that findings provide an important basis for additional research assessing the utility of DA for indexing distal outcomes and for identifying students who require tertiary prevention in a more timely way. The present database indicates the potential utility of DA for predicting math problem-solving generalization across third grade. Parallel work, with larger samples, appears warranted to examine other aspects of academic learning.
Acknowledgments
This research was supported in part by Grant #1 RO1 HD46154 and Core Grant #HD15052 from the National Institute of Child Health and Human Development to Vanderbilt University. Statements do not reflect agency position or policy, and no official endorsement should be inferred.
Appendix I
Instructional Scaffolding Levels for DA Skill A
For DA Skill A, during Instructional Scaffolding Level 1, the tester works problems for the student without explanation. The tester says, “I’m going to work some problems for you. Watch carefully while I work because I’ll ask you to do some more problems like these in a few minutes.” The tester then demonstrates three problems. Then the tester says, “Now you try to do some problems like these” and readministers the 6-item test.
During Instructional Scaffolding Level 2, the tester explains the plus and equal signs mean and what the problem means/is asking. The tester says, “The plus sign tells us to add (point). And the problem asks us to figure out what number x stands for. What number (point) can we add to 6 (point) to make the total 8 (point)? If correct: That’s right! 2 + 6 adds to 8. So the missing number is 2. I write x equals 2 (write). Now let’s look at another problem. If incorrect. That’s not quite right. 2 plus 6 equals 8. So the missing number is 2. I write x equals 2 (write). Let’s try another problem. Now try to do this practice problem (guide student using same procedure).”
During Instructional Scaffolding Level 3, the tester elaborates on what x means, relating x to the “blank” that is used more commonly in the primary grades. The tester explains, “The blank (point) stands for the missing number, just like the x stands for the missing number in this problem (point). These two problems mean the same thing. They ask us to figure out what number x, or the blank, stands for. The problem asks, “What number (point) can we add to 6 (point) to make the total 14 (point)?” 6 plus what number equals 14? If correct: That’s right! 8 + 6 equals 14. So I write 8 in the blank. That tells me that the missing number, x, equals 8. If incorrect: That’s not quite right. 6 (point) plus 8 equals 14. So, the missing number is 8. So I write 8 in the blank. That tells me that the missing number, x, equals 8. After you figure out what the missing number is, you write the missing number like this: “x = 8” We read the problem like this: 6 + x = 14; x = 8. Let’s try another problem, but this time you’ll try to do the work (guide student using same procedures).
During Instructional Scaffolding Level 4, the tester provides the student with the min counting strategy for finding the missing number. The tester says, What number (point) do we add to x (point)? (Student: 7) Yes, this problem tells us, 7 plus x. Put the number being added to x, 7, in your head. Now count up to the total, 13 (point). When I count up, I use my fingers until I reach the total (point), like this. I already have 7 in my head (point to head). I start counting up using the next number: 8 (put up one finger), 9 (put up second finger, and continue putting up fingers for each subsequent number), 10, 11, 12, 13. How many fingers am I holding up? (Student: 6). Yes, I have 6 fingers up. So, x equals 6. I know that 7 (point) + 6 (write 6 above the x) equals 13 (point). So, I know that x equals 6, and I write my answer like this: x = 6. You write the answer for me (student writes). If correct: That’s right! # + # equals #. So I write # in the blank. That tells me that the missing number, x, equals #. If incorrect: That’s not quite right. # (point) plus # equals #. So, the missing number is #. So I write # in the blank. That tells me that the missing number, x, equals #. Let’s try another one, but this time you’ll try to do it on your own (guide student using same procedures).
During Instructional Scaffolding Level 5, the tester adds color coding to help the student discriminate the salient components of the min strategy, thereby increasing the level of scaffolding with concreteness. The tester says, “This problem asks us to find what number x stands for. The problem asks, ‘What number (point) can we add to 3 (point) to make the total 5 (point)?’ What number (point) do we add to x (point)? (Student: 3) Yes, this problem tells us, 3 plus x. This number is written in green to help you remember to start counting here (point). Put the green number, 3 (point), in your head. Now count up to the total, 5 (point). What color is the total in this problem? (Student: Red.) Yes, the total is written in red to tell us when to stop counting up. We put the green number in our head. Then, we count up with our fingers until we reach the red total, like this. When I count up, I use my fingers until I reach the total (point). I already have the green 3 in my head (point to head). I start counting up using the next number: 4 (put up one finger), 5 (put up second finger). How many fingers am I holding up? (Student: 2). Yes, I have 2 fingers up. So, x equals 2. I know that 3 (point) + 2 (write 2 above the x) equals 5 (point). I know that x equals 2, and I write my answer like this: x = 2. You write the answer for me (student writes). If correct: That’s right! # + # equal #. So I write # in the blank. That tells me that the missing number, x, equals #. If incorrect: That’s not quite right. # (point) plus # equals #. So, the missing number is #. So I write # in the blank. That tells me that the missing number, x, equals #. Let’s try another one, but this time you’ll try to do the work (guide student using same procedures).
Footnotes
We excluded Byrne’s work (e.g., Byrne, Fielding-Barnsley, & Ashley, 2000) because it conceptualizes DA as the student’s rate of acquisition in response to schooling; it is not an assessment conducted to predict responsiveness to schooling. Therefore, as an assessment paradigm, Byrne’s work is more similar to responsiveness-to-intevention than to DA.
Concerning classroom as a potential source of dependency in the data, we explained the following in the revision. We calculated intra-class correlations (ICCs) for classrooms on the outcomes measures, which is where important context effects might be revealed. We found minimal ICCs for the far-transfer measures (.003 to .03). By contrast, the ICCs for the near-transfer measures were sizeable (.5 to .7). However, the ICCs for the near-transfer measures dropped to levels comparable to the far-transfer measures when the effects of treatment were controlled, as in the SEM models. So in the SEM models, variance in the outcomes is essentially at the individual not the classroom level, making it unnecessary to account for classroom in the SEM models.
References
- Agness PJ, McClone DG. Learning disabilities: A specific look at children with spina bifida. Insights. 1987:9–9. [Google Scholar]
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders. 4. Washington, DC: Author; 1994. [Google Scholar]
- Bernstein IH, Garbin CP, Teng GK. Applied multivariate analyses. New York: Springer-Verlag; 1988. [Google Scholar]
- Bransford JC, Delclos VR, Vye NJ, Burns MS, Hasselbring TS. State of the art and future directions. In: Lidz CS, editor. Dynamic assessment: An interactional approach to evaluating learning potential. New York: Guilford Press; 1987. pp. 479–496. [Google Scholar]
- Bransford JD, Schwartz DL. Rethinking transfer: A simple proposal with multiple implications. In: Iran-Nejad A, Pearson PD, editors. Review of research in education. Washington, DC: American Educational Research Association; 1999. pp. 61–100. [Google Scholar]
- Bryant DP, Bryant BR, Kim SA, Gersten R. Three-tier mathematics intervention: Emerging model and preliminary findings. Poster presented at the 14th annual meeting of the Pacific Coast Research Conference; San Diego. 2006. Feb, [Google Scholar]
- Budoff M. Learning potential among institutionalized young adult retardates. American Journal of Mental Deficiency. 1967;72:404–411. [PubMed] [Google Scholar]
- Bull R, Johnston RS. Children’s arithmetical difficulties: Contributions from processing speed, item identification, and short-term memory. Journal of Experimental Child Psychology. 1997;65:1–24. doi: 10.1006/jecp.1996.2358. [DOI] [PubMed] [Google Scholar]
- Burton GM, Maletsky EM. Math Advantage. Orlando, FL: Harcourt Brace Jovanovich; 1999. [Google Scholar]
- Byrne B, Fielding-Barnsley R, Ashley L. Effects of preschool phoneme identity training after six years: Outcome level distinguished from rate of response. Journal of Educational Psychology. 2000;92:659–667. [Google Scholar]
- Campione JC. Assisted testing: A taxonomy of approaches and an outline of strengths and weaknesses. Journal of Learning Disabilities. 1989;22:151–165. doi: 10.1177/002221948902200303. [DOI] [PubMed] [Google Scholar]
- Campione JC, Brown AL. Linking dynamic assessment with school achievement. In: Lidz C, editor. Dynamic assessment: An interactional approach to evaluating learning potential. New York: Guilford Press; 1987. [Google Scholar]
- Chard DJ, Clarke B, Baker S, Otterstedt J, Braun D, Katz R. Using measures of number sense to screen for difficulties in mathematics: Preliminary findings. Assessment for Effective Intervention. 2005;30(2):3–14. [Google Scholar]
- Chi MTH, Feltovich PJ, Glaser R. Categorization and representation of physics problems by experts and novices. Cognitive Science. 1981;5:121–152. [Google Scholar]
- Cirino PT, Ewing-Cobbs L, Barnes M, Fuchs LS, Fletcher JM. Cognitive arithmetic differences in learning disability groups and the role of behavioral inattention. Learning Disabilities Research and Practice. 2007;22:25–35. [Google Scholar]
- Clarke B, Shinn MR. A preliminary investigation into the identification and development of early mathematics curriculum-based measurement. School Psychology Review. 2004;33:234–248. [Google Scholar]
- Cooper G, Sweller J. Effects of schema acquisition and rule automation on mathematical problem solving transfer. Journal of Educational Psychology. 1987;79:347–362. [Google Scholar]
- CTB/McGraw-Hill. TerraNova technical manual. Monterey, CA: Author; 1997. [Google Scholar]
- Daneman M, Carpenter PA. Individual differences in working memory and reading. Journal of Verbal Learning and Verbal Behavior. 1980;19:450–466. [Google Scholar]
- Day JD, Engelhardt JL, Maxwell SE, Bolig EE. Comparison of static and dynamic assessment procedures and their relation to independent performance. Journal of Educational Psychology. 1997;89:358–368. [Google Scholar]
- Ferrara RA, Brown AL, Campione JC. Children’s learning and transfer of inductive reasoning rules: Studies of proximal development. Child Development. 1986;57:1087–1099. doi: 10.1111/j.1467-8624.1986.tb00438.x. [DOI] [PubMed] [Google Scholar]
- Fletcher JM, Shaywitz SE, Shankweiler DP, Katz L, Liberman IY, Stuebing KK, Francis DJ, Fowler A, Shaywitz BA. Cognitive profiles of reading disability: Comparisons of discrepancy and low achievement definitions. Journal of Educational Psychology. 1994;85:1–18. [Google Scholar]
- Fuchs D, Fuchs LS. Peer-Assisted Learning Strategies: Promoting word recognition, fluency, and comprehension in young children. Journal of Special Education. 2005;39:34–44. [Google Scholar]
- Fuchs LS, Fuchs D, Stuebring K, Fletcher JM, Hamlett CL, Lambert WE. Problem-solving and computational skills: Are they shared or distinct aspects of mathematical Cognition? Journal of Educational Psychology. 2008;100:30–47. doi: 10.1037/0022-0663.100.1.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant JD, Hamlett CL. The prevention, identification, and cognitive determinants of math difficulty. Journal of Educational Psychology. 2005;97:493–513. [Google Scholar]
- Fuchs LS, Fuchs D. Mathematical problem-solving profiles of students with mathematics disabilities with and without comorbid reading disabilities. Journal of Learning Disabilities. 2002;35:563–573. doi: 10.1177/00222194020350060701. [DOI] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Powell SR, Seethaler PM, Capizzi AM, Schatschneider C, Fletcher JM. The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology. 2006;98:29–43. [Google Scholar]
- Fuchs LS, Fuchs D, Craddock C, Hollenbeck KN, Hamlett CL, Schatschneider C. Effects of small-group tutoring with and without validated classroom instruction on at-risk students’ math problem solving: Are two tiers of prevention better than one? Journal of Educational Psychology. doi: 10.1037/0022-0663.100.3.491. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Finelli R, Courey SJ, Hamlett CL. Expanding schema-based transfer instruction to help third graders solve real-life mathematical problems. American Educational Research Journal. 2004a;41:419–445. [Google Scholar]
- Fuchs LS, Fuchs D, Karns K, Hamlett CL, Dutka S, Katzaroff M. The importance of providing background information on the structure and scoring of performance assessments. Applied Measurement in Education. 2000;13:1–34. [Google Scholar]
- Fuchs LS, Fuchs D, Kazdan S, Allen S. Effects of peer-assisted learning strategies in reading with and without training in elaborated help giving. Elementary School Journal. 1999;99:201–220. [Google Scholar]
- Fuchs LS, Fuchs D, Prentice K, Hamlett CL, Finelli R, Courey SJ. Enhancing mathematical problem solving among third-grade students with schema-based instruction. Journal of Educational Psychology. 2004b;96:635–647. [Google Scholar]
- Fuchs LS, Hamlett CL, Fuchs D. Test of Computational Fluency. 1990. Available from L.S. Fuchs, 328 Peabody Vanderbilt University, Nashville, TN 37203. [Google Scholar]
- Fuchs LS, Hamlett CL, Powell SR. Grade 3 Math Battery. 2003. Available from L.S. Fuchs, 328 Peabody, Vanderbilt University, Nashville, TN 37203. [Google Scholar]
- Fuchs LS, Seethaler PM, Powell SR, Fuchs D, Hamlett CL, Fletcher JM. Effects of preventative tutoring on the mathematical problem solving of third-grade students with math and reading difficulties. Exceptional Children. doi: 10.1177/001440290807400202. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feuerstein R. The dynamic assessment of retarded performers. The Learning Potential Assessment Device, theory, instruments, and techniques. Baltimore, MD: University Park Press; 1979. [Google Scholar]
- Geary DC, Brown SC, Samaranayake VA. Cognitive addition: A short longitudinal study of strategy choice and speed-of-processing differences in normal and mathematically disabled children. Developmental Psychology. 1991;27:787–797. [Google Scholar]
- Gick ML, Holyoake KJ. Analogical problem solving. Cognitive Psychologist. 1980;12:306–355. [Google Scholar]
- Grigorenko EL, Sternberg RJ. Dynamic testing. Psychological Bulletin. 1998;124:85–111. [Google Scholar]
- Greenes C, Larson M, Leiva MA, Shaw JM, Stiff L, Vogeli BR, Yeatts K. Houghton Mifflin Math. Boston: Houghton Mifflin; 2007. [Google Scholar]
- Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning disabilities. Journal of Educational Psychology. 2001;93:615–626. [Google Scholar]
- Harris RJ. A primer of multivariate statistics. San Diego, CA: Academic; 1975. [Google Scholar]
- Hedges LV, Olkin I. Statistical methods for meta-analysis. Orlando: Academic; 1985. [Google Scholar]
- Hitch GJ, McAuley E. Working memory in children with specific arithmetical learning disabilities. British Journal of Psychology. 1991;82:375–386. doi: 10.1111/j.2044-8295.1991.tb02406.x. [DOI] [PubMed] [Google Scholar]
- Hoover HD, Dunbar SB, Frisbie DA. Iowa Test of Basic Skills. Rolling Meadows, IL: Riverside Publishing; 2001. [Google Scholar]
- Hu L, Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparametrized model specification. Psychological Methods. 1998;3:424–453. [Google Scholar]
- Huberty CJ. Discriminant analysis. Review of Educational Research. 1975;45:543–598. [Google Scholar]
- Jaccard J, Wan CK. LISREL approaches to interaction effects in multiple regression. Thousand Oaks, CA: Sage Publications; 1996. [Google Scholar]
- Jordan NC, Hanich LB. Mathematical thinking in second-grade children with different forms of LD. Journal of Learning Disabilities. 2000;33:567–578. doi: 10.1177/002221940003300605. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. Arithmetic fact mastery in young children: A longitudinal investigation. Journal of Experimental Child Psychology. 2003;85:103–119. doi: 10.1016/s0022-0965(03)00032-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Levine SC, Huttenlocher J. Calculation abilities in young children with different patterns of cognitive functioning. Journal of Learning Disabilities. 1995;28:53–64. doi: 10.1177/002221949502800109. [DOI] [PubMed] [Google Scholar]
- Kansas State Board of Education. Kansas Quality Performance Accreditation. Topeka: Author; 1991. [Google Scholar]
- Kern B. Wirkungsformen der Ubung (Effects in training) Munster, Germany: Helios; 1930. [Google Scholar]
- Kintsch W, Greeno JG. Understanding and solving word arithmetic problems. Psychological Review. 1985;92:109–129. [PubMed] [Google Scholar]
- Kirk S, McCarthy J, Kirk W. Examiner’s Manual: Illinois Test of Psycholinguistic Ability Grammatic Closure. Urbana: Illinois University Press; 1968. [Google Scholar]
- Kline RB. Principles and practice of structural equation modeling. NY: Guilford Press; 1998. [Google Scholar]
- Landerl K, Began A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8–9-year-old students. Cognition. 2004;93:99–125. doi: 10.1016/j.cognition.2003.11.004. [DOI] [PubMed] [Google Scholar]
- LeBlanc MD, Weber-Russell S. Text integration and mathematics connections: A computer model of arithmetic work problem-solving. Cognitive Science. 1996;20:357–407. [Google Scholar]
- Lemaire P, Siegler RS. Four aspects of strategic change: Contributions to children’s learning of multiplication. Journal of Experimental Psychology: General. 1995;124:83–97. doi: 10.1037//0096-3445.124.1.83. [DOI] [PubMed] [Google Scholar]
- Lembke E, Foegen A. Monitoring student progress in early math. Paper presented at the 14th annual meeting of the Pacific Coast Research Conference; San Diego. 2006. Feb, [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenger O. SAS system for mixed models. 2. Cary, NC: SAS Institute; 2006. [Google Scholar]
- Luria AR. Higher cortical functions in man. 2. New York: Basic Books; 1980. [Google Scholar]
- MacCallum RC. Model specification: Procedures, strategies, and related issues. In: Hoyle RH, editor. Structural equation modeling: Concepts, issues, and applications. Thousand Oaks: Sage; 1995. pp. 16–36. [Google Scholar]
- Mayer RE. Thinking, problem solving, cognition. 2. New York: Freeman; 1992. [Google Scholar]
- Mayer RE, Quilici JL, Moreno R. What is learned in an after-school computer club? Journal of Educational Computing Research. 1999;20:223–235. [Google Scholar]
- McGrew K, Woodcock RW. In: Woodcock-Johnson psycho-educational battery-III: Technical manual. McGrew K, Woodcock RW, editors. Riverside; Chicago: 2001. [Google Scholar]
- Murray BA, Smith KA, Murray GG. The test of phoneme identities: Predicting alphabetic insight in pre-alphabetic readers. Journal of Literacy Research. 2000;32:421–477. [Google Scholar]
- Newcomer PL, Hammill DD. Test of Language Development (rev) Austin, TX: Pro-Ed; 1988. [Google Scholar]
- Nich C, Carroll K. Now you see it, now you don’t: A comparison of traditional versus random-effects regression models in the analysis of longitudinal follow-up data from a clinical trial. Journal of Consulting and Clinical Psychology. 1997;65:252–261. doi: 10.1037//0022-006x.65.2.252. [DOI] [PubMed] [Google Scholar]
- Passolunghi MC, Siegel LS. Working memory and access to numerical information in children with disability in mathematics. Journal of Experimental Child Psychology. 2004;88:348–367. doi: 10.1016/j.jecp.2004.04.002. [DOI] [PubMed] [Google Scholar]
- Passolunghi MC, Cornoldi C, De Liberto S. Working memory and inhibition of irrelevant information in poor problem solvers. Memory & Cognition. 1999;27:779–790. doi: 10.3758/bf03198531. [DOI] [PubMed] [Google Scholar]
- Penrose LS. Mental defect. New York: Farrar and Rinehart; 1934. [Google Scholar]
- Perfetti CA. The representation problem in reading acquisition. In: Gough PB, Ehri LC, Treiman R, editors. Reading acquisition. Hillsdale, NJ: Erlbaum; 1992. pp. 145–174. [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children. London: The Psychological Corporation; 2001. [Google Scholar]
- Quilici JL, Mayer RE. Role of examples in how students learn to categorize statistics word problems. Journal of Educational Psychology. 1996;88:144–161. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2. Newbury Park, CA: Sage; 2002. [Google Scholar]
- Raudenbush SW, Liu X. Statistical power and optimal design for multisite randomized trials. Psychological Methods. 2000;5:199–213. doi: 10.1037/1082-989x.5.2.199. [DOI] [PubMed] [Google Scholar]
- Raven JC. Standard progressive matrices, sets A, B, C, D, and E. Cambridge: Lewis and Co; 1960. [Google Scholar]
- Rey A. D’un procede pour evaluer l’educabilite [A method for assessing educability] Archive de Psychologie. 1934;24:297–337. [Google Scholar]
- Riley MS, Greeno JG. Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction. 1988;5:49–101. [Google Scholar]
- Riley MS, Greeno JG, Heller JI. The development of mathematical thinking. Academic Press; 1983. Development of children’s problem-solving ability in arithmetic; pp. 153–196. [Google Scholar]
- Rivera-Batiz FL. Quantitative literacy and the likelihood of employment among young adults in the United States. The Journal of Human Resources. 1992;27:313–328. [Google Scholar]
- Ryan JJ, Carruthers CA, Miller LJ, Souheaver GT, Gontkovsky ST, Zehr MD. The Wasi Matrix Reasoning Subtest: Performance in traumatic brain injury, stroke, and dementia. International Journal of Neuroscience. 2005;115(1):129–136. doi: 10.1080/00207450490512704. [DOI] [PubMed] [Google Scholar]
- Seaman MA, Levin JR, Serlin RC. New developments in pairwise multiple comparisons: Some powerful and practical problems. Psychological Bulletin. 1991;110:577–586. [Google Scholar]
- Siegel LS, Linder B. Short-term memory process in children with reading and arithmetic disabilities. Developmental Psychology. 1984;20:200–207. [Google Scholar]
- Spector JE. Predicting progress in beginning reading: Dynamic assessment of phonemic awareness. Journal of Educational Psychology. 1992;84:353–363. [Google Scholar]
- Speece DL, Cooper DH, Kibler JM. Dynamic assessment, individual differences, and academic achievement. Learning and Individual Differences. 1990;2:113–127. [Google Scholar]
- Steinberg D, Colla P. CART: Tree-structured non-parametric data analysis. San Diego, CA: Salford Systems; 1995. [Google Scholar]
- Sternberg RJ. Successful intelligence. New York: Simon & Schuster; 1996. [Google Scholar]
- Swanson HL. Cross-sectional and incremental changes in working memory and mathematical problem solving. Journal of Educational Psychology. 2006;98:265–281. [Google Scholar]
- Swanson HL, Beebe-Frankenberger M. The relationship between working memory and mathematical problem-solving in children at risk and not at risk for serious math difficulties. Journal of Educational Psychology. 2004;96:471–491. [Google Scholar]
- Swanson H, Lee, Howard CB. Children with reading disabilities: Does dynamic assessment help in the classification? Learning Disability Quarterly. 2005;28:17–34. [Google Scholar]
- Swanson HL, Cooney JB, Brock S. The influence of working memory and classification ability on children’s word problem solution. Journal of Experimental Child Psychology. 1993;55:374–395. [Google Scholar]
- Swanson HL, Sachse-Lee C. Mathematical problem-solving and working memory in children with learning disabilities: Both executive and phonological processes are important. Journal of Experimental Child Psychology. 2001;79:294–321. doi: 10.1006/jecp.2000.2587. [DOI] [PubMed] [Google Scholar]
- Swanson J, Schuck S, Mann M, Carlson C, Hartman K, Sergeant J, Clevenger W, Wasdell M, McCleary R. Categorical and dimensional definitions and evaluations of symptoms of ADHD: The SNAP and the SWAN rating scales. 2004 Downloaded from www.adhd.net on 12/20/2004. [PMC free article] [PubMed]
- The Psychological Corporation. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: Harcourt Brace & Company; 1999. [Google Scholar]
- Tzuriel D, Haywood HC. The development of interactive-dynamic approaches for assessment of learning potential. In: Haywood HC, Tzuriel D, editors. Interactive assessment. New York: Springer-Verlag; 1992. pp. 3–37. [Google Scholar]
- Vaughn S, Fuchs LS. Redefining learning disabilities as inadequate response to intervention: The promise and potential problems. Learning Disabilities Research and Practice. 2003;18:137–146. [Google Scholar]
- Vygotsky LS. Mind and society. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Vygotsky LS. Thought and language. Cambridge, MA: MIT Press (Original work published 1934); 1962. [Google Scholar]
- Webster RE. Visual and aural short-term memory capacity deficits in mathematics disabled students. Journal of Educational Research. 1979;72:272–283. [Google Scholar]
- Weschler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: Psychological Corporation; 1999. [Google Scholar]
- West SG, Finch JF, Curran PJ. Structural equation models with nonnormal variables. In: Hoyle RH, editor. Structural equation modeling: Concepts, issues, and applications. Thousand Oaks, CA: Sage; 1994. pp. 56–75. [Google Scholar]
- Wilson KM, Swanson HL. Are mathematics disabilities due to a domain-general or a domain-specific working memory deficit? Journal of Learning Disabilities. 2001;34:237–248. doi: 10.1177/002221940103400304. [DOI] [PubMed] [Google Scholar]
- Woodcock RW. Woodcock Reading Mastery Tests - Revised. Circle Pines, MN: American Guidance Service; 1998. [Google Scholar]
- Woodcock RW. Woodcock Diagnostic Reading Battery. Itasca, IL: Riverside; 1997. [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III Tests of Cognitive Abilities. Itasca, IL: Riverside; 2001. [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock-Johnson Psycho-Educational Battery -Revised. Allen, TX: DLM Teaching Resources; 1989. [Google Scholar]
- Zhu J. WASI manual. San Antonio, TX: 1999. [Google Scholar]