Abstract
E. coli RecBCD is a highly processive DNA helicase involved in double strand break repair and recombination that possesses two helicase/translocase subunits with opposite translocation directionality (RecB (3’ to 5’) and RecD (5’ to 3’)). RecBCD has previously been shown to melt out ∼5−6 base pairs upon binding to a blunt-ended duplex DNA in a Mg2+-dependent, but ATP-independent reaction. Here we examine the binding of E. coli RecBC helicase (minus RecD), also a processive helicase, to duplex DNA ends in the presence and absence of Mg2+ in order to determine if RecBC can also melt a duplex DNA end in the absence of ATP. Equilibrium binding of RecBC to DNA substrates with ends possessing pre-formed 3’ and/or 5’-single stranded (ss)-(dT)n flanking regions (tails) (n varying from zero to 20 nucleotides) was examined by competition with a fluorescently labeled reference DNA and by isothermal titration calorimetry (ITC). The presence of Mg2+ enhances the affinity of RecBC for DNA ends possessing 3’ or 5’-(dT)n ss-DNA tails with n < 6 nucleotides, with the relative enhancement decreasing as n increases from zero to six nucleotides. No effect of Mg2+ was observed for either the binding constant or the enthalpy of binding (ΔHobs) for RecBC binding to DNA with ss-DNA tail lengths, n ≥ 6 nucleotides. Upon RecBC binding to a blunt duplex DNA end in the presence of Mg2+, at least four base pairs at the duplex end become accessible to KMnO4 attack, consistent with melting of the duplex end. Since Mg2+ has no effect on the affinity or binding enthalpy of RecBC for a DNA end that is fully pre-melted, this suggests that the role of Mg2+ is to overcome a kinetic barrier to melting of the DNA by RecBC and presumably also by RecBCD. These data also provide an accurate estimate (ΔHobs = 8 ± 1 kcal/mol) for the average enthalpy change associated with the melting of a DNA base pair by RecBC.
Keywords: fluorescence; motor protein; helicase; recombination; kinetics, thermodynamics
Introduction
Helicases are a class of motor enzymes that play critical roles in all aspects of DNA and RNA metabolism. These enzymes catalyze the separation of double-stranded (ds) DNA (or RNA) to form the single stranded (ss) DNA intermediates required for DNA replication, recombination and repair via the coupling of energy from nucleoside triphosphate (NTP) binding and hydrolysis 1; 2; 3; 4. To function processively, helicases must also translocate along the DNA filament. Such enzymes can also disrupt protein-DNA complexes 5; 6 and this appears to provide an important biological function 7; 8.
The E. coli RecBCD helicase is responsible for the majority of recombinational repair at dsDNA breaks 9; 10. RecBCD is a heterotrimeric enzyme consisting of the RecB (134 kDa), RecC (129 kDa) and RecD (67 kDa) subunits. Both the RecB and RecD subunits are superfamily 1 (SF1) DNA helicases 11, but unwind dsDNA with opposite polarities; RecB is a 3’ to 5’ helicase/translocase 12, while RecD is a 5’ to 3’ helicase/translocase 13; 14. RecBCD binds and initiates DNA unwinding from a blunt or nearly blunt DNA end, the enzyme generates a 3’-ended ssDNA intermediate after encountering a recombination hotspot, called Chi (χ) (5’-GCTGGTGG-3’)15; 16; 17. After Chi recognition, RecBCD then facilitates the loading of the RecA protein onto the unwound 3’-ssDNA 18. The RecA-bound ssDNA filament then forms a joint molecule with a homologous region of DNA to initiate a recombination event. The RecBC enzyme, lacking the RecD subunit, can also function as a processive helicase and is capable of facilitating homologous recombination in vivo 19; 20. However, the nuclease activity of RecBC is greatly attenuated 21; 22; 23; 24 even though the nuclease site is located within the 30-kDa C-terminal domain of the RecB subunit 25; 26; 27, indicating that the nuclease activity is stimulated by the RecD subunit.
Both RecBCD and RecBC enzymes initiate DNA unwinding from duplex ends, including blunt ends 28; 29; 30; 31; 32; 33. Studies of initiation complexes formed between RecBCD and a blunt-ended duplex DNA show that the RecB subunit can be crosslinked to the 3’-strand of the duplex end while the RecC and RecD subunits can be crosslinked to the 5’-strand 34. Furthermore, five to six base pairs (bp) at the duplex end within the RecBCD-dsDNA initiation complex become accessible to KMnO4 attack in a Mg2+-dependent but ATP-independent manner 35, suggesting that RecBCD melts out or unwinds 4−5 bp upon binding to a blunt DNA end. A crystal structure of a RecBCD-DNA complex, formed in the presence of Ca2+, but without ATP, shows a melting of ∼ four bp at the duplex DNA end 27.
Equilibrium binding of both RecBCD and RecBC to duplex DNA ends is enhanced if the DNA end possesses pre-formed 3’ and/or 5’ ssDNA flanking regions36, with RecBC showing optimal binding to a DNA end with both 3’-(dT)6 and 5’-(dT)6 tails, whereas RecBCD binds optimally to a DNA end with a 3’-(dT)6 tail, but a 5’-(dT)10 tail 37. These results suggest that both enzymes are capable of disrupting ∼six bp upon binding to a blunt duplex DNA end 37; however, melting of a duplex DNA end by RecBC has not been demonstrated. In the current study, we have compared the effects of Mg2+ on the equilibrium binding of RecBC to duplex DNA ends possessing variable lengths of pre-existing ssDNA tails as well as on the patterns of KMnO4 protection. These results demonstrate that RecBC is also able to melt out at least four bp upon binding to a duplex DNA end in a Mg2+-dependent, but ATP-independent reaction. Our studies also suggest that the effect of Mg2+ is to relieve a kinetic block to DNA melting by RecBC, rather than to affect the equilibrium binding affinity of RecBC for the DNA.
Results
DNA substrate design
The experiments described here were performed using the series of 60-bp Cy3-labeled reference DNA (I to III) and the unlabeled DNA molecules (IV to VI) shown schematically in Figure 1a. The 60-bp duplex length ensures that one molecule of RecBC can bind independently to each duplex end without interference from protein binding to the other end 37. The almost identical ends within each DNA duplex molecule simplify the data analysis as RecBC binds to both ends with the same affinity within experimental error 37. The equilibrium constant for RecBC binding to an end of a Cy3-labeled reference DNA molecule (I to III) is referred to hereafter as KBC,R, while KBC denotes the equilibrium constant for RecBC binding to an unlabeled duplex DNA end (IV to VI). The sequences of DNA strands used to form the duplex DNA molecules in Figure 1a are given in Figure 1c.
Figure 1.
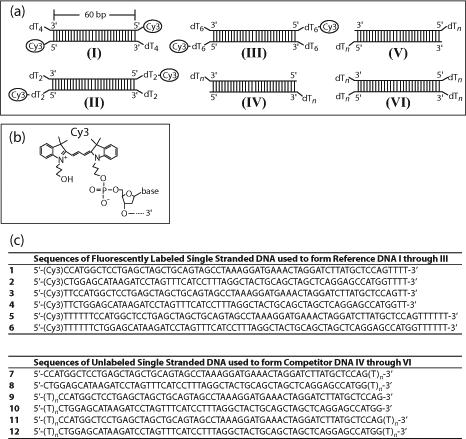
DNA molecules used for RecBC equilibrium binding studies. (a) Schematic representations of Cy3-labeled reference DNA molecules I through III and the non-fluorescent competitor series DNA IV to VI. (b) Structure of the Cy3 fluorophore and its covalent attachment to the phosphate group on the 5’-end of the DNA via a three-carbon linker. (c) Sequences of all DNA strands used to form DNA molecules shown in (a). Reference DNA I was formed from strands 1 and 2; reference DNA II was formed from strands 3 and 4; reference DNA III was formed from strands 5 and 6; DNA series IV was formed from strands 7 and 8; DNA series V was formed from strands 9 and 10; and DNA series VI was formed from strands 11 and 12.
Effects of Mg2+ on RecBC binding to reference DNA I
Generally, an increase in the bulk solution [NaCl] will decrease the equilibrium binding constant for most protein-DNA interactions due to the fact that the Na+ counterion is displaced from the DNA when the protein binds 38; 39; 40; 41. If there is a mixture of Na+ and Mg2+ in the buffer and if Mg2+ interacts only with the DNA and not the protein, then the Mg2+ should compete with both the Na+ and protein for binding to the DNA. Thus, if Mg2+ were only serving as a competitor for DNA binding, then the protein-DNA binding constant measured in the presence of Mg2+ should always be less than or equal to the binding constant measured in the absence of Mg2+ at the same [NaCl] 42; 43.
We examined the effects of Mg2+ on the [NaCl]-dependence of the equilibrium constant for RecBC binding to a duplex DNA end that we expect will be partially melted in the presence of Mg2+. For this purpose we examined RecBC binding to reference DNA I which has a Cy3 fluorophore on each 5’-end of the DNA and a 3’-(dT)4 tail. Based on our previous studies 37, RecBC binding to each end of this DNA is expected to melt an additional 2 bp in the presence of Mg2+. We first examined the dependence of the RecBC-DNA end binding constant, KBC,R, on [NaCl] by performing “salt-back titrations” in the presence and absence of 10 mM MgCl2 as described 44; 45 (see Materials and Methods) and the results are plotted in Figure 2. At the starting [NaCl] of 0.10 M, RecBC binds with higher affinity to the DNA end in the presence of 10 mM MgCl2 (KBC,R = (4.8 ± 0.3) × 107 M−1 in 10 mM MgCl2 vs. (2.3 ± 0.2) × 107 M−1 in the absence of MgCl2). Upon increasing the [NaCl] we observe a decrease in KBC,R both in the presence and absence of 10 mM MgCl2. Plots of log KBC,R vs. log [NaCl] are linear within experimental error over the range from 0.1 to 0.85 M NaCl, with log-log slopes of −1.9 ± 0.4 in the presence of 10 mM MgCl2 and −4.5 ± 0.6 in the absence of MgCl2. Therefore, at any [NaCl], KBC,R is always larger in the presence of 10 mM MgCl2 with the relative effect of MgCl2 increasing with increasing [NaCl] (Figure 2). This result is opposite to the expected result if Mg2+ were to bind only to the DNA and compete for binding of Na+ and RecBC since under those circumstances the values of KBC,R should converge, rather than diverge at high [NaCl] 42; 43. This result provides a clear indication that Mg2+ also binds directly to the RecBC protein and/or the RecBC-DNA complex, and facilitates RecBC binding to the DNA end. The simplest interpretation of the slopes of the plots in Figure 2 indicates that approximately five ions (Na+ and/or Cl−) are released upon RecBC binding to an end of reference DNA I in the absence of MgCl2, while ∼two ions (Na+ and/or Cl−) are released when RecBC binds to a DNA I end in the presence of 10 mM MgCl2.
Figure 2.
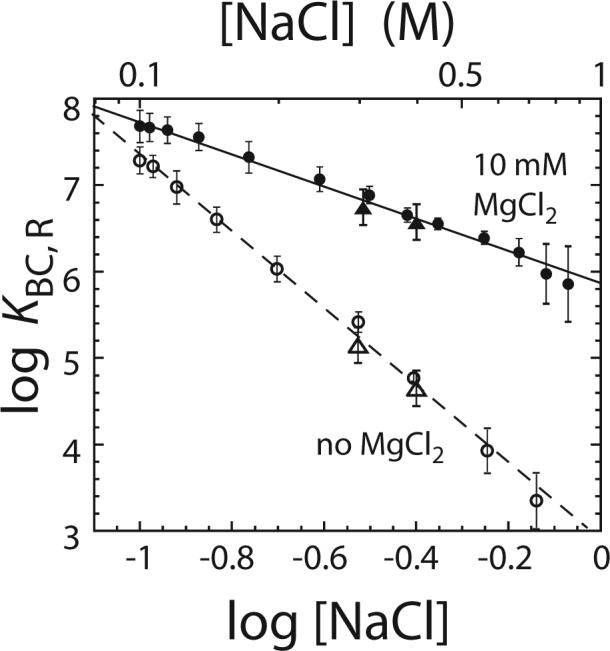
Effects of Mg2+ on the [Na+]-dependence of the equilibrium constant (KBC,R) for RecBC binding to an end of reference DNA I. Values of log KBC,R for reference DNA I are plotted as a function of log [Na+]. The data were obtained from “salt-back titrations” as described in Materials and Methods in buffer M at 25°C in the presence of 10 mM MgCl2 (●) or in the absence of MgCl2 (○). Data were also obtained from direct measurement of KBC,R in buffer M plus the indicated [NaCl] in the presence of 10 mM MgCl2 (▲) or in the absence of MgCl2 (△). The solid and short dash lines are linear fits to the data obtained in buffer M with or without 10 mM MgCl2, respectively. The slopes obtained from the linear fits are −1.9 ± 0.4 in the presence of 10 mM MgCl2 and −4.5 ± 0.6 in the absence of MgCl2.
Independent experiments indicated that the fluorescence intensity of the Cy3 labeled DNA is unaffected by increases in [NaCl], thus enabling us to use “salt back” titrations to obtain estimates of KBC,R. As a further check, we also measured KBC,R directly at 300 and 400 mM NaCl by determining a full binding isotherm (titrating RecBC into DNA I and monitoring the Cy3 fluorescence increase). The values of KBC,R determined directly (triangles in Figure 2) and by the salt back titration (circles in Figure 2) agree within experimental uncertainty.
The pre-existing ss-(dT)n tail length influence the effects of Mg2+ on RecBC binding to DNA ends
The data in Figure 2 show that KBC,R for RecBC binding to a DNA end with a 3’-(dT)4 ssDNA tail is increased in the presence of 10 mM MgCl2. As mentioned above, we anticipate that two bp within the duplex region at the ss-ds-DNA junction should be melted upon RecBC binding to such a DNA end. We next determined the relative equilibrium constants for RecBC binding to DNA ends possessing different lengths of pre-existing ss-(dT)n tails. For these studies we measured equilibrium constants, KBC, for RecBC binding to the non-fluorescent DNA series IV (variable 3’-(dT)n tail) and V (variable 5’-(dT)n tail) in the presence and absence of 10 mM MgCl2 using competition titration experiments. These experiments were performed by titrating a mixture of reference DNA I and one of the competitor DNA IV or V series molecules with RecBC as described 37. For each competitor DNA molecule, three experiments were performed in which the concentration of reference DNA I was maintained constant (20 nM) while the concentration of the non-fluorescent competitor DNA molecule was increased in each successive experiment. Data from all three experiments were analyzed globally to obtain KBC using non-linear least square (NLLS) methods as described 37 and the values of KBC are presented in Table 1. The competition binding isotherms obtained from a representative experiment performed using a DNA IV series molecule with n = 8 nucleotides are shown in Figure 3a. The relative fluorescence enhancement (ΔFobs, defined in equation (2) in Materials and Methods) is plotted as a function of total [RecBC] together with simulated isotherms based on the best fit values of KBC (Table 1) as described 37.
Table 1.
Equilibrium constants (KBC) for RecBC binding to the non-fluorescent DNA IV to VI series molecules at 25°C.
| DNA IVa |
DNA Va |
||||
|---|---|---|---|---|---|
| 3′-(dT)n tail length (n) | KBC (107 M−1) in 10 mM MgCl2 | KBC (107 M−1) in 0 mM MgCl2 | 5′-(dT)n tail length (n) | KBC (107 M−1) in 10 mM MgCl2 | KBC (107 M−1) in 0 mM MgCl2 |
| 0 | 1.6 ± 0.3 | 0.56 ± 0.05 | 0 | 1.6 ± 0.3 | 0.56 ± 0.05 |
| 2 | 4.3 ± 0.4 | 1.96 ± 0.2 | 2 | 2.2 ± 0.4 | 0.79 ± 0.05 |
| 4 | 18 ± 2 | 13 ± 2 | 4 | 3.8 ± 0.4 | 1.7 ± 0.3 |
| 6 | 39 ± 3 | 39 ± 3 | 6 | 4.8 ± 0.5 | 4.6 ± 0.4 |
| 8 | 19 ± 2 | 19 ± 2 | 8 | 4.7 ± 0.4 | 4.5 ± 0.4 |
| 10 | 8.2 ± 0.9 | 9.0 ± 0.9 | 10 | 5 ± 0.5 | 4.9 ± 0.3 |
| 20 | 0.82 ± 0.09 | 0.90 ± 0.06 | 20 | 4.7 ± 0.5 | 4.7 ± 0.4 |
| DNA VI (twin-tails)b | ||
|---|---|---|
| (dT)n tail length (n) | KBC (106 M−1) in 10 mM MgCl2 | KBC (106 M−1) in 0 mM MgCl2 |
| 6 | 13 ± 1 | 13 ± 1 |
buffer M plus 100 mM NaCl and the indicated [MgCl2]
buffer M plus 750 mM NaCl and the indicated [MgCl2]
Figure 3.
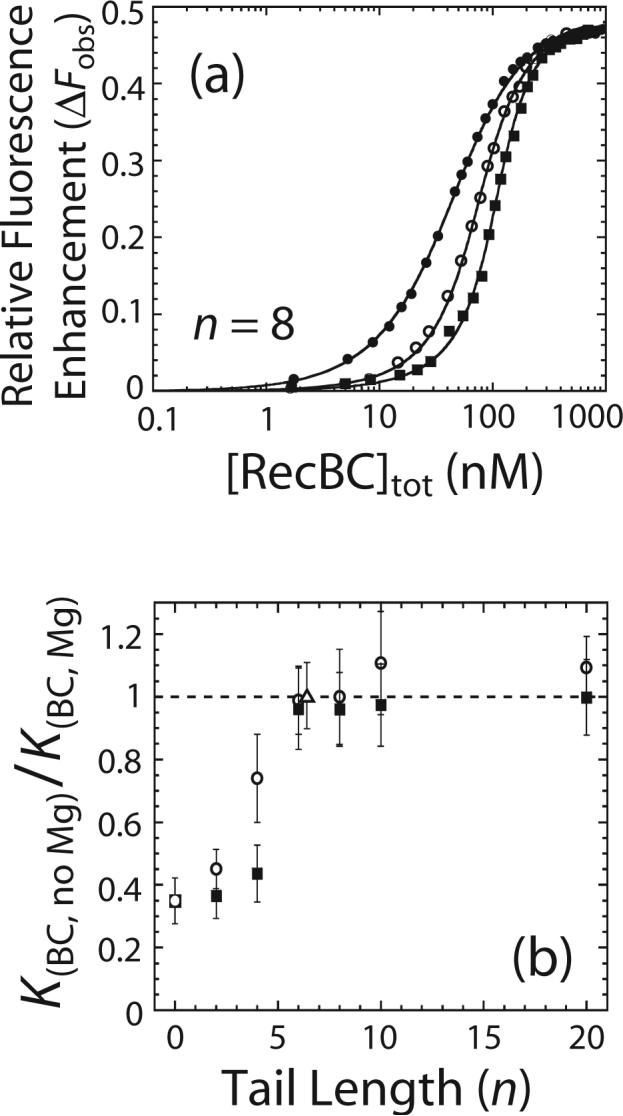
Effects of Mg2+ on the equilibrium constants (KBC) for RecBC binding to DNA ends containing pre-formed ss-(dT)n tails. (a) Representative equilibrium competition titrations to determine KBC for binding to the ends of a non-fluorescent DNA IV series molecule containing 3’-(dT)8 tails. Mixtures of Cy3 labeled reference DNA I (20 nM) and the non-fluorescent DNA IV molecule was titrated with RecBC in buffer M, 10 mM MgCl2 plus 100 mM NaCl at 25°C and the relative Cy3 fluorescence enhancement (ΔFobs) is plotted as a function of total [RecBC]. Three separate titration experiments were performed in which a constant total reference DNA I concentration was used for all experiments but the total concentrations of the competitor DNA IV substrates were varied in each titration. (●) represents a titration performed in the presence of only reference DNA I (20 nM), while (○) and (■) represent experiments performed in the presence DNA I (20 nM) and 20 or 40 nM DNA IV with 3’-(dT)8, respectively. Solid lines are simulations using the best fit values of KBC (Table 1) as described previously 37. (b) Ratios of KBC measured in the absence of Mg2+ (Table 1) to KBC measured in 10 mM MgCl2 (Table 1) are plotted as a function of the length of pre-existing ss-(dT)n tail (n). (○) represents ratios of KBC for the DNA IV series with pre-existing 3’-(dT)n tails; (■) represents ratios of KBC for the DNA V series with pre-existing 5’-(dT)n tails; and (△) represents ratio of KBC for a DNA VI molecule with pre-existing twin-(dT)6 tails.
Figure 3b shows plots of the ratio of KBC measured in the absence of MgCl2 to KBC measured in the presence of 10 mM MgCl2 as a function of the length of the preexisting ss-(dT)n tail. The dependences of KBC on the length of the pre-existing ss-(dT)n tail are qualitatively similar in the presence or absence of 10 mM MgCl2 (Table 1). In both cases, a maximum in KBC is observed for a DNA end with a pre-existing 3’- or a 5’-(dT)n tail with n ≥ 6 nucleotides. Importantly, the values of KBC for the DNA IV and V series measured in the absence of MgCl2 are lower than KBC measured in 10 mM MgCl2 when n < 6 nucleotides (Table 1); however, for n ≥ 6 nucleotides, KBC is the same in the absence or presence of 10 mM MgCl2. As shown in Figure 3b, the difference between KBC measured in the absence and presence of MgCl2 decreases as the length of the preexisting ss-(dT)n tail increases from zero to six nucleotides, with the values of KBC becoming independent of the presence of Mg2+ for n ≥ 6 nucleotides. The largest difference is observed for a blunt DNA end such that KBC is ∼3 times higher in the presence of 10 mM MgCl2. We also observed no effect of 10 mM MgCl2 on the values of KBC for a DNA VI molecule possessing pre-existing twin ss-(dT)6 tails on both ends (open triangle in Figure 3b). Hence, Mg2+ only affects KBC for RecBC binding to a DNA end with a 3’- or 5’-(dT)n tail if n < 6 nucleotides. This suggests that the effect of Mg2+ is observed only when RecBC can potentially melt out some base pairs within a duplex DNA end.
Effects of Mg2+ on melting of a DNA end by RecBC as examined by chemical protection of DNA
Although the above binding studies suggest that RecBC melts some of the bp within the duplex DNA end region in the presence of Mg2+, we performed additional independent experiments to test this hypothesis. We performed KMnO4 footprinting experiments on the RecBC-blunt-ended-DNA complex to examine if base pairs are melted out in a Mg2+-dependent manner. KMnO4 preferentially oxidizes the C5-C6 double bond within unstacked thymine bases within DNA 46 and thus should detect melting of a duplex region containing thymidine base pairs. In fact, this approach was used by Farah and Smith 35 to demonstrate that RecBCD melts out four to five bp upon binding to a blunt duplex end. We used a blunt-ended DNA (the same DNA used in the fluorescence titration experiments discussed above) radiolabeled with 32P at the 5’-end of the top strand (Figure 4). In addition to performing the experiments in buffer M in the presence or absence of 10 mM MgCl2, we also performed experiments in both 30 and 100 mM NaCl to determine if this range of monovalent salt concentration influences bp melting. As shown in Figure 4, the thymine base at position four (T4) is significantly more susceptible to KMnO4 attack in the presence of 10 mM MgCl2 and RecBC, regardless of the [NaCl]. This is the only thymine base within the six base pair region from the end of the 5’-32P-labeled strand. None of the other thymines at other positions (T8 and beyond in Figure 4) exhibit any enhancement in susceptibility to KMnO4 attack in the presence of RecBC and 10 mM MgCl2. This indicates that at least four base pairs at the end of a blunt-ended DNA are melted upon binding of RecBC in a Mg2+-dependent manner.
Figure 4.

Effects of Mg2+ on the chemical protection patterns of a blunt-ended DNA bound by RecBC. KMnO4 footprinting experiments of the RecBC-blunt-ended-DNA complex were performed in buffer M plus the indicated [NaCl] and [MgCl2] at 25°C as described in Materials and Methods. Lane 1 is a control with just the 5’-32P-labeled ssDNA top strand alone. The contents of lanes 2 through 9 are indicated in the figure. The asterisk in the inset shows the position of the 32P-label on the DNA. The reference DNA band is indicated by ref and the uncut sample DNA band is denoted by uncut.
Dependence of DNA melting by RecBC on Mg2+ concentration
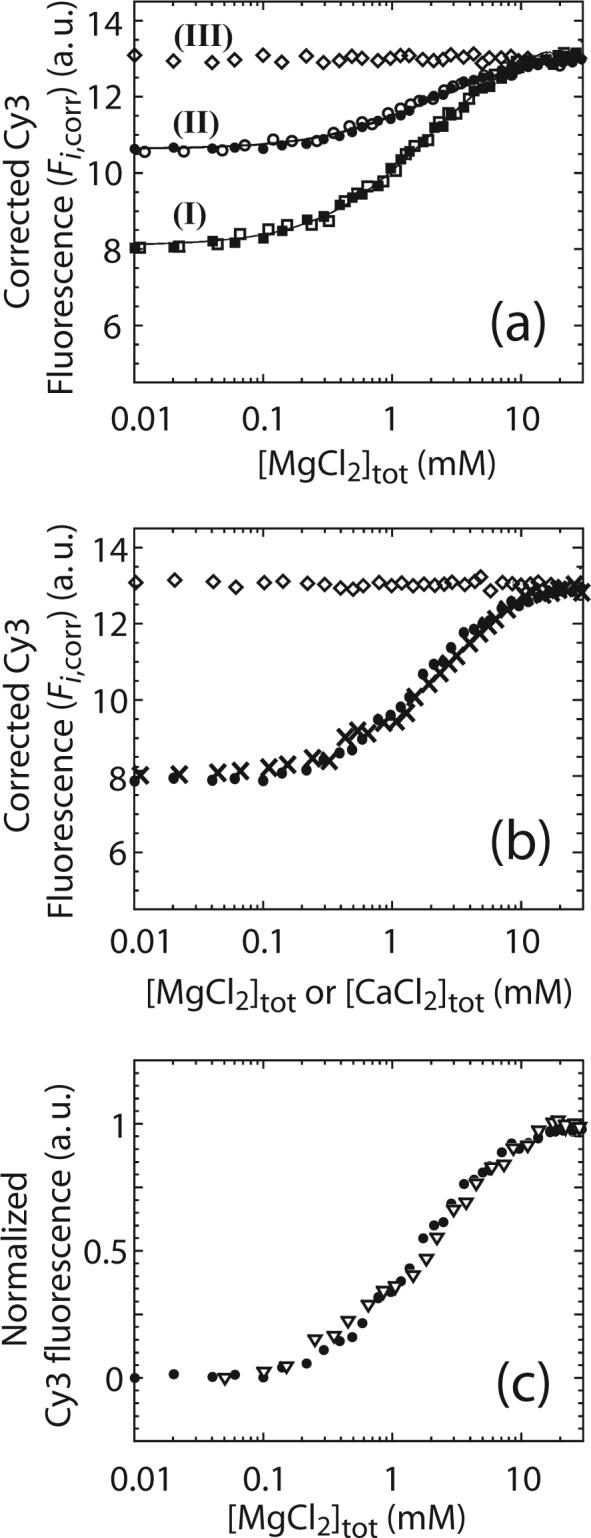
The effects of Mg2+ on the equilibrium constant for RecBC binding to a DNA end, KBC,R and KBC, indicate that the binding of Mg2+ to RecBC increases its affinity for DNA ends containing pre-existing ss-(dT)n tails only if the tails are shorter than six nucleotides. The KMnO4 chemical protection experiments indicate that base pair melting by RecBC is also dependent on the presence of Mg2+. Together, these results indicate that the binding of Mg2+ to RecBC and/or the RecBC-DNA complex is linked to base pair melting by RecBC as has been demonstrated previously to be the case for RecBCD 35. To further study these two processes and to estimate the equilibrium constant for Mg2+ binding to the RecBC-DNA complex, we examined the fluorescence intensity of Cy3 labeled reference DNA molecules (DNA I through III) when pre-bound with RecBC as a function of [MgCl2]. As shown in Figure 1a, DNA I has a Cy3 label on the 5’-end of the duplex and each end has a 3’-(dT)4 tail, DNA II has twin 3’ and 5’-(dT)2 tails and a Cy3 label at the end of the 5’-(dT)2 tail and DNA III has twin 3’ and 5’-(dT)6 tails and a Cy3 label at the end of the 5’-(dT)6 tail. Therefore, we expect that RecBC will melt out 2 bp from each end of DNA I and 4 bp from each end of DNA II in a Mg2+-dependent reaction. Experiments were performed by first saturating each reference DNA with RecBC in the absence of MgCl2 (buffer M plus 100 mM NaCl at 25°C) and then titrating with MgCl2 while monitoring the Cy3 fluorescence signal.
The results of these experiments are presented in Figure 5a where the corrected Cy3 fluorescence (Fi,corr as defined in equation (1) in Material and Methods) is plotted as a function of the total [MgCl2]. The fluorescence intensities of Cy3 within the RecBCDNA I and RecBC-DNA II complexes were enhanced upon titrating with MgCl2. In contrast, the Cy3 fluorescence signal of the RecBC-bound reference DNA III, which has twin ss-(dT)6 tails on both ends, does not change upon addition of MgCl2. The largest enhancement in Cy3 fluorescence (∼58%) is observed for the RecBC-bound DNA I, which has a 3’-(dT)4 tail, while the RecBC-bound DNA II, which has twin ss-(dT)2 tails, exhibits a smaller Cy3 fluorescence enhancement (∼21%). Since the Cy3 fluorescence of reference DNA alone is independent of [MgCl2] (data not shown), the observed enhancement of the Cy3 fluorescence signals of the RecBC-DNA I and RecBC-DNA II complexes upon titration with MgCl2 is due to the effects of Mg2+ on the RecBC-reference DNA complexes. The final fluorescence levels for all RecBC-reference DNA complexes are the same within experimental error, indicating that the final environments of the Cy3 fluorophores in all RecBC-DNA complexes are the same. The fact that only the reference DNA with ss-(dT)n tails shorter than six nucleotides (DNA I and DNA II) exhibit fluorescence enhancement suggests that the increase in Cy3 fluorescence is due to DNA melting. No enhancement of the Cy3 signal was observed for reference DNA III which has twin ss-(dT)6 tails, consistent with the expectation that no additional base pair melting should occur upon RecBC binding.
Figure 5.
Effects of Mg2+ on the Cy3 fluorescence signal of a RecBC-reference DNA complex. (a) 10 nM of DNA I (■), DNA II (●) or DNA III (◇) was pre-bound with 2.4, 2.2 or 1.3 μM RecBC, respectively, and titrated with MgCl2 in buffer M plus 100 mM NaCl at 25°C and the corrected Cy3 fluorescence (Fi,corr) was plotted as a function of total [MgCl2]. The same experiments were performed in buffer M plus 400 mM NaCl for DNA I (□) and DNA II (○). Solid lines are simulations using equations (13) to (15) and the best fit values of and (, and (8 ± 3) M−1 respectively). (b) Comparisons of 10 nM of DNA I pre-bound with 2.4 μM RecBC titrated with MgCl2 (●) or CaCl2 (×) in buffer M plus 100 mM NaCl at 25°C. Fi,corr is plotted as a function of total [MgCl2] or [CaCl2]. 10 nM of DNA III pre-bound with 1.3 μM RecBC was also titrated with CaCl2 (◇) in buffer M plus 100 mM NaCl at 25°C. (c) Comparisons of 10 nM of DNA I pre-bound with either 2.4 μM RecBC (●) or 2.4 μM RecBΔnucC (▽) and titrated with MgCl2 in buffer M plus 100 mM NaCl at 25°C. Fi,corr from each experiment was normalized arbitrarily to one and plotted as a function of [MgCl2].
We also performed a MgCl2 titration of DNA I and DNA II in the presence of 400 mM NaCl, since this higher [NaCl] should further reduce Mg2+ binding to the DNA. As shown in Figure 5a, the results obtained in 400 mM NaCl are identical to the those obtained in 100 mM NaCl, thus the binding of Mg2+ to the DNA appears to be weak enough at these high [NaCl] that it does not compete with the binding of Mg2+ to the RecBC-DNA complex. To examine this further, we calculated the expected extent of Mg2+ binding to a DNA duplex under these salt concentrations using the values of the Mg2+ binding constant determined as a function of [NaCl] from the study of non-specific interactions between lac repressor and calf thymus DNA42 as well as pentalysine and T7 DNA 43. Based on these results one can calculate the probability (PNa) that a nucleotide within the duplex DNA has only Na+ and no Mg2+ associated with it when the duplex DNA is placed in a buffer containing both Na+ and Mg2+ (see Appendix). These calculations indicate that at 100 mM NaCl, PNa ≈ 0.62 at the end of the titration when 10 mM MgCl2 is present. At 400 mM NaCl, PNa ≈ 0.95 at the end of the titration when 10 mM MgCl2 is present. We also note that the equilibrium constants for Mg2+ binding to duplex DNA used in the above calculations were determined for Mg2+ binding to long duplex DNA. Since the DNA used in our experiments is only 60 bp long, there will be less Mg2+ binding to the shorter DNA than estimated from the calculations. Therefore we conclude that there should be relatively little Mg2+ bound to the DNA even at 10 mM Mg2+, especially at 400 mM NaCl. Although these results suggest that the binding of Mg2+ to the RecBC-DNA complex is relatively insensitive to the [NaCl], this may be complicated by any compensating effects due to the [NaCl]-dependence of Mg2+ binding to the DNA.
As shown in Figure 5a, the midpoint of the Mg2+ titrations for DNA I performed in either 100 or 400 mM NaCl is ∼ 1.6 (± 0.4) mM MgCl2 while titrations for DNA II exhibit a midpoint of 1.8 (± 0.4) mM MgCl2. This indicates that the melting of base pairs in both DNA I and II has the same dependence on MgCl2 concentration despite the expectation that a different number of base pairs are melted in DNA I vs. II (2 vs. 4 bp, respectively).
To obtain estimates of the apparent equilibrium constant for Mg2+ binding to the RecBC and RecBC-DNA complex we analyzed the MgCl2 titrations quantitatively using a simple model that assumes only one Mg2+ binding site per RecBC (see Scheme 1 and Materials and Methods). This model ignores any binding of Mg2+ to duplex DNA; however, as discussed above, this is expected to be small at the high [NaCl] (100 mM and 400 mM) used in our experiments. NLLS analysis of the data using equation (17) (see Materials and Methods) yields a value of for the equilibrium constant for Mg2+ binding to either a RecBC-DNA I or a RecBC-DNA II complex, and a value of for the equilibrium constant for Mg2+ binding to RecBC, assuming only one Mg2+ binding site per RecBC.
Somewhat surprisingly, Ca2+ has identical effects on the Cy3 fluorescence signals of RecBC-DNA complexes as Mg2+. As shown in Figure 5b, the traces obtained from titrations of the RecBC-DNA I complex with CaCl2 and MgCl2 are identical within experimental uncertainty. Titration of the RecBC-DNA III complex with CaCl2 also exhibits no change in Cy3 fluorescence intensity (Figure 5b). We also observed that RecBC binds to reference DNA I with the same affinity (KBC,R = (4.8 ± 0.5) × 107 M−1) in either 10 mM MgCl2 or 10 mM CaCl2 (data not shown). These data indicate that the observed equilibrium constant for the RecBC-DNA complex binding to one Ca2+ ion is identical to that for Mg2+. Even though a crystal structure of RecBCD bound to a duplex DNA in the presence of Ca2+ shows that RecBCD can melt out four bp at the end of the duplex 27, our quantitative studies are somewhat surprising since Mg2+ and Ca2+ binding sites on proteins are expected to be different 47; 48.
Since a Ca2+ ion is observed bound at the RecB nuclease domain active site in the crystal structure of RecBC-DNA complex 27, we next tested if this site is responsible for the observed binding of Mg2+ by examining RecBΔnucC, which was reconstituted from RecC and a RecB nuclease domain deletion mutant (RecBΔnuc) 26. Figure 5c shows that the [MgCl2]-dependence of the normalized enhancement of the Cy3 fluorescence signal of a RecBΔnucC-DNA I complex is the same as observed for the normalized Cy3 fluorescence signal for a RecBC-DNA I complex. Therefore the nuclease domain of RecB is not responsible for the observed effect of Mg2+ on DNA melting.
Effects of Mg2+ on the observed enthalpy and heat capacity changes for RecBC binding to DNA ends
As shown above, for RecBC binding to a DNA end possessing a pre-existing twin-ss-(dT)6 tail (DNA VI), there is no effect of Mg2+ on KBC and thus on the standard state binding free energy change, ΔG°obs= −RT ln KBC, (Figure 3b and Table 1). While this suggests that there is no effect of Mg2+ on the energetics of the RecBC-DNA VI (n = 6) interaction, it is possible that there is an enthalpy/entropy compensation under the conditions used resulting in similar values of KBC. We therefore performed isothermal titration calorimetry (ITC) experiments to measure ΔHobs for RecBC binding to the ends of a DNA VI molecule with n = 6 in the presence and absence of 10 mM MgCl2 over a temperature range from 5 to 25°C. We also compared the ΔHobs for RecBC binding to a DNA VI molecule with n = 6, for which no bp melting is expected, to that for RecBC binding to a blunt-ended DNA molecule (DNA VI with n = 0) for which bp melting is only expected to occur in the presence of Mg2+.
The results of two representative ITC experiments are shown in Figure 6a and b where the heat of each injection normalized to the amount of DNA injected (ΔQi,norm as defined in equation (20) in Materials and Methods) is plotted as a function of the ratio of total [DNA]/total [RecBC] (Buffer M, 100 mM NaCl). The data were analyzed (see equations (18) to (20) in Materials and Methods) and the values of the observed enthalpy change (ΔHobs) for RecBC binding to one DNA end are presented in Table 2 and Figure 6c. In the temperature range between 5 to 25°C, ΔHobs for RecBC binding to a DNA end containing twin-ss-(dT)6 tails (DNA VI with n = 6) is the same within experimental error, in the absence or presence of 10 mM MgCl2. This indicates that the complete thermodynamic profile (ΔG°obs, ΔHobs, ΔS°obs, and ΔCp,obs) for RecBC binding to the pre-melted ends of DNA VI (with n = 6) is identical in the absence or presence of MgCl2. Hence, Mg2+ has no effect on the energetics of RecBC binding to a fully pre-melted DNA end over the temperature range from 5 to 25°C. RecBC binding to the DNA with twin-ss-(dT)6 tails (DNA VI with n = 6) exhibits the same ΔCp,obs in the presence or absence of 10 mM MgCl2 ((−1.6 ± 0.3) and (−1.6 ± 0.4) kcal mol−1 K−1, respectively).
Figure 6.
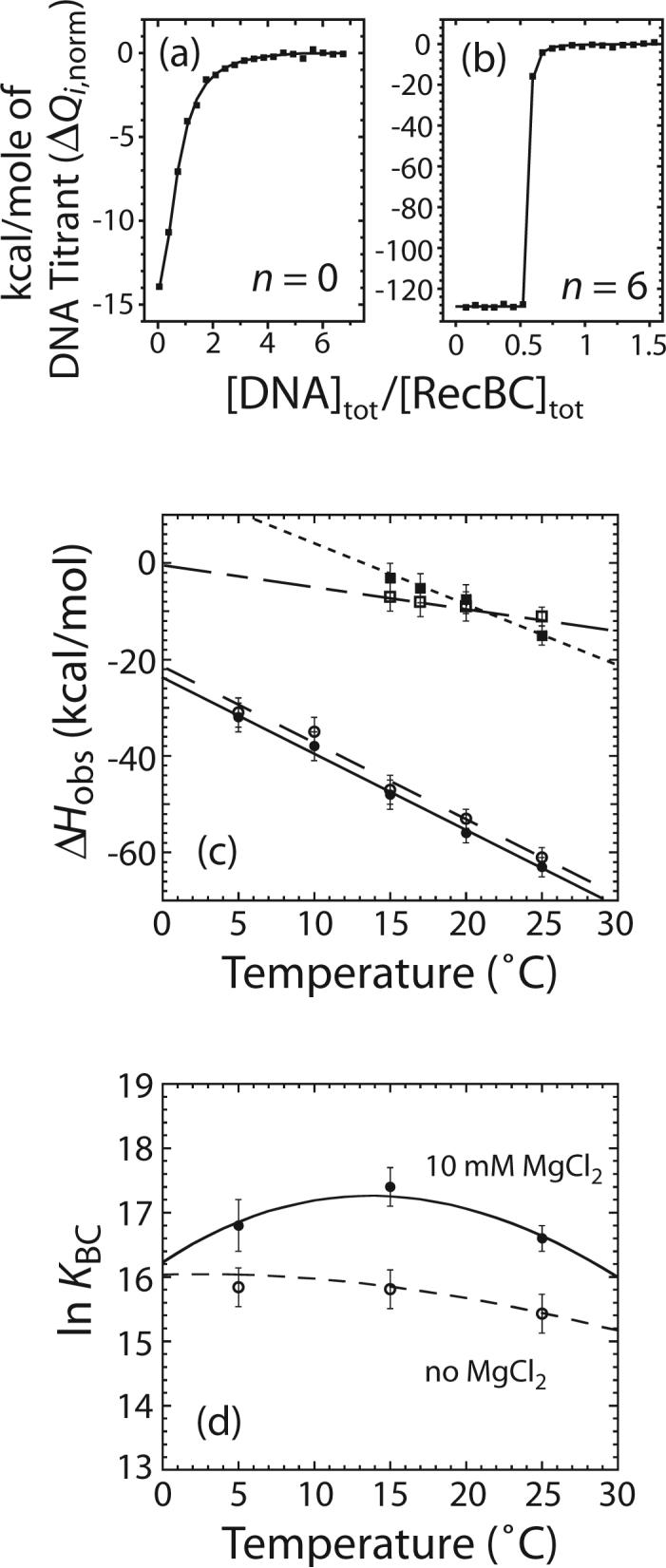
Effects of Mg2+ on the temperature dependence of the observed enthalpic change (ΔHobs) for RecBC binding to one end of the DNA VI series molecules with n = 0 or 6. Experiments were performed in buffer M plus 100 mM NaCl and the indicated [MgCl2] at the indicated temperature. (a) and (b) are representative ITC experiments to determine the enthalpic change for RecBC binding the ends of DNA VI series molecules with n = 0 or 6 in the presence of 10 mM MgCl2 at 25°C. The heat of each injection normalized to the amount of DNA injected (ΔQi,norm as defined in equation (20)) is plotted as a function of total [DNA]/total [RecBC]. (a) 710 nM RecBC was titrated with 15.2 μM DNA VI with n = 0; (b) 885 nM RecBC was titrated with 9 μM DNA VI with n = 6. Solid lines are simulations using equations (18) to (20) and the best fit values of ΔHobs (Table 2) and KBC = (1.6 ± 0.3) × 107 M−1 in (a) while K BC ≥ 109 M−1 in (b). (c) Effects of Mg2+ on values of ΔCp,obs for RecBC binding to a DNA end. ΔHobs for RecBC binding to an end of DNA VI with n = 6 in the presence of 10 mM MgCl2 (●) or in the absence of MgCl2 (○) and ΔHobs for RecBC binding to a blunt DNA end in the presence of 10 mM MgCl2 (■) or in the absence of MgCl2 (□) are plotted as a function of temperature (°C). Straight lines represent results obtained from linear least-square analysis of each set of data and the value of ΔCp,obs obtained from each set of data is presented in Table 2. (d) Effects of Mg2+ on the temperature dependence of equilibrium constant (KBC) for RecBC binding to a blunt DNA end measured by competition fluorescence titration experiments. Experiments were performed in buffer M, 100 mM NaCl with or without 10 mM MgCl2 at the indicated temperature. Values of ln KBC measured in 10 mM MgCl2 (●) or 0 mM MgCl2 (○) are plotted as a function of temperature (°C). The solid and broken lines are simulations using equation (22) and the ΔHobs and ΔCp,obs values obtained from ITC experiments in the presence or absence of 10 mM MgCl2, respectively (Table 2).
Table 2.
Temperature dependence of the observed enthalpic change (ΔHobs) for RecBC binding to one end of the DNA VI series molecules with n = 0 or 6. Observed heat capacity change (ΔCp,obs) values are obtained from linear least-square analyses of the observed enthalpic change data. (buffer M plus 100 mM NaCl and the indicated [MgCl2])
| Temperature (°C) | DNA with twin (dT)6 tails |
Blunt-ended DNA |
||
|---|---|---|---|---|
| ΔHobs (kcal mol−1) in 10 mM MgCl2 | ΔHobs (kcal mol−1) in 0 mM MgCl2 | ΔHobs (kcal mol−1) in 10 mM MgCl2 | ΔHobs (kcal mol−1) in 0 mM MgCl2 | |
| 5 | −32 ± 3 | −31 ± 3 | ND | ND |
| 10 | −38 ± 3 | −35 ± 3 | ND | ND |
| 15 | −48 ± 3 | −47 ± 3 | −3 ± 3 | −7 ± 3 |
| 17 | ND | ND | −5 ± 3 | −8 ± 3 |
| 20 | −56 ± 3 | −53 ± 2 | −8 ± 3 | −9 ± 3 |
| 25 | −64 ± 3 | −61 ± 2 | −15 ± 2 | −11 ± 2 |
| ss-(dT)n tail length (n) | ΔCp,obs (kcal mol−1 K−1) in 10 mM MgCl2 | ΔCp,obs (kcal mol−1 K−1) in 0 mM MgCl2 |
|---|---|---|
| 0 | −1.2 ± 0.2 | −0.5 ± 0.3 |
| 6 | −1.6 ± 0.3 | −1.6 ± 0.4 |
On the other hand, we observe a definite effect of Mg2+ on the values of ΔHobs and its heat capacity change (ΔCp,obs= (dΔHobs/dT)P) for RecBC binding to a blunt DNA end (DNA VI with n = 0) (Table 2 and Figure 6c) measured over the temperature range from 15 to 25°C. Interestingly, ΔCp,obs for RecBC binding to a blunt-ended DNA in the presence of 10 mM MgCl2 is very similar ((−1.2 ± 0.2) kcal mol−1 K−1), to ΔCp,obs for RecBC binding to the twin-ss-(dT)6 tailed DNA, although the values of ΔHobs are much smaller in magnitude for RecBC binding to the blunt DNA end. In contrast, ΔCp,obs for RecBC binding to a blunt-ended DNA in the absence of MgCl2 ((−0.5 ± 0.3) kcal mol−1 K−1) is about 2.5 times smaller in magnitude. Hence, a larger negative value of ΔCp,obs is observed under conditions where the final state of the DNA has 6 unpaired bases when bound to RecBC.
We also used the competition fluorescence titration experiments to examine the effects of 10 mM MgCl2 on KBC for RecBC binding to a blunt DNA end (DNA VI with n = 0) at 5, 15 and 25°C and compared these values with the predicted temperature dependence of KBC based on the ΔCp,obs and ΔHobs values obtained from the ITC studies (Table 2). The results are presented in Table 3 and plotted in Figure 6d. The lines in Figure 6d are simulations using equation (22) and the ΔHobs and ΔCp,obs values from Table 2. As shown in Figure 6d, there is excellent agreement between the measured values of ln KBC both in the presence and absence of MgCl2 and those calculated using the parameters obtained from the ITC studies.
Table 3.
Temperature dependence of the equilibrium constants (KBC) for RecBC binding to a blunt-ended DNA. (buffer M plus 100 mM NaCl and the indicated [MgCl2])
| Temperature (°C) | KBC (107 M−1) in 10 mM MgCl2 | KBC (107 M−1) in 0 mM MgCl2 |
|---|---|---|
| 5 | 2.0 ± 0.7 | 0.8 ± 0.1 |
| 15 | 3.7 ± 0.7 | 0.8 ± 0.1 |
| 25 | 1.6 ± 0.3 | 0.56 ± 0.05 |
Enthalpic cost of base pair melting
We next performed a series of experiments to obtain an estimate of the ΔHobs for melting a base pair within the RecBC-DNA end complex. For this purpose, we measured ΔHobs for RecBC binding to the ends of the series of DNA VI molecules containing twin ss-(dT)n tails, with n = 0, 2, 4, 6, 8, 10 and 20, in the presence of 10 mM MgCl2. We reasoned that, in the presence of MgCl2, six base pairs should be melted upon RecBC binding to a blunt DNA end (DNA VI with n = 0), while no base pairs should be melted upon RecBC binding to a DNA end with twin ss-(dT)n tails, where n ≥ 6. Thus the difference between ΔHobs for RecBC binding to a blunt DNA end and ΔHobs for RecBC binding to a DNA end with twin ss-(dT)6 tails should provide a measure of the enthalpic cost for melting six base pairs. Of course, this assumes that the energetic state of the final RecBC-DNA complex (with 6 bp melted) is unaffected by DNA base composition.
The results of these experiments are presented in Table 4 and Figure 7. ΔHobs for RecBC binding to one end of DNA VI is always negative and decreases linearly from (−17 ± 4) kcal mol−1 to (−64 ± 3) kcal mol−1 as the lengths of the pre-formed twin ss-(dT)n tails increase from zero to six nucleotides; however, ΔHobs remains unchanged at (−64 ± 3) kcal mol−1 for n ≥ 6 nucleotides. A linear fit to the length dependence of ΔHobs for n = 0 to 6 yields a value of −8 (± 1) kcal mol−1. Therefore, the average enthalpic cost of melting one DNA base pair by RecBC is (8 ± 1) kcal mol−1 bp−1.
Table 4.
Observed enthalpic change (ΔHobs) for RecBC binding to one end of the DNA VI series molecules. (buffer M plus 10 mM MgCl2 and 100 mM NaCl at 25°C)
| (dT)n tail length (n) | ΔHobs (kcal mol−1) for DNA VI (twin tails) |
|---|---|
| 0 | −17 ± 4 |
| 2 | −34 ± 3 |
| 4 | −49 ± 3 |
| 6 | −64 ± 3 |
| 8 | −63 ± 3 |
| 10 | −65 ± 3 |
| 20 | −64 ± 3 |
Figure 7.
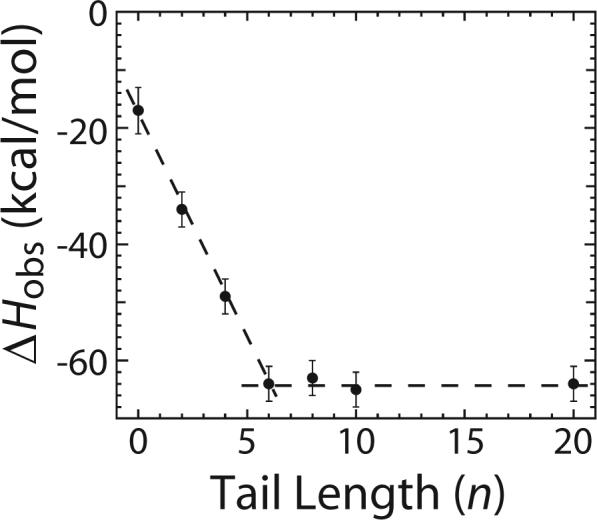
Enthalpic cost of base pair melting by RecBC upon binding to a duplex DNA end. The observed enthalpic change (ΔHobs) for RecBC binding to one end of the DNA VI series containing twin ss-(dT)n tails with n varying from zero to 20 nucleotides were measured in buffer M plus 10 mM MgCl2 and 100 mM NaCl at 25°C . ΔHobs for RecBC binding to one end of the DNA DNA VI series (●) are plotted as a function of pre-existing ss-(dT)n tail length (n).
Discussion
Previous studies of RecBCD binding to a blunt DNA duplex end have shown that the last four to five bp at the end of the duplex become accessible to KMnO4 attack in a Mg2+-dependent but ATP-independent manner 35. The last four bp of a blunt ended duplex DNA are also observed to be unpaired in a crystal structure of a RecBCD-DNA complex formed in the presence of Ca2+ 27. Equilibrium binding studies performed in the absence of ATP also show that RecBCD binds tightest to a DNA end containing preexisting 3’-ss-(dT)6 and 5’-ss-(dT)10 tails 37. These observations indicate that RecBCD is capable of melting out the last four to six base pairs upon binding to a blunt duplex DNA end in a divalent cation-dependent, but ATP-independent reaction. Here we have shown that RecBC is also able to carry out a similar bp melting reaction upon binding a blunt-ended DNA.
Base pair melting by RecBC is Mg2+-dependent
Divalent cations such as Mg2+ can always compete with monovalent cations and protein for the binding of DNA and thus the presence of Mg2+ will generally decrease the equilibrium constant for protein binding to DNA and the magnitude of its dependence on [NaCl] 40; 41. Although for RecBC binding to DNA I we observe that the dependence of the equilibrium constant (KBC,R) on [NaCl] is affected by the presence of 10 mM MgCl2, the effects are very different from those expected if Mg2+ only acted as a competitor. The fact that KBC,R measured in the presence of Mg2+ is always higher than KBC,R measured in the absence of Mg2+ at all [NaCl] examined indicates that Mg2+ facilitates RecBC binding to DNA. This Mg2+-dependent increase in KBC,R is consistent with the hypothesis that RecBC requires Mg2+ in order to melt a region of the duplex DNA end upon binding.
The effects of varying the lengths of the pre-existing tails on KBC for the DNA IV and V series in the absence of MgCl2 are qualitatively similar to the effects observed in the presence of 10 mM MgCl2. Therefore, these data by themselves cannot be used to conclude whether RecBC melts out six base pairs in a Mg2+-dependent manner. However, the quantitative differences between KBC measured in the absence and presence of MgCl2 are consistent with the hypothesis that six base pairs at the blunt DNA end are melted out by RecBC only in the presence of Mg2+. For DNA ends with pre-existing (dT)n tails shorter than six nucleotides, the difference between KBC measured in the presence and absence of Mg2+ is expected to increase in magnitude as the lengths of the pre-existing (dT)n tails decreases because the number of base pairs melted by RecBC (6 − n) increases as n decreases. Indeed we observe that the magnitude of the difference between KBC measured in the presence and absence of 10 mM MgCl2 decreases as the length of the pre-existing tail increases from zero to six nucleotides, whereas no difference was observed in KBC for DNA possessing ss-(dT)n tails with n ≥ 6 nucleotides. The KMnO4 footprinting data also directly shows a Mg2+-dependent melting by RecBC of at least four base pairs at the end of a blunt DNA end.
The effects of [MgCl2] on the Cy3 fluorescence of DNA I through III molecules when pre-bound with RecBC also indicate that binding of Mg2+ by RecBC facilitates base pair melting at the end of DNA. The RecBC-DNA III complex, which possesses pre-existing twin ss-(dT)6 tails and therefore no melting is expected to occur upon binding of RecBC, failed to show an increase in the Cy3 fluorescence, whereas both RecBC-bound DNA I and II (with ss-DNA tails shorter than six nucleotides) exhibit an enhancement in Cy3 fluorescence upon titration of MgCl2 consistent with bp melting being associated with the fluorescence enhancement upon addition of MgCl2. The same final fluorescence level exhibited by all RecBC-DNA complexes at the end of titration indicating that all the RecBC-DNA complexes are in the same final state (i.e., six base pairs at the end are unpaired) at the end of titration.
Mg2+ overcomes a kinetic barrier to facilitate base pair melting by RecBC
For RecBC-induced melting of duplex DNA to occur, the favorable free energy change accompanying RecBC binding to DNA (ΔG°bind) must be sufficient to overcome the unfavorable free energy change associated with base pair melting (ΔG°melt). One potential explanation for the requirement of Mg2+ for this process is if Mg2+ increases the affinity of RecBC for the final fully melted DNA product so that (ΔG°bind + ΔG°melt < 0), whereas in the absence of Mg2+, (ΔG°bind + ΔG°melt > 0). However, the fact that ΔG°obs (= −RT ln KBC) for RecBC binding to a DNA end possessing pre-existing ss-(dT)n tails with n ≥ 6 nucleotides is the same with or without 10 mM MgCl2 indicates that there is already sufficient binding free energy available from the RecBC-DNA interaction even in the absence of Mg2+, to achieve a melted structure. Yet, bp melting by RecBC does not occur in the absence of Mg2+. Therefore, our results suggest that base pair melting by RecBC binding to DNA is thermodynamically favored in the presence and absence of Mg2+, but is kinetically blocked in the absence of Mg2+.
Interestingly, the Cy3 fluorescence data suggest that Ca2+ can also facilitate base pair melting by RecBC. This observation is consistent with the fact that four bp are unpaired in the RecBCD-blunt-ended DNA crystal structure formed in the presence of Ca2+ 27. The one surprising observation is that the effect of Ca2+ is indistinguishable from Mg2+. Even if Ca2+ and Mg2+ bind to the same site to facilitate bp melting, it is not expected that they would have the same affinity for the same site on RecBC or the RecBC-DNA complex given the distinctly different ion sizes and requirements for Ca2+ and Mg2+ binding sites within proteins 47; 48. In fact, Ca2+ is observed bound in the expected Mg2+ binding site within the RecB nuclease domain 27 and does inhibit the nuclease activity of RecBCD 49. It is possible that there are multiple sites for Mg2+ and Ca2+ and that there is a fortuitous compensation of effects such that the apparent affinity of Mg2+ and Ca2+ appear to be the same. Since both Ca2+ and Mg2+ appear to function to relieve a kinetic block associated with DNA melting by RecBC and RecBCD, this could potentially mask any difference in affinity of these two ions for the RecBCD-DNA complex.
A Ca2+ ion is observed bound at the Mg2+ binding site within the nuclease domain in the crystal structure of a RecBCD-DNA complex 27. Yet, our data indicate that deletion of the nuclease domain to form RecBΔnucC, has no influence on the ability of Mg2+ to facilitate DNA melting by RecBC. Therefore the site for Mg2+ binding that facilitates bp melting by RecBC is not located on the nuclease domain of RecB. The ATP binding site on RecB is a potential site for binding Mg2+ but it is also possible that the Mg2+ binding site is present on the RecC subunit. The structural fold of RecC is similar to that of RecB and it has been suggested that RecC may have been a defunct RecB helicase 50.
Thermodynamics of RecBC-DNA complex formation and base pair melting
We observe that ΔCp,obs for RecBC binding to a blunt DNA end in the presence of Mg2+ (−1.2 ± 0.2 kcal mol−1 K−1) is very similar to the ΔCp,obs for RecBC binding to a DNA end possessing two pre-existing twin-(dT)6 tails (DNA VI with n = 6 nucleotides) (−1.6 ± 0.3 kcal mol−1 K−1 in 10 mM MgCl2 and −1.6 ± 0.4 kcal mol−1 K−1 in no MgCl2). This similarity suggests that there is little heat capacity change associated with bp melting, at least as it occurs within the RecBC complex. This is consistent with the conclusion that unstacking of bases does not contribute significantly to the ΔCp,obs of duplex disruption 51. In contrast, ΔCp,obs for RecBC binding to blunt DNA end in the absence of Mg2+ is less negative (−0.5 ± 0.3 kcal mol−1 K−1). The potential origins of the heat capacity change associated with any protein-DNA complex or any macromolecular interaction are numerous 52; 53; 54; 55; 56; 57, and a determination of the origins of ΔCp,obs for this system are beyond the scope of this work. Further studies are required to elucidate the linked equilibria responsible for the large and negative ΔCp,obs for RecBC binding to DNA ends and the difference between ΔCp,obs for the formation of the “melted” versus “un-melted” complexes.
We estimated the average enthalpic cost of melting six base pairs at a blunt DNA end by RecBC in the presence of Mg2+ from the measurements of ΔHobs for RecBC binding to a DNA end possessing pre-existing twin ss-(dT)n tails (DNA VI) with n varying from 0 to 6 nt. This estimate is based on two assumptions. The first is that the end state of a RecBC-DNA VI complex is the same for 0 ≤ n ≤ 6 in the presence of 10 mM MgCl2, i.e. the last six base pairs are unpaired in 100% of the RecBC-DNA complexes. The second assumption is that ΔHobs is independent of base sequence and composition. With these assumptions, we estimate a value of 47 ± 7 kcal mol−1 for the enthalpic cost to melt out the last six base pairs at the blunt DNA end used in our experiments, which consists of four G/C and two A/T base pairs. This corresponds to a value of (8 ± 1) kcal mol−1 bp−1 for the average enthalpic cost of melting out one base pair at 25°C. Since this estimate is based on the difference in ΔHobs for binding of a series of RecBC-DNA VI complexes, the contributions to ΔHobs from the RecBC-DNA interactions should cancel if the final RecBC-DNA complexes are the same and independent of base composition. Previous estimates of ΔHobs for base pair melting are: 4.3 to 9 kcal mol−1 bp−1 58, 5.2 to 15 kcal mol−1 bp−1 51 and ∼7 kcal mol−1 bp−1 from the nearest neighbor model 59. Our value of (8 ± 1) kcal mol−1 bp−1 falls within this range. Since determinations of ΔHobs for base pair melting from DNA melting experiments is generally difficult due to the uncertainties associated with obtaining accurate baselines at low and high temperatures, our determination may represent a more accurate estimate of this average quantity.
Implications for the helicase mechanism of RecBC and RecBCD
We have shown that when RecBC binds the end of a blunt-ended DNA, it melts out six base pairs at the DNA end in a Mg2+-dependent but ATP-independent manner. Our results suggest that Mg2+ functions by overcoming a kinetic barrier to the RecBC-mediated DNA melting process. The binding of RecBCD to a blunt DNA end also results in the unpairing of the last 4 to 5 base pairs at the end of the duplex DNA 35. The number of base pairs melted out by RecBCD upon binding to a blunt DNA end is very similar to the “kinetic step size” of 3.9 ± 0.6 bp s−1 estimated for RecBCD unwinding of DNA from pre-steady state kinetic studises of DNA 31; 32; 33. Recall that a kinetic unwinding step size of 4 bp indicates that some rate-limiting step in the unwinding process is repeated every 4 bp on average during the unwinding process. The similarity between these two values suggests that DNA unwinding by RecBCD may occur in a two-step process in which 4−6 base pairs of DNA are melted upon binding of RecBCD to the duplex region independent of ATP, followed by more rapid ATP-dependent translocation of RecBCD to the newly formed ss/dsDNA junction 31; 32; 33. Since RecBC also melts out base pairs upon binding to a duplex DNA end, it is possible that RecBC also unwinds DNA by this same mechanism, such that the RecBC binding alone is sufficient to actively open the next 4 bp.
Materials and Methods
Buffers
Buffers were made from reagent grade chemicals using double-distilled water that was further deionized with a Milli-Q purification system (Millipore Corp., Bedford, MA). Buffer C contains 20 mM potassium phosphate (pH 6.8), 0.1 mM 2-mercaptoethanol (2-ME), 0.1 mM EDTA, 10% (v/v) glycerol. Buffer M contains 20 mM MOPS-KOH (pH 7.0), 1 mM 2-ME, 5% (v/v) glycerol. The concentration of MgCl2 stocks was determined by measuring the refractive index of a stock solution in water using a Mark II refractometer (Leica Inc., Buffalo, NY) and a standard table relating refractive index to [MgCl2] 60.
Proteins
E. coli RecB and RecC proteins were purified and reconstituted to form RecBC as described 32. RecBΔnuc was purified and reconstituted with RecC to form RecBΔnucC as described 61. RecBC and RecBΔnucC concentrations were determined spectrophotometrically in buffer C using extinction coefficients of ε280 = 3.9 × 105 M−1 cm−1 32 and ε280 = 3.4 × 105 M−1 61, respectively. All protein concentrations reported refer to the RecBC or RecBΔnucC heterodimer. Bovine serum albumin (BSA) was from Roche (Indianapolis, IN) and its concentration was determined using an extinction coefficient of ε280 = 4.3 × 104 M−1 cm−1 in buffer C 37. All proteins were dialyzed into the particular reaction buffer before use. Dialyzed RecBC or RecBΔnucC were stored at 4°C for up to five days, since a loss of activity (∼15%) was observed after five days at 4°C.
Oligodeoxynucleotides
Oligodeoxynucleotides were synthesized using an ABI model 391 synthesizer (Applied Biosystems, Foster City, CA) using reagents and phosphoramidites from Glen Research (Sterling, VA). A first purification step of each single-stranded oligodeoxynucleotide was performed using polyacrylamide gel electrophoresis under denaturing conditions followed by removal of the DNA from the gel by electroelution 62. The resulting oligodeoxynucleotides were then further purified chromatographically by reverse phase HPLC using an XTerra MS C18 column (Waters, Milford, MA). The concentration of each DNA strand was determined by completely digesting the strand with phosphodiesterase I (Worthington, Lakewood, NJ) in 100 mM Tris-Cl pH 9.2, 3 mM MgCl2, at 25°C and measuring the absorbance of the resulting mixture of mononucleotides at 260 nm as described 51. The extinction coefficients at 260 nm used in this analysis are: 15340 M−1 cm−1 for AMP, 7600 M−1 cm−1 for CMP, 12160 M−1 cm−1 for GMP, 8700 M−1 cm−1 for TMP 63 and 5000 M−1 cm−1 for Cy3 (Glenn Research). Duplex DNA substrates were prepared by mixing equimolar concentrations (usually 3 μM) of the appropriate DNA strands in reaction buffer, which was subsequently heated to 90°C for five minutes followed by slow cooling to 25°C. Reference DNA I (Figure 1a) was formed from strands 1 and 2 (Figure 1c); reference DNA II was formed from strands 3 and 4; reference DNA III was formed from strands 5 and 6; competitor DNA series IV was formed from strands 7 and 8; competitor DNA series V was formed from strands 9 and 10; and competitor DNA series VI was formed from strands 11 and 12. The sequences of the oligodeoxynucleotides used in this study are given in Figure 1c.
Fluorescence Titrations
Fluorescence titrations were performed as described 37 using a PTI QM-4 fluorometer (Photon Technology International, Lawrenceville, NJ) equipped with a 75 watt Xe lamp. All slit widths were set at 0.5 mm. The temperature of sample in the 10-mm pathlength Type 3 quartz fluorometer cuvette (3 mL) (NSG Precision Cells Inc., Farmingdale, NY) was controlled using a Lauda RM6 recirculation water bath (Brinkmann, Westbury, NY). Stirring was maintained throughout each experiment using a P-73 cylindrical cell stirrer with a diameter of 8 mm (NSG Precision Cells Inc., Farmingdale, NY). The corrected Cy3 fluorescence intensity (Fi,corr) after the i-th addition of protein and the initial corrected Cy3 fluorescence of the reference DNA (F0,corr) were obtained as described previously 37. Briefly, Fi,corr is defined as in equation (1):
| (1) |
where Fi is the fluorescence intensity after the i-th addition of titrant, Fb is the background fluorescence of the buffer which is always negligible 37, Vi is the volume of the i-th addition and V0 is the volume before the first addition.
The observed relative fluorescence change (ΔFobs) is defined as in equation (2),
| (2) |
ΔFobs reaches its maximum value (ΔFmax) when both ends of the reference DNA are bound with protein. Hence ΔFobs/ΔFmax (0 ≤ Fobs/ΔFmax ≤ 1) equals the average of protein molecules bound per DNA end, and thus the average number of protein molecules bound per DNA molecule is given by (2ΔFobs/ΔFmax).
“Salt-back” titrations
“Salt-back” titrations 44; 64 were performed after completion of a regular titration, i.e., after all additions of RecBC have been made. A buffer containing the same components as the reaction buffer but with 4 M NaCl was titrated into to the cuvettes and fluorescence measurements were made as described above. Data from “salt-back” titration experiments were analyzed using the same model used to describe the binding of RecBC to the ends of reference DNA, which has been described in detail 37. In this model, RecBC (hereafter referred to as B) binds to each end of reference DNA (D) with the same binding constant, KR, because the reference DNA has nearly identical ends. The binding polynomial for this model, which has two independent and identical sites, is given in equation (3),
| (3) |
where Bf is the free concentration of protein.
The average number of protein molecules bound per DNA molecule is given by equation (4),
| (4) |
where Bbound = ([DB]+2[B2D]), [DB] is the concentration of D with only one of its ends bound by B and [B2D] is the concentration of D with both of its ends bound by B.
As described previously 37, ΔFobs/ΔFmax can be expressed explicitly in terms of total protein concentration (BT), total reference DNA concentration (DT) and KR as in equation (5).
| (5) |
Experimental fluorescence titrations, plotted as ΔFobs vs. [BT], were obtained at three different reference DNA concentrations, DT, and analyzed by global non-linear least squares (NLLS) analysis using equation (5) to obtain the best fit values of KR and ΔFmax.
To calculate KR at each [NaCl] during a “salt-back” titration, equation (5) is rearranged and ΔFobs is substituted using equation (2) to become equation (6),
| (6) |
where ΔFobs,[NaCl] is the relative fluorescence change observed after each addition of NaCl and ΔFmax is determined previously from an independent titration experiment of reference DNA with RecBC.
Competition methods to determine equilibrium binding to non-fluorescent DNA
Equilibrium constants for RecBC binding to non-fluorescent DNA molecules (N) were obtained from analysis of competition binding studies 65. The analysis of competition data has been described previously 37 and the same analysis is used here. Briefly, three separate titration experiments were performed at three different non-fluorescent competitor DNA concentrations (N1, N2 or N3). In each titration experiment, a constant concentration of competitor DNA (N1, N2 or N3) was added to a cuvette containing a Cy3 labeled reference DNA at 20 nM and then titrated with protein. Since the competitor DNA molecules used here have nearly identical ends (DNA IV and V), B should bind to both ends of N with binding constant KN. Then BT and Bf can be related to the total concentration of non-fluorescent DNA concentration (NT), KN, KR and DT as shown in equation (7),
| (7) |
Data from the three titration experiments at competitor DNA concentrations N1, N2 and N3 were analyzed simultaneously using equations (4) and (7) and the “implicit fitting” NLLS algorithm in Scientist (Micromath, St Louis, MO) without the need to obtain an explicit expression for Bf. The value of KN was allowed to float in this analysis while the values of KR and ΔFmax were fixed at values determined from the analysis of independent titrations with reference DNA in the absence of competitor. The uncertainties for the independently determined values of KR and ΔFmax were propagated into the reported uncertainties in KN.
Equilibrium binding of Mg2+ to RecBC and RecBC-Reference DNA complex
The MgCl2 titration data were analyzed by assuming there is one Mg2+-binding site on RecBC as well as RecBC bound at one end of the reference DNA and no significant binding of Mg2+ ions to the reference DNA. This model is sufficient in describing the data (Figure 5a) and therefore we did not consider more complicated models involving more than one Mg2+-binding site per RecBC. This one-Mg2+-site model is represented in Scheme 1, where K1,no Mg and K1 are the stepwise macroscopic binding constants for forming BD (D with only one of its ends bound by B) in the absence and presence of MgCl2, respectively, while K2,no Mg and K2 are the stepwise macroscopic
Scheme 1.
binding constants for forming B2D (D with both of its ends bound by B) in the absence and presence of MgCl2, respectively. The equilibrium constant of B binding to D in the presence of Mg2+ (KR) is related to K1 and K2 as described in equation (8),
| (8) |
Similarly, K1,no Mg and K2,no Mg can be expressed in terms of equilibrium constant for B binding to D in the absence of Mg2+ (KR,no Mg) as given in equation (9):
| (9) |
is the equilibrium constant for one molecule of B binding to one Mg2+ ion while is the equilibrium constant for one molecule of B bound at one end of D binding to one Mg2+ ion. Expressions for BT, DT and total Mg2+ concentration (MgT) in terms of Bf, Df, free Mg2+ concentration (Mgf), KR, KR,no Mg, and are given in equations (10), (11) and (12) respectively:
| (10) |
| (11) |
| (12) |
In our experiment, since all the reference DNA molecules were bound with two molecules of RecBC before addition of Mg2+, [BD] = [BD]•Mg2+ = 0 and DT = [B2D] + [B2D] •Mg2+ + [B2D] •(Mg2+)2. Therefore equations (10) to (12) become equations (13) to (15):
| (13) |
| (14) |
| (15) |
By combining equations (13) through (15), one obtains equation (16),
| (16) |
which relates MgT to Mgf, BT, DT, and .
ΔFobs,[Mg] in this experiment reaches its maximum value (ΔFmax,[Mg]) when Mg2+ ions are bound at both ends of B2D to form B2D•(Mg2+)2. Hence, ΔFobs,[Mg]/ΔFmax,[Mg] (0 ≤ ΔFobs,[Mg]/ΔFmax,[Mg] ≤ 1) equals the average number of Mg2+ ions bound per RecBC-bound DNA end. The average number of Mg2+ ions bound per RecBC-saturated DNA molecule is given by equation (17):
| (17) |
where Mgbound = 2([B2D•(Mg2+)] + [B2D•(Mg2+)2]), Fi,corr,[Mg] is the corrected fluorescence intensity after the i-th addition of Mg2+, F0,corr,[Mg] is the corrected fluorescence intensity before the addition of Mg2+ and Fmax,corr,[Mg] is the maximum value reached by Fi,corr,[Mg] after Mg2+ ions are bond at both ends of B2D. Data were analyzed using equations (16) and (17) and the “implicit fitting” NLLS algorithm in Scientist (Micromath, St. Louis, MO) without the need to obtain an explicit expression for Mgf. In this analysis, the values of , and Fmax,corr,[Mg] were allowed to float. All uncertainties are reported at the 68% confidence limit (±one standard deviation).
Isothermal titration calorimetry
ITC experiments were performed in a VP-ITC calorimeter (Microcal, Northampton, MA) as described 37. The analysis of the calorimetric data has been described in detail 37 and the same analysis is used here. Briefly, experiments were carried out by titrating RecBC (0.7 to 1.1 μM in the sample cell) with 10 μL aliquots of DNA (8 to 14 μM in the syringe) at four-minute intervals and at a stirring rate of 140 rpm. All samples were degassed prior to use. The heat of reaction was obtained by integration of the peak obtained after each injection of titrant, using the software (Origin 7.0) provided by the manufacturer. Separate control experiments were performed to determine the heat of dilution for each injection by injecting the same volumes of DNA into the sample cell containing only buffer. The observed heat for the i-th injection (ΔQi) was obtained after correcting for the heat of dilution as described 66 and is related to the total heat after the i-th injection (Qitot) as in equation (18):
| (18) |
where dVi is the volume of the i-th injection and V0 is the active cell volume (1.43 mL). Since the DNA molecules used here have nearly identical ends (DNA VI series in Figure 1a), the same model of two identical and independent sites (see equation (7)) was used to analyze Qitot, as given by equation (19):
| (19) |
where ΔHobs is the observed enthalpy change for RecBC binding to one end of DNA, DiT is the total DNA concentration in the cell after the i-th injection, KN is the binding constant for RecBC binding to one DNA end and Bif and BiT are the concentrations of free and total RecBC, respectively, in the cell after the i-th injection. ΔHobs and KN were obtained from NLLS analysis using equations (18) and (19) and the ITC NLLS algorithm contained within the Origin 7.0 software as described 66.
In Figure 6a and b, the observed heat released upon the i-th injection normalized to the amount of injected DNA (ΔQi,norm) is obtained using equation (20):
| (20) |
where DT is the concentration of DNA in the syringe. The continuous lines in Figure 6a and b are simulations based on equations (18) to (20) and the best fit values of ΔHobs (Table 4) and KN indicated in the figure legends.
Observed heat capacity change (ΔCp,obs) was obtained from a linear regression of ΔHobs obtained at different temperature using equation (21),
| (21) |
where ΔHobs,ref is the observed enthalpy change at some reference temperature (Tref). The dependence of KBC on temperature is described by the van't Hoff equation ∂ln KBC/∂(1/T = −δHobs/R, where R is the gas constant. By substituting equation (21) into the van't Hoff equation and integrating it between Tref to T, one can express ln KBC in terms of ln KBC,ref, ΔHobs,ref, ΔCp,obs, Tref and T as shown in equation (22),
| (22) |
KMnO4 footprinting
A 5’-32P-labeled blunt-ended DNA (Figure 5) was made by annealing an unlabeled DNA strand 10 (n = 0) (Figure 1c) with a 5’-32P-labeled DNA strand 9 (n = 0) (Figure 1c) as described above. Strand 9 was labeled using T4 polynucleotide kinase (US Biochemical Corp., Cleveland, OH) and γ-32P-ATP (Perkin Elmer, Wellesley, MA) followed by purification as described 62. 2 nM of this 5’-32P-labeled dsDNA was incubated with 1 μM of RecBC in buffer M plus the indicated [MgCl2] and [NaCl] over ice for 20 min. Freshly prepared KMnO4 solution was added to the RecBC-DNA mixture to a final concentration of 2 mM. This reaction was allowed to proceed for 3 min at 25°C and was quenched by adding 2-ME to a final concentration of 2 M. A 5’-32P-labeled ssDNA strand 9 with n = 15 nucleotides was also added at this point to a final concentration of 2 nM as a control. DNA was then extracted by phenol extraction as described 67 and followed by ethanol precipitation and piperidine digestion as described elsewhere 68. The samples were run on a 20% polyarcrylamide gel with 7 M urea at 55°C for one hour as described 68 and the gel was exposed to a phosphor screen and quantified with a Storm 840 system (Molecular Dynamics, Sunnyvale, CA).
Acknowledgements
We thank Drs. Roberto Galletto, Gerry Smith and Aaron Lucius and Colin Wu for stimulating discussions and comments on the manuscript and T. Ho for synthesis and purification of DNA. This research was supported in part by NIH grant GM45948 to T.M.L.
Appendix
The probability of a nucleotide within a duplex DNA is bound with only Na+ and no Mg2+ when the duplex DNA is placed in a buffer containing both cations is calculated using equation A(1) as described 42; 43.
| A(1) |
where [D] is the total nucleotide concentration, [D0] is the concentration of nucleotides associated with only Na+ and is the observed intrinsic constant for Mg2+ binding to each DNA site. As shown by equation A(1), PNa equals one before any addition of Mg2+ and it will decrease as [Mg2+] increases, indicating an increasing probability of Mg2+ binding to the DNA. The dependence of on [NaCl] has been determined from the non-specific interactions between lac repressor and duplex DNA 42 as well as pentalysine and duplex DNA 43 and given in equations A(2) and A(3), respectively:
| A(2) |
| A(3) |
In the presence of 100 mM NaCl, using either equation A(2) or A(3), one obtains an estimate for . Thus in the presence of 10 mM MgCl2 and 100 mM NaCl one obtains a value of PNa ≈ 0.62 using equation A(1). Similarly, in the presence of 400 mM NaCl, and PNa ≈ 0.95 when 10 mM MgCl2 is present.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Matson SW, Bean DW, George JW. DNA helicases: enzymes with essential roles in all aspects of DNA metabolism. Bioessays. 1994;16:13–22. doi: 10.1002/bies.950160103. [DOI] [PubMed] [Google Scholar]
- 2.Lohman TM, Bjornson KP. Mechanisms of Helicase-Catalyzed DNA Unwinding. Ann.Rev.Biochem. 1996;65:169–214. doi: 10.1146/annurev.bi.65.070196.001125. [DOI] [PubMed] [Google Scholar]
- 3.Delagoutte E, von Hippel PH. Helicase mechanisms and the coupling of helicases within macromolecular machines. Part I: Structures and properties of isolated helicases. Q Rev Biophys. 2002;35:431–78. doi: 10.1017/s0033583502003852. [DOI] [PubMed] [Google Scholar]
- 4.Singleton MR, Dillingham MS, Wigley DB. Structure and Mechanism of Helicases and Nucleic Acid Translocases. Annu Rev Biochem. 2007;76:23–50. doi: 10.1146/annurev.biochem.76.052305.115300. [DOI] [PubMed] [Google Scholar]
- 5.Eggleston AK, O'Neill TO, Bradbury EM, Kowalczykowski SC. Unwinding of Nucleosomal DNA by a DNA Helicase. J.Biol.Chem. 1995;270:2024–2031. doi: 10.1074/jbc.270.5.2024. [DOI] [PubMed] [Google Scholar]
- 6.Byrd AK, Raney KD. Displacement of a DNA binding protein by Dda helicase. Nucl. Acids Res. 2006;34:3020–9. doi: 10.1093/nar/gkl369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Veaute X, Jeusset J, Soustelle C, Kowalczykowski SC, Le Cam E, Fabre F. The Srs2 helicase prevents recombination by disrupting Rad51 nucleoprotein filaments. Nature. 2003;423:309–12. doi: 10.1038/nature01585. [DOI] [PubMed] [Google Scholar]
- 8.Veaute X, Delmas S, Selva M, Jeusset J, Le Cam E, Matic I, Fabre F, Petit MA. UvrD helicase, unlike Rep helicase, dismantles RecA nucleoprotein filaments in Escherichia coli. EMBO J. 2005;24:180–9. doi: 10.1038/sj.emboj.7600485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kowalczykowski SC, Dixon DA, Eggleston AK, Lauder SD, Rehrauer WM. Biochemistry of homologous recombination in Escherichia coli. Microbiological Reviews. 1994;58:401–465. doi: 10.1128/mr.58.3.401-465.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Smith GR. Homologous recombination near and far from DNA breaks: alternative roles and contrasting views. Annu Rev Genet. 2001;35:243–74. doi: 10.1146/annurev.genet.35.102401.090509. [DOI] [PubMed] [Google Scholar]
- 11.Gorbalenya AE, Koonin EV. Helicases: amino acid sequence comparisons and structure-function relationships. Curr.Op.Struct.Biol. 1993;3:419–429. [Google Scholar]
- 12.Boehmer PE, Emmerson PT. The RecB subunit of the Escherichia coli RecBCD Enzyme Couples ATP Hydrolysis to DNA Unwinding. J.Biol.Chem. 1992;267:4981–4987. [PubMed] [Google Scholar]
- 13.Dillingham MS, Spies M, Kowalczykowski SC. RecBCD enzyme is a bipolar helicase. Nature. 2003;423:893–897. doi: 10.1038/nature01673. [DOI] [PubMed] [Google Scholar]
- 14.Taylor AF, Smith GR. RecBCD enzyme is a DNA helicase with fast and slow motors of opposite polarity. Nature. 2003;423:889–893. doi: 10.1038/nature01674. [DOI] [PubMed] [Google Scholar]
- 15.Smith GR, Kunes SM, Schultz DW, Taylor A, Triman KL. Structure of chi hotspots of generalized recombination. Cell. 1981;24:429–36. doi: 10.1016/0092-8674(81)90333-0. [DOI] [PubMed] [Google Scholar]
- 16.Taylor AF, Schultz DW, Ponticelli AS, Smith GR. RecBC enzyme nicking at Chi sites during DNA unwinding: location and orientation-dependence of the cutting. Cell. 1985;41:153–63. doi: 10.1016/0092-8674(85)90070-4. [DOI] [PubMed] [Google Scholar]
- 17.Ponticelli AS, Schultz DW, Taylor AF, Smith GR. Chi-dependent DNA strand cleavage by RecBC enzyme. Cell. 1985;41:145–51. doi: 10.1016/0092-8674(85)90069-8. [DOI] [PubMed] [Google Scholar]
- 18.Anderson DG, Kowalczykowski SC. The Translocating RecBCD Enzyme Stimulates Recombination by Directing RecA Protein onto ssDNA in a χ-regulated Manner. Cell. 1997;90:77–86. doi: 10.1016/s0092-8674(00)80315-3. [DOI] [PubMed] [Google Scholar]
- 19.Chaudhury AM, Smith GR. A new class of Escherichia coli recBC mutants: implications for the role of RecBC enzyme in homologous recombination. Proc Natl Acad Sci U S A. 1984;81:7850–4. doi: 10.1073/pnas.81.24.7850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Thaler DS, Stahl FW. DNA double-chain breaks in recombination of phage λand of yeast. Ann.Rev.Genet. 1988;22:169–197. doi: 10.1146/annurev.ge.22.120188.001125. [DOI] [PubMed] [Google Scholar]
- 21.Chaudhury AM, Smith GR. Role of Escherichia coli RecBC enzyme in SOS induction. Mol Gen Genet. 1985;201:525–8. doi: 10.1007/BF00331350. [DOI] [PubMed] [Google Scholar]
- 22.Amundsen SK, Taylor AF, Chaudhury AM, Smith GR. recD: the gene for an essential third subunit of exonuclease V. Proc.Natl.Acad.Sci.USA. 1986;83:5558–5562. doi: 10.1073/pnas.83.15.5558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Palas KM, Kushner SR. Biochemical and Physical Characterization of Exonuclease V from Escherichia coli. Comparson of the Catalytic Activities of the RecBC and RecBCD Enzymes. J.Biol.Chem. 1990;265:3447–3454. [PubMed] [Google Scholar]
- 24.Chen HW, Randle DE, Gabbidon M, Julin DA. Functions of the ATP hydrolysis subunits (RecB and RecD) in the nuclease reactions catalyzed by the RecBCD enzyme from Escherichia coli. J Mol Biol. 1998;278:89–104. doi: 10.1006/jmbi.1998.1694. [DOI] [PubMed] [Google Scholar]
- 25.Yu M, Souaya J, Julin DA. Identification of the Nuclease Active Site in the Multifunctional RecBCD Enzyme by Creation of a Chimeric Enzyme. J.Mol.Biol. 1998;283:797–808. doi: 10.1006/jmbi.1998.2127. [DOI] [PubMed] [Google Scholar]
- 26.Yu M, Souaya J, Julin DA. The 30-kDa C-terminal domain of the RecB protein is critical for the nuclease activity, but not the helicase activity, of the RecBCD enzyme from Escherichia coli. Proc.Natl.Acad.Sci.,U.S.A. 1998;95:981–986. doi: 10.1073/pnas.95.3.981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Singleton MR, Dillingham MS, Gaudier M, Kowalczykowski SC, Wigley DB. Crystal structure of RecBCD enzyme reveals a machine for processing DNA breaks. Nature. 2004;432:187–93. doi: 10.1038/nature02988. [DOI] [PubMed] [Google Scholar]
- 28.Taylor AF, Smith GR. Substrate specificity of the DNA unwinding activity of the recBC enzyme of Escherichia coli. J.Mol.Biol. 1985;185:431–443. doi: 10.1016/0022-2836(85)90414-0. [DOI] [PubMed] [Google Scholar]
- 29.Roman LJ, Kowalczykowski SC. Characterization of the helicase activity of the Escherichia coli RecBCD enzyme using a novel helicase assay. Biochemistry. 1989;28:2863–2873. doi: 10.1021/bi00433a018. [DOI] [PubMed] [Google Scholar]
- 30.Korangy F, Julin DA. Kinetics and Processivity of ATP Hydrolysis and DNA Unwinding by the RecBC Enzyme from Escherichia coli. Biochemistry. 1993;32:4873–4880. doi: 10.1021/bi00069a024. [DOI] [PubMed] [Google Scholar]
- 31.Lucius AL, Vindigni A, Gregorian R, Ali JA, Taylor AF, Smith GR, Lohman TM. DNA Unwinding Step-size of E. coli RecBCD Helicase Determined from Single Turnover Chemical Quenched-flow Kinetic Studies. J. Mol. Biol. 2002;324:409–428. doi: 10.1016/s0022-2836(02)01067-7. [DOI] [PubMed] [Google Scholar]
- 32.Lucius AL, Jason Wong C, Lohman TM. Fluorescence stopped-flow studies of single turnover kinetics of E.coli RecBCD helicase-catalyzed DNA unwinding. J. Mol. Biol. 2004;339:731–50. doi: 10.1016/j.jmb.2004.04.009. [DOI] [PubMed] [Google Scholar]
- 33.Lucius AL, Lohman TM. Effects of temperature and ATP on the kinetic mechanism and kinetic step-size for E.coli RecBCD helicase-catalyzed DNA unwinding. J. Mol. Biol. 2004;339:751–71. doi: 10.1016/j.jmb.2004.04.010. [DOI] [PubMed] [Google Scholar]
- 34.Ganesan S, Smith GR. Strand-specific binding to duplex DNA ends by the subunits of the Escherichia coli RecBCD enzyme. J.Mol.Biol. 1993;229:67–78. doi: 10.1006/jmbi.1993.1008. [DOI] [PubMed] [Google Scholar]
- 35.Farah JA, Smith GR. The RecBCD Enzyme Initiation Complex for DNA Unwinding: Enzyme Positioning and DNA Opening. J.Mol.Biol. 1997;272:699–715. doi: 10.1006/jmbi.1997.1259. [DOI] [PubMed] [Google Scholar]
- 36.Taylor AF, Smith GR. Strand Specificity of Nicking of DNA at Chi Sites by RecBCD Enzyme. J.Biol.Chem. 1995;270:24459–24467. doi: 10.1074/jbc.270.41.24459. [DOI] [PubMed] [Google Scholar]
- 37.Wong CJ, Lucius AL, Lohman TM. Energetics of DNA end binding by E.coli RecBC and RecBCD helicases indicate loop formation in the 3′-single-stranded DNA tail. J. Mol. Biol. 2005;352:765–82. doi: 10.1016/j.jmb.2005.07.056. [DOI] [PubMed] [Google Scholar]
- 38.Anderson CF, Record J,MT. Salt-Nucleic Acid Interactions. Annu.Rev.Phys.Chem. 1995;46:657–700. doi: 10.1146/annurev.pc.46.100195.003301. [DOI] [PubMed] [Google Scholar]
- 39.Record MT, Jr., Lohman ML, De Haseth P. Ion effects on ligand-nucleic acid interactions. J Mol Biol. 1976;107:145–58. doi: 10.1016/s0022-2836(76)80023-x. [DOI] [PubMed] [Google Scholar]
- 40.Record MT, Anderson CF, Lohman TM. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Quart.Rev.Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 41.Lohman TM, Mascotti DP. Thermodynamics of ligand-nucleic acid interactions. Methods Enzymol. 1992;212:400–24. doi: 10.1016/0076-6879(92)12026-m. [DOI] [PubMed] [Google Scholar]
- 42.Record MT, Jr., deHaseth PL, Lohman TM. Interpretation of monovalent and divalent cation effects on the lac repressor-operator interaction. Biochemistry. 1977;16:4791–6. doi: 10.1021/bi00641a005. [DOI] [PubMed] [Google Scholar]
- 43.Lohman TM, de Haseth PL, Record MT. Pentalysine-deoxyribonucleic acid interactions: a model for the general effects of ion concentrations on the interactions of proteins with nucleic acids. Biochem. 1980;19:3522–3530. doi: 10.1021/bi00556a017. [DOI] [PubMed] [Google Scholar]
- 44.Overman LB, Bujalowski W, Lohman TM. Equilibrium binding of Escherichia coli single-strand binding protein to single-stranded nucleic acids in the (SSB)65 binding mode. Cation and anion effects and polynucleotide specificity. Biochemistry. 1988;27:456–71. doi: 10.1021/bi00401a067. [DOI] [PubMed] [Google Scholar]
- 45.Lohman TM, Mascotti DP. Nonspecific ligand-DNA equilibrium binding parameters determined by fluorescence methods. Methods Enzymol. 1992;212:424–58. doi: 10.1016/0076-6879(92)12027-n. [DOI] [PubMed] [Google Scholar]
- 46.Hayatsu H, Ukita T. The selective degradation of pyrimidines in nucleic acids by permanganate oxidation. Biochem Biophys Res Commun. 1967;29:556–61. doi: 10.1016/0006-291x(67)90521-9. [DOI] [PubMed] [Google Scholar]
- 47.Nayal M, Di Cera E. Predicting Ca2+-binding sites in proteins. Proc. Natl. Acad. Sci. U.S.A. 1994;91:817–821. doi: 10.1073/pnas.91.2.817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yamashita MM, Wesson L, Eisenman G, Eisenberg D. Where metal ions bind in proteins. Proc Natl Acad Sci U S A. 1990;87:5648–52. doi: 10.1073/pnas.87.15.5648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rosamond J, Telander KM, Linn S. Modulation of the action of the recBC enzyme of Escherichia coli K-12 by Ca2+. J Biol Chem. 1979;254:8646–52. [PubMed] [Google Scholar]
- 50.Rigden DJ. An inactivated nuclease-like domain in RecC with novel function: implications for evolution. BMC Struct Biol. 2005;5:9. doi: 10.1186/1472-6807-5-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Holbrook JA, Capp MW, Saecker RM, Record MT., Jr. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 1999;38:8409–22. doi: 10.1021/bi990043w. [DOI] [PubMed] [Google Scholar]
- 52.Sturtevant JM. Heat capacity and entropy changes in processes involving proteins. Proc Natl Acad Sci U S A. 1977;74:2236–40. doi: 10.1073/pnas.74.6.2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Spolar RS, Record MT. Coupling of local folding to site-specific binding of proteins to DNA. Science. 1994;263:777–784. doi: 10.1126/science.8303294. [DOI] [PubMed] [Google Scholar]
- 54.Kozlov AG, Lohman TM. Adenine base unstacking dominates the observed enthalpy and heat capacity changes for the Escherichia coli SSB tetramer binding to single-stranded oligoadenylates. Biochemistry. 1999;38:7388–7397. doi: 10.1021/bi990309z. [DOI] [PubMed] [Google Scholar]
- 55.Kozlov AG, Lohman TM. Large Contributions of Coupled Protonation Equilibria to the Observed Enthalpy and Heat Capacity Changes for ssDNA Binding to Escherichia coli SSB Protein. PROTEINS: Structure, Function, and Genetics. 2000;(Suppl 4):8–22. doi: 10.1002/1097-0134(2000)41:4+<8::aid-prot20>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 56.Kozlov AG, Lohman TM. Effects of monovalent anions on a temperature-dependent heat capacity change for Escherichia coli SSB tetramer binding to single-stranded DNA. Biochemistry. 2006;45:5190–205. doi: 10.1021/bi052543x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ladbury JE, Wright JG, Sturtevant JM, Sigler PB. A thermodynamic study of the trp repressor-operator interaction. J.Mol.Biol. 1994;238:669–681. doi: 10.1006/jmbi.1994.1328. [DOI] [PubMed] [Google Scholar]
- 58.Vesnaver G, Breslauer KJ. The contribution of DNA single-stranded order to the thermodynamics of duplex formation. Proc Natl Acad Sci U S A. 1991;88:3569–73. doi: 10.1073/pnas.88.9.3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.SantaLucia J,J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc.Natl.Acad.Sci.,U.S.A. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wolf AV, Brown MG, Prentiss PG. Concentrative properties of aqueous solutions: conversion tables. In: Weast RC, editor. CRC Handbook of Chemical and Physical Data. 55 edit. CRC Press; Cleveland: 1974. [Google Scholar]
- 61.Wong CJ, Rice RL, Baker NA, Ju T, Lohman TM. Probing 3′-ssDNA Loop Formation in E. coli RecBCD/RecBC-DNA Complexes Using Non-natural DNA: A Model for “Chi” Recognition Complexes. J. Mol. Biol. 2006;362:26–43. doi: 10.1016/j.jmb.2006.07.016. [DOI] [PubMed] [Google Scholar]
- 62.Wong I, Chao KL, Bujalowski W, Lohman TM. DNA-induced dimerization of the Escherichia coli rep helicase. Allosteric effects of single-stranded and duplex DNA. J Biol Chem. 1992;267:7596–610. [PubMed] [Google Scholar]
- 63.Gray DM, Hung SH, Johnson KH. Absorption and Circular Dichroism Spectroscopy of Nucleic Acid Duplexes and Triplexes. Methods in Enzymology. 1995;246:19–34. doi: 10.1016/0076-6879(95)46005-5. [DOI] [PubMed] [Google Scholar]
- 64.Mascotti DP. Ph.D. thesis. Texas A&M University; 1992. Charged oligopeptide-nucleic acid interactions as models of the electrostatic component of protein-nucleic acid interactions. [Google Scholar]
- 65.Jezewska MJ, Bujalowski W. A General Method of Analysis of Ligand Binding to Competing Macromolecules Using the Spectroscopic Signal Originating from a Reference Macromolecule. Application to Escherichia coli Replicative Helicase DnaB Protein-Nucleic Acid Interactions. Biochemistry. 1996;35:2117–2128. doi: 10.1021/bi952344l. [DOI] [PubMed] [Google Scholar]
- 66.Kozlov AG, Lohman TM. Calorimetric studies of E-coli SSB protein single-stranded DNA interactions. Effects of monovalent salts on binding enthalpy. Journal of Molecular Biology. 1998;278:999–1014. doi: 10.1006/jmbi.1998.1738. [DOI] [PubMed] [Google Scholar]
- 67.Maniatis T, Fritsch EF, Sambrook J. Molecular Cloning: A Laboratory Manual. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 1982. [Google Scholar]
- 68.Ausubel FM, Brent R, Kingston RE, Moore DD, Seidman JG, Smith JA, Struhl K. Current Protocols in Molecular Biology. John Wiley and Sons, Inc.; 1987. [Google Scholar]