Mutual information reveals variation in temperature-dependent sex determination in response to environmental fluctuation, lifespan and selection

Abstract

Quantifying the degree to which sex determination depends on the environment can yield insight into the evolution, ecological dynamics, and functional aspects of sex determination. In temperature-dependent sex determination (TSD), theory often predicts a complete dependence of sex on temperature, with a switch-like reaction norm. However, empirical data suggest more shallow relationships between sex and temperature. Here, we demonstrate the usefulness of an index, mutual information (MI), to reflect the degree of temperature dependence in sex. MI depends on both the shape of a reaction norm and the natural temperature variation, thus providing a measure of TSD that is ecologically dependent. We demonstrate that increased lifespan and decreased environmental fluctuation predict reaction norms with high MI (switch-like). However, mutation and weaker selection on sex-specific performance reduce average MI in a population, suggesting that mutation–selection balance can resolve some of the conflict between theoretical predictions of individual-based optimality and population-based empirical results. The MI index allows clear comparison of TSD across life histories and habitats and reveals functional similarities between reaction norms that may appear different. The model provides testable predictions for TSD across populations, namely that MI should increase with lifespan and decrease with historical environmental fluctuations.

1. Introduction

Environmental sex determination (ESD) describes the phenomenon of individual sex being determined by environmental conditions during development. For example, in some fish and reptiles (e.g. many turtles, all crocodilians, some lizards), sex is determined early during development by incubation temperature (temperature-dependent sex determination (TSD); Janzen & Paukstis 1991; Valenzuela & Lance 2004). TSD is hypothesized to be adaptive when fitness is influenced by developmental temperature in a sex-specific fashion and individuals cannot choose the temperature at which they develop (Charnov & Bull 1977; Bull 1981b).

Research on the evolution of TSD has frequently aimed to explain the shape of the reaction norm that describes sex as a function of temperature (Janzen & Paukstis 1991; Mrosovsky & Pieau 1991; Valenzuela & Lance 2004). Empirical research has demonstrated that pivotal temperatures (temperature at which there is a 50% probability of developing as male) vary little across geographical ranges or are higher at higher latitudes, and transitional ranges of temperature (TRT: range of temperatures from which both sexes are produced) typically span a few degrees (Bull et al. 1982a,b; Janzen & Paukstis 1991; Mrosovsky & Pieau 1991; Ewert et al. 1994; Ewert et al. 2004). Additionally, quantitative approaches to determine these parameters have been applied successfully (Girondot 1999).

TSD reaction norms are most easily measured in a laboratory setting, and knowing the shape of a reaction norm provides vital information. While this laboratory approach is indispensable, temperature-sensitive transitions in sex ratio, as measured in the laboratory, are only relevant when they are demonstrated to occur in natural nests over a range of naturally occurring nest temperatures (Bull 1985; Schwarzkopf & Brooks 1987; Janzen & Paukstis 1991; Doody et al. 2006; Robert et al. 2006; Bull 2008). To better understand the evolution of TSD, it would be valuable to have a description of TSD reaction norms that accounts for the natural temperatures experienced by populations.

(a) Theoretical background

Whereas empirical approaches typically examine sex and temperature across clutches and report population-based reactions norms that vary from highly switch-like to more gradual transitions (i.e. variable TRT; Ewert et al. 2004), early theory of TSD and ESD predicted individual reaction norms that are entirely switch-like (Bull 1981a; Charnov & Bull 1989). More recently, theory has aimed to identify the conditions under which gradual transitions are predicted (Bull & Bulmer 1989; van Dooren & Leimar 2003; Leimar et al. 2004), focusing on the potential role of fluctuations in the environment (e.g. temperature distributions; Bull & Bulmer 1989; van Dooren & Leimar 2003). Fluctuations among patches may occur when spatially isolated mating pools have different temperature distributions, or when annual temperature distributions fluctuate among generations (Bull 1981b; Bull & Bulmer 1989; van Dooren & Leimar 2003). When populations are confined to local fluctuating patches (low mating among patches), switch-like reaction norms are selected against due to the production of biased cohort sex ratios in extreme-environment years, which translate to biased adult sex ratios in isolated populations (van Dooren & Leimar 2003). For spatially isolated populations with variable migration and no overlapping generations, van Dooren & Leimar (2003) showed that the maintenance of non-switch-like reaction norms in populations with TSD requires either very high fluctuations in the environment or very low migration among patches.

In addition to sampling across patches spatially through migration, many species that exhibit TSD (e.g. turtles and crocodilians) can live at least 20 years (Janzen & Paukstis 1991) and will sample across patches through time as well (Bull & Bulmer 1989), making temporal isolation of populations low. In fact, Bull & Bulmer (1989) have shown that longer lifespan in fluctuating environments can favour switch-like reaction norms due to greater averaging over temporal patches. In these theoretic approaches, shallow reaction norms persist only in short-lived, spatially isolated populations (Bull & Bulmer 1989; van Dooren & Leimar 2003). Empirically, many taxa that display TSD are long-lived, with at least some amount of dispersal, yet may still exhibit gradual transitions in sex across developmental temperature (Ewert et al. 2004). Thus, theory and empiricism conflict in the approaches and conclusions of TSD research. This disparity may be due to an incomplete understanding of the organisms' ecology and how it selects for individual reaction norms. In addition, variation in pivotal temperatures among clutches with switch-like reaction norms may lead to broader reaction norms when measured at the population level (broader TRT; Mrosovsky & Pieau 1991; Janzen 1992; Rhen & Lang 1998; Bowden et al. 2000; Dodd et al. 2006). Therefore, predicting patterns of TSD measured across individuals may be a fruitful approach to reconciling theoretical predictions with empirical patterns.

Here, we approach these challenges to TSD research by examining the evolution of TSD in fluctuating environments in a simulation model. First, we introduce a new metric of TSD, mutual information (MI), which provides a single measure of TSD by incorporating all components of the reaction norm and which reflects ecological reality by relying on the natural distribution of temperatures. We demonstrate that this measure of TSD is predicted to change in response to lifespan and environmental fluctuation. Second, we explore how mutation–selection balance may produce mean population reaction norms that are less switch-like than individual optimal reaction norms. We aim to identify and interpret the influence of important ecological variables on the evolution of TSD and provide a predictive framework for comparison among populations.

2. The model

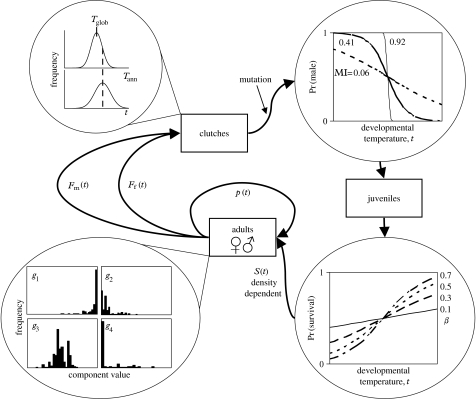
We model the evolution of TSD in a single population with overlapping generations (figure 1; table 1). Each year, the annual mean developmental temperature T_ann is drawn from an interannual distribution of mean temperatures, with mean T_glob and variance ${\sigma }_{\text{glob}}^2$. For each clutch produced in that year, the developmental temperature of the clutch, t, is drawn from the annual distribution of developmental temperatures with mean T_ann and variance ${\sigma }_{\text{ann}}^2$.

Figure 1.

Schematic of the simulation model. In each generation, clutches are described by a developmental temperature, t, drawn from a distribution with mean T_ann. T_ann is drawn from an annual temperature distribution with mean T_glob. A portion of offspring undergo mutation, after which all offspring are assigned to being male or female. The shape of the sex-versus-temperature reaction norm and the total environmental variance determine the MI (${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=1.5), the amount of information shared between sex and temperature. First-year adults are sampled from clutches. Adults vary in their genotypic components (g₁–g₄). Adults contribute to the next round of clutches.

Table 1.

Definitions of model symbols.

symbol	definition
Tglob, ${\sigma }_{\text{glob}}^{\text{2}}$	mean and variance of annual temperature distribution
Tann, ${\sigma }_{\text{ann}}^2$	mean and variance of clutch temperature distribution
Ff, Fm	reproductive competition function, female and male
φ, Q	power of reproductive competition function, female and male
pf, pm	annual adult survival function, female and male
γf, γm	slope of annual adult survival function, female and male
Sf, Sm	juvenile survival function, female and male
βf, βm	slope of juvenile survival function, female and male
g1, g2, g3, g4	components of the TSD reaction norm

(a) Reaction norm

The reaction norm of sex versus temperature is described by a sigmoidal curve with four components, g₁, g₂, g₃ and g₄,

$$\text{Pr}(\text{male})=g_1+\frac{(g_2-g_1)}{1+\text{exp}(-(t-g_3)/g_4)}.$$ (2.1)

In the reaction norm, g₁ is the extreme y-value at low t; g₂ is the extreme y-value at high t; g₃ is the inflection point of the curve (i.e. pivotal temperature); and g₄ is the inverse of the steepness of the curve (i.e. TRT). Thus, the reaction norms that are highly temperature dependent have g₁, g₂ of 0, 1 or 1, 0, respectively, and g₄ near 0. When g₁ and g₂ equal 1 and 0, the population shows Type Ia TSD (male to female transition), and when they equal 0 and 1, the population demonstrates Type Ib TSD (female to male transition).

Here, we refer to the temperature that predicts sex ratio as a single ‘developmental’ temperature. Because temperature varies in natural systems, the mean of temperature may not accurately predict clutch sex ratios (Georges 1989). For application to a particular TSD system, a different measure, such as a constant temperature equivalent (Georges 1989; Georges et al. 2004, 2005), may provide a better predictor of sex ratio and be the variable of interest for measuring intra- and interannual variation.

(b) Dynamics

In our population, adult population size, N, is set at 1000. For each clutch produced in a generation (figure 1), a developmental temperature, t, is assigned based on the annual temperature distribution. Each individual is defined by its developmental temperature and four genotypic components of the reaction norm (g₁–g₄). The individual is assigned to be a male with a probability given by t and the reaction norm. Otherwise, the individual is assigned to be a female. Offspring are sexually mature in 1 year. Population size is maintained by density-dependent survival of offspring to adulthood, with relative juvenile survival of S_m and S_f, where $S_{\text{m}}=S_{\text{m}\min }+(S_{\text{m}\max }-S_{\text{m}\min })/(1+\exp (-(t-T_{\text{glob}}){\beta }_{\text{m}}))$ and $S_{\text{f}}=S_{\text{f}\min }+(S_{\text{f}\text{max}}-S_{\text{f}\text{min}})/(1+\text{exp}(-(t-T_{\text{glob}}){\beta }_{\text{f}}))$. First-year adults are sampled from the pool of offspring based on relative juvenile survival. Adult breeding success is provided by power functions of developmental temperature. Females produce clutches of offspring number $F_{\text{f}}=t^{\phi }$. Adult males compete to fertilize clutches with a relative fertility given by $F_{\text{m}}=t^Q$. Adults survive to the following year with probability p_m and p_f, for males and females, respectively, where $p_{\text{m}}=p_{\text{m}\text{min}}+(p_{\text{m}\text{max}}-p_{\text{m}\text{min}})/(1+\text{exp}(-(t-T_{\text{glob}}){\gamma }_{\text{m}}))$ and $p_{\text{f}}=p_{\text{f}\text{min}}+(p_{\text{f}\text{max}}-p_{\text{f}\text{min}})/(1+\text{exp}(-(t-T_{\text{glob}}){\gamma }_{\text{f}}))$. Individual fitness components of juvenile survival, adult survival and breeding success are all functions of developmental temperature. The dependence of the fitness components on temperature is determined by φ, Q, γ_f, γ_m, β_f and β_m. When a parameter is set to zero, the fitness component does not depend on temperature. In this paper, we examined the evolution of TSD when daughters gain in juvenile survival with warmer t, but sons do not (β_f>β_m=0). Temperature does not influence adult breeding success (Q=φ=0) or adult survival (both γ=0).

Prior to determining offspring sex, 2% of all offspring are chosen randomly as mutants. For mutants, we assume pleiotropy in the determination of the reaction norm and induce mutation in all four components (g₁–g₄) simultaneously. For g₁, g₂ and g₃, a change in the value is chosen randomly from a normal distribution with mean 0 and variance 0.01 (for g₁ and g₂) or 0.02 (for g₃). For g₄, a change in the value is chosen from a uniform distribution with range 0–5 and randomly subtracted or added to the pre-mutation value. g₁ and g₂ are constrained to be between 0.0001 and 0.9999 and g₄ is constrained to be greater than 1×10⁻¹⁰ to allow mathematical calculation of MI (see below). Sexes are assigned following mutation because sex determination naturally occurs after meiotic mutation, during embryonic development.

Each simulation was initiated with a population homogenous for genotype (g₁=0.5, g₂=0.5, g₃=22, g₄=1) and iterated 10 000 times. At the end of each simulation, MI (see below) was calculated for the reaction norm of each individual, and the mean MI and mean value of each reaction norm component across the population were calculated.

We considered the influence of multiple parameter values. First, we varied the environmental fluctuation, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$ (${\sigma }_{\text{glob}}^2+{\sigma }_{\text{ann}}^2=1.5$). Second, we varied adult survival by setting both p_min and p_max to different values. Third, we varied the differential fitness advantage that daughters have in juvenile survival by varying β_f. All the simulations were performed in Matlab v. 7.1.

(c) Mutual information

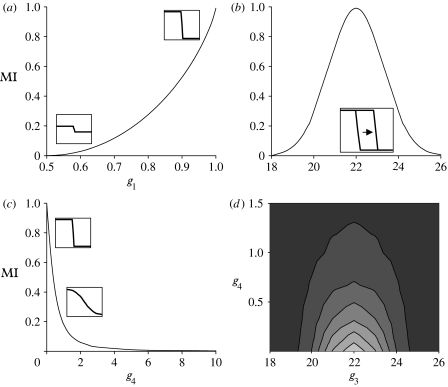
To use a single measure of the degree of temperature dependence in sex determination, we employ information theory to find, for a given reaction norm, the MI between temperature and sex. MI has broad application in information theory (Cover & Thomas 2006; Yeung 2006), but the application to a biological reaction norm is novel. Here, MI captures how much information about sex is shared with information about the environment. The calculation of MI reflects all components of the reaction norm and the probability distribution of developmental temperatures. The measure, therefore, provides an ecologically relevant measure of TSD. MI ranges between 0 and ln(2) and is the highest when g₄ is near 0, g₁ and g₂ are at opposite extreme values and g₃ equals T_glob (see §3; figures 1 and 2). To allow better comparison among parameter sets, all values of MI were divided by ln(2) and are thus measures of relative MI with maximum 1.

Figure 2.

The relationship between MI and components of the reaction norm. (a) MI as a function of g₁, when g₂ mirrors values in g₁ about the 0.5 midpoint; g₃=22, g₄=0.0001. (b) MI as a function of g₃, when g₁=0.9999, g₂=0.0001 and g₄=0.0001. (c) MI as a function of g₄, when g₁=0.9999, g₂=0.0001 and g₃=22. (d) Contours of MI as a function of g₃ and g₄. For all, T_glob=22 and ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=1.5.

MI is calculated as the difference between the joint entropy between temperature and sex (HTS) and the sum of the entropy associated with sex (HS) and the entropy associated with temperature (HT), or

$$\text{MI}=\text{HTS}-(\text{HT}+\text{HS}).$$ (2.2)

The entropies are given by the following equations:

$$\text{HT}=\int \text{Pr}(t)\text{ln}(\text{Pr}(t))\text{d}t,$$ (2.3)

$$\text{HS}=\int \text{Pr}(\text{male}|t)\text{Pr}(t)\text{d}t*\text{ln}\left(\int \text{Pr}(\text{male}|t)\text{Pr}(t)\text{d}t\right)+\int \text{Pr}(\text{female}|t)\text{Pr}(t)\text{d}t*\text{ln}\left(\int \text{Pr}(\text{female}|t)\text{Pr}(t)\text{d}t\right),$$ (2.4)

and

$$\text{HTS}=\int \text{Pr}(\text{male}|t)\text{Pr}(t)\text{ln}(\text{Pr}(\text{male}|t)\text{Pr}(t))\text{d}t+\int \text{Pr}(\text{female}|t)\text{Pr}(t)\text{ln}(\text{Pr}(\text{female}|t)\text{Pr}(t))\text{d}t.$$ (2.5)

Pr(t) is a normal distribution with mean T_glob and variance $({\sigma }_{\text{glob}}^2+{\sigma }_{\text{ann}}^2)$,

$$\text{Pr}(t)=\frac{1}{\sqrt{2\pi ({\sigma }_{\text{glob}}^2+{\sigma }_{\text{ann}}^2)}}\text{exp}\left(\frac{-{(t-T_{\text{glob}})}^2}{2({\sigma }_{\text{glob}}^2+{\sigma }_{\text{ann}}^2)}\right).$$ (2.6)

Pr(male|t), the probability of developing as a male given the developmental temperature, is given by equation (2.1), and $\text{Pr}(\text{female}|t)=1-\text{Pr}(\text{male}|t)$.

MI can be calculated for an individual or for a population, depending on the source of the data used to generate the reaction norm. However, it is not immediately obvious that one can scale from one level to another. A homogenous population would show congruence between mean individual MI and population-level MI, whereas a heterogeneous population composed of individuals of high MI may show low MI when measured at the population level (e.g. if some individuals show TSD Ia while others show TSD Ib).

3. Results

(a) Mutual information

Changes in MI reflect changes in the components of the reaction norm (figures 1 and 2). MI increases as g₁ and g₂ approach opposite extreme values. As g₃ moves away from T_glob, MI decreases, reflecting the importance of the natural temperature distribution in defining the degree to which sex depends on temperature. MI changes dramatically with g₄, allowing fine distinction over changes in slope that are likely to represent functional variation in TSD (i.e. g₄<2). However, it does not distinguish well between reaction norms that are very shallow and unlikely to represent functional differences (i.e. 2<g₄<10). When MI is high, temperature and sex are strongly linked, whereas low MI reflects more randomness in sex determination. In general, MI measures the tendency of a reaction norm to produce one sex versus the other over the natural range of temperatures, by any combination of g₁–g₄.

(b) Environmental fluctuation and lifespan

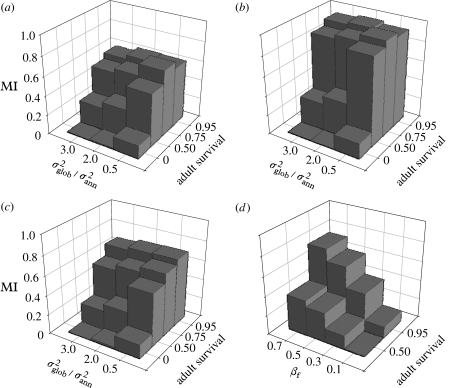
We examined the reaction norm for three levels of environmental fluctuation (${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=0.5, 2 and 3) and for four adult annual survival probabilities (p=0, 0.5, 0.75 and 0.95), where β_f=0.5. Each parameter set was replicated in 10 simulations and the results are means from the 10 replicates.

We found that, for semelparous organisms, the reaction norm was very shallow even in the more stable environment (figure 3a). MI increased with lifespan, as longer lived individuals experience increasingly more year types during their lifetimes. For iteroparous organisms, as environmental fluctuation increased, the reaction norm became shallower and MI decreased. Environmental fluctuation had little impact on the degree of TSD in the most short- and long-lived organisms. All simulations with p=0.95 were continued until 20 000 iterations due to directional movement near the 10 000th iteration. The mean MI values after 20 000 were slightly higher than those presented for 10 000 iterations.

Figure 3.

MI as a function of environmental fluctuation, annual adult survival and female juvenile survival advantage. In (a), MI values are averages of population mean values from 10 separate simulations. In (b), MI values are averages of 10 replicate runs from two simulations each where mutation was turned off for 10 000 iterations. In (c), mutation was returned for another 10 000 iterations to all replicates in (b). In (a–c), β_f=0.5 and β_m=0. (d) MI when β_f=0.1, 0.3, 0.5 or 0.7, β_m=0, p=0.5 or 0.95 and ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2 (after 10 000 iterations).

(c) Mutation

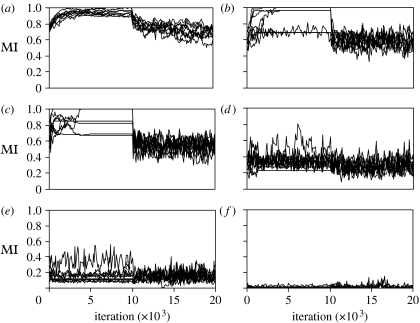
The results of our simulations are in populations experiencing regular mutation. Thus, the mean reaction norm of populations may reflect the balance of mutation and selection. To understand the extent to which our results were altered by mutation, we continued some simulations without mutation. Specifically, we chose haphazardly two replicate simulations from each parameter set, and replaced 50 of the adults (5%) of the 10 000th iteration with a ‘switch-like mutant’ (g₁=0.9999, g₂=0.0001, g₃=22, g₄=0.00001). This mutant was introduced to ensure that a switch-like genotype was present in the population as a source of variation for selection. Mutation was turned off, and the population was iterated for another 10 000 generations. This ‘invasion’ was replicated 10 times for each of the original simulations. Based on trajectories, these runs all led to stasis, and often fixation of a genotype.

For moderate- and long-lived organisms (p=0.75, 0.95), turning off mutation always led to an increase in MI (figures 3b and 4). In fact, when the artificially introduced invader genotype did not become fixed, an existing resident genotype that had even higher MI often went to fixation. In general, switch-like reaction norms appear to be optimal for long-lived organisms, even in fluctuating environments, consistent with van Dooren & Leimar (2003). This was also the case for short-lived organisms in more stable environments (p=0.5, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=0.5), where MI also increased with the removal of mutation. In more fluctuating environments, short-lived organisms were subjected to variable influences of mutation, and a non-switch-like reaction norm appeared to be optimal. For semelparous organisms, turning off mutation had very little effect on mean MI, which remained low or near zero (no TSD) with or without mutation.

Figure 4.

MI over time for 10 replicates where mutation is removed (at iteration=0) and then returned (at iteration 10 000) at the end of a single simulation run. Panels represent runs with particular parameter values. (a) p=0.95, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2, population mean MI at iteration 0=0.4904. (b) p=0.75, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2, population mean MI at iteration 0=0.3063. (c) p=0.5, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=0.5, population mean MI at iteration 0=0.3560. (d) p=0.5, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2, population mean MI at iteration 0=0.1879. (e) p=0, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=0.5, population mean MI at iteration 0=0.0809. (f) p=0, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2, population mean MI at iteration 0=0.0104.

When mutation was returned to these populations for another 10 000 iterations, MI returned to values similar to those before mutation was turned off (figure 3c). The difference in MI between populations with and without mutation measures the phenotypic effect of mutation load in the population.

(d) Strength of differential fitness

We next explored how the strength of the fitness differential influences the reaction norm. Ten replicate simulations were run for three additional values of juvenile female survival (β_f=0.1, 0.3 and 0.7) in a fluctuating environment (${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2), for short- and long-lived organisms (p=0.5 and 0.95, respectively). In all cases, β_m=0.

The strength of the differential fitness effect influenced the average reaction norm (figure 3d). When the selective advantage for developing as a female was reduced, the resulting MI was reduced. For a given level of selective advantage, greater MI was predicted in longer-lived individuals. However, even in long-lived organisms, a low fitness differential could lead to low MI across the population.

4. Discussion

(a) Mutual information

Organisms may develop in a heterogeneous environment, where environmental conditions (i.e. temperature) influence fitness in a sex-specific fashion. As a result, selection will favour ESD (here, TSD). However, if the distribution of temperatures fluctuates, populations will exhibit extremely biased cohort sex ratios, and frequency-dependent selection can lead to the evolution of less extreme TSD (Bull & Bulmer 1989). The degree to which sex depends on temperature is difficult to encapsulate in a single measure, with research focusing on a few components of the TSD reaction norm (e.g. pivotal temperature and TRT).

Here, we analysed the evolution of TSD by calculating a single value that integrates multiple components of the sex-versus-temperature reaction norm and the natural variation in incubation temperatures. MI allows easy interpretation of predictions for TSD across varied life histories and habitats in a fashion that would be difficult to accomplish by comparing multiple components of a reaction norm separately. In particular, it can reveal functional similarity between reaction norms that have different values for their reaction norm components, as well as functional differences between reaction norms that appear to have similar steep slopes. In addition, this index takes into account the natural variation in incubation temperatures encountered in a population (e.g. mean nest temperatures or constant temperature equivalents; Georges et al. 2004), thereby providing a measure of the dependence of sex on temperature that is ecologically relevant and apparent to natural selection (Bull et al. 1982a,b). Reaction norms can still be measured in the laboratory; however, natural nest temperatures must be measured to calculate MI, potentially limiting the empirical application of this index. However, in order to increase our understanding of the ecology and evolution of TSD, it will be necessary in the future to place reaction norms in the context of a population's ecology. Thus, the collection of field-based data will probably increase in the future.

(b) Population patterns

We showed that the impact of environmental fluctuation on TSD depends on the lifespan of the organism, confirming earlier findings of Bull & Bulmer (1989). At one extreme, the breeding adults of a semelparous population consist of a single cohort, so any biases in cohort sex ratio greatly impact demography. In these populations, even modest fluctuations in annual temperature distributions led to the loss of TSD. For organisms of long lifespan, the adult breeding population averages across many separate cohorts and their annual temperature distributions, so that fluctuations have little impact on demography. In these populations, MI was high regardless of environmental fluctuation, indicating the evolution of more switch-like reaction norms. In organisms of intermediate adult lifespan, the interaction between degree of temporal averaging (i.e. lifespan) and that of temporal patchiness (i.e. environmental fluctuation) was important. For moderately long-lived species, the index of MI has the ability to discriminate among reaction norms predicted to have steep but variable slopes.

How much isolation among patches is required to predict populations of low MI? In van Dooren & Leimar's (2003) model of mating pools with spatial isolation (migration), a 0.5 probability of migration among patches predicted switch-like reaction norms in strongly fluctuating environments. This suggests that even modestly isolated populations in the wild (migration less than 0.5) may be expected to demonstrate gradual reaction norms. However, the expectation of gradual reaction norms was greatly reduced in less fluctuating environments (migration must be less than 0.1 probability for gradual reaction norms). In addition, sampling across multiple temporal patches due to increased lifespan will reduce the effective isolation of populations. Thus, we might expect that long-lived organisms must either live in more fluctuating environments or have reduced migration compared with populations in van Dooren & Leimar in order to expect gradual reaction norms. In our model, we found that a high degree of temporal isolation (i.e. adult lifespan less than or equal to 2 years) was required to always expect gradual reaction norms. Relatively high MI may be expected even in moderately long-lived organisms in highly fluctuating environments.

Most reptile species with TSD have very long lifespans (approx. 20 years, Janzen & Paukstis 1991) yet show variable reaction norms. Our model and its predecessors (Bull & Bulmer 1989; van Dooren & Leimar 2003) provide predictions for variation among natural populations exhibiting TSD which have yet to be tested with empirical patterns. Because migration may also contribute to patterns in reaction norms (van Dooren & Leimar 2003), a model incorporating both spatial and temporal patch sampling would further advance our predictive ability. If populations are responding to frequency-dependent selection on the TSD reaction norm, we would expect that the steepness of the reaction norms should correlate negatively with historical fluctuations in climate among years (steeper reaction norms in less-fluctuating environments) and correlate positively with lifespan.

(c) Mutation and selection

When mutation was removed from our populations, we found that very high MI was expected in all but the most short-lived populations living in highly fluctuating environments. This indicates that switch-like reaction norms are optimal under most ecological situations. With the addition of mutation, however, we saw the persistence of maladaptive genotypes that led to decreased mean MI, or shallower reaction norms when sampled across a population. Although MI does not directly translate into individual fitness under all parameter sets, it is clear that there is an optimal MI (optimal genotype) in the population which readily becomes fixed when mutation is turned off. The genetic variance around the optimum represents the mutation load as measured through the phenotypic effects on sex ratio. While the mutation load cannot be calculated directly owing to the frequency-dependent nature of sex ratio evolution, we can compare the phenotypic effects of this load. Mutation load had a relatively large phenotypic effect in populations with moderate adult lifespan in high-fluctuation environments (p=0.75, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=2) and in populations with short lifespan in low-fluctuation environments (p=0.5, ${\sigma }_{\text{glob}}^2/{\sigma }_{\text{ann}}^2$=0.5).

Similarly, the phenotype effect of the mutation–selection balance can also be seen across the varied levels of sex-specific fitness. Reduced levels of differential fitness led to reductions in predicted MI. In particular, long-lived organisms in moderately fluctuating environments are predicted to demonstrate shallow reaction norms if the selection differential is small enough. In line with Bull & Bulmer (1989), we found that a much stronger fitness differential was required in short-lived organisms to predict reaction norms of equivalent MI as in long-lived organisms. Therefore, detecting the fitness differentials may be easier in short-lived species with TSD.

(d) Summary

With our model, we demonstrated the usefulness of a single measure of temperature dependence to study the evolution of TSD. The index of MI represents multiple components of the TSD reaction norms simultaneously and should be adaptable to other shapes of reaction norms (e.g. TSD II female–male–female pattern). In addition, MI provides a biologically relevant measure by incorporating natural variation in incubation temperatures and providing high discrimination of reaction norms across the range that is most functionally relevant. We found that environmental fluctuation and lifespan interact to determine the mean MI in a population. This finding provides predictions for empirical patterns across populations with TSD. Mutation in a population can maintain the mean degree of TSD in a population below what would be expected from the individual optimum. In addition, weak selection can also lead to reduced mean MI. Thus, we found that, while switch-like reaction norms are optimal for individuals with at least moderate lifespan, environmental fluctuation, mutation and weak selection can lead to a reduction in the MI recorded in the population. That individual variation in reaction norms can lead to shallower population patterns may resolve some of the conflict between the switch-like reaction norms predicted by individual-based optimality models and the more gradual reaction norms recorded in population-based empirical measures.

Supplementary Material

How to use MATLAB code to calculate MI

Instructions for how to implement the Matlab code for calculating mutual information

MATLAB code to calculate MI

Matlab m-file to modify and call in Matlab

MATLAB code for MI function

Matlab m-file that serves as a function to calculate mutual information