Initial Training with Difficult Items Facilitates Information-Integration but not Rule-Based Category Learning

Abstract

Previous research has disagreed about whether a difficult cognitive skill is best learned by beginning with easy or difficult examples. Two experiments are described that clarify this debate. Participants in both experiments received one of three types of training on a difficult perceptual categorization task. In one condition participants began with easy examples, then moved to examples of intermediate difficulty, and finished with the most difficult examples. In a second condition this order was reversed, and in a third condition, participants saw examples in a random order. The results depended on the type of categories that participants were learning. When the categories could be learned via explicit reasoning (a rule-based task), all three training procedures were equally effective. However, when the categorization rule was difficult to describe verbally (an information-integration task), participants who began with the most difficult items performed much better than participants in the other two conditions.

Conventional wisdom suggests that the best way to learn a difficult cognitive skill is to begin with easy examples, master those, and then gradually increase example difficulty. A variety of evidence supports this general hypothesis. For example, a popular training procedure, called the method of errorless learning (Baddeley, 1992; Terrace, 1964), adopts an extreme form of this strategy in which the initial examples are so easy and each subsequent increase in difficulty is so small that participants never make errors. The basic assumption of this method is that errors that occur during training strengthen incorrect associations and are therefore harmful to the learning process. Errorless learning has proven to be an effective training procedure in a wide variety of tasks (e.g., Squires, Hunkin, & Parkin, 1997; Wilson, Baddeley, Evans, & Shiel, 1994). Similar results have been reported in perceptual learning tasks (e.g., Ahissar & Hochstein, 1997).

On the other hand, other studies have reported opposite results. For example, Lee et al. (1988) trained separate groups of participants to classify a variety of stimuli. Each successive group began with the stimuli that the previous group had classified incorrectly. Presumably, these were the more difficult items in the two categories. In all experiments, later groups made fewer errors than earlier groups, thus suggesting that learning may be better when training begins with the most difficult items and concludes with the easiest.

We report the results of two experiments that clarify the role that initial difficulty plays in category learning. Participants in both experiments received one of three types of training on a difficult perceptual categorization task. In one condition participants began with easy examples, then moved to examples of intermediate difficulty, and finished their training with the most difficult examples. In a second condition this order was reversed, and in the third condition, participants saw examples in a random order. Our results suggest that the effect of these different training orders depends on the type of categories that participants are learning. When the categories can be learned via explicit reasoning (i.e. a rule-based task), all three training procedures were equally effective. However, when the categorization rule was difficult to describe verbally (i.e., an information-integration task), participants who began with the most difficult examples performed much better than participants in the other two conditions.

There is now good evidence that humans have multiple category learning systems, which are each best suited for learning certain types of category structures, and are each mediated by different neural circuits (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & O’Brien, 2005; Erickson & Kruschke, 1998; Nosofsky, Palmeri, & McKinley, 1994; Reber, Gitelman, Parrish, & Mesulam, 2003). In rule-based category-learning tasks, the categories can be learned via some explicit reasoning process. Frequently, the rule that maximizes accuracy is easy to describe verbally (Ashby et al., 1998). In information-integration (II) category-learning tasks, accuracy is maximized only if information from two or more stimulus components (or dimensions) is integrated at some pre-decisional stage, and the optimal strategy is difficult or impossible to describe verbally (Ashby et al., 1998).

The II and rule-based categories used in Experiments 1 and 2 are described in Figure 1. Note that each category contains 15 circular sine-wave gratings that vary in the width and orientation of the dark and light bars. The solid lines denote the category boundaries. On each trial in both experiments, one randomly selected disk was shown to the participant, whose task was to press a response key to indicate category membership. Each response was followed by feedback indicating whether that response was correct or incorrect. In the case of the II categories, note that no simple verbal rule correctly separates the disks into the two categories. Nevertheless, many studies have shown that people reliably learn such categories, provided they receive consistent and immediate feedback after each response (for a review, see Ashby & Maddox, 2005). With the rule-based categories, the correct rule is the logical conjunction: respond A if the bars are wide and the orientation is steep; otherwise respond B. Despite depending on both dimensions, this is a rule-based task because the optimal rule is easy to verbalize.

Figure 1.

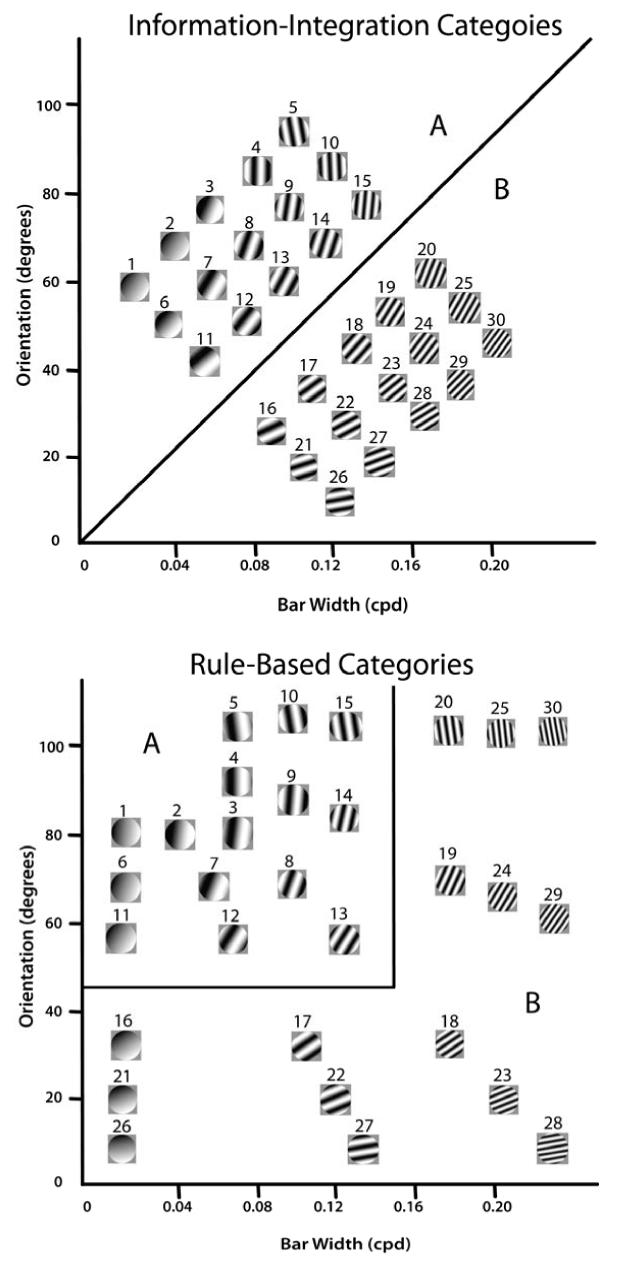
Stimuli and categories used in the Experiments 1 and 2. Each stimulus was a circular sine-wave grating that varied across trials in bar width and bar orientation. The solid lines denote the category boundaries. The stimulus numbers refer to Tables 1 and 2.

A prominent neuropsychological theory of category learning, called COVIS (Ashby et al., 1998; Ashby & Waldron, 1999), proposes that II categories are learned via procedural-learning, whereas rule-based categories are learned via logical reasoning, and that both types of learning depend on the same memory systems that have been identified by memory researchers (Ashby & O’Brien, 2005). COVIS correctly predicts many of the empirical dissociations between rule-based and II tasks that have been reported. First, II category learning requires immediate feedback after the response, whereas rule-based learning is relatively unaffected if the feedback is delayed by as much as 10 sec (Maddox, Ashby, & Bohil, 2003), or if the category label is shown before stimulus presentation (Ashby, Maddox, & Bohil, 2002). Rule-based learning is even possible in the absence of any feedback (Ashby, Queller, & Berretty, 1999). Second, effective II learning requires a consistent mapping between category and response, whereas rule-based learning does not (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004). Third, rule-based learning requires working memory and executive attention, whereas II learning does not (Maddox, Ashby, Ing, & Pickering, 2004; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006).

EXPERIMENT 1

COVIS predicts that when participants begin with easy examples in an II task, they will use simple explicit rules that succeed with the training examples, but might not work as well with the difficult examples. In contrast, when participants begin with difficult examples, they should quickly realize that no explicit strategies will succeed, which should facilitate procedural learning. The following experiment provides a strong test of this prediction.

Method

Participants

There were 26, 24, and 31 participants respectively in the Hard-to-Easy, Easy-to-Hard, and Random conditions. All participants were from the UCSB community and they all reported 20/20 vision or vision corrected to 20/20. Each participant completed one 60 minute session.

Stimuli

Each stimulus was a circular sine-wave grating of constant size and contrast. Stimuli varied across trials in bar width (i.e., spatial frequency) and bar orientation. The categories were created from the values in Table 1. We hereafter refer to the 5 stimuli in each outer row as Easy (stimuli 1-5 and 26-30), the 5 stimuli in each middle row as Medium (stimuli 6-10 and 21-25), and the 5 stimuli in the inner rows as Hard (stimuli 11-20). The diagonal line shown in the top panel of Figure 1 denotes the category boundary. The most accurate one-dimensional categorization rule (i.e., a vertical or horizontal line in Figure 1), would achieve 60%, 80%, and 100% correct, respectively, for the Hard, Medium, and Easy stimuli. Each grating subtended a visual angle of approximately 3.3°, and was generated using Brainard’s (1997) Psychophysics Toolbox and displayed on a 21-inch monitor with 1280 × 1024 resolution.

Table 1.

Stimulus Values

Category	Stimulus Number	Bar Width1	Orientation2
A	1	0.010	56.09
	2	0.033	67.07
	3	0.056	78.04
	4	0.079	89.02
	5	0.102	100.0
	6	0.026	48.41
	7	0.049	59.39
	8	0.072	70.36
	9	0.095	81.34
	10	0.118	92.31
	11	0.0424	40.73
	12	0.065	51.70
	13	0.088	62.68
	14	0.111	73.65
	15	0.135	84.63
B	16	0.074	25.36
	17	0.098	36.34
	18	0.121	47.31
	19	0.144	58.29
	20	0.167	69.26
	21	0.091	17.68
	22	0.114	28.65
	23	0.137	39.63
	24	0.160	50.61
	25	0.183	61.58
	26	0.107	10.00
	27	0.130	20.97
	28	0.153	31.95
	29	0.176	42.92
	30	0.200	53.90

¹cycles per degree

²degrees counterclockwise from horizontal

Procedure

Participants were tested individually in a dimly lit room. They were told to emphasize accuracy without worrying about response time. On each trial, a stimulus and category labels were presented on the screen until the participant responded by depressing a computer key labeled “A” or “B”. Participants were given 5 sec to respond. If they did not respond within 5 sec a message appeared on the screen, “PLEASE RESPOND FASTER”, accompanied by a saw-tooth tone. Immediately following the response, corrective audio feedback was presented for 500 ms. Feedback was a sine-wave tone for a correct response and a saw-tooth tone for an incorrect response. The feedback was followed by a pause of 1500 ms.

During training, each stimulus was presented 15 times. In the Easy-to-Hard condition, Easy stimuli were shown first in random order, then Medium stimuli, and finally Hard stimuli. In the Hard-to-Easy condition, this ordering was reversed. In the Random condition, all stimuli were presented in random order. During transfer, each stimulus was presented 5 times in random order in all three conditions.

Results

Accuracy-Based Analyses

Average accuracy is shown in Figure 2. The data of most interest are from the transfer block (i.e., block 4), where all groups categorized all stimuli. Block 2 is also of interest because the Hard-to-Easy and Easy-to-Hard participants received training on the exact same stimuli during this block (i.e., Medium stimuli). A visual inspection of Figure 2 indicates that accuracy was highest in the Hard-to-Easy condition during both of these blocks (i.e., blocks 2 and 4). This conclusion is supported by 1-way ANOVAs [with 3 levels of condition (Hard-to-Easy, Easy-to-Hard, and Random)], in which both main effects were significant [Block 2: F(2, 80) = 6.15, p = .003, p_rep = .98; Block 4: F(2, 80) = 8.05, p < .001, p_rep = .99]. Post hoc tests revealed a significant accuracy difference in both blocks between the Hard-to-Easy and Easy-to-Hard conditions [Block 2: F(1,50) = 8.39, p = .018, p_rep = .97; Block 4: F(1,50) = 5.96, p = .018, p_rep = .94] and between the Hard-to-Easy and Random conditions [Block 2: F(1,55) = 7.11, p = .010, p_rep = .96; Block 4: F(1,55) = 19.23, p < .001, p_rep > .99]. In addition, neither accuracy difference between the Easy-to-Hard and Random conditions was significant [Block 2: F(1,55) = .35, p = .554, p_rep = .46; Block 4: F(1,55) = 1.39, p = .24, p_rep = .68].

Figure 2.

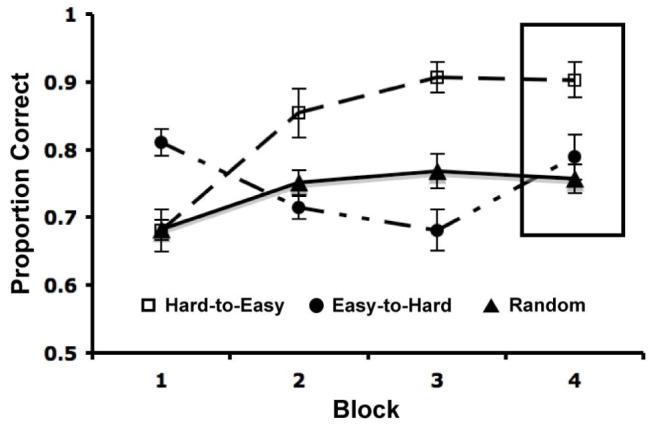
Proportion correct for Hard-to-Easy (empty squares), Easy-to-Hard (filled circles), and Random (filled triangles) conditions in each block (with standard error bars) during Experiment 1. Proportions from the transfer block are boxed.

Figure 3 shows how each group performed on the easiest items (stimuli 1-5, 26-30), the items of intermediate difficulty (stimuli, 6-10, 21-25), and the most difficult items (stimuli 11-20). Note that the Hard-to-Easy group performed substantially better than either other group on all items, except for the most difficult items during training. These, of course, were the first stimuli the Hard-to-Easy group saw, so their undifferentiated performance here is not surprising. During the critical transfer block, Hard-to-Easy accuracy is significantly better than either other group on all three types of items [3 × 3 ANOVA, main effect of condition: F(2, 78) = 8.45, p < 0.001, p_rep = 0.999; post hoc tests: all p < .001, p_rep > 0.99].

Figure 3.

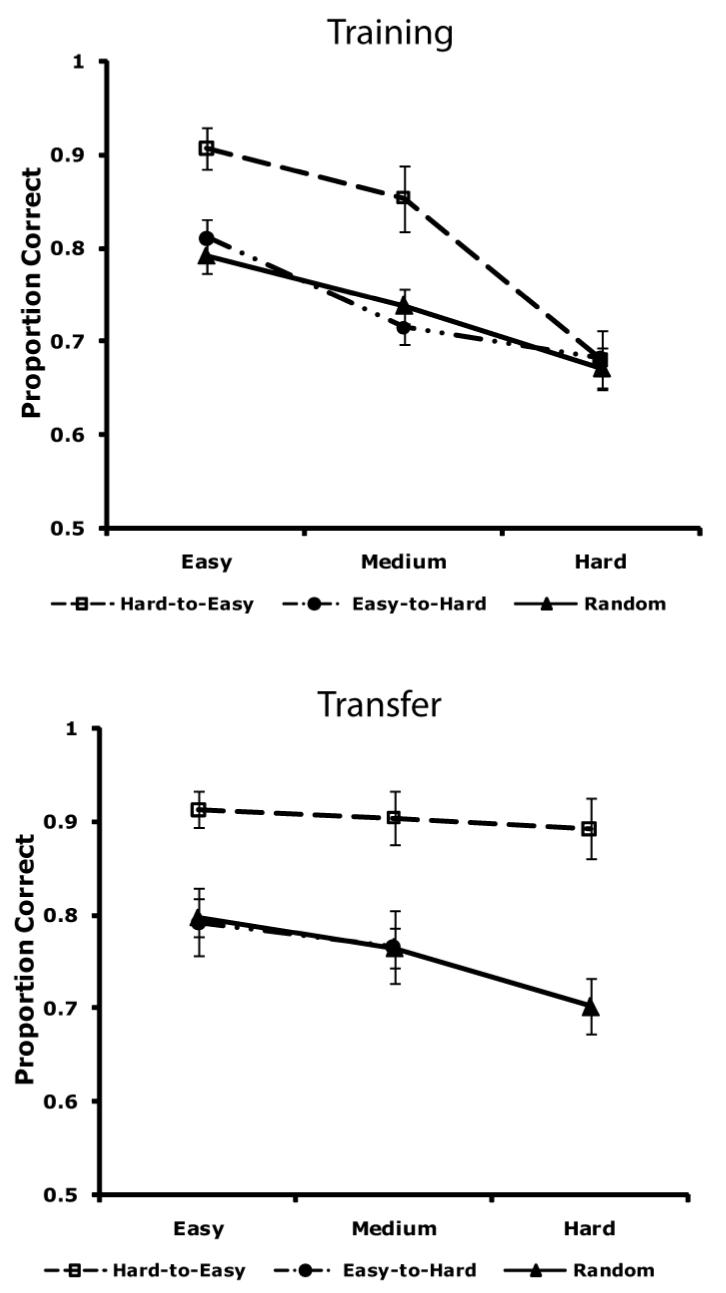
Proportion correct for each group in Experiment 1 during training and transfer on easy, medium, and difficult items.

Model-Based Analyses

The accuracy-based analyses suggest that performance in the Hard-to-Easy condition was better than in the Easy-to-Hard or Random conditions. Before concluding that Hard-to-Easy training is superior, however, it is important to confirm that the Hard-to-Easy participants used an II strategy. To answer this question, we fit three different types of decision bound models (e.g., Maddox & Ashby, 1993) to the data from each individual participant: II, rule-based, and random response models (see the Appendix for details). The random response models assume participants guess randomly on every trial. The II and rule-based models make no detailed process assumptions, but they assume that each participant’s responses are compatible with either an II or rule-based strategy, respectively.

Figure 4 shows the percentage of participants in each condition whose data were best fit by a model that assumed an II strategy, separately for block 2 and for the transfer block. In both blocks, participants in the Hard-to-Easy condition were significantly more likely to use an II strategy than participants in the Easy-to-Hard condition [binomial test; Block 2: t(50) = 1.97, p = .05, p_rep = .87; Block 4: t(50) = 2.53, p = .015, p_rep = .94] or in the Random condition [Block 2: t(57) = 5.37, p < .001, p_rep > .99; Block 4: t(57) = 4.071, p < .001, p_rep > .99]. Also in both blocks, the percentages of participants using an II strategy in the Easy-to-Hard and Random conditions were not significantly different [Block 2: t(55) = 3.73, p < .001, p_rep = .99; Block 4: t(55) = 1.50, p = .140, p_rep = .77].

Figure 4.

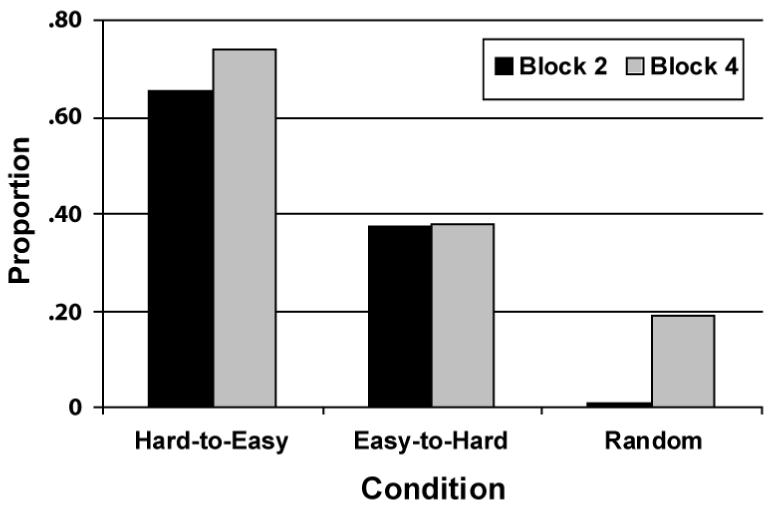
Proportion of Experiment 1 participants whose data were best fit by a model assuming an II decision strategy for blocks 2 and 4 in each of the three experimental conditions.

Overall, II models gave good accounts of the data. For example, during the transfer block, the best fitting II models accounted for an average of 97.8%, 96.3%, and 94.6% of the variance in the data from the Hard-to-Easy, Easy-to-Hard, and Random conditions, respectively. In addition, the mean p_reps on all decisions that a data set was best fit by an II model was greater than .999 for block 4 in all three conditions (i.e., p_reps computed using the method of Ashby & O’Brien, 2008). In block 2, mean p_rep was greater than .999 in the Hard-to-Easy condition and .777 in the Easy-to-Hard condition. Thus, we can be highly confident that participants were using an II strategy when their data were best fit by an II model.

Discussion

The Hard-to-Easy group had dramatically higher transfer accuracy on all stimuli than either other group. In fact, Hard-to-Easy transfer accuracy was about 15 percentage points higher than Easy-to-Hard accuracy, and the Hard-to-Easy advantage over the Random group was greater still. In addition, participants in the Hard-to-Easy condition were also much more likely to use a decision strategy of the optimal type - that is, an II strategy - than participants in either other group. Further, these dramatic differences were already apparent by block 2.

A finding of secondary interest was that the Easy-to-Hard group outperformed the Random group, both in terms of transfer accuracy and probability of using an II strategy. Although these differences were not significant, this trend lends tentative support to the claim that errorless learning techniques are superior to general random training.

Ahissar and Hochstein (1997) reported that in simple feature detection tasks the more difficult the initial training, the more specific the transfer benefits. Consistent with this result, Doane, Sohn, and Schreiber (1999) reported that initial training with difficult perceptual same-different judgments led to improved transfer performance on difficult, but similar judgments, relative to initial training with easy judgments. In other words, results from the perceptual learning literature suggest that training on difficult items might prove beneficial to subsequent testing on similar difficult items. Note however, that this result cannot account for our block 4 results since prior to block 4 all three groups received an equal amount of training on the most difficult category members (i.e., stimuli 11-20).

It is also important to note that our results are incompatible with the two most popular single system theories of categorization - namely prototype theory and exemplar theory. Prototype theory assumes that when an unfamiliar stimulus is encountered, it is assigned to the category with the most similar prototype (Homa et al., 1981; Posner & Keele, 1968; Reed, 1972; Rosch, 1973; Smith & Minda, 1998). Exemplar theory assumes that when an unfamiliar stimulus is encountered, its similarity is computed to the memory representation of every previously seen exemplar from each relevant category (Brooks, 1978; Estes, 1986; Hintzman, 1986; Lamberts, 2000; Medin & Schaffer, 1978; Nosofsky, 1986).

To see what these theories predict in the present experiment, consider block 2 where participants in the Hard-to-Easy and Easy-to-Hard conditions only saw stimuli of medium difficulty. Consider a trial when a stimulus is shown from category A. For the Easy-to-Hard group the prototype will be somewhere near the center of the Easy stimuli and for the Hard-to-Easy group it will be near the center of the Hard stimuli. Stimuli of medium difficulty then will be equally near the category A prototype for both groups. However, medium category A stimuli will be further from the B prototype for the Easy-to-Hard group than for the Hard-to-Easy group. Thus, prototype theory predicts that categorization will be easier for the Easy-to-Hard group and that they should therefore have higher block 2 accuracy than the Hard-to-Easy group. Of course, this is exactly opposite to the observed results.

The argument is similar for exemplar theory. A category A stimulus of medium difficulty is equally similar to the Easy and Hard category A exemplars. However, such stimuli are less similar to the Easy category B exemplars than to the Hard category B exemplars. Thus, exemplar theory also incorrectly predicts that block 2 accuracy should be higher in the Easy-to-Hard condition.

EXPERIMENT 2

Experiment 1 strongly contradicts predictions of errorless training, but seems consistent with the results of Lee et al. (1988). Of the four category structures studied by Lee et al. (1988), at least one seemed like an II task (was the handwriting written by a man or a woman?), and at least one seemed like a rule-based task (does the sentence indicate an upward or a downward direction?). The results for these two category structures were similar. In both cases, overall accuracy was higher for participants who first trained on stimuli that other participants found particularly difficult. In contrast, COVIS predicts that the learning advantage of the Hard-to-Easy group in Experiment 1 depends critically on the fact that II categories were used. To clarify this issue, Experiment 2 replicates Experiment 1 exactly, except using the rule-based categories shown in bottom panel of Figure 1.

Method

Participants

There were 31 participants each in the Hard-to-Easy, Easy-to-Hard, and Random conditions. All participants were from the UCSB community reported 20/20 vision or vision corrected to 20/20. Each participant completed one 60 minute session.

Stimuli

The stimuli were constructed in the same manner as in Experiment 1. The exact dimensional values are shown in Table 2.

Table 2.

Stimulus Values

Category	Stimulus Number	Bar Width1	Orientation2
A	1	0.103	90.00
	2	0.116	90.00
	3	0.128	90.00
	4	0.128	98.89
	5	0.128	107.78
	6	0.100	76.67
	7	0.123	76.67
	8	0.147	76.67
	9	0.147	93.33
	10	0.147	110.00
	11	0.103	63.33
	12	0.134	63.33
	13	0.165	63.33
	14	0.165	85.56
	15	0.165	107.78
B	16	0.103	36.67
	17	0.153	36.67
	18	0.203	36.67
	19	0.203	72.22
	20	0.203	107.78
	21	0.106	23.33
	22	0.164	23.33
	23	0.221	23.33
	24	0.221	64.44
	25	0.221	105.56
	26	0.100	10.00
	27	0.170	10.00
	28	0.240	10.00
	29	0.240	60.00
	30	0.240	110.00

¹cycles per degree

²degrees counterclockwise from horizontal

Procedure

The procedures were identical to those outlined in Experiment 1 except Experiment 2 used the stimuli and categories shown in Figure 4.

Results

Accuracy-Based Analyses

Mean accuracy is shown in Figure 5. The data of most interest are again from the transfer block and from block 2. A visual inspection indicates that accuracy was approximately the same during both of these blocks. This conclusion is supported by 1-way ANOVAs, in which neither main effect was significant [Block 2: F(2, 90) = .045, p > .50, p_rep = .11; Block 4: F(2, 90) = .851, p > .40, p_rep = .55].

Figure 5.

Proportion correct for Hard-to-Easy (empty squares), Easy-to-Hard (filled circles), and Random (filled triangles) conditions in each block (with standard error bars) of Experiment 2. Proportions from the transfer block are boxed.

Figure 6 shows how each group performed on the easiest items (stimuli 1-5, 26-30), the items of intermediate difficulty (stimuli, 6-10, 21-25), and the most difficult items (stimuli 11-20). During training, the Hard-to-Easy group was worse than the other groups on the most difficult items [F(2, 90) = 5.11, p < 0.01, p_rep > 0.95], but there was no difference among any of the groups on the intermediate or easy items (p > 0.3, p_rep < 0.64). During transfer, the Easy-to-Hard group performed best on all items, but none of these differences reached significance [F(2,90) = .669, p = .515, p_rep = 0.49].

Figure 6.

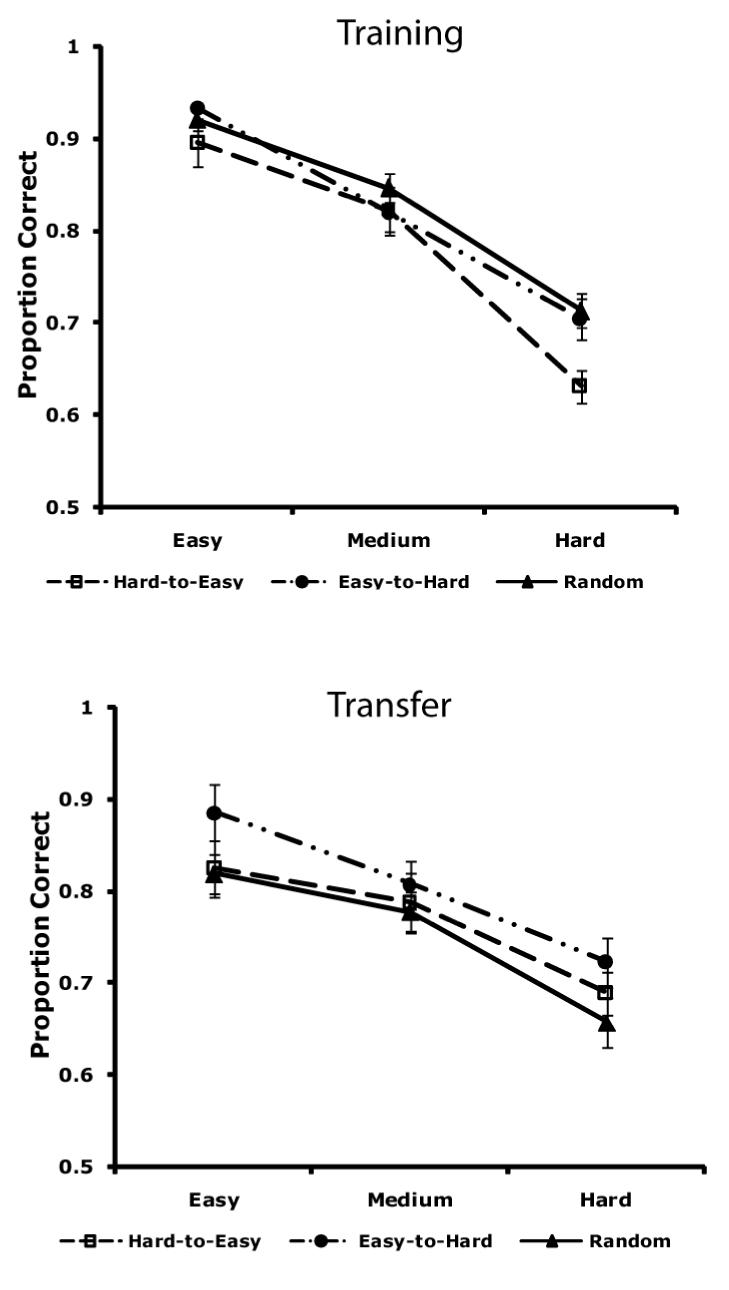
Proportion correct for each group in Experiment 2 during training and transfer on easy, medium, and difficult items.

Model-Based Analyses

To confirm that all groups used similar decision strategies, we fit the same decision bound models used in Experiment 1 to the responses of each participant. Figure 7 shows the percentage of participants in each condition whose block 2 and transfer block data were best fit by a model that assumed a logical conjunction decision rule. Note that in all blocks and conditions, a model of this type was the best fitting model for at least 75% of participants. Furthermore, there were no significant differences in these percentages across conditions [all p > 0.35].

Figure 7.

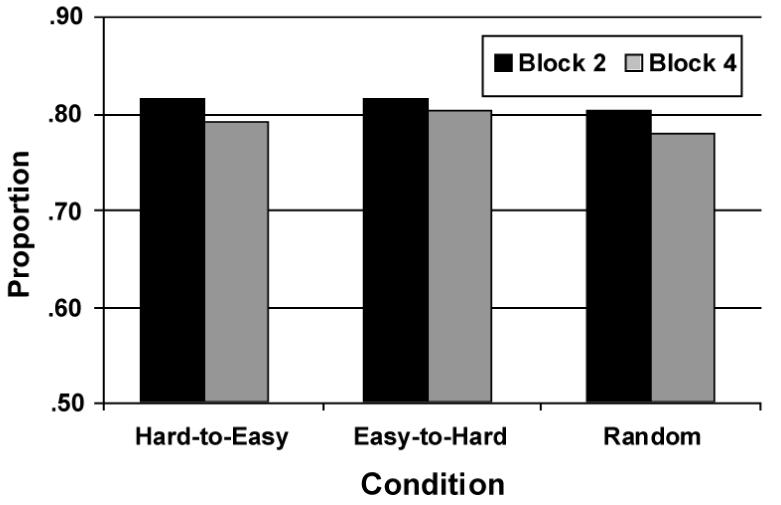
Proportion of Experiment 2 participants whose data were best fit by a model assuming the decision rule was a logical conjunction for blocks 2 and 4 in each of the three experimental conditions.

Discussion

When the optimal rule was a logical conjunction, there was no difference in any of the training procedures, either in overall accuracy or in the likelihood that participants learned the correct categorization rule. There was a trend toward better performance by the Easy-to-Hard group, as predicted by errorless learning, but this difference was not significant. These results appear to contradict the results of Lee et al. (1988), who reported that overall accuracy in a rule-based task was higher for participants who first trained on stimuli that other participants found particularly difficult. One complication in interpreting the Lee et al. results is that they did not include a transfer block, like our block 4. For this reason, they were unable to assess whether there was any real learning advantage of their Hard-to-Easy group. Unfortunately, the higher overall accuracy of this group does not necessarily imply a learning advantage. For example, in a rule-based task where accuracy is at chance before the correct rule is learned and where all-or-none learning occurs (i.e., in one trial), it is straightforward to show that participants who begin with the most difficult items will have higher accuracy than participants who begin with easy items. This is because beginning with difficult items means more easy items later, after the rule is learned (and thus, more chances to respond correctly). In summary, higher accuracy in the Lee et al. (1988) design does not guarantee better learning.

GENERAL DISCUSSION

The results of Experiments 1 and 2 were dramatically different. With II categories, initial training on the most difficult items led to higher accuracy and a greater probability that the correct rule was learned. With rule-based categories however, there were no differences among any of the training methods, either in accuracy or the strategy that was learned. This difference is especially striking since both category structures required participants to attend to both stimulus dimensions, and the stimuli used in the two experiments were essentially the same.

The COVIS theory of category learning (Ashby et al., 1998; Ashby & Waldron, 1999) predicts that the advantage of the Hard-to-Easy group with II categories occurred because the other groups were rewarded early in training for using simple explicit rules. For example, participants using a one-dimensional rule in Experiment 1 could achieve perfect accuracy during block 1 in the Easy-to-Hard condition, 80% correct in the Random condition, but only 60% correct in the Hard-to-Easy condition. Participants who used a simple rule during block 1 may then have persisted with explicit strategies in later blocks¹. This hypothesis is supported by the lower percentages of Easy-to-Hard and Random participants whose data were best fit by a model assuming an II decision strategy in blocks 2 and 4. In contrast, the Hard-to-Easy group was punished from the outset (with low accuracy) for using one-dimensional rules. This may have encouraged Hard-to-Easy participants to quickly give up on explicit rules and instead use some nondeclarative similarity-based strategy (which in this experiment was optimal).

The present results suggest that optimal training procedures in difficult categorization tasks may depend on the nature of the categories that are being trained. In particular, our results suggest that if the optimal rule is not easily verbalized and accurate performance requires integrating information from different perceptual dimensions, then the most effective training procedure might be to begin with difficult examples and only introduce easy examples later, after participants have learned that no simple verbal rule will succeed.

APPENDIX

This appendix describes the models that were fit to each participant’s data and the model fitting procedure. For more details, see Maddox and Ashby (1993).

Rule-Based Models

The One-Dimensional Classifier assumes participants set a decision criterion on a single stimulus dimension (i.e., bar width or orientation), and has two parameters (a criterion on the relevant dimension, and perceptual noise variance). The General Conjunctive Classifier assumes that the decision rule is a logical conjunction, and has 3 parameters (a criterion on each dimension, and perceptual noise variance).

Information-Integration Models

The General Linear Classifier (GLC) assumes participants divide the stimulus space using a linear decision bound. The GLC has 3 parameters: the slope and intercept of the linear decision bound, and a perceptual noise variance.

Random Response Models

Two models assumed random responding - one with unbiased guessing (zero parameters) and one with biased guessing (one parameter).

Model Selection

Parameters were estimated using the method of maximum likelihood, and the Bayesian Information Criterion (BIC; Schwarz, 1978) was used for model selection:

$$\mathrm{BIC}=r\ln N-2\ln L,$$

where r is the number of free parameters, N is the sample size, and L is the likelihood of the model given the data.