Abstract
We present a mathematical model of the genetic regulation controlling skeletogenesis and the influence of the physical environment on a branching sponge with accretive growth (e.g. Haliclona oculata or Lubomirskia baikalensis). From previous work, it is known that high concentrations of silicate induce spicule formation and upregulate the silicatein gene. The upregulation of this gene activates locally the production of spicules in the sponge and the deposition of the skeleton. Furthermore, it is known that the expression of the gene Iroquois induces the formation of an aquiferous system, consisting of exhalant and inhalant pores. We propose a model of the regulatory network controlling the separation in time and space of the skeletogenesis and the formation of the aquiferous system. The regulatory network is closely linked with environmental influences. In building a skeleton, silicate is absorbed from the environment. In our model, silicate is transported by diffusion through the environment and absorbed at the surface of a geometric model of the sponge, resulting in silicate gradients emerging in the neighbourhood of the sponge. Our model simulations predict sponge morphology and the positioning of the exhalant pores over the surface of the sponge.
Keywords: morphogenesis, sponges, regulatory networks, body plan formation
1. Introduction
Within the metazoans, sponges represent the phylum with the simplest body plan (Pilcher 2005). This makes these organisms an excellent case study for understanding morphogenesis and the physical translation of the genetic information into a growth form, using a combination of a geometric model of the growth form and a model of the spatial and temporal expression of developmental genes.
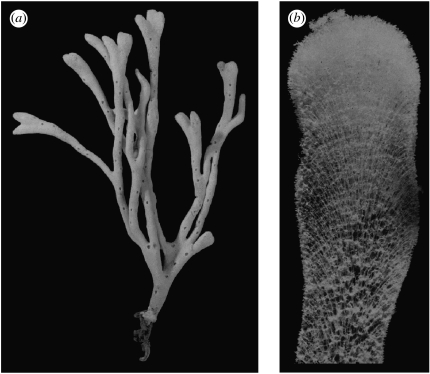
In sponges, only species (as, for example, Haliclona oculata and Lubomirskia baikalensis) with a certain kind of skeletal architecture can develop erect tree-like growth forms (Kaandorp & Kűbler 2001; Kaluzhnaya et al. 2005a,b), as shown in figure 1a. The skeletal architecture emerges in an accretive growth process where the individual skeleton elements (the spicules) are arranged in a radiate accretive architecture (Wiedenmayer 1977). In this growth process, growth occurs only at the tip of the sponge, where new layers are deposited on top of the previous layers, while the previous growth stages remain unchanged. An example of this architecture is shown in figure 1b. In some Haliclona species (Haliclona simulans), the spicules in the growth layers are arranged in triangles, and in H. oculata the spicules are arranged in a polygonal pattern, which can be subdivided again in a triangular pattern (for detailed drawings of the spicule architecture in Haliclona species, see Kaandorp & Kűbler 2001).
Figure 1.
(a) Growth form of the sponge H. oculata showing the distribution of the growth zones at the tips and the exhalant pores over the surface of the sponge. (b) Section through a branch of the sponge H. oculata in which all soft tissues have been removed showing the radiate accretive architecture of the skeleton.
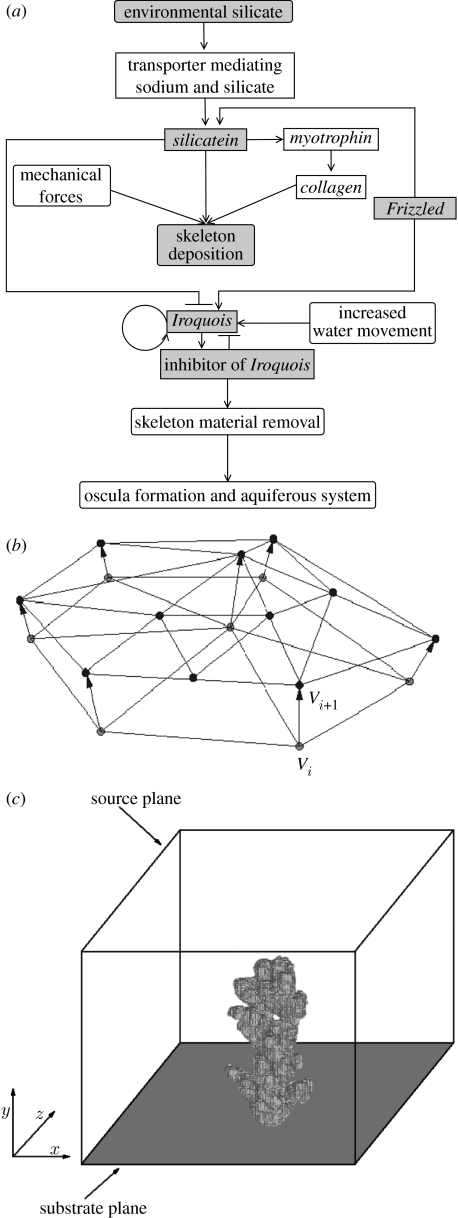
Recently, new details (Adell et al. 2003; Le Pennec et al. 2003; Müller et al. 2003, 2004; Perovic et al. 2003; Schröder et al. 2007) about the genetic regulation of growth and form of sponges have become available, including evidence for spatial and temporal gradients of morphogens controlling the growth in a positional information system. The regulatory network, together with environmental influences, controlling the formation of the skeleton and the aquiferous system in a sponge is summarized in figure 2a. The genes (gene products) and the external environment influence the two major biomechanical processes shaping the sponge: the deposition of the skeleton and the formation of the aquiferous system. Triangular arrows indicate activation of a gene or process, while blocked arrows indicate suppression of a gene or process.
Figure 2.
(a) Regulatory genes (rectangular boxes) and (external) environmental influences (round-edged boxes) controlling the two major morphogenetic biomechanical processes, viz. the deposition of the skeleton and the formation of exhalant pores and the aquiferous system in a sponge through removal of material. Triangular arrows indicate activation of a gene or process, while blocked arrows indicate suppression of a gene or process. Only the shaded components in the diagram have been included in the model. (b) Small detail of the accretive growth model showing the construction of a new layer (layer i+1) on top of the previous layer (layer i). The thickness li+1 of the new layer and the distance between the vertices Vi and Vi+1 are determined by the growth function in equation (2.2). (c) Basic idea of the coupled simulation model. The simulated form consisting of triangulated growth layers is mapped onto a discrete lattice. The discrete representation is used for computing the diffusion model and the flux of nutrients into the sponge surface. Simulated silicate is exclusively distributed by diffusion, and the top plane is the source of silicate, while all silicate is absorbed at the surface of the growth form and periodic boundary conditions are applied at the vertical faces of the simulation box.
For building a skeleton, two species of silicate (silicic acid) are absorbed by the sponge from the environment. Silicate is transferred over the diffusive boundary layer around the sponge and locally silicate is depleted. When there is a constant supply of silicate from the environment and the silicate is continuously being absorbed, silicate gradients will emerge in the direct neighbourhood of the sponge.
High concentrations of silicate (or ferric ions) induce spicule formation and upregulate the silicatein, collagen and myotrophin genes (Le Pennec et al. 2003). The upregulation of the genes activates the production of spicules in the sponge and leads to deposition of the skeleton. The second major morphogenetic event is the construction of the aquiferous system together with the formation of the exhalant pores. The aquiferous system is constructed, only after the skeleton has been built. The expression of the gene Iroquois is induced by increased water current and activates the formation of exhalant pores and the aquiferous system (Perovic et al. 2003; Müller et al. 2004). During the formation of this aquiferous system, some material has to be removed from the original skeleton and skeletogenesis is stopped in the regions of the sponge where the aquiferous system is formed. Exhalant pores are formed at more or less regular distances from each other (figure 1a), this suggests a feedback mechanism preventing Iroquois from being expressed everywhere on the surface, which would lead to a disintegration of the sponge. The regulator suppressing Iroquois is not yet known. Furthermore, both the skeletogenesis and the formation of exhalant pores are processes occurring more or less at the surface of the sponge. It has been demonstrated in the sponge Suberites domuncula that the gene Frizzled works as a polarity factor in the sponge (Adell et al. 2003). In S. domuncula, Frizzled is expressed at the surface of the sponge. It is hypothesized here that Frizzled works as a positional information system, indicating the ‘upward’ direction (the direction towards the external environment in a branching sponge).
In this study, we have translated the observations and hypotheses discussed above and which are summarized in figure 2a, into a mathematical model, with the aim to test the idea whether this knowledge is sufficient to predict the body plan and morphology of the sponge.
2. Material and methods
(a) The sponge Haliclona oculata
The sponge H. oculata was used as a case study for our model. All materials shown in this paper were collected in the eastern Scheldt in The Netherlands. Details on environmental conditions are provided elsewhere (Kaandorp & de Kluijver 1992).
(b) Model of accretive growth and environment
In the model, we have simplified the environmental influence and assumed that the accretive growth process is entirely determined by a diffusion-limited supply of silicate and the influence of water current is neglected. In reality, this describes a physical environment under stagnant conditions. Although this is a major simplification, in some cases the sponge H. oculata may grow at very sheltered and almost stagnant locations (Kaandorp & de Kluijver 1992). The growth velocity of the sponges (approx. 1–2 cm in one month; see Kaandorp & de Kluijver 1992) is much slower compared with the diffusion process. The distribution of silicate in the environment will be in a steady state with a source of silicate and absorption of silicate at the surface of the sponge. The distribution of silicate can be modelled by a Laplace equation
| (2.1) |
To model the growth process, we have used a diffusion-limited accretive growth model that can lead to the spontaneous formation of branches (Merks et al. 2003; Kaandorp et al. 2005). The growth process is modelled as a surface-normal deposition process, where new material is deposited along the normal vectors that are constructed on the surface of the previous growth stage. In the model, the growth layers are represented by layers of triangles. A small detail of the model is shown in figure 2b, where a new layer of triangles (layer i+1 with vertices Vi+1) is constructed on top of the previous layer (layer i with vertices Vi). We based the simulation model on the hypothesis that silicate is the main limiting factor in skeletogenesis, and growth is limited by the local amount of silicate available to the sponge. The nutrient distribution was simulated using a lattice-based diffusion model (for a more detailed description of this model see Kaandorp et al. 2005). The diffusion model was coupled to the accretive growth model, by mapping the geometric representation (the layers of triangles) onto a lattice of 2003 nodes (figure 2c). The lattice representation was used for computing the gradients around the simulated growth form. After the gradients have been computed, the normalized flux of nutrients into the sponge surface can be calculated.
The simulated skeleton is constructed from discrete and nearly equal-sized elements (the spicules) with basic unit size s. The surface is covered with triangles with almost equal-sized edges, varying slightly about this basic unit s. Triangles that become very large when the growth layer is expanding split up into new ones, while the small ones in a shrinking growth layer are deleted. In figure 2b, it can be observed that a number of triangles in the previous layer i have split up into smaller ones during the construction in layer i+1. For further details about the splitting up and deletion of triangles, we refer to a previous paper on the accretive growth model (Merks et al. 2003). The linear extension rate of the simulated skeleton is driven by the amount of absorbed simulated silicate. The thickness of a new layer li+1, the distance between two successive vertices Vi and Vi+1 from the previous growth layer i and the new growth layer i+1 are computed using the growth function
| (2.2) |
where is the normal vector in vertex Vi (the average of the normal vectors of the surrounding triangles); is the normalized amount of absorbed silicate in an area around vertex Vi; and s is the maximal thickness of a growth layer (the length of an individual spicule). In this growth function, we assume a linear relationship between the local amount of deposited material and the local amount of absorbed silicate from the environment.
(c) Regulatory network model
In our model, we have tried to simplify the network of figure 2a as much as possible; the aim here was to have a network model that can predict some aspects of the body plan formation and still can be investigated by numerical simulation. In §2b, we explained the first simplification step where we model the influence of the physical environment as a diffusion-limited process. We have simplified the genes involved in the regulatory network of figure 2a into a system consisting of four genes: silicatein; Frizzled; Iroquois; and an inhibitor of Iroquois (all components included in our model are shaded in figure 2a). In this simplification, we have lumped all influences of the genes involved in the deposition of the skeleton into one gene, viz. silicatein. This gene plays the central role in this process. In the model, Frizzled is only expressed at the surface of the sponge. We hypothesize that only in the presence of (a constant amount of) Frizzled, the other gene products can be activated. Therefore, all simulated interactions take place only at the sponge surface. In the model, silicatein product (sil), Iroquois product (irq) and the inhibitor of Iroquois (inh) can freely diffuse over the sponge surface, not hindered by cells, spicules or other sponge structures. It should be noted here that in the network, skeletal growth can only be downregulated by decreasing environmental silicate concentrations and is not influenced by Iroquois or its inhibitor.
After determining the amount of silicate absorbed by the area around each vertex of the mesh object in the accretive growth model, a system of coupled differential equations is used to simulate the regulatory network controlling the formation of the exhalant pores. Three gene products are considered: silicatein (sil); Iroquois (irq); and an inhibitor of Iroquois (inh). The amount of silicatein is set equal to the amount of normalized absorbed silicate at each growth step. Iroquois is produced when the concentration of silicatein drops below a certain threshold. The third gene product inhibits the production of Iroquois. To simulate the expression pattern of Iroquois, we use a Gierer–Meinhardt model (1972) for the production of Iroquois and the inhibition of Iroquois. Equation (2.2) describes the regulatory system
| (2.3) |
where are the concentrations of Iroquois and its inhibitor, respectively; x is a two-dimensional spatial variable on the surface; t is time; and D and λ are the diagonal matrices with the respective diffusion and decay coefficients. The first term in the equation describes the diffusion of the gene products over the sponge surface. Decay of the products is modelled by the second term, while the third term governs the reaction between the gene products. In addition, Iroquois is suppressed by silicatein, which is due to the absorption process predominantly present at the top of the branches. To obtain a regular pattern of Iroquois in the regions below the top of the branches, the diffusion coefficient for Iroquois is much smaller than that for the inhibitor of Iroquois. Furthermore, Iroquois has a negative regulation by the inhibitor and a positive autoregulation, while the inhibitor is positively regulated by Iroquois. Equations (2.4) and (2.5) specify the production of activator (Iroquois) and inhibitor, respectively. In case the local silicatein concentration ρsil is below the threshold δsil, we apply the normal production rule for Iroquois. Otherwise, we set the production term in the Iroquois equation to zero as a simple way of simulating strong inhibition by silicatein,
| (2.4) |
| (2.5) |
The reaction–diffusion calculations are done after the silicate absorption. We use a method for surface diffusion on triangulated manifolds (Zemlin 2002) to update the concentrations of all the gene products at each iteration of the reaction–diffusion processes on the triangulated growth layer. After each growth step, equation (2.2) is solved until steady state. Note that this approach implicitly assumes a separation of time scales: a slow accretive growth and a fast reaction–diffusion process in the surface of the sponge.
(d) Coupling the accretive growth model and the regulatory network model
The coupling of the accretive growth model with the other model components can be described in an algorithmic form as follows:
initialization of the accretive growth model with a spherical object,
growth_step=0,
while (growth_step<max_growth_step) do,
map geometrical object onto the 2003 lattice,
compute diffusion silicate until steady state (equation (2.1)) using the lattice representation,
compute thickness new growth layer (equation (2.2)), and construct a new growth layer geometric model,
compute regulatory network on the surface using a new geometric model (equations (2.3)–(2.5)), and
growth_step=growth_step+1.
3. Results and discussion
In figure 3, a series of successive growth stages of the simulated sponge is shown; the light blue spots with a relatively high upregulation of Iroquois indicate the future positions of the exhalant pores. The simulation is initialized with a small spherical triangulated object consisting of 2562 vertices (figure 3a). Furthermore, there is a constant source of silicate at the top plane in the three-dimensional simulation box and silicate is absorbed at the surface of the simulated growth form and at the bottom of the simulation box (figure 2c). In figure 3, there is a clear separation in time and space of the growing zones (dark blue regions at the tips without spots, where silicatein is expressed and Iroquois is suppressed) and the zones where exhalant pores are formed. Growth occurs in the dark blue regions without spots where relatively high concentrations of environmental silicate activate silicatein. The gene product of silicatein is produced near the surface (with high concentrations of Frizzled product) and diffuses through the sponge. As soon as the growth process stops when the silicate concentration is nearly depleted, the silicatein gene is suppressed and the Iroquois gene is activated.
Figure 3.
Simulated growth forms and body plan of a branching sponge after respectively (a) 0, (b) 17, (c) 34, (d) 51, (e) 68 and (f) 84 construction steps. The light blue spots indicate relatively high concentrations of Iroquois and mark the future positions of the exhalant pores. An animation of this object is provided in figure4.mov of the electronic supplementary material.
In figure 3, it can be observed that under the diffusion-limited conditions, we get a branching object. Under the diffusion-limited conditions, the accretive growth model produces branches as an emergent phenomenon (Merks et al. 2003); there are no explicit branching rules in the model. In section, the model displays a radiate accretive architecture comparable to the structure shown in figure 1b (an example of a section through the accretive growth model is shown in figure 4). In figure 3, the growing zones are visible as dark blue regions without light blue spots. An exception can be seen at the lower left branch, which is shielded by the other branches; growth stopped due to a local depletion of silicate and suppression of Iroquois is stopped, leading to the formation of exhalant pores on the tip. This phenomenon can also be observed in actual sponges (an example is shown in figure S1 of the electronic supplementary material). The exhalant pores are formed near the surface (with high concentrations of Frizzled product). Since Iroquois is suppressed by silicatein, the formation of exhalant pores can only occur at low silicatein product concentrations. In the simulations, the positions of exhalant pores are formed at more or less regular equal distances. In figure3.mov of the electronic supplementary material showing the entire development in time of this object, it can be seen that the spots indicating the future exhalant pores only appear below the growing tips and the position of the spots does not change in time. In actual sponges, the position of the exhalant pores also remains fixed. The model also predicts the position of a new pore if a pore is removed in an experiment or if the space between neighbouring pores becomes too large.
Figure 4.
Section (b) through an object (a) simulated with the accretive growth model under diffusion-limited conditions. The radiate accretive architecture can be constructed by tracing the growth trajectories of the nodes of the triangles on the surface within the successive growth layers.
In our simulations, we have hypothesized a feedback system, where an Iroquois inhibitor is controlling the positions of the spots with high Iroquois expression. Without some feedback mechanism controlling the distance between neighbouring exhalant pores, activation of Iroquois would lead to the removal of the material everywhere at the surface. Although we have selected the simplest system producing a stable pattern of spots in space in time, the simulated pattern in figure 3 resembles the pattern of exhalant pores in sponges, as shown in figure 1a. Although the molecular evidence that Iroquois and its inhibitor interact in the way as described by our model is absent, our model presents a number of testable predictions on the positioning of the exhalant pores over the sponge morphology.
In the absence of quantitative data on the interaction between Iroquois and its inhibitor, results from Gierer–Meinhardt models have to be interpreted carefully. It has been shown by several authors (see Koch & Meinhardt 1994) that such systems are capable of producing a large variety of patterns observed in organisms.
In the case of the sponge H. oculata with its large variety in complex-shaped growth forms (Kaandorp & Kűbler 2001) under different environmental conditions, it is conceivable that a relatively simple mechanism, which is effective in a large range of morphologies as presented above, is controlling the positioning of the exhalant pores. Our model predicts the existence of a diffusible inhibitor of Iroquois. Iroquois genes (Iro) play a major role in patterning the nervous system in vertebrates. Iro genes show a complex interaction with Wnt and BMP4 signalling pathways, where they act as antagonists (Cavodeassi et al. 2001). The diffusible inhibitor might be a product stemming from the Wnt or BMP4 signalling pathway.
Acknowledgments
We thank S. Portegies Zwart and three anonymous referees for their constructive comments on the manuscript. We would like to thank S. L. M. Kaandorp for her help in creating the illustrations. This work is supported by grants from The Netherlands Organization for Scientific Research (635.100.0.10) and the EC (MORPHEX, NEST contract no. 043322).
Appendix A. Parameters regulatory network model
Table 1 describes the parameters used in equations (2.3)–(2.5) in the regulatory network model. In a paper by Koch & Meinhardt (1994), an analysis has been done of the Gierer–Meinhardt model. Our regulatory network model corresponds to their model used for the insertion of new maxima of activator during growth. The authors demonstrate that pattern formation requires a parameter setting where Dinh≫Dirq and λinh>λirq; in our case, we used a similar parameter setting and the additional constraint that the model reaches a steady state. In the parameters.pdf of the electronic supplementary material, we show additional experiments for different parameters settings. It should be noted here that these parameter values are arbitrary and not based on experimentally measured quantities.
Table 1.
Parameters of the regulatory network model described in equations (2.3)–(2.5).
| parameter | value | description |
|---|---|---|
| δsil | 0.025 | silicatein–Iroquois suppression threshold value |
| Dirq | 5×10−6 | diffusion constant for Iroquois |
| Dinh | 1×10−3 | diffusion constant for the inhibitor of Iroquois |
| λirq | 0.1 | decay parameter for Iroquois |
| λinh | 0.11 | decay parameter for the inhibitor of Iroquois |
| k1 | 0.1 | Gierer–Meinhardt model parameter |
| k2 | 0.01 | Gierer–Meinhardt model parameter |
| k3 | 0.1 | Gierer–Meinhardt model parameter |
| k4 | 0.001 | Gierer–Meinhardt model parameter |
Supplementary Material
Animation of the simulated growth form of a branching sponge shown in figure 4. The light blue spots indicate relatively high concentrations of Iroquois and mark the future positions of the exhalant pores
The sponge Haliclona oculata showing the formation of exhalant pores in one of the lower branches (indicated with a white arrow)
Additional experiments for different parameters settings used in the equations (2.3)–(2.5) of the regulatory network model
References
- Adell T, Nefkens I, Müller W.E.G. Polarity factor ‘Frizzled’ in the demosponge Suberites domuncula: identification, expression and localization of the receptor in the epithelium/pinacoderm. FEBS Lett. 2003;554:363–368. doi: 10.1016/s0014-5793(03)01190-6. doi:10.1016/S0014-5793(03)01190-6 [DOI] [PubMed] [Google Scholar]
- Cavodeassi F, Modolell J, Gomez-Skarmeta J.L. The Iroquois family of genes: from body building to neural patterning. Development. 2001;128:2847–2855. doi: 10.1242/dev.128.15.2847. [DOI] [PubMed] [Google Scholar]
- Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetic. 1972;12:30–39. doi: 10.1007/BF00289234. doi:10.1007/BF00289234 [DOI] [PubMed] [Google Scholar]
- Kaandorp J.A, de Kluijver M.J. Verification of fractal growth models of the sponge Haliclona oculata (Porifera; class Demospongiae) with transplantation experiments. Mar. Biol. 1992;113:133–143. doi:10.1007/BF00367647 [Google Scholar]
- Kaandorp J.A, Kűbler J.E. Springer; Heidelberg, Germany: 2001. The algorithmic beauty of seaweeds, sponges and corals. [Google Scholar]
- Kaandorp J.A, Sloot P.M.A, Merks R.M.H, Bak R.P.M, Vermeij M.J.A, Maier C. Morphogenesis of the branching reef coral Madracis mirabilis. Proc. R. Soc. B. 2005;272:127–133. doi: 10.1098/rspb.2004.2934. doi:10.1098/rspb.2004.2934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaluzhnaya O.V, Belikov S.I, Schröder H.C, Zapf S, Borejko A, Kaandorp J.A, Krasko A, Müller I.M, Müller W.E.G. Dynamics of skeletal formation in the Lake Baikal sponge Lubomirskia baicalensis. Part I. Biological and biochemical studies. Naturwissenschaften. 2005a;92:128–133. doi: 10.1007/s00114-004-0599-4. doi:10.1007/s00114-004-0599-4 [DOI] [PubMed] [Google Scholar]
- Kaluzhnaya O.V, Belikov S.I, Schröder H.C, Wiens M, Giovine M, Krasko A, Müller I.M, Müller W.E.G. Dynamics of skeletal formation in the Lake Baikal sponge Lubomirskia baicalensis. Part II. Molecular biological studies. Naturwissenschaften. 2005b;92:134–138. doi: 10.1007/s00114-004-0600-2. doi:10.1007/s00114-004-0600-2 [DOI] [PubMed] [Google Scholar]
- Koch A.J, Meinhardt H. Biological pattern formation: from basic mechanisms to complex structures. Rev. Mod. Phys. 1994;88:1481–1507. doi:10.1103/RevModPhys.66.1481 [Google Scholar]
- Le Pennec G, Perovic S, Ammar M.S.A, Grebenjuk V.A, Steffen R, Brummer F, Mueller W.E.G. Cultivation of primmorphs from the marine sponge Suberites domuncula: morphogenetic potential of silicon and iron a review. J. Biotechnol. 2003;100:93–108. doi: 10.1016/s0168-1656(02)00259-6. doi:10.1016/S0168-1656(02)00259-6 [DOI] [PubMed] [Google Scholar]
- Merks R.M.H, Hoekstra A.G, Kaandorp J.A, Sloot P.M.A. Models of coral growth: spontaneous branching, compactification and the Laplacian growth assumption. J. Theor. Biol. 2003;224:153–166. doi: 10.1016/s0022-5193(03)00140-1. doi:10.1016/S0022-5193(03)00140-1 [DOI] [PubMed] [Google Scholar]
- Müller W.E.G, Krasko A, Pennec G, Steffen R, Ammar M.S.A, Müller I.M, Schröder H.C. Molecular mechanism of spicule formation in the demosponge Suberites domuncula: silicatein–collagen–myotrophin. Prog. Mol. Subcell. Biol. 2003;33:195–231. doi: 10.1007/978-3-642-55486-5_8. [DOI] [PubMed] [Google Scholar]
- Müller W.E.G, Wiens M, Adell T, Gamulin V, Schröder H.C, Müller I.M. Bauplan of urmetazoa: basis for genetic complexity of metazoa. Int. Rev. Cytol. 2004;235:53–92. doi: 10.1016/S0074-7696(04)35002-3. doi:10.1016/S0074-7696(04)35002-3 [DOI] [PubMed] [Google Scholar]
- Perovic S, Schröder H.C, Sudek S, Grebenjuk V.A, Batel R, Stifanic M, Müller I.M, Müller W.E.G. Expression of one sponge Iroquois homeobox gene in primmorphs from Suberites domuncula during canal formation. Evol. Dev. 2003;5:240–250. doi: 10.1046/j.1525-142x.2003.03023.x. doi:10.1046/j.1525-142X.2003.03023.x [DOI] [PubMed] [Google Scholar]
- Pilcher H. Back to our roots. Nature. 2005;435:1022–1023. doi: 10.1038/4351022a. doi:10.1038/4351022a [DOI] [PubMed] [Google Scholar]
- Schröder H.C, Natalio F, Shukoor I, Tremel W, Schlossmacher U, Wang X, Müller W.E.G. Apposition of silica lamellae during growth of spicules in the demosponge Suberites domuncula: biological/biochemical studies and chemical/biomimetical confirmation. J. Struct. Biol. 2007;159:325–334. doi: 10.1016/j.jsb.2007.01.007. doi:10.1016/j.jsb.2007.01.007 [DOI] [PubMed] [Google Scholar]
- Wiedenmayer F. Birkhäuser; Basel, Switzerland; Stuttgart, Germany: 1977. Shallow-water sponges of the western Bahamas. [Google Scholar]
- Zemlin, C. 2002 Rhytms and wave propogation in the heart. PhD thesis, Humboldt-Universität zu, Berlin.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Animation of the simulated growth form of a branching sponge shown in figure 4. The light blue spots indicate relatively high concentrations of Iroquois and mark the future positions of the exhalant pores
The sponge Haliclona oculata showing the formation of exhalant pores in one of the lower branches (indicated with a white arrow)
Additional experiments for different parameters settings used in the equations (2.3)–(2.5) of the regulatory network model