Bayesian analysis of amino acid substitution models

Abstract

Models of amino acid substitution present challenges beyond those often faced with the analysis of DNA sequences. The alignments of amino acid sequences are often small, whereas the number of parameters to be estimated is potentially large when compared with the number of free parameters for nucleotide substitution models. Most approaches to the analysis of amino acid alignments have focused on the use of fixed amino acid models in which all of the potentially free parameters are fixed to values estimated from a large number of sequences. Often, these fixed amino acid models are specific to a gene or taxonomic group (e.g. the Mtmam model, which has parameters that are specific to mammalian mitochondrial gene sequences). Although the fixed amino acid models succeed in reducing the number of free parameters to be estimated—indeed, they reduce the number of free parameters from approximately 200 to 0—it is possible that none of the currently available fixed amino acid models is appropriate for a specific alignment. Here, we present four approaches to the analysis of amino acid sequences. First, we explore the use of a general time reversible model of amino acid substitution using a Dirichlet prior probability distribution on the 190 exchangeability parameters. Second, we then explore the behaviour of prior probability distributions that are ‘centred’ on the rates specified by the fixed amino acid model. Third, we consider a mixture of fixed amino acid models. Finally, we consider constraints on the exchangeability parameters as partitions, similar to how nucleotide substitution models are specified, and place a Dirichlet process prior model on all the possible partitioning schemes.

1. Introduction

The statistical phylogenetic analysis of amino acid data presents problems that are not associated with nucleotide data. The instantaneous rate matrix is 20×20 in dimension for amino acid data. For the most general model of amino acid substitution, a model that may not be time reversible, there are a total of 20×19=380 parameters to be estimated. For a general time reversible (GTR) model of amino acid substitution, isomorphic to the GTR model used in phylogenetic analysis of DNA sequences (Tavaré 1986), there would be a total of 20+190=210 parameters.1 Unlike the case with codon models in which many rates between states may be zero because the changes involve two or more substitutions in an instant of time, there are no easy ways to reduce the number of parameters to be estimated for amino acid data. The most common approach used for the phylogenetic analysis of amino acid sequence data is to use a continuous-time Markov model in which all of the rates are fixed to specific values. There are a number of such fixed rate matrices that have rates based on the analysis of inferred amino acid changes from various databases. These models include the Jones (Jones et al. 1992), Dayhoff (Dayhoff et al. 1978), Mtrev (Adachi & Hasegawa 1996), WAG (Whelan & Goldman 2001), Mtmam (Cao et al. 1998; Yang et al. 1998), Rtrev (Dimmic et al. 2002), Cprev (Adachi et al. 2000), Blosum (Henikoff & Henikoff 1992), ECM (Empirical Codon Model; Kosiol et al. 2007) and Vt (Muller & Vingron 2000). The Poisson model, which is isomorphic to the Jukes & Cantor (1969) nucleotide substitution model, can also be considered a member of the family of fixed amino acid models (Bishop & Friday 1987).

The fixed amino acid models are useful not only because they reduce the number of parameters to be estimated in a phylogenetic analysis, but also because they can be applied to small alignments (datasets involving a small number of taxa and sites). It is unlikely that the rates of substitution for an amino acid model that had the rates of change free to vary could be reliably estimated for typical (small) amino acid alignments. However, the use of fixed amino acid models also complicates matters because, for any specific alignment of amino acid sequences, it is not clear which of the many potential models is the most appropriate. Often, one can make a good guess of which model should be used; for example, if the alignment is of plastid genes, then the Cprev model (Adachi et al. 2000) might be appropriate because its rates are based on a database of plastid genes. Similarly, the Mtmam model is probably the most appropriate for an alignment of mammalian mitochondrial genes. Yet, there is no guarantee that any specific amino acid model is the most appropriate for a particular alignment, even in cases where the amino acid model is based upon a database of genes similar to the one to be analysed. Another approach is to use the fixed model that has the maximum likelihood. This is sensible, but involves optimizing likelihoods under the current models. Also, this approach does not allow one to spread one's bets across amino acid models if several of the models have similar likelihoods.

Even the best-fitting fixed amino acid model, however, may not be particularly suitable for the data at hand. It is interesting to note that biologists who adopt the approach of using fixed amino acid substitution models are, in a sense, adopting a Bayesian perspective, even if they do not use Bayesian methodology to estimate the parameters of the phylogenetic model. The fixed amino acid model that is assumed in the analysis can be considered a prior probability distribution on the rates of amino acid substitution for the data at hand. In fact, by using a model of amino acid substitution in which all of the rates are fixed to specific values, the biologist has adopted the strongest form of a prior that can be imagined; a fixed amino acid model places a point mass probability on the rates specified by the model, but zero probability on other rate combinations, even those rates that are slightly different from the fixed rates. An intermediate solution, in which the assumptions of the fixed amino acid model are tempered, might be more appropriate.

In this paper, several Bayesian approaches to the analysis of amino acid models are developed. We consider (i) inference of amino acid rates under a GTR model, (ii) inference of amino acid data when the rates of substitution have been ‘centred’ on a fixed amino acid model, but which still allow rates to vary, (iii) a model averaging approach, in which the results of a phylogenetic analysis are averaged over a candidate set of fixed amino acid models, and (iv) a model averaging approach in which all possible partitions of the exchangeability/rate parameters are considered.

2. Material and methods

(a) Specifying a ‘centred’ prior distribution for amino acid substitution rates

We adopt a Bayesian perspective to statistical estimation, in which inferences are based on the posterior probability distribution of a parameter, which can be calculated using Bayes' theorem as

$$\mathbb{P}(\text{Parameter}|\text{Data})=\frac{\mathbb{P}(\text{Data}|\text{Parameter})\mathbb{P}(\text{Parameter})}{\mathbb{P}(\text{Data})},$$

where $\mathbb{P}(\text{Parameter}|\text{Data})$ is the posterior probability distribution of the parameter; $\mathbb{P}(\text{Data}|\text{Parameter})$ is the likelihood; $\mathbb{P}(\text{Parameter})$ is the prior probability distribution of the parameter; and $\mathbb{P}(\text{Data})$ is the marginal likelihood, obtained by summing and/or integrating over all possible combinations of the model parameters. We consider the observations to be an alignment of s amino acid sequences each n in length, denoted X. (We ignore the possibility that the amino acid sequences might be misaligned.) For a phylogenetic model, the parameters include a tree, with branch lengths specified in terms of expected number of substitutions per site, and a continuous-time Markov model describing how the characters, in our case amino acid sequences, change over time. We will forgo a thorough treatment of the phylogenetic model which would include a description of how the likelihood is calculated; suffice it to say that we use standard methods for calculating the likelihood (Felsenstein 1981) and use Markov chain Monte Carlo (MCMC) to numerically calculate the posterior probability distribution of the parameters (e.g. Larget & Simon 1999). Moreover, we accommodate among-site rate variation by assuming that the rate at a particular amino acid site (column in the alignment) is a random variable drawn from a mean-one gamma distribution with parameter γ (Yang 1993, 1994).

We assume that amino acid substitutions occur according to a continuous-time Markov model with instantaneous rates of change described by the following rate matrix

$$\mathit{Q}=\left\{q_{ij}\right\}=\left(\begin{array}{ccccccc}-& {\theta }_{\text{AR}}{\pi }_{\text{R}}& {\theta }_{\text{AN}}{\pi }_{\text{N}}& \cdots & {\theta }_{\text{AW}}{\pi }_{\text{W}}& {\theta }_{\text{AY}}{\pi }_{\text{Y}}& {\theta }_{\text{AV}}{\pi }_{\text{V}}\\ {\theta }_{\text{AR}}{\pi }_{\text{A}}& -& {\theta }_{\text{RN}}{\pi }_{\text{N}}& \cdots & {\theta }_{\text{RW}}{\pi }_{\text{W}}& {\theta }_{\text{RY}}{\pi }_{\text{Y}}& {\theta }_{\text{RV}}{\pi }_{\text{V}}\\ {\theta }_{\text{AN}}{\pi }_{\text{A}}& {\theta }_{\text{RN}}{\pi }_{\text{R}}& -& \cdots & {\theta }_{\text{NW}}{\pi }_{\text{W}}& {\theta }_{\text{NY}}{\pi }_{\text{Y}}& {\theta }_{\text{NV}}{\pi }_{\text{V}}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ {\theta }_{\text{AW}}{\pi }_{\text{A}}& {\theta }_{\text{RW}}{\pi }_{\text{R}}& {\theta }_{\text{NW}}{\pi }_{\text{N}}& \cdots & -& {\theta }_{\text{WY}}{\pi }_{\text{Y}}& {\theta }_{\text{WV}}{\pi }_{\text{V}}\\ {\theta }_{\text{AY}}{\pi }_{\text{A}}& {\theta }_{\text{RY}}{\pi }_{\text{R}}& {\theta }_{\text{NY}}{\pi }_{\text{N}}& \cdots & {\theta }_{\text{YW}}{\pi }_{\text{W}}& -& {\theta }_{\text{YV}}{\pi }_{\text{V}}\\ {\theta }_{\text{AV}}{\pi }_{\text{A}}& {\theta }_{\text{RV}}{\pi }_{\text{R}}& {\theta }_{\text{NV}}{\pi }_{\text{N}}& \cdots & {\theta }_{\text{WV}}{\pi }_{\text{W}}& {\theta }_{\text{YV}}{\pi }_{\text{Y}}& -\end{array}\right)\mu ,$$

which corresponds to a GTR model of amino acid substitution. (The dots represent rows and columns that are not shown because the rate matrix is too large to be printed in its entirety.) The amino acid substitution model has 20 states, corresponding to the 20 possible amino acids: $\mathit{S}=(\text{A},\text{R},\text{N},\text{D},\text{C},\text{Q},\text{E},\text{G},\text{H},\text{I},\text{L},\text{K},\text{M},\text{F},\text{P},\text{S},\text{T},\text{W},\text{Y},\text{V})$ (which are the IUPAC codes for the amino acids; Cornish-Bowden 1985). The diagonal elements of the rate matrix are specified such that each row sums to 0. The GTR model of amino acid substitution has a total of 210 parameters. Twenty of the parameters are the stationary frequencies of the amino acids. Similar to other phylogenetic models, the stationary frequencies of the process are parameters of the model, specified as components of the rate matrix. The other 190 parameters are rate parameters, sometimes referred to as exchangeability parameters; the exchangeability parameters are the rate factors θ_AR, θ_AN, θ_AD, …, θ_YV.

The 20 amino acid frequencies, π=(π_A, π_R, π_N, …, π_V) are, of course, constrained to sum to one. The 190 exchangeability parameters, θ=(θ_AR, θ_AN, θ_AD, …, θ_YV), on the other hand, are ideally measured in terms of the expected number of substitutions per unit time, and would not have any constraint (other than the common-sense one that the rates be positive). However, without any reference to time on a tree, the values of the rate parameters cannot be estimated; only divergence—the product of substitution rate and time—can be measured on a phylogenetic tree in the absence of a calibration. Because only divergence on a tree can be estimated, only the relative substitution rates can be estimated. For example, the relative substitution rates θ_AR=1, θ_AN=3, θ_AD=2, … are equivalent to θ_AR=2, θ_AN=6, θ_AD=4, … In this study, we impose the constraint that the 190 rate parameters sum to one. The rate matrix is scaled by a factor μ to ensure that the mean rate of substitution is one. Branch lengths of the tree, then, are interpreted as the expected number of amino acid substitutions per site. The scaling factor is equal to $\mu =-1/{\sum }_{\mathit{S}}{\pi }_s{q}_{ss}$, where $\mathit{S}\in (\text{A},\text{R},\text{N},\dots ,\text{W},\text{Y},\text{V})$.

We assume that both the amino acid frequency parameters, π, and the exchangeability parameters, θ, follow different Dirichlet prior probability distributions. The use of a Dirichlet prior probability distribution for the exchangeability parameters of the GTR model of DNA substitution was first described by Zwickl & Holder (2004). Let X=(X₁, X₂, …, X_K) be K random variables that are constrained to sum to one. The Dirichlet probability density is

$$f(\mathit{x}|\mathit{\alpha })=\frac{1}{b(\mathit{\alpha })}\prod _{i=1}^K{x}_i^{{\alpha }_i-1},$$

where α=(α₁, α₂, …, α_K) are the parameters of the distribution and the constant of integration is a well-known ratio of gamma functions given by

$$b(\mathit{\alpha })=\frac{\prod _{i=1}^K\Gamma ({\alpha }_i)}{\Gamma ({\alpha }_0)}.$$

$({\alpha }_0={\sum }_{i=1}^K{\alpha }_i)$.The marginal probability distribution of the ith Dirichlet random variable is a beta distribution with parameters α_i and α₀−α_i. The expected value for the ith Dirichlet random variable is $E(X_i)={\alpha }_i/{\alpha }_0$ and the variance is $\text{var}(X_i)=({\alpha }_i({\alpha }_0-{\alpha }_i)/{\alpha }_0^2({\alpha }_0+1))$.

We assume that the amino acid frequencies follow a flat Dirichlet prior distribution in which ${\alpha }_1={\alpha }_2=\cdots ={\alpha }_{20}=1$ (K=20). We consider several different prior distributions for the exchangeability parameters, θ. In general, the exchangeability parameters have the following Dirichlet probability distribution:

$$f(\mathit{\theta }|{\rm X}\mathit{\nu })=\frac{1}{b({\rm X}\mathit{\nu })}\prod _{i<j\in \mathit{S}}{\theta }_{ij}^{{\rm X}{\nu }_{ij}-1},$$

where S is the set of ordered amino acid states. The constant of integration is, again, a ratio of gamma functions. The parameters ν_ij are constrained to sum to one. We interpret the parameter Χ as a concentration parameter that controls the variance of the Dirichlet prior distribution. The expectation and variance of the exchangeability parameters are E(θ_ij)=ν_ij and $\text{var}({\theta }_{ij})=({\nu }_{ij}(1-{\nu }_{ij})/{\rm X}+1)$, respectively. Note that the maximum variance allowed is ν_ij(1−ν_ij) that occurs at the improper prior Χ=0 and is the variance associated with a single draw from a binomial with proportion ν_ij. One can also show that $\text{cov}({\theta }_{ij},{\theta }_{mn})=-({\nu }_{ij}{\nu }_{mn}/{\rm X}+1)$; θ_ij and θ_mn will be most correlated when Χ=0 which corresponds to the covariance associated with a single draw from a multinomial $({\nu }_{ij},{\nu }_{mn},1-{\nu }_{ij}-{\nu }_{mn})$.

We consider Dirichlet prior distributions for the exchangeability parameters that are centred on different values. To centre the prior distribution on a particular fixed amino acid rate matrix, we set the ν_ij such that they are equal to the scaled entries of the fixed rate matrix. (A similar approach of using an informative Dirichlet prior was described by Zwickl & Holder 2004.) Consider, for example, the following fixed rate matrix with only three states

$$\mathit{Q}=\left(\begin{array}{ccc}-& 1.0{\pi }_1& 1.2{\pi }_2\\ 1.0{\pi }_0& -& 1.4{\pi }_2\\ 1.2{\pi }_0& 1.4{\pi }_1& -\end{array}\right)\mu .$$

A Dirichlet prior distribution centred on this rate matrix would have ${\nu }_{01}=1.0/(1.0+1.2+1.4)=0.278$, ${\nu }_{02}=1.2/(1.0+1.2+1.4)=0.333$ and ${\nu }_{12}=1.4/(1.0+1.2+1.4)=0.389$. The concentration parameter, Χ, specifies how the probability density is spread around the centred rate value. When Χ is small, the prior probability, while still centred on the values of the fixed rate matrix, has more prior density on values that are quite different from those specified by the rate matrix. On the other hand, large values of Χ put very little prior probability density on rates that are different from those specified by the fixed model. Note, in fact, that as Χ→∞, the variance decreases to zero; the centred model becomes equivalent to the fixed model, with no probability density on rate values even slightly different from the fixed rates. The small example given here involves only three rates. However, the reader should see that the 3-state model is isomorphic with a 20-state amino acid model, but with

$$\left(\begin{array}{c}20\\ 2\end{array}\right)=190,$$

centred rates instead of

$$\left(\begin{array}{c}3\\ 2\end{array}\right)=3,$$

centred rates.

Our parametrization of the Dirichlet prior for the exchangeability parameters allows us to explore a large number of prior models on the rates. For example, we can specify the GTR model, with a flat prior, by setting all ν_ij=1/190 and Χ=190. Similarly, we can explore the sensitivity of rate parameter estimates centred on fixed amino acid models by varying the concentration parameter Χ.

(b) Model choice and model averaging

In this paper, we consider 10 amino acid models, denoted M₁, M₂, …, M₁₀. The 10 amino acid models correspond to the Poisson (M₁; Bishop & Friday 1987), Jones (M₂; Jones et al. 1992), Dayhoff (M₃; Dayhoff et al. 1978), Mtrev (M₄; Adachi & Hasegawa 1996), Mtmam (M₅; Cao et al. 1998; Yang et al. 1998), WAG (M₆; Whelan & Goldman 2001), Rtrev (M₇; Dimmic et al. 2002), Cprev (M₈; Adachi et al. 2000), Vt (M₉; Muller & Vingron 2000) and Blosum (M₁₀; Henikoff & Henikoff 1992) models.

In a Bayesian analysis, inferences are based upon the joint posterior probability distribution of the model parameters. For the phylogeny problem, the joint posterior probability is calculated using Bayes' theorem as

$$f({\tau }_i,v_i,M_j|\mathit{X})=\frac{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M_j)f({\mathit{v}}_i)\frac{1}{T(s)}\frac{1}{10}}{{\sum }_{j=1}^{10}\left({\sum }_{j=1}^{10}\left({\int }_{v_i}f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M_j)f({\mathit{v}}_i)\right)\text{d}{\mathit{v}}_i\frac{1}{T(s)}\right)\frac{1}{10}},$$

where $f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M_j)$ is the likelihood for the ith tree and jth amino acid model; f(ν_i) is the prior probability density distribution for branch lengths; and T(s) is the number of unrooted trees possible for s species $[T(s)=(2s-5)!!]$. In this study, all trees and all amino acid models are considered to be equally probable, a priori. If one is interested only in the phylogeny of the species, then inferences are based upon the marginal posterior probability distribution of phylogenetic trees. The marginal posterior probability of the ith tree is obtained by integrating over the other model parameters:

$$f({\tau }_i|\mathit{X})=\sum _{j=1}^{10}\left({\int }_{{\mathit{v}}_i}f({\tau }_i,{\mathit{v}}_i,M_j|\mathit{X})\text{d}{\mathit{v}}_i\right).$$

Note that the estimate of phylogeny does not depend upon any particular fixed model of amino acid substitution; the posterior probability of a tree is averaged over all 10 amino acid models. This formulation of the problem does not force the biologist to choose a particular amino acid model.

The posterior probability distribution of phylogenetic trees cannot be calculated analytically. MCMC (Metropolis et al. 1953; Hastings 1970), however, can be used to approximate the posterior probability of a tree. The details of MCMC as applied to the phylogeny problem have been described elsewhere (see Larget & Simon 1999; Huelsenbeck et al. 2001). In short, the posterior probability distribution of parameters is approximated using a Markov chain which has a stationary distribution that is the posterior probability distribution of the parameters. New states for the chain (trees and branch lengths) are proposed using a stochastic mechanism and accepted or rejected according to the formula of Metropolis et al. (1953) and Hastings (1970). States are sampled from the chain when at stationarity. The fraction of the time the chain dwells on any particular tree is a valid approximation of the posterior probability of that tree. We note one important change in implementing the mixed model analysis of amino acid data; in addition to proposal mechanisms that change the tree and branch lengths, we also include a proposal mechanism that changes the amino acid rate matrix that is used to calculate likelihoods. The proposal mechanism works as follows. The current amino acid model is denoted M. We propose a new model, denoted M′, by choosing one of the other nine models with equal probability. The proposed model is accepted with probability

$$R=\text{min}\left(1,\frac{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M^{\prime })}{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M)}\times \frac{f(M^{\prime })}{f(M)}\times \frac{f(M|M^{\prime })}{f(M^{\prime }|M)}\right)=\text{min}\left(1,\frac{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M^{\prime })}{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M)}\times \frac{1/10}{1/10}\times \frac{1/9}{1/9}\right)=\text{min}\left(1,\frac{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M^{\prime })}{f(\mathit{X}|{\tau }_i,{\mathit{v}}_i,M)}\right).$$

In a Bayesian analysis, model choice is often guided by Bayes factors. The Bayes factor for a comparison of two models (M₁ and M₂) is calculated as the ratio of the marginal likelihoods

$$B{F}_{12}=\frac{f(\mathit{X}|M_1)}{f(\mathit{X}|M_2)}=\frac{\frac{f(M_1|\mathit{X})}{f(M_2|\mathit{X})}}{\frac{f(M_1)}{f(M_2)}}.$$

The Bayes factor measures the ‘the change in the odds in favour of the hypothesis when going from the prior to the posterior’ (Lavine & Schervish 1999, p. 120). In this study, we calculate the Bayes factor for each model, against all of the other models. The Bayes factor for amino acid model i, then, is

$$B{F}_i=\frac{\frac{f(M_i|\mathit{X})}{1-f(M_i|\mathit{X})}}{\frac{f(M_i)}{1-f(M_i)}}.$$

(c) Considering amino acid models as partitions

Consider, again, the three-state model of change with instantaneous rate matrix

$$\mathit{Q}=\left(\begin{array}{ccc}-& {\theta }_{01}{\pi }_1& {\theta }_{02}{\pi }_2\\ {\theta }_{01}{\pi }_0& -& {\theta }_{12}{\pi }_2\\ {\theta }_{02}{\pi }_0& {\theta }_{12}{\pi }_1& -\end{array}\right)\mu$$

and exchangeability parameters θ_ij, where 0≤i≤j≤2. This rate matrix is analogous to the GTR model of DNA or amino acid substitution, but with three states instead of 4 or 20. The exchangeability parameters can be restricted to give submodels of the most general model. For example, if rates are constrained to be equal, with θ₀₁=θ₀₂=θ₁₂, then the model is isomorphic to the model first described by Felsenstein (1981). Other possible models apply the restriction θ₀₁=θ₀₂, θ₀₁=θ₁₂ and θ₀₂=θ₁₂. The last possible model does not constrain equalities among the exchangeability parameters. We label possible models by introducing a notation that allows all of the possible models to be labelled. Here, there are three exchangeability parameters, and the possible labels for the models are

$$\begin{array}{ccc}01& 02& 12\\ 1& 1& 1\\ 1& 1& 2\\ 1& 2& 1\\ 1& 2& 2\\ 1& 2& 3\end{array}.$$

The first model, with label $1,1,1$, constrains the three exchangeability parameters to be equal to one another. Similarly, the second model listed, $1,1,2$, constrains θ₀₁=θ₀₂, but allows θ₁₂ to vary freely (subject to the constraint that the three exchangeability parameters sum to one). Huelsenbeck et al. (2004) introduced this notation to describe all of the submodels of the GTR model of nucleotide substitution. Here, the set of exchangeability parameters is considered a partition, and the possible partitions are labelled according to the restricted growth function notation of Stanton & White (1986). The same scheme for labelling nucleotide models is implemented in the program PAUP^* (Swofford 1998), but with the indices being letters instead of numbers.

The number of possible partitions of n elements is described by the Bell numbers (Bell 1934). The Bell numbers are defined as

$$\mathcal{B}(n)=\sum _{k=0}^n{\mathcal{S}}_2(n,k),$$

where ${\mathcal{S}}_2(n,k)$ is the Stirling number of the second kind

$${\mathcal{S}}_2(n,k)=\frac{1}{k!}\sum _{i=0}^{k-1}{(-1)}^i\left(\begin{array}{c}k\\ i\end{array}\right){(k-i)}^n$$

and is the number of ways to partition n elements into k subsets. For the small example given above consisting of three states, the total number of ways to partition the rates is $\mathcal{B}(3)=5$. Similarly, when only the exchangeability parameters are considered, there are a total of $\mathcal{B}(6)=203$ possible time-reversible four-state nucleotide models (Huelsenbeck et al. 2004). (Note that there are many more possible models when stationary frequencies are considered to be fixed or estimated parameters of the model.) The number of possible time-reversible amino acid models is vast. A general time-reversible model of amino acid substitution has 190 exchangeability parameters, meaning that there are a total of $\mathcal{B}(190)=6.59\times {10}^{258}$ possible models, the most parameter rich of which has 190 independently estimated rates and the simplest of which has a common rate for all 190 exchangeability parameters.

We consider phylogenetic analysis of amino acid data when the candidate pool of substitution models consists of all 6.59×10²⁵⁸ time-reversible substitution models. Huelsenbeck et al. (2004) performed analysis of nucleotide data on the set of 203 possible time-reversible nucleotide models, placing a uniform prior probability distribution on all possible models. However, directly extending the approach of Huelsenbeck et al. (2004) to the amino acid data is not feasible for several reasons. First, if a uniform prior probability distribution is placed on all possible amino acid models, the result is a prodigious amount of probability on models with an intermediate number of substitution rates. For example, models with k=48 substitution types have a probability of ${\mathcal{S}}_2(190,48)/\mathcal{B}(190)=0.133$, whereas models with only k=3 rate classes have a probability of ${\mathcal{S}}_2(190,3)/\mathcal{B}(190)=1.14\times {10}^{-169}$. The posterior probability of the number of substitution types is strongly affected by the prior, and is drawn to models with approximately 50 rate classes simply because there are so many more models with an intermediate number of rate classes. Second, the MCMC used in the Huelsenbeck et al. (2004) paper does not work efficiently for a problem with 190 substitution types.

We take a different approach in this paper. We use a Dirichlet process prior model (Ferguson 1973; Antoniak 1974) as a prior probability on substitution models. The Dirichlet process prior is a probability model on partitions and has been usefully applied in several contexts in phylogenetics and evolutionary biology (Lartillot & Philippe 2004; Huelsenbeck et al. 2006). Moreover, robust MCMC methods have been developed for this model, which allow effective exploration of the space of partitions (Neal 2000). The Dirichlet process prior has a single parameter, here denoted β>0, that controls the ‘clumpiness’ of the process. A simple description of the Dirichlet process prior is as follows. Consider adding rate classes sequentially. Let the probability that a new rate class is added at the ith step be $\beta /(i-1+\beta )$. If we keep track of the number of rate classes added, by letting Y_i be a binary random variable that is equal to one, when a new rate class is added, then the total number of rate classes is $K={\sum }_{i=1}^n{Y}_i$. Here n is the total number of possible rates (n=190). Therefore, $E(K)=\beta {\sum }_{i=1}^n\frac{1}{i-1+\beta }\approx \beta \text{ln}(i+\beta )$. Small values for β result in only a few groups of substitution types (k) whereas large values of β place more probability on large values of k. In fact, the prior probability of two rate parameters being placed in the same group is 1/1+β. Since the number of substitution types is on the order of the natural logarithm of the total number of substitutions, the prior gives more weight to fewer classes than the uniform prior on partitions.

(d) Data

We analysed eight alignments of amino acid sequences: (i) adh sequences from s=23 Drosophila species (Cao et al. 1998; Yang et al. 2000), (ii) β-globin sequences from s=17 vertebrates (Yang et al. 2000), (iii) coat protein sequences from s=9 viruses from the family Leviviridae (Bollback & Huelsenbeck 2001), (iv) env sequences from s=23 Japanese encephalitis viral samples (Yang et al. 2000), (v) pol sequences from s=23 HIV samples (Yang et al. 2000), (vi) s=28 hemagglutinin sequences from influenza virus (type A; Fitch et al. 1997; Yang et al. 2000), (vii) replicase sequences from s=9 viruses from the family Leviviridae (Bollback & Huelsenbeck 2001) and (viii) E-glycoprotein sequences sampled from s=18 flavivirus (Zanotto et al. 1996; Yang et al. 2000).

3. Results

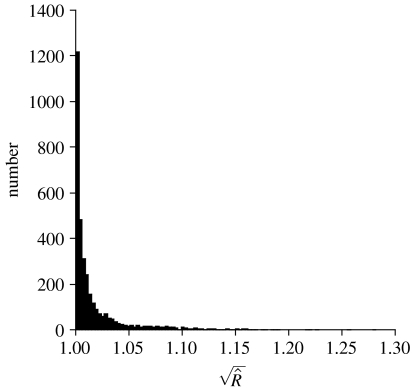
For each analysis of this paper, two MCMC analyses, each of four million cycles, were performed. Paired chains were checked for convergence to the same marginal probability distribution for the 190 exchangeability, 20 state frequency and gamma-shape parameters using the program Tracer (Rambaut & Drummond 2007) and boa (Smith 2007). Inferences were based on samples taken after the one millionth MCMC cycle. Analysis of the post-burn-in samples taken by each pair of chains shows that all analyses had estimated sample sizes greater than 100 (for the combined analyses) and resulted in very similar (by eye) marginal posterior probability distributions for all of the exchangeability parameters. We also calculated the ‘potential scale reduction factor’ statistic $\left(\sqrt{\hat{R}}\right)$ of Gelman & Rubin (1992) using the program boa (Smith 2007). The potential scale reduction compares the between-chain variance to the within-chain variance and approaches one from above. Values of $\sqrt{\hat{R}}$ less than 1.2–1.3 are taken as evidence that the chain has converged for that parameter (Gelman 1996). Figure 1 shows the values of $\sqrt{\hat{R}}$ for all of the parameters shown in this paper. The vast majority of these parameters have $\sqrt{\hat{R}}$ less than 1.05, with only a few having values of $\sqrt{\hat{R}}$ between 1.2 and 1.3.

Figure 1.

A frequency histogram of the potential scale reduction statistics $\left(\sqrt{\hat{R}}\right)$ for the parameters examined in this study.

(a) Analysis under the GTR model of amino acid substitution

We estimated the exchangeability parameters of the GTR model of amino acid substitution under a flat Dirichlet prior probability distribution. In our formulation, the flat Dirichlet distribution has all ν_ij=1/190 and Χ=190. We used MCMC to approximate the joint posterior probability distribution of the exchangeability parameters (θ), amino acid frequency parameters (π), gamma-shape parameter (γ), phylogenetic tree (τ) and branch-length parameters (ν).

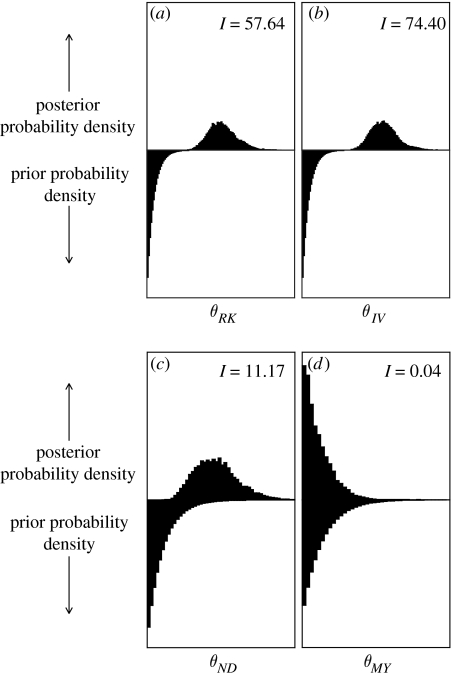
Figure 2 shows the marginal posterior and prior probability distributions of four of the exchangeability parameters for the HIV alignment. The marginal posterior probability distribution for a parameter integrates over uncertainty in all of the other model parameters. Hence, the marginal distributions shown in figure 2 are not conditioned on any particular phylogenetic tree, set of branch lengths, etc., but rather account for uncertainty in these nuisance parameters. The prior probability distribution of a single exchangeability parameter follows a beta distribution with parameters 1 and 189. The posterior distribution differs for each of the parameters. The posterior probability distribution for the rate of substitution between amino acids M and Y closely resembles the prior probability distribution; there is very little information in the data about this particular parameter. However, for the other three exchangeability parameters shown in figure 2, the data are informative and the marginal posterior probability distribution is shifted away from the prior distribution.

Figure 2.

The marginal prior and posterior probability distribution for four of the exchangeability parameters for the HIV pol alignment. The Kullback–Leibler divergence, I, is shown for each parameter and measures the dissimilarity between the prior and posterior probability distributions. Note that the Kullback–Leibler divergence is small for the M↔Y parameter where the prior and posterior distributions are similar. The data are more informative for the other parameters shown, and the Kullback–Leibler divergence is correspondingly larger.

Summarizing the results of a Bayesian analysis of a parameter-rich model can be difficult. We summarize the results of the Bayesian analyses of the exchangeability parameters in two ways. First, we examine the mean of the marginal posterior probability distribution for each rate. Second, we also calculate the Kullback–Leibler divergence (Kullback & Leibler 1951) between the prior and posterior probability distributions for each exchangeability parameter. The Kullback–Leibler divergence between two continuous probability distributions, f(x) and g(x), is defined as

$$I(f,g)=\int f(x)\text{ln}\left(\frac{f(x)}{g(x)}\right)\text{d}x,$$

where integration is over all possible values of the random variable x. We assume that the posterior probability distribution can be closely approximated by a beta distribution with parameters that are estimated from the MCMC output. The Kullback–Leibler divergence between two beta distributions, one with parameters a₁ and b₁ and the other with parameters a₂ and b₂ is

$$I=\text{ln}\frac{b(a_2,b_2)}{b(a_1,b_1)}-(a_2-a_1)\psi (a_1)-(b_2-b_1)\psi (b_1)+(a_2-a_1+b_2-b_1)\psi (a_1+b_1),$$

where, as earlier, the beta function $b(x,y)=\Gamma (x)\Gamma (y)/\Gamma (x+y)$ is the ratio of gamma functions and $\psi (x)={\Gamma }^{\prime }(x)/\Gamma (x)$ is the digamma function. Figure 2 shows the Kullback–Leibler divergence between the prior and posterior distributions for the exchangeability parameters, R↔K, I↔V, N↔D and M↔Y. Note that the Kullback–Leibler divergence is large when the prior and posterior distributions are dissimilar. The Kullback–Leibler divergence can be interpreted as a measure of the informativeness of the data about the value of the exchangeability parameter.

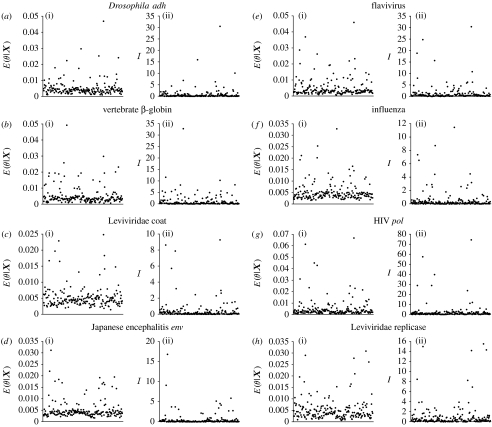
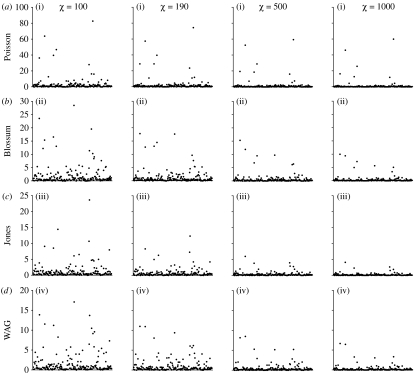
The amino acid sequence data are informative for some, but not all, of the exchangeability parameters. Figure 3 shows a summary for each of the eight alignments examined in this study. For each alignment, the mean of the posterior distribution and the Kullback–Leibler divergence are shown for the 190 exchangeability parameters. Note that the Kullback–Leibler divergence is small for many of the exchangeability parameters. In these cases, the data are not particularly informative about the value of the parameter. However, in some cases, the Kullback–Leibler divergence is large. The data are informative about the realized value of these exchangeability parameters.

Figure 3.

The mean of the marginal posterior probability distribution [$[E(\theta |\mathit{X})]$] and the Kullback–Leibler divergence (I) for the 190 exchangeability parameters for each of the eight alignments examined in this study. The 190 exchangeability parameters are ordered along the x-axes.

(b) Analysis under ‘centred’ fixed amino acid prior models

We analysed one of the eight alignments (the HIV alignment) under four ‘centred’ prior models. Specifically, we analysed the data under a prior centred on the Poisson (Bishop & Friday 1987), Blosum (Henikoff & Henikoff 1992), Jones (Jones et al. 1992) and WAG (Whelan & Goldman 2001) models. These analyses were designed to address three questions: (i) How are the substitution rates affected by the prior model? (ii) How informative is the data about the substitution rates? and (iii) What is the effect of the concentration parameter, Χ, on the exchangeability parameters?

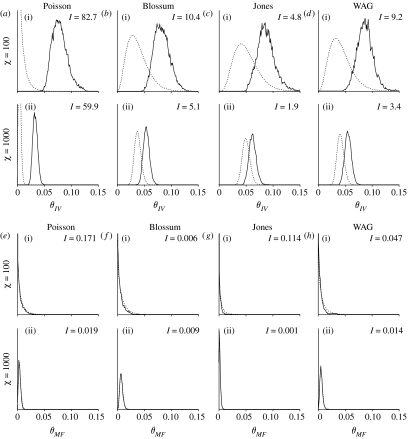
Figure 4 shows the marginal prior and posterior probability densities for a few of the substitution rates. Specifically, figure 4 shows the marginal prior and posterior probability densities of the I↔V (θ_IV) and M↔F (θ_MF) parameters for the HIV alignment. In each case, the exchangeability parameters were chosen to display an instance in which the data are informative (I↔V) and rather uninformative (M↔F) about the parameter's value. Note that the posterior distribution is shifted away from the prior distribution for the case in which the data are informative. This shift towards larger values of the exchangeability parameter results in a larger Kullback–Leibler divergence when compared with the case in which the data are uninformative. The prior and posterior probability densities are almost indistinguishable for the uninformative rate, resulting in a small Kullback–Leibler divergence. Figure 5 shows the Kullback–Leibler divergences for all 190 exchangeability parameters for the HIV alignment. In general, the posterior probability distribution of an exchangeability parameter becomes more similar to the prior distribution as the concentration parameter, Χ, is increased.

Figure 4.

The prior (dashed line) and posterior (solid line) marginal probability density for two of the 190 exchangeability parameters for analyses of the HIV alignment. The y-axis is the marginal posterior probability density of the rate.

Figure 5.

The Kullback–Leibler divergences (y-axes) of the 190 exchangeability parameters (arranged along the x-axes) under four different centred prior distributions for the HIV alignment.

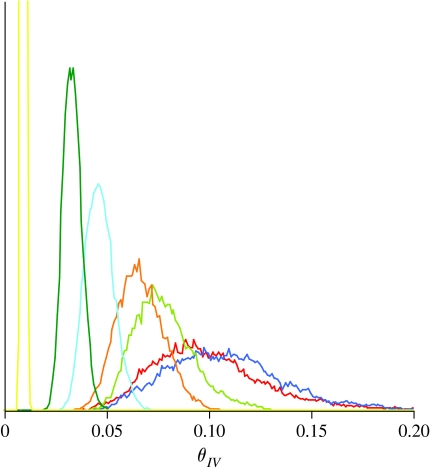
The concentration parameter, Χ, strongly influences the posterior probability distributions of the exchangeability parameters. Figure 6 shows the marginal posterior probability distribution for one of the exchangeability parameters (I↔V) for the HIV alignment when the prior is centred on the Poisson model. The marginal posterior distributions are most similar when Χ is small (e.g. when Χ=0.1 and Χ=1), but quite different for larger values of Χ. A large value for the concentration parameter states that many prior observations of exchanges (substitutions) between amino acids were observed. Why do we say this? For most statistical problems, the Dirichlet probability distribution is used as a prior for multinomially distributed data. The Dirichlet distribution is conjugated with the multinomial distribution, which means that when a Dirichlet prior distribution is combined with a multinomial-likelihood function, the posterior distribution is also a Dirichlet distribution (but with different parameter values than the prior). The parameter values of the Dirichlet prior are interpreted as the prior number of observations. Hence, a Dirichlet with parameters α₁=1, α₂=1, α₃=1 and α₄=1 essentially assumes four prior observations (one for each of the four categories). In our use of the Dirichlet prior distribution, the Χ parameter can be interpreted as the prior number of observations. Hence, a value of Χ=100 might be interpreted as there being 100 prior observations. For many datasets, even a value of Χ=100 might be considered large, and potentially swamp the information in the alignment about the values of the exchangeability parameters. Small values of Χ, however, do not appear to strongly affect the posterior distribution of substitution rate.

Figure 6.

The marginal posterior probability distribution of the I↔V exchangeability parameter for the HIV alignment when Χ varies. The y-axis is the marginal posterior probability density of the rate. Red line, 0.1; blue line, 1; light green line, 100; orange line, 190; light blue line, 500; green line, 1000; yellow line, 10 000.

(c) Averaging over fixed amino acid models

We performed phylogenetic analyses under a mixture of the fixed amino acid models. The mixture model was not applied on a per site basis (i.e. the likelihood for each site is calculated as an average over the 10 fixed amino acid models), but rather each amino acid model was applied to the entire alignment (i.e. only a single amino acid model is used to calculate the likelihood for the alignment, and MCMC is used to perform the model averaging). We summarize the results of these analyses using the posterior probabilities and Bayes factors for the 10 fixed amino acid models (tables 1 and 2). In general, the M₂ (Jones et al. 1992), M₃ (Dayhoff et al. 1978) and M₆ (Whelan & Goldman 2001) models performed the best for the eight alignments examined in this study.

Table 1.

The posterior probabilities of the 10 fixed amino acid models for each of the eight alignments. (A, Drosophila adh; B, vertebrate β-globin; C, Leviviridae coat; D, Japanese encephalitis env; E, flavivirus; F, influenza; G, HIV pol; H, Leviviridae replicase.)

model	A	B	C	D	E	F	G	H
M1	6.20×10−101	3.69×10−119	1.33×10−66	1.52×10−72	1.56×10−151	9.01×10−55	5.35×10−254	2.54×10−95
M2	6.20×10−3	1.04×10−10	1.41×10−8	9.99×10−1	9.99×10−1	9.99×10−1	9.99×10−1	1.69×10−10
M3	2.81×10−11	9.99×10−1	1.39×10−8	2.11×10−15	1.71×10−18	1.27×10−14	4.12×10−45	1.09×10−26
M4	5.55×10−34	2.59×10−53	1.52×10−60	3.40×10−33	2.47×10−87	3.16×10−33	3.04×10−131	3.95×10−91
M5	5.46×10−44	8.65×10−78	7.53×10−89	3.72×10−32	1.92×10−113	5.07×10−37	2.56×10−143	6.65×10−121
M6	9.88×10−1	5.04×10−6	9.99×10−1	4.10×10−8	7.81×10−6	1.54×10−8	7.22×10−31	2.27×10−2
M7	4.53×10−3	1.04×10−13	4.14×10−9	2.68×10−32	3.21×10−20	4.11×10−24	1.99×10−12	6.91×10−10
M8	6.67×10−4	5.65×10−19	1.97×10−9	2.99×10−10	5.26×10−7	1.20×10−8	6.49×10−17	5.68×10−10
M9	2.24×10−7	1.77×10−27	5.14×10−5	1.34×10−15	9.83×10−17	2.96×10−17	1.31×10−44	4.28×10−18
M10	1.51×10−10	8.13×10−24	4.43×10−5	6.40×10−23	2.21×10−20	4.00×10−22	3.12×10−67	9.77×10−1

Table 2.

The Bayes factors of the 10 fixed amino acid models for each of the eight alignments. (A, Drosophila adh; B, vertebrate β-globin; C, Leviviridae coat; D, Japanese encephalitis env; E, flavivirus; F, influenza; G, HIV pol; H, Leviviridae replicase.)

model	A	B	C	D	E	F	G	H
M1	5.58×10−100	3.32×10−118	1.19×10−65	1.41×10−71	1.41×10−150	8.11×10−54	4.81×10−253	2.29×10−94
M2	5.61×10−2	9.41×10−10	1.26×10−7	2.17×108	1.08×106	3.26×108	4.51×1012	1.52×10−9
M3	2.53×10−10	1.78×106	1.25×10−7	1.89×10−14	1.54×10−17	1.14×10−13	3.71×10−44	9.81×10−26
M4	5.00×10−33	2.33×10−52	1.37×10−59	3.06×10−32	2.22×10−86	2.84×10−32	2.73×10−130	3.56×10−90
M5	4.91×10−43	7.78×10−77	6.78×10−88	3.34×10−31	1.73×10−112	4.56×10−36	2.31×10−142	5.99×10−120
M6	7.80×102	4.53×10−5	9.39×104	3.69×10−7	7.03×10−5	1.39×10−7	6.49×10−30	2.09×101
M7	4.09×10−2	9.44×10−13	3.73×10−8	2.41×10−31	2.89×10−19	3.70×10−23	1.79×10−11	6.22×10−9
M8	6.01×10−3	5.09×10−18	1.77×10−8	2.69×10−9	4.74×10−6	1.08×10−7	5.84×10−16	5.12×10−9
M9	2.02×10−6	1.60×10−26	4.62×10−4	1.21×10−14	8.85×10−16	2.66×10−16	1.17×10−43	3.85×10−17
M10	1.36×10−9	7.32×10−23	3.98×10−4	5.76×10−22	1.98×10−19	3.60×10−21	2.81×10−66	3.86×102

(d) Considering the substitution model as a partition of substitution rates

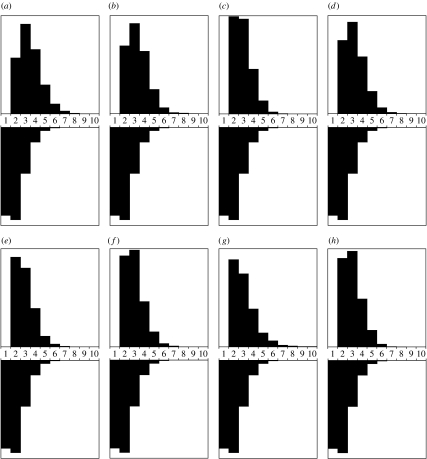
We performed analyses in which the substitution models were considered partitions of the 190 substitution rates. As described above, we assumed a Dirichlet process prior probability model that places some probability on all 6.59×10²⁵⁸ possible time-reversible amino acid substitution models and explored the consequence of using different values for the concentration parameter of the Dirichlet process prior (β). Specifically, we fixed β such that the prior mean for the number of rate categories (K) was 2, 5 and 10 (which are achieved by using β=0.18, 0.81 and 2.09, respectively). Figure 7 summarizes one important aspect of the MCMC analyses: the number of rate categories explored by the Markov chain. Note that in none of the analyses was there much posterior probability on K=1, even when a lot of prior probability was placed on the simplest possible amino acid model, as was the case when E(K)=2. The posterior probability for K=1 was close to zero for all eight analyses and for each prior on K that we explored. Although the data were informative about small values of K, they were less so for large values of K. The prior and posterior probability distributions on the number of substitution rate categories were similar when the prior mean for the number of categories was E(K)=10.

Figure 7.

The prior and posterior probability distributions (upside down and right side up, respectively) for the number of exchangeability parameter groups for the analyses where the concentration parameter is fixed such that the prior mean of the number of substitution categories is 2 (i.e. E(K)=2). (a) Drosophila adh; (b) vertebrate β-globin; (c) Leviviridae coat; (d) Japanese encephalitis env; (e) flavivirus; (f) influenza; (g) HIV pol and (h) Leviviridae replicase.

Even though the posterior probability distribution on the number of substitution types varied from one analysis to another, mostly depending on the prior placed on K, summaries of the substitution models visited were remarkably consistent. Figure 8 shows the ‘mean partition’ for each of the three analyses we conducted for each alignment. The mean partition is the partition that minimizes the squared distance to all of the sampled partitions (Huelsenbeck & Andolfatto 2007). We use a distance on partitions, described by Gusfield (2002). The distance between two partitions is the minimum number of elements that must be moved between subsets to make one of the partitions identical to the other. (Or, equivalently, it is the minimum number of elements that must be deleted to make the induced partitions the same.) The mean partitions are similar under the three different choices of β we examined for each alignment, with the same exchangeability parameters usually being grouped together.

Figure 8.

The mean partitions of the exchangeability parameters for each of the analyses. For each alignment, three mean partitions are shown, with the top most having a prior mean of 2 and the bottom most having a prior mean of 10.

4. Discussion

Amino acid substitution models are quite complex and parameter rich with regard to both the number of substitution rates to be estimated and the number of ways to partition rates. No single dataset is expected to contain enough information to resolve the phylogeny while simultaneously providing accurate estimates of all parameters. A synthesis of various data sources is necessary, and the Bayesian approach described above provides a statistically rigorous framework that performs this synthesis. We explored several different approaches to the analysis of amino acid data, three of which extend previous work on the development of fixed amino acid models, and one of which extends work on model averaging of DNA substitution models (Huelsenbeck et al. 2004).

One possible approach, explored here and implemented in MrBayes (Ronquist & Huelsenbeck 2003), is to simply average inferences over a set of fixed amino acid models. This approach has the advantage that it automates the choice of fixed amino acid models, selecting the model or models that are most appropriate for the data in hand. In practice, however, we found that little averaging occurred, because virtually all of the posterior probability is placed on a single amino acid model. Moreover, this approach assumes that one of the fixed amino acid models is appropriate for the data in hand, though in reality none of the models in the candidate pool of models may be particularly appropriate.

Unlike the fixed amino acid models, the centred model allows for the possibility that the data in hand do not conform to any particular amino acid model. The treatment of amino acid substitutions under either the centred models or the GTR model (a model ‘centred’ on the Poisson model rates) does not entail a significant computational burden when posterior probabilities are approximated using MCMC. Maximum-likelihood estimation of the substitution parameters, by contrast, is expected to be difficult not only owing to the large number of parameters to estimate but also because the likelihood surface is likely to be flat as there is little information in a small alignment about many of the exchangeability parameters. Furthermore, by using a substitution model centred about a fixed amino acid model, one can use prior information about amino acid substitution processes combined with the data at hand to produce valid phylogenetic inferences. Indeed, an alternative to producing fixed amino acid models is to produce distributions of substitution rates from databases of alignments, such as the Pandit database (Whelan et al. 2003, 2006).

Perhaps the most intriguing possibility for the analysis of amino acid models is directly motivated by work on nucleotide models that are all four-state time-reversible continuous-time Markov chains. Several different substitution models have been described, such as those described by Jukes & Cantor (1969), Kimura (1980) and Tamura & Nei (1993), which are all simply special cases of the GTR model of DNA substitution (Tavaré 1986) but with restrictions on the substitution rates. There are a total of 203 possible models of nucleotide substitution, with about a half dozen being formally described. As we have shown here, this approach can be directly extended to the analysis of amino acid data, with the total number of restrictions on substitution rates now being 6.59×10²⁵⁸. Substitution models in this framework are considered partitions, and in our implementation, we placed a Dirichlet process prior probability distribution on the model partitions, using MCMC to explore the space of models. The number of parameters to be estimated is determined by how the amino acid substitution rates are partitioned into equivalence classes. The data suggest a relatively small number of partitions. Thus, a uniform prior on partitions, as described by Huelsenbeck et al. (2004), places too much weight on an intermediate number of rate classes and is inefficient. The Dirichlet process prior provides a flexible class of priors, where the number of classes can be controlled by a single parameter β and the influence of the choice of β on the posterior can be assessed. Importantly, we find that the mean number of partitions to be very similar for a variety of choices of β.