Fractal reorientation clocks: Linking animal behavior to statistical patterns of search

Abstract

The movement ecology framework depicts animal movement as the result of the combined effects of internal and external constraints on animal navigation and motion capacities. Nevertheless, there are still fundamental problems to understand how these modulations take place and how they might be translated into observed statistical properties of animal trajectories. Of particular interest, here, is the general idea of intermittence in animal movement. Intermittent locomotion assumes that animal movement is, in essence, discrete. The existence of abrupt interruptions in an otherwise continuous flow of movement allows for the possibility of reorientations, that is, to break down previous directional memories of the trajectory. In this study, we explore the potential links between intermittent locomotion, reorientation behavior, and search efficiency. By means of simulations we show that the incorporation of Lévy intermittence in an otherwise nonintermittent search strongly modifies encounter rates. The result is robust to different types of landscapes (i.e., target density and spatial distribution), and spatial dimensions (i.e., 2D, 3D). We propose that Lévy intermittence may come from reorientation mechanisms capable of organizing directional persistence on time (i.e., fractal reorientation clocks), and we rationalize that the explicit distinction between scanning and reorientation mechanisms is essential to make accurate statistical inferences from animal search behavior. Finally, we provide a statistical tool to judge the existence of episodic and strong reorientation behaviors capable of modifying relevant properties of stochastic searches, ultimately controlling the chances of finding unknown located items.

The movement ecology framework explicitly recognizes animal movement as the result of a constant “dialogue” between environment (external factors) and animal internal states. This dialogue affects organisms' motion and/or navigation capacities to finally produce the actual movement (1). Beyond phenomenological descriptions of movement, the random paradigm (1) should seek to understand how interactions between the four components of the movement ecology framework (i.e., internal states, external forces, motion, and navigation capacities) might be translated into observed statistical patterns of movement (2, 3). In the present work, we suggest that a major advance in bridging the gap between animal behavior (mechanistic approach) and the statistical properties of search strategies involves a statistical reinterpretation of the idea of intermittent locomotion (4–6).

The biological principle of intermittent locomotion assumes that animal behavior unavoidably produces observable punctuations in the movement (e.g., stops, strong changes in speed). Thus, the forces generating movement operate discontinuously, producing pauses and speeding patterns on the move. Intermittent locomotion (also known as stop-and-go movement, pause-travel locomotion) occurs in terrestrial, aquatic, and aerial environments, embracing very different ecological contexts, e.g., food search, directed travel toward hoarding sites, active pursuit of preys, habitat assessment (4).

To understand why intermittent locomotion has evolved it is essential to take into account all relevant costs and benefits (5). However, an often disregarded but very general aspect of intermittency is that, any type of abrupt change in the continuous flow of movement (e.g., morphological changes of the body plan, sensorial failures, pauses) allows for the possibility of breaking down previous directional memory. Indeed, intermittence may be closely related to turning behavior: after pauses, new directions (not correlated with the previous ones) are more prone to be chosen, producing strong reorientations on the move. Thus, patterns of intermittence can be mapped into patterns of reorientation behavior.

The existence of episodic behaviors resulting in sequential breaks of previous-directions can strongly modify the success of a search process. The probability distribution of time intervals between reorientations can determine strong changes in the diffusive properties of movement and in relevant spatial properties of the trajectories (6, 7). These distributions may not necessarily involve Gaussian statistics but can also involve Lévy type of statistics (8, 9). Thus, changes in animal behavior affecting the tempo and modes of reorientation can generate different anomalous diffusion regimes (8–11) or involve macroscopic transitions between normal and anomalous diffusion (12, 13), which in turn, can affect the search efficiency of random exploration processes (7, 14). When information availability and/or searcher detection capabilities are low, and thus, orientation mechanisms cannot be used, animals still can improve the chances of locating targets by relying on statistical properties provided by their motility patterns (e.g., refs. 15–17). Given the energetic costs of large-scale searching, behavioral features favoring an intermittent locomotion that promotes efficient search patterns may represent a real adaptive advantage. Hence, when exploring natural resource fields across different scales, animals could complement fine-tuned sensorial capabilities with the generation of efficient (e.g., Lévy-like) intermittency (15, 17).

By means of biphasic (scanning–reorientation) models of search we explore the connections between intermittency, reorientation behavior, and efficient statistical patterns of search. We develop two behavioral models of search (with and without intermittence) and quantify the effects of Lévy intermittence in search efficiency in relation to (i) nonintermittent animal movement, (ii) non-Lévy types of intermittence, and (iii) increases in searchers' detection capability and cruising speed. We also present a statistical method based on maximum likelihood and Akaike Information Criteria (AIC) model selection (18, 19) capable of detecting the presence of intermittence (i.e., reorientations) on the basis of empirical turning angle distributions. Our study introduces the general concept of fractal reorientation clocks as adaptive memory losses of previous behavior, controlling the diffusivity and other relevant properties of stochastic search processes.

Two Behavioral Models of Search

We present two contrasting behavioral models of animal search: with and without intermittence. In the simplest case (without intermittence) we model organisms' local scanning behavior by means of correlated random walks (CRW). CRW are a natural way to model the emergence of angular correlations in animal trajectories coming from local scanning behavior (2, 20–23). In the intermittent model, we generate a class of random walks, named Lévy-modulated CRW (LMCRW), by incorporating a time-discrete reorientation behavior (with Lévy statistics) into the background continuous scanning process modeled as a CRW (7). The LMCRW generalizes the idea of Lévy walk models as search strategies proposed by Shlesinger and Klafter (24) and developed by Viswanathan et al. (14).

In CRW models, angular correlations are introduced on the basis of a continuously decaying probability distribution of turning angles (−π≤ θ ≤ π) centered at the value θ = 0 (maximum probability) (7, 21, 23). In our model, the turning angles are selected at each step from a wrapped Cauchy distribution (WCD) (25),

where ρ ∈ [0,1], although other distributions (e.g., circular Gaussian, von Mises) might be as good (26, 27). The shape parameter ρ of the WCD distribution controls the directional persistence or correlation length of the random walk (20, 22, 26, 27). In the intermittent model (LMCRW), reorientation phenomena are added to the above CRW model. By definition, a reorientation breaks the directional persistence introduced by the scanning behavior, involving a change of direction that should be uncorrelated (or else strongly anticorrelated) to the previous direction. For the sake of simplicity, but without loss of generality, we have assumed that reorientation behavior generates turning angles that are not correlated to previous directions. In statistical terms, this means that reorientation turning angles θ are being sampled from a uniform distribution (UD) θ ∈ [−π, π]. Therefore, in our model, at each reorientation time the turning angle is no longer sampled from a WCD (scanning behavior), but instead it is sampled from a UD (reorientation behavior). The time intervals t between these reorientations (UD sampling) are drawn from a power law distribution: P(t) ∼ t^−μ, where 1 < μ ≤ 3. These power laws represent the tail of a Lévy-stable distribution, so that if the power law exponent μ, also known as the Lévy index, lies in the interval 1 < μ < 3, then the tail of the corresponding Lévy stable distributions have exponent μ_L = 1 − μ. For μ ≥ 3, provided the conditions of the Generalized Central Limit Theorem (28), the tail converges to a Gaussian distribution (29). In the latter case, the time intervals between reorientations will show an intrinsic characteristic scale (in this sense, intermittence is non-Lévy). To compare the role of Lévy intermittence with non-Lévy types of intermittence we also show the results of a search model where the time intervals t between reorientations (UD sampling) are drawn from an exponential distribution: P(t) ∼ e^−t/τ, with characteristic time τ = βλ_p, where β ∈ [0.01, 1] and λ_p is the average distance (or travel-time) between patches [see supporting information (SI) Text].

Search Efficiency Simulations

We consider search scenarios in which random walkers look for fixed target sites in 2D and 3D spaces with periodic boundary conditions. To make comparable the encounter rates of diffusive-like searching processes at distinct dimensional space (i.e., 2D, 3D) the mean free path λ, defined as the average Euclidean distance between sites, is fixed at a constant value (30). For each dimension we considered two target-density scenarios, represented by patchy landscapes with different average distances between patches λ_p = 1,000 (low-resource scenario) and λ_p = 100 (high-resource scenario). We also consider 2D fractal-like landscapes with the same target densities (see SI Text).

Along each step the walker “scans” for circular targets of radius r_t with a detection radius r_d. The walkers perform CRW (nonintermittent model) or LMCRW (intermittent model) with steps of fixed length (ℓ₀ = 0.5). Taking into consideration some variability in ℓ through Gaussian or exponential distributions of move lengths does not change qualitatively the results. In CRW the turning angles are sorted from a WCD at each step. In LMCRW, the turning angles are sorted from a WCD and following Lévy time intervals from a UD. If it finds a target, i.e., if the distance between the walker and the target is equal or less than the detection distance R, the step is truncated because detection has occurred. Once detected, with probability P = 0.5, the walker can capture the target. If the walker captures the target, it proceeds to the target location, and the number of encounters increases by one. If it does not, the number of encounters remains the same. Whether there is capture or not, after detecting a target, the walker draws a turning angle from a UD in both models, which assumes that target detection always forces subsequent reorientation. A full run ends after the walker travels a total of N = 10⁷ steps. To ensure stationary averages throughout the simulations, we delete targets once they are found (local depletion) but we maintain global target densities by randomly adding a new target each time an encounter is computed. Targets are relocated, preserving the basic statistical properties of the initial landscape structures (see SI Text).

We define the search efficiency function η = n_e/d_total as the ratio of the final number of target sites visited n_e to the total distance traversed by the searcher d_total, and we scale the whole search process in terms of the mean free path between patches λ_p, which represents the average distance between two patches (see SI Text). Results of the search efficiency simulations are presented as the percentage of relative change on search efficiency (i.e., Δη) of the intermittent behavioral model (I), which can be Lévy or non-Lévy (i.e., exponential), against the nonintermittent model (G), that is,

Statistical Analysis of Trajectories: Detecting Intermittent Behavior

In animal movement data, the common assumption that the behavior of a random variable (related to movement) can be described with the same probability distribution throughout all its range cannot be guaranteed a priori. This is so because the underlying mechanisms of movement differ on different scales, or alternatively because the same core mechanism generates different outcomes at different scales. For instance, one usually assumes that turning angles follow an exponential-like or a Gaussian-like distribution, decaying from small (≈0°) to large values (≈180°). However, if intermittence exists, the observed probability distribution of the turning angles would arise as a combination of the turning angles generated by (at least) two behaviors, scanning and reorientation. On the average, scanning turning angles (gleaned in our models from a WCD) are smaller (closer to 0) than reorientation turning angles (gleaned in our models from a UD). Because of that, the effect of reorientation behavior on turning angle distributions should be particularly conspicuous at the “tail” of the distribution.

We compute the turning angle distributions of two trajectories (N = 10³) generated with the nonintermittent (ρ = 0.9) and the Lévy intermittent model (ρ = 0.9, μ = 2), and we perform AIC-based pointwise model selection tests (PWMS) to determine whether the tail of the respective turning angle distribution is uniform. PWMS is a rigorous method to: (i) identify different qualitative regimes within statistical data and (ii) select the probabilistic model that suits better the different regimes. The model selection is based on Akaike Information Criteria weights corrected for small data samples (wAICc) (18, 19) (see SI Text). In particular, we run tests where an exponential distribution (the simplest decaying function) and a UD are confronted to fit the turning angle data from the two behavioral models of search. The data are ranged in ascending order and the model selection tests are done sequentially from the smallest to the largest angle values.

Results

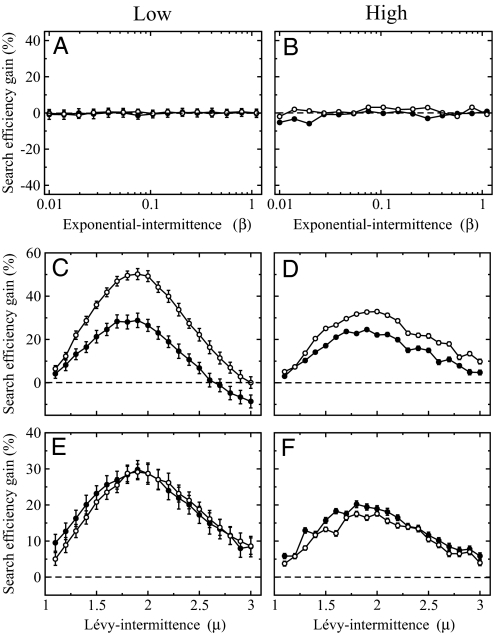
Plots of the search efficiency gain Δη (Fig. 1) show that exponential intermittence (Fig. 1 A and B) does not impact (there is almost no effect) the search efficiency. This is true for the 2-fold range of characteristic times τ chosen. On the basis of the parameter β ∈ [0.01, 1], we choose a range of characteristic times τ that would represent a range from 1% to 100% of the average travel time between patches (see SI Text). Below this range, exponential intermittence starts to break the directional persistence of the trajectory in excess, leading to significant decreases in the search efficiency when compared with a nonintermittent search. Above this range, the effects of exponential intermittence remain insignificant. On the contrary, the incorporation of Lévy intermittence (Fig. 1 C–F) can produce a substantial increase in the number of encounters at different target densities (compare Fig. 1 C vs. D and E vs. F or Fig. S1 a vs. b), landscape dimensions (compare Fig. 1 C vs. E and D vs. F), and target spatial distributions (compare Fig. 1 C and D vs. Fig. S1 a and b). The overall range of search efficiency gain Δη goes from −40% to 50%, but more importantly, optimal Lévy intermittent behavior does emerge. In our scenarios the range of optimal Lévy indexes is 1.5 ≤ μ_opt ≤ 2. Optimal values for patchy landscapes (i.e., μ_opt ∼2) are larger than for fractal-like landscapes (i.e., μ_opt ∼1.5). In general, optimal Lévy indexes seem to be more sensitive to target spatial distributions than to target densities or dimensionality. The gain in search efficiency Δη is smaller when target density increases (compare Fig. 1 C vs. D and E vs. F and Fig. S1 a vs. b), when the system changes from 2D to 3D (compare Fig. 1 C vs. E and D vs. F), and when target spatial distributions go from patchy to fractal-like (compare Fig. 1 C and D vs. Fig. S1 a and b). In 2D systems, the larger the directional persistence during the scanning process (ρ = 0.9 vs. ρ = 0.7) the larger the benefits of intermittence. In 3D systems (Fig. 1 E and F), even though the effects of intermittence are reduced, Lévy intermittence always increases search efficiency and large changes in the sinuosity of the paths (from ρ = 0.7 to ρ = 0.9) seem not be as determinant for search efficiency as could be in 2D systems. In any case, in low-density patchy landscapes, the search efficiency gain caused by optimal Lévy-intermittent behavior is comparable to the gain obtained by a nonintermittent searcher if increasing almost 2-fold the speed and 4-fold the size (i.e., perceptual capabilities) (2D systems), and 1.5-fold the speed or size (3D systems) (Fig. S2).

Fig. 1.

Search efficiency gain Δη (%) comparing search processes with and without exponential-intermittence in 2D patchy landscapes (A and B) and with and without Lévy intermittence in 2D (C and D) and 3D (E and F) patchy landscapes. Results are shown for λ_P = 1,000 (low patch densities) (A, C, and E) and λ_P = 100 (high patch densities) (B, D, and F) for different scanning behaviors: ρ = 0.7 (●) and ρ = 0.9 (○), and for different intermittent reorientation behaviors: exponential-intermittent (0.01 ≤ β ≤ 1]) and Lévy intermittent (1 < μ ≤ 3). In the former case, the β values cover characteristic time-scales of intermittence (i.e., τ = βλ_P) that go from 1% to 100% of the λ_P value [i.e., the average distance, or travel time, between patches (see SI Text)]. Dashed lines indicate zero search efficiency gain (Δη = 0%).

Interestingly, in some conditions, certain classes of Lévy intermittence can decrease the search efficiency because of an excessive breakage of the overall directional persistence of the walk (Fig. 1, ρ = 0.07, for the interval 2.5 < μ ≤ 3; Fig. S1, for the interval 2 < μ ≤ 3). Indeed, it is well known that the Lévy type of statistics not only increases but can also decrease (depending on the conditions) average encounter rates (30). All together, Fig. 1 and Fig. S1 suggest that the incorporation of Lévy intermittence into realistic scanning/reorientation models of search significantly modifies (either increase or decrease) encounter rates in different types of landscapes and different spatial dimensions. In addition, Fig. S2 illustrates the fact that Lévy intermittence might be of evolutionary relevance.

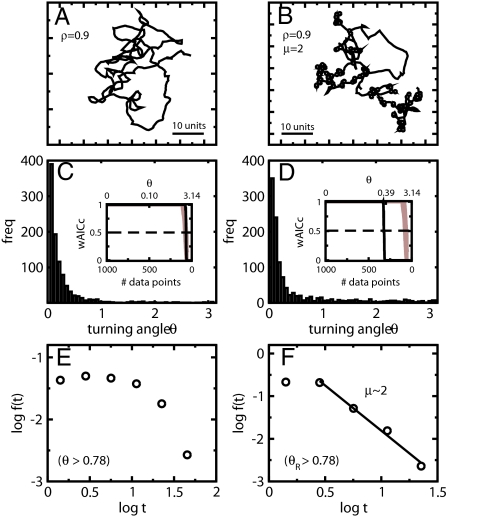
Even though the two “behavioral” search modes (Lévy-intermittent and nonintermittent) involve large differences in the search efficiency (Fig. 1 and Fig. S1), the realized trajectories are almost indistinguishable (Fig. 2 A and B). Concordantly, the resulting turning angle distributions look very similar (Fig. 2 C and D). Only the use of powerful statistical methods (i.e., PWMS) can help us to distinguish the two searching modes (Fig. 2 C and D Insets). Contrary to the nonintermittent case, the PWMS can detect uniformity in the tail of the turning angle distribution generated with the Lévy-intermittent model. The critical turning angle at which the regime shift from exponential to uniform behavior occurs is θ_c = 0.39 rad. Turning angle values above θ_c are uniformly distributed and so we can expect those to be produced mainly because of reorientation (and not scanning) behavior. In Fig. 2 E and F we estimate the distribution (i.e., probability density function) of time intervals between “observable” reorientations θ_R. We define an observable reorientation θ_R to occur if the turning angle approximately doubles the critical value θ_c, so we can ensure that we are not in the transition regime. In our case θ_R ≥ 2θ_c ≥ 0.78 rad. Even though in our computation we are definitely missing many reorientation-based turning angles (θ_R ≤ 0.78) and we might wrongly include some scanning-based turning angles (θ ≥ 0.78), we still can recover the correct scaling exponent μ ∼ 2 that characterizes the intermittent behavior of our model. As a matter of comparison, if we compute the time-interval distribution for angles such that θ ≥ 0.78 rad in the nonintermittent model, we do not observe a power-law distribution for the time intervals (i.e., straight line in a log-log plot). Instead, we obtain an exponential-like distribution consistent with what we expect to observe in the absence of intermittent behavior. Exponential distributions can be well characterized as straight lines in semilog plots. In a log-log plot, the exponential-like behavior shows up as a strongly curved line (Fig. 2E). Note that in those cases where intermittence exists (uniform tail) but it has an intrinsic characteristic scale (μ ≥ 3 or exponential intermittence), exponential-like behavior for the time-interval distributions can also be observed.

Fig. 2.

Trajectories of length N = 1,000 (A and B), turning angle distributions (C and D), and log-log probability distributions for the time intervals between turning angles θ such that θ > 0.78 rad (E and F) in the absence (Left) and presence of Lévy intermittence (Right). In both cases, scanning behavior was set at ρ = 0.9 and reorientation behavior was set at μ = 2. Filled circles in B indicate reorientation locations. Insets in C and D show the results of PWMS) contrasting an exponential versus a uniform model for the respective turning angle frequency distributions (C and D). A value of wAICc = 1(0) gives the maximum weight of evidence in favor of the exponential (uniform) model. A wAICc = 0.5 divides the area of selection of one model against the other (dashed line). Shaded areas show the widths of the standard deviation of 100 tests performed on 100 Monte Carlo replicates of turning angle series (N = 1,000, ρ = 0.0) (for more details on PWMS see SI Text). In F, a regression line is computed for the range of values where power law behavior (straight line in a log-log plot) is observable. In E and F note the distinction between θ > 0.78 (E) and θ_R > 0.78 representing scanning-related (θ) and reorientation-related (θ_R) turning angles, respectively.

Discussion

The general idea that animals exhibit a set of different behaviors (movement modes) that are statistically distinguishable (31) can also be applied to the search behavior. By definition, in the search mode animals do not have much environmental information, and learning from the environment should represent a challenge. As such, the search mode should be distinguished from other movement modes driven by strong environmental cues (e.g., ref. 32) or by learning processes occurring in predictable and static ecological conditions, which typically generate highly repetitive and cyclical movement behavior (e.g., ref. 33).

An efficient search mode not only would involve the existence of specific search strategies that can be effective in particular situations but, more generally, the flexibility to deal efficiently with a changing environment (4). It is within this ecological and evolutionary framework that we propose the existence of background reorientation mechanisms (i.e., fractal reorientation clocks) that can generate Lévy intermittence, efficiently alternating scanning (whether continuous or not) and reorientation behavior. Such mechanisms might co-occur with more localized/specialized scanning mechanisms and could substantially improve the search efficiency across natural exploration scales (e.g., refs. 15 and 17). Our results in Fig. 1 and Fig. S1 show that such a set of reorientation mechanisms could strongly modify encounter rates by amounts that depend on: (i) the dimensionality of the system (i.e., 2D, 3D), (ii) the type of landscape (i.e., spatial distribution and target densities), (iii) the background scanning behavior (i.e., correlation length of the walk), and (iv) the specific scaling exponent (i.e., Lévy index) governing the time-interval distribution between reorientations. Considering the energetic costs associated with enhancing search efficiency by increasing the cruising speed and/or the perceptual capabilities (see Fig. S2), the “timing” of specific reorientation mechanisms surely must be a strong target for natural selection.

Scanning, Reorientations, and Lévy-Intermittent Behavior.

From a purely statistical perspective, scanning behavior can produce different amounts of angular correlations during a walk. These correlations depend mainly on local environmental features, and thus, represent an emergent property from the complex mechanic-sensorial responses of animals to the local environment. The emerging statistical patterns produced by scanning behavior cannot be considered as part of a large-scale search strategy ruled by the animal. First, it is difficult to imagine a scanning mechanism evolved to mold angular statistical correlations at scales much larger than the scales of the detection process itself. Second, and more importantly, several studies suggest that if animals have some degree of control on angular correlations, this aptitude would only be relevant at short scales (e.g., patch exploitation) (27, 34, 35). In the long run, the correlations generated by scanning behavior can either vanish (as in CRW processes; e.g., refs. 7, 21, and 23) or else be retained mainly because of the constant feedback between scanning behavior and the landscape (as is assumed in composite Brownian walks; e.g., refs. 36 and 37).

During a search process, scanning behavior can be continuous or discontinuous (i.e., saltatory or intermittent search). In the latter case, the proportion of time spent in relocation displacements and scanning phases also affects the search efficiency (38, 39). However, either if the exploration of space is based on continuous scanning behavior (e.g., refs. 7, 14, and 30) or a saltatory process (e.g., refs. 38 and 39), the key element impacting on the efficiency of stochastic searching is the generation of Lévy-like reorientation patterns (7, 30, 40, 41).

Our results (Fig. 1, Fig. S1, and Fig. S2) suggest that the effects of Lévy intermittence are important and robust in a variety of landscapes, target densities, and types of scanning behavior (see also refs. 30 and 42). This fact does not come as a surprise if one notes that Lévy intermittence has direct impact on general statistical properties that shape the long-term spatial pattern of exploration (e.g., diffusivity, first-passage times, resampling rates, returning probabilities). From a biological perspective, what is important is that the distinction between scanning and reorientation behavior seems crucial to understand the relationships between animal behavior and statistical patterns of search (see also ref. 6). The concept of fractal reorientation clocks, which involves the ability to organize directive memory losses of previous behavior/movement, brings the possibility to look for a variety of biological mechanisms under a common perspective and may square different types of stochastic search strategies (i.e., area-restricted search, Lévy search strategies and saltatory search processes) under a common framework.

Biological Mechanisms for Lévy Intermittence.

To think rigorously about Lévy-intermittent phenomena in biology, one should first identify a precise biological mechanism of reorientation that can be switched on and off, triggered as a response to the environment. Environmental cues acting on reorientation behaviors are expected to be different from those acting on scanning or “detection” mechanisms (6). Although reorientation mechanisms might be triggered by detailed, localized environmental information such as in scanning or detection mechanisms, the idea of fractal reorientation clocks involves the existence of a “reorientation plan of action” that could be triggered by coarse-grained, landscape-level environmental cues, which need to be integrated in time (e.g., absence/presence of food, absence/presence of enemies) and might be closely associated to the internal states of the animal (e.g., starvation, fatigue, sexual attraction).

In searches where scanning is continuous, reorientation behavior may involve any biological mechanism capable of breaking apart previous directional persistence of the scanning process itself. In saltatory searches, where scanning is discontinuous, reorientation behavior might be linked to decision-making mechanisms capable of stopping and/or starting relocation moves in different directions. In both cases, the mechanisms themselves could consist of simple internal biological programs (6, 43) or could emerge as interactive processes with other individuals (i.e., collective mechanisms of intermittence) or the environment (i.e., relocation displacements). As occurs in dispersal processes, for example, many animals could actively take benefit of external transportation devices (e.g., winds, ocean currents, other animals) as part of a search strategy.

In general, any biological mechanism acting like a reorientation clock, adjustable either to environmental forcing or to changes of the animal internal state, could be under selective pressure to stochastically control the search efficiency. There are some examples in the literature showing that at least for “simple” organisms (e.g., bacteria, flagellates, fruit flies) motor-related neuronal configurations (43, 44) and biochemical paths (45) could be responsible for a Lévy timing of reorientations (12, 13, 44, 46). Empirical evidence of such fractal reorientation clocks at different levels of biological organization (e.g., neuronal, biochemical, physiological, behavioral) could explain, to some extent, the presence of Lévy flights and scale-free (i.e., fractal) properties in the movement patterns of some animals (e.g., refs. 12, 13, and 44). However, the explicit links between reorientation behavior and statistical properties of movement have yet to be systematically explored.

When Lévy Intermittence Is Advantageous as a Search Pattern.

When animals find food or localize a particular environment where resource exploitation may be predictable and profitable, they can switch behavior to a local search mode [i.e., area-restricted search (ARS)]. ARS explains the common observation that the amount of time spent by animals in food rich areas is much larger than the time spent in bare environments (e.g., ref. 47). However, prey capture does not always induce ARS (48). If resource patterns within food-rich areas are complex enough, the problem of efficiently exploiting resource patches is not a matter of finding a patch and fully exploiting it, but instead involves visiting several resource areas of potential interest at the right moments. This fact imposes a tradeoff between constantly revisiting nearby areas and exploring new potential resource areas. In terms of stochastic processes, this situation resonates more with an N-passage than with a first-passage search problem. In such cases, the simple ARS behavior combined with ballistic-like movement (e.g., refs. 36 and 47) would not be, in general, the most efficient stochastic search strategy. If the exploration involves either continuous or saltatory scanning, whenever there are potential benefits in randomly revisiting and reexploring close areas aside from exploring new landscape, Lévy intermittence can strongly modify search efficiency. This main result holds for different target spatial distributions and densities (Fig. 1 and Fig. S1). However, the power of Lévy intermittence decreases with increasing dimensionality and target densities (Fig. 1 and Fig. S1; see also ref. 30). Of note is the fact that animals living in 2D and 3D environments actually can move in a much more reduced spatial dimensionality (see, for example, ref. 49) enhancing the potential effects of Lévy intermittence during a search.

The similar dependency of different stochastic search processes (i.e., LMCRW, pure Lévy strategies, and saltatory searches) on both target densities and dimensionality (e.g., refs. 7, 30, 39, and 50), indicates the universal character of some basic stochastic search properties. Analogous essential properties might explain the general result that Lévy intermittence can strongly modify the search efficiency of N-passage stochastic search problems. Yet if the exploration of an area can be considered an N-passage search problem, our simulations illustrate the fact that in LMCRW models, other particular conditions are needed for Lévy intermittence to significantly increase the search efficiency. For example, if the scanning behavior of the animal leads to extremely sinuous paths (ρ < 0.5), reorientation mechanisms will not convey any effect at large scales. In other words, the larger the sinuosity of the path, the lower the power of Lévy intermittence. Also, as we show in Fig. 1C and Fig. S1, the combination of certain target spatial arrangements and densities can account for regimes of Lévy intermittence (3 ≥ μ > 2) that decrease the number of encounters by excessively breaking the directional memory that scanning behavioral processes can provide.

Detecting Lévy Intermittence in Trajectories.

Animal movement can be understood as a sequence of scanning and reorientation behavior, the latter also including relocation displacements (i.e., saltatory search). Even though a search process might incorporate Lévy intermittence, trajectories might not look as pure Lévy walks or flights (e.g., Fig. 2B). Therefore, it is necessary to develop new segmentation methods on trajectories capable of recovering intermittence. The method proposed here should be considered a step toward this goal. In fact, empirical data (i.e., small datasets, large sampling errors), and certain natural contexts (i.e., high sinuosity trajectories, high resource scenarios) may challenge the identification of Lévy intermittence by means of AIC-based PWMS on turning angle distributions. In some solutions, the turns originated by episodic reorientation behavior can be mostly screened by those coming from scanning behavior.

In addition to developing new statistical tools to analyze recorded trajectories, it would be important to move closer toward measurements of reorientation (i.e., proxys of reorientation events) rather than try to detect reorientation signals indirectly from the plotted track. In the near future, the detection of Lévy intermittence can be powered by the advancement of biotelemetry, that is, the remote monitoring of the physiology, behavior, and energetic status of free animals in combination with the more standard tracking procedures (e.g., ref. 51).

Challenging the Movement Ecology Framework.

Beyond the quantitative analysis of movement, the random paradigm (1) should provide clear rationale to link animal behavior to statistical patterns of movement (e.g., refs. 31 and 33). We suggest that the recognition of intermittent locomotion and the explicit distinction between scanning and reorientation mechanisms is essential to make accurate statistical inferences from searching behavior. Furthermore, adequate null models of search behavior could help to build more realistic links between individual and populational scales, improving the understanding of spatially structured population dynamics (e.g., ref. 52). Therefore, a major challenge within the movement ecology framework (1) is to understand how reorientation mechanisms are integrated into the set of traits enabling the execution of movement (motion capacity) and how navigation capacity (scanning behavior) and/or internal states of the animal can control and modify reorientation patterns based on different external stimuli. Merging the concepts essayed in this work with the movement ecology framework will definitely help to discriminate between different causes for Lévy patterns in animal movement (e.g., refs. 15, 36, 53, and 54) and to know whether there could be room for adaptive behaviors, such as those proposed here i.e., fractal reorientation clocks, relying on essential properties of stochastic search processes.