Ordered cyclic motifs contribute to dynamic stability in biological and engineered networks

Abstract

Representation and analysis of complex biological and engineered systems as directed networks is useful for understanding their global structure/function organization. Enrichment of network motifs, which are over-represented subgraphs in real networks, can be used for topological analysis. Because counting network motifs is computationally expensive, only characterization of 3- to 5-node motifs has been previously reported. In this study we used a supercomputer to analyze cyclic motifs made of 3–20 nodes for 6 biological and 3 technological networks. Using tools from statistical physics, we developed a theoretical framework for characterizing the ensemble of cyclic motifs in real networks. We have identified a generic property of real complex networks, antiferromagnetic organization, which is characterized by minimal directional coherence of edges along cyclic subgraphs, such that consecutive links tend to have opposing direction. As a consequence, we find that the lack of directional coherence in cyclic motifs leads to depletion in feedback loops, where the number of nodes affected by feedback loops appears to be at a local minimum compared with surrogate shuffled networks. This topology provides more dynamic stability in large networks.

Complex systems can be abstracted to directed graphs where physical components are represented as nodes and interactions are represented as links. Because such systems are difficult to visualize, system-level topological properties such as connectivity distribution (1), clustering (2), and network motifs (3–6) are used to characterize the global organization of such systems. These properties, although useful, do not fully explain the underlying topology of large directed networks. For example, although many networks were found to display power-law connectivity distribution, such networks can still have low or high clustering. Similarly, characterizing small-size network motifs explains local network organization, but not how these motifs are juxtaposed to form higher-order structures. Enumeration of a collection of small-to-large network motifs may provide a better overview of how global topological properties can arise from local properties. Finding all network motifs is nondeterministic polynomial-time (NP) hard (7) and practically unfeasible for motifs of size greater than 10 nodes in moderate-size networks (e.g., networks with ≈2,000 nodes/links). Approaches to overcome this difficulty include sophisticated heuristics (8), parallelization (9), and sampling (5).

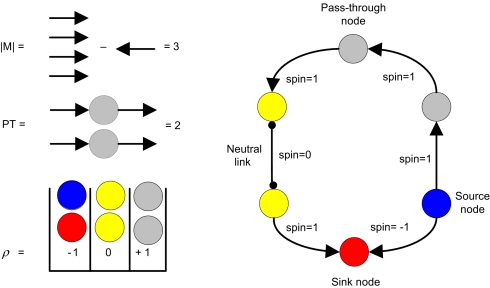
The task of detecting network motifs involves identifying and counting the motifs, classifying them into isomorphic groups, and determining whether the various types of motifs appear more abundantly in real networks as compared with shuffled networks created from the original topologies. Classifying network motifs into all their possible isomorphic groups quickly becomes intractable because the number of possible unique configurations grows exponentially with n. Thus, we focus here only on classifying cycles. The number of all possible n-node configurations for cycles with 2 types of links, directional and nondirectional (neutral), scales as 3ⁿ/2n [supporting information (SI) Appendix sections S1 and S5, Figs. S1–S4, and Tables S1–S6]. Hence, we developed a concise description for cycles using 3 different measures: (i) Nodes in a cycle can be “pass-through” (PT),“source,” or “sink” nodes, if the nodes in the cycle are not connected to a neutral link (Fig. 1). PT nodes have 1 input and 1 output, source nodes have 2 outputs, and sink nodes have 2 inputs. In the absence of neutral links, there are as many sink-nodes as source-nodes in a cycle, and therefore the number of PT plus twice the total number of source-nodes adds to the number of nodes in the cycle. (ii) When there are nondirectional or bidirectional links (heretofore called neutral links), as is the case in several of the networks studied, it is convenient to introduce another term to describe the relationship between pairs of links along a cycle: The link–link correlation ρ for a node is defined with “1” for PT, “−1” for sinks and sources, and “0” when at least 1 link connecting a node in a cycle is neutral (i.e., nondirectional or bidirectional) (SI Appendix section S7). This definition is consistent with a formal analogy between directed cycles and “spin” (or magnet) systems with circular topology (Fig. 1). (iii) Using the spin representation, we defined cycle “magnetization,” M, as the absolute value of the disparity between clockwise and counterclockwise links in the cycle. For spin systems, M is the magnitude of the sum of spins over all links in a cycle. The value of the link–link correlation ρ at a given node is the product of the spins coincident at that node. This measure formalizes the notion of how much coherence, or lack thereof, there is in the directionality of the directed links along cycles throughout the network. Thus, an alternative name for magnetization could be “cyclic directional coherence.” Networks with a high or low density of directed feedback loops will be characterized as “ferromagnetic” or coherent or “antiferromagnetic” or noncoherent, respectively. In this study, we first analyze this topological property across several real networks, and then explore the functional implications of such measurement, in particular its effect on the dynamics of networks.

Fig. 1.

Cycle characterization. The spins assigned to clockwise, counterclockwise, and neutral links are 1, −1, and 0, respectively. The directional coherence of the cycle on the right is characterized by having absolute value of magnetization |M| = 3, 2 nodes with link–link correlation ρ = 1 (PT nodes), 2 nodes with ρ = −1 (source and sink nodes), and 2 nodes with ρ = 0 (those with impinging neutral links).

To deal with the NP-hardness of identifying large cycles, we used a previously published algorithm (10), applied a sampling approach (6), and parallelized the code. We also implemented several enhancements to reduce execution time and used a high-performance massively parallelized supercomputer (BlueGene) for program execution (11) (SI Appendix section S2). Any cluster computer can be used to execute the motifs search program we developed.

Results

The networks we analyzed are as follows: Saccharomyces cerevisiae gene regulation (12) (hereafter called yeast), Escherichia coli gene regulation (4, 13) (E. coli), mammalian cell signaling (10) (signaling), Caenorhabditis elegans neuronal connectivity (14, 15) (neuronal), ecosystem food-web (16) (foodweb), functional brain map created from fMRI images (17, 18) (brain), small airplane air traffic control (19) (FAA), benchmark electrical circuit (20) (electrical), and internet connectivity map (tracert). For details and network construction and statistics see SI Appendix section S3 and Table S7.

For all of the networks considered, we analyzed n-node cycles with 3 ≤ n ≤ 15 (for some analyses 3 ≤ n ≤ 20). We did not explicitly include in our analysis self-loops and 2-node loops (Table S8). We first calculated the average of the absolute value of the magnetization 〈|M_n|〉 as a function of the number of nodes n. For cycles with no neutral links and random direction of links, it can be shown that:

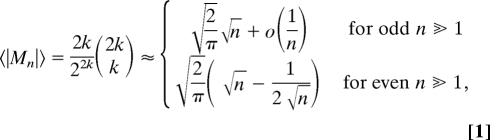where k is the integer part of (n +1)/2 (SI Appendix section S6 provides derivation of Eq. 1 and its generalization to the case of cycles with finite number of neutral links). Thus, for n = 3, 4, 5, 6, 7, 8, …. 〈|M_n|〉 is equal to the nondecreasing sequence 1.5, 1.5, 1.875, 1.875, 2.1875, 2.1875, … However, for the real networks, except for the FAA, we found that the observed 〈|M_n|〉 alternates as n increases (Fig. 2).

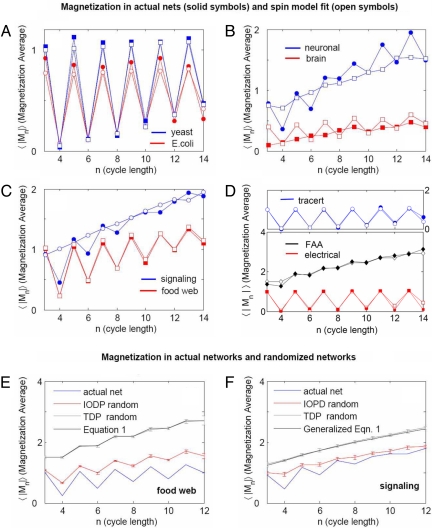
Fig. 2.

Directional coherence of cyclical motifs as measured by the magnetization. (A–D) Solid symbols correspond to the real networks and open symbols to the spin model fit. (E and F) The magnetization for the foodweb and signaling networks, the IODP randomization, the TDP randomization, and the fit from the independent-link model from Eq. 1 (E) and its generalization (F).

Spin Model for Antiferromagnetic Behavior of Cycles.

For several networks (e.g., yeast and E. coli), the magnetization approaches the minimal possible values of 0 for even cycles and 1 for odd cycles. This observation is inconsistent with the nondecreasing trend of Eq. 1, which assumes independence between neighboring links. To account for the dependence between neighboring links, we modeled the cycles as a system of interacting spins. Using statistical physics, an energy function H (21) can be defined as:

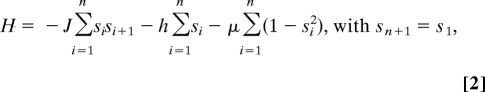where the ss are the spins (0, −1, +1), J is the parameter that determines the nature of the interaction between links (magnetic coupling), h is an external magnetic field, and μ is the chemical potential for neutral links. Because the energy tends to be minimized when the system is at equilibrium if J > 0 neighboring links are aligned, i.e., nodes in a cycle are PT (having 1 input and 1 output link), whereas when J < 0, neighboring links are pointing in opposite directions (sources or sinks in a cycle). In our case, h is set to 0 because of symmetry (SI Appendix section S4). The last term μ accounts for the presence or absence of neutral links in cycles.

We analytically computed 〈M_n²〉 as a function of J and μ for each network and fitted the best values over the range of cycle lengths 3 ≤ n ≤ 15. The results show that with the exception of the FAA network (J = 0, no link–link interactions), all other real networks have negative J (Table 1), indicating that cycles in real networks exhibit low magnetization and are antiferromagnetic; in other words, cycles tend to be “anticoherent”. The average of the absolute value of the magnetization as a function of cycle length for all of the networks, along with the spin model fit values taken from Table 1 are shown in Fig. 2 A–D. The fits obtained from the spin model capture the trend of the magnetization as a function of cycle length for all networks. However, with the neuronal, brain, and signaling networks, the fit is less precise. This discrepancy can be explained because of the abundance of neutral links in these networks. Except for the FAA (J = 0), the negative values of J suggest that nodes along cycles tend to be either sinks or sources. This hypothesis is confirmed by the histograms of ρ (Fig. S5). The result for the FAA (J = 0) is because of the fact that planes coming into airports are balanced with planes leaving airports.

Table 1.

The parameters J and μ fitted for the real networks using the spin-system representation for the cyclic motifs and the exclusion degree 〈x²〉

Network	J	μ	〈x2〉 in 10% most-connected nodes
Brain	−2.2	1.10	0.93
E. coli	−1.55	−1.00	0.86
Electrical	−1.35	−∞	0.52
Yeast	−1.25	−∞	0.96
Tracert	−1.35	−∞	0.27
Foodweb	−0.80	−∞	0.79
Neuronal	−0.65	0.20	0.32
Signaling	−0.35	−0.05	0.45
FAA	0.00	−∞	0.22

A negative J rewards source and sink nodes, whereas a negative μ indicates a tendency for cycles to exclude neutral links. The rightmost column is a measure of the exclusion degree 〈x²〉 averaged for the 10% most-connected nodes.

The realization that most real networks can be described by using a negative J suggests that nodes with high degree (hubs) are either mostly source or sink nodes. To confirm this conjecture, we defined a measure, the exclusion degree, that assesses the extent to which a node is exclusively a sink or a source: The difference between the in-degree (d_in) and out-degree (d_out), normalized by the maximum of d_in and d_out (neutral links are not included in this calculation). If nodes are purely sinks, having exclusion degree of x = 1, or purely sources x = −1, the average of the exclusion-degree coefficient 〈x²〉 would be 1. Alternatively, if the directionality is random, 〈x²〉 would be 0.33. The rightmost column in Table 1 shows 〈x²〉 for hubs, defined as nodes in the top 10th percentile based on connectivity degree (Figs. S6 and S7 and SI Appendix sections S8 and S9). Table 1 shows that a high exclusion degree corresponds with a high antiferromagnetic coupling (e.g., E. coli, yeast, and brain networks, with J < −1). Hence, source and sink hubs contribute to the antiferromagnetism observed in real networks (Fig. S8). However, it is possible that networks can still have a relatively high antiferromagnetic trend while displaying low 〈x²〉 as observed for the electrical and tracert networks.

To further explore additional contributions to the antiferromagnetism besides the bias of hubs, we compared the magnetization obtained in real networks with networks randomized by 2 different methods: (i) total degree-preserving (TDP) randomization, in which we keep the degree for each node and shuffle both the targets of sources' nodes and the directionality of links; and (ii) in- and out-degree-preserving (IODP) randomization, in which we keep the in- and out-degree for all nodes, shuffling only the targets (22) (SI Appendix section S10). These 2 methods of randomization preserve nodal-connectivity degree while destroying the global structure of the original networks. In particular, IODP conserves 〈x²〉, which is useful for exploring the contribution of other factors to antiferromagnetism. We compared the real and randomized network magnetization for all networks (Fig. 2 E and F and Fig. S9). Except for the FAA network, the magnetization level of the real networks is lower than the magnetization observed in all randomized networks. For the TDP randomization, the magnetization coincides with the model with statistically independent directed links in a cycle. This agreement is expected because directionality is completely destroyed with TDP randomization. The observation that real networks are more antiferromagnetic than networks with IODP randomization, which have a 〈x²〉 identical to that of the real networks, indicates that there are additional factors besides the hubs exclusion that contribute to the antiferromagnetic observation. Another contributing source to antiferromagnetism may be redundancy through bifans [motifs made of 2 source nodes targeting 2 target nodes (3)]. Using FANMOD (23), we confirmed that bifans are enriched in most networks (Fig. S10).

A further indication that the exclusion principle and the abundance of bifans contribute to the antiferromagnetic behavior of the networks studied was obtained by applying a protocol where in- and out-degree hubs and bifan are gradually removed (SI Appendix section S13). Indeed, we observed that surrogate networks generated by excising links from high-degree hubs display consistently higher magnetization than the original networks with all of the links implemented (Figs. S11 and S12). This trend is also present when nodes with high bifan degree are excised (Figs. S13 and S14), which emphasizes that antiferromagnetism is both a local and a global topological property.

Depletion of Feedback Loops.

The presence or absence of feedback loops can have profound effects on the dynamical behavior of systems (24–27), whereas a cycle that is not a feedback loop, having sinks and sources, is always linearly stable (Fig. 3A). A feedback loop of size ≥3, even if negative, can have an infinite region of parameter space in which it is linearly unstable (Fig. 3B and SI Appendix section S11). The observed antiferromagnetic organization of cycles means that cycles in real networks are mostly made of sinks and sources, reducing the chance for forming feedback loops. Because feedback loops can have dramatic effects on the behavior of dynamical systems, we further explored how the antiferromagnetic topology observed for real networks affects dynamic stability.

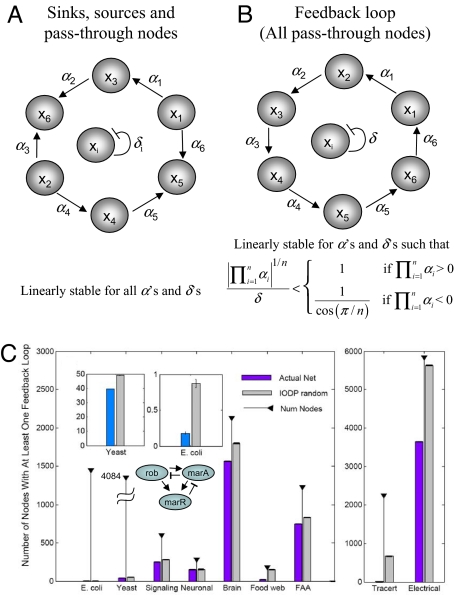
Fig. 3.

Nodes in feedback loops. (A and B) Linear stability conditions for generic cycles without (A) and with (B) feedback loop connectivity. (C) The number of nodes that participate in feedback loops for the 9 networks (purple bars) and their IODP-randomized versions (gray bars). The stems topped with solid triangles indicate the number of nodes in the corresponding network. (Insets) Enlargements of the yeast and E. coli results. For the latter, the only feedback loop found is shown.

Although antiferromagnetism suggests depletion of feedback loops, negative J does not reveal how many feedback loops “survive”. For this quantitation, we computed the number of nodes involved in at least 1 feedback loop of size 3 or greater. For networks with undirected/bidirectional links, we randomly assigned direction to these links, biasing the direction based on existing in- or out-degree, and computed the average and standard error resulting from N = 1,000 realizations. As a control, we also computed the number of nodes involved in feedback loops in the IODP-randomized networks (Fig. 3C). The number of nodes affected by feedback loops relative to the total number of nodes in the network is the smallest for the E. coli (0.05%) and yeast (1%) networks. All networks, biological and engineered, have a significantly smaller number of nodes involved in feedback loops compared with their randomized counterparts [one-tailed t test P values of <6.3 × 10⁻²³ (E.coli), <1 × 10⁻¹⁰⁰ (yeast), < 1 × 10⁻¹⁰⁰ (signaling), 3.3 × 10⁻⁷³, (neuronal), <1 × 10⁻¹⁰⁰ (brain), <1 × 10⁻¹⁰⁰ (foodweb), <1 × 10⁻¹⁰⁰ (electrical), <1 × 10⁻¹⁰⁰ (tracert), and <1 × 10⁻¹⁰⁰ (FAA)] (Fig. 3C). It appears that 1 common design principle developed to accomplish stability in biological and engineered networks could be reduction in feedback loops, thereby lowering the potential of destabilization of the systems.

The distribution of feedback loops of lengths 1 and 2 was also computed and compared with larger size loops (Fig. S15). For some of the networks (E. coli, foodweb, tracert) the distribution is a decreasing function, with most nodes being self-regulatory, some participating in 2-node loops, and very few being part of 3 or more node loops. For the yeast, signaling, FAA, and electrical networks, however, nodes are mostly affected by longer feedback loops. Even though the inclusion of 1- and 2-node loops (disregarded in the process of redirecting neutral links) could change the absolute number of nodes affected by feedback loops shown in Fig. 3C, the 1- and 2-node loops are treated exactly the same when creating the IODP-randomized networks. Therefore, the conclusion of Fig. 3C, that feedback loops are minimized, is not changed by the exclusion of feedback loops of sizes 1 and 2.

Dynamic Stability Because of Depletion of Feedback Loops.

To test whether real networks, having fewer nodes in feedback loops compared with IODP randomizations, tend to be more dynamically stable, we analyzed the networks as dynamical systems. To simulate the dynamics of the networks, we made the assumption that each node has an associated dynamic variable, y_i. In the signaling network, this variable could be, for example, the level of a protein that is dynamically regulated by synthesis and degradation. We constructed a dynamical system of the form

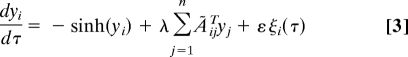for 1 ≤ i ≤ n (SI Appendix section S12 has justification for Eq. 3). Although this equation models the network dynamics around a fixed point, large deviations from fixed points (if they exist) do not produce divergences because of the dissipative nature of the sinh term. Therefore, these equations can capture the effects of linear instabilities on the collective dynamics of coupled nodes beyond small perturbations around a fixed point. However, specific behaviors such as intermittent bursts, observed in neuronal networks, are not intended to be captured by this simplified dynamical modeling.

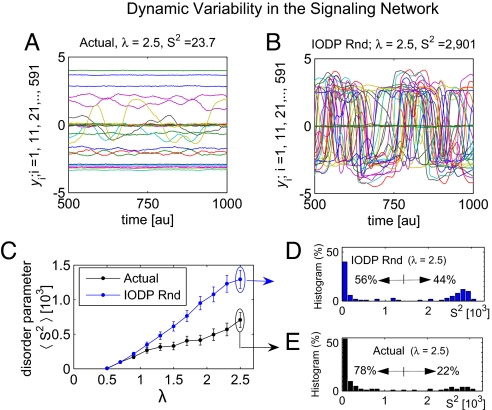
The magnitude of the interaction between different nodes is given by λ, and the identity of the interacting nodes is determined by the nonzero elements of the adjacency matrix Ã, which in the case of the signaling is either positive or negative. Each node is affected by a white-in-time noise εξ_i(t), whose magnitude ε was chosen to be 0.05 as a mid-range value after initial parameter variation analysis, because it provides a reasonable window within which dynamic stability can be assessed. A representative simulation for the signaling network, where undirected links were randomly assigned a direction for λ = 2.5, is shown (Fig. 4A). All dynamical simulations were performed on networks where neutral links where randomly redirected as described above. To quantify the amount of variability in the y_is around their stationary averages, we define the quantity S² as the sum over all of the variances σ_i² ≡ 〈(y_i − 〈y_i〉)²〉 of y_is. We call S² the disorder parameter, because it represents the dynamical disorder of the entire network. For λ = 0, it can be analytically shown that σ_i² ≡ 〈(y_i − 〈y_i〉)²〉 = ε²/2, and therefore for the 599 nodes in the signaling network, we have S² = 0.75. The S² value for the simulation for λ = 2.5 was 23.7 (Fig. 4A). Comparing this value with the representative example simulation for the IOPD-randomized signaling network, it is clear that the variability in this latter case is substantially larger than that for the actual signaling network (Fig. 4B). Indeed, S² was 2,901 for λ = 2.5. This observation constitutes one representative example that the real signaling network gives rise to less disordered dynamics compared with shuffled networks. The average disorder parameter S² over 100 different assignments of directions to undirected links (black line), with the error bars indicating the standard errors, shows that the average disorder parameter S² grows from 0.75 to 707, with λ ranging from 0 to 2.5 (Fig. 4C). For the IODP-randomized networks, the variability grows from 0.75 to 1,294 for λ ranging from 0 to 2.5. The differences between the 2 curves begin to be statistically significant with a P value of <10⁻³ when λ ≥ 1.4 (Fig. 4C). It is relevant to note that the averages of S² come from bimodal distributions (Fig. 4 D and E). These 2 distributions are different at a P value of 5 × 10⁻³ (2-sample Kolmogorov–Smirnov test). The bimodality of the S² distribution indicates that there are 2 regimes of topologies: those that support relatively stable dynamics with low disorder parameter (S² < 1,000) and those that support relatively unstable dynamics with high disorder parameter (S² > 2,000). Approximately 80% of the topological realizations for the actual signaling network show low disorder parameter. In contrast, only 56% of IODP-random topologies yield the less disordered dynamics. The IODP-randomized networks are on average twice as often dynamically disordered compared with the real signaling network topology. Hence, the dynamics of the real signaling network are less chaotic than the dynamics of networks with similar local (but not global) topological properties. Similar analyses were conducted for all other networks. In all cases, the actual networks were found to be dynamically more ordered (according to the disorder parameter) than their shuffled counterparts (Fig. S16).

Fig. 4.

Dynamics of the signaling network. (A and B) Simulations of the dynamics (Eq. 3) endowed to the actual signaling network (A) and the IODP-randomized version of this network (B). au, Arbitrary units. The enhanced instabilities in B are typical, as quantified in C, with the parameter S² defined as the sum of the variances over all of the dynamic variables for the actual network (black line) and the IODP-randomized (blue line) as a function the interaction strength between nodes, λ. The error bars in C correspond to the standard error in 100 simulations. For λ = 2.5, the distribution of S² shows a bimodal distribution both for the actual (D) and the IODP-randomized (E) networks.

The stability of the dynamical system modeled using Eq. 3 cannot be accounted for by Gershgorin's diagonal dominance condition, which states that if the coupling between “neighboring” nodes is sufficiently small, then the system is linearly stable (28). Indeed, the Gershogorin theorem predicts the same stability for both actual and IODP-randomized networks; the higher disorder in the IODP-randomized networks is because of the nonlocal topological changes induced by the randomization.

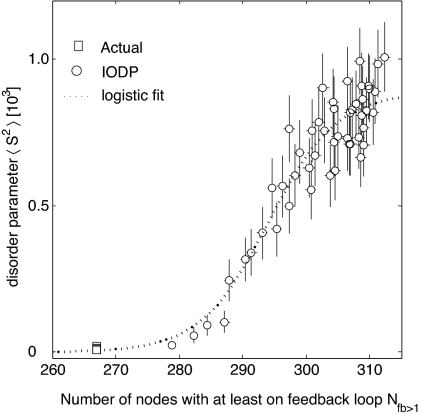
As was previously shown, one difference between the real networks and the IODP-randomized networks is the number of nodes involved in feedback loops. We expect that the number of nodes involved in feedback loops in real biological networks will be less than their randomized counterparts. Indeed, the signaling network has 268 nodes involved in feedback loops (Fig. 3C), whereas the IODP network that produces the unstable dynamics in Fig. 4B has ≈320 nodes involved in feedback loops. This difference is consistent with our hypothesis that networks with fewer nodes involved in feedback loops have a wiring configuration that gives rise to more stable dynamics (Fig. 5).

Fig. 5.

Average of the disorder coefficient S² as a function of N_fb>1, the number of nodes in at least 1 feedback loop (open symbols), and a logistic fit (dotted line, r = 0.93), for the signaling network and its IODP-randomized surrogates. Error bars indicate the standard error around the mean indicated by the open symbols.

To further investigate this claim, we performed gradual, partial IODP randomizations of the signaling network, thereby creating an ensemble of networks. The networks in this ensemble have nodes participating in at least 1 feedback loop, N_fb>1, ranging from ≈270 to ≈320. For each of these networks we simulated the dynamics to compute the disorder coefficient S², plotted as a function of N_fb>1 (Fig. 5). A logistic relationship can be fitted (r = 0.93) to the dependence of the average S² as a function of the number of nodes involved in at least 1 feedback loop. Two conclusions can be drawn from the results: First, in all randomizations, the number of nodes involved in feedback loops was greater than 268 (the value observed for the real network), suggesting that real network topologies are likely to exist at, or close to, the minimal possible number of nodes participating in feedback loops consistent with the local connectivity. A second observation is that on average, the disorder coefficient S² increases with the number of nodes associated with feedback loops. Conversely, removing feedback loops has the effect of decreasing the disorder parameter (Fig. S17). Together these observations suggest that keeping the number of nodes associated with feedback loops close to a minimum has a stabilizing effect on the dynamics of the signaling network. Similar results were observed for all other networks (Fig. S16).

Discussion

Biological regulatory networks may have evolved to reduce the number of feedback loops because feedback loops, positive or negative, can be destabilizing. It has been hypothesized that biological networks have minimized the number of feedback loops for driving connections in the mammalian visual cortex (29). This observation was generalized to form the conjecture that driving connections between cortical areas do not form higher-order loops, because such excitatory loops would result in uncontrolled cortical oscillations. At the same time, there are a few circuits specifically designed to produce oscillations through feedback loops, such as the central pattern generators required for locomotion (30). Hence, when present, feedback loops are required for specific system behaviors. To quantify the potential effects of feedback loops in the dynamics of a network, we represented the networks as a generic dynamical system resembling a linearized version of the full dynamics around a stationary point saturated by nonlinearities to avoid divergences. We observed that networks with fewer nodes involved in feedback loops (Figs. 4 and 5 and Fig. S16) are more stable than corresponding shuffled networks with more nodes involved in feedback loops. It appears that carefully placing feedback loops is a guiding design principle of complex biological networks.

Even though we have simulated a fixed network topology, it is clear that for some of the biological networks, such as the signaling and transcription networks where the spatiotemporal consideration is omitted (31), our analysis still captures important qualitative dynamical concepts. Indeed, if the entire network is antiferromagnetic with few feedback loops, individual modules within the network, i.e., in a particular cell compartment, or at a particular time scale, would have to also be antiferromagnetic, because it is a subset of the entire antiferromagnetic network assembly.

In this study, we characterized the ensemble of cyclic motifs by using properties such as magnetization and edge–edge correlation. This approach helped us understand higher-order structures in real networks. Our ability to explain the topological properties of cyclical motifs by using a 2-parameter model from statistical physics provides a way to understand the topological organization of large-scale real networks. The resulting antiferromagnetic order in 8 of the 9 networks we analyzed yields, as a natural outcome, depletion of feedback loops. Such a depletion results in a modular architecture that ensures that information processing remains local. Overall, this architecture leads to complex systems with substantial dynamic capabilities that are nevertheless relatively dynamically stable.

For some of the networks studied, the interactions between components might be time lagged (e.g., for gene regulatory networks). We previously showed (32) that the linear stability of feedback loops with time delays is equivalent to the linear stability of a longer feedback loop without time delay. Therefore, the effect of adding time delays on the dynamics based on Eq. 3 will result in a less stable system than a system with no time delays with the same value of λ. However, the effect of destabilizing the time delays would be identical for both the actual networks and the IODP-randomized networks.

It can be argued that some additional feedback loops will be at work in the signaling network when the gene transcriptional network is combined with the signaling network. However, it is important to consider that in eukaryotic cells there is a defined time-scale separation between transcriptional (slow) and signaling (fast) processes. Therefore, the study of the signaling network should be considered in a fast time scale, where the feedback produced through transcriptional processes has not yet taken place.

Although several of the networks analyzed can be considered completely mapped (i.e., foodweb, electrical, C. elegans neuronal), other networks are incomplete. Our analysis indicates that the antiferromagnetic property of many real networks is a robust property and will likely not change as more information is acquired, given that even incomplete networks provide considerable sampling of the entire real topology.

In conclusion, our ability to identify large cycles in real networks, using a powerful high-performance computing platform, has helped us to characterize the ensemble of cyclic motifs in real directed networks. Our characterization of cycles has allowed us to relate local topological properties with global network structure and function, thus providing an initial view of how complex biological and engineered systems may be configured.