Local kinetic measures of macromolecular structure reveal partitioning among multiple parallel pathways from the earliest steps in the folding of a large RNA molecule

Summary

At the heart of the RNA folding problem is the number, structures, and relationships among the intermediates that populate the folding pathways of most large RNA molecules. Unique insight into the structural dynamics of these intermediates can be gleaned from the time-dependent changes in local probes of macromolecular conformation (e.g. reports on individual nucleotide solvent accessibility offered by hydroxyl radical (•OH) footprinting). Local measures distributed around a macromolecule individually illuminate the ensemble of separate changes that constitute a folding reaction. Folding pathway reconstruction from a multitude of these individual measures is daunting due to the combinatorial explosion of possible kinetic models as the number of independent local measures increases. Fortunately, clustering of time progress curves sufficiently reduces the dimensionality of the data so as to make reconstruction computationally tractable. The most likely folding topology and intermediates can then be identified by exhaustively enumerating all possible kinetic models on a super-computer grid. The folding pathways and measures of the relative flux through them were determined for Mg²⁺- and Na⁺-mediated folding of the Tetrahymena thermophila group I intron using this combined experimental and computational approach. The flux during Mg²⁺-mediated folding is divided among numerous parallel pathways. In contrast, the flux during the Na⁺-mediated reaction is predominantly restricted through three pathways, one of which is without detectable passage through intermediates. Under both conditions, the folding reaction is highly parallel with no single pathway accounting for more than 50% of the molecular flux. This suggests that RNA folding is non-sequential under a variety of different experimental conditions even at the earliest stages of folding. This study provides a template for the systematic analysis of the time-evolution of RNA structure from ensembles of local measures that will illuminate the chemical and physical characteristics of each step in the process. The applicability of this analysis approach to other macromolecules is discussed.

Introduction

The ability of polypeptides and polynucleotides to fold into discrete tertiary structures is central to their biological function^1-4. Some macromolecules (e.g. small proteins) adopt their native structure through a simple two-state folding process without the formation of discernible intermediates^5-7. In contrast, a defining characteristic of RNA folding is the presence of multiple, highly populated and long-lived intermediates^8-12. Navigation through the rugged RNA folding landscapes is at the heart of the RNA folding problem. The ability to represent and model RNA folding landscapes is key to the development of a comprehensive understanding of the principles underlying RNA folding.

Local probes of macromolecular structure are measurements that are sensitive to the environment of a relatively small region within a macromolecule. These include, but are not limited to, NMR deuterium exchange and shift perturbation analysis^13,14, Fluorescence Resonance Energy Transfer (FRET)¹⁵, and RNA/DNA protein footprinting^16,17. The separate transitions reported by individual probes yield unique insight into folding intermediates. While simultaneous acquisition of many unique local transitions provides a cornucopia of information, creating an accurate global description of folding that remains faithful to local details is very challenging. We are particularly interested in one such local measure: the quantization of the solvent accessible surface of RNA or DNA with single nucleotide resolution by hydroxyl radical (•OH) footprinting. In the case of RNA folding, •OH footprinting effectively discriminates the inside from the outside¹⁸ of a molecule as a function of time or a thermodynamic variable^12,19.

In studies of the cation-dependent folding of the Tetrahymena thermophila group I intron, tens of discrete regions of •OH protection or enhancement were separately identified and quantified as a function of time^17,20,21. Such an ensemble of •OH protection progress curves can help define and structurally characterize the folding intermediates of a large RNA molecule. If folding is a two-state transition, then all of the •OH protection progress curves are identical; such behavior has not been observed for the wild type T. thermophila group I intron. Instead heterogeneity among the progress curves is observed as illustrated in Figure 1 due to the presence of intermediates along the folding pathways of the RNA molecule^22-24. However, the observed •OH protection progress curves are not completely heterogeneous (Figure 1b). Among the thirty •OH protections identified for the T. thermophila ribozyme are regions of the polynucleotide that are distant in primary sequence but juxtaposed in the folded three-dimensional structure. Similar progress curves can be found among participants in a tertiary contact (i.e. a tetraloop – tetraloop receptor motif) or within structural domains^25,26. Understanding how individual RNA structural elements define an RNA folding pathway is a key goal in the analysis of time-resolved •OH footprinting data. A recent time-resolved •OH footprinting study of the RNA polymerase/T7A1 promoter complex illustrates how site-specific progress curves can yield kinetic insight into molecular recognition events¹⁶.

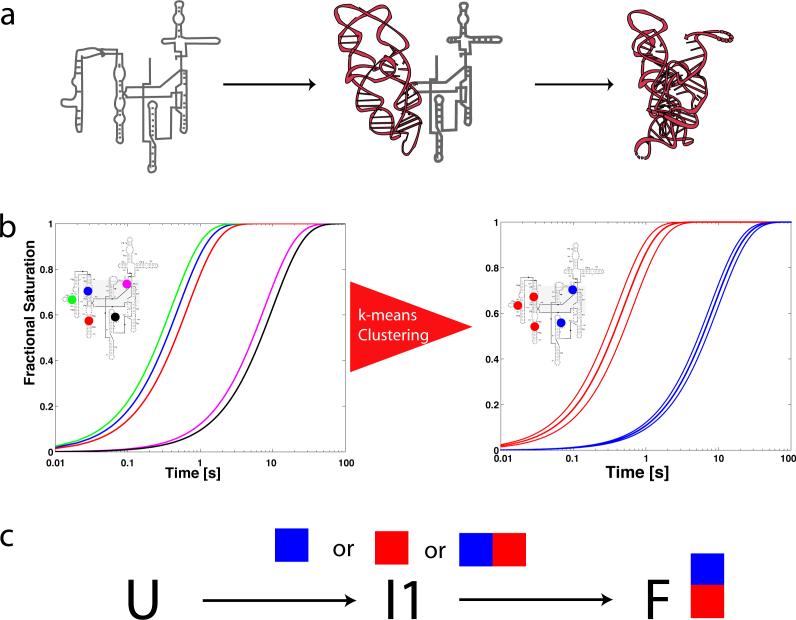
Figure 1.

Illustration of the effect of intermediates on progress curves for local probes of macromolecular structure. a) In this example a single intermediate is present along the folding pathway of the molecule, in which the brown (P4-P6) domain folds first. b) If five sites on the molecule were monitored with •OH footprinting (in this case colored blue, green, red, magenta and black) one would observe heterogeneous progress curves. The thick lines in the right hand plot indicate average time-progress curves based on a k-means clustering of the data. c) Once the data are clustered the problem of reconstructing the kinetic model that best fits the data is solved by exhaustively fitting all possible mappings of intermediates to progress curves. In this very simple case, three mappings must be tested (blue curve to I1, red curve to I1, or blue and red curve to I1).

Because of the great difficulty in creating and validating coherent quantitative models, the interpretation of time-resolved •OH footprinting data published to date has been qualitative and phenomenological in nature. The emergence of inexpensive parallel computers now provides the ability to tackle problems of unprecedented size and complexity. In this paper, we present an exhaustive optimization strategy to determine the best-fitting kinetic models for particular RNA folding reactions. These models define the folding pathways of RNA molecules and allow for a quantitative comparison of the flux through these different pathways. The flux analysis in turn allows prediction of the number of significant folding pathways and their relative importance.

To exploit the power of this combined experimental and computational approach, we have analyzed the folding of the T. thermophila group I intron upon the addition of either sodium or magnesium ions^10,20 from a common initial condition with the goal of identifying and characterizing the dominant folding pathways for each reaction. The resulting kinetic models make quantitative predictions of the time-evolution and structural characteristics of the folding intermediates providing a basis for the rational design of single-molecule experiments and direct comparison with rates predicted by molecular simulation. Given the exhaustive nature of the optimization approach, these results also help establish the limits of detection of the experiment. The quantitative comparison of folding pathways provides further insight into the role of divalent versus monovalent cations in RNA folding. Furthermore, it establishes a framework for the computational analysis of collections of local measures of macromolecular conformational change.

Results

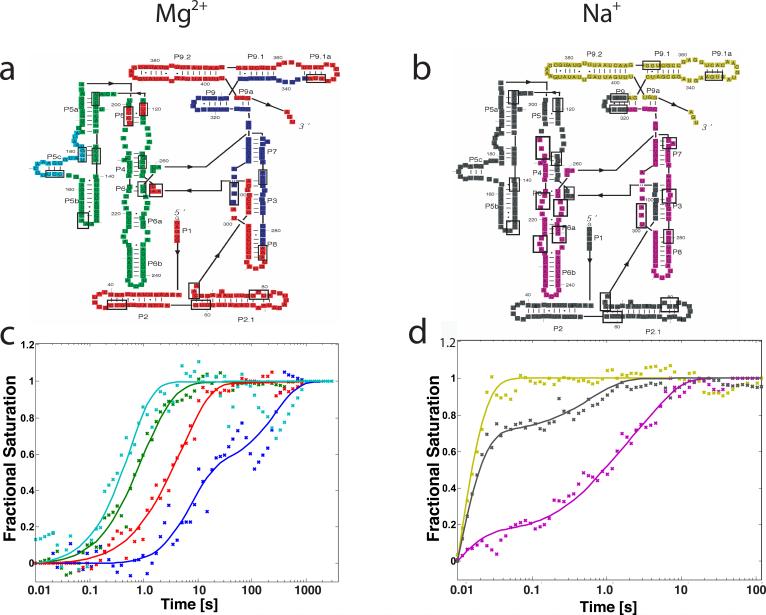
Kinetics progress curves reporting local changes in the solvent accessibility of the polynucleotide backbone during Mg²⁺- and Na⁺-dependent folding of the T. thermophila ribozyme from a common initial condition were acquired by synchrotron X-ray (hydroxyl radical) footprinting^10,17,27. The local sites chosen for this analysis (Figure 2a, 2b and Supplementary Material) exhibit robust changes in their •OH radical reactivity under both solution conditions that correlate with the inside vs. outside predictions of the molecular model of the ribozyme^10,27,28. Two to four independent progress curves were collected for each •OH protection included in this analysis. The data were binned, normalized and averaged as described in the Materials and Methods yielding a set of progress curves amenable for clustering.

Figure 2.

a) and b) Colored secondary structure diagram representation of the L-21 T. thermophila group I intron. Colors represent regions of molecule exhibiting similar time-progress curves during folding in the Mg²⁺ and Na⁺ mediated folding, as determined by k-means clustering of site-specific progress curves. Boxes indicate sites of protection that were monitored on the molecule, these are also listed in the Supplementary Material. c) and d) Best fitting kinetic model predictions (lines) to time-progress curves for the Mg²⁺ and Na⁺ mediated folding, respectively. Fractional saturation calculated based on hydroxyl radical footprinting protection data is plotted with × symbols. Colors correspond to the different regions of the molecule as defined in a) and b).

Clustering of time-progress curves

K-means clustering identified the •OH protections characterized by similar time-progress curves. The number of statistically significant clusters was determined by the Gap statistic²⁹ as described in the Materials and Methods. A more detailed analysis of cluster dispersion is provided in the Supplementary Material. Four distinct clusters emerge from the Mg²⁺-mediated folding reaction data set¹⁰. These clusters correspond to the P5c helix, P4-P6 stem, periphery and catalytic core of the molecule (Figure 2a cyan, green, red and blue, respectively). For the Na⁺-mediated folding reaction, three clusters emerge corresponding to the P9 peripheral helix, P5abc and the P2 peripheral helix, and the P6 helix and catalytic core (Figure 2b yellow, gray and magenta, respectively).

We computed time progress-curve cluster centroids for the Mg²⁺- and Na⁺-mediated folding reactions that represent the average folding behavior of each group of •OH protection progress curves (Figures 2c & d). For example, the blue data in Figure 2c corresponds the time-evolution of the •OH protections indicative of formation of the catalytic core of the ribozyme. As was previously noted, Na⁺-mediated folding of the T. thermophila ribozyme is much magnitude faster than the Mg²⁺-mediated folding reaction at this experimental condition (Figures 2c & d)^10,30,31. In addition, the structural hierarchy of the clusters and the shapes of the time-progress curves are unique for each cation. While such differences are readily discernible from the model-independent clustering analysis, it is not clear whether a common kinetic model underlies Mg²⁺- and Na⁺-mediated folding. For this reason, we constructed and tested kinetic models based upon the clustered •OH progress curves described above.

The number of clusters restricts the number of required kinetic intermediates

A fundamental problem for the determination of a unique kinetic model describing any folding reaction is the explosive combinatorial number of possible model topologies as the number of proposed intermediate species increases (Materials and Methods, Equation 3). The combinatorial nature of the problem stems from the fact that a priori, the mapping of clusters of progress curves to the reaction intermediates is not known (Figure 1c). Therefore, all possible mappings must be tested to determine the best fitting model with certainty. While the definition of intermediate species from global folding measures would typically imply distinct kinetic phases, local progress curves such as those shown in Figure 2 provide a set of independent folding measures that, in principle, could all follow their own particular time course. Critical to our approach is the assumption that these local curves can be combined to create the major “modes” of folding for different parts of the overall structure. This assumption is supported by the data, as it is possible to identify cluster boundaries such that the within cluster dispersion (W_k) is significantly smaller then the inter-cluster dispersion (see Supplementary Material).

Since any reaction must have an initial state and a final state (referred to as unfolded (U) and folded (F) herein), a kinetic model must include at least one intermediate to predict two progress curves clusters (Figure 1). Extrapolating from this example it becomes apparent that to accommodate k progress curves, at least k – 1 intermediates are required in the kinetic model. Since each intermediate can potentially be mapped to one or more progress curve clusters, the combinatorial explosion defined by Equation 3 becomes the next hurdle to overcome in the quest for a solution to the RNA folding problem.

Model topology resolution through parallel optimization

All possible mappings of intermediates to progress curves must be tested to rigorously determine the kinetic model that best fits a given set of data. Since four clusters were determined for the Mg²⁺-mediated folding reaction, at least three intermediates are required to model the data. Equation 3 with k = 4 and I = 3 yields 680 unique model topologies. Least squares optimization was used to fit each kinetic model to the data shown in Figure 2c. The optimizations were distributed to a large computational grid, running a single optimization per node. Table 1 summarizes the root mean square error (RMSE) for the top three kinetic models tested in each folding reaction. As can be seen in Row C, the RMSE of the best model is 13.4% better than the second best model. The predicted time-progress curve evolution for the second and third best fitting models are shown in Supplementary Material Figure S3a and S3b, respectively. For the Na⁺-mediated folding reaction solution, k = 3 and thus I ≥ 2. The best fitting model in this case has a 30.6% better RMSE than the second best fitting model (Table 1, Row E, and Supplementary Material Figure S3c and S3d). Therefore, a single kinetic model best fits each of the folding reactions.

Table 1.

Summary of RMSE values for testing of different kinetic models

	Folding Reaction	k¥	I¥	N¥	RMSE of best model	RMSE 2nd best model	RMSE 3rd best model	% RMSE 1st to 2nd
A	Mg2+	3	2	28	0.98	2.03	2.76	107%
B	Mg2+	3	3	84	0.95	1.02	1.08	7.4%
C	Mg2+	4	3	680	1.72	1.95	2.05	13.4%
D	Mg2+	4	4	3060	1.69	1.72	1.73	1.8%
E	Na+	3	2	28	0.36	0.47	0.98	30.6%
F	Na+	3	3	84	0.34	0.36	0.37	5.9%

^¥k, I and N are the number of clusters, the number of intermediates in the model, and the total number of models tested, respectively.

Gray shading indicates best models based on Gap Statistic analysis²⁹.

To establish whether a better fit to the data is possible by adding additional intermediates to the kinetic models, least squares optimizations were repeated with I = 4 and 3 for the Mg²⁺- and Na⁺-mediated folding reactions, respectively (Table 1, Rows D & F, respectively). Adding an additional intermediate does not significantly lower the RMSE of the best fitting kinetic model with respect to the original analysis (Table 1; 1.7% and 5.3% for the Mg²⁺- and Na⁺-mediated reactions, respectively). The top three models in both cases have similar RMSE, consistent with the data being unable to distinguish among more complex models. We conclude from this analysis that the minimal number of intermediates in the kinetic models defined by Equation 3 is necessary and sufficient to describe the data.

Kinetic models predict the time-dependent evolution of the different species

The lines in Figures 2c and 2d depict the time course of the progress curve clusters predicted from the models with the minimum number of intermediates for the Mg²⁺- and Na⁺-mediated folding reactions that had the lowest RMSE (Table 1, Rows C and E, respectively). The biphasic behavior of some of the different progress curve clusters is well reproduced by the kinetic models (for example the gray progress curve in Figure 2d, which corresponds to the P2 and P5abc region of the T. thermophila ribozyme).

Numerical integration of the constitutive differential equations (Equation 2) defining the best fitting kinetic models yields the time-evolution of the different species (Figures 3a and 3b) that begins to paint a quantitative picture of the folding landscape of the ribozyme. Graphical representations of the kinetic models are shown in Figures 3c and 3d for the Mg²⁺- and Na⁺-mediated folding reactions, respectively. Each node on the graphs represents a species in solution, and each arrow an inter-conversion rate. The coloring scheme indicates the mapping of intermediates to specific progress curves. For example, when I3 (Figure 3c) is present in solution, protections are observed in the cyan, green and red regions of the molecule (indicated by a cyan, green and red square), which correspond to the P4P6 and peripheral regions of the molecule. Thus, for each intermediate a specific set of structural characteristics is predicted.

Figure 3.

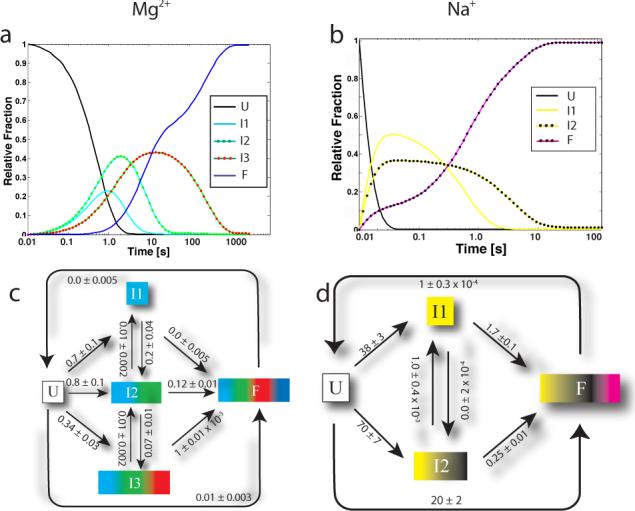
a) and b) Time-evolution of the different species in solution for Mg²⁺ and Na⁺ mediated folding, respectively. c) and d) Best fitting kinetic model diagrams for Mg²⁺ and Na⁺ mediated folding, respectively (rate constants are in s⁻¹). Errors on the kinetic parameters were computed using a bootstrap procedure and can also be found in the Supplementary Material. Reverse rates were constrained to zero as an equivalently good fit to the data was obtained with and without these constraints. The I1→I3 rate is not shown for clarity but is 0.3±0.02 s⁻¹. All other rates not shown are ≤0.01 s⁻¹ and are reported in the Supplementary Material Tables.

Pathway flux analysis

Inspection of the rate constants in Figures 3c and 3d suggests the presence of multiple folding pathways. For example, the rates of conversion of U→I1 and U→I2 for Mg²⁺-mediated folding (0.7 and 0.8 s⁻¹, respectively) give rise to similar initial time evolution curves for I1 and I2 in Figure 3a. Furthermore, it is evident that the main folding pathway for the T. thermophila group I intron for Mg²⁺ mediated folding is U→I2→F, as the I2→F rate is significant (0.12 s⁻¹). While the movement of molecules through the model can be inferred by consideration of the rate constants, an analysis of the reaction flux, where rate constants are transformed into transition probabilities as indicated in Equation 4 (Materials and Methods), yields a quantitative assessment of the pathways that dominate the folding reaction.

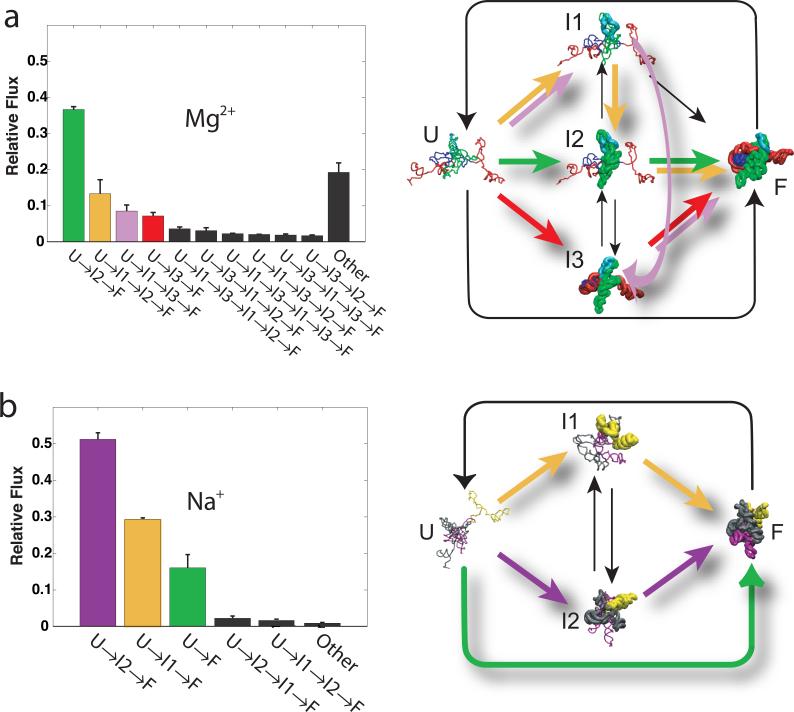
We computed the relative flux through the different possible folding pathways by numerical simulation. There are, in theory, an infinite number of possible pathways through the graphs shown in Figures 3c and 3d. The stochastic approach used preferentially samples the most probable pathways to give an accurate measure of their flux. For both solution conditions, the folding of 10⁵ independent molecules was simulated and the different pathways clustered. The histograms shown in Figures 4a and 4b illustrate the relative flux through the ribozyme's most common folding pathways during Mg²⁺- and Na⁺-mediated folding, respectively.

Figure 4.

Relative flux through the different major folding pathways of the T. thermophila group I intron sorted from highest to lowest. Each intermediate is illustrated as a cartoon structure in which the protected regions of the molecule are rendered in the native conformation (thick lines) and the unprotected regions are rendered with formed secondary structures, but arranged in a random manner (thin lines). Thus, U is shown with all thin lines because only the secondary structure is formed. In contrast, F has thick lines because it is entirely in the native conformation. The intermediates (I1, I2, I3) are shown with a mixture of thick lines (for native protections formed) and thin lines (for regions of the molecule not adopting native protections). These structures are shown for illustration purposes only. Colored arrows illustrate the dominant folding pathways. a.) and b.) correspond to Mg²⁺ and Na⁺ mediated folding reactions. The “Other” bar in the histograms represents the relative flux through alternative pathways with flux below 1%. Error bars were computed based on three standard deviations for 10³ repeats of flux analysis.

The most populated folding pathway during Mg²⁺-mediated folding is U→I2→F (Figure 4a). The regions •OH of protection mapped to the I2 intermediate correspond to the P4-P6 domain of the ribozyme. This correspondence is illustrated by the structural models represented in Figure 4a. Therefore, the kinetic model predicts that formation of P4-P6 occurs early in the folding process. Although the U→I2→F pathway might appear dominant, only 36% of the molecules fold through it. The second most common pathway is U→I1→I2→F (15% flux), where P5c precedes formation of P4P6. The remaining 49% of the flux is distributed over many other pathways including more complex pathways such as U→I1→I3→I1→ I2→F. Insignificant flux passes through the two-state pathway (U→F) during this Mg²⁺-mediated reaction.

In contrast, three pathways dominate Na⁺-mediated folding (Figure 4b). The most populated pathway is U→I2→F with over 50% of the relative flux. This pathway involves initial formation of the P9, P2 and P5abc (gray and yellow structural regions in I2, Figure 4b) followed by coincident formation of the core and P6 (magenta region). The second most common pathway is U→I1→F. This pathway involves initial formation of the P2 helix protections (yellow region) followed by coincident formation of the catalytic core, P6, and P5abc regions (grey and magenta). The two-state folding pathway (U→F) accounts for about 18% of the total flux in Na⁺-mediated folding. Comparing Figures 4a and 4b it is evident that both the dominant pathways and the structures of the intermediates are different in Mg²⁺ versus Na⁺ mediated folding.

Analysis of the kinetic model's sensitivity to k

The number of clusters k defines the minimum number of intermediates (k-1) required to kinetically model folding of an RNA. Values of k are determined using the Gap Statistic²⁹ which analyzes the relative within cluster dispersion and thus identifies the optimal value of a given data set. The Gap Statistic analysis will yield a larger value of k when more precise data allows the resolution of more clusters. Since more information is contained within a more complex model (when it is robustly defined by the data) we deemed it important to assess the effect of the resolved value of k on the predicted kinetic models as a function of data precision.

A Mg²⁺-mediated folding reaction data set acquired in 1998²⁰ with less precisely defined time progress curves was clustered and analyzed as described above. In this case, the Gap statistic revealed only three (k=3) clusters (See Supplementary Material, Figure S2); the P5c •OH protections are not resolved from the remainder of the P4P6 domain (green). These data were tested against the 28 models possible with the minimum number of intermediates (I=2) consistent with two clusters. The average time-progress curves generated from the three clusters are shown in the Supplementary Material with the simulated curves generated from the model with the lowest RMSE (Table 1, Row A). The RMSE for this model is 107% better than the next best model, identifying it as the best fitting model (Table 1 and Supplementary Material Figure S3). Repeating the analysis with an additional intermediate (k=3 and I=3; Table 1, Row B) did not improve the quality of the fit, showing that three intermediates is sufficient to accurately model this data set (Table 1, Row B).

The time evolution of the intermediate, initial and final species as well as the best-fit model is summarized in Supplementary Material Figure S2. Analysis of the clustered protections reveals that the I2 and I3 intermediates are structurally identical in both the two and three intermediate models. The relationships between the two intermediate model resolved from the less precise data to the three intermediate model (Figure 4a) are most readily visualized in the analysis of the flux through the pathways (Supplementary Material Figure S2). The consistency of the analysis of the two sets of data is seen in the emergence of the flux through the separately distinguished P5c helix cluster from that of the P4P6 cluster. The flux of molecules in the U→I2→F pathway for the two intermediate model splits between the U→I1→F and U→I1→I2→F pathways in the three intermediate kinetic model. It should be noted that the model resolves a very subtle difference in the time progress curves as the P5c and P4-P6 clusters; these clusters differ by only a factor of two in their rates. The Gap statistic is thus an effective tool to determine the sensitivity limit of models to the data and thus insures that kinetic models do not attempt to over interpret the experiments.

Time evolution of catalytic activity

The models derived above from the •OH footprinting data predict the time evolution of the native structure. An advantage to studying the folding of a molecule with catalytic activity is that this activity can be used as an independent measure of the formation of the native structure. As an independent evaluation of the kinetic models for Mg²⁺-mediated folding, the fraction of catalytically active T. thermophila ribozymes was determined as a function of time. The earliest time that could be measured in this assay was 1.25 s. The predicted time-evolution of the folded species corresponds within experimental error to the observed onset of activity of the ribozyme as a function of time (Figure 5). Thus, independent experimental measures agree upon the time evolution of the folded catalytically active ribozyme. Given that Mg²⁺ ions are directly involved in T. thermophila ribozyme catalysis, a similar analysis could not be done for the Na⁺-mediated folding reaction¹⁹.

Figure 5.

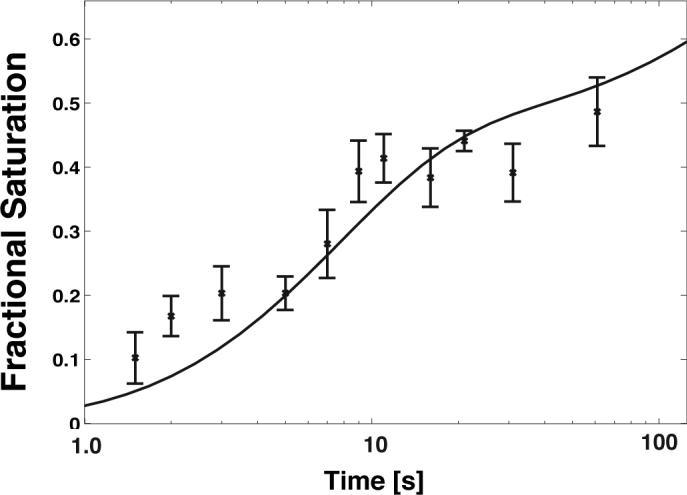
Catalytic activity measurements (×) for the T. thermophila group I intron as measured from the amplitude of burst phase in multiple turnover experiments. The black line is the predicted evolution of the folded species (F) based on the kinetic model depicted in Figure 3c. Error bars represent three standard deviations based on three repeats of the experiment.

Discussion

The ability of protein and RNA molecules to spontaneously fold into unique three-dimensional structures is essential to fulfilling their biological functions. At the heart of the folding problem is the ability to quantitatively describe the process by which these large polymers adopt their native conformation. One such description is a kinetic model that structurally defines the different species in solution and their inter-conversion rates. The hydroxyl radical's virtues as a local probe of RNA structure include reporting a well-defined physical property, the solvent accessible surface of the polynucleotide backbone^12,32,33. Furthermore a single •OH footprinting experiment can separately report the change in accessible surface of each and every nucleotide of a molecule^34,35. In this manuscript we describe a general and novel approach to automatically reconstruct a kinetic model from local probes of structure such as •OH footprinting experiments.

The kinetic model that best describes the Mg²⁺-mediated folding reaction (Figure 4a) presents a dramatically different picture compared to its previous interpretation²⁰ as a sequential reaction. Only about 10% of the folding flux passes through the U→I1→I3→F sequential pathway (Figure 4a). It is simply not possible to fit the footprinting data to the sequential model. The parallel folding pathways are a direct consequence of the data. Parallel folding pathways for RNA folding reactions in general and the T. thermophila ribozyme in particular have been observed previously^36,37. However, the previous studies of Mg²⁺-mediated folding focused primarily on the partitioning between a longed lived (tens of minutes to hours) misfolded catalytically inactive species and the pathway(s) leading to the active native structure that has been studied herein. The temperature and solution conditions at which the folding reactions were carried out in this study do not favor formation of this particular misfolded species³⁸. If we view these previous studies as discerning the partitioning folding of the Tetrahymena ribozyme between ‘slow’ and ‘rapid’ pathways, the parallel folding pathways revealed in our analysis reflect further partitioning of the ‘rapid’ pathway. As such they appear to be an integral part to the RNA folding process. The resolution of kinetic models and analysis of the flux that flows through the different pathways will allow direct and critical comparisons to be made of folding under different solution conditions. These comparisons have the potential of revealing whether a common set of intermediates and the transitions between them describe a general folding mechanism for this RNA.

The time-evolution for the different species shown in Figure 3a reveals the nearly simultaneous formation of I1, I2 and I3 early in folding. Indeed, the peripheral contacts that distinguish I3 from I2 impede folding, providing direct evidence that I3 is kinetically trapped. This conclusion is consistent with the effect of mutation and sub-denaturing concentrations of urea on the ribozymes folding^3,39-41. It is also notable that I3 rarely unfolds to either I1 or I2. Folding to native is either rapid from the P4-P6 scaffold or encumbered by the embrace of a structured periphery (Figure 4a, red regions). From the distribution of the flux it can be clearly concluded that this folding reaction proceeds via parallel pathways.

The analysis of more complete and higher precision data allowed the folding of the P5c substructure to be resolved and its independence assessed. While the two-fold faster folding of P5c had been previously noted²⁷, the small magnitude of its separation from the remainder of the P4-P6 domain left uncertain its significance. That the flux through the P5c intermediate (Figure 4a, I1) is extracted only from the P4-P6 domain intermediate (Supplementary Material Figure S2) attests to its absence of influence in the remainder of the ribozyme folding mechanism. Thus, kinetic modeling can discern autonomy as well as interdependence in the structurally distinct steps of folding.

Comparison of folding models resolved for the Mg²⁺- and Na⁺-mediated folding reactions reveals similarities and important differences (Figures 3c & 3d). A clear difference is the order of magnitude acceleration of the Na⁺-mediated reaction. A clear similarity is simultaneous formation of intermediates early in the folding reaction. However, the structures of the folding intermediates are distinctly different (Figure 4). In the Na⁺-mediated reaction, I1 encompasses the P9 peripheral helix while I2 includes structuring of the P5abc/P2 regions (Figure 3d). The differences in the structures of the intermediate reflects the partial inversion of the folding hierarchy that characterizes the Mg²⁺-mediated folding reaction from this initial condition.

A result of the modeling is that forward conversion rates from I2 (P4P6 formed) to I3 (P4P6 and periphery formed) for Mg²⁺ mediated folding (0.07 s⁻¹) contrast with the negligible values observed for the I1 to I2 interconversion in Na⁺ mediated folding (Figure 3d). Thus, sequential folding contributes negligibly to the Na⁺-mediated reaction. The flux through the three most populated pathways account for 98% of the Na⁺-mediated folding reaction. Among this group is the direct U→F pathway and the two most direct pathways that pass through a single intermediate each, U→I1→F and U→I2→F. This behavior contrasts with the negligible population of the direct U→F pathway in the Mg²⁺-mediated reaction and the appreciable flux passing along pathways of two or more intermediates. Of the two reactions, Na⁺-mediated folding is thus more direct as well as faster. These characteristics highlight a unique contribution of Mg²⁺ _to RNA folding.

The approach presented in this manuscript to quantify the relationships among reaction intermediates is generally applicable to any ensemble of local measures of conformational change. It allows distilling potentially overwhelming amounts of information into kinetic models with intermediates having well-defined structural characteristics. This intersection of kinetic modeling and structure is a unique opportunity to illuminate relationships between structure and folding pathway. The main challenge associated with structural modeling of the intermediates (such as those illustrated in Figure 4) is the coarse view of the folding pathway that this approach generates. Coarse-grained models must therefore be developed that match the resolution of such techniques, as there is insufficient data to constrain atomic level models. Nonetheless, these data are sufficient to rule in/out classes of structural transitions consistent with the observed intermediate protection patterns. Structural models of these transitions provide the next significant computational challenge in understanding the RNA folding process.

Materials and Methods

Preparation of the experimental data for analysis

Time-resolved hydroxyl radical footprinting progress curves were acquired for the Mg²⁺-mediated^10,20 and Na⁺-mediated¹⁰ folding of the T. thermophila ribozyme from an initial condition of 10 mM Sodium Cacodylate and 0.1 mM EDTA, pH 7.5 (CE buffer) at 42 °C. Mg²⁺-mediated folding was initiated with 10 mM MgCl₂ while Na⁺ mediated folding was initiated with 1.5M NaCl. Footprinting progress curves were scaled to the fractional saturation (Ȳ ) of the ·OH protection from the initial condition (Ȳ = 0.0 ) to a control sample at equilibrium in CE buffer plus 10 mM MgCl₂ (Ȳ = 1.0 ). Multiple independent sets of experimental data for each folding reaction were combined for subsequent analysis by binning. Approximately 70 equally log-spaced time bins were defined and populated with data and the fractional saturation values within each bin averaged. Two sets of Mg²⁺ mediated folding data (the original data published in 1998²⁰ and recently acquired measurements of greater precision¹⁰) were analyzed separately to ascertain the effect of signal to noise on the predicted kinetic models.

Progress curve clustering

The binned progress curves were clustered using the k-means clustering algorithm with a Manhattan distance metric implemented in Matlab 7.01 (The Mathworks, Natick Ma.). The optimal number of clusters was determined using the Gap Statistic²⁹. Briefly, a series of 100 different sets of random time-progress curves were generated based on a normal distribution of random, single exponential kinetic curves. These random data sets were then clustered using k-means clustering. The within cluster dispersion ($W_k^{\ast }$) for the random sets and for the data (W_k) was then computed as a function of increasing k by applying k-means clustering. The Gap score was computed as indicated in Equation 1 and the optimal value of k was chosen such that Gap(k) ≥ Gap(k+1)–s_k+1 where s_k+1 is the standard deviation of the Gap parameter for the B=100 random sets of time-progress curves.

$$Gap\left(k\right)=1∕B\sum _b\log \left(W_k^{\ast }\right)-\log \left(W_k\right)$$ (1)

The cluster centroids for the data were computed and subsequently used as time-progress curves for the kinetic modeling.

Formulation of kinetic models

A kinetic model can be represented by a fully connected graph, where the nodes represent species in solution and the edges represent the conversion rates. The general form for this model is

$$\frac{d\overrightarrow{C}}{dt}=K^{\prime }•\overrightarrow{C}$$ (2)

where C̄ is the vector containing the concentrations of the different species in solution and K is a square matrix with diagonal elements equal to zero. The off-diagonal elements in K are the forward (top) and reverse (bottom) rate constants. Numerical integration of Equation 2 was carried out using a Matlab implementation of an explicit Runge-Kutta pair as described by Bogacki and Shampine⁴². Integration of Equation 2 yields the time-evolution of the relative fraction of each species in solution for a given set of kinetic parameters.

Kinetic model optimization

Kinetic parameter optimization was carried out using an Ansi-C implemented version of a non-linear large scale bounded least squares optimization routine based on the interior reflective Newton method⁴³. In general the reverse rate parameters of the kinetic model were initially bound to zero as equivalently good fits were obtained with and without bounds. For a given number of clusters, all possible mappings of intermediates to time-progress curve clusters were enumerated. Equation 3 relates the number of possible mappings (N) given a specific number of intermediates (I), and time-progress curves (k).

$$N=\sum _{j=1}^I\left(\begin{array}{c}\hfill 2^k\hfill \\ \hfill j\hfill \end{array}\right)\times \left(\begin{array}{c}\hfill k\hfill \\ \hfill j-1\hfill \end{array}\right)$$ (3)

Each mapping represents a specific kinetic model that is tested by least squares optimization to the experimental data (see Figure 1c for the trivial example of a single intermediate). The model with the lowest root mean square error (RMSE) is then reported. If the relative RMSE of the best fitting model to that of the second best fitting model is greater than 10%, then only the best-fitting model is reported. Errors in the kinetic model parameters are estimated using a standard bootstrap^44,45.

Pathway flux analysis

A stochastic algorithm was implemented to determine the flux through the pathways of the best-fitting kinetic models. Equation 4 relates the probability of transitioning to the rate constant (k_abs) for a transition from state A to state B over a given period of time (Δt).

$$p_{ab}\left(\Delta t\right)=1-e^{k_{ab}\Delta t}$$ (4)

The simulations start with a population of 10⁵ molecules all in the U (or unfolded state). A time step is chosen based on the total number of species in solution and the maximum observed rate in the model (Δt = Alog(num_species)/max_rate where A=0.1). This procedure keeps the transition probabilities small, guaranteeing a Markovian behavior of the simulation. During the simulation, the paths of the molecules through the kinetic model are stored. These paths are then clustered, and the relative flux computed for each pathway.

Catalytic activity

The fraction of catalytically active molecules as a function of time following the addition of Mg²⁺ was determined by quantifying the amplitude of burst phase in multiple turnover experiments³⁸. The burst phase in these experiments reports the fraction of molecules capable of catalysis at a given time. The ribozyme in CE buffer was mixed with equal volume of MgCl₂ in a three syringe KinTek® quench-flow mixer at 42 °C. After aging the reaction solution for the indicated time, it was expelled into an equal volume of solution containing GTP and a mixture of unlabeled and 5′-end-³²P-labeled 11-nucleotide substrate of the sequence CCCUCUAAAAA being held at 42 °C. The final concentrations of the solution components were 10 mM sodium cacodylate, pH 7.6, 0.1 mM EDTA, 10 mM MgCl₂, 1 mM GTP, 1μM substrate, 100 nM intron. Aliquots of 3 μL were taken 5, 15, 25 35, 45 and 60 s after mixing and added to an equal volume of iced loading buffer. The samples were maintained on ice until the substrate and product of the reaction were resolved by electrophoresis on 20% denaturing polyacrylamide gels. The folding time of the ribozyme was calculated to be equal to the aging time plus the half-time of the chemical reaction. The substrate docking is rate-limiting step for the reaction under the above described conditions with t_1/2 = 1 sec³⁸. It has been shown that under this experimental condition a portion of the RNA misfolds into a long-lived an inactive structure³⁸. Therefore, the fraction of native molecules determined herein was normalized to a measure of ribozyme incubated for 30 min in buffer containing 260 mM NaCl and 10 mM MgCl₂ at 50°C, conditions under which 100% catalytic activity is obtained^38,46.