Deadly competition between sibling bacterial colonies

Abstract

Bacteria can secrete a wide array of antibacterial compounds when competing with other bacteria for the same resources. Some of these compounds, such as bacteriocins, can affect bacteria of similar or closely related strains. In some cases, these secretions have been found to kill sibling cells that belong to the same colony. Here, we present experimental observations of competition between 2 sibling colonies of Paenibacillus dendritiformis grown on a low-nutrient agar gel. We find that neighboring colonies (growing from droplet inoculation) mutually inhibit growth through secretions that become lethal if the level exceeds a well-defined threshold. In contrast, within a single colony developing from a droplet inoculation, no growth inhibition is observed. However, growth inhibition and cell death are observed if material extracted from the agar between 2 growing colonies is introduced outside a growing single colony. To interpret the observations, we devised a simple mathematical model for the secretion of an antibacterial compound. Simulations of this model illustrate how secretions from neighboring colonies can be deadly, whereas secretions from a single colony growing from a droplet are not.

Bacteria are not the simple solitary creatures of limited capabilities they were long believed to be. When exposed to harsh environmental conditions such as starvation, hard surfaces, extreme heat, and hazardous chemicals, the bacteria can collectively develop sophisticated strategies for adaptation and survival. One aspect of this cooperative behavior is the formation of complex colonies with different spatiotemporal patterns, as needed for efficient response to the environmental conditions (1–13).

To coordinate such cooperative ventures, bacteria have developed methods of cell-to-cell signaling (14–19), including direct physical interactions by extra membrane polymers (20–21), secretion of extracellular materials like lubricating surfactin (22–23), biochemical communication such as quorum sensing and chemotaxis signaling (by using mediators ranging from simple molecules and polymers to peptides and complex proteins) (24–29), and exchange of genetic information (by plasmids and viruses) (30–32). Bacterial communication-based cooperation can lead to colony morphogenesis, coordinated gene expression, regulated cell differentiation, and division of tasks. Intercellular communication is achieved through highly complex and intricate intracellular mechanisms involving signal transduction networks (33) and gene network dynamics to turn genes on and off (34).

Bacteria competing with unrelated or distantly related strains for limited resources in the same niche cooperate to secrete antibacterial compounds to attack the competing strains (35–36). Although antibacterial compounds such as bacteriocins affect only similar or closely related bacteria, such “chemical weapons” can even be used to attack sibling cells within the same colony (37–39). An example is “fratricide” in Streptococcus pneumoniae (during the transition to competence) (39–41). Another example is “cannibalism” in Bacillus subtilis, where bacteria during the early stages of sporulation produce chemicals that kill some siblings, which become food for the surviving bacteria (37–38). This complex behavior involves the activation of many genes and ensures the survival of the colony as a whole.

Based on these observations, one expects that there must also be competition between sibling colonies for survival. Indeed, communication between sibling colonies has been observed in a preliminary study of interaction between 2 colonies of Paenibacillus dendritiformis; neighboring colonies showed inhibited growth, and it was suggested, based on comparison with model simulations, that the repulsion was not simply due to food depletion but was due to mutual inhibition through some signaling factor (42–44).

In this article, we report a quantitative experimental investigation of competition between 2 growing sibling bacterial colonies. We study the Gram-positive lubricating bacterial strain P. dendritiformis, which develops complex colonial (bush-like) branching patterns that are sensitive to small changes in the environment when grown on nutrient-limited surfaces (9, 11, 12). The patterns slowly grow to several centimeters in diameter, which makes these bacteria ideal for studying pattern development, internal structure of branches, and mutual inhibition between 2 colonies.

Results

Competing Sibling Colonies.

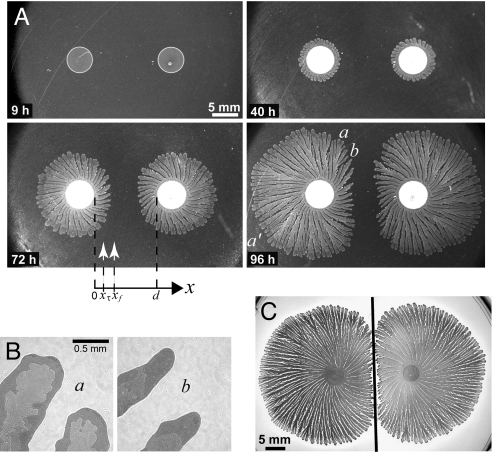
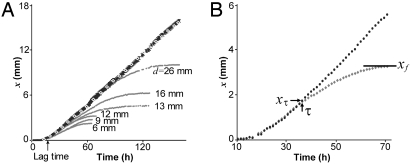
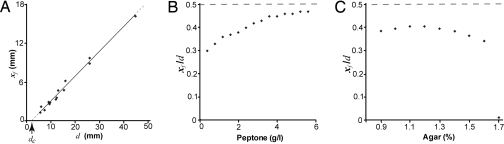
Two sibling colonies of P. dendritiformis were inoculated simultaneously on an agar plate at the same distance from the plate's center. We refer to the colonies as “siblings” because they were taken from the same bacterial culture. The time development of such a pair of colonies (separated in distance d) is presented in Fig. 1A. The initial development of each colony is just the same as for a single isolated colony: After a lag time of ≈18 h, a colony starts to expand outward, developing an intricate branched pattern within a well-defined circular envelope. The speed of the growth envelope is isotropic (see Fig. 1A, 40 h) and constant, as illustrated by the straight line of white diamonds in Fig. 2A [see also supporting information (SI) Movie S1 and Movie S2]. However, after a well-defined time τ(d) when a colony has grown a distance x_τ(d), a colony's front facing its neighbor starts to decelerate, and the growth front finally stops at x_f(d), leaving a gap between the colonies (see Fig. 2A for different d). The final separation between colonies depends linearly on their initial separation (see Fig. 3A); this separation is smaller for larger peptone levels (Fig. 3B) and almost independent of agar concentration (Fig. 3C). These results led us initially to suspect that food depletion leads to the growth inhibition, as has been observed in studies of the growth of B. subtilis (45).

Fig. 1.

Interaction between neighboring P. dendritiformis colonies growing on a 1.5% agar gel with 2 g/L peptone nutrient. (A) Images of growing nearby colonies: 9 h after inoculation, no growth; 40 h, the onset of inhibition; 72 h, inhibited growth; 96 h, where growth has stopped in region b but not in regions a and a′. The labels on the x axis indicate the initial distance d between the 2 colonies (here 12 mm); the position x_τ(d) is where growth begins to decelerate, and the position x_f(d) is where growth stops. (B) Magnified images of region a (uninhibited) and b (inhibited) of A at 96 h show different morphology of both the branches and their interior structures. (C) Colony growth when a glass partition (black line) was inserted midway between 2 inoculation points. There is no growth inhibition: Each colony grew until it hits the partition.

Fig. 2.

The dynamics of competing bacterial colonies. (A) Position x of the growth front as a function of time for initial colony separations d from 6 to 26 mm; black symbols, aligned on the straight line, correspond to the uninhibited growth in regions a and a′, whereas gray symbols, aligned on the curved lines represent growth toward region b (see 72-h and 96-h data in Fig. 1A). The white diamonds (on the straight line) represent the growth of a single colony for the same conditions. For both the single colony and for neighboring colonies with any separation d, there is the same lag time (18 h), followed by growth with velocity 0.11 mm/h. (B) A well-defined transition (at τ = 36 h, x_τ = 1.8 mm) from uninhibited to inhibited growth for the colony in Fig. 1A; the growth velocity decelerates, and the growth front stops at x_f.

Fig. 3.

The robustness of the growth inhibition and the deceleration to a stop is demonstrated by these measurements of the final positions x_f of growth fronts for different conditions. (A) x_f as a function of the initial separation d between 2 colonies (for 2 g/L peptone and 1.5% agar). The data fall on a straight line with an x axis intercept at d_c = 2.1 mm. (B) x_f/d as a function of peptone level (for d = 17 mm and 1.5% agar). The colonies do not coalesce even at high peptone levels, i.e., x_f/d remains below the dashed line, where x_f/d = 0.5. (C) x_f/d as a function of agar concentration (for d = 17 mm and 2 g/L peptone). The value of x_f/d changes little for agar concentrations 0.9–1.7%, which is the range in which the P. dendritiformis T morphotype strain grows.

To distinguish between the food depletion and signaling mechanisms, we measured the diffusion constant of peptone in the agar gel and found it to be too large (1.6 × 10⁻⁵ cm²/s), given the length and time scales for colony growth, for the inhibition to be explained by food depletion. The signaling hypothesis was then confirmed by inserting a thin glass partition between the colonies to block any transport of inhibitory factors—each colony then grew until it hit the partition (Fig. 1C). A partition between 2 colonies might be expected to serve as a mirror so that nearby colonies would sense similar inhibitor levels whether or not a partition were between them. The observation that the colonies actually grow until they hit the partition suggests that the signaling proteins stick to the glass, either binding or degrading them (46–47). When 2 colonies are grown on agar with a gap in the gel midway between the 2 colonies, the 2 colonies do not grow to the barrier as in the case of the glass barrier (Fig. 1C), but instead the growth pattern is similar to that with no barrier (Fig. S1).

To gain insight into the observed growth inhibition, we developed an integrated incubation-imaging system to track the growth development for periods of weeks, simultaneously for 10 independent samples. We found that nearby colonies did not even start to grow toward one another if d < d_c (where d_c = 2.1 mm; see Fig. 3A). Remarkably, for d > d_c the initial velocity was the same, independent of d (see Fig. 2A). Measurements of the time development of the front position for different initial separations d of competing colonies (Fig. 2A) suggested the existence of a sharp threshold governing the stopping process, because 2 colonies always exhibited a well-defined time τ(d) marking the onset of growth inhibition, irrespective of the initial separation d between the 2 inoculation locations. Moreover, the resultant front deceleration (0.0012 mm/h²) was also independent of d, indicating that once colonies with different separations sense an inhibitor level above a threshold, they are affected in exactly the same way.

There is a transition in the growth morphology as well as a change in the growth speed when the inhibitor signal exceeds the threshold—compare the inhibited region b with the nearby uninhibited region a in Fig. 1B. In the small region between a and b, there are branches that have been inhibited but have not yet stopped completely.

Deadly Inhibition.

To further exclude the possibility of a food depletion mechanism, we isolated bacteria from different regions of the colonies and used them to inoculate LB broth. In every case, the bacteria extracted from an uninhibited region of growing neighboring colonies (e.g., near a and a′ in Fig. 1A at 96 h) and also from the growing tips of single colonies exhibited normal growth, reaching in 24 h an optical density of 1.00 ± 0.03, corresponding to ≈1 × 10⁸ bacteria per milliliter. In contrast, bacteria collected from tips near b of Fig. 1A showed no growth in LB broth for a period of more than a week; thus the bacteria in the mutually inhibited regions are dead. These results indicate that the growth inhibition illustrated by Fig. 1 does not arise just from repulsive chemotaxis or from decreased motility or from a bacterial transition into a nonmotile prespore state, because in those cases, bacteria from the inhibited regions would grow in LB broth.

Inhibition of a Single Colony by Extracted Material.

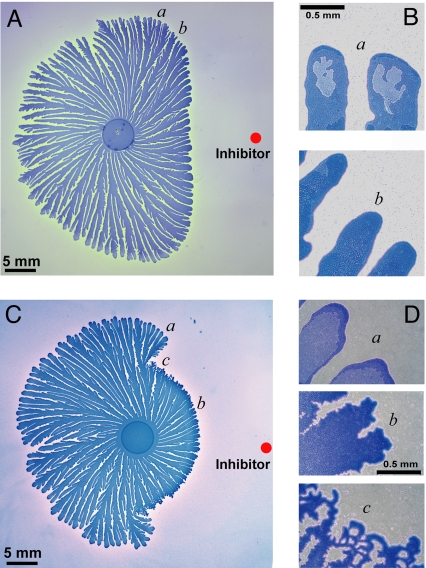
To explore further the hypothesis of the existence of a threshold level for an inhibitory signaling factor (inhibitor), we extracted material from the agar gel between 2 competing colonies and introduced it near a growing single colony. The extract's inhibiting influence on the colonial growth (Fig. 4A) and the transition in the colony's interior structure (Fig. 4B) were found to be very similar to the observations for neighboring colonies (Fig. 1 A and B). The close proximity of regions a and b in Fig. 4A indicates a sharp threshold for the effect of the inhibitor. Moreover, bacteria collected from uninhibited regions (e.g., a) showed normal growth in LB broth, reaching in 24 h an optical density of 1.00 ± 0.03, whereas bacteria collected from the inhibited regions (e.g., b) showed no growth, just as observed for 2 competing colonies. Experiments for a higher concentration of the gel extract (Fig. 4C) revealed an even more striking transition from the branching morphology of the P. dendritiformis to the chiral one (7, 11), as is shown in Fig. 1B.

Fig. 4.

Inhibition of growth of a single P. dendritiformis bacterial colony by material extracted from the region between competing colonies (region b in Fig. 1A at 96 h). (A) Growth inhibition resulting from the introduction, 4 days after the inoculation (at the red dot) of the gel with a 5-μL droplet of extract, containing 1 mg of extracted material. (Introduction of a droplet of extract only 1 h after an inoculation inhibited the growth of an entire colony.) (B) Magnified images of normal (e.g., a) and inhibited (e.g., b) growth branches, illustrating the transition in morphology. (C) Same as A, except that here, the gel extract is 10 times more concentrated. There is an abrupt transition from inhibited to normal growth as the distance from the inhibitor increases and the inhibitor level drops below a threshold. (D) Magnified images of normal (e.g., a) and inhibited (e.g., b) growth branches; c shows the transition region between a and b.

Having established that an inhibitor above a threshold concentration leads to bacterial death, the natural question is: Why doesn't a single droplet-inoculation colony inhibit its own growth? We address this question with the aid of a simple model.

Model.

We propose a model that oversimplifies the biochemistry yet is sufficient to describe the generation and diffusion of an inhibitor (self-toxin) in growing colonies. We use the model to make predictions about growth for different inoculation geometries. The model is based on our observations of bacteria grown from droplet inoculations, as in Figs. 1–3. Bacteria at the rim of a growing colony are active and motile, whereas prespores(sporulating bacteria) exist mainly in annular ring that encircles a region containing spores (Fig. 5). The prespores are assumed to secrete an inhibitor, which is in accord with previous observations of the secretion of inhibiting proteins by prespores (37, 43). The growing outer edge of the colony is at R_c(t), and the outer edge of the region containing prespores is at R_p(t) (see Fig. 5). Fig. 2A shows that after a lag time, t_lag = 18 h, the radius of a single colony increases linearly with time, i.e., R_c(t) = Vt − Vt_lag. The spatial distribution of prespores is not known; we assume that R_p(t) is constrained to R_c(t), i.e., R_p(t) = α R_c(t), where α is a positive constant <1. These considerations lead to the following equation for the generation and diffusion of an inhibitor of concentration u(r→,t) that depends on position r→ and time t:

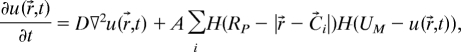where D is the diffusion coefficient of the inhibitor, A is an amplitude, H(x) is a Heaviside step function, and C→_i is the position of the center of the ith inoculation droplet. The first step function limits the inhibitor generation to the sporulating region, whereas the second step function limits the inhibitor generation to u < U_M; for larger values of u(r→,t) it is assumed that prespores at r→ have finished the sporulation process and no inhibitor is generated locally. Guided by the laboratory observations (Fig. 2A), we assume growth of the colony edge starts to decelerate locally when the concentration u(r→,t) exceeds a threshold U_T.

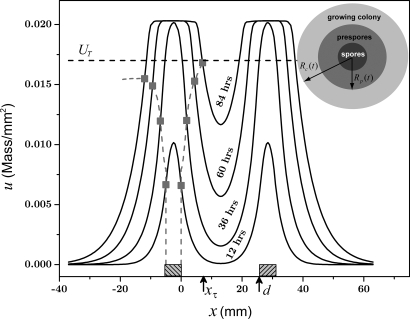
Fig. 5.

Model prediction for the case of 2 competing colonies. The Inset in the upper right is a schematic diagram of a droplet-inoculated colony that has an inner circle (dark gray) corresponding to spores, a ring (gray) corresponding to prespores that produce inhibitor, and an outer ring (pale gray) corresponding to motile bacteria. The graph shows inhibitor concentration u(x,t) at different times as a function of position along a line connecting 2 centers of inoculation; the locations of the inoculation droplets are indicated by shaded boxes to the left of x = 0 and to the right of x = d. The horizontal dashed line marks the level of the threshold, U_T = 0.017 mass/mm². The square points, connected with a dashed line, show the position of the outer edge of the colony on the left; the colony starts decelerating toward the right colony when u reaches the threshold U_T. At 84 h, the inhibitor concentration at the right edge reaches the threshold, and the inhibitor concentration at the left edge has reached a maximum below U_T and has started to decline.

In the experiment, bacteria in the region labeled a and a′ in Fig. 1A (at 96 h) are always below the inhibitor threshold level, whereas bacteria in region b, at some time τ and position x_τ (see Fig. 2A), start to sense inhibitor levels above a threshold, and the front starts to decelerate. In just the same way, in the model, the inhibitor concentration at the growing outer edge of a single colony never reaches the threshold, even with a front velocity as low as 0.05 mm/h, whereas the inhibitor level between 2 nearby colonies growing toward one another reaches the threshold U_T and growth slows and then stops (Fig. 5).

Test of the Model.

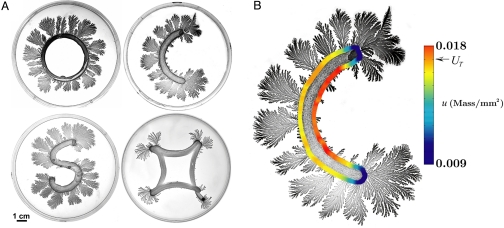
To test our model, we have conducted experiments with quasi-1-dimensional inoculations for various geometries, as illustrated by 4 examples in Fig. 6A. Bacteria in regions that were close (e.g., inside the letter “O” or letter “S”) did not grow or grew very little, even though the nutrient level was sufficient. Food depletion cannot explain the growth patterns in Fig. 6A, but a high level of inhibitor in the nongrowing regions can explain each case. Further, the absence of growth on both the insides and the outsides of the edges of the distorted square geometry excludes possible bacterial growth preference for a convex or concave front.

Fig. 6.

Bacterial growth for different inoculation geometries. (A) Inoculation lines of different shapes (on a 1.5% agar gel with 2 g/L peptone nutrient): Ring (O shape), where bacteria grow on the convex edge of the inoculated ring but not on the concave edge, even though the medium has a sufficient nutrient level on the concave side; (for much larger ring diameters, some growth occurs on the concave edge); C shape, where bacteria grow on the convex edge but exhibit little growth on the concave edge; S shape, where, as in the O-and C-shaped inoculations, the bacteria grow on the convex but not the concave edges; note the change in the growth behavior when the curvature changes from convex to concave; and distorted square, where the bacteria grow on the corners but not on either the convex interior edges or on the outer concave edges. (B) The local inhibitor concentration u( r→,t) at the edge of the initial inoculation at the end of the lag time, calculated by the model, is shown by the color bar. The experimental observation is that the colony grows very little in regions where the calculated inhibitor concentration exceeds the level U_T.

The geometry of an inoculation determines the spatial distribution of the inhibitor's source and the subsequent diffusion of it. The model explains well why bacteria grow in particular regions, as Fig. 6A illustrates. For example, given the C-shaped colony geometry, we computed the inhibitor concentration u(r→,t) along the edge of the inoculation region (at the end of the lag time), and the results are shown by color code in Fig. 6B. As predicted by the model, almost no growth occurs in the region where the inhibitor concentration exceeds the threshold U_T.

Discussion

Bacterial colonies in natural environments can spontaneously grow at a close proximity, leading to competition for resources. The question that motivated the present work is whether sibling bacterial colonies have developed sophisticated mechanisms to deal with such a competition.

We have performed detailed quantitative experimental investigations of the competition between 2 nearby sibling P. dendritiformis bacterial colonies grown on nutrient-limited surfaces. Our results suggest that the 2 colonies mutually secrete an inhibitor that leads to death of bacteria in competing colonies when the inhibitor exceeds a threshold level. This can be concluded for the following reasons: (i) Bacteria in the inhibited regions are dead; no growth was observed in LB broth for a period of more than a week. (ii) The deceleration of a front is independent of the initial separation between colonies (Fig. 2A), indicating that once a colony senses an inhibitor level above a certain threshold it is affected in the same way. Further, whatever the initial separation d of 2 colonies, there exists a well-defined time τ(d) marking the onset of growth inhibition. (iii) Extracted material from the inhibited region between colonies was found to inhibit the growth of a single colony (see Fig. 4). Higher concentration of the extracted material provides even more striking evidence of a well-defined threshold (Fig. 4C). (iv) A mathematical model for the inhibitor concentration demonstrates how inhibitor from competing colonies kills bacteria if the inhibitor exceeds a threshold level (Fig. 5). The model provides a putative explanation how nearby regions in quasi-1-dimensional inoculations do not show any growth (Fig. 6); for example, inside a C shape, there is little growth, whereas there is growth outside the C (Fig. 6B). The distorted square geometry demonstrates that even convex regions, if bounding a nearby region, will not show growth because of the diffusion of the inhibitor from the other boundaries (Fig. 6A).

The existence of a sharp threshold indicates that P. dendritiformis bacteria have developed a well-orchestrated deadly response to the presence of a sibling colony. Bacteria in sibling colonies are killed and not just inhibited. In contrast to bacterial cannibalism, where killed siblings serve as a source of food for the surviving bacteria, there is no obvious advantage of killing bacteria in a sibling colony.

New insight may come from investigating how the bacteria die. There are 2 possible ways: The inhibitor acts as a bacteriocin (self-toxin) that kills bacteria directly, or the inhibitor acts indirectly by triggering a complex response in the bacteria similar to the one observed in B. subtilis (37–38). The long deceleration observed in the affected regions (see Fig. 2) suggests that the second possibility is more likely. In future experiments, the inhibitor-containing agar taken from the region between colonies should be analyzed because identification of the inhibitor may reveal new clues about the inhibition mechanism and may even point toward the evolutionary advantage of the deadly competition between sibling colonies.

Materials and Methods

Strain and Growth Media.

We used a spore-forming Gram-positive motile bacterial strain, Paenibacillus dendritiformis (T morphotype) (7). Each bacterium is rod-shaped with dimensions ≈4 × 1 μm (7, 11). The bacteria secrete lubricating substances (such as surfactin), and they move in this thin lubricant layer on top of a substrate such as a high-concentration agar gel (7, 11). The morphology of the patterns and the dynamics of the growth are sensitive to the nutrient level, substrate hardness, temperature, and humidity (7, 11).

The bacteria were maintained at −80 °C in LB broth (Sigma) with 25% glycerol. LB broth was inoculated with the frozen stock and grown for 24 h at 30 °C with shaking; it reached an OD₆₅₀ of 1.0, corresponding to ≈1 × 10⁸ bacteria per milliliter.

The peptone medium contained NaCl (5 g/L), K₂HPO₄ (5 g/L), Bacto Peptone (0.4–10 g/L). Difco Agar (Becton Dickinson) was added at concentrations 0.7–1.7%, as indicated. Twelve milliliters of molten agar was poured into 8.8-cm-diameter Petri plates, which were dried for 4 days at 25 °C and 50% humidity until the weight decreased by 1 g.

Growth Pattern Experiments.

The agar plates were inoculated by placing 5-μL droplets of the culture on the surface. For intercolony competition experiments, 2 droplets were inoculated equidistant from the center, along a line through the plate's center. The plates were mounted on a rotating stage inside a 1-m³ chamber maintained at 30.0 ± 0.5 °C and 90 ± 2% humidity (see Fig. S2). The rotating stage system enabled us to monitor growth development of 10 plates simultaneously; the rotation had no influence on any of the bacterial properties. The stage was controlled by a stepper motor that stopped sequentially for each bacterial colony to be imaged. A rotation period of 1 h is sufficiently short to capture the growth of the colony, the tips of which move typically at 0.11 mm/h. The reproducibility of positioning of the agar plates was ±15 μm, allowing successive images of a given colony to be subtracted to determine growth patterns.

Images were obtained with a 10-megapixel Nikon D200 camera with a 60-mm lens. The camera was placed above the rotating stage and programmed to take an image and store the data when a sample was stationed below it. Each Petri dish was mounted above a 6-cm-diameter hole in the stage and illuminated from below the stage by a 8-cm-diameter ring of 5-mm white LEDs, which yielded cold-bright-uniform-white illumination. No direct light from the lamps could reach the camera lens. For plates imaged only at a single point in time, colonies were stained with 0.1% Coomassie brilliant blue to obtain higher-contrast images than those obtained in the sequences of images.

Inhibitor Extraction.

Sections of agar (5 mm × 40 mm) were excised from the zone of inhibition between colonies of 20 plates and suspended in 10 mL of deionized water for 3 days. The supernatant was filtered through a 0.2-μm filter, and an equal volume of 100% trichloroacetic acid was added. The solution was incubated for 2 h at 4 °C and then centrifuged for 1 h at room temperature and 9,000 × g (13,000 rpm). The pellet was washed with acetone and then centrifuged again for 10 min at the same rate. The pellet was resuspended in 100 μL of deionized water, creating a solution that presumably contained chemical agents secreted by the colonies, including the inhibitor. The existence of the latter was tested by application of the solution to growing single colonies. This led to inhibited colony growth similar to the effect of a growing nearby colony; hence, we assume that the solutions do indeed contain the relevant inhibitor.

Modeling and Simulation.

The model was numerically integrated by a finite element method in a circular domain with a no-flux condition at the boundary. As a check, the simulations were done also by a spectral method, and good quantitative agreement between the 2 computational methods was found. Among the parameters, the results were most sensitive to the diffusion constant D, which we estimated from experimental results such as those in Fig. 2A. For example, for colonies initially separated by a distance d = 26 mm, the colonies grow x_τ(d) = 7.5 mm during the 85 h before starting to slow down. Given a diffusion length l_D ≈ 10 mm and time scale T_D = 85 h, we obtain D ≈ l_D²/T_D ≈ 1 mm²/h. Other parameters are constrained by experimental results in Figs. 2A and 6.

Because we did not have a way to estimate the rate of secretion of the inhibitor or its concentration in the colony, we used an arbitrary unit for the mass, denoted by “mass.” In the end, we found the following parameters fit the experiments best: D = 1.66 mm²/h, A = 0.1 (mass/mm²)/s, α = 0.9 and U_M = 0.02 mass/mm².

To define a region in which the bacteria secrete an inhibitor in inoculations of arbitrary shape, such as the C shape in Fig. 6A, we manually identified the boundary of an original inoculation and then generated a binary image in which only the inoculated region was in white, as shown in Fig. S3A. The mean width of the inoculation was w = 5 mm. Then, an erosion algorithm was applied to the binary image to shrink the white region. The erosion length was defined as (1 − α)w/2. The binary image after erosion with α = 0.5 (chosen for presentation purpose) is shown in Fig. S3B). The white region in Fig. S3B was defined as the inhibitor secretion region. In Fig. S3C, the inhibitor secretion region (in gray) is overlaid on top of the original inoculation (in white) for comparison. After the inhibitor secretion region was identified, the model was integrated with the parameters given above to predict the inhibitor concentration at the end of the lag time.