Abstract
FtsZ, a bacterial homologue of tubulin, plays a central role in bacterial cell division. It is the first of many proteins recruited to the division site to form the Z-ring, a dynamic structure that recycles on the time scale of seconds and is required for division to proceed. FtsZ has been recently shown to form rings inside tubular liposomes and to constrict the liposome membrane without the presence of other proteins, particularly molecular motors that appear to be absent from the bacterial proteome. Here, we propose a mathematical model for the dynamic turnover of the Z-ring and for its ability to generate a constriction force. Force generation is assumed to derive from GTP hydrolysis, which is known to induce curvature in FtsZ filaments. We find that this transition to a curved state is capable of generating a sufficient force to drive cell-wall invagination in vivo and can also explain the constriction seen in the in vitro liposome experiments. Our observations resolve the question of how FtsZ might accomplish cell division despite the highly dynamic nature of the Z-ring and the lack of molecular motors.
Keywords: bacterial cell division, constriction force, FtsZ, mathematical model, cytokinesis
FtsZ is a fundamental bacterial division protein that is conserved across nearly all bacterial and archaeal species, and has been found to play a role in chloroplast division in plants as well as in mitochondrial division in algae (1, 2). It is a cytoskeletal protein, homologous to tubulin, that assembles into short filaments (3) that are the building blocks of the bacterial division ring referred to as the Z-ring. The Z-ring forms at midcell (4, 5) under the regulating influence of a nucleoid-associated signal (6, 7) and the Min system (8).
By analogy with eukaryotic cell division, one might expect bacterial division to proceed by a filament sliding motion similar to that of actin and myosin. However, bacteria have no known cytoskeletal molecular motors to generate the sliding force. In addition, FtsZ filaments sometimes form “Z-spirals” that are capable of invaginating despite not forming a closed loop structure around the cell (9). An alternate hypothesis (10) is that the Z-ring constricts by progressively bending into a more highly curved structure. This idea is supported by the observation that FtsZ has a GTP hydrolysis cycle, similar to that of tubulin, that allows it to take on 2 preferred states. When bound to GTP, filaments prefer to be straight but, upon hydrolysis, the preferred conformation is curved with a radius of curvature of ≈12–13 nm (10, 11). The fact that FtsZ alone is capable of generating a constriction force was clearly demonstrated by Osawa et al. (12). In their in vitro liposome-FtsZ assay, FtsZ rings formed on the inside of tubular liposomes and proceeded to constrict the liposomes in a GTP-dependent manner, in the absence of any other protein. The viability of this hydrolyze-and-bend hypothesis, in either the in vivo or in vitro context, has not been rigorously tested yet in the sense of quantitative modeling. In vivo, the Z-ring forms early in the cell cycle and is maintained at a constant size for tens of minutes until constriction begins (13). During this time, it contains ≈30% of the total FtsZ available in the cell (14, 15). However, throughout this period, either FtsZ subunits or short FtsZ filaments are constantly being incorporated into and removed from the ring, resulting in a turnover half-time on the order of tens of seconds, as indicated by FRAP measurements (14, 15). This rapid turnover is coordinated with nucleotide state in that GDP-bound subunits tend to disassemble from the ring more rapidly than GTP-bound subunits (16). The half-time is consistent with in vitro measurement of FtsZ polymerization kinetics, in particular, hydrolysis and disassembly rates that are reported to be ≈0.1 s−1 and 3 s−1, respectively (14, 17, 18). However, given that the filaments themselves are allegedly generating the constriction force, it is not clear that significant force can be generated when disassembly follows hydrolysis so rapidly. There seems to be a narrow window of force-generating opportunity.
Although much progress has been made in understanding FtsZ biochemistry, the details of the molecular structure of the in vivo Z-ring and its maintenance are still largely unknown. For example, an important question is whether the dominant pathway for Z-ring maintenance is growth by direct subunit addition or incorporation of preformed filaments. One recent electron cryotomographic study of fixed cells reported that Z-rings appeared to consist of a scattering of short filaments loosely connected by lateral contacts (19). Like tubulin, FtsZ forms filaments with a strong longitudinal bond (20) and can also associate laterally (10). Lateral bonds are weak (0.1 − 0.3 kBT per subunit) (21) compared with longitudinal bonds and with lateral bonds in microtubules (22, 23). However, lateral bonding of longer filaments would have proportionally higher energy and could lead to a greater net contribution to Z-ring maintenance.
The notion that the Z-ring is built by lateral association of cytosolic filaments to filaments already incorporated into the ring is bolstered by the finding that MinC, an inhibitor of in vivo Z-ring assembly, inhibits lateral association of filaments in vitro (24).
In the last few years, much theoretical work has been published on the kinetics and mechanics of FtsZ. Several models of FtsZ in vitro kinetics have been proposed (20, 21, 25–29). Surovtsev et al. (29) also studied in vivo kinetics of the Z-ring but did not address the question of how energy is transduced into a mechanical constriction force.
Using a formalism derived from elasticity theory, Andrews and Arkin (30) and Horger et al. (31) recently provided a comprehensive numerical characterization of the shapes that a linear polymer can take on when constrained to a cylindrical geometry. This provided an appealing explanation for the helical and ring shapes formed by many bacterial polymers. Their work has implications for the mechanics of FtsZ constriction but was focused on the shapes of static polymers rather than the mechanical interaction between dynamic polymers and the cell membrane/wall.
By modeling the process of cell-wall growth, Lan et al. (32) derived estimates of the force required to drive cell-wall invagination. By treating the Z-ring force as a free parameter in their detailed cell-wall model, they concluded that the Z-ring must generate at least 8 pN of force.
Through these studies, much has been elucidated about the kinetics and mechanics of the Z-ring. However, no one has yet addressed the question of whether any particular putative force-generating mechanism is capable of generating sufficient force to explain the observed constriction phenomena in vivo or in vitro. Furthermore, the issue of how the Z-ring can generate this constriction force over a period of minutes, despite the fact that its component parts are turning over on the scale of seconds, has also not been resolved.
In this article, we propose a simple mathematical model that describes the mechanism originally suggested by Erickson et al. (10) for Z-ring constriction. We use this model to examine in vivo Z-ring maintenance and force generation in the context of rapid turnover. We also consider the observed phenotype of the ftsZ84 mutant, whose FtsZ GTPase activity is reduced. Next, we apply the model to the in vitro Z-ring reconstitution experiments of Osawa et al. (12), taking into consideration the balance of forces between Z-ring and membrane including the GTP dependence of the observed constriction phenomenon. Our results quantitatively support the hydrolyze-and-bend mechanism.
Model
Our model consists of 2 components: (i) a kinetic description of Z-ring maintenance including the incorporation of new filaments into the ring, hydrolysis of GTP-bound subunits in the ring, and disassembly of GDP-bound subunits from the ring and (ii) a mechanical characterization of the Z-ring used for analysis of both in vivo and in vitro force generation. Our formal description of the ring treats it as a collection of filaments with weak lateral bonds that maintain their individual identities as far as kinetics are concerned but cohere as a single mechanical structure. An illustration of the relevant structures is provided in Fig. 1. The kinetic model tracks 2 primary quantities: the length distribution of filaments in the ring, p(l,t), where l is measured in numbers of subunits, and the number of hydrolyzed subunits, SD(t), in the ring. From these 2 primary quantities, several secondary quantities can be calculated: the total number of FtsZ subunits in the ring S = ∫0∞lp(l,t)dl; the total number of filaments, and hence the total number of filament tips, in the ring, F = ∫0∞p(l,t)dl; the cytosolic concentration of FtsZ, ZT − S/(NCV), where ZT is the total concentration of FtsZ, and the factor NCV converts numbers of molecules to concentration in micromoles.
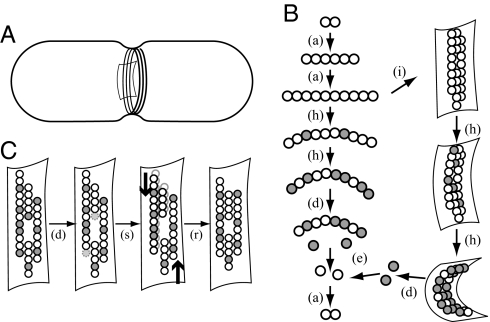
Fig. 1.
A schematic illustration of FtsZ kinetics and mechanics. (A) A rod-shaped bacterial cell (E. coli) shown with an invagination in the cell wall and a Z-ring composed of a collection of filaments. (B) From top left: FtsZ-GTP assembles into straight filaments [denoted (a)]; filaments incorporate into the Z-ring (i); subunits hydrolyze their GTP to GDP [white-to-gray transition, denoted (h)] and upon doing so, adopt a highly curved conformation; those in the Z-ring exert a force on the membrane and cell wall; GDP-bound subunits dissociate from the filament tips (d), exchange GDP for GTP (e) and continue to cycle. (C) Four filaments within the Z-ring. From left to right: Hydrolyzed subunits at the tips of filaments disassemble (d); under the influence of the curvature-induced constriction force (thick arrows), weak lateral bonds are broken, filaments slide past each other (s) and reconnect (r).
Filaments of all lengths are assumed to be randomly distributed throughout the ring. Changes in the length distribution p(l,t) arise through incorporation of FtsZ filaments from the cytosol and dissociation of hydrolyzed subunits from filament tips.
We assume a quasi-steady exponential length distribution for FtsZ filaments in the cytosol, which is consistent with polymer kinetics, independent of the issue of cooperative versus isodesmic assembly or the presence of fragmentation and annealing (25). The assumption of a cytosolic filament distribution is justified by the fact that the cytosolic concentration is well above the critical concentration (15). Additionally, FRAP experiments of cytosolic FtsZ give a half-time approximately twice that of monomeric GFP, consistent with predictions for an exponential length distribution [see supporting information (SI) Appendix]. We use a mean length λ = 30 subunits (17) and an amplitude determined by the current cytosolic concentration. The incorporation rate of filaments of length l is proportional to the cytosolic concentration of filaments of that length. We assume that cytosolic filaments consist entirely of GTP-bound subunits. Although incorporated filaments certainly contain some fraction of hydrolyzed subunits, explicitly including this in the model is equivalent to scaling the hydrolysis rate (see SI Appendix).
Dissociation of subunits is governed by 2 factors: position in a filament and nucleotide state. Because interior subunits are stabilized by the lattice, disassembly is biased to the tips of filaments, whose flux is proportional to koffp. Because GDP-bound subunits disassemble more rapidly than GTP-bound ones (16), this tip expression is multiplied by a prefactor SD/S, the fraction of subunits that are GDP-bound. In a simpler model described in SI Appendix, we assume that disassembly is uniform throughout the lattice instead of restricted to filament tips, leading to force estimates that are insufficient to explain constriction. The equation for p(l,t) is
The 4πR accounts for the number of available binding sites for new filaments that we assume can only attach along the outer edges of the barrel-shaped Z-ring.
The number of GDP-bound subunits in the ring, SD, evolves according to
The first term accounts for hydrolysis, which is independent of subunit position in a filament, and the second term accounts for disassembly, found by integrating the disassembly term in the p equation. Parameter values are given in Table 1.
Table 1.
Parameter values used in the model
| Parameter | Description | Value | Source |
|---|---|---|---|
| λ | Average no. of subunits in a filament | 30 subunits | Chen and Erickson (17) |
| δ | Size of FtsZ subunit | 4 nm | Erickson et al. (10) |
| B | Bending modulus of FtsZ filament | 1.2 · 104 pN nm2 | Mickey and Howard (38) |
| koff | Depolymerization rate of FtsZ-GDP | 3.5 s−1 | Chen and Erickson (17) |
| khyd | GTP hydrolysis rate (wild type) | 0.13 s−1 | Stricker et al. (14), Anderson et al. (15) |
| Khyd84 | GTP hydrolysis rate (ftsZ84 mutant) | 0.013 s−1 | Stricker et al. (14), Anderson et al. (15) |
| κD | Intrinsic curvature of FtsZ-GDP | 0.08 nm−1 | Lu et al. (11) |
| NC | Conversion factor | 600 μM−1 μm−3 | – |
| In vivo | |||
| kin | Membrane association rate | 2.1 · 10−4 μM−1 nm−1 s−1 | Estimated here |
| R | Radius of Z-ring | 0 → 400 nm | Erickson et al. (10) |
| ZT | Total concentration of FtsZ in cell | 11 μM | Lu et al. (39) |
| V | Volume of cell | 2 μm3 | – |
| In vitro | |||
| kin | Membrane association rate | – | See Results |
| R0 | Intrinsic radius of liposome | 1 μm | Osawa et al. (12) |
| ZT | Concentration of FtsZ in solution | 4 μm | Osawa et al. (12) |
| V | Per-ring liposome volume | 41 μm3 | Osawa et al. (12) |
| SR | No. of subunits in each ring | >1,500 | Estimated range |
| FM | Scale of membrane resistance force | – | See Results and SI Appendix |
For the mechanical properties of the Z-ring, we assume that the ring always forms a stable and smooth circle of radius R. The spring energy of an individual hydrolyzed subunit E = Bδκ = 150 pN nm would tend to tear apart neighboring filaments of differing nucleotide state. However, the energy of membrane attachment, which is several hundred pN nm per α-helix (33, 34), is sufficient to counteract this destabilizing effect. The lateral bond energies [≈0.1 kBT (21)] alone would not be enough to stabilize the structure. The assumption of a smooth ring is justified by a mechanical averaging across the thickness of the ring due to the uniform distribution of hydrolyzed subunits and the influence of the cell membrane and/or cell wall.
An expression, ℋ, for the mechanical energy stored in a Z-ring is derived in SI Appendix. Taking the derivative of this expression with respect to R gives the radial force generated by the ring,
where B is the bending modulus of a filament, δ is the size of a subunit, fD = SD/S is the fraction of hydrolyzed subunits in the ring, and κD is the preferred curvature of a hydrolyzed subunit. We use this expression to understand in vivo force generation by the Z-ring, a quantity that we compare with the 8-pN estimate of Lan et al. (32) as a test of the viability of the hydrolyze-and-bend mechanism.
When considering the in vitro experiments of Osawa et al. (12), we must include the membrane's resistance to constriction in a force-balance calculation. We treat the membrane force as linear in the deviation from the preferred radius of the tubular liposome (R0 ≈ 1 μm). The resulting force balance equation, which we take to be in mechanical equilibrium, can be written as
where FM is the membrane force scale. This approximation is valid for relatively small deformations observed by Osawa et al. (12). For larger deformations, the nonlinear elastic energy should be considered as should the possibility of membrane rupture (see SI Appendix).
Results
In Vivo Z-Ring Constriction Forces.
The force generated by the Z-ring has been hypothesized to be the primary driving force behind constriction during cell division (10). The mechanics of the invagination process are complicated by the fact that the cell wall is relatively stiff and must be remodeled rather than simply pulled inward. A model for this process was recently proposed by Lan et al. (32), through which the authors derive the aforementioned estimate of 8 pN required for constriction to proceed. To determine whether our Z-ring model has such a force-generating capacity, we consider the expression for the radial force (Eq. 3) given in Model above.
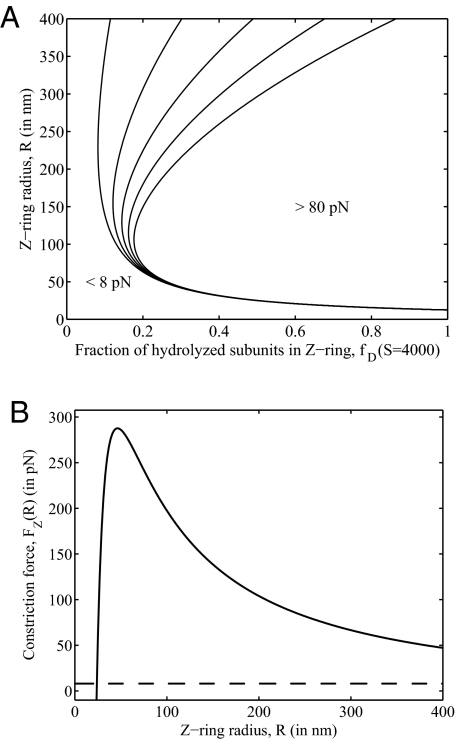
This expression provides a map of the force-generating capacity of the Z-ring as a function of parameters. For a ring consisting of S = 4,000 subunits [≈30% of the total FtsZ (14)], the force of constriction is shown in Fig. 2A as a family of level curves over the plane of possible values of ring radius R and fraction of subunits hydrolyzed fD. To the right of the rightmost curve, the force is >80 pN. To the left of and below the leftmost curve, it is <8 pN; this corresponds to a small fraction of FtsZ–GDP subunits and/or a small ring radius. Note that the absolute minimal radius for which this constriction mechanism can generate an inward force is the intrinsic radius of curvature of FtsZ–GDP, κD−1 = 12.5 nm (11). For radii R > 60 nm, the force is always >8 pN, provided fD > 0.2. Thus, we predict that ≈20% or more of the FtsZ in the ring must be hydrolyzed.
Fig. 2.
Predicted Z-ring forces. (A) The inward radial force, represented as a contour plot, varies with the fraction of subunits that are hydrolyzed, fD, and with the radius of the ring, R, from Eq. 3, for S = 4,000. In this plot, fD and R are treated as parameters. (B) Predicted constriction force generated for different radii, R, calculated by using the full model with the kinetic Eqs. 1 and 2 in quasi-steady state. For radii >25 nm, the force (solid curve) is always >8 pN (dashed line), the required constriction force predicted by Lan et al. (32).
This purely mechanical analysis indicates that FtsZ filaments with a small preferred radius of curvature are capable of generating the required force under the conditions described. However, the kinetics of FtsZ turnover in the ring are surprisingly fast, with half-times as small as 9 s (14, 15). With a disassembly rate of hydrolyzed subunits significantly faster than the hydrolysis rate (see Table 1), it is not obvious that the ring can maintain a sufficient fraction of hydrolyzed subunits (>20%) or even a sufficient total number of subunits.
Assuming R changes slowly according to a mechanism such as the one described by Lan et al. (32), we calculate the quasi-steady state of the kinetic Eqs. 1 and 2 for fixed R and use the resulting values of S and SD in Eq. 3 to calculate the force generated by rings of various sizes. For the in vivo parameters shown in Table 1, we find that for a cell starting with a radius of 400 nm, the dynamic ring is capable of generating the requisite 8 pN of constriction force all the way down to a radius of ≈25 nm. This force–radius relationship is depicted in Fig. 2B.
It is important to note that for the in vivo rate of filament incorporation kin, no estimate could be found in the literature. However, Stricker et al. (14) and Anderson et al. (15) both observed that ≈30% of the total FtsZ in a cell is found in the Z-ring. This observation provides a phenomenological means of determining kin, as described in SI Appendix. No further fitting of parameters was required.
The model also provides an estimate for the fraction of the subunits in the ring that are GDP bound, fD = 0.53 (see SI Appendix). Currently, there is no reported value to which this can be compared, even in vitro, so this stands as a prediction of the model. Interestingly, a simpler model for Z-ring kinetics that does not account for any spatial structure, with subunit dissociation occurring anywhere from within the ring, predicts a value of fD = 0.036 (see SI Appendix). As shown in Fig. 2A, this is clearly too small to generate sufficient forces for constriction. The model presented here introduces enough structure to account for constriction forces without adding details that are not resolved experimentally.
Reduced GTPase Mutant and FRAP Recovery.
The mutant ftsZ84 hydrolyzes GTP at a rate one tenth that of wild-type cells (14, 15). In vivo, this reduced GTPase activity was found to increase the fraction of FtsZ in the ring to 65% (14). By FRAP analysis Anderson et al. (15) found a half-time for the mutant Z-ring of 30 ± 10 s, a slowing of the subunit turnover by a factor of 3 compared with the wild-type half-time of 9 ± 3 s. An earlier study under different conditions found slower rates of 248 and 32 s for mutant and wild type, respectively (14).
To simulate this mutant phenotype, we used an appropriately reduced hydrolysis rate khyd84 and calculated the steady-state value of S for a radius of R = 400 nm, with all other parameters unchanged. The fraction of FtsZ in the ring increased to 69%, fairly close to the observed 65%.
To explain the half-times in both wild-type and mutant cells, we consider an estimate for the average time a subunit resides in the ring:
The first term is the time required for subunit hydrolysis, and the second is the average time required for an arbitrary subunit to be released by disassembly. This gives an estimated half-life of 8.3 s for wild type and 56 s for the mutant.
To support these estimates, we simulated the FRAP experiment numerically by holding the cell radius fixed and integrating the system of Eqs. 1 and 2 starting from an initially empty ring until a steady state was reached. We found that wild type recovers with a half-time of 5.2 s, whereas the mutant half-time is 15.7 s. Thus, the model accurately reproduces the 3-fold increase observed by Anderson et al. (15). The half-times themselves are faster than those reported by Anderson et al. (15). This difference could be due to variability in khyd and koff in vivo, where the FRAP assay was carried out, as compared with the in vitro kinetic measurements from which we took our parameter values.
The model predicts a hydrolyzed fraction of subunits in the Z-ring of fD = 0.1 for the mutant cells. With such a reduction in the hydrolyzed fraction, it seemed possible that the constriction force might fall below the required 8 pN. This would be inconsistent with the observation that the mutant cells still manage to divide (14). We find that force generated by the mutant's Z-ring is sufficient by the criterion of Lan et al. (32) down to a radius of ≈135 nm, in contrast with the 25-nm result for wild-type cells.
Z-Rings in Liposomes.
In the in vitro experiments of Osawa et al. (12), the physical problem is simpler than that described by Lan et al. (32) in that the Z-ring is only competing against the elastic resistance of the tubular vesicle wall. Thus, no model for cell-wall production is required. To model this system, we use the same kinetic Eqs. 1 and 2 as in the in vivo context with changes only in the values of those parameters listed under “in vitro” in Table 1. At every moment, the dynamic values of S and SD determine the mechanical equilibrium value of R, which solves Eq. 4.
Can the hydrolyze-and-bend mechanism generate constrictions that are consistent with experiment? Osawa et al. (12) report that Z-rings colocalize with membrane constrictions that vary in their extent. Our own measurements from their published images and movies indicate that Z-ring-associated constriction radii range from ≈60% of the liposome radius to a complete lack of perceptible constriction for faint rings. In addition, Osawa et al. (12) report that thinner-walled liposomes could not be successfully produced.
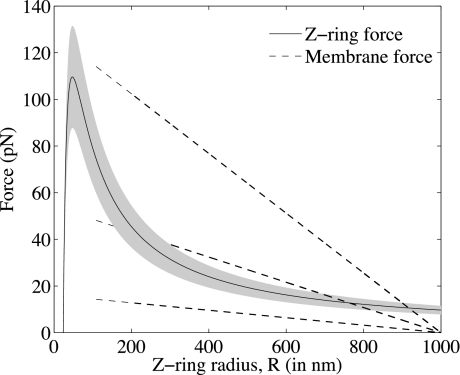
In the physiological regime, the steady-state ring radius given by our model does not depend on the values of FM and kin independently but rather on their ratio (see SI Appendix); a stiffer membrane can be balanced by a thicker Z-ring. Fig. 3 illustrates the 2 sides of the force-balance equation (Eq. 4) for the wild-type value of kin and an estimate of the membrane force scale for liposomes with 2, 3, and 4 bilayers (see SI Appendix), but the analysis applies equally well to other parameter combinations with the same ratios. The membrane force curves (dashed lines) fade out below 400 nm, where the linear approximation is no longer valid and where we hypothesize membrane rupture might occur (see SI Appendix). The solid curve corresponds to the force exerted by the Z-ring. For the middle dashed curve (two bilayers), the steady constriction radius is 765 nm. The shaded region represents variation of kin by 20%, which is an ad hoc means of representing stochastic variation in S (S = 4,000 ± 800). This predicts a range of constriction radii from ≈690–820 nm.
Fig. 3.
Plots of the membrane force (left-hand side of Eq. 4, dashed lines) and Z-ring force (right-hand side of Eq. 4, solid line) with S set to its steady-state value as a function of R for kin = 2.1 · 10−4 s−1 μM−1 nm−1 and FM = 16, 54, and 128 pN, which correspond to liposomes 2, 3, and 4 bilayers thick. Notice that for FM corresponding to 2 bilayers, there is no solution.
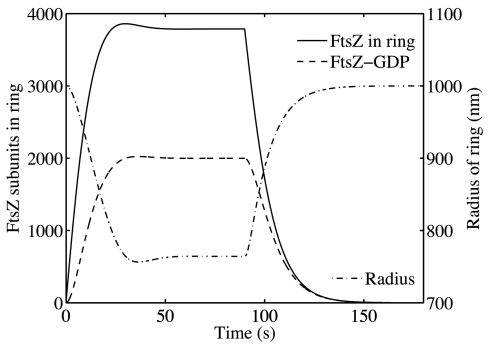
When the in vitro assays were carried out at concentrations of GTP that would allow for complete GTP depletion Osawa et al. (12) found that the Z-ring relaxed over a period of ≈20 s,, and the liposome returned to its original radius. We replicated this experiment by first allowing the system to find its steady state (90 s) and then imposed ZT = 0 (see SI Appendix) using the in vivo value of kin and the 3-bilayer liposome force scale. The resulting time course is shown in Fig. 4. Association of new polymers ceased and S and SD decreased, whereas R increased to its original radius. The constriction and release had half-times of 6.4 s and 8.8 s, respectively.
Fig. 4.
Constriction of the Z-ring in a liposome. For kin = 2.1 · 10−4 s−1 μM−1 nm−1 and FM = 54 pN, the ring constricts from 1,000 nm to 765 nm with a half-time of 6.4 s. Once the ring is in steady state, at 90 s, GTP is artificially depleted by imposing ZT = 0. The ring dissolves and the radius expands to its original 1,000 nm with a half-time of 8.8 s.
Discussion
We have developed a model of the bacterial Z-ring based on the hydrolyze-and-bend mechanism first proposed by Erickson et al. (10). Our model explains how FtsZ can generate the required force for cell division and sustain the force to almost total constriction (25 nm in wild type), even while the individual subunits are turning over rapidly.
The model provides estimates of the time scale for subunit turnover that are consistent with both wild-type and ftsZ84 mutant FRAP measurements. It also makes predictions for the relative abundance of GTP and GDP in the Z-ring. These results depend on the assumption that disassociation from the ring is from filament tips only. A Z-ring that allows dissociation of subunits from within filaments loses its hydrolyzed subunits too quickly and cannot generate the required force.
The model also reproduces the in vitro experiments of Osawa et al. (12) where the Z-ring was reconstituted inside liposomes. Constriction of the liposomes is slight (down to ≈60% of the original radius) and depends on the ratio of membrane resistance FM and the polymer incorporation rate kin, but not on either parameter individually. Our results are therefore robust to inaccuracy in parameter estimates provided the ratio is correct. Estimates from data of the number of lipid bilayers and of the number of subunits in the ring would provide a good test of the model.
An alternative hypothesis for force generation in the absence of motors is a Hill sleeve-type mechanism, where polymers slide relative to one another, reducing free energy by increasing the number of lateral bonds (35). However, the mutants described by Addinall and Lutkenhaus (9) (ftsZ26 and rodAsui) were capable of forming “Z-spirals” and “Z-arcs” that did not form closed loops but were nonetheless capable of generating invaginations. Although a sliding mechanism, which requires tension along the length of the structure, could still accomplish this, it would require selective anchoring of the FtsZ structure at its open ends. In addition, the lateral bonding not only provides an energy gradient and, hence, force but also comes with an energy barrier through the necessity of breaking bonds. Our estimates indicate that the force generated is significant but, relative to the thermal energy scale, so is the barrier (see SI Appendix).
The Z-ring has been observed to maintain 30% of the FtsZ in a cell even during constriction (14). Our model does not reproduce this result but instead predicts that the ring shrinks as it constricts. This could be reconciled by the up-regulation of kin or down-regulation of khyd or koff coincident with the onset of constriction, which is certainly possible given the multiple FtsZ regulatory pathways (36).
Osawa et al. (12) were not able to produce tubular liposomes with thinner walls. One possible reason is suggested by Fig. 3. By accounting for only small deformations in the membrane force calculation, we implicitly assumed that membrane stretch was minimal. In the case of large constrictions, our estimate of the stretch (see SI Appendix) indicates that for constriction radii <0.7 R0, membrane rupture becomes a possibility. For thick-walled liposomes, the upper solution prevents the system from entering this regime, but thin-walled liposomes have no such protection. It may be that thin-walled liposomes initially tubulate but are ruptured as soon as Z-rings form. This could also explain why constriction radii <0.6R0 were never seen.
A more detailed mechanical model, similar to the work of VanBuren et al. (22, 37) on microtubule dynamic instability, would be a valuable step forward from the model presented here. However, such a mechanically detailed treatment requires a better understanding of the details of in vivo kinetics, including the still elusive ultrastructure of and kinetic rates within the Z-ring.
Supplementary Material
Acknowledgments.
We thank B. Marshall, D. Fagnan, R. Wong, and A. Mogilner for useful discussion and the Pacific Institute for Mathematical Sciences International Graduate Training Centre Summer School in Mathematical Biology. This work was supported by the National Sciences and Engineering Research Council of Canada.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0808657106/DCSupplemental.
References
- 1.Vaughan S, Wickstead B, Gull K, Addinall S. Molecular evolution of FtsZ protein sequences encoded within the genomes of archaea, bacteria, and eukaryota. J Mol Evol. 2004;58:19–29. doi: 10.1007/s00239-003-2523-5. [DOI] [PubMed] [Google Scholar]
- 2.Miyagishima S. Origin and evolution of the chloroplast division machinery. J Plant Res. 2005;118:295–306. doi: 10.1007/s10265-005-0226-2. [DOI] [PubMed] [Google Scholar]
- 3.Bi E, Lutkenhaus J. FtsZ ring structure associated with division in Escherichia coli. Nature. 1991;354:161–164. doi: 10.1038/354161a0. [DOI] [PubMed] [Google Scholar]
- 4.Lutkenhaus J. FtsZ ring in bacterial cytokinesis. Mol Microbiol. 1993;9:403–409. doi: 10.1111/j.1365-2958.1993.tb01701.x. [DOI] [PubMed] [Google Scholar]
- 5.Ma X, Ehrhardt D, Margolin W. Colocalization of cell division proteins FtsZ and FtsA to cytoskeletal structures in living Escherichia coli cells by using green fluorescent protein. Proc Natl Acad Sci USA. 1996;93:12998–13003. doi: 10.1073/pnas.93.23.12998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sun Q, Yu X, Margolin W. Assembly of the FtsZ ring at the central division site in the absence of the chromosome. Mol Microbiol. 1998;29:491–503. doi: 10.1046/j.1365-2958.1998.00942.x. [DOI] [PubMed] [Google Scholar]
- 7.Bernhardt T, de Boer P. SlmA, a nucleoid-associated, FtsZ binding protein required for blocking septal ring assembly over chromosomes in E. coli. Mol Cell. 2005;18:555–564. doi: 10.1016/j.molcel.2005.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lutkenhaus J. Assembly dynamics of the bacterial MinCDE system and spatial regulation of the Z ring. Annu Rev Biochem. 2007;76:539–562. doi: 10.1146/annurev.biochem.75.103004.142652. [DOI] [PubMed] [Google Scholar]
- 9.Addinall S, Lutkenhaus J. FtsZ-spirals and -arcs determine the shape of the invaginating septa in some mutants of Escherichia coli. Mol Microbiol. 1996;22:231–237. doi: 10.1046/j.1365-2958.1996.00100.x. [DOI] [PubMed] [Google Scholar]
- 10.Erickson H, Taylor D, Taylor K, Bramhill D. Bacterial cell division protein FtsZ assembles into protofilament sheets and minirings, structural homologs of tubulin polymers. Proc Natl Acad Sci USA. 1996;93:519–523. doi: 10.1073/pnas.93.1.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lu C, Reedy M, Erickson H. Straight and curved conformations of FtsZ are regulated by GTP hydrolysis. J Bacteriol. 2000;182:164–170. doi: 10.1128/jb.182.1.164-170.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Osawa M, Anderson D, Erickson H. Reconstitution of contractile FtsZ rings in liposomes. Science. 2008;320:792–794. doi: 10.1126/science.1154520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Den Blaauwen T, Buddelmeijer N, Aarsman M, Hameete C, Nanninga N. Timing of FtsZ assembly in Escherichia coli. J Bacteriol. 1999;181:5167–5175. doi: 10.1128/jb.181.17.5167-5175.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stricker J, Maddox P, Salmon E, Erickson H. Rapid assembly dynamics of the Escherichia coli FtsZ-ring demonstrated by fluorescence recovery after photobleaching. Proc Natl Acad Sci USA. 2002;99:3171–3175. doi: 10.1073/pnas.052595099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Anderson D, Gueiros-Filho F, Erickson H. Assembly dynamics of FtsZ rings in Bacillus subtilis and Escherichia coli and effects of FtsZ-regulating proteins. J Bacteriol. 2004;186:5775–5781. doi: 10.1128/JB.186.17.5775-5781.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mukherjee A, Lutkenhaus J. Dynamic assembly of FtsZ regulated by GTP hydrolysis. EMBO J. 1998;17:462–469. doi: 10.1093/emboj/17.2.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen Y, Erickson H. Rapid in vitro assembly dynamics and subunit turnover of FtsZ demonstrated by fluorescence resonance energy transfer. J Biol Chem. 2005;280:22549–22554. doi: 10.1074/jbc.M500895200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huecas S, et al. The interactions of cell division protein FtsZ with guanine nucleotides. J Biol Chem. 2007;282:37515–37528. doi: 10.1074/jbc.M706399200. [DOI] [PubMed] [Google Scholar]
- 19.Li Z, Trimble M, Brun Y, Jensen G. The structure of FtsZ filaments in vivo suggests a force-generating role in cell division. EMBO J. 2007;26:4694–4708. doi: 10.1038/sj.emboj.7601895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Romberg L, Levin P. Assembly dynamics of the bacterial cell division protein FtsZ: Poised at the edge of stability. Annu Rev Microbiol. 2003;57:125–154. doi: 10.1146/annurev.micro.57.012903.074300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lan G, Dajkovic A, Wirtz D, Sun S. Polymerization and bundling kinetics of FtsZ filaments. Biophys J. 2008;95:4045–4056. doi: 10.1529/biophysj.108.132837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.VanBuren V, Odde DJ, Cassimeris L. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc Natl Acad Sci USA. 2002;99:6035–6040. doi: 10.1073/pnas.092504999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Molodtsov MI, Grishchuk EL, Efremov AK, McIntosh JR, Ataullakhanov FI. Force production by depolymerizing microtubules: A theoretical study. Proc Natl Acad Sci USA. 2005;102:4353–4358. doi: 10.1073/pnas.0501142102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dajkovic A, Lan G, Sun S, Wirtz D, Lutkenhaus J. MinC spatially controls bacterial cytokinesis by antagonizing the scaffolding function of FtsZ. Curr Biol. 2008;18:235–244. doi: 10.1016/j.cub.2008.01.042. [DOI] [PubMed] [Google Scholar]
- 25.Chen Y, Bjornson K, Redick S, Erickson H. A rapid fluorescence assay for FtsZ assembly indicates cooperative assembly with a dimer nucleus. Biophys J. 2005;88:505–514. doi: 10.1529/biophysj.104.044149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hörger I, et al. Langevin computer simulations of bacterial protein filaments and the force-generating mechanism during cell division. Physical Review E. 2008;77:11902. doi: 10.1103/PhysRevE.77.011902. [DOI] [PubMed] [Google Scholar]
- 27.Huecas S, et al. Energetics and geometry of FtsZ polymers: Nucleated self-assembly of single protofilaments. Biophys J. 2008;94:1796–1806. doi: 10.1529/biophysj.107.115493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Miraldi E, Thomas P, Romberg L. Allosteric models for cooperative polymerization of linear polymers. Biophys J. 2008;95:2470–2486. doi: 10.1529/biophysj.107.126219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Surovtsev I, Morgan J, Lindahl P. Kinetic modeling of the assembly, dynamic steady state, and contraction of the FtsZ ring in prokaryotic cytokinesis. PLoS Comput Biol. 2008;4:e1000102. doi: 10.1371/journal.pcbi.1000102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Andrews S, Arkin A. A mechanical explanation for cytoskeletal rings and helices in bacteria. Biophys J. 2007;93:1872–1884. doi: 10.1529/biophysj.106.102343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hörger I, Velasco E, Rivas G, Velez M, Tarazona P. FtsZ bacterial cytoskeletal polymers on curved surfaces: The importance of lateral interactions. Biophys J. 2008;94:L81–3. doi: 10.1529/biophysj.107.128363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lan G, Wolgemuth C, Sun S. Z-ring force and cell shape during division in rod-like bacteria. Proc Natl Acad Sci USA. 2007;104:16110–16115. doi: 10.1073/pnas.0702925104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Contera SA, Lemaitre V, de Planque MRR, Watts A, Ryan JF. Unfolding and extraction of a transmembrane alpha-helical peptide: Dynamic force spectroscopy and molecular dynamics simulations. Biophys J. 2005;89:3129–3140. doi: 10.1529/biophysj.105.061721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Oesterhelt F, et al. Unfolding pathways of individual bacteriorhodopsins. Science. 2000;288:143–146. doi: 10.1126/science.288.5463.143. [DOI] [PubMed] [Google Scholar]
- 35.Hill T. Theoretical problems related to the attachment of microtubules to kinetochores. Proc Natl Acad Sci USA. 1985;82:4404–4408. doi: 10.1073/pnas.82.13.4404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Weiss D. Bacterial cell division and the septal ring. Mol Microbiol. 2004;54:588–597. doi: 10.1111/j.1365-2958.2004.04283.x. [DOI] [PubMed] [Google Scholar]
- 37.VanBuren V, Cassimeris L, Odde D. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys J. 2005;89:2911–2926. doi: 10.1529/biophysj.105.060913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mickey B, Howard J. Rigidity of microtubules is increased by stabilizing agents. J Cell Biol. 1995;130:909–917. doi: 10.1083/jcb.130.4.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lu C, Stricker J, Erickson H. FtsZ from Escherichia coli, Azotobacter vinelandii, and Thermotoga maritima—Quantitation, GTP hydrolysis, and assembly. Cell Motil Cytoskeleton. 1998;40:71–86. doi: 10.1002/(SICI)1097-0169(1998)40:1<71::AID-CM7>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.