Nonlinear threshold behavior during the loss of Arctic sea ice

Abstract

In light of the rapid recent retreat of Arctic sea ice, a number of studies have discussed the possibility of a critical threshold (or “tipping point”) beyond which the ice–albedo feedback causes the ice cover to melt away in an irreversible process. The focus has typically been centered on the annual minimum (September) ice cover, which is often seen as particularly susceptible to destabilization by the ice–albedo feedback. Here, we examine the central physical processes associated with the transition from ice-covered to ice-free Arctic Ocean conditions. We show that although the ice–albedo feedback promotes the existence of multiple ice-cover states, the stabilizing thermodynamic effects of sea ice mitigate this when the Arctic Ocean is ice covered during a sufficiently large fraction of the year. These results suggest that critical threshold behavior is unlikely during the approach from current perennial sea-ice conditions to seasonally ice-free conditions. In a further warmed climate, however, we find that a critical threshold associated with the sudden loss of the remaining wintertime-only sea ice cover may be likely.

The retreat of Arctic sea ice during recent decades (1) is believed to be augmented by the difference in albedo (i.e., reflectivity) between sea ice and exposed ocean waters (2). Because bare or snow-covered sea ice is highly reflective to solar radiation, the increasing area of open water that is exposed as sea ice recedes leads to an increase in absorbed solar radiation, thereby contributing to further ice retreat. A number of recent studies have discussed the possibility that this positive ice–albedo feedback will cause the rapidly declining annual minimum (September) sea-ice cover to cross a critical threshold, after which the sea ice will melt back on an irreversible trajectory to a seasonally ice-free state (3–9).

Heuristically, one might expect in a simple annual mean picture of the Arctic Ocean that completely ice-covered and ice-free stable states could coexist under the same climate forcing. The ice-free state would remain warm because of the absorption of most incident solar radiation, whereas the ice-covered state would reflect most solar radiation and remain below the freezing temperature. In such a picture, these two stable states would be separated by an unstable intermediate state in which the Arctic Ocean is partially covered by ice and absorbs just enough solar radiation such that it remains at the freezing temperature: Adding a small amount of additional sea ice to this unstable state would lead to less solar absorption, cooling, and a further extended sea-ice cover. If the background climate warmed, the unstable state would require an increased ice extent to reflect sufficient solar radiation to remain at the freezing temperature. Beyond a critical threshold, the background climate would become so warm that the ice-covered state would reach the freezing temperature. At this point the stable ice-covered state and unstable intermediate state would merge and disappear in a saddle-node bifurcation, leaving only the warm ice-free state (10–12). This scenario suggests that if an ice-covered Arctic Ocean were warmed beyond the bifurcation point, there would be a rapid transition to the ice-free state. It would be an irreversible process in the sense that the Arctic Ocean would refreeze only after the climate had cooled to a second bifurcation point at which even an ice-free Arctic Ocean would become sufficiently cold to freeze, representing a significantly colder background climate than the original point at which the ice disappeared. Thus, the ice–albedo feedback could, in principle, cause a hysteresis loop in the Arctic climate response to warming.

Here, we investigate the central physical processes underlying the possibility of such a bifurcation threshold in future sea-ice retreat. We illustrate the discussion with a seasonally varying model of the Arctic sea ice–ocean–atmosphere climate system.

Arctic Sea Ice and Climate Model

The theory presented here describes the thermal evolution of sea ice, ocean mixed layer, and an energy balance atmosphere that is in steady-state with the underlying surface forcing, including also representations of dynamic sea-ice export and atmospheric meridional heat transport. The sea-ice thermodynamics in this model is an approximation of the full heat conduction equation of Maykut and Untersteiner (13), which provides the thermodynamic basis for most current sea ice models. Ice grows during the winter at the base, and when the surface reaches the freezing temperature in summer, ablation occurs at the surface as well as at the base. Our model produces an observationally consistent simulation of the modern Arctic sea ice seasonal cycle using a single 1-dimensional nonautonomous ordinary differential equation with observationally based seasonally varying parameters. Here we provide a brief summary of the model equations, which are fully derived from basic physical principles in the SI Appendix. The state variable E represents the energy per unit area stored in sea ice as latent heat when the ocean is ice covered or in the ocean mixed layer as sensible heat when the ocean is ice free,

where L_i is the latent heat of fusion for sea ice, h_i is the sea-ice thickness, c_ml is the mixed-layer specific heat capacity, and H_ml is the mixed-layer depth. The ocean mixed-layer temperature is written in terms of departure from the freezing point, T_ml ≡ T̃_ml − T̃_fr, where T̃_ml is the ocean mixed-layer temperature and T̃_fr is taken to be 0 °C. The time evolution of E is proportional to the net energy flux,

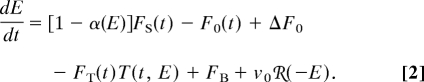Here, the Stefan–Boltzmann equation for outgoing longwave radiation has been linearized in the surface temperature departure from the freezing point, T(t, E) ≡ T̃ (t, E) − T̃_fr, as F₀(t) + F_T(t)T(t, E), where the parameters also account for the effects of a partially opaque atmosphere and atmospheric heat flux convergence that is a function the meridional temperature gradient. The seasonally varying values of F₀(t) and F_T(t) are derived by using an atmospheric model that incorporates observations of Arctic cloudiness (14), surface air temperature south of the Arctic (15), and atmospheric transport into the Arctic (16).

The term ΔF₀ represents a specified perturbation to the surface heat flux, which is zero by default but can be increased to prescribe a warming in the model. Incident surface shortwave radiation F_S(t) and basal heat flux F_B are specified at central Arctic values (13). The final term in Eq. 2 accounts for an observationally based constant ice export of v₀ = 10% year⁻¹ (17) when ice is present (E < 0), with the ramp function ℛ(x) defined to equal x when x ≥ 0 and to equal 0 when x < 0.

The surface temperature T(t, E) can evolve among 3 different regimes. (i) When ice is present (E < 0) and the surface temperature is below the freezing point [T(t, E) < 0], it is calculated from a balance between the energy flux above the ice surface and upward heat flux in the ice, −[1 − α(E)]F_S(t) + F₀(t) − ΔF₀ + F_T(t)T(t, E) = −k_i T(t, E)/h_i = k_iL_iT(t, E)/E. (ii) When the surface temperature warms to the freezing point [T(t, E) = 0], it remains at this point while the ice undergoes surface ablation. (iii) When the ice ablates entirely, the ocean mixed layer is represented as a thermodynamic reservoir by using T(t, E) = T_ml = E/(c_mlH_ml). Using the ramp function as a convenient notation for combining cases (i) and (ii), the surface temperature can be expressed as

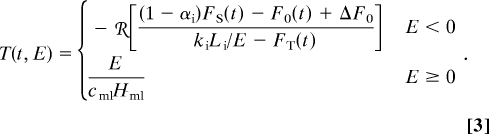The ocean is represented as either ice covered or ice free at any given time. To model the gradual transition between these regimes in a partially ice-covered Arctic Ocean, the albedo varies between values for ice (α_i) and ocean mixed layer (α_ml) with a characteristic smoothness given by the thickness parameter h_α,

We also consider a partially linearized version of the model in which Eq. 3 is replaced with

and there is no ice export (v₀ = 0). This causes the model equations to be linear with the exception of the ice–albedo feedback (Eq. 4).

Results

Seasonal Cycle.

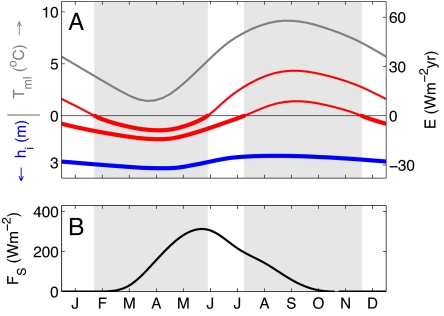
In a seasonally varying Arctic climate, warming might be expected to cause the sea ice to initially melt back to the point where the entire Arctic Ocean is ice free during part of the year, in contrast to the current perennial sea-ice cover in the central Arctic. Further warming would cause the ice-free period to increase until the Arctic Ocean becomes perennially ice free. We study this scenario theoretically by increasing the imposed surface heat flux ΔF₀ in Eqs. 2–4. In Fig. 1A, steady-state seasonal cycle solutions are plotted in regimes with perennial ice cover (blue curve), seasonally ice-free conditions (red curves), and perennially ice-free conditions (gray curve).

Fig. 1.

Sea ice seasonal cycle in a warming climate and solar radiation. (A) Seasonal cycle of stable solutions of the full nonlinear model are illustrated by plotting the model state E (energy per unit area in ocean mixed layer sensible heat or sea ice latent heat) versus time of year. Four solutions are plotted, each with different levels of surface heating ΔF₀: a perennial ice state (blue curve, ΔF₀ = 0), seasonally ice-free states with most of the year ice covered (lower red curve, ΔF₀ = 21 Wm⁻²) or most of the year ice free (upper red curve, ΔF₀ = 23 Wm⁻²), and a perennially ice-free state (gray curve, ΔF₀ = 19 Wm⁻²). As described in Eq. 1, when E > 0, it represents the mixed-layer temperature of an ice-free ocean (E = c_mlH_mlT_ml). At E = 0, the ocean mixed layer reaches the freezing point (T_ml = 0 °C), and further cooling will cause ice to grow. When E < 0, it represents the sea-ice thickness (E = −L_i h_i); note that ice thickness increases downward. Model solutions are drawn with thicker lines when the ocean is ice covered and thinner lines when the ocean is ice free. Solutions are obtained by integrating Eqs. 2–4 with seasonally varying parameter values given in Table S1 in SI Appendix until the model has converged on a steady-state seasonal cycle. The light-gray shaded region to the right represents the first months to become ice free in a warming climate (demarcated by zero-crossings of the seasonally ice-free solution with ΔF₀ = 21 Wm⁻²), whereas the light-gray shaded region to the left represents the last months that are ice covered in a further warmed climate (demarcated by zero-crossings of the seasonally ice-free solution with ΔF₀ = 23 Wm⁻²). (B) Seasonal cycle of incident solar radiation specified in the model based on central Arctic surface observations (13), indicating that the first months to become ice free in a warming climate (light-gray region to right) and the last months to be ice covered in a further warmed climate (light-gray region to left) experience similar amounts of solar radiation. Note that the radiation curve is asymmetric because of seasonal differences in Arctic cloudiness, but the qualitative results presented here do not depend on this asymmetry.

The annual minimum sea-ice area and thickness is commonly referred to as “summer” sea ice, and the annual maximum is commonly referred to as “winter” sea ice. This nomenclature may carry with it the implication that the ice–albedo feedback, which depends on the magnitude of the incident solar radiation, would be most prominent during the retreat of the summer sea-ice cover. Indeed, it is often conjectured that a critical threshold for the loss of summer Arctic sea ice may be more likely than a threshold for the loss of winter ice (8). However, as is illustrated by Fig. 1B, this terminology can be misleading because the ice cover receives a similar amount of incident solar radiation during the period of annual maximum as at annual minimum. The light-gray shaded regions in Fig. 1 illustrate the key transition periods in the state of the Arctic Ocean during the transition from perennial ice cover to seasonally ice-free conditions (light gray region to right) and from seasonally ice-free conditions to perennially ice-free conditions (light gray region to left). Both of these periods experience approximately equivalent amounts of incident solar radiation (Fig. 1B), with somewhat more solar radiation occurring during the period associated with the loss of winter ice (light gray region to left). Hence the ice–albedo feedback should be expected to be similarly strong during a transition to perennially ice-free conditions in a very warm climate (i.e., loss of winter ice) as during a more imminent possible warming to seasonally ice-free conditions (i.e., loss of summer ice).

Bifurcation Thresholds.

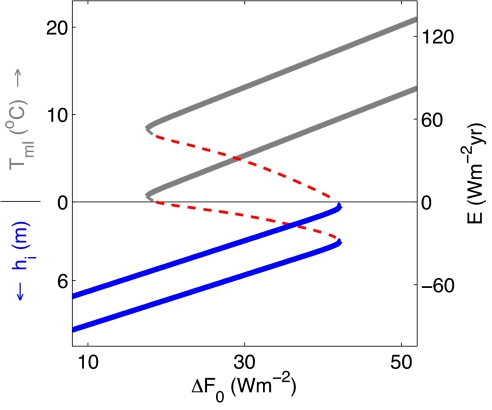
We begin the bifurcation analysis using the partially linearized version of the model (Eqs. 2, 4, and 5) to focus on the effect of albedo in the absence of other nonlinearities. In this representation, the Arctic Ocean is viewed as a simple radiating thermal reservoir with a temperature-dependent albedo, and the model exhibits a linear relaxation to a stable solution in each albedo regime. As would be expected by analogy with the discussion above of an annual mean Arctic Ocean with a variable sea ice edge, Fig. 2 illustrates that when ΔF₀ becomes sufficiently large for the ocean to remain perennially ice free with α = α_ml, an unstable seasonally ice-free solution (red dashed curves) appears in a saddle-node bifurcation of cycles [for a discussion of the theory of bifurcations in periodic systems, see, e.g., Strogatz (18)].

Fig. 2.

Bifurcation diagram for the partially linearized model, where nonlinear sea-ice thermodynamic effects have been excluded but the ice–albedo feedback has been retained (Eqs. 2, 4, and 5). For each value of the surface heating ΔF₀, the model is integrated until it converges on a steady-state seasonal cycle, and the annual maximum (upper curve) and annual minimum (lower curve) values of E are plotted. Solutions with perennial sea-ice cover are indicated in blue, seasonally ice-free solutions in red, and perennially ice-free solutions in gray. Dashed lines indicate unstable solutions, which have been determined by constructing an annual Poincaré map and finding the fixed points (i.e., numerically integrating the model for 1 year starting from an array of initial conditions and identifying the solutions with the same value of E at the end of the year as the initial condition). The curves have been smoothed with a boxcar filter to suppress a small level of noise associated with numerical integration. Note that the lines are slightly curved at the 2 bifurcation points because of the smooth albedo transition associated with h_α > 0. The vertical axis is labeled as in Fig. 1A.

The unstable solution separates stable solutions with perennial ice (blue curves) or perennially ice-free conditions (gray curves). The perennial ice regime collides with the unstable seasonally ice-free state and disappears in a second saddle-node bifurcation of cycles at the point where ΔF₀ becomes sufficiently large that the ice completely melts at the time of annual maximum E in the cold stable state. Because there is significant incident solar radiation during both the maximum and minimum periods of the seasonal cycle of E (Fig. 1), the ice–albedo feedback ensures that all seasonally ice-free solutions will be unstable (Fig. 2).

When nonlinear sea-ice thermodynamic effects are included (Eqs. 2–4), basal ice formation is controlled by a diffusive vertical heat flux of k_iΔT/h_i, where ΔT is the difference between surface and basal temperatures and the base is assumed to be at the freezing point. This causes thin ice to grow significantly faster than thick ice (13). It would also cause thin ice to experience greater basal ablation during the summer melt season, but the surface temperature only warms until it reaches the freezing point (ΔT = 0) and surface melt begins, making the rate of melt less sensitive to thickness. These 2 effects, both nonlinear in E, are expressed in Eq. 3 by the −k_i/h = k_iL_i/E term in the denominator and the ramp function ℛ(x), respectively. The result is an increase in the rate of growth for thin ice that is more stabilizing for thinner ice, as pointed out (19) and applied (20) in previous studies. This is in contrast to the state-independent linear mixed-layer stabilizing term, −F_T(t)E/c_mlH_ml, which applies when E > 0 (Eqs. 2 and 3).

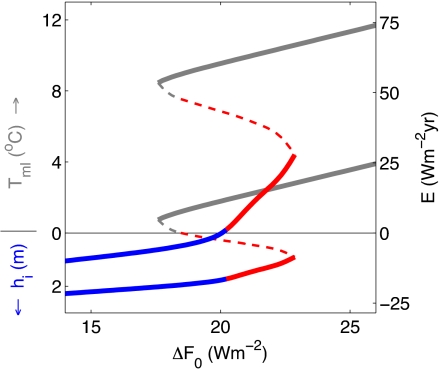
These nonlinearities allow for the existence of a stable seasonally ice-free solution (Fig. 3). When a sufficiently large value of ΔF₀ is chosen such that the cold solution becomes ice free during a small part of the year, a slight increase in temperature would lead to a longer open-water period and a thinner seasonal ice cover. Although the increased period of open water promotes warming through the ice–albedo feedback, the thinner ice grows significantly faster because of the sea-ice thermodynamic effects that are nonlinear in E. During the ice-covered portion of the year, the stability of the solution is controlled by this strong nonlinear stabilizing effect, but during the ice-free portion of the year, it is replaced by the weaker linear mixed-layer stabilizing term. This causes the stabilizing sea-ice thermodynamic effects to dominate the destabilizing ice–albedo feedback and allow a stable seasonally ice-free solution only when there is ice cover during a sufficiently long portion of the year. Nonetheless, the ice–albedo feedback causes this regime to warm at an increased rate in response to increasing heat flux (compare slopes of red and blue curves in Fig. 3). As the ice-covered fraction of the year decreases in a warming climate, the stabilizing ice thermodynamic effects become less pronounced in the full annual cycle, and a bifurcation occurs when ice covers the Arctic Ocean during a sufficiently small fraction of the year to allow the ice–albedo feedback to dominate. Hence, when the Arctic warms beyond this point, the system supports only an ice-free solution (Fig. 3).

Fig. 3.

Bifurcation diagram for the full nonlinear model (Eqs. 2–4). Axes and colors are as described in the Fig. 2 legend. The inclusion of nonlinear sea-ice thermodynamic effects stabilizes the model when sea ice is present during a sufficiently large fraction of the year, allowing stable seasonally ice-free solutions (red solid curves). Under a moderate warming (ΔF₀ = 15 Wm⁻²), modeled sea-ice thickness varies seasonally between 0.9 and 2.2 m. Further warming (ΔF₀ = 20 Wm⁻²) causes the September ice cover to disappear, and the system undergoes a smooth transition to seasonally ice-free conditions. When the model is further warmed (ΔF₀ = 23 Wm⁻²), a saddle-node bifurcation occurs, and the wintertime sea ice cover abruptly disappears in an irreversible process. Although the specific values of ΔF₀ at which the transitions occur are sensitive to parameter choices, the qualitative features of Fig. 3 are highly robust to changes in model parameter values (Fig. S4 in SI Appendix).

Discussion

Comparison with Results of Other Models.

The theoretical treatment presented here is constructed to facilitate simple conceptual interpretation, and to this end many processes have been neglected. Factors including possible sea ice-cloud feedbacks (refs. 21–23 and D.S. Abbot, C.C. Walker, E. Tziperman, unpublished manuscript), the dependence of sea ice surface albedo on snow and melt pond coverage (24, 25), ocean heat flux convergence feedbacks (6, 26), changes in wind-driven ice dynamics (7), and changes in ice rheology (27) in a thinning ice cover (28) could potentially lead to other bifurcation thresholds or smooth out the threshold investigated here, akin to the smoothing of a first order phase transition because of statistical fluctuations (29). We are emboldened in our approach, however, because behavior consistent with the mechanism proposed here can be found in the published results of models with a broad range of complexities. (i) A “toy model” that is forced by a step-function seasonal cycle produced no stable seasonally ice-free solution in the published parameter regime (30), but by a slight adjustment of the tunable model parameters one can find a stable seasonally ice-free solution that coexists with a stable perennially ice-free solution (Fig. S5 in SI Appendix), consistent with the findings presented here. (ii) In a variant of the model used in this study that is significantly more complex (representing the simultaneous evolution of fractional Arctic sea-ice coverage, mean thickness, and surface temperature, as well as ocean mixed-layer temperature), increasing the level of greenhouse gas forcing leads to a gradual transition to seasonally ice-free solutions followed by a bifurcation threshold during the transition to perennially ice-free conditions (31), as in Fig. 3. (iii) Turning to the most complex current climate models, approximately half the coupled atmosphere–ocean global climate models used for the most recent IPCC report (32) predict seasonally ice-free Arctic Ocean conditions by the end of the 21st century, and none predict perennially ice-free conditions by the end of the 21st century. However, perennially ice-free Arctic Ocean conditions occur in 2 of the model simulations after CO₂ quadrupling. Neither of the models exhibits an abrupt transition when the annual minimum (September) ice cover disappears, but after further warming 1 of the models abruptly loses its March ice cover when it becomes perennially ice free (26). The physical mechanism presented here may help explain this abrupt simulated loss of March ice following the gradual simulated loss of September ice.

Conclusions.

Our analysis suggests that a sea-ice bifurcation threshold (or “tipping point”) caused by the ice–albedo feedback is not expected to occur in the transition from current perennial sea ice conditions to a seasonally ice-free Arctic Ocean, but that a bifurcation threshold associated with the sudden loss of the remaining seasonal ice cover may occur in response to further heating. These results may be interpreted by viewing the state of the Arctic Ocean as comprising a full seasonal cycle, which can include ice-covered periods as well as ice-free periods. The ice–albedo feedback promotes the existence of multiple states, allowing the possibility of abrupt transitions in the sea-ice cover as the Arctic is gradually forced to warm. Because a similar amount of solar radiation is incident at the surface during the first months to become ice free in a warming climate as during the final months to lose their ice in a further warmed climate, the ice–albedo feedback is similarly strong during both transitions. The asymmetry between these two transitions is associated with the fundamental nonlinearities of sea-ice thermodynamic effects, which make the Arctic climate more stable when sea ice is present than when the open ocean is exposed. Hence, when sea ice covers the Arctic Ocean during fewer months of the year, the state of the Arctic becomes less stable and more susceptible to destabilization by the ice–albedo feedback. In a warming climate, as discussed above, this causes irreversible threshold behavior during the potential distant loss of winter ice, but not during the more imminent possible loss of summer (September) ice.

The relevance of any basic theory to the actual future evolution of the complex climate system must be carefully qualified. Because the time scale associated with the sea-ice response to a change in forcing may be decadal, and the time scale associated with increasing greenhouse gas concentrations may be similar, the system may not be operating close to a steady-state. In the gradual approach to steady-state under a continual change in forcing, the difference between a region of the steady-state solution with increased sensitivity to the forcing and an actual discontinuous bifurcation threshold (as in Fig. 3) could be difficult to discern. If greenhouse gas concentrations were reduced after crossing a bifurcation threshold, however, the possible irreversibility of the trajectory would certainly be expected to be relevant.