Abstract
Physiological changes that result in changes in bacterial gene expression are often accompanied by changes in the growth rate for fast adapting enteric bacteria. Because the availability of RNA polymerase (RNAP) in cells depends on the growth rate, transcriptional control involves not only the regulation of promoters, but also depends on the available (or free) RNAP concentration, which is difficult to quantify directly. Here, we develop a simple physical model describing the partitioning of cellular RNAP into different classes: RNAPs transcribing mRNA and ribosomal RNA (rRNA), RNAPs nonspecifically bound to DNA, free RNAP, and immature RNAP. Available experimental data for Escherichia coli allow us to determine the 2 unknown parameters of the model and hence deduce the free RNAP concentration at different growth rates. The results allow us to predict the growth-rate dependence of the activities of constitutive (unregulated) promoters, and to disentangle the growth-rate-dependent regulation of promoters (e.g., the promoters of rRNA operons) from changes in transcription due to changes in the free RNAP concentration at different growth rates. Our model can quantitatively account for the observed changes in gene expression patterns in mutant E. coli strains with altered levels of RNAP expression without invoking additional parameters. Applying our model to the case of the stringent response after amino acid starvation, we can evaluate the plausibility of various scenarios of passive transcriptional control proposed to account for the observed changes in the expression of rRNA and biosynthetic operons.
Keywords: constitutive promoters, ribosomal RNA, stringent response, transcription
Bacteria are able to grow with wildly different growth rates in different media. Depending on the growth conditions, the quality and availability of nutrients, they differ in cell size and macromolecular compositions, e.g., the ratio of protein, RNA, and DNA (1, 2). For bacteria in exponential growth phase, this dependence was found empirically as a dependence on growth rate rather than as a dependence on the specific growth medium, because bacteria grown in different media that support the same growth rate exhibited the same macromolecular composition (1–3). For this reason, many parameters of the bacterial cell have been characterized as functions of the growth rate (4). Many of these parameters affect gene expression, e.g., the cellular abundance of transcription and translation machinery. Gene expression is therefore expected to exhibit a generic growth-rate dependence in addition to the specific genetic regulation (5). Indeed, even unregulated (or “constitutively expressed”) promoters exhibit growth-rate-dependent activities (5, 6). Some genes, e.g., the ribosomal RNA operons (rrn), are additionally regulated in a growth-rate-dependent fashion (7, 8).
One difficulty in elucidating various mechanisms of growth-rate-dependent transcriptional control lies in the fact that the activity of a promoter depends not only on the active control mechanisms, but also directly on the availability of RNA polymerase (RNAP), which is growth-rate dependent. For example, the total number of RNAPs per cell was determined to increase from 1,500 at slow growth (0.6 doublings per hour) to 11,400 at fast growth (2.5 doublings per hour) (4). How the concentration of free RNAPs, which is crucial to the initiation of transcription, depends on growth rate is less clear. Nevertheless, “passive transcriptional control” (3), i.e., changes in gene expression due to changes of the free RNAP concentration alone, was proposed to play a role in the growth-rate-dependent regulation of rRNA transcription (7, 9), based on observations that similar behaviors could be induced by RNAP mutations (9, 10). Passive control has also been proposed to account for changes in transcription on sudden depletion of nutrients, during the so-called “stringent response.” Surprisingly, both decreasing and increasing free RNAP concentrations have been proposed to occur during the stringent response, and were invoked by different authors to explain either the down-regulation of rrn operons (6, 9) or the up-regulation of biosynthetic operons (10, 11). These proposals are hard to test experimentally, because the concentration of the free RNAPs in cells is difficult to measure directly. Also, indirect inference based on measurements of the cytoplasmic fraction of RNAPs (12, 13) and promoter activities (6, 14) rely on assumptions that may be questioned (see below).
In this study, we developed a method to estimate the free RNAP concentration in Escherichia coli cells growing with different growth rates. Our method is based on a physical model that partitions the RNAPs in a cell into fractions representing RNAPs transcribing mRNA and rRNA, RNAPs nonspecifically bound to DNA, free RNAPs, and RNAP assembly intermediates. Our model combined features from previous studies of RNAP partitioning (15–17), none of which, however, included all of these fractions. By integrating the available data from both direct and indirect measurements of the free RNAP concentration with the growth-rate dependence of the macromolecular composition of E. coli cells (4), this model allowed us to predict the growth-rate-dependent partitioning of RNAPs, thereby providing a quantitative picture of the various activities of RNAPs in the cell. The results for the concentration of free RNAP allowed us to predict the growth-rate dependence of the activities of the constitutive promoters, as well as to disentangle the various growth-rate-dependent factors affecting the activity of the rrn promoters. We finally applied our model to investigate the change in free-RNAP concentration during the stringent response and test several scenarios for passive control. The results suggest that passive control, both positive and negative, should not be expected to play a major role in the stringent response, at least in the early stage immediately after sudden starvation.
Model and Results
The concentration of free RNAPs in cells is difficult to measure. Two approaches have been described in the literature. The first one is indirect and uses transcription from a constitutive (unregulated) promoter (6, 7, 14, 18). This approach yields only RNAP concentrations relative to the Michaelis constant of that promoter. To estimate an absolute value of the free RNAP concentration under this approach, one has to rely on the kinetic parameters of the promoter measured in vitro (18), which depend on experimental conditions and may not be representative for the situation in vivo. The interpretation of such data is further complicated by controversies about whether specific promoters (in particular, the rRNA promoter P2 used in refs. 6 and 7) are actually constitutive (see below). The second, more direct approach is to use DNA-free minicells and compare the RNAP content of minicells and normal cells to obtain the fraction of cytoplasmic RNAPs (12, 13). The cytoplasmic RNAP measured in these experiments, however, includes free RNAPs and RNAP assembly intermediates, and possibly other forms such as RNAPs sequestered on 6S RNA (19) in stationary or very slowly growing cells. The advantage of this approach is that it yields absolute RNAP concentrations. However, to link the results to the free-RNAP concentration, we need to understand quantitatively the partitioning of total RNAP, which is the subject of this section.
Model for the Partitioning of RNA Polymerases.
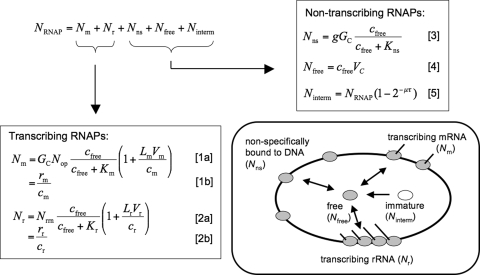
We developed a model for the partitioning of RNAP based on the assumption that, in exponentially growing cells, all RNAP in the cell falls into 1 of 5 different classes: (i) RNAPs transcribing mRNA, (ii) RNAPs transcribing rRNA, (iii) RNAPs nonspecifically bound to DNA, (iv) free RNAPs in the cytoplasm available for transcription, and (v) RNAP subunits and assembly intermediates (see Fig. 1). Some of these classes require further explanation.
Fig. 1.
Model for the partitioning of RNAPs. In exponentially growing cells all RNAPs are taken to fall into 5 classes, RNAPs transcribing mRNA (Nm) and rRNA (Nr), RNAPs nonspecifically bound to DNA (Nns), free RNAPs (Nfree), and RNAP assembly intermediates (immature RNAPs, Ninterm). The total number of RNAPs per cell (NRNAP) is the sum of the number of RNAPs in these classes. Our model describes the numbers of RNAPs in each class by equations that link them to measured biophysical parameters of the cell (see SI Text for a detailed description and Tables S1 and S2 for the parameter values, many of which are growth-rate dependent). The numbers of transcribing RNAPs (Nr and Nm) are both described by a microscopic model Eqs. 1a, 2a, and estimated directly from measured RNA synthesis rates Eqs. 1b and 2b.
RNAPs nonspecifically bound to DNA.
Nonspecific binding of RNAP to DNA, as demonstrated in vitro (20, 21), is much weaker than the specific binding of RNAPs to promoters, but is nevertheless expected to play an important role in vivo, because the number of sites for nonspecific binding greatly exceeds the number of promoters (22, 23). In vitro, nonspecifically bound RNAPs have been directly shown to slide along DNA (24, 25), which may play a role in the kinetics of promoter binding. In vivo, nonspecific binding has not been directly demonstrated for RNAP. Nonspecific binding (26) and sliding along DNA (27) have, however, been demonstrated in vivo for transcription factors, which exhibit nonspecific binding to DNA similar to that of RNAPs in vitro (22, 28). Furthermore, nonspecific binding of RNAP in vivo is consistent with the observation that a large fraction of RNAPs, larger than the fraction of actively transcribing RNAPs, is associated with the nucleoid (13).
Assembly intermediates.
Intermediates of RNAP assembly (immature RNAPs) have to be taken into account (13), because the RNAP content of cells is determined by measuring the fraction of total protein mass that is in β and β′ subunits of RNAP (4). Some of these subunits are not or are only partially assembled into functional RNAPs in the cell (29). These assembly intermediates are located in the cytoplasm and radioactively labeled β and β′ subunits appear in the nucleoid after ≈5 and 2.5 min, respectively (29). The larger of these times is likely to correspond to the time needed to fully assemble an RNAP plus the transition to the nucleoid, thereby providing an upper bound for the maturation time τ.
Additional classes of RNAP.
Under conditions different from exponential growth there may be fractions of RNAPs in addition to the 5 listed above. Additional classes are clearly present under various stress conditions and for cells in the stationary phase, where alternative sigma factors play important roles, so that RNAPs have to be partitioned according to their sigma factors (16, 30), and where a fraction of RNAPs is inactivated by the regulatory 6S RNA (19). In this study, we focus on exponentially growing cells, for which the concentration of the housekeeping sigma factor, sigma 70, is very high (16, 31), and concentrations of alternative sigma factors are considerably lower (16, 30). In addition, alternative sigma factors have lower affinities for core RNAP than sigma 70 (32). These 2 features allow us to neglect the competition of sigma factors for exponentially growing cells. Furthermore the affinity of sigma 70 for the RNAP core enzyme is very high (32, 33), so that essentially all free RNAPs are bound to sigma factor.
RNAPs pausing in transcription.
The models of Bremer et al. (15) and of Tadmor and Tlustly (17) consider RNAPs pausing in transcription as an additional class. We take pausing to be an integral part of transcript elongation, because the measured elongation speeds are average values that include pauses (34, 35). An incentive for Bremer et al. to separate pauses from active transcription is the assumption that there are specific “pause genes,” for which pausing is strongly enhanced during the stringent response, so that these genes sequester RNAPs. There is, however, little experimental support for the existence of such pause genes and the transcription speeds assumed in these models are far lower than measured values (34, 35). The main difference between our model and the models of refs. 15 and 17 is thus the description of nontranscribing RNAPs associated with the nucleoid: In our model, these RNAPs are considered as nonspecifically bound to DNA, whereas nonspecific binding is not included in the models of refs. 15 and 17, where these RNAPs are assumed to be pausing in transcription.
To determine the partitioning of RNAPs into these 5 classes, we derived quantitative expressions for the numbers of RNAPs in each class that link these numbers to measured parameters of the cell [Fig. 1 and supporting information (SI) Text]. The numbers of RNAPs transcribing mRNA and rRNA (Nm and Nr) are estimated directly from measured RNA synthesis rates (rm and rr) and RNAP speeds (cm and cr) at different growth rates. In addition we link these numbers to the biophysical properties of the corresponding promoters by using a Michaelis–Menten model of transcription activity, which relates the transcription rates to the concentration cfree of free RNAP (15). This description is used below to study growth-rate-dependent regulation of transcription.
The main task of our model is to quantify the partitioning of the nontranscribing RNAPs into the other 3 classes, namely free RNAPs (Nfree), nonspecifically bound RNAPs (Nns), and assembly intermediates (Ninterm). In our model, the number of nonspecifically bound RNAPs is determined by equilibrium binding to DNA, with a growth-rate-dependent number of possible binding sites. As mentioned above, sliding of nonspecifically bound RNAPs along DNA may play a role for the kinetics of promoter binding; this kinetic effect is not explicitly described in our model, which describes only the (quasi-)equilibrium binding of RNAPs to promoters and nonspecific sites. In this thermodynamic description, the numbers of transcribing RNAPs depend only on the concentration of free RNAPs even though nonspecifically bound RNAPs may start transcribing without dissociation from the DNA. The number of free RNAPs is described by a concentration of free RNAPs (cfree), which we determine below as a function of growth rate, and the cellular volume (VC), and the number of immature RNAPs is described by a maturation time τ after which newly synthesized RNAPs are functional.
Most parameters of our model have been measured (see ref. 4, SI Text, and Tables S1 and S2), but the model contains 2 unknown parameters, the dissociation constant for nonspecific RNAP-DNA binding, Kns, and the maturation time τ of newly synthesized RNAPs. We assume these parameters are independent of the growth rate themselves and determine them by matching the fraction of cytoplasmic RNAPs predicted by our model to data from minicell experiments (12, 13) (see SI Text and Fig. S1). This procedure leads to a maturation time τ of 3.4 min and a dissociation constant for nonspecific binding of 3,100 μM. These values are consistent with experimental data, as discussed in SI Text, and will be used throughout the following. However, 2-fold changes in the values of these 2 parameters lead to very similar results (Fig. S2). We note that the dissociation constant might be growth-rate dependent if the level of macromolecular crowding changes with the growth rates (17). This question has not been addressed directly by experiments, but indirect evidence does not suggest a strong change (see SI Text).
Predicted Growth-Rate Dependence of RNAP Partitioning.
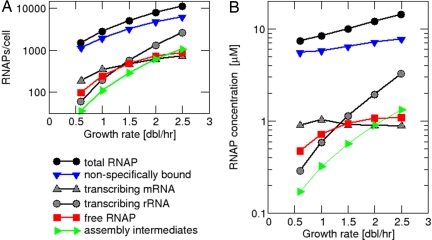
By using the model above, we computed the partitioning of RNAP into each of the 5 classes for growth rates ranging from 0.6 to 2.5 doublings per hour; the results are shown as total number per cell in Fig. 2A and as concentration (after taking into account the growth-rate-dependent cell size; see Table S1) in Fig. 2B. In these plots, gray symbols indicate the species of transcribing RNAPs that are estimated directly from RNA synthesis rates (using Eqs. 1b and 2b in Fig. 1), whereas colored symbols indicate the predicted partitioning of the nontranscribing RNAPs: nonspecifically bound (blue), free (red), assembly intermediates (green). Fig. 2A shows that the actual numbers of RNAPs per cell (measured and predicted) increase with the growth rate for each of the 5 species. However, the numbers of RNAPs transcribing rRNA (gray circles) and those involved in assembly (green triangles) increase more strongly (44-fold and 31-fold, respectively) than the numbers of RNAPs of the other species (at most, 9-fold) and more strongly than the measured total number of RNAPs per cell (black circles), which exhibits a 7.6-fold increase.
Fig. 2.
Partitioning of RNAPs at different growth rates. (A) Total number of RNAPs per cell and numbers of RNAPs in the different classes as predicted by our model. (B) Concentrations of total RNAP and RNAPs in the different classes.
Fig. S3 shows the same RNAP partitioning as fractions of the total RNAP number. For all growth rates, nonspecific binding to DNA (blue triangles) is predicted to make up the largest fraction of RNAPs, despite the fact that nonspecific binding is very weak. Nonspecific binding accounts for 75% of all RNAPs at slow growth (0.6 doubling per hour). This fraction decreases to 54% at 2.5 doublings per hour. The strongest increase is seen for the fraction of RNAPs transcribing rRNA, which increases ≈5.8-fold, from 4% to 23%. Likewise, the fraction of RNAP assembly intermediates exhibits a 4-fold increase, whereas the fraction transcribing mRNA and the fraction of free RNAPs exhibit only small changes (<2-fold). Note that the total fraction of cytoplasmic RNAP (red + green) is <20% and the fraction of assembly intermediates is <10% even at the highest growth rate studied.
We finally turn to the free RNAPs that is the focus of our study. As shown by the red curve in Fig. 2B, the concentration of free RNAPs is predicted to increase from 0.47 μM for a growth rate of 0.6 doublings per hour to 1.1 μM for 2.5 doublings per hour. The range of the free RNAP concentration is substantially higher than the estimate of 30 nM made by McClure (for a doubling time of 50–60 min) based on a comparison of in vivo transcription rates from various promoters with their Michaelis constants measured in vitro (18). Our result (red curve of Fig. 2B) has 2 remarkable features that will be elaborated below: (i) the overall change of the free RNAP concentration over the studied range of growth rates is only ≈2-fold, significantly less than previous estimates (6, 14, 15), and (ii) the growth rate dependence of the free RNAP concentration saturates at high growth rates.
Discussion
Constitutive Promoters.
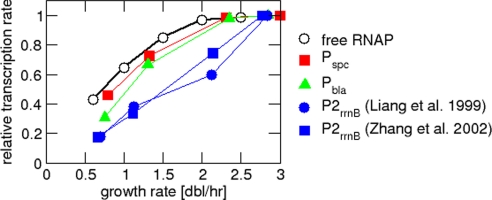
The transcription from unregulated (constitutive) promoters is expected to depend on the growth rate in a way that is completely determined by the growth-rate dependence of the free RNAP concentration.* Based on this idea, Liang et al. (6) have studied the transcription of promoters believed to be constitutive to determine the growth rate dependence of the free RNAP concentration. They found that, at slow growth rates, the transcription from these promoters† increased approximately in parallel with increasing growth rate, i.e., the ratio of the levels of transcription from these promoters remained approximately constant (see also Fig. S4 A and B). At fast growth, the transcription rate from most promoters saturated, but transcription from the ribosomal RNA promoter P2 kept increasing (purple line in Fig. S4A or ref. 6). Liang et al. suggest the following interpretation of these results: The increase of transcription of rrn P2 reflects the increase of the free-RNAP concentration, as P2 appears not to be saturated with RNAPs under their experimental conditions. The other constitutive promoters, however, become saturated with RNAP at fast growth, thereby reflecting the increase of the free RNAP concentration only at slow growth.
Although the argument of Liang et al. (6) is very elegant, this interpretation has several difficulties. First, the parallel increase of transcription from these promoters is only approximate. Comparing the 2 smallest growth rates studied by Liang et al. (where all of their promoters should be far from saturation with RNAPs), the increase in transcription varies between 1.4-fold and 2-fold (see also Fig. 3). This may not be sufficient to distinguish constitutive expression from weakly regulated expression. Second, a comparison of their results for wild type cells and for the relaxed strain devoid of ppGpp shows that, at a given growth rate, the transcription from P2 is almost the same in both strains (figure 3 of ref. 6; see also Fig. S5A). According to their interpretation, the free-RNAP concentration is thus also the same in both strains and one would expect the transcription rates of other constitutive promoters also to be the same. Their data show, however, that the transcription from most other constitutive promoters is reduced in the relaxed strain at high growth rates compared with the wild type (figure 2 of ref. 6; see also Fig. S5B). Finally, the method is based on the assumption that P2 is a constitutive promoter, which is controversial (see SI Text).
Fig. 3.
Growth-rate-dependent transcription from constitutive promoters. Growth-rate dependence of the transcription rates from several constitutive promoters and the rrn promoter P2. Data are taken from ref. 6 and have been normalized to the maximal value per promoter. (For P2 we also included corresponding data from ref. 14.) The black curve indicates the free RNAP concentration from Fig. 2, which is proportional to the predicted transcription rate from an unsaturated constitutive promoter.
By using our result for the free-RNAP concentration, we can predict the growth-rate dependence of the transcription rate for an unregulated promoter, i.e., the rate of mRNA synthesis, which corresponds to the mRNA level assuming that mRNA lifetime is not growth-rate dependent. The growth-rate dependence of an unsaturated constitutive promoter should be proportional to the growth-rate dependence of the free RNAP concentration. In Fig. 3, we plotted the data of Liang et al. (6) for the growth rate dependence of several constitutive promoters (Pbla, Pspc, P2) together with the growth-rate dependence of the free-RNAP concentration (red curve of Fig. 2B). All curves were normalized to their respective maximal value. This plot shows that the growth-rate dependence of those promoters with saturating expression at fast growth (Pbla, Pspc) approximately parallels the growth-rate dependence of the free RNAP concentration. This observation suggests a rather different interpretation of the data of Liang et al. (6): Transcription from these promoters directly reflects the free RNAP concentration at all growth rates. The apparent saturation of these promoters at fast growth does not indicate that these promoters are saturated with RNAPs, but according to our picture, results from the fact that free RNAP saturates for high growth rates. This interpretation also suggests that the observed increase of transcription from the P2 promoter of rRNA (6, 14) is due to growth-rate-dependent regulation, with the implication that P2 is not a constitutive promoter. (See SI Text for a detailed discussion of the P2 promoter, including a review of the salient arguments in the literature.) We note that the 2 interpretations could be distinguished experimentally by overexpressing RNAP in fast-growing cells. While the original interpretation of Liang et al. (6) predicts that transcription from the constitutive promoters should be unaffected by the increased RNAP level, our interpretation predicts an increase in the transcription of the constitutive promoters. Such an experiment has so far only been done with slowly growing cells (see below).
Growth-Rate-Dependent Regulation of Promoter Activity.
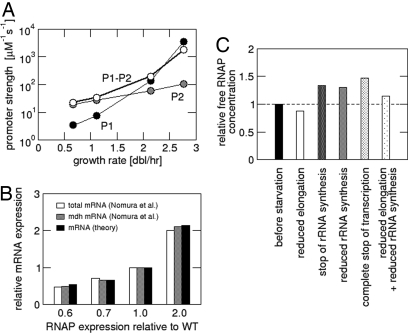
Next, we used our result for the free-RNAP concentration to study the growth-rate-dependent regulation of the rrn promoters. (A corresponding calculation for the average mRNA-synthesizing promoter is described in SI Text.) Over the range of growth rates studied here, there is a 44-fold increase in rRNA synthesis (Table S1), which is based on a 2.9-fold increase in of the operons copy number (4) and a 2.3-fold increase of the free RNAP concentration (Fig. 3). As a consequence, a 6.6-fold increase in rrn transcription is achieved by an increase in promoter strength, which reflects growth-rate-dependent regulation, isolated from the change in free RNAP concentration.‡ To determine promoter strengths at different growth rates, we use a Michaelis–Menten model of transcription (Eqs. 1a and 2a), with the ratio of the maximal transcription rate and its Michaelis constant, Ar = Vr/Kr taken to be a measure of the promoter strength. Fig. 4A shows the promoter strengths for the promoter pair P1-P2 of the rrn operons as well as those for the individual rrn promoters P1 and P2, calculated in this way from the transcription rates measured in ref. 14. The P1-P2 promoter strength Ar increases ≈80-fold over the studied range of growth rates (calculating Ar from the transcription rates given in ref. 4 leads to smaller values, but a similar growth-rate dependence; see Fig. S6A). The P1 promoter exhibits strong growth-rate-dependent regulation, with a predicted ≈1,000-fold increase of its promoter strength. As discussed above, we expect the strength of P2 to be regulated as well, but Fig. 4A suggests that its regulation is much weaker than that of P1, with only a 5.4-fold increase of the promoter strength. We note that over the range of growth rates where Liang et al. observed covariation of P2 with constitutive promoters (≈0.6–1.3 doublings per hour) (6), our model gives only a ≈1.5-fold change in the strength of P2, which is probably too small to be distinguished from covariation in that experiment. Our conclusion of a weak growth-rate-dependent regulation of P2 is in agreement with the conclusion of Murray et al. (36) based on in vitro studies (see also SI Text). However, our model additionally allows us to separate the regulation of the promoter from the growth-rate dependence of the free RNAP concentration.
Fig. 4.
Consequences of the predicted free RNAP concentration. (A) Growth-rate-dependent regulation of the rrn promoters: Effective promoter strengths for the rrn promoters P1 (black), P2 (gray), and the pair P1-P2 (white) as calculated from the transcription rates measured in ref. 14. (B) Predicted mRNA expression for over- and under expression of RNAP and comparison with data from ref. 37. (C) Passive control during the stringent response: Concentration of free RNAPs during the stringent response relative to the concentration during the exponential growth (with a rate of 2.5 doublings per hour) before starvation.
Transcription with Over- and Underproduction of RNAP.
We next used our model to study the effect of changing the total amount of RNAPs per cell. This has been studied experimentally by Nomura et al., who either increased the level of RNAPs per cell by expressing RNAP core enzyme subunits on a plasmid or decreased the RNAP level by replacing the chromosomal β and β′ genes with β and β′ genes controlled by the lac promoter and controlling its level of induction (37). For E. coli growing on glycerol-amino acids medium (with a growth rate of ≈1.5 doublings per hour), they found that an up to 2-fold change of the amount of RNAP per cell in either direction had little or no effect on the growth rate and on the transcription of rRNA, but resulted in a proportional change in the transcription of both the total mRNA and of the mdh mRNA, with the latter serving as a probe for the transcription from an unregulated promoter (37). To check whether our model can account for this result, we varied the total RNAP number and determined the predicted transcription rate of mRNA (see SI Text). The results shown in Fig. 4B (black bars) are in excellent agreement with the data of Nomura et al. (37) without invoking any additional parameters.
Passive Control in the Stringent Response.
Finally, we addressed the change in free-RNAP concentration during the stringent response and used our model to test several scenarios for the passive control of rRNA or mRNA synthesis. As mentioned in the introduction, both increasing and decreasing free RNAP concentrations have been proposed during the stringent response. We consider the immediate response to starvation (within the first few minutes), before the composition of the cell, in particular, the RNAP and ribosome content, is substantially changed. This situation is implemented in our model by changing one or several parameters according to what was measured during the stringent response, while keeping all other parameters fixed at the values they had before starvation. This simplification is based on the fact that the parameter changes are due to an increase of the cellular concentration of the regulatory nucleotide ppGpp, which increases very quickly (38, 39), whereas changes in protein content are expected to occur more slowly. We then calculate the partitioning of RNAPs according to the changed parameters.
We first tested the proposal that a decreased mRNA elongation speed (cm) sequesters RNAPs in transcription and that rRNA synthesis is down-regulated by the resulting reduction of the free RNAP concentration (6, 9). The elongation speed of mRNA is reduced to 19–28 nt/s during the stringent response, most likely because of increased RNAP pausing induced by ppGpp (38, 40). The elongation of rRNA is unchanged at their value of 85 nt/s, because RNAPs transcribing rRNA are protected against ppGpp-induced pausing by the rRNA antitermination complex (40). When we change cm from 55 nt/s to 20 nt/s, our model exhibits a decrease of the free RNAP concentration of only 13% (Fig. 4C, white bar). [The exact value depends on the growth rate before starvation, which is 2.5 doublings per hour in Fig. 4C; the results for slower growth rates are very similar (see Fig. S7A).] This decrease of the RNAP concentration has a very small effect on the synthesis of rRNA (<10%; Fig. S7B), whereas measured reductions are at least 5- to 10-fold (see, e.g., refs. 39, 41, and 42). Our model predicts that much slower cm would be needed to affect rRNA synthesis substantially. For example, to obtain even a modest 2-fold suppression of rRNA synthesis by sequestering RNAPs in transcription, we have to reduce cm to <5 nt/s (data not shown), which is far below the experimentally observed range. We can thus conclude that sequestering of RNAPs in transcript elongation plays only a minor role in the suppression of rRNA synthesis during the stringent response. This conclusion is in agreement with experimental results for a NusA mutant, which exhibits a normal stringent response without a reduction of the mRNA elongation speed (41).
We then tested whether the suppression of rRNA synthesis due to ppGpp-dependent regulation of the rrn promoters (7, 8) increases the free RNAP concentration. This increase has been proposed to explain the positive regulation of biosynthetic operons during the stringent response (10, 11). We find, however, that, even if rRNA synthesis is shut off entirely, the free-RNAP concentration increases only by 35% (Fig. 4C, third bar). A more realistic estimate for the suppression of rRNA synthesis (Kr ≈ 20 μM during the stringent response; see SI Text) leads to almost the same result (fourth bar in Fig. 4C). A further increase of the free-RNAP concentration could be due to the repression of a fraction of protein-coding operons (other than the biosynthetic operons). However, even for the extreme case that all transcription (mRNA and rRNA) is completely stopped in the stringent response, we obtained only a 1.5-fold increase of the free RNAP concentration (Fig. 4C, fifth bar), not sufficient to explain the observed 2- to 3-fold stimulation in the transcription of, e.g., the his operon (43). We finally studied the combined effect of a decrease in mRNA elongation speed and decreased transcription of rRNA and found a weak decrease of the free RNAP concentration (by ≈10%) for slowly growing cells (violet curve, Fig. S7) and a similarly weak increase (up to 15%) for fast-growing cells (Fig. 4C, bar 6). These results strongly suggest that passive control by increased RNAP concentration plays only a limited role in the positive control of biosynthetic operons during the stringent response. This conclusion is consistent with the recent experimental demonstration that ppGpp has a direct stimulating effect on the transcription of biosynthetic operons in vitro, an effect not noticed before because it requires the coregulator DksA (43). The relative importance of direct and passive effects has, however, remained unclear and our results suggest that the direct control dominates.
Finally, evidence has accumulated in recent years indicating that altered sigma factor competition plays an important role in the stringent response (44–47). This is to some extent an effect of altered expression of sigma factors and their regulators such as anti-sigma factors (42) and therefore expected to be important during later stages rather than in the immediate response. However, direct effects of ppGpp on sigma factors, e.g., favoring at least some alternative RNAP-sigma complexes, may also contribute. It has therefore been proposed that during the stringent response, the concentration of free RNAP with bound sigma 70 is reduced (45). An alternative proposal suggests that, because of the suppression of rRNA transcription, more RNAP core enzymes become available to bind alternative sigma factors, so that operons controlled by alternative sigma factors could be up-regulated passively (46, 47). Based on our analysis above we expect the latter effect to be small; but at the moment we cannot test these ideas quantitatively, because the effect of ppGpp on the formation and the activity of alternative holoenzymes is unclear and important parameters such as affinities of sigma factors to core RNAP and sigma factors concentrations are unknown in the stringent response. This important question must therefore be postponed to future research.
Supplementary Material
Acknowledgments.
We thank Eduard Mateescu, Hans Bremer, Patrick Dennis, Richard Gourse, Sarah Ades, and Moselio Schaechter for discussions during the course of this work. This work was supported by National Science Foundation Grant PHY-0822283 through the Center for Theoretical Biological Physics, Deutsche Forschungsgemeinschaft Fellowship KL818/1-1 and 1/2 (to S.K.), and National Science Foundation Grant MCB-0746581 (to T.H.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0804953105/DCSupplemental.
This assumes again that there is no strong effect due to changes in macromolecular crowding (see SI Text).
In this study, transcription rates were determined by measuring the β-galactosidase activity for LacZ expressed from the promoter of interest. The relative β-galatosidase activity obtained from 2 different promoters at the same growth rate provides a measure of the relative transcription rate. Absolute values of the transcription rates have been determined from the relative activities of the promoters compared with that of the rrn promoter pair P1-P2 and the absolute values of the transcription rate from P1-P2 as obtained from the rRNA content of the cells and the rrn operon multiplicity (6).
The increase in promoter strength is expected to be larger than 6.6-fold, because the promoter approaches saturation with RNAPs for fast growth (see SI Text for estimates of the maximal transcription rate).
References
- 1.Schaechter M, Maaløe O, Kjeldgaard NO. Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. J Gen Microbiol. 1958;19:592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
- 2.Neidhardt FC, Ingraham JL, Schaechter M. Physiology of the Bacterial Cell: A Molecular Approach. Sunderland, MA: Sinauer; 1990. [Google Scholar]
- 3.Maaloe O. An analysis of bacterial growth. Dev Biol Suppl. 1969;3:33–58. [Google Scholar]
- 4.Bremer H, Dennis PP. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt FC, editor. Escherichia coli and Salmonella. 2nd Ed. Washington DC: ASM Press; 1996. pp. 1553–1569. [Google Scholar]
- 5.Wanner BL, Kodaira R, Neidhardt FC. Physiological regulation of a decontrolled lac operon. J Bacteriol. 1977;130:212–222. doi: 10.1128/jb.130.1.212-222.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liang ST, et al. Activities of constitutive promoters in Escherichia coli. J Mol Biol. 1999;292:19–37. doi: 10.1006/jmbi.1999.3056. [DOI] [PubMed] [Google Scholar]
- 7.Dennis PP, Ehrenberg M, Bremer H. Control of rRNA synthesis in Escherichia coli: A systems biology approach. Microbiol Mol Biol Rev. 2004;68:639–668. doi: 10.1128/MMBR.68.4.639-668.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schneider DA, Ross W, Gourse RL. Control of rRNA expression in Escherichia coli. Curr Opin Microbiol. 2003;6:151–156. doi: 10.1016/s1369-5274(03)00038-9. [DOI] [PubMed] [Google Scholar]
- 9.Jensen KF, Pedersen S. Metabolic growth-rate control in escherichia-coli may be a consequence of subsaturation of the macromolecular biosynthetic apparatus with substrates and catalytic components. Microbiol Rev. 1990;54:89–100. doi: 10.1128/mr.54.2.89-100.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhou YN, Jin DJ. The rpoB mutants destabilizing initiation complexes at stringently controlled promoters behave like “stringent” RNA polymerases in Escherichia coli. Proc Natl Acad Sci USA. 1998;95:2908–2913. doi: 10.1073/pnas.95.6.2908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Barker MM, Gaal T, Gourse RL. Mechanism of regulation of transcription initiation by ppGpp. II. Models for positive control based on properties of RNAP mutants and competition for RNAP. J Mol Biol. 2001;305:689–702. doi: 10.1006/jmbi.2000.4328. [DOI] [PubMed] [Google Scholar]
- 12.Rünzi W, Matzura H. Distribution of RNA polymerase between cytoplasm and nucleoid in a strain of Escherichia coli. In: Kjeldgaard NO, Maaløe O, editors. Control of Ribosome Synthesis. Copenhagen: Munksgaard; 1976. pp. 115–116. [Google Scholar]
- 13.Shepherd N, Dennis P, Bremer H. Cytoplasmic RNA polymerase in Escherichia coli. J Bacteriol. 2001;183:2527–2534. doi: 10.1128/JB.183.8.2527-2534.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang X, Dennis P, Ehrenberg M, Bremer H. Kinetic properties of rrn promoters in Escherichia coli. Biochimie. 2002;84:981–996. doi: 10.1016/s0300-9084(02)00010-x. [DOI] [PubMed] [Google Scholar]
- 15.Bremer H, Dennis P, Ehrenberg M. Free RNA polymerase and modeling global transcription in Escherichia coli. Biochimie. 2003;85:597–609. doi: 10.1016/s0300-9084(03)00105-6. [DOI] [PubMed] [Google Scholar]
- 16.Grigorova IL, Phleger NJ, Mutalik VK, Gross CA. Insights into transcriptional regulation and sigma competition from an equilibrium model of RNA polymerase binding to DNA. Proc Natl Acad Sci USA. 2006;103:5332–5337. doi: 10.1073/pnas.0600828103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tadmor AD, Tlusty T. A coarse-grained biophysical model of E. coli and its application to perturbation of the rRNA operon copy number. Plos Comput Biol. 2008;4:e1000038. doi: 10.1371/journal.pcbi.1000038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McClure WR. A biochemical analysis of the effect of RNA polymerase concentration on the in vivo control of RNA chain initiation frequency. In: Lennon DLF, Stratman FW, Zahlten RN, editors. Biochemistry of Metabolic Processes. New York: Elsevier; 1983. pp. 207–217. [Google Scholar]
- 19.Wassarman KM. 6S RNA: a small RNA regulator of transcription. Curr Opin Microbiol. 2007;10:164–168. doi: 10.1016/j.mib.2007.03.008. [DOI] [PubMed] [Google Scholar]
- 20.Chamberlin MJ. Interaction of RNA polymerase with the DNA template. In: Losik R, Chamberlin MJ, editors. RNA Polymerase. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory; 1976. pp. 159–191. [Google Scholar]
- 21.de Haseth PL, Lohman TM, Burgess RR, Record MT. Nonspecific interactions of Escherichia-Coli RNA polymerase with native and denatured DNA: Differences in binding behavior of core and holoenzyme. Biochemistry. 1978;17:1612–1622. doi: 10.1021/bi00602a006. [DOI] [PubMed] [Google Scholar]
- 22.von Hippel PH, Revzin A, Gross CA, Wang AC. Nonspecific DNA binding of genome regulating proteins as a biological control mechanism: 1. The lac Operon: Equilibrium aspects. Proc Natl Acad Sci USA. 1974;71:4808–4812. doi: 10.1073/pnas.71.12.4808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gerland U, Moroz JD, Hwa T. Physical constraints and functional characteristics of transcription factor-DNA interaction. Proc Natl Acad Sci USA. 2002;99:12015–12020. doi: 10.1073/pnas.192693599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kabata H, et al. Visualization of single molecules of RNA polymerase sliding along DNA. Science. 1993;262:1561–1563. doi: 10.1126/science.8248804. [DOI] [PubMed] [Google Scholar]
- 25.Harada Y, et al. Single-molecule imaging of RNA polymerase-DNA interactions in real time. Biophys J. 1999;76:709–715. doi: 10.1016/S0006-3495(99)77237-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kao-Huang Y, et al. Nonspecific DNA binding of genome-regulating proteins as a biological control mechanism: Measurement of DNA-bound Escherichia coli Lac repressor in vivo. Proc Natl Acad Sci USA. 1977;74:4228–4232. doi: 10.1073/pnas.74.10.4228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Elf J, Li GW, Xie XS. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang YM, Austin RH, Cox EC. Single molecule measurements of repressor protein 1D diffusion on DNA. Phys Rev Lett. 2006;97 doi: 10.1103/PhysRevLett.97.048302. 048302. [DOI] [PubMed] [Google Scholar]
- 29.Saitoh T, Ishihama A. Biosynthesis of RNA polymerase in Escherichia Coli. VI. Distribution of RNA-polymerase subunits between nucleoid and cytoplasm. J Mol Biol. 1977;115:403–416. doi: 10.1016/0022-2836(77)90162-0. [DOI] [PubMed] [Google Scholar]
- 30.Ishihama A. Functional modulation of Escherichia coli RNA polymerase. Annu Rev Microbiol. 2000;54:499–518. doi: 10.1146/annurev.micro.54.1.499. [DOI] [PubMed] [Google Scholar]
- 31.Mooney RA, Landick R. Tethering sigma(70) to RNA polymerase reveals high in vivo activity of sigma factors and sigma(70)-dependent pausing at promoter-distal locations. Genes Dev. 2003;17:2839–2851. doi: 10.1101/gad.1142203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Maeda H, Fujita N, Ishihama A. Competition among 7 Escherichia coli sigma subunits: Relative binding affinities to the core RNA polymerase. Nucleic Acids Res. 2000;28:3497–3503. doi: 10.1093/nar/28.18.3497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gill SC, Weitzel SE, Von Hippel PH. Escherichia Coli Sigma-70 and NusA proteins. I. Binding interactions with core RNA polymerase in sSolution and within the transcription complex. J Mol Biol. 1991;220:307–324. doi: 10.1016/0022-2836(91)90015-x. [DOI] [PubMed] [Google Scholar]
- 34.Vogel U, Jensen KF. The RNA chain elongation rate in Escherichia coli depends on the growth rate. J Bacteriol. 1994;176:2807–2813. doi: 10.1128/jb.176.10.2807-2813.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Klumpp S, Hwa T. Stochasticity and traffic jams in the transcription of ribosomal RNA: Intriguing role of termination and antitermination. Proc Natl Acad Sci USA. 2008;105:18159–18164. doi: 10.1073/pnas.0806084105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Murray HD, Appleman JA, Gourse RL. Regulation of the Escherichia coli rrnB P2 promoter. J Bacteriol. 2003;185:28–34. doi: 10.1128/JB.185.1.28-34.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nomura M, Bedwell DM, Yamagishi M, Cole JR, Kolb JM. RNA polymerase and regulation of rRNA synthesis in Escherichia coli: RNA polymerase concentration, stringent control, and ribosome feedback regulation. In: Reznikoff WS, et al., editors. RNA Polymerase and the Regulation of Transcription. New York: Elsevier; 1987. pp. 137–149. [Google Scholar]
- 38.Vogel U, Sorensen M, Pedersen S, Jensen KF, Kilstrup M. Decreasing transcription elongation rate in Escherichia-Coli exposed to amino-acid starvation. Mol Microbiol. 1992;6:2191–2200. doi: 10.1111/j.1365-2958.1992.tb01393.x. [DOI] [PubMed] [Google Scholar]
- 39.Murray HD, Schneider DA, Gourse RL. Control of rRNA expression by small molecules is dynamic and nonredundant. Mol Cell. 2003;12:125–134. doi: 10.1016/s1097-2765(03)00266-1. [DOI] [PubMed] [Google Scholar]
- 40.Vogel U, Jensen KF. Effects of the antiterminator boxA on transcription elongation kinetics and ppGpp inhibition of transcription elongation in Escherichia coli. J Biol Chem. 1995;270:18335–18340. doi: 10.1074/jbc.270.31.18335. [DOI] [PubMed] [Google Scholar]
- 41.Vogel U, Jensen KF. NusA is required for ribosomal antitermination and for modulation of the transcription elongation rate of both antiterminated RNA and mRNA. J Biol Chem. 1997;272:12265–12271. doi: 10.1074/jbc.272.19.12265. [DOI] [PubMed] [Google Scholar]
- 42.Durfee T, Hansen AM, Zhi H, Blattner FR, Jin DJ. Transcription profiling of the stringent response in Escherichia coli. J Bacteriol. 2008;190:1084–1096. doi: 10.1128/JB.01092-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Paul BJ, Berkmen MB, Gourse RL. DksA potentiates direct activation of amino acid promoters by ppGpp. Proc Natl Acad Sci USA. 2005;102:7823–7828. doi: 10.1073/pnas.0501170102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jishage M, Kvint K, Shingler V, Nystrom T. Regulation of sigma factor competition by the alarmone ppGpp. Genes Dev. 2002;16:1260–1270. doi: 10.1101/gad.227902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Magnusson LU, Farewell A, Nystrom T. ppGpp: A global regulator in Escherichia coli. Trends Microbiol. 2005;13:236–242. doi: 10.1016/j.tim.2005.03.008. [DOI] [PubMed] [Google Scholar]
- 46.Bernardo LMD, Johansson LUM, Solera D, Skarfstad E, Shingler V. The guanosine tetraphosphate (ppGpp) alarmone, DksA and promoter affinity for RNA polymerase in regulation of sigma(54)-dependent transcription. Mol Microbiol. 2006;60:749–764. doi: 10.1111/j.1365-2958.2006.05129.x. [DOI] [PubMed] [Google Scholar]
- 47.Costanzo A, et al. ppGpp and DksA likely regulate the activity of the extracytoplasmic stress factor sigma(E) in Escherichia coli by both direct and indirect mechanisms. Mol Microbiol. 2008;67:619–632. doi: 10.1111/j.1365-2958.2007.06072.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.