Thermodynamics and kinetics of protein folding under confinement

Abstract

Understanding the effects of confinement on protein stability and folding kinetics is important for describing protein folding in the cellular environment. We have investigated the effects of confinement on two structurally distinct proteins as a function of the dimension d_c and characteristic size R of the confining boundary. We find that the stabilization of the folded state relative to bulk conditions is quantitatively described by R^−γ_c, where the exponent γ_c is ≈5/3 independent of the dimension of confinement d_c (cylindrical, planar, or spherical). Moreover, we find that the logarithm of the folding rates also scale as R^−γ_c, with deviations only being seen for very small confining geometries, where folding is downhill; for both stability and kinetics, the dominant effect is the change in the free energy of the unfolded state. A secondary effect on the kinetics is a slight destabilization of the transition state by confinement, although the contacts present in the confined transition state are essentially identical to the bulk case. We investigate the effect of confinement on the position-dependent diffusion coefficients D(Q) for dynamics along the reaction coordinate Q (fraction of native contacts). The diffusion coefficients only change in the unfolded state basin, where they are increased because of compaction.

Protein folding in the cell occurs in a crowded, heterogeneous environment, a perturbation that may alter both the thermodynamics and kinetics of folding relative to observations made in dilute solutions. Experimental and theoretical studies have shown that effects arising from excluded volume interactions either due to macromolecular crowding (1–15) or localization (confinement) of the protein in a small volume (16–31), such as the ribosome tunnel (32) or a chaperonin cavity (33–35), can indeed have significant effects on folding. In the limit where the crowding particles are much bigger and heavier than the protein, the macromolecular crowding effects can be approximated by confinement; the shape and dimensions of the cavity will depend on the crowding concentration. This approach was shown to be applicable for a range of conditions in an insightful study by Cheung, Klimov, and Thirumalai (9). Specifically, they showed that the effect of crowding on protein-folding kinetics can be mimicked by confining the protein within a spherical cavity. The effect of crowding at low concentrations will be different from encapsulation in a spherical cavity and may be better represented by the weaker confining environment within a cylinder or between two planes. Because all of these confinement configurations may also appear naturally (e.g., cylindrical confinement for protein passage through a ribosome tunnel and planar confinement for proteins at interfaces or near surfaces), it is instructive to study the effects of varying the reduced dimensions due to confinement (d_c = 1, 2, and 3 for planar, cylindrical, and spherical, respectively) on protein stability and kinetics.

Considerations from polymer physics suggest that the free energy of confinement within repulsive boundaries should have a simple power law dependence (13, 36, 37) on the size of the cavity. A scaling law based on a simple coarse-grained model for the shift in protein-folding temperature with respect to bulk in a chaperonin-like cage (cylindrical cage with length L twice as big as radius R) was reported by Takagi et al. (20). The folding temperature was shown to vary with the radius of the confining cage as (T_f − T_f)^bulk/T_f^bulk ∝ R^−γ_c, where γ was found to be 3.25. Previous studies on protein folding under spherical confinement (30) and in a crowded solution (9) have observed an exponent γ close to 2, the value expected for an ideal chain (13). Another study of protein folding under spherical confinement found that the scaling exponent γ varied with the protein and repulsive confinement model (26). For an excluded volume chain confined in a spherical cavity, the free energy of confinement is expected to scale with γ = 3.75 (37). It is therefore not clear whether protein-folding thermodynamics follows a polymer-like scaling behavior under confinement and what γ value will be relevant. Although folding kinetics is known to be affected by confinement, no quantitative explanation for the observed increase in rates exists. The essential features of protein-folding kinetics in bulk can be captured by diffusion along a well-defined reaction coordinate (38–40). How confinement affects the diffusion coefficient along such a coordinate is also not known.

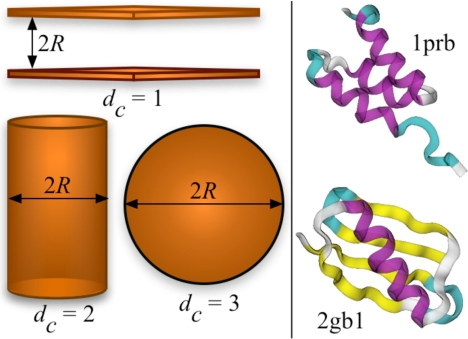
In this work, we examine the effect of different confining geometries on protein-folding thermodynamics and kinetics, relative to the corresponding properties in dilute (“bulk”) conditions. As the most elementary models of confinement (Fig. 1), we consider planar (d_c = 1), cylindrical (d_c = 2), and spherical (d_c = 3) confining potentials to restrict protein conformations and mobility to 1, 2, and 3 dimensions, respectively. We study the effect of confinement on two structurally dissimilar proteins, a 3-helix bundle protein prb (PDB ID code 1PRB) and protein G (PDB ID code 2GB1), by using coarse-grained folding models (see Model and Simulation Methods). Such models allow a thorough exploration of conformational space and statistically accurate determination of the folding stabilities and rates and have been very successful in describing various aspects of protein folding (41). First, we show that the shift in the folding temperature with respect to bulk can be approximated by (T_f − T_f^bulk)/T_f^bulk ∝ R^−γ_c, where γ_c is independent of the protein model as well as d_c. Remarkably, we also find that the increase in folding rates for both the proteins follows the scaling ln(k_f/k_f^bulk) ∝ R^−γ_c, with deviations occurring only for the smallest confining geometries. We show that this scaling arises because the dominant effect of confinement is on the unfolded protein. In agreement with previous observations (42), we find that the transition state ensemble is only marginally affected by confinement when analyzed in terms of the fraction of native contacts formed. However, because the bulk transition state ensemble includes expanded conformations (which are essentially indistinguishable by extent of native contact formation from the more compact ones), it is slightly destabilized by confinement. Thus, there is also a slight slowdown of unfolding rates with increasing confinement.

Fig. 1.

Confinement geometries and protein structures. (Left) Schematic illustration of different confinement models (planar: d_c = 1, cylindrical: d_c = 2 and spherical: d_c = 3). (Right) The native state structure of the 3-helix bundle protein (1PRB) and protein G (2GB1).

Results and Discussion

Scaling of Stability with Confinement Is Approximately Independent of Confining Dimension.

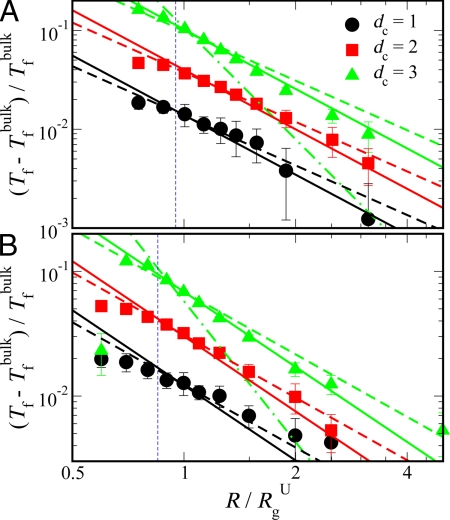
To characterize the effect of confinement by using different reduced dimensions d_c (see Fig. 1), we have determined the folding temperature T_f as a function of characteristic confinement size R. We identify T_f for a given system from the maximum in heat capacity C_v as a function of temperature T. The confinement-induced shift in T_f with respect to the bulk folding temperature T_f^bulk, as shown in Fig. 2, gives a measure of the stabilizing effect of confinement. We find that the shift in folding temperature from bulk follows a power law scaling with the size of the cavity, (T_f − T_f^bulk)/T_f^bulk ∝ (R/R_g^U)^−γ_c, where R_g^U is the bulk radius of gyration of the unfolded state (R_g^U ≈ 15.9 Å for prb and 20.0 Å for protein G).

Fig. 2.

Effect of confinement on folding thermodynamics. The shift in folding temperature with respect to bulk as a function of characteristic confinement size R/R_g^U for prb (A) and protein G (B) is shown by symbols. Lines represent the scaling form given by (T_f − T_f^bulk)/T_f^bulk ∝ (R/R_g^U)^−γ_c (see text), where solid and dashed lines are for γ_c = 2 and 5/3, respectively, and dotted–dashed lines are for γ_c = 15/4. Vertical dashed lines indicate R = R_max/2, where R_max is the length of the folded protein along its longest axis.

We fit the data in Fig. 2 by using exponents γ_c = 2 (solid lines) and 5/3 (dashed lines), corresponding respectively to the expected scaling of confinement-free energy with size R for a Gaussian chain (γ_c = 2; d_c = 1, 2 and 3), and for an excluded volume chain (γ_c = 5/3; d_c = 1, 2) (36): The data for the planar and cylindrical cases are well fit with either scaling (Fig. 2). A power law fit with a free exponent to the data for cylindrical confinement (which have smaller errors than planar confinement) yielded exponents γ_c of 1.66 and 1.62 for prb and protein G, respectively. Because least squares fitting of power laws can produce biased estimates of the parameters for small samples (43) and polymer scaling exponents don't reach their limiting values for small chain lengths studied here, it will be difficult to distinguish whether γ_c = 2 or 5/3 will in general be the more probable exponent but γ_c = 5/3 seems to fit better over the full R range, at least for d_c = 2. For practical purposes, either of these can be used to predict the confinement effect on protein stability with reasonable accuracy.

For an excluded volume chain confined in a spherical cavity (d_c = 3), the change in free energy is expected to scale more strongly with the cavity radius, with an exponent γ_c = 15/4 (37) for sufficiently small cavities, because of the increase in effective monomer concentration. This scaling prediction was recently confirmed via molecular simulations for excluded volume chains confined in cavity sizes less than ≈0.7 R_g (44), where R_g is the radius of gyration of an unconfined chain. However, it is clear that there must be a crossover to the weaker planar/cylindrical-like scaling for large spherical cavities (see figure 3 in ref. 44). Our data for spherical confinement were fitted to the Gaussian chain γ_c= 2, and cylindrical/planar γ_c = 5/3 and spherical γ_c = 15/4 excluded volume scalings. The dependence of stability on confining radius is clearly much weaker than the expected spherical-excluded volume scaling. We interpret these results to mean that we are closer to the weak confinement limit (37); similar scalings have been observed in previous simulations for protein confinement in a spherical cavity (9, 19, 30). Note that for the intermediate cavity sizes (R_g/R_g^U ≈ 1), the scaling in fact appears stronger than γ_c = 5/3, 2, which suggests that we may be approaching the crossover to the strong confinement regime (γ_c = 15/4). Because the single-domain proteins used here are relatively short chains, and possibly because of compaction due to residual native-like interactions in the unfolded state, very small geometries would be required to see γ_c = 15/4 scaling. However, for the smallest geometries (R_g/R_g^U < 1), we find that the scaling becomes weaker again. The weak scaling is most likely due to the destabilization of the folded structure as predicted in the theoretical analysis of Zhou and Dill (17) because R is approaching the radius of protein's minimal bounding sphere. The radius of a sphere that can accommodate the protein without distorting it is estimated as R_max/2, where R_max is the length of the protein along its longest axis. This radius is shown in Fig. 2 by dashed vertical lines. As discussed earlier, a previous study found a scaling exponent of 3.25 for confinement in a capped cylinder, close to the expected 15/4 for spherical confinement (20). The reason for the different scaling exponent observed in that work may be that range of confinement sizes used to fit the data are close to the strong confinement regime.

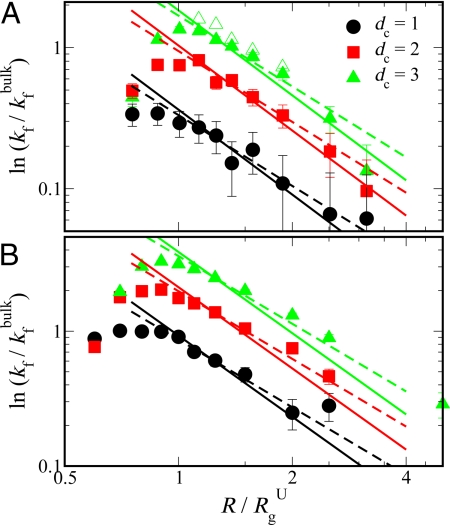
Fig. 3.

Effect of confinement on folding kinetics. Logarithm of folding rates under confinement k_f with respect to the bulk value k_f^bulk as a function of characteristic confinement size R/R_g^U for prb (A) and protein G (B) is shown by filled symbols. Lines represent the scaling form given by ln(k_f/ k_f^bulk) ∝ (R/R_g^U)^−γ_c (see text), where solid and dashed lines are for γ_c = 2 and 5/3, respectively. For comparison, folding rates estimated from long equilibrium trajectories are also shown for prb confined in a spherical cavity by open triangles in A.

Thus, we find that the power law relating free energy of confinement to the confining radius is approximately independent of the reduced dimension d_c due to confinement, although the magnitude of the confinement effects differ because of the prefactor; because of its more expanded unfolded state, protein G is more affected by confinement than prb.

Protein Folding Kinetics Under Confinement Scales with R, Independent of d_c.

Because the folding rates of proteins in vivo may be just as important as their stabilities, we have also investigated the dependence of folding kinetics on confining geometry. We estimate the folding rates from mean first passage times by using 400–800 folding trajectories. The starting unfolded configurations are selected from trajectories at the relevant temperature T and confinement size R. Folding rates for both proteins under different confinements d_c = 1, 2, 3 are shown in Fig. 3. Remarkably, we find that the folding rates shown by filled symbols are well described by ln(k_f/k_f^bulk) ∝ (R/R_g)^−γ_c, where γ_c can be 2 (solid lines) or 5/3 (dashed lines), similar to the exponents found for the shift in the folding temperature. However, there is a turnover at very small cavity sizes (R/R_g^U ≈ 1), which has also been observed in previous studies (9, 19, 20).

To explain the folding rate data, we project the dynamics onto a 1D reaction coordinate. This mapping is justified by the energy landscape theory of protein folding, a consequence of which is that folding dynamics can be represented as diffusion in a low-dimensional coordinate space (38, 39). Previous studies have shown that the projection of the multidimensional folding dynamics onto a suitable 1D coordinate can be well approximated as Markovian diffusion along that coordinate (38, 40, 45, 46).

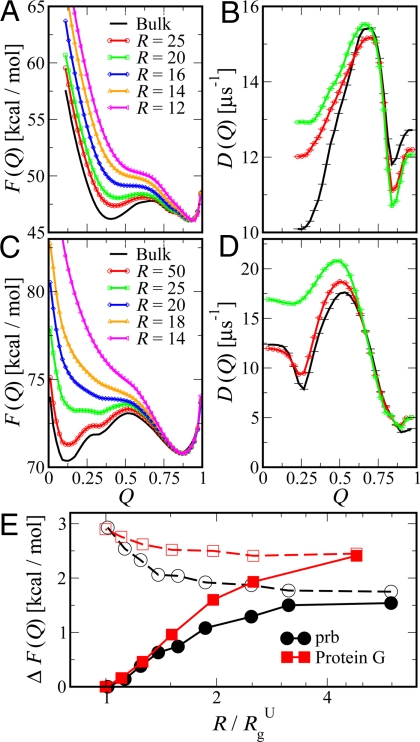
As a 1D coordinate, we choose Q, the fraction of native contacts. Q has previously been shown to be a good coordinate for prb (40, 47), and we find that it is similarly good for protein G (data not shown); thus, it can be used to describe transition states accurately as well as unfolded and folded free-energy minima. To provide more detailed insight into the effect of confinement on the folding free-energy surface, we calculate the potential of mean force (PMF) as a function of Q, defined as F(Q) = −k_BT ln[P(Q)/ΔQ], where P(Q) is the equilibrium probability of observing configurations for a given Q. Fig. 4 A and C shows these free-energy profiles in bulk and confined within a spherical cavity at the respective bulk folding temperatures (T_f^bulk ≈ 292 K for prb and 312 K for protein G). The primary effect of confinement, the destabilization of the unfolded state, is clearly visible from the upward shift in the unfolded basin with decreasing cavity radius R. A secondary effect shown in Fig. 4 A and C is the increase in the barrier height with decreasing R.

Fig. 4.

Position-dependent free-energies and diffusion coefficients. (A and C) The potential of mean force F(Q) as a function of native contacts Q at the bulk folding temperature is shown for prb (A) and protein G (C). For clarity, the curves have been shifted by an arbitrary constant to match the free energy of the folded state. (E) The difference in free energy between the barrier and folded (filled symbols) and unfolded (empty symbols) basins (i.e., filled and empty symbols correspond to ΔF = F_barrier − F_unfolded and ΔF = F_barrier − F_folded, respectively). (B and D) The local diffusion coefficient along Q is given for prb (B) and protein G (D) in bulk and under spherical confinement.

To a first approximation, the folding rates k_f can be estimated from high-friction Kramers kinetics (48) by using k_f ∝ D exp[−ΔF/k_BT], where D is an effective diffusion coefficient over the 1D PMF, k_B the Boltzmann constant, and the barrier height for folding ΔF is the difference in energy between the unfolded state and the transition state. To illustrate how free-energy surface modifications due to confinement may affect the folding rates within the Kramers model, we plot the free-energy difference ΔF between the barrier top and the unfolded basins in Fig. 4E as filled symbols. A simple approximation to the shift in k_f (R) with respect to its bulk value (k _f^bulk) is given by [k_f(R)/ k_f^bulk] = [D(R)/D^bulk] exp[−β(F_barrier(R) − F_barrier^bulk + F_unfolded^bulk − F_unfolded(R))]. A similar approach was used to build a simple semiempirical model for protein folding under confinement (49). Now, if we assume that D(R) ≈ D^bulk and F_barrier(R) ≈ F_barrier^bulk, we get ln(k_f(R)/k_f^bulk) = β(F_unfolded(R) − F_unfolded^bulk). These assumptions become less accurate for proteins confined to very small cavities (more so for prb) as shown in Fig. 4. Also, the excluded volume scaling of the folding temperature strongly suggests that the primary effect of confinement is to destabilize the unfolded state. The confinement reduces the entropy of the chain by excluding configurations that are larger than the confining potential radius R. Therefore, β(F_unfolded(R) − F_unfolded^bulk) will scale as (R/R_g)^−γ_c and folding rates should scale with confinement radius as ln(k_f(R)/k_f^bulk) ∝ (R/R_g^U)^−γ_c. Note that, although the functional dependence on R is remarkably similar, the absolute effect of confinement is larger for protein G because confinement more strongly affects its larger unfolded state, as reflected also in the larger change in ΔF due to confinement.

The above approximation assumed that the only effect of confinement on folding dynamics was through the free-energy surface. However, as has been suggested before, confinement could also alter the effective diffusion coefficient. To describe diffusion over a 1D free energy surface, we approximate the dynamics as 1D diffusion along Q and use a propagator based formalism (50) to determine position-dependent free-energies F(Q) and diffusion coefficients D(Q). A similar approach has been successfully applied to protein folding dynamics and kinetics (40, 51). As shown in Fig. 4 B and D, confinement causes only small shifts in the local diffusion coefficients, D(Q), from the bulk. The largest change in diffusion coefficient is for the unfolded state of protein G, where it is increased by almost a factor of 2 relative to bulk. This increase is most likely because the formation and breaking of contacts, reflected in Q, is enhanced by compaction (12). We find that there is almost no change in diffusion coefficient for more compact states.

We find there is a “turnover” or slowdown of folding rates for very small cavities (R_g/R_g^U ≈ 1) based on mean first passage times. However, under these extreme confinement conditions, the barrier between the folded and the unfolded state disappears and folding is effectively “downhill” (see Fig. 4E) (52); under conditions where there is a barrier, the folding rates continue to follow R^−γ_c scaling. We note that turnover in rates may also result from other effects. For example, turnover in folding rates in small cavities can result from restricted conformational fluctuations, which are necessary to move from the unfolded to the folded state (9), and slowdown of chain dynamics due to hydrodynamic effects (13).

Decreased Protein Unfolding Rates for Small R Due to Transition State Destabilization.

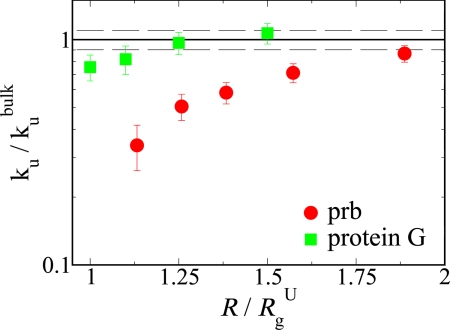
In addition to the expected decrease in folding barrier height with confinement, we also observe a slight increase in the unfolding barrier, mainly arising from the effect of confinement on the transition state energy as shown in Fig. 4 A, C, and E. We compute the unfolding rates k_u from mean first passage times by using at least 100 unfolding trajectories. The unfolding rates for both proteins confined within a spherical cavity (d_c = 3) are shown in Fig. 5. The decrease in unfolding rate is larger for prb because its unconfined transition state is more aspherical than that of protein G (Fig. S1), leading to a larger change in barrier height, ΔF (empty symbols in Fig. 4E) with confinement.

Fig. 5.

Unfolding rates under spherical confinement k_u with respect to its bulk value k_u^bulk as a function of characteristic confinement size R/R_g^U. The errors in individual k_u are estimated as σ[k_u]√, where σ[k_u] is the standard deviation in k_u and N is the number of first passage time samples. The dashed line represents the standard deviation in bulk rates for prb and protein G.

Key Features of Folding Mechanism Are Unchanged with Confinement.

A qualitative picture of the influence of confinement on folding pathways can be formed by examining the transition paths (segments of trajectories linking folded and unfolded states) in the presence and absence of confining boundaries. Fig. S2 shows typical transition paths for protein G in bulk and in a confining sphere of radius R = 22.5. It is clear that many of the unfolded configurations of the protein in bulk would be excluded by the cavity, whereas the transition state would be less affected. Because confinement clearly does have a small affect on the transition state free energy as shown in Fig. 4 A and C, we have investigated more closely its effect on the folding “transition-state ensemble.”

Transition state structure can be quantified experimentally in terms of Φ values, which give an estimate of how native-like the environment of a given residue is in the transition state on a scale from 0 to 1 (53). A simple way to estimate Φ values from simulation is from the fraction of native contacts formed in the transition state, that is Φ_i ≈ N_i(TS)/N_i(NS), where N_i(TS) and N_i(NS) are the number of native contacts formed by residue i in the transition state and native state, respectively. Fig. 6 A and B shows Φ estimated from the fraction of native contacts in the transition state in bulk and confined within a spherical cavity. The Φ values for each protein confined in a spherical cavity (symbols) are almost unchanged from the bulk values (black line), confirming that the key features of the folding transition state are the same. We also compare the experimentally determined Φ data for protein G (filled gray circles) (54) with our simulation data in Fig. 6B. The agreement between the two is quite good, validating the coarse-grained protein models used here (there are no experimental Φ values for prb). Average contact maps calculated from the transition states for prb and protein G confirm the results from the Φ values and are provided in Fig. S3. However, although the transition states are similar in terms of contacts, the distribution of radius of gyration, R_g, Fig. 6 shows that confinement does lead to an increase in compactness for the unfolded state and transition state. The effect is clearly much greater in the unfolded state, where the mode of the distribution is strongly shifted, whereas in the transition state, only the tail of the distribution at large R_g is truncated (except for small cavities where the folding is already downhill). We similarly find that confinement also affects the protein shape, as characterized by an asphericity parameter (Fig. S1). Similar to what we observed for the radius of gyration distribution, the effect is negligible for the folded state and largest for the unfolded state.

Fig. 6.

Effect of confinement on folding mechanism. (A and B) Fraction of native contacts per residue Φ as a function of residue number for prb (A) and protein G (B). (B) The experimentally observed Φ values for protein G (gray circles). (We have excluded the negative values observed in experiments.) (C–H) Distributions of radius of gyration R_g for prb (C–E) and protein G (F–H) in the folded state, transition state, and unfolded state (left to right).

Conclusions

We present extensive simulation results for two structurally dissimilar proteins (i.e., prb and protein G) that show that the shift in protein-folding thermodynamics and kinetics as a function of confinement size is remarkably similar for proteins confined within a planar, cylindrical, or a spherical confining boundary. Although this behavior was expected from polymer scaling for the planar and cylindrical cases, the appropriate scaling for spherical confinement was not clear a priori because the free energy of confinement of an excluded volume chain in a spherical pore may be different for very small cavities. However, we find that under the weaker confining conditions likely to be encountered in the cell, spherical confinement obeys a similar empirical scaling law to the plane/cylinder cases. Although attractive interactions with the confining boundary (42) or effects of solvent confinement (30) may play an additional role, the exclusion of configurations by repulsive interactions with the cavity walls, which we study here, is likely to be the primary effect. In addition to the common scaling behavior for folding temperatures and rates, there are effects specific to the protein under consideration. We find that the effect of confinement on the folding rate is much stronger for protein G than for prb, which is probably due to protein G having a more disordered unfolded state. The difference in the effect of confinement on transition-state free energy is due to the shape distribution within the transition state, as was recently noted (29). The stabilization of these proteins in various confinement conditions produces absolute changes in T_f from 0 to 50 °C, in the same range as experimental results on proteins confined within sol-gel matrices and gels (5, 18, 23). Our predictions for the scaling behavior can be further tested via experiments by localizing proteins in well-controlled matrices and pores.

Model and Simulation Methods

We use a Go-like protein model in which each amino acid residue is represented by a single particle. We use a standard procedure to build the model from the experimental native-state structure (55). This model treats interactions between residues in contact in the native state as attractive and nonnative contacts as repulsive. We ran Langevin dynamics simulations by using CHARMM (56), with a time step of 15 fs and in the low friction limit (0.2 ps⁻¹). To confine the protein in a restricted space, we use a repulsive quartic potential of the form V_c(r) = 0.2 (r − R)² [(r − R)² − 0.1], r > R along with the shape specification for plane, cylinder, and sphere as implemented in the CHARMM MMFP module. Both the proteins exhibit 2-state folding when monitored with a standard reaction coordinate, the fraction of native contact Q. We generate relatively long trajectories (9 μs) by using an umbrella biasing potential of the form, V_u(Q) = $\frac{1}{2}$κ(Q − Q_t)², where Q_t is the target Q value and κ = 300 kcal/mol is the force constant. To speed up equilibration, we use replica exchange moves every 30 ps between 12 replicas spanning Q = 0 to 1 at a given temperature. We then use the weighted histogram analysis method (WHAM) (57) to extract the required thermodynamic information. The folding and unfolding rates were calculated from the mean first passage time starting from the protein configurations in the unfolded and the folded state, respectively. We also generate long (15 μs) equilibrium trajectories without any biasing potential for several temperatures and confinement conditions. We use a Bayesian description of transition states to extract transition-state configurations from the equilibrium trajectories (47).