Epifluorescence-based Quantitative Microvasculature Remodeling Using Geodesic Level-Sets and Shape-based Evolution

Abstract

Accurate vessel segmentation is the first step in analysis of microvascular networks for reliable feature extraction and quantitative characterization. Segmentation of epifluorescent imagery of microvasculature presents a unique set of challenges and opportunities compared to traditional angiogram-based vessel imagery. This paper presents a novel system that combines methods from mathematical morphology, differential geometry, and active contours to reliably detect and segment microvasculature under varying background fluorescence conditions. The system consists of three main modules: vessel enhancement, shape-based initialization, and level-set based segmentation. Vessel enhancement deals with image noise and uneven background fluorescence using anisotropic diffusion and mathematical morphology techniques. Shape-based initialization uses features from the second-order derivatives of the enhanced vessel image and produces a coarse ridge (vessel) mask. Geodesic level-set based active contours refine the coarse ridge map and fix possible discontinuities or leakage of the level set contours that may arise from complex topology or high background fluorescence. The proposed system is tested on epifluorescence-based high resolution images of porcine dura mater microvasculature. Preliminary experiments show promising results.

I. Introduction

Analysis of vessel characteristics is useful in many medical applications i.e. in quantifying effects of certain drugs or in determining the state of various diseases that cause measurable structural changes in blood vessels such as stenoses and aneurysms [1]. Vessel segmentation is the first step in extraction of features such as diameter, wall profile, volume, surface area, permeability, extrinsic curvature and tortuosity [2], and any further analysis on microvascular networks i.e. registration, bifurcations and crossovers analysis [3], [4]. Given the importance, many recent works focus on vessel segmentation [5]. Most of these work concentrate on angiogram imaging to characterize retinal, brain, or heart blood vessels. In the proposed system, we focus on segmentation of epifluorescence-based high resolution images of dura mater microvasculature. These images pose unique challenges due to broad range of vessel diameters in close neighborhood (from large arteries and veins to venules and capillaries), leakage of the epifluorescent dye out of the vessels, and non-homogeneous distribution of epifluorescence within the vessels. Leakage makes the segmentation particularly challenging since it smooths the vessel edges and causes nonuniform background fluorescence making intensity based methods difficult to use. This paper presents a novel system that combines methods from mathematical morphology, differential geometry, and active contours to reliably detect and segment microvasculature under varying background fluorescence conditions. The system consists of three main modules: (1) vessel enhancement, (2) shape-based initialization, and (3) level-set based segmentation explored in the following sections.

II. Vessel Enhancement

Vessel enhancement is used to improve vessel segmentation, increasing the separability of vessel and background classes by adjusting nonuniform background fluorescence and by decreasing image noise. The preprocessing step improves the overall performance, but is less crucial for our shape-based initialization and geodesic contour evolution compared to intensity based segmentation approaches, particularly those using intensity thresholding. Three main aspects addressed by vessel enhancement include: (1) sharp intensity changes within the blood vessel caused by localized concentration of epifluorescent dye, (2) smoothly varying nonuniform background fluorescence caused by leakage, and (3) spatially varying image noise. To equalize the background, we use the morphological top-hat operation and adaptive histogram equalization. The top-hat operation (Eq. 1) returns the original image minus its morphological opening.

$$\begin{array}{r}\mathit{tophat}(I)=I-((I\ominus se)\oplus se)\\ (I\ominus se)(s,t)=\mathit{min}\{I(s+x,t+y)+se(x,y)\}\\ (I\oplus se)(s,t)=\mathit{max}\{I(s+x,t+y)+se(x,y)\}\\ \mathit{where}(s+x,t+y)\in D_f\cap (x,y)\in D_{se}\end{array}$$ (1)

Opening with a structuring element (se) larger than the widest vessel provides an estimation of the background fluorescence distribution. Subtracting the opened image from the original image tends to equalize the background. Unlike background subtraction with local mean or median, top-hat operation does not blend vessel intensity into background model and approximates epifluorescent dye leakage better than homomorphic filter that assumes an input signal with multiplicative components. To smooth the localized concentration of epifluorescence within the vessels, we use a second top-hat operation, this time with a structuring element smaller than the narrowest vessel. Image noise and localized concentration of epifluorescent dye along the vessels result in sharp intensity changes and locally jagged intensity ridges. Both shape-based initialization (section III) and geodesic active contours (section IV) involve differentiation and are sensitive to noise. Particularly curvature computation in section III is affected by noise because of the second-order derivatives involved. We use anisotropic diffusion [6] to smooth out noise without blurring the vessel edges. Further information on anisotropic diffusion can be found in [7].

III. Shape-based Initialization

Shape-based initialization produces a coarse vessel mask that is used to initialize the active contour vessel segmentation described in Section IV. Active contour methods are initialization sensitive since evolution of PDEs converge to a local minimum of the energy function. For the coarse segmentation, shape-based properties are chosen because of their robustness to image contrast and intensity variations. Since vessels produce ridges/creases in the intensity map, we explore ridge-based vessel detection. Various definitions and associated detection methods for ridges/creases can be found in [8]. These methods can be roughly classified as: curvature-based [8], [9], directional derivative-based [8]–[11], and (3) height definitions or Hessian-based [12]–[17]. In this work, ridge detection approaches based on curvatures and Hessian matrix have been used. Principal curvature and directions of a surface L correspond to the eigenvalues κ₁ ≥ … ≥ κ_n−1 and eigenvectors ξ₁ ≥ … ≥ ξ_n−1 of the shape operator matrix on the tangent space W defined as Eq. 2 where I and II are the first and second fundamental forms and $c=\frac{L_x\times L_y}{\mid L_x\times L_y\mid }$ [8].

$$W={\mathbf{I}}^{-1}\mathbf{II}={\left[\begin{array}{cc}{L}_x·L_x& L_x·L_y\\ L_x·L_y& L_y·L_y\end{array}\right]}^{-1}\left[\begin{array}{cc}{L}_{xx}·c& L_{xy}·c\\ L_{xy}·c& L_{yy}·c\end{array}\right]$$ (2)

Ridges can be defined as local extrema of principal curvatures, where the differentiation is taken in the principal directions [8]. Since computation of eigenvalues, thus individual principal curvatures is expensive, mean curvature H (Eq. 3) is often used to classify a surface patch as as ridge, flat, or valley [8], [9].

$$H=\frac{({\kappa }_1+{\kappa }_2)}{2}=\frac{\mathit{trace}(W)}{2}=\frac{I_y^2{I}_{xx}+I_x^2{I}_{yy}-2I_x{I}_y{I}_{xy}}{2{(I_x^2+I_y^2)}^{\frac{3}{2}}}$$ (3)

Height definition [8] is a generalization of local extrema for real-valued functions of a vector variable. A point x₀ is classified as maximum if ∇L(x₀) = 0 (critical point) and ℋ(L(x₀)) is negative definite (all eigenvalues λ_i are negative). Hessian matrix ℋ (Eq. 4) describes the second order structure of local intensity variations around each point of the image L(x, y):

$$\mathcal{H}=\left[\begin{array}{cc}{L}_{xx}& L_{xy}\\ L_{xy}& L_{yy}\end{array}\right]$$ (4)

Table I shows possible orientation patterns based on the value of the eigenvalues λ_1,2 (Eq.5) of the Hessian matrix ℋ.

TABLE I.

Possible orientation patterns based on the value of eigenvalues λ₁, λ₂ (H=high, L=low, |λ₁| ≥ |λ₂|) [14].

λ1	λ2	orientation pattern
L	L	Flat or Noise no preferred direction
H−	L	Bright tubular structure
H+	L	Dark tubular structure
H−	H−	Bright blob-like structure
H+	H+	Dark blob-like structure

$${\lambda }_{1,2}=\frac{1}{2}(L_{xx}+L_{yy}\pm \sqrt{{(L_{xx}-L_{yy})}^2+{(2L_{xy})}^2})$$ (5)

When the height condition holds (critical points, ∇L = 0), according to the Taylor series expansion and curvature definitions, eigenvalues λ_i and eigenvectors v_i of the Hessian matrix correspond to principal curvatures κ_i and principal directions ξ_i respectively [18]. Eigenvalues and eigenvectors of the Hessian matrix have been used in many medical image processing applications as a ridgeness measure for linear/tubular structure enhancement and detection [12]–[17]. Laplacian, (Δ(L) = trace(ℋ) = λ₁ + λ₂), is a good approximation of the sign of the eigenvalues of the Hessian matrix without the expensive eigenvalue decomposition (particularly for high dimensions). Because of this property, Laplacian or its regularized version Laplacian of Gaussian have been used in many recent vessel detection papers such as [19]–[21]. In this work, we produce a coarse vessel mask by thresholding trace(ℋ) as below:

$$\mathit{Mas}{k}_{\mathit{vesse}l}(x,y)=\{\begin{array}{ll}1\hfill & \mathit{trace}(\mathcal{H})<\epsilon \hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}$$ (6)

IV. Segmentation Using Geodesic Level-sets with Spatially Adaptive Force

Intensity ridges are good initializations for vessel networks, but because of their local nature, obtained ridge maps may have spurious results or discontinuities, particularly for cases of complex topology (bifurcations, crossings etc.), nonuniform leakage of the fluorescent material), irregular vessel diameters. To refine the ridge-based vessel mask, we propose a spatially adaptive geodesic active contour segmentation, tuned to image differential geometric information (i.e. ridges) as well as edge information.

In level set-based active contour methods, a curve is represented implicitly via a Lipschitz function ϕ by = {(x, y)|ϕ(x, y) = 0}, and the evolution of the curve is given by the zero-level curve of the function ϕ(t, x, y) [22]. We use geodesic active contours [23] where the level set function ϕ is evolved using the speed function,

$$\frac{\partial \varphi }{\partial t}=g(\nabla \mathbf{I})(F_c+\mathcal{K}(\varphi ))\mid \nabla \varphi \mid +\nabla \varphi ·\nabla g(\nabla \mathbf{I})$$ (7)

where F_c is a constant, is the curvature term Eq. 8, and g(∇I) is the edge stopping function, a decreasing function of the image gradient, defined as Eq. 9 in this application.

$$\mathcal{K}=\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)=\frac{{\varphi }_{xx}{\varphi }_y^2-2{\varphi }_x{\varphi }_y{\varphi }_{xy}+{\varphi }_{yy}{\varphi }_x^2}{{({\varphi }_x^2+{\varphi }_y^2)}^{\frac{3}{2}}}$$ (8)

$$g(\nabla \mathbf{I})=\mathit{exp}(-\mid \nabla G_{\sigma }(x,y)\ast \mathbf{I}(x,y)\mid )$$ (9)

The constant velocity F_c pushes the curve inwards or outwards depending on its sign. The regularization term 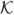ensures boundary smoothness. g(∇I) is used to stop the curve evolution at vessel boundaries. The geodesic active contours are more robust against nonuniform background fluorescence compared to intensity based approaches such as intensity thresholding or Chan-Vese type minimal variance models [22]. However, since they are designed to evolve until edges, they suffer from early stopping on background edges, and contour leaking across weak boundaries. We overcome the first problem by starting the contour close to the vessels using ridge-based initialization. To reduce the effects of the second problem, we propose a spatially adaptive geodesic active contour approach, where the constant force F_c in Eq. 7 is replaced by the proposed adaptive differential geometric force F_A:

$$F_A(x,y)=c_1\times (\text{trace}(\mathcal{H}(I(x,y)))+c_2)$$ (10)

trace(ℋ(I)) returns positive values for intensity valleys, negative values for intensity ridges, and small absolute values in homogeneous regions with small noise. To obtain F_A, trace(ℋ(I)) is normalized into the [−1 : +1] range, a constant force c₂ (0 < c₂ < 1) is added to ensure expansion in homogeneous regions, and the sum is multiplied with a coefficient c₁ (c₁ > 0) that tunes the speed of expansion. In our tests c₁ and c₂ are set to 1 and 0.5 respectively. Using this differential geometric adaptive force F_A instead of a constant balloon force increases the convergence speed on homogeneous regions and decreases contour leaks around weak boundaries. The overall vessel segmentation approach is summarized in Algorithm 1.

Algorithm 1.

Vessel Segmentation

Require: Enhanced epifluorescence-based vessel image I

Ensure: Background-Vessel mask MaskVessel (1:Vessel, 0:BG)

1: ℋ(I)←Hessian(I)

2: g(∇I) = exp(−|∇Gσ(x, y) * I(x, y)|) // Edge stopping function

3: FA(x, y) = c1 × (trace(ℋ(I(x, y))) + c2) // Differential geometric adaptive force

4: Maskridge(x, y)←Initialize ridge mask

5: Maskridge(trace(ℋ) < ε)←1 // Set ridge (vessel) pixels to 1

6: Maskridge = Maskridge ⊕ se // Dilate ridges

7: ϕ = SignedDist( Maskridge) //Initialize ϕ using signed distance transform of Maskridge; Maskridge = = 0→ϕ > 0

8: while stopping/convergence condition not met do

9: Evolve ϕ using g(∇I) and spatially adaptive force FA.

10: end while

11: MaskVessel(x, y)←0; MaskVessel(ϕ < 0)←1 // 1: Vessel, 0:BG

V. Results and Analysis

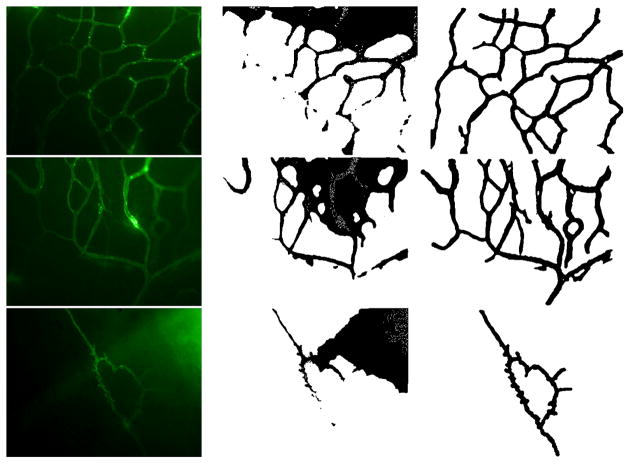
The biological motivaton is to study the influence of hormone treatments on angiogenesis and vasculature remodeling. In an ex vivo process, brain dura mater endothelial cells are stained by infusing fluorescently labeled lectin SBA. The epifluorescence images were then acquired with a 10x lens, at 0.56 μ/pixel resolution using Laborlux 8 microscope and QICAM digital CCD camera. 100 images from 6 female porcine specimens, three with intact ovary, three with excised ovary were used for characterizing normal microvasculature and OVX case respectively. Figure 1 shows intermediate results for vessel enhancement described in section II and ridgeness measures explored in section III. Top-hat and anisotropic filters are quite effective in correcting the non-uniform background caused by epifluorescent dye leakage and smoothing the jagged edges caused by localized concentration of epifluorescent dye respectively. Compared to Laplacian and λ₁, mean curvature H produces noisier results. As expected, λ₁ and Laplacian produces comparable results, with smoother ridges and less blobs in λ₁. λ₂ shows blob/corner like features. Figure 2 shows results for three cases including original epifluorescence imagery, comparison to the Chan and Vese level-set segmentation results initialized with uniformly distributed disks, and the vessel segmentation mask from our method which is accurate and clearly provides a superior vessel mask. Once an accurate segmentation of the microvasculature is obtained a number of quantitative parameters can be extracted to characterize the morphological and architectural features of terminal microvasulature networks.

Fig. 1.

Row 1:Vessel enhancement(a) Original intensity map, (b) background estimation (opening), (c) background adjusted image (top-hat filter), (d) smoothed image (anisotropic diffusion filter + sqrt transformation). Row 2: Ridgeness measures(a) Mean curvature H, (b) Laplacian, (c) λ₁, (d) λ₂ (|λ₁| ≥ |λ₂|). Images in second row have been obtained by shifting the actual values. Dark: negative values, bright: positive values.

Fig. 2.

Comparison of the segmentation results. Column 1: original epifluorescence imagery for three distinct cases; column 2: Chan and Vese level-set segmentation [22] initialized with uniformly distributed disks; column 3: vessel mask from the proposed method.

VI. Conclusion

The focus of this paper is the novel biomedical application of microvasculature segmentation using epifluorescence imagery of ex vivo brain dura mater (outermost lining of the brain surface) at very high half-micron per pixel spatial resolution. Previous studies on blood vessel segmentation have typically used angiogram imaging modalities to characterize retinal as well as brain and heart blood vessels. This paper is novel in both the medical imaging epifluorescence modality as well as the tissue vasculature studied. Current approaches to vessel segmentation lead to poor results with epifluorescence imagery. We showed that our new approach using morphology-based background fluorescence correction, differential geometry-based ridge and curvature detection, combined with adaptive geodesic level sets leads to extremely good results for the automatic segmentation of the vasculature regions. The approach is robust to a variety of challenging image conditions including non-uniform spatially varying background fluorescence, leakage of flourescent material outside the vasculature walls, non-homogeneous interior regions of the vessel lumen, with random spatial accumulation of fluorescent material. The proposed segmentation system will be used in characterization of OVX (ovary removed) versus normal cases for studying systemic influence of hormone therapy.