A 7 µm mini-beam improves diffraction data from small or imperfect crystals of macromolecules

An X-ray mini-beam of 8 × 6 µm cross-section was used to collect diffraction data from protein microcrystals with volumes as small as 150–300 µm³. The benefits of the mini-beam for experiments with small crystals and with large inhomogeneous crystals are investigated.

Abstract

A simple apparatus for achieving beam sizes in the range 5–­10 µm on a synchrotron beamline was implemented in combination with a small 125 × 25 µm focus. The resulting beam had sufficient flux for crystallographic data collection from samples smaller than 10 × 10 × 10 µm. Sample data were collected representing three different scenarios: (i) a complete 2.0 Å data set from a single strongly diffracting microcrystal, (ii) a complete and redundant 1.94 Å data set obtained by merging data from six microcrystals and (iii) a complete 2.24 Å data set from a needle-shaped crystal with less than 12 × 10 µm cross-section and average diffracting power. The resulting data were of high quality, leading to well refined structures with good electron-density maps. The signal-to-noise ratios for data collected from small crystals with the mini-beam were significantly higher than for equivalent data collected from the same crystal with a 125 × 25 µm beam. Relative to this large beam, use of the mini-beam also resulted in lower refined crystal mosaicities. The mini-beam proved to be advantageous for inhomogeneous large crystals, where better ordered regions could be selected by the smaller beam.

1. Introduction

Progress in some of the most important and challenging problems in structural biology often stumbles upon the inability to grow crystals that are large enough or sufficiently homogeneous to produce diffraction data that are suitable for solution of the structure. Exhaustive efforts, sometimes exceeding years, do not always lead to the growth of larger or more perfect crystals. Some examples include supramolecular assemblies, membrane proteins, especially the generally small crystals grown from lipidic mesophases (Cherezov & Caffrey, 2006 ▶; Landau & Rosenbusch, 1996 ▶; Misquitta et al., 2004 ▶; Ng et al., 2008 ▶), crystals grown from nanolitre volumes and molecules that can form fibrils (Nelson et al., 2005 ▶). In addition, many projects, especially those based on integrated high-throughput methods, would be more productive if initial microcrystals were used for structure determination directly without further optimization of crystallization conditions.

There is now ample evidence that a small X-ray beam can be used to collect useful microdiffraction data from very small or imperfect crystals of biological macromolecules. Several publications have described successful data-collection experiments in which a small X-ray beam, defined as having a diameter of <10 µm, intersected small volumes of 5–10 µm thick plate-shaped crystals or needle crystals with 10 × 10 µm cross-sections (Cusack et al., 1998 ▶; Dimasi et al., 2007 ▶; Fotinou et al., 2001 ▶; Li et al., 2004 ▶; Pebay-Peyroula et al., 1997 ▶; Weichenrieder et al., 2000 ▶; Xiao et al., 2003 ▶). The minimum crystal size that can yield reasonably complete diffraction data has been variably estimated to be in the range 20–30 µm in all three dimensions based on radiation-damage considerations (Burmeister, 2000 ▶; Glaeser et al., 2000 ▶; Sliz et al., 2003 ▶; Teng & Moffat, 2000 ▶, 2002 ▶). The smallest volume samples reported to have produced useful crystallographic data were a 30 × 7.5 × 5 µm crystal of insulin measured with a 25 × 5 µm beam (Norrman et al., 2007 ▶) and 2 × 2 × 2 µm crystals of cypovirus polyhedra (Coulibaly et al., 2007 ▶). Small beams have also been used with large crystals to address a variety of problems including crystal inhomogeneity (Renault et al., 2001 ▶), radiation damage (Fotinou et al., 2001 ▶) and high mosaicity (Xiao et al., 2003 ▶). At the beamlines of the GM/CA Collaborative Access Team (CAT), located at Sector 23 of the Advanced Photon Source (APS), we observe a growing number of user samples of 5–10 µm size or with special problems (high mosaicity, extreme sensitivity to radiation damage, irregular spot shapes, multiple or cracked crystals on the mount) that could benefit from the use of a small beam. Thus, there is a growing need to apply small X-ray beams to important problems in macromolecular crystallography and to learn how best to use these beams.

X-ray beams at modern synchrotron beamlines for macromolecular crystallography are typically ellipsoids with the major axis in the range 50–200 µm (http://biosync.rcsb.org/). For samples that are much smaller than the incident beam, the intrinsically weak diffracted intensities can be overwhelmed by high backgrounds from the large beam. The portion of the beam cross-section that does not intercept the sample crystal contributes only background to the diffraction image and reduces the signal-to-noise ratio. The effective diffraction limit is also reduced by loss of weak diffracted intensities into background noise. The beam size at the sample position depends significantly on the beam convergence/divergence and on the position of the beam-defining slits relative to the sample and the focusing optical elements. The general practice of reducing the beam size by closing the beam-defining slits has limitations because these slits are typically located too far upstream of the sample. For example, on GM/CA beamline 23ID-B the minimum achievable beam size at the sample was ∼38 × 16 µm defined by slits located 230 mm upstream. In this case, the focused full beam was 125 × 25 µm at the sample with a vertical convergence of 136.6 µrad and the smallest setting of the beam-defining slits was 13 µm in both the horizontal and vertical directions.

In addition to simply reducing the beam size, the requirements for the beamline experimental apparatus are more stringent for small-beam experiments than for standard-beam experiments. The so-called ‘sphere of confusion’ at the sample position must be small relative to the sample and beam size. For a 10 µm sample and 10 µm beam, the X-ray beam, sample-goniometer axis, sample-visualization system and sample-alignment system should converge within 2 µm and be stable over the time of an experiment. The stringent requirements for stability and a small sphere of confusion may explain why few facilities with such capabilities exist today despite the need for small beams in macromolecular crystallography. The first synchrotron beamline to offer a small beam for biological crystallography was the multi-disciplinary ID13 at the ESRF (Cusack et al., 1998 ▶; Engstrom et al., 1997 ▶; Riekel, 2004 ▶). A dedicated microdiffractometer was developed for these experiments (Perrakis et al., 1999 ▶) and is in use at several beamlines, although not in all cases with a small beam. Beam sizes down to 20 µm have also been achieved with capillary optics (Huang & Bilderback, 2006 ▶). We have developed a mini-beam apparatus enabling reduction of the beam size at the sample down to near 5 µm diameter while maintaining adequate flux for crystallographic data collection (manuscript in preparation).

Despite the number of structure determinations that have employed a small X-ray beam (as cited above), no systematic study of the utility of a small beam has been reported. In this work, we report several crystallographic experiments with a mini-beam of less than 10 µm diameter to study the advantages of measuring diffraction data from small crystals of less than 1000 µm³ volume and from larger crystals that are inhomogeneous.

2. Methods and materials

2.1. Mini-beam apparatus

The GM/CA mini-beam apparatus, a description of which will be published elsewhere (Fischetti et al., in preparation), was implemented on both of the GM/CA-CAT insertion-device beamlines, 23ID-D and 23ID-B (Fischetti et al., 2007 ▶). The typical focal spots achievable with the existing focusing Kirkpatrick–Baez bi­morph mirrors are 70 × 25 µm on 23ID-D and 125 × 25 µm on 23ID-B (Yoder et al., in preparation). Briefly, a beam-defining 5 or 10 µm diameter aperture was placed 30 ± 0.5 mm upstream of the sample and was encapsulated in a scatter-guard construction: upstream and downstream tubes and the housing (Fig. 1 ▶). The beam-defining assembly is manipulated with linear stages (M-111.1DG, Physik Instrumente GmbH & Co. KG) with 0.1 µm reproducibility. Sample X and Y translations are carried out with the same M-111.1DG motors mounted on an air-bearing rotation axis of 0.027 arcsec resolution (ABR1000, Aerotech). A motor assembly with 0.012 µm resolution was used for the Z motion of the sample. Rotation-axis alignment was performed with a 0.1 µm resolution assembly. The goniometer sphere of confusion was less than 1 µm r.m.s. over 360°. The maximum magnification of the on-axis visualization camera was 32-fold with a numerical aperture of 0.3. The X-ray beam intensity on 23ID-B had 1% r.m.s. deviation on the time scale of data collection. The beam size through the 10 µm aperture, measured with a knife-edge scan, was 7.8 × 6.3 µm (full-width at half-maximum; FWHM) at the sample position. The flux of the mini-beam, 1 × 10¹¹ photons s⁻¹ (100 mA)⁻¹, measured with an ion chamber, was sufficient to conduct data-collection experiments from protein crystals. The beam size through the 5 µm aperture was 6.8 × 3.8 µm and the flux at the sample position was 7 × 10¹⁰ photons s⁻¹ (100 mA)⁻¹. The flux values varied between the reported experiments, mostly owing to the use of different focal parameters at different times, as demanded by concurrent user experiments. On 23ID-B the beam divergence in the vertical direction, measured using the rocking curves of a Si(220) analyzer crystal, was 103.3 µrad with and 136.6 µrad without the mini-beam apparatus. A greater reduction of the divergence is expected in the horizontal plane, although it could not be measured with the single-axis horizontal gonio­meter. Indeed, placing the mini-beam aperture in the 125 × 25 µm beam reduced the vertical beam size by a factor of four, while in the horizontal plane this reduction was 16-fold.

Figure 1.

Mini-beam apparatus. (a) Location of the beamline optical elements relative to the X-ray source and the sample on beamline 23ID-B. All distances are shown for the centers of the elements except for the mirrors: each rectangle in the figure represents a pair of mirrors and the indicated distance is the average of the center distances in the pair. Details of the mini-beam apparatus are shown below the beamline schematic and its placement is indicated with a dashed arrow. 1, upstream scatter guard; 2, beam-defining aperture; 3, housing for beam-defining aperture; 4, downstream scatter guard. (b) Mini-beam apparatus in the sample environment. The mini-beam apparatus is positioned between the on-axis visualization lens and the sample. The beam stop is not visible as it is automatically lowered when the hutch door is open.

2.2. Crystallization

Tetragonal crystals of hen egg-white lysozyme and Thaumatococcus daniellii thaumatin were grown by the hanging-drop vapor-diffusion technique in 24-well culture plates (Hampton Research) at 293 K. Lyophilized lysozyme (Sigma) was dissolved in water to a concentration of 40 mg ml⁻¹. 2 µl protein solution was mixed with an equal volume of well solution comprising 1 M NaCl, 50 mM sodium acetate pH 4.6 and 28–30% glycerol. Droplets were streak-seeded 15–17 h after setup. Previously grown large lysozyme crystals were touched with an acupuncture needle, which was then swiped through the droplets. Crystals appeared within 4–12 h of seeding and reached sizes of 5–500 µm. Thaumatin (Sigma) was dissolved in water to 30–40 mg ml⁻¹. 2 µl protein solution was mixed with an equal volume of well solution comprising 0.75 M potassium sodium tartrate, 0.1 M sodium citrate pH 5.6 and 26–28% glycerol. Crystals grew in 2–5 d. The crystal size was manipulated by varying the protein concentration. The largest crystals were obtained with 30 mg ml⁻¹ protein stock and microcrystals were obtained with 40 mg ml⁻¹ protein stock.

Pikromycin thioesterase (TE) mutant T77V was prepared as previously described for the wild-type protein (Akey et al., 2006 ▶). The protein was crystallized at 277 K by vapor diffusion in a hanging drop with a well buffer containing 20% PEG 4000, 0.2 M lithium acetate, 100 mM bis-tris pH 6.5, 2 mM DTT. Crystals were transferred to an equivalent solution containing 30% PEG 4000 for freezing.

2.3. Crystallographic data collection and analysis

Crystal sizes were measured in the beamline sample-visualization microscope by translation with the high-resolution (0.01 µm) goniometer motors. The mini-beam (8 × 6 µm beam) was defined with the 10 µm aperture and the ‘standard’ beam (75 × 25 µm beam defined by guard slits on 23ID-B). Crystallographic data-collection experiments, including manipulations of the experimental station motors, were carried out with the Blu-Ice software (McPhillips et al., 2002 ▶), which was adapted for an Experimental Physics and Industrial Control System (EPICS) environment (Stepanov et al., unpublished work). All diffraction data were recorded at an X-ray energy of 12 keV (λ = 1.033 Å) on beamline 23ID-B equipped with a 4 × 4 tiled MAR Mosaic charge-coupled device (CCD) detector with a 300 × 300 mm sensitive area and a 4096 × 4096 pixel array (MAR USA, now Rayonix). Data were integrated and scaled with HKL-2000 (Otwinowski & Minor, 1997 ▶). Coordinates with PDB codes 193l and 1rqw were used as starting models for the refinement of lysozyme and thaumatin, respectively. CNS (Brünger et al., 1998 ▶) and REFMAC5 (Murshudov et al., 1997 ▶) were used for refinement. To remove model bias during refinement, one macrocycle comprising simulated annealing (3000 K) and overall and individual isotropic B-factor refinement followed by positional refinement was carried out with CNS. After inspecting the model and manually correcting errors, refinement was continued with REFMAC5 as implemented in CCP4i (Collaborative Computational Project, Number 4, 1994 ▶). The same subset of reflections was used to calculate R _free in both CNS and REFMAC refinements. No solvent was included in the initial models. Water O atoms and other solvent atoms were identified and included first automatically with the program Coot (Emsley & Cowtan, 2004 ▶) as implemented in CCP4 and then manually. Model inspection and corrections were carried out with O (Jones et al., 1991 ▶). Refinements of the lysozyme and thaumatin models against the data collected from large crystals were carried out using the same protocol as described above for microcrystals. The figures for the refined structures were prepared with PyMOL (http://www.pymol.org; DeLano Scientific, LLC).

3. Results

Diffraction data were collected from a number of crystals (Table 1 ▶) to mimic several scenarios of typical user experiments and to study the effects of reduced beam size and divergence on the quality of data from small and large crystals.

Table 1. Summary of data-collection experiments.

Data set	Description	Purpose
Experiment 1
LSS	Lysozyme, small crystal, small beam	Complete data from a single microcrystal
LLL1	Lysozyme, large crystal, large beam	To compare with LSS when data-collection parameters are optimized for each case independently
Experiment 2
TSS	Thaumatin, small crystals, small beam	Complete data collection from multiplemicrocrystals
TLL1	Thaumatin, large crystal, large beam	To compare with TSS when data-collection parameters are optimized for each case independently
Experiment 3
TENS	Thioesterase, needle crystal, small beam	Comparison of data with small and large beams measured from the same small crystal to determine the effects of the beam size on signal-to-noise ratio
TENL	Thioesterase, needle crystal, larger beam
Experiment 4	No complete data, only mosaicity measurements
Experiment 5
LLL2	Lysozyme, large crystal, large beam	To compare data quality measured with large and small beams from an inhomogeneous sample
LLS1	Lysozyme, large crystal, small beam
Experiment 6
LLS2	Lysozyme, large crystal, small beam	Used together with LLL3 and LLL4 for comparisons
LLL3	Lysozyme, large crystal, large beam	Used together with LLS2 to compare data collected with small and large beams from the same large crystal with the same peak flux density
LLL4	Lysozyme, large crystal, large beam	Used together with LLS2 to compare data collected with small and large beams from the same large crystal with the same integrated beam intensity

3.1. Experiment 1. Proof of principle: complete data from a single microcrystal

The goal of this experiment was to demonstrate that complete good-quality data can be measured from a single microcrystal using a small beam. Data sets LSS (lysozyme, small crystal, small beam) and LLL1 (lysozyme, large crystal, large beam) were compared. A complete 2.0 Å data set (LSS) was collected from a single crystal of lysozyme using the 8 × 6 µm mini-beam. The 15 × 7 × 7 µm crystal (Fig. 2 ▶) diffracted beyond 2 Å but a relatively low dose (2.5-fold attenuation) was used to ensure com­pleteness of data before substantial decay of diffracted intensities. A 180° swath of data was collected with a 1° frame width and 2 s exposure per frame. Frames 1–125 were kept for further analysis. Frames 126–180 were rejected because of substantial radiation damage as revealed by decreased diffracted intensities and increased R _merge as a function of frame number (R _merge was <15% for frames 1–125 and up to 30% for frames 126–180). Two tests confirmed that the loss of diffracted intensity was a consequence of radiation damage and not beam fluctuations or crystal mis-centering. The mean intensity per pixel on the CCD detector was monitored to ensure that the crystal received a constant incident X-ray flux. After completion of the 180° scan, 20 frames were re-measured from the starting crystal orientation. Equivalent diffraction spots were threefold less intense at the end of the experiment compared with the beginning, which is indicative of severe radiation damage. The first 125 frames produced a complete and redundant data set that was successful in model refinement and resulted in high-quality electron density (Table 2 ▶; Fig. 2 ▶). This experiment demonstrated the capability to record complete and redundant data from one microcrystal and to obtain good-quality electron density from the data. A comparison data set, LLL1, was measured from a 300 × 200 × 150 µm lysozyme crystal during crystallographic commissioning of the beamline. The beam was focused 300 mm downstream of the sample, leading to a beam size of 90 × 45 µm at the sample. An attenuation factor of 1000 was used, resulting in a flux of 2 × 10¹⁰ photons s⁻¹ (100 mA)⁻¹. The ex­posure time was 2 s and the frame width was 0.5°. The data and density quality are superior from the larger crystal examined with the larger beam.

Figure 2.

Lysozyme (left) and thaumatin (right) crystals and electron densities. The single lysozyme crystal (15 × 7 × 7 µm) was used for the experiment depicted. The thaumatin microcrystals were spread over the MiTeGen mount. Refined models and electron-density maps correspond to data sets from microcrystals with the mini-beam (above) and large crystals with a large beam (below). |2F _o − F _c| electron densities are contoured at the r.m.s. density level.

Table 2. Data-collection and refinement statistics for experiments 1 and 2.

Data for TSS are merged from multiple crystals. Flux values, when multiplied by the attenuation factors, differ between experiments, reflecting differences in optimization of the setup and varying focal parameters for data-collection experiments conducted over several weeks. Values in parentheses correspond to the outermost shell of data.

	LSS	LLL1	TSS	TLL1
Data collection
Space group	P43212	P43212	P41212	P41212
Flux at the sample [photons s−1 (100 mA)−1]	8.1 × 109	2 × 1010	5.4 × 1010	1 × 1010
Attenuation (fold)	2.5	1000	1	1000
Exposure time (s)	2	2	1.5	2
Total rotation range (°)	125	120	106	90
Resolution (Å)	50–2.0 (2.07–2.0)	50.0–1.52 (1.55–1.52)	50.0–1.94 (2.01–1.94)	50.0–1.15 (1.19–1.15)
Average mosaicity (°)	0.52	0.34	0.1–0.2	0.17
Unique reflections	8211 (758)	18502 (920)	19873 (1911)	84000 (8268)
Completeness (%)	98.8 (92.4)	99.9 (99.9)	99.5 (98.6)	92.3 (92.7)
Multiplicity	8.7 (5.0)	9.3 (7.0)	4.2 (3.7)	7.1 (7.0)
I/σ(I)	19.1 (3.2)	61.0 (7.8)	20.2 (5.3)	40.7 (5.6)
Rmerge† (%)	11.7 (42.5)	3.8 (23.8)	9.9 (27.6)	4.1 (26.4)
Refinement
dmin (Å)	55.6–2.0 (2.05–2.0)	55.6–1.52 (1.56–1.52)	41.1–1.94 (1.99–1.94)	53.8–1.15 (1.18–1.15)
Rcryst‡ (%)	18.6 (21.4)	17.7 (22.2)	16.9 (19.3)	16.5 (15.5)
Rfree§ (%)	22.4 (29.8)	19.7 (25.3)	18.9 (22.3)	18.5 (19.5)
Correlation coefficient	0.94 (0.90)	0.96 (0.95)	0.95 (0.94)	0.97 (0.93)
Protein atoms	1001	1001	1552	1552
Water O atoms	75	152	207	297
Other atoms	4 Cl−	4 Cl−	10 tartrate	10 tartrate
Deviations
Bond lengths (Å)	0.009	0.009	0.008	0.007
Bond angles (°)	1.129	1.208	1.083	1.051
Torsion angles (°)	5.65	5.79	6.095	6.08

^† R _merge = , where I_i(hkl) is the intensity of the ith observation and 〈I(hkl)〉 is the mean intensity.

^‡ R _cryst = 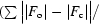) × 100, where F _o is the observed structure factor and F _c is the calculated structure factor used in the refinement.

^§ R _free corresponds to a 5% subset of the data.

3.2. Experiment 2. Proof of principle: complete data from several microcrystals

The goal of this experiment was to demonstrate that a complete data set can be assembled from partial data sets from several microcrystals. Data sets TSS (thaumatin, small crystals, small beam) and TLL (thaumatin, large crystal, large beam) were compared.

Microcrystals of thaumatin were retrieved from a drop containing a crystalline shower. All crystals were mounted on a single MiTeGen micromount (http://www.mitegen.com) as removing a single crystal from the growth solution was not possible (Fig. 2 ▶). The small beam size allowed us to isolate individual crystals for data collection from numerous neighbors on the micromount. This experiment aimed to record data to the full diffraction limit of the crystals by use of the un­attenuated beam and to minimize the effects of radiation damage by merging partial data sets from several crystals. Incomplete data sets were collected from eight thaumatin crystals ranging in size from 6 × 5 × <5 to 12 × 12 × <5 µm. All crystals were oriented with the smallest dimension perpendicular to the plane of the mount, so this dimension was not measured reliably. From each crystal, 10–25 frames were kept, corresponding to 50–89% of the unique data (Table 3 ▶). Two data sets were identified as outliers in inter-crystal scaling and were excluded. The data from the remaining six crystals were merged to produce a complete and redundant 1.94 Å data set that was used successfully in refinement and resulted in an electron-density map of high quality (Table 2 ▶; Fig. 2 ▶). The comparison data set, TLL, was measured during crystallo­graphic commissioning of the beamline from a crystal of dimensions 300 × 150 × 150 µm. The 125 × 25 µm beam was focused at the sample and an attenuation factor of 1000 was used, resulting in a flux of 1 × 10¹⁰ photons s⁻¹ (100 mA)⁻¹. The exposure time was 2 s and the frame width was 0.5°. This experiment demonstrated the feasibility of avoiding radiation-damage effects by assembling multi-crystal data sets obtained from several microcrystals using the mini-beam.

Table 3. Data-processing statistics for the data sets collected from eight thaumatin microcrystals in experiment 2.

Crystals are represented by their size in two dimensions. Sizes in the third dimension were less than the two shown but could not be measured reliably. Crystals 2 and 3 were not included in the final set. Crystal 2 diffracted weakly and data beyond 2.3 Å had low completeness. Data from crystals 2 and 3 did not scale well with the other sets. Statistics of the six merged sets are given in Table 2 ▶. Values in parentheses are for the last shell.

Crystal	Crystal size (µm)	dmin (Å)	No. of images	Rmerge† (%)	Completeness (%)	Average multiplicity	Rmerge† for 8 crystals (%)	Rmerge† for 6 crystals (%)
1	10 × 4	1.94 (2.01–1.94)	20	7.2 (18.5)	88.8 (83.4)	1.7 (1.7)	11.1	6.8
2	10 × 5	2.30 (2.38–2.30)	10	12.1 (34.0)	50.4 (40.8)	1.4 (1.3)	20.5
3	10 × 6	1.94 (2.01–1.94)	25	9.9 (27.6)	68.9 (69.1)	2.8 (2.5)	23.1
4	11 × 5	1.94 (2.01–1.94)	20	8.5 (32.8)	82.4 (67.9)	1.8 (1.6)	11.9	8.6
5	12 × 12	1.94 (2.01–1.94)	13	8.2 (29.2)	56.7 (43.1)	1.7 (1.6)	17.0	14.4
6	12 × 6	1.94 (2.01–1.94)	23	11.9 (28.5)	72.4 (72.2)	2.4 (2.1)	11.8	9.2
7	6 × 5	1.94 (2.01–1.94)	10	10.8 (27.3)	49.6 (41.7)	1.5 (1.4)	13.0	12.2
8	8 × 5	1.94 (2.01–1.94)	20	11.4 (29.3)	70.9 (68.3)	2.1 (1.9)	16.0	10.7

^† R _merge = , where I_i(hkl) is the intensity of the ith observation and 〈I(hkl)〉 is the mean intensity.

3.3. Experiment 3. Improved signal-to-noise ratio for a small crystal with a small beam

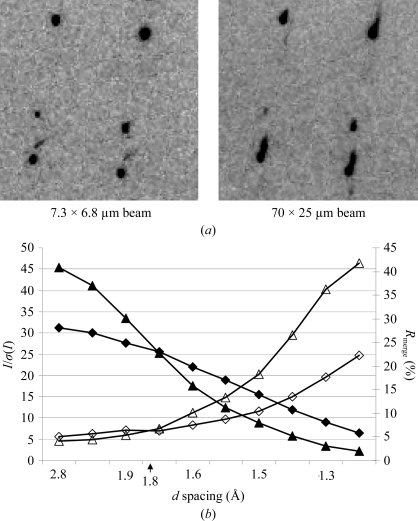
In this experiment, we compared the quality of data measured from a single crystal with small and large beams. A single-site variant (Thr77→Val) of pikromycin thio­esterase yielded only long needle-shaped crystals, in contrast to the larger crystals of the wild-type protein (Akey et al., 2006 ▶). Data sets TENS (thioesterase, needle crystal, small beam) and TENL (thioesterase, needle crystal, large beam) were compared. A data set was obtained by merging partial data sets collected from two segments along a 200 µm needle-shaped crystal with a small (<12 × 10 µm) cross-section. The long axis of the crystal was oriented 30–40° away from the axis of data collection. Three data sets were measured with the fivefold attenuated mini-beam by irradiating fresh segments 30 µm apart. The third data set was excluded owing to a 2.6 Å diffraction limit and poor data-processing statistics (R _merge exceeded 50% for data beyond 2.9 Å). The two remaining sets were merged to produce an 89% complete 2.24 Å merged data set (TENS). Data set TENL was collected from the unexposed end of the crystal 70 µm away from the nearest irradiated segment. All data-collection parameters were identical to those used for TENS, except that the beam size was 70 × 25 µm. Details of the structure will be published elsewhere. Data collected with the small beam had an improved diffraction limit compared with the large-beam data (2.24 versus 2.4 Å) and were of better quality as indicated by greater I/σ(I) and lower R _merge values (Table 4 ▶ and Fig. 3 ▶).

Table 4. Processing statistics for data included in experiments 3, 5 and 6.

The TENS data set was obtained by merging data from two segments of the crystal. All other data were measured from single regions of the corresponding samples. Values in parentheses are for the last shell.

	Experiment 3			Experiment 5		Experiment 6
Data set	TENS to 2.24 Å	TENS to 2.4 Å	TENL	LLS1	LLL2	LLS2	LLL3	LLL4
Space group	P212121	P212121	P212121	P43212	P43212	P43212	P43212	P43212
Beam size (µm)	7.8 × 6.3	7.8 × 6.3	70 × 25	7.8 × 6.3	75 × 25	7.8 × 6.3	75 × 25	75 × 25
Exposure time (s)	5	5	5	2	2	2	2	2
Angular range of data collection (°)	120	120	120	75	75	120	120	120
Data range (Å)	50–2.24 (2.32–2.24)	50.0–2.4 (2.49–2.4)	50.0–2.4 (2.49–2.4)	50–1.29 (1.34–1.29)	50–1.29 (1.34–1.29)	50–1.80 (1.86–1.80)	50–1.28 (1.33–1.28)	50–1.28 (1.33–1.28)
Average mosaicity (°)	0.31	0.31	1.0	0.4–1.2†	0.6–1.1†	0.10	0.14	0.11
Unique reflections	31144 (1610)	27595 (2174)	27805 (1906)	28637 (2208)	28935 (2710)	10678 (740)	28941 (2299)	28884 (2205)
Completeness (%)	88.8 (46.9)	96.4 (77.1)	80.2 (56.5)	95.7 (74.9)	96.7 (91.9)	94.4 (67.3)	94.6 (77.0)	94.3 (73.8)
Multiplicity	4.0 (1.8)	4.3 (2.6)	4.0 (2.4)	5.0 (3.1)	5.2 (4.7)	8.4 (3.9)	9.0 (5.1)	8.9 (4.5)
I/σ(I)	12.9 (1.6)	13.3 (1.8)	10.9 (1.7)	30.1 (2.2)	27.2 (6.5)	18.4 (2.2)	46.9 (3.6)	44.7 (3.3)
Rmerge‡	11.3 (39.4)	11.2 (38.2)	11.6 (62.8)	5.5 (41.8)	6.0 (22.2)	9.8 (37.1)	4.6 (29.6)	4.6 (29.4)

^†The mosaicity of this crystal displayed strong anisotropy.

^‡ R _merge = , where I_i(hkl) is the intensity of the ith observation and 〈I(hkl)〉 is the mean intensity.

Figure 3.

Comparison of mini-beam and large-beam data from a needle-shaped crystal. I/σ(I) (solid symbols) and R _merge (open symbols) are plotted for data sets collected from a thioesterase crystal with the mini-beam (triangles; TENS) and with a large beam (diamonds; TENL). Owing to higher background and a poorer signal-to-noise ratio, the TENL data have a reduced effective diffraction limit and overall poorer statistics than the TENS mini-beam data.

The most obvious reason for the improved diffraction data obtained using the mini-beam was the improved signal-to-noise ratio in the diffraction images, which ranged from 1.5-­fold to 3.5-fold based on pixel counts in the raw data (Fig. 4 ▶). We cannot exclude the possibility that the large-beam data (TENL) were recorded from a poorer region of the sample than that used to record the small-beam data. However, the large beam was considerably larger than the crystal in the direction perpendicular to the needle, leading to much higher background counts per pixel in the large-beam diffraction images (Fig. 4 ▶). Another reason for the higher quality of the data from the mini-beam experiment may have been mechanical flexibility of the crystal, which had a length ratio of 20:1. Any bending of the crystal would have been ‘seen’ by the large beam, while the small beam may have sampled a less bent region of the crystal. This possibility is consistent with the refined mosaicities, which were 0.31° for TENS and 1.0° for TENL.

Figure 4.

Comparison of signal-to-noise ratios for diffraction from a needle-shaped thioesterase crystal obtained with a large beam (left column) and with the mini-beam (right column). All panels are depicted with the same gray levels (0→344 counts, white→black). For each of the (a) high, (b) medium and (c) low resolutions, identical reflections are compared from the large-beam and mini-beam data sets. In the corner insets, the peak intensity (peak), average background around the spot (Bkgr.) and signal-to-noise ratio (S/N) are shown. S/N was calculated by summing the four largest pixel values in the diffraction spot and dividing by four times the average background around the spot. To ensure that the largest pixel values were chosen for both beams, adjacent diffraction images were also inspected.

3.4. Experiment 4. Crystal inhomogeneity: mosaicity

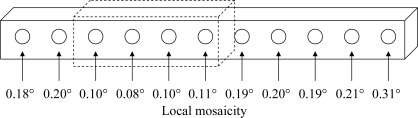
To study the variation of mosaicity within a sample, a lysozyme crystal of 350 × 50 × 50 µm was probed using the mini-beam. Ten frames of 0.2° width were collected from each of 11 segments along the crystal. The centers of adjacent segments were 30 µm apart. The crystal mosaicity refined for each segment varied between 0.08 and 0.31° (Fig. 5 ▶). The low values of the refined mosaicity indicate the good overall quality of the sample. The smooth variation of mosaicity along the crystal length indicates that the mosaicity values are reliable. A 100 µm segment of the crystal had twofold lower mosaicity than other regions, demonstrating the utility of the mini-beam for the isolation of well ordered local segments of the sample.

Figure 5.

Variation of mosaicity within a crystal. The large rod-shaped lysozyme crystal used for mosaicity measurements is drawn. The circles and arrows indicate the spots at which six diffraction images were recorded. The crystal was translated 30 µm between spots. Mosaicity estimates are as refined in HKL-2000. The dashed box indicates the best region of the crystal.

3.5. Experiment 5. Crystal inhomogeneity: diffraction-spot shapes

Next, we investigated the application of the mini-beam to a crystal with streaked diffraction spots. Two data sets, LLS1 (lysozyme, large crystal, small beam) with the mini-beam and LLL2 (lysozyme, large crystal, large beam) with the ‘standard’ beam, were collected from two regions of a large (200 × 80 × 40 µm) lysozyme crystal (Table 4 ▶). Viewed with the large beam, this low-quality sample had streaked diffraction spots arising from either an invisible crack or a satellite crystal; however, the mini-beam produced well shaped diffraction spots (Fig. 6 ▶ a). The beam attenuation was adjusted to maintain a constant total X-ray dose for the two data collections, while the other parameters were identical. The processing statistics to 1.8 Å spacing were better for the data measured with the small beam (LLS1) than for the large-beam data (LLL2). Beyond 1.8 Å, better statistics were obtained for the large-beam data (Fig. 6 ▶ b). While the mini-beam and the large-beam data sets were collected from different segments of the crystal in order to avoid possible artifacts arising from radiation damage, similar patterns of mosaicity values indicate similar sample quality in the two cases. We interpret the difference in data quality as the mini-beam intercepting a more homogeneous region of the crystal whereas the large beam intercepted a split or doubled crystal. Within 1.8 Å, the doubled diffraction spots were not resolved with the large beam but they were easily separated with the mini-beam (Fig. 6 ▶ a). For data beyond 1.8 Å from the large beam, either the two patterns were better resolved or the satellite crystal did not diffract strongly. In this situation, the advantage of a larger beam bathing a larger diffracting volume became the dominant factor and the large-beam data were of superior quality.

Figure 6.

Effect of beam size on data from a large inhomogeneous lysozyme crystal. (a) Identical region of reciprocal space imaged with the mini-beam (left) and with the large beam (right). (b) Comparison of data measured with the mini-beam (triangles) and a large beam (diamonds). I/σ(I) (solid symbols) and R _merge (open symbols) are plotted. Data from the mini-beam within a 1.8 Å limit are of higher quality, whereas beyond 1.8 Å the quality of the large-beam data is superior.

3.6. Experiment 6: Comparison of mini-beam and large-beam data from a large homogeneous crystal

In a final experiment, we compared mini-beam and large-beam data recorded from a large homogeneous crystal under conditions of either equal peak flux density or equal integrated intensity (Fig. 7 ▶ a). Three complete data sets were collected from a large (300 × 40 × 40 µm) lysozyme crystal using small and large beams: LLS2 (lysozyme, large crystal, small beam), LLL3 (lysozyme, large crystal, large beam, constant flux density with LLS2) and LLL4 (lysozyme, large crystal, large beam, constant integrated intensity with LLS2). Firstly, the rod-shaped crystal was probed with the mini-beam to ensure its high quality throughout. Six frames of 0.5° each were collected with 100-fold attenuation and the crystal mosaicity was refined. Mosaicities varied from 0.07° at one end of the crystal to 0.3° at the other and spot shapes were uniform throughout. Data set LLL3 was collected with a large (70 × 25 µm) beam from the higher mosaicity end of the crystal (Fig. 7 ▶ a). X-ray flux [200-fold attenuation, 5 × 10¹⁰ photons s⁻¹ (100 mA)⁻¹] and exposure time (2 s) were chosen to achieve maximum diffraction intensity while avoiding overloaded detector pixels for the data collection of highest total dose. Integration and scaling parameters showed no evidence of radiation damage, consistent with our experience with many lysozyme crystals. The LLS2 data set was collected from the center of the crystal using the mini-beam with attenuation and exposure time as for data set LLL3. Data set LLL4 was collected using the large beam from the previously unexposed end of the crystal using increased beam attenuation (flux density decreased) so that the integrated beam intensity was identical to that in the mini-beam experiment (LLS2). Exposure times were identical for the three experiments.

Figure 7.

Effect of the beam size on data from a large homogeneous lysozyme crystal. (a) Schematic diagram of the experiment. The rectangle represents the 300 µm long rod-shaped lysozyme crystal. The beam size, shape and flux for each experiment are shown as ellipses and profiles. The peak flux is matched in the LLS2 and LLL3 experiments; the integrated intensity is matched in the LLS2 and LLL4 experiments. (b) Comparison of data quality. I/σ(I) (solid symbols) and R _merge (open symbols) are plotted for the LLS2 (triangles), LLL3 (squares) and LLL4 (circles) experiments. Data from the large-beam experiments (LLL3 and LLL4) are superior to mini-beam data (LLS2) throughout the diffracting range of the experiment.

Both data sets measured with the larger beam were of superior quality to the mini-beam data set (Table 4 ▶, Fig. 7 ▶), demonstrating that the larger beam produces better data from large homogeneous sample crystals. We expected the data quality to decrease when the total beam flux was decreased (LLL3 versus LLL4); however, the data quality was indistinguishable in these two large-beam experiments. The observed effect may partially be a consequence of the crystal diffracting power, which extended well beyond the limits of the experiment, and partially of the fact that the crystal was better ordered in the region of the LLL4 data collection. It is noteworthy that the experiment with the larger diffracting volume (LLL4) produced significantly better data than the experiment with the smaller diffracting volume (LLS2) when the total integrated intensity of the incident beam was unchanged. This illustrates how the larger beam and larger diffracting volume allowed the use of lower flux density, thus better preserving the sample.

4. Discussion

The experiments presented here show conclusively that the best quality diffraction data were obtained when the size of the X-ray beam was matched to the size of the sample crystal to the upper limit of the beam size. This is seen most directly in the experiments on the needle crystal of thioesterase (experiment 2, Table 4 ▶, Fig. 4 ▶), in which low background scattering with the mini-beam led to substantial improvements in the signal-to-noise ratio, R _merge and effective diffraction limit relative to data from the same sample obtained using the large beam (TENS versus TENL). In this case, improvements are seen over the full diffracting range of the crystal.

The intrinsically weak diffraction from crystals of biological macromolecules is best recorded when the X-ray beam intercepts the largest possible number of unit cells. In experiment 6, the quality of the data sets collected using the large beam was superior to that of the mini-beam data by all measures: effective diffraction limit, I/σ(I) and R _merge (Table 4 ▶). The superiority of the large-beam data is even more striking in comparisons of individual reflections in diffraction images. For example, we compared the total counts in the largest four pixels for two Bragg reflections in the LLS2 and LLL4 data sets. These data sets were collected with beams of identical integrated intensities but different sizes, illuminating larger and smaller diffracting volumes of the same crystal. A Bragg reflection with d = 12 Å was 12 times stronger with the larger beam than with the smaller beam. A Bragg reflection with d = 2.2 Å was nine times stronger with the larger beam. The preference for a large beam is also clear from the improved diffraction limits in the data sets from large crystals of lysozyme and thaumatin relative to the data from microcrystals of these proteins (experiments 1 and 2, Table 2 ▶).

However, data from large crystals are only superior when the X-ray beam intercepts a homogeneous volume of the crystal. Diffraction quality is reduced when the intercepted crystal volume is inhomogeneous. Unfortunately, such in­homogeneities are common in crystals of biological macromolecules and arise from effects such as split or multiple crystals, bent crystals, satellite crystals and crystals with damaged or imperfect local regions. In practice, the length scale of many such crystal inhomogeneities lies between 10 and 100 µm. Thus, by selecting more homogeneous regions of such crystals, the 7 µm mini-beam affords the opportunity to measure data that are superior to large-beam data even though fewer unit cells contribute to the measured diffraction with the mini-beam than with the large beam. This is illustrated by the thioesterase crystal (experiment 3, Table 4 ▶), in which crystal mosaicity was reduced threefold when the beam intercepted 7 µm of the needle crystal (TENS) compared with 70 µm (TENL). It is also apparent in the lysozyme crystal, with streaked diffraction spots in the large beam but not in the mini-beam (experiment 5, Fig. 6 ▶).

Radiation damage can be viewed as time-dependent in­homogeneity. For several cases of extreme sensitivity to radiation, useful data have been recorded using a mini-beam in raster fashion to collect data from several spots on a large crystal (see, for example, Rasmussen et al., 2007 ▶). Experiment 2 also illustrates the usefulness of merging partial data sets, each collected at a high X-ray dose from a very small crystal volume, to yield a good-quality complete data set (Tables 2 ▶ and 3 ▶, Fig. 2 ▶).

The results presented here have several implications for ordinary data collection in macromolecular crystallography. It is abundantly clear that small protein crystals approaching 100 µm³ in volume can produce useful data with X-ray beams of a few micrometres in size mainly because of improved signal-to-noise ratios relative to data from large beams. It is noteworthy that in our experiments the ‘standard’ beam, 70 × 25 or 125 × 25 µm, was considerably smaller than the standard beam on most beamlines. Therefore, the benefits of the mini-beam demonstrated relative to our ‘standard’ beam are expected to be greater when compared with even larger beams. The experiments reported here and many results in the literature lead to the obvious conclusion that a mini-beam should be used with small crystals to maximize diffraction quality.

The mini-beam also has many advantages for large sample crystals that display the inhomogeneities discussed above. A mini-beam can be used routinely to probe large crystals for their most perfect regions. Many GM/CA-CAT users have taken exactly this approach when large crystals have un­desirable diffraction properties (poor spot shapes or high mosaicity). The mini-beam apparatus at GM/CA-CAT is quickly exchangeable with the scatter-guard tube for large-beam experiments, allowing users to select the beam best suited to the sample.

Improvements in the capability of the mini-beam will make it a better general tool. For example, smaller diffracting volumes necessitate higher X-ray doses to maintain diffraction limits, leading to faster decay of sample crystals. This is typically remedied by translating the sample to expose fresh parts to the beam. For more robust and streamlined operations, new tools are needed to automate this process. Another challenge is the visualization and centering of samples of ever-decreasing size. In several cases on the GM/CA beamlines, samples could not be seen optically owing to their small size or to peculiarities of the mounted sample. New tools are needed to aid reliable centering of samples by optical or other means.

A current trend in structural biology is the demand for the solution of structures from small or imperfect crystals. Technologies exist to achieve beam sizes of several hundred nanometres or smaller (Bilderback et al., 1994 ▶, and references therein; Jark et al., 2006 ▶; Lagomarsino et al., 2006 ▶; Snigirev et al., 2007a ▶,b ▶). With current efforts in nanoscale sciences, such capabilities promise to become more robust and more readily available. However, many of these techniques pose additional challenges in crystallographic data collection, for example by increases in exposure times owing to lowered beam intensities and decreased diffracting volumes, by more stringent re­quirements for beam and sample stability, by increased beam divergence, by limited usable energy range and by limited sample-to-detector distance range. The feasibility of using sub-micrometre beams with similarly sized crystals has not been investigated. Nevertheless, these possibilities for an even smaller beam are intriguing for future development. For the present, an X-ray mini-beam of several micrometres in diameter is proving to be an excellent practical resource and its use promises to increase substantially over the coming years.