Enthalpy (ΔH) and Entropy (ΔS) for π-Stacking Interactions in near-Sandwich Configurations: The Relative Importance of Electrostatic, Dispersive, and Charge-Transfer Effects

Abstract

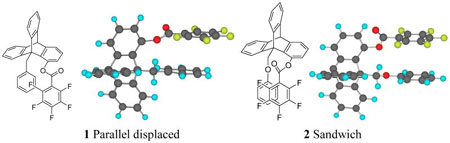
Interactions between two aromatic rings with various substituents in a near-sandwich configuration have been quantitatively studied using the triptycene derived molecular models. This model system allows a stacking arrangement of two arenes to assume a near perfect face-to-face configuration in its ground state conformation. Comparing to our previous study of the parallel displaced configuration, repulsive interactions are predominant for most arenes currently studied. However, if one arene is strongly electron-deficient (Ar₂ = pentafluorobenzoate), attractive interactions were observed regardless of the character of the other arene (Ar₁). For stacking interactions between Me₂NC₆H₄ and C₆F₅CO groups, a ΔH of −1.84 ± 0.2 kcal/mol and a ΔS of −2.9 ± 0.8 cal/mol·K were determined. The general trend in the attractive stacking interaction towards a pentafluorobenzoate is Me₂NC₆H₄ > Me₃C₆H₂> Me₂C₆H₃> MeC₆H₄ > MeOC₆H₄ > C₆H₅ > O₂NC₆H₄. The observed trend is consistent with a donor-acceptor relationship and the acceptor is a C₆F₅CO group.

Introduction

Aromatic interactions play important roles in biological recognition and crystal engineering.^1,2 Widespread interest have been shown in the development of models to improve our understanding of these interactions.^3–5 The two most noted models with strategies to quantify aromatic interactions in the stacking conformation include the 1,8-diarylnaphthalene system by Cozzi, Siegel, and co-workers and the double mutant cycle system by Hunter and coworkers.^6–9 However, each model system has its limitations and the previous models were either too restrictive or too flexible.^8–11 There has not been enough quantitative studies to compare and reach a generally-agreed value for the magnitude of aromatic interactions in solution.⁵ Other studies involving the edge-to-face conformation have been reported.^12–14 This study is focused on the face-to-face or sandwich configuration.

Recently we reported our studies on aromatic interactions using the triptycene derived model system,^15,16 which allows the arenes to interact near their van der Waals’ contact and quantitative determination of the magnitude of interaction was achieved. Our previous study involved arene-arene interactions in the parallel displaced configurations (1), i.e., the two arenes are parallel to each other with the center of one arene on top of the edge of the other. Through molecular modeling, we have found that by a small modification to the previous model compound, the arenes can be arranged to assume a near-sandwich configuration in the syn rotamer of 2.

Currently little experimental data are available on the magnitude of arene interactions in solution. Although the significant role played by quadrupole moments of benzene and hexafluorobenzene has been elegantly presented,^17–20 it seems that no agreement has been reached on whether electrostatic interactions alone control aromatic interactions.⁵ The consideration of quadrupole moments provides a simple way to visualize the charge distribution of aromatics and correctly predicts the preferred geometry of symmetrically substituted arene interactions. However, if the arenes are stacked at van der Waals distance, it would not be appropriate for the interactions to be quantitatively modeled as just a quadrupole-quadrupole interaction.^20,21 In fact, recent high level theoretical studies have indicated that electrostatic forces alone cannot rationalize the energetic ordering of substituent effects.²² In general, theoretical studies have demonstrated the importance of dispersive forces.⁵ Our study has shown that in addition to electrostatic and dispersive forces, charge transfer or donor-acceptor interactions also play a role in aromatic interactions.¹⁶ We have recently reported the observation that a charge-transfer band was observed in the stacking interactions between a N,N-dimethylaminophenyl group and a pentafluorobenzoate group in a parallel-displaced configuration.¹⁶ This study shows that charge transfer interactions are also present for the same arene pair in a near sandwich configuration. Our data are consistent with the view that electrostatic, dispersive, and donor-acceptor forces all play a role in aromatic interactions in organic solvents. The relative importance of each force depends on the characteristics of the two arenes involved.

Results

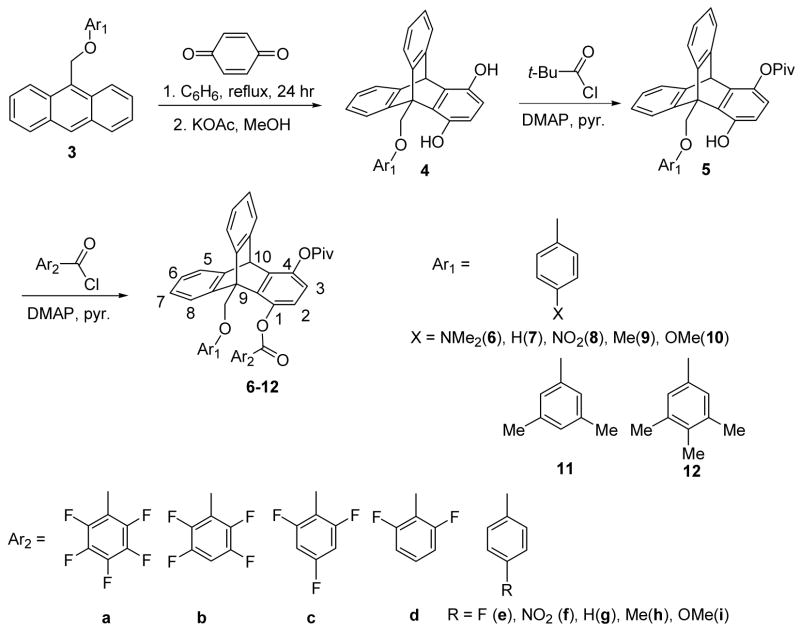
As a result of molecular modeling studies, a modification to our recently reported model compounds was made in order to study aromatic interactions in the sandwich configuration. This calls for an insertion of an oxygen atom into our previous model between the bridgehead (C9) CH₂ group and the phenyl group. The compounds used in this study and their syntheses are summarized in Scheme 1. We will briefly describe the synthetic procedures.

Scheme 1.

Synthesis of the model compounds

The preparation of the desired compounds 6a-12i started with a Diels-Alder reaction. Various anthraceny ethers 3 were prepared according to literature procedures^23,24 and were allowed to react with the dienophile p-benzoquinone. The Diels-Alder reaction was followed by an equilibration/aromatization with KOAc to produce the triptycene derivative 4. The less sterically hindered phenolic OH group at C4 was protected by a pivaloyl group to produce ester 5. The pivaloyl group was chosen to be the spectator group to increase the solubility of these model compounds. The synthesis was completed with acylation reaction with substituted benzoyl chloride Ar₂COCl to afford the desired model compounds 6a-12i.

Conformations of the syn and anti isomers

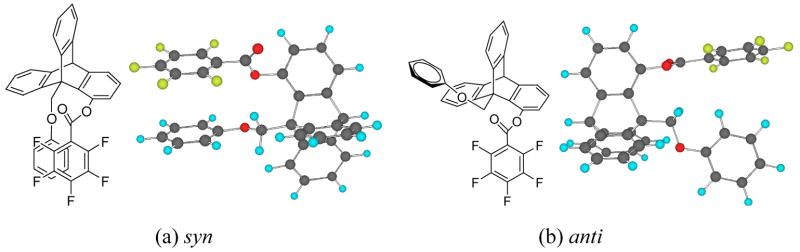
The two arenes are denoted as Ar₁ and Ar₂ with Ar₁ attached to the bridgehead carbon (C9) and Ar₂ attached to C1 of the triptycene system. Ar₁ and Ar₂ are face-to-face and within van der Waals’ contact distance in the syn conformation. In the anti conformation, the Ar₁ group bisects the triptycene skeleton and the Ar₂ group assumes the perpendicular arrangement from the triptycene skeleton. It appears to be an edge-to-face arrangement between Ar₁ and Ar₂ in the anti conformation. However, the distance between the C-H of Ar₁ and the π–face of Ar₂ is not optimal and the substituent effects do not correlate with the potential edge-to-face interaction in the anti conformation. As shown in Scheme 1, the Ar₁ groups range from mono-substituted para-X-phenyl to multiple methyl or methoxy substituted phenyl groups. The substituent X is varied from a strongly electron-donating group such as NMe₂ to an electron-withdrawing group such as NO₂. The Ar₂ groups also involve both mono-substituted benzoate and an increasingly electron-deficient arene by the increase of fluorine atoms on the aromatic ring. Molecular modeling via MacroModel (version 7.0, force field: MMFFs) shows a stable near-sandwich configuration between Ar₁ and Ar₂ in model compound 7a where Ar₂ = C₆F₅, Figure 1. It is important to point out that the structures shown here were modeled by molecular mechanics, therefore, the sandwich conformation is stable based on steric and electrostatic effects alone. Other electronic effects such as dispersion forces can only be estimated by using more sophisticated electronic models. The only apparent repulsive close contact in the syn conformation (a, Figure 1) is between the oxygen atom at C1 and the one at the bridgehead CH₂. The arenes are far enough from each other in the anti conformer (b, Figure 1), neither steric and nor stacking interactions are present. The only potential interaction between Ar₁ and Ar₂ in the anti conformation is the attractive edge-to-face interaction mentioned above. Therefore any preference for the syn conformation should be the results of attractive interactions from the stacking orientation rather than repulsions from the anti conformer.

Figure 1.

Global ground state conformations for (a) syn and (b) anti isomers. Ar₁ = phenyl, Ar₂ = pentafluorobenzoate.

Variable Temperature NMR Spectroscopy

A variable temperature NMR study was carried out using these model compounds. Two conformational isomers, the syn and the anti, can be observed at low temperatures. This is due to the slow rotation of the bridgehead CH₂ group in these compounds on the NMR time scale, which allows the integration and the determination of the syn/anti isomer ratio for each compound (Figure 2). It is important to point out that the conformational freedom is rather limited for either the anti or the syn isomers. The C1 ester linkage prefers the s-trans conformation (Figure 1) by ~4.5 kcal/mol to the alternative s-cis conformation to avoid oxygen lone pair repulsion.^25,26 Furthermore, the Ar₂C(=O)-O bond prefers to be nearly perpendicular to the triptycene arene plane which allows a parallel alignment between Ar₁ and Ar₂, Figure 1. Thus the syn/anti ratio is effectively the equilibrium constant between the stacked (or syn) and the separated (or anti) arene conformations. Since statistically two syn and one anti conformer are expected, the equilibrium constant, K_eq, should be 1/2·syn/anti ratio. The Ar₁OCH₂ protons are diastereotopic in the syn conformational isomer and display an AB quartet while they are enantiomeric in the anti conformation and appear as a singlet. The experimentally determined syn/anti ratios in CDCl₃ at different temperatures are shown in Table 1.

Figure 2.

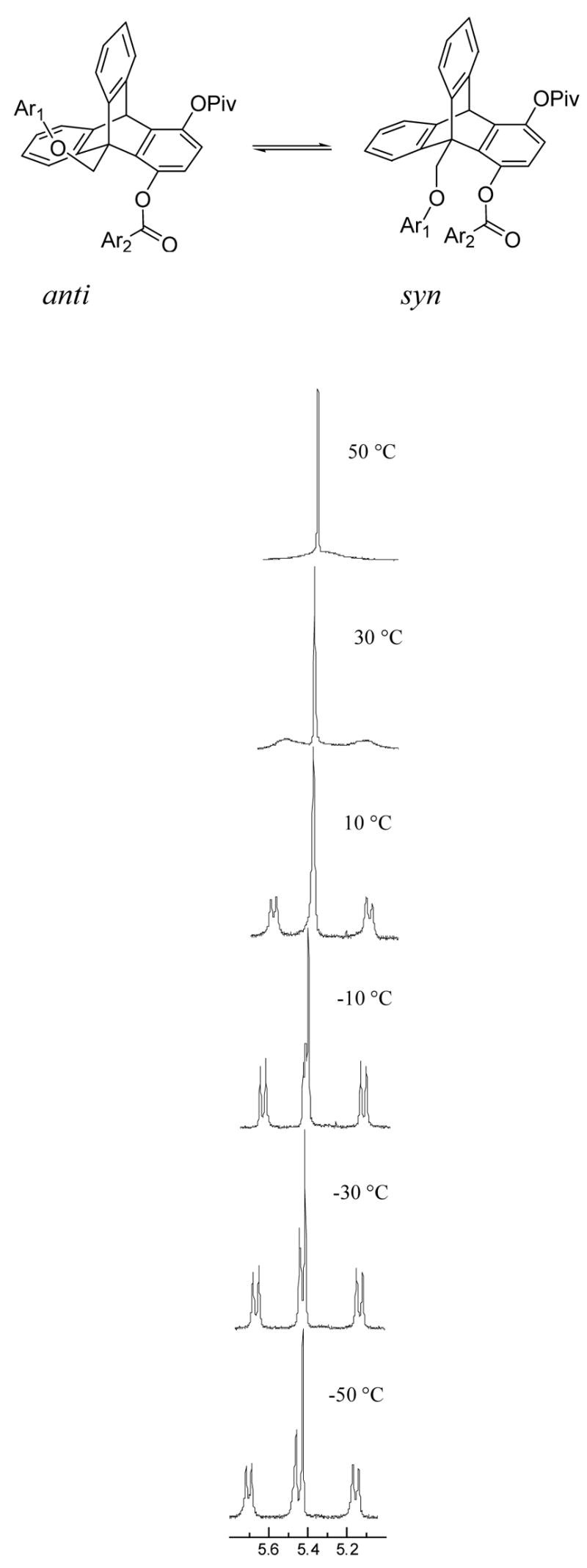
The temperature-dependent NMR signals (300 MHz in CDCl₃) from the bridgehead C(9)H₂ protons of compound 7f. The sharp singlet is the bridgehead CH at C10.

Table 1.

Ratios of syn/anti Isomers at Different Temperatures for Model Compounds 6a-14a. The experiments were performed in CDCl₃ unless stated otherwise.

Entry	Compound	Ar1	Ar2	syn/anti Ratio in CDCl3 at different temp.
				−10	−20	−30	−40	−50 (°C)
1	6a	C6H4NMe2	C6F5	15.7	17.5	20.7	26.5	28.0
2	6b	C6H4NMe2	C6HF4	5.37	6.04	6.61	7.36	8.87
3	6c	C6H4NMe2	C6H2F3	1.62	1.70	1.83	1.90	1.93
4	6d	C6H4NMe2	C6H3F2	0.72	0.71	0.72	0.72	0.74
5	6e	C6H4NMe2	C6H4F	0.54	0.53	0.48	0.47	0.47
6	7a	C6H5	C6F5	11.0	11.7	13.7	15.7	18.0
7	7f	C6H5	C6H4NO2	2.63	2.78	2.94	3.08	3.27
8	7e	C6H5	C6H4F	0.55	0.54	0.53	0.50	0.47
9	7g	C6H5	C6H5	0.30	0.29	0.26	0.24	0.21
10	7h	C6H5	C6H4Me	0.19	0.17	0.16	0.14	0.12
11	7i	C6H5	C6H4OMe	0.23	0.22	0.19	0.18	0.17
12	8a	C6H4NO2	C6F5	5.6	6.0	6.8	7.6	8.9
13	8f	C6H4NO2	C6H4NO2	2.66	2.73	2.85	2.94	3.05
14	8e	C6H4NO2	C6H4F	0.96	0.92	0.90	0.89	0.89
15	8g	C6H4NO2	C6H5	0.59	0.56	0.55	0.53	0.50
16	8h	C6H4NO2	C6H4Me	0.54	0.51	0.48	0.46	0.44
17	8i	C6H4NO2	C6H4OMe	0.61	0.59	0.57	0.54	0.52
18	9a	C6H4Me	C6F5	13.5	15.2	17.2	18.7	21.3
19	10a	C6H4OMe	“	10.6	12.0	13.1	15.8	18.2
20	11a	C6H3Me2	“	15.2	17.5	19.8	21.0	23.3
21	12a	C6H2Me3	“	17.1	19.1	21.3	23.8	26.1
22	13	C6H4Me	CH3	1.99	2.08	2.27	2.40	2.58
23	14	CH3	CH3	0.32	0.32	0.30	0.28	0.27

The ratio changes significantly with temperature when a model compound displays a large syn/anti ratio. This enables us to obtain both ΔH and ΔS by using the van’t Hoff equation (1). Considering the importance of entropic effects in noncovalent interactions,¹¹ this study provides information for π– stacking that has not been reported from previous systems. Thermodynamic parameters are collected in Tables 2–4. Some caution should be taken with these data since the enthalpy and entropy obtained using the van’t Hoff equation assume a constant enthalpy value in the surveyed temperature range which may or may not be true.

Table 2.

The Effect of the Number of Fluorine Atoms of Ar₂ on ΔH and ΔS for Arene-Arene Interactions in CDCl₃. The standard errors are calculated using linear regression analysis.²⁷

Entry	Compound	Ar1	Ar2	ΔH° anti→syn,a	ΔS°anti→synb	ΔGanti→sync
1	6a	C6H4NMe2	C6F5	−1.84 ± 0.2	−2.9 ± 0.8	−0.99 ± 0.2
2	6b	C6H4NMe2	C6HF4	−1.41 ± 0.1	−3.4 ± 0.3	−0.41 ± 0.1
3	6c	C6H4NMe2	C6H2F3	−0.53 ± 0.1	−2.4 ± 0.3	−0.17 ± 0.1
4	6d	C6H4NMe2	C6H3F2	−0.08 ± 0.1	−2.4 ± 0.2	0.62 ± 0.1
5	6e	C6H4NMe2	C6H4F	0.46 ± 0.1	−0.9 ± 0.5	0.72 ± 0.1

^ain units of kcal/mol.

^bin units of cal/mol·K.

^cin units of kcal/mol at 293 K.

Table 4.

Comparison between Sandwich and Parallel-displaced π-Stacking

Entry	Compound	Ar1	Ar2	Ratio (syn/anti, at −15 °C)
				Sandwicha	Parallel-displacedb
1	6a	C6H4NMe2	C6F5	16.6	21.7
2	10a	C6H4OMe	C6F5	11.2	16.8
3	7a	C6H5	C6F5	11.3	13.7
4	7f	C6H5	C6H4NO2	2.71	9.0
5	7e	C6H5	C6H4F	0.55	2.9
6	7g	C6H5	C6H5	0.30	1.9
7	7i	C6H5	C6H4OMe	0.23	1.7

^aThis work.

^bReference ¹⁶.

$$ln{\text{K}}_{\text{eq}}=-\mathrm{\Delta }\text{H}°/\text{RT}+\mathrm{\Delta }\text{S}°/\text{R}({\text{K}}_{\text{eq}}=\mathbf{1}/\mathbf{2}·\text{syn}/\text{anti},\text{R}=\text{gas}\text{constant})$$ (1)

Discussion

As shown in Table 1, the largest syn/anti ratio was obtained for compound 6a, where Ar₁ = C₆H₄NMe₂ and Ar₂ = C₆F₅. This corresponds to a ΔH of −1.84 ± 0.2 kcal/mol and a ΔS of −2.86 ± 0.83 cal/mol·K (Table 2) in favor of the stacking configuration. Hunter and co-workers have reported a study for a pair of arenes with similar structures using their chemical double mutant model system.⁸ Only room temperature study was conducted and a free energy of 0.4 kcal/mol was deduced for the stacking interactions between pentafluoro-aminophenyl and N,N-dimethylaminobenzoate grouping (see below) in CDCl₃. From our experiments, the ΔH and ΔS in Table 2 give a free energy of 0.99 ± 0.2 kcal/mol at 293 °K in the same solvent.

The difference in the structures between that used in Hunter’s experiments and the current experiment may partially account for the difference in observed free energies. The donor and acceptor groups in our model system are more electron-rich and deficient, respectively, than that used in Hunter’s experiments. This difference in arene structures may well account for the fact that the attractive interactions in our model system are twice as strong as that determined by the chemical double mutant cycle experiments. Double mutant cycle experiments offer a sophisticated and laborious approach to dissecting a complex system to a single weak interaction. However the method suffers in accuracy as suggested previously,^10,11 because the flexibility of the system and the uncertainty was multiplied because four different binding studies were required.

The entropies for edge-to-face interactions have been determined by Jennings and coworkers.¹⁴ However, to our knowledge, the entropies for stacking aromatic interactions are for the first time determined experimentally. The entropy values shown in Tables 2–3 are significantly negative when the interactions are strongly attractive. On the other hand, negligible or positive values are obtained when the interactions are small or repulsive. Thus to a certain degree, an enthalpy-entropy compensation is shown in this conformational equilibrium.²⁸ However the entropy decreasing does not completely offset the enthalpy gained through substituent effects. This is evidenced by the different free energies observed for different arene pairs. The errors associated with the entropy values should be greater than the corresponding enthalpy values since the ΔS is derived from the intercept and the ΔH is determined from the slope.

Table 3.

Substituent Effect on the ΔH and ΔS for Arene-Arene Interactions. The standard errors are calculated using linear regression analysis.²⁷

Entry	Compound	Ar1	Ar2	ΔH°anti→syn,	ΔS°anti→syn in CDCl3
1	7a	C6H5	C6F5	−1.49 ± 0.08 kcal/mol	−2.3 ± 0.3 cal/mol·K
2	7f	C6H5	C6H4NO2	−0.63 ± 0.02	−1.8 ± 0.1
3	7e	C6H5	C6H4F	0.46 ± 0.06	−0.8 ± 0.3
4	7g	C6H5	C6H5	1.06 ± 0.1	0.3 ± 0.4
5	7h	C6H5	C6H4Me	1.30 ± 0.1	0.3 ± 0.4
6	7i	C6H5	C6H4OMe	0.93 ± 0.1	−0.8 ± 0.5
7	8a	C6H4NO2	C6F5	−1.36 ± 0.1	−3.2 ± 0.3
8	8f	C6H4NO2	C6H4NO2	−0.41 ± 0.1	−1.0 ± 0.1
9	8e	C6H4NO2	C6H4F	0.21 ± 0.1	−0.7 ± 0.3
10	8g	C6H4NO2	C6H5	0.45 ± 0.1	−0.7 ± 0.2
11	8h	C6H4NO2	C6H4Me	0.59 ± 0.1	−0.4 ± 0.2
12	8i	C6H4NO2	C6H4OMe	0.48 ± 0.1	−0.6 ± 0.1

^aNegative values indicate attractive and positive values repulsive interactions.

Figure 3 shows a plot of free energy vs. number of fluorine atoms for compounds 6a–6e, Table 2. The general trend is such that more fluorine substitution leads to higher attractive interaction. This trend follows the reasoning that electrostatic forces dominate the interactions. The quadrupole moments of the fluorinated aromatic rings gradually change from negative to positive as the number of fluorine atoms increases.¹⁷ It follows that attractive interactions occur between the tetra- and penta-fluorinated arene and the Me₂NC₆H₄ group while either repulsive interactions occur between the mono-, di-, and tri-fluorinated benzoate and the Me₂NC₆H₄ group or the anti conformation becomes attractive in the latter three model compounds. It is interesting to note that although the enthalpies of compounds 6c (Ar₂ = trifluorophenyl) and 6d (Ar₂ = difluorophenyl) have negative signs, the free energies have positive signs, meaning that entropic effects may play a role for these two compounds.

Figure 3.

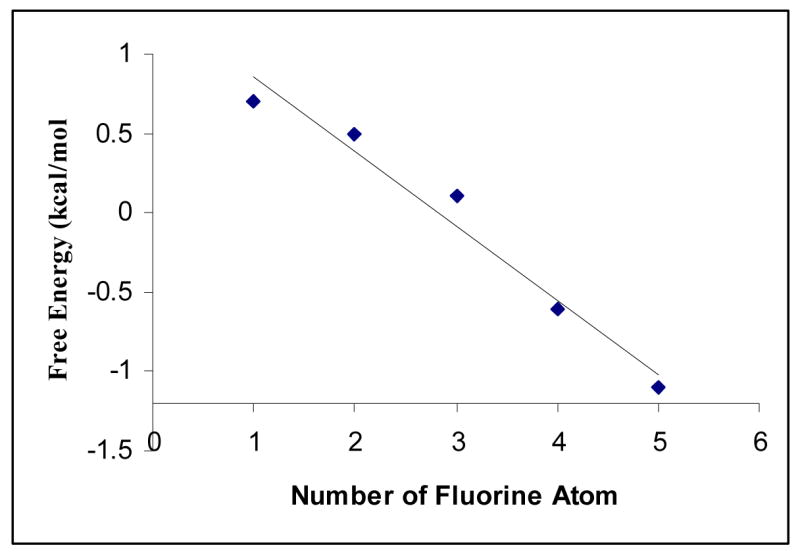
Plot showing the trend in stacking free energy for compounds 6a–6e as a function of the number of fluorine substitution on Ar₂ (Ar₁ = C₆H₄NMe₂). Primary data are given in Table 1 and Table 2.

The trend in Figure 3 is also consistent with a donor-acceptor mechanism, in which the donor is the C6H4NMe2 group and the acceptors are fluorinated benzoate groups. As the acceptor becomes more electron-deficient, the interaction becomes stronger. The pentafluoro substitution has a stronger attractive interaction than the trend line would predict. A UV band at 318 nm was observed for compound 6a, which was absent in the precursors’ spectra. None of the other model compounds showed such UV absorption. We attribute this to charge-transfer interactions. It is consistent with our previous suggestion that in order to observe a charge transfer band in the UV spectrum, a certain threshold of a high HOMO for the donor and low LUMO for the acceptor must be met in order to narrow the energy gap between the donor and the acceptor. When the arene is a relatively weak acceptor,²¹ such as the pentafluorobenzoate group, it appears that the donor must be at least as electron rich as an N,N-dimethylaminophenyl group.

Anti conformation was dominant for all compounds studied where Ar₁ is either a phenyl or a nitrophenyl group except where Ar₂ = C₆F₅ or C₆H₄NO₂ (Table 3). This is in contrast to our recent report on parallel displaced models,¹⁶ where most arenes prefer the syn conformation. The only favorable syn conformation in the current models is when Ar₂ = C₆F₅ or C₆H₄NO₂. Two possible reasons can account for the difference. The first possibility is that sandwich configuration between two aromatic rings are repulsive unless one of the arenes is reasonably electron-deficient. The second possibility is that the imperfect edge-to-face interaction in the anti conformation plays a role in the syn-anti equilibrium. Currently we prefer the first explanation because the highest anti preference (anti/syn = 8.3) is exhibited by model compound 7h where Ar₁ = C₆H₅ and Ar₂ = C₆H₄CH₃ rather than compound 8g (anti/syn = 2.3) where Ar₁ = C₆H₄NO₂ and Ar₂ = C₆H₄CH₃. If the edge-to-face interaction in the anti conformation plays a dominant role, one would expect 8g has a higher anti preference because the nitro group increases the phenyl CH acidity.

A comparison of the observed ratios of syn vs. anti isomers for the two different model systems is summarized in Table 4. The energy-optimized structures for the two models with C₆F₅ and C₆H₅ are shown in Figure 4 (with triptycene skeleton omitted for clarity). The parallel-displaced model has a smaller interplanar distance. In general, the parallel-displaced models give a greater percentage of syn isomers. When one arene is the strongly electron-deficient pentafluorophenyl group, both models prefer the syn conformation significantly, but by a comparable margin. The general trend in the attractive stacking interaction towards a pentafluorobenzoate is consistent with a donor-acceptor relationship. For example, the order of preference for the syn conformation is Me₂NC₆H₄ > C₆H₅ > O₂NC₆H₄ and in the multi-methyl series the order of preference is Me₃C₆H₂> Me₂C₆H₃> MeC₆H₄ > C₆H₅. The observed trend applies when the acceptor is a C₆F₅CO group. When Ar₁ = C₆H₄OMe, the syn/anti ratio is smaller than expected. This may be explained by considering the sandwich structure in the syn conformation. In the stacked conformation, the oxygen atom of the methoxy substituent is in close proximity to a fluorine atom from the C₆F₅, which causes repulsive interactions. The fact that a charge-transfer band is observed for compound 6a, where Ar₁ = Me₂NC₆H₄ and Ar₂ = C₆F₅, supports the notion that donor-acceptor interactions play a role.

Figure 4.

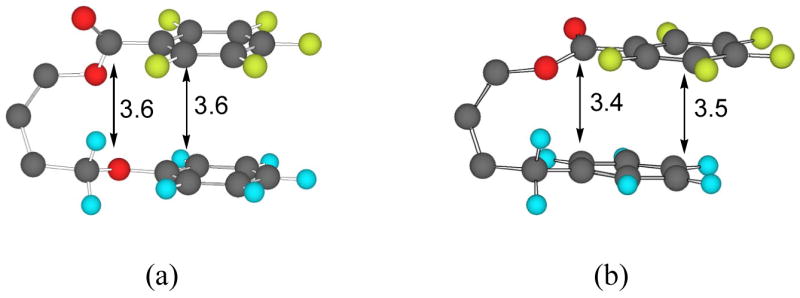
Chem3D representations of (a) sandwich and (b) parallel-displaced models with the triptycene skeleton omitted for clarity. Structures were optimized using MacroModel (version 7.0, force field: MMFFs). Interplanar distances are labeled in angstroms.

A much greater difference in syn/anti ratio between the two configurations is observed when neither of the arenes is strongly electron-deficient. In these cases, the ratio of the syn/anti isomers for the parallel-displaced model is greater than three times of that of the sandwich model. The sandwich model shows a much greater preference for the anti isomer indicating either a greater repulsive interaction in the syn conformation or a potential attractive interaction in the anti conformation although less likely.

Considering the data in whole, we interpret these results by a combination of electrostatic, London dispersive, and charge-transfer effects. When one arene is the strongly electron-deficient pentafluorophenyl group, the dominant role is played by electrostatic (including quadrupolar/dipolar) interactions which exist in both sandwich and the parallel-displaced configurations. In addition donor-acceptor interactions also play a role as evidenced by the substituent effects and the observation of a charge-transfer band of compound 6a. The parallel-displaced configuration has the advantage of allowing a closer interplanar distance which enhances London dispersive forces.²¹ This explains why the parallel-displaced configuration in general has a stronger binding energy than the sandwich configuration. When none of the arenes is strongly electron-deficient, electrostatic forces are repulsive in the sandwich configuration while attractive in the parallel-displaced configuration, which explains why the syn/anti ratio is three times greater with the parallel-displaced configuration. Thus both electrostatic and dispersive forces favor the parallel-displaced configuration. A further argument for the role of dispersion is to point out that one would mistakenly predict a preferred sandwich conformation for C₆F₆-C₆H₆ interactions if quadrupole moments alone were considered. Recent theoretical studies of C₆F₆-C₆H₆ complex indicate that the parallel-displaced configuration is the energy minimum even for the completely symmetrical aromatic complex.^21,29

Summary

Triptycene-derived molecular model system has been used to quantitatively study arene-arene interactions in the near-sandwich configuration. Both enthalpy and entropy are obtained for 21 different compounds via variable temperature NMR spectroscopy. Similar to models with arenes in the parallel-displaced configuration, arene-arene interaction in the sandwich configurations also prefers the syn conformation if the two arenes are of opposite polarity, i.e., one electron-rich and the other electron-poor. Overall the sandwich configuration shows a smaller attractive interaction than the parallel-displaced configuration. Electrostatic model based on quadrupole moments alone cannot completely explain the preference for the parallel-displaced arrangement. Our recent theoretical study in conjunction with our previous results has appeared which shows that dispersive forces are important in determining the energy minimum.²¹ The origin of the preference for the parallel-displaced conformation with regard to C₆F₆-C₆H₆ is related to the closeness of stacking.

Experimental Section

Representative procedure for the preparation of the model compounds: 9-(4-Dimethylaminophenoxymethyl)-1-(4-fluorobenzoyloxy)-4-pivaloyloxytriptycene (6e)

9-(4-dimethylamino phenoxymethyl)-1-hydroxy-4-pivaloyloxy triptycene (5) (0.15 mmol) was treated with 4-fluoro benzoyl chloride (0.19 mmol) and 4-(dimethylamino) pyridine (50 mg, 0.42 mmol) in pyridine (1 ml) at ambient temperature for 24 h. Then 5 ml of 1N HCl was added to quench the reaction. The mixture was extracted with methylene chloride and the extract was washed with aqueous HCl solution two times and dried over MgSO₄. The solvent was removed under reduced pressure. Further purification of the crude via flash column chromatography provided compound 6e as a solid (96%); M.P. 249–251 °C, ¹H NMR (300 MHz, CDCl₃) δ 7.78–8.36 (2H, m), 7.31–7.42 (5H, m), 6.73–7.03 (7H, m), 6.50–6.52 (4H, m), 5.08–5.62 (3H, m), 2.83 (6H, s), 1.53 (9H, m); ¹³C NMR (75 MHz, CDCl₃) δ 176.4, 164.1, 162.2, 144.3, 143.4, 133.2, 125.7, 125.7, 125.4, 124.6, 123.9, 121.2, 120.3, 116.5, 115.2, 66.3, 55.0, 48.5, 39.4, 32.6, 27.4. HRMS calcd for C₄₁H₃₆FNO₅ + H 642.2656, found 642.2655.

Variable Temperature NMR Experimental Procedure

The ¹H NMR spectra were recorded on a 300 MHz instrument with a variable temperature probe. A 0.05 M solution of the sample in a deuterated solvent such as chloroform was placed in a high quality NMR tube. All samples were degassed using a needle to bubble nitrogen through the sample for ~1 minute. The NMR tube was then capped with a cap and sealed with parafilm. The sample tube was placed into the NMR probe and the air line to the probe was replaced with liquid nitrogen transfer line. The desired temperature was set on the variable temperature unit and the sample was allowed to equilibrate for 10 ~15 minutes at each set temperature. Then the ¹H NMR spectrum at each temperature was recorded. The ratios of rotamers were obtained through the integrations of selected peaks.

Supplementary Material

si20061212_025. Supporting Information Available.

Experimental procedures for the preparation of compounds 3–13 and their ¹H NMR spectra. This material is available free of charge via the Internet at http://pubs.acs.org.