Measuring Specific, Rather than Generalized, Cognitive Deficits and Maximizing Between-Group Effect Size in Studies of Cognition and Cognitive Change

Abstract

While cognitive impairment in schizophrenia is easy to demonstrate, it has been much more difficult to measure a specific cognitive process unconfounded by the influence of other cognitive processes and noncognitive factors (eg, sedation, low motivation) that affect test scores. With the recent interest in the identification of neurophysiology-linked cognitive probes for clinical trials, the issue of isolating specific cognitive processes has taken on increased importance. Recent advances in research design and psychometric theory regarding cognition research in schizophrenia demonstrate the importance of (1) maximizing between-group differences via reduction of measurement error during both test development and subsequent research and (2) the development and use of process-specific tasks in which theory-driven performance indices are derived across multiple conditions. Use of these 2 strategies can significantly advance both our understanding of schizophrenia and measurement sensitivity for clinical trials. Novel data-analytic strategies for analyzing change across multiple conditions and/or multiple time points also allow for increased reliability and greater measurement sensitivity than traditional strategies. Following discussion of these issues, trade-offs inherent to attempts to address psychometric issues in schizophrenia research are reviewed. Finally, additional considerations for maximizing sensitivity and real-world significance in clinical trials are discussed.

Introduction

In studies of cognition in schizophrenia, or of cognitive change as the result of an intervention, a primary goal is to measure a specific cognitive process, free from the influence of other cognitive processes, and other factors that can affect cognitive functioning (eg, sedation, low motivation, anxiety, etc). The more precise the measurement of the cognitive process, the clearer the link will be to the associated neurophysiology, allowing for more sensitive assessments of treatment effects. Accomplishing this goal has proven difficult, however, due to a number of methodological and psychometric issues. The purpose of this article is to review these issues and to suggest potential solutions. The topics discussed below are organized into the following categories: (1) measuring specific vs generalized deficits; (2) the differential deficit and matched tasks research design; (3) optimizing effect size in between-groups comparisons, including considerations of the related issues of reliability, within-group variation, and between-group variation; (4) alternatives to task matching; (5) trade-offs inherent in choosing solutions to psychometric issues; and (6) other suggestions to maximize effect sizes.

Measuring Specific Vs Generalized Deficits

There are numerous obstacles to isolating variance in test scores that is related to a single cognitive process. One of these is that neuropsychological tests are generally confounded by multiple cognitive processes (ie, many tests involve attention, working memory, and decision making components in addition to the specific process purportedly being measured). Also, noncognitive factors such as low frustration tolerance, loss of motivation in the face of repeated failure, and sedation due to medication side effects can affect performance.^1–3

Based on these considerations, and based on the common factor model, performance on a typical neuropsychological test can be represented as

where z_j = an individual's standardized score on test j, s_p = true score for source of variance p, a_jp = influence of variance source p on test j, E_j = sources of measurement error on z_j, e_j = influence of E_j on z_j⁴

Because the influence of extraneous cognitive and noncognitive factors (ie, additional instances of “s”) clouds interpretation of test performance, the ideal test would be represented as z_j = a_jps_p + e_jE_j, where a person's score reflects only a single cognitive source of variance that accounts for (ideally) most of the observed variance, with only (ideally) a small contribution of error variance to observed scores. For the purposes of maximizing effect sizes between groups, the sources of variance that must be eliminated are those that do not discriminate between groups. To do this, we need to either eliminate all“nonspecific” sources of true score variance (s), or minimize effects of these sources (a) on test scores. While conceptually simple to grasp, the isolation of single cognitive processes has proven extraordinarily difficult in practice, as reflected in the multiple strategies to solving this problem that have been developed over the past 35 years.

The Differential Deficit Strategy and the Matched Tasks Solution

Because a single test score can reflect multiple sources of variance, many investigators have designed studies to detect a differential deficit across 2 tasks. The logic behind such designs is that if patients' performance compared with controls is differentially worse on one test than another, this could be taken as evidence of a specific deficit. However, as Chapman and Chapman^5–7 noted, this pattern of scores does not necessarily indicate the presence of a specific cognitive deficit, and in fact, it can be due to a psychometric artifact. In particular, a differential deficit could be due to the greater discriminating power of one of the tests. A test that is more reliable and/or has more variance (often associated with being more difficult, though not always) will discriminate between subjects better than a less reliable or less variable test. Therefore, a differential deficit is only meaningful under 3 conditions: (1) the patient group achieves superior performance on one of the tests; (2) differences between groups are greater on the task with poorer discriminating power; and/or (3) both tests have equivalent reliability and variance.^6–8

Chapman and Chapman⁶ suggested that the best way to ensure construct validity was to use a matched tasks approach (No. 3 above)—using two tasks that are matched on reliability and variance. The logic of this strategy was that a deficit that was identified using this approach could not be due either to a generalized deficit or to psychometric artifact. However, while this strategy can reduce the likelihood of findings being due to psychometric artifacts, it does not ensure construct validity (process specificity). This is because the matched tasks can still each be confounded by multiple cognitive processes, and so a difference in scores between the 2 tasks may also reflect the contribution of multiple cognitive processes. Moreover, matching on difficulty level is a problem for cognitive neuroscience tasks where parameter manipulations necessarily change difficulty levels across multiple conditions (eg, examining the effects of manipulating the number of noise elements in visual search tasks, exposure duration on recall, or extent of stimulus degradation on visual perception, etc, all involve manipulating difficulty level as well). In some cases, researchers have attempted to get around this issue by either altering tasks to ensure equivalent difficulty and variance levels across conditions (typically by removing more difficult items in more difficult conditions) or introducing additional cognitive requirements into one condition of a task (ie, increasing memory load in one condition of a perception task) to make this normally easier condition more difficult. It can be shown in such cases, however, that these manipulations reduce construct validity by lessening the range of the cognitive function that is assessed either by a single condition or the overall test and/or by making test scores more difficult to interpret in terms of a single cognitive process.²

Optimizing Effect Size in Between-Groups Comparisons, Including Considerations of the Related Issues of Reliability, Within-group Variation, and Between-Group Variation

Perhaps the most important limitation of the matched tasks solution, however, is that matching on reliability and difficulty level does not maximize between-groups discriminating power.^2,9 This can be seen by examining the following equation for reliability: 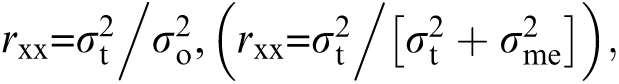where σ_t² = true score variance, σ_o² = observed score variance, and σ_me² = measurement error. From this view of reliability, it can be seen that reliability of a test can be increased by reducing measurement error (σ_me²) or by increasing true score variance (σ_t²). Reducing measurement error will always reduce within-group variance and increase sensitivity to between-group sources of variance. Increasing true score variance will increase within-group variance/discrimination, but if it does not also increase between-group separation, between-group effect size will decrease.¹⁰

The latter point can be demonstrated using formulas derived from the noncentrality parameter, the equation that represents effect size in between group comparisons.¹⁰ As Neufeld¹⁰ demonstrated, the magnitude of a between-group difference can be expressed as (ct + β)/(t + e), where β is the effect on group separation of a variable unique to group membership (eg, a pathognomonic variable), t reflects the size of the combined distribution of both groups' distributions on a nonpathognomic variable (ie, the extent of individual differences, as might be revealed in a population sample), and c represents the amount of separation between the 2 group distributions whose overall magnitude make up t (ie, as t-related group separation increases, c increases). For example, in a study comparing people with schizophrenia vs people with depression on visual integration (a process in which an impairment is thought to be found only in schizophrenia), β would reflect variance due to visual integration ability, t would reflect the contribution of variance from individual differences on a factor present in both groups, such as varying motivation level to perform the task, and c would represent the degree to which the groups differ on the variable whose variance is reflected by t. Note that in cases where c is large and β is small, findings may appear to be due to a generalized deficit.

In a standardization (test development) sample, c and β are irrelevant because there is no between-group comparison. In such a case, within group discrimination is therefore t/(t + e), and maximizing t will increase reliability and sensitivity to individual differences. However, in typical clinical research contexts, where 2 (or more) groups are being compared, a measure becomes less group discriminating as its standardization group psychometric precision (ie, within-group variation) goes up.¹⁰ That is, as within-group variance is increased, the ability to discriminate groups will be reduced unless the sources of within-group variance overlap considerably with the source of between-group variance.¹¹ Increasing t will only increase between-group separation when β < c × e,¹⁰ with the extent of separation increasing as c increases. However, such cases are not desirable for clinical researchers because there are potential confounds from other cognitive processes, the specific process of interest is contributing relatively little to test scores, and between-group separation will only be a function of the cognitive process of interest to the extent that c and β covary in the sample.

For example, with a task that is only minimally sensitive to a putative pathognomonic variable (β) such as context processing, it can be made to separate groups more by modifying it so that it relies more heavily on other nonpathognomonic variables (t) where patients may nevertheless obtain lower values than controls. However, such a test would be relatively useless in an experimental study or clinical trial focused on context processing ability. Only in the case where there is significant overlap between c and β, such as in the case of context processing in a task such as the AX-continuous performance task and working memory, would increases in t and c overlap with an increase in β. Even in this case though, between-group separation is won at the cost of reduced clarity regarding why patients are performing poorly (eg, context processing per se vs working memory load), and therefore, typically, reduced clarity regarding which neurophysiological circuits are associated with abnormal test performance. As can be seen by these examples, attending to issues of true score variance (or reliability) without regard to the extent to which a test isolates a pathognomonic cognitive process can be counterproductive, in terms of identifying a measure that is useful for probing a specific neural circuit or for maximizing sensitivity to the effects of a medication.

In contrast, recalling that (ct + β)/(t + e), when group separation is a function primarily of β (specifically, when β > c × e), separation goes up as t goes down. That is, as the overall distribution of scores on a measure is reduced by elimination of variance due to nonpathognomonic factors and error, the between-group effect size will remain high as long as the primary source of the between-group differences is the single variable that is pathognomonic. Continuing with the example used in the above paragraph, with a task that is maximally sensitive to a pathognomonic variable such as context processing (and so where β is high), increasing within-group variance by modifying the task so that it also relies heavily on other factors will only reduce the value of statistical between-group tests (eg, the F test reflecting the main effect of group in an analysis of variance) by increasing the within-group variance reflected in the denominator relative to the between-group variance reflected in the numerator.

Based on these constraints, it has been demonstrated that for 2 tests of the same construct that differ by as much as 3-fold in true score variance, a test with higher σ_t² was associated with a lower between-group effect size, due to σ_t² being increased via score variance from processing requirements that increase within-group variation but that are not related to between-group separation.¹⁰ Increasing σ_t² will invariably increase between-group separation only if there is one source of true score variance and reliability and between-group differences act exclusively through this source, a condition which is rare. If there is more than one source of σ_t², increasing σ_t² will only increase between-group separation if it is not associated with adverse effects on c; raising t in this case also risks changing a measure's structure so as to reduce group separation, as discussed above. Relatedly, measures of the same construct and of equal reliability can differ by a factor of greater than 2 in terms of between-group separation, due to reliability being achieved more by increases in σ_t² in one case, and more by reductions in σ_me² in the other case, with the former method leading to reductions in between-group separation.⁴ Finally, increasing β, like decreasing e, inevitably increases between-groups discriminating power.

The issues are similar with increasing the length of a task, a strategy sometimes assumed to automatically increase reliability. Adding trials to a task may increase test-retest reliability, but it can reduce between-group separation if new items are associated with sources of within-group variance that are independent of β. Increasing task length can be useful only if the test is unifactorial, or if the covariance structure of the task does not change with added items. Even so, however, this can add significant time and cost to clinical trials. Relatedly, in within-group correlational studies, where wider distributions of scores are often seen as optimal, effect sizes can be increased when within-group variance is reduced, if that reduction is achieved by eliminating sources of variance that are unrelated to the processes being examined. A good demonstration of this can be seen in a magnetic resonance imaging study by Mathalon et al¹², where head size correction removed irrelevant within-group true score variance, which reduced reliability yet increased the correlations between region-of-interest variables and validity criteria such as age and diagnostic status.

In short, neither matching on reliability and difficulty nor maximizing within-group true score variance ensures either that a specific process is being measured or that between-group separation is maximized. However, we need to maximize between group discriminating power so that we can (1) create process-specific measures that discriminate schizophrenia from other conditions and (2) sensitively test whether effects of one treatment (eg, N-methyl-D-aspartate (NMDA) receptor coagonist) are different from effects of another (eg, D₂ blocker). Therefore, strategies other than task matching are needed. Below, several alternatives are reviewed.

Alternatives to Task Matching

Analysis of Covariance

Analysis of covariance (ANCOVA) can control for the influence of one test score on another, and therefore, prima facie appears to be a useful method to remove variance due to one or more cognitive functions from scores on the test of interest. This of course, assumes that the control tests are specific measures of the confounding cognitive processes. More importantly, however, in clinical research ANCOVA typically is not appropriate as a control for another cognitive process as represented by a second task score. This is because ANCOVA assumes independence of the covariate and the independent variable (eg, diagnostic group). In studies with preexisting groups (eg, schizophrenia vs control), the covariate and the independent group are often not independent. As such, ANCOVA is most appropriate when there is random assignment to groups. It was designed to reduce within-group variance rather than between-group variance.¹³

Item Response Theory

Item response theory (IRT) is a sophisticated and increasingly popular approach to test development that mathematically models individual responses based on model-derived item and person parameters. However, it requires large samples to construct measures. Moreover, it cannot resolve the issue that a focus on t and e cannot ensure a match on group discriminating power.¹⁰ Also, while IRT has many advantages for developing tests in normative samples, it assumes that item parameters do not differ across groups, and this assumption may not be met when comparing people with specific psychopathology-related cognitive processing impairments to people with intact functioning.

Profile Analysis

The goal of profile analysis is to compare 2 or more groups on multiple tests to see where the greatest differences emerge. However, this strategy is vulnerable to the same psychometric artifacts as the differential deficit strategy. That is, unless it can be demonstrated that the largest group differences are not on the most group-discriminating tests, it is possible that the findings reflect psychometric artifacts of the differential discriminating power of the tests, rather than a specific deficit.

Aggregation of Scores into Cognitive Subdomains

The goal of this strategy is to reduce the negative effects of single tests being confounded by multiple processes by combining or averaging scores on tests thought to measure the same process into a single a priori factor score. However, this strategy can exacerbate the effects of measurement error and of variance that is due to sources other than the construct of interest when the individual test scores reflect significant variance from such sources. In cases where confounds from other cognitive processes are less of an issue, aggregation can increase power. However, while aggregate scores can potentially be more reliable than single test scores, aggregation itself cannot ensure construct validity (ie, that a single process is being measured).

Principal Components Analysis and Factor Analysis

Factor analytic approaches are more sophisticated than a priori aggregation approaches because scores loading on the same factor are known to be highly correlated. However, tests with the same confound(s) may load on the same factor/cluster, thereby confounding interpretation. For example, tests of different cognitive processes (eg, working memory and problem solving) that both have a significant attentional demand may load on the same factor due to the requirement for this secondary process for test performance. Despite this caution, these approaches can be useful for understanding the factor structure of single tests.

Partially Ordered Sets (POSET)¹⁴

This approach assumes that tests are multifactorial and accommodates this by organizing test scores into a hierarchical, conceptual network, based on the cognitive functions that are thought (according to expert consensus) to be shared between tests and functions that are unique to tests. Patients are then classified as belonging to one functional state in this network, based on their test scores, and Bayesian analysis techniques are used to determine the likelihood that these assignments are correct. An important consideration here is that the POSET approach would not be necessary with unifactorial tests, which is the goal of much cognitive neuroscience and the Cognitive Neuroscience Treatment Research to Improve Cognition in Schizophrenia (CNTRICS) process.¹⁵ Moreover, this approach requires the use of multiple tests, which may not be feasible or desired for clinical trials (due to cost and time considerations or due to a particular focus on one cognitive system). In addition, this approach works best with extreme test scores, whereas researchers typically want scores to be within midrange intervals.

Process-Oriented Strategies

Unlike the approaches noted above, the process-oriented approach typically uses tasks that are based in cognitive psychology, not neuropsychology (ie, tests that were developed based on a theoretical model of cognition, and validated in healthy samples or animals, as opposed to tests developed to discriminate between people with brain injury and health controls). The tasks used in process-oriented studies typically include multiple conditions where specific parameters are varied to probe the integrity of an underlying process, and the adequacy of the target process is understood in terms of the pattern of scores across conditions, or the pattern of psychophysiological correlates, as opposed to a single test score. Importantly, process-oriented tasks are guided by theoretical models that make specific, falsifiable predictions that can be tested against other hypotheses, including what would be predicted from a generalized deficit.

Knight¹⁶ outlined 4 major process-oriented research strategies for cognitive studies of schizophrenia. Of these, 2 are particularly relevant to the CNTRICS process and to clinical trials in general. One is called the superiority strategy. Here, a cognitive task is designed so that the hypothesized cognitive deficit leads to an absolute performance advantage (compared with controls) in at least one condition of the task. A classic example of this is the perceptual organization study of Place and Gilmore.¹⁷ In that study, which used very rapid presentation times (20 ms), schizophrenia patients' impairment in automatically and initially grouping visual features into configurations allowed them to attend to and count individual features more accurately than controls. The second strategy is called the relative superiority strategy. This involves a specific reversal of performance, compared with controls, in at least 2 conditions. An example of this strategy is the study by Silverstein et al.¹⁸ In that study, the perceptual organization impairment led to a subtype of schizophrenia patients' visual search performance being faster in an ungrouped display with fewer elements compared with a display with more elements but where the target was grouped apart from distractors (ie, a display size effect). In contrast, other groups demonstrated the normal performance pattern of faster search times in the easy target distractor grouping condition, even though this had more elements than the nongrouped condition (ie, a grouping effect).

Examples of superiority or relative superiority have been found in multiple cognitive domains (eg, latent inhibition,¹⁹ working memory,²⁰ language,^21–23 and auditory²⁴ and visual^25,26 perception), suggesting the potential for wider adoption of these strategies. The development of additional process-oriented tasks in more cognitive domains will allow for greater process specificity, stronger cognition-neurobiology links, and better cognitive probes for treatment studies.

Simply identifying tasks developed from within cognitive psychology or cognitive neuroscience is not a panacea, however. There are a number of issues involving such tasks that pose a challenge for clinical researchers. One is that these tasks are typically developed to maximize between-condition differences and are less concerned with individual differences and group differences. This raises the question: how do we convert tests that aim to minimize individual differences and maximize between-condition differences into measures that can reliably assess individual differences in the service of maximizing between-group differences?² Second, although moving away from the use of single test scores is desirable, it is less clear what the best method is to classify subjects based on scores across multiple conditions. Several possibilities present themselves, such as classification of subjects by profile types and quantification of aspects of a linear or nonlinear profile across conditions (eg, extent of slope or curve, intercept, root mean square error), etc. At this point, the relative validity of these approaches has not yet been explored,¹⁶ although these approaches have each demonstrated utility.^27–30 By capturing the essential aspects of performance or more accurately characterizing task performance, such indices can increase sensitivity to task manipulations and/or treatment effects; this is not the same as breaking a continuous variable into categories, which typically reduces sensitivity to change. Below, the use of a simple yet surprisingly robust, albeit misunderstood index, the difference score, will be discussed.

Difference Scores

In the process-oriented approach, integrity of performance is typically characterized by a pattern of scores across more than one condition. This has several advantages over single performance scores on one condition or task or over residualized scores that reduce performance across 2 conditions to a single value representing one with the variance due to another score removed. For example, straight performance scores contribute both specific and generalized variance (ie, t and β). In addition, residualized scores are difficult to interpret, and it has been suggested that they never should be used to characterize level of change.^30–35 Although a simple difference score would seem to avoid the interpretive difficulties inherent in a residualized score, a potential problem is that the reliability of a difference score decreases as the correlation between tasks (or conditions within a task) increases.³⁶

In much real-world clinical research, however, difference scores are the preferred index of change (although see suggestion below regarding the collection of multiple data points) because the conditions inherent in such research can render them highly reliable. Much of the earlier caution about the unreliability of difference scores came from psychometricians or researchers who assumed that the phenomena to be measured were trait-like and therefore highly stable over time.^37,38 However, in typical clinical trials, we are measuring state-related features that are expected to change over time (at least for one treatment arm), and in such cases, difference scores can be sufficiently reliable. The influence of score stability on reliability of difference scores can be seen clearly by examining the following equation for reliability of difference scores, which holds for typical measurement conditions:

³⁹

Traditionally, it was assumed that adequate validity required high ρ₁₂ (trait stability), so low ρ_gg. When there is little change among people, or if all people change to a similar degree, the reliability of difference scores will be low. However, when there is heterogeneity in true change (ie, the rank ordering of people changes significantly over time), there is low or moderate ρ₁₂ (or even high but negative ρ₁₂) and reliability of difference scores can be high under these conditions, reflecting real differences in change over time or across conditions as a result of a task manipulation or treatment.

This can be seen in the 2 following examples. Again, assuming that ρ_gg' = ρ_xx' – (ρ₁₂ /1 − ρ₁₂), where ρ₁₂ (correlation between pre- and posttest scores) is low (eg, .2), the reliability of the difference score can be high (.75): .75 = (.8 − .2) /(1 − .2). In contrast, where ρ₁₂ is high (.7), the reliability of the difference score is lower (.33): .33 = (.8 - .7) /(1 − .7). Also, note that in the above examples, the first term in the numerator, the average reliability of each score, is high (.8); this value typically comes from an internal consistency estimate.

The above examples are consistent with the point that differences between conditions may be heterogeneous across people, even when a test is perfectly construct valid. This is an important consideration for clinical trials research, because, eg, in a typical clinical trial comparing a new vs an older treatment, heterogeneity in change is the means by which a treatment effect is observed. Importantly, under conditions where change is heterogeneous and real (ie, where it is not due to error variance but to known factors such as treatment type), the reliability of a difference score can actually be higher than the reliabilities of the individual scores that make up the index.³⁴ In addition, the reliability of difference scores increases monotonically as individual differences in real change increase.³⁴ The critical issue is whether we can understand/model the change in terms of measurable variables. That is, our goal is not to identify processes (or test indices) that do not change over time. Rather, it is to sensitively measure change and then to be able to predict it, whether in terms of group status, medication type, psychosocial intervention, etc.

The discussion above demonstrated that the use of difference scores across 2 conditions or time points can produce a sensitive assessment of change that is reliable and valid. However, to maximally characterize change across conditions or time, performance should be measured across more than 2 conditions or time points, via slope or nonlinear functions. These strategies will increase reliability, reduce SE, and increase sensitivity, especially when change is nonlinear.^34,35,40,41 Moreover, they are feasible for clinical trials because many trials collect data at time points other than baseline and completion of treatment, and many use tasks where performance can be more accurately expressed across multiple conditions (eg, slope of verbal learning curve during a session or slope of psychometric function in a visual perception task) than when using an index such as total number correct. Data analytic strategies that initially model individual change, followed by analysis of group differences in patterns of individual change (see below), are increasingly being used in longitudinal research on patient outcomes (eg, studies using latent growth modeling),^42–44 and these same strategies are applicable to performance analysis of single cognitive tasks that include multiple conditions.

In cases where patterns of scores are characterized in terms of extent of slope or curve, individual performance can be characterized in terms of multiple variables (eg, baseline value, slope across all data points with first-order autoregressive component removed, and root mean square error or variability around the trend line or curve). In addition to traditional multivariate analysis of variance procedures that compare groups on multiple variables, cluster analysis can be used to identify subgroups of subjects in 3-dimensional space, for subsequent identification of (single, or sets of) factors that predict heterogeneity in degree of change (either across conditions within a task or across time with multiple testing points).^28,30 An advantage of this type of multivariate characterization of subjects is that by including baseline and change indices as separate variables, they are not confounded by each other, as can be the case when only extent of change is included in the analysis. In predicting change, it is important to note that the effects of group and other predictor variables (and sets of variables) on rate of within-person change may be linear or nonlinear.^10,34

Once change is measured in terms of more than 2 data points, appropriate modeling of covariance structure further increases sensitivity. For example, repeated-measures data rarely meet the assumptions of compound symmetry. Although corrections for violations of this assumption are ubiquitous in statistical programs, a better estimate of reality involves determining which type of covariance structure (eg, compound symmetry, first order autoregressive, general autoregressive, unstructured, etc) best fits the observed data and then analyzing effects across multiple conditions taking this into account.

Trade-offs Inherent in Choosing Solutions to Psychometric Issues

The strategies discussed above all convey advantages over traditional single-score indices of cognitive functioning. Nevertheless, these strategies can also create psychometric artifacts. Below, a number of these potential trade-offs are briefly discussed.

Although measurement sensitivity can be increased by increasing the number of conditions within a task,⁴⁰ there are limits to the number of conditions (and therefore, typically, trials) that can be added before measurement is compromised. For example, adding conditions and trials can create fatigue, or reduce motivation, and therefore confound interpretation of results. The possibility of adding conditions but reducing trials within each condition to avoid such confounds carries with it the risk of reducing the number of trials to the point where the reliability of each condition's score is reduced below an acceptable value. Therefore, the trade-off of increasing measurement sensitivity by adding measurement points (conditions) vs ensuring adequate numbers of trials for within-condition measurement must always be considered.

A second, but related, trade-off involves measurement of the full range of a construct vs optimizing discriminating power in each condition. It is often desirable to ensure that a full range of ability is being measured. This allows the researcher to determine under which conditions groups are similar or different and allows for comparison of full psychometric functions for each group, which can help rule out effects of poor attention or low motivation. However, measuring the full range of a construct typically involves including conditions where ceiling and floor effects may be present, and this can lead to attention, motivation, and fatigue effects. In such cases, it is tempting to optimize between-group discriminating power by only including those conditions that maximally discriminate between groups. While this of course maximizes effect sizes, important information may be missed regarding the abilities of one or more groups to process stimuli at levels that may be meaningful. On the other hand, including a fuller range of conditions can add undesired time and costs to a clinical trial.

A third trade-off, related to the second one above, involves the choice of using staircase procedures (adaptive testing) vs using standardized trial presentation. With staircase procedures, the researcher essentially individualizes the test for each subject by reducing the range of trial types so that they vary around each subject's threshold level. Because, especially for more impaired subjects, accuracy may be greater under these conditions than when using a standardized set of trials, motivation may also be higher during the task. But, this approach can lead to different trials and different difficulty levels being given to different subjects, which can create interpretative difficulties, especially if there are qualitative differences between trial types at different difficulty levels (eg, if longer stimulus durations allow for greater attentional allocation and for eye movements, whereas briefer stimulus durations recruit primarily perceptual operations). Staircase or adaptive procedures are widely used in nonclinical studies of perception and cognition and have been applied to studies of schizophrenia.⁴⁵ However, the conditions under which using such procedures are more or less useful have generally not been explored in clinical research.

A fourth trade-off concerns test-retest reliability/stability vs sensitivity to change. While test-retest reliability is a desirable test characteristic under conditions in which no change is expected, a test that is insensitive to real change (eg, change produced by an effective intervention) is not useful for clinical trials researchers. The ideal test for treatment studies is one that is sensitive to specific forms of change and where the extent of the score change can be predicted by independent variables such as treatment history, premorbid functioning, medication type/dose, etc.

With tasks that cannot be given more than once, there can be a conflict between construct validity and test-retest reliability. For example, with the Wisconsin Card Sorting Test, if a person learns the sorting rule during the first administration, the test is basically a different test the second time. In cases like this, alternate forms with low face validity are necessary. At this point, however, these have not been developed.

As discussed above, process-oriented tasks can be superior to the use of matched tasks designs for isolating specific cognitive processes. However, even with process-oriented tasks, it is critical to ensure that the hypothesized, theory-driven pattern of results cannot be accounted for in terms of differences in the difficulty levels of the conditions. Both the superiority and relative superiority strategies avoid this potential confound.

Finally, clinical trials researchers must weigh the trade-off of accounting for patient heterogeneity against adding time and costs to studies. It is critical to account for patient heterogeneity (eg, disorder subtypes, illness course, gender, age, genetic factors) in clinical trials because, thus far, degree of cognitive improvement seen in people with schizophrenia is much smaller than the variability between patients in cognitive functioning and the variability in change over time—a situation where the increases in the numerator in parametric statistical tests (eg, t, F, etc) will be offset by larger increases in the denominator (reflecting within-group variability) unless more homogeneous subgroups can be identified. Moreover, many examples exist where diagnostic subtypes perform differently on cognitive measures.^16,46–49 The danger of not accounting for heterogeneity is that potential treatment effects within a meaningful subgroup of patients can be underestimated or even missed if all patients' scores are averaged. Heterogeneity can be taken into account by only including specific subtypes of patients into clinical trials or by assessing relevant characteristics (eg, premorbid functioning, paranoid vs nonparanoid status) and then having sufficient power to explore subgroup differences after the trial is completed. However, the latter suggestion can mean added time and costs for the trial, although it may allow for greater sensitivity to detect treatment effects in specific subgroups of patients.

Other Suggestions to Maximize Effect Sizes

In this final section, several other considerations relevant to maximizing between-groups discrimination will be briefly noted. One is to aim for overall performance levels that are optimally discriminating. Within-group and between-group effect sizes decrease as the difficulty level of a task departs from optimally discriminating levels.⁸ In addition, overly difficult tasks can impair motivation, thus confounding interpretation of test scores. Discrimination can also be improved by carefully designing tests so that they are as unconfounded by extraneous cognitive processes as possible. For example, in a perception test, it is important to ensure that trial blocks are short to minimize the effects of attention on performance. Second, it is important to choose tests that are sensitive to the changes that occur within the time frame of a clinical trial. Tests whose scores can be considered state markers or mediating vulnerability markers (ie, trait markers but where scores still vary within the abnormal range as a function of state factors)⁵⁰ are ideal for this purpose. It is also important to distinguish between performance and ability; ie, what someone typically does and what they can do under optimal (ie, reinforcing, motivation-enhancing) conditions. Research demonstrating that social or tangible reinforcement can improve and, in some cases, normalize scores on cognitive tests (including some that are considered vulnerability markers)^51–54 highlights the influence of environmental effects on cognitive performance and the need to evaluate both performance and potential. The gain from clinical trials can also be improved if researchers abandon null hypothesis significance testing.⁵⁵ Testing specific predictions about the magnitude of change will lead to a more meaningful body of evidence regarding the effectiveness of interventions. Relatedly, for measurement of change, an alternative hypothesis should be that of known practice effects, which can be significant.^56,57 Finally, the generalized deficit undoubtedly includes variance from a number of measurable factors, such as negative symptoms (including amotivation), distractibility from hallucinations, sedation, and low self-efficacy. Assessment of the extent to which these variables contribute variance to cognitive performance, or change in cognitive performance, can help clarify the effects of the intervention that is being studied.

The Utility of Analytic Mathematical Modeling (or Quantitative Clinical Cognitive Science)

The above discussion has focused on measurement issues related to the application of experimental psychological, neuropsychological, and neuroscience methods for measuring specific cognitive deficits unconfounded by other cognitive deficits or extraneous sources of error (eg, poor motivation, medication side effects). The focus was limited to these methods because tasks in these categories were the foci of the CNTRICS project and the earlier Measurement and Treatment Research to Improve Cognition in Schizophrenia (MATRICS) initiative from which CNTRICS emerged. As a result, mathematical modeling as a method to clarify cognitive processing deficits in schizophrenia was not a focus of the discussion. However, it is important to note that in recent years, formal mathematical models have led to significant advances in our understanding of a number of issues that are relevant to an understanding of schizophrenia, including visual processing, memory search, decision making, electrophysiology, and the relationships between cognitive deficits and symptoms.^10,58–61 Moreeover, formal models have also demonstrated utility in addressing the psychometric artifact issues noted early in the article. And, they can clarify aspects of sample performance that are normally seen more simply as part of global constructs such as “difficulty level”—such as intertrial dispersion and between-condition variability.^10,60 Formal mathematical models are perhaps the best methods available at present for aiding researchers in understanding the distributional properties of data, and the insights gained can be applied to both within- and between-group discrimination issues. Finally, while there is always the danger that formal models can be developed that are internally consistent but biologically implausible,² advances in model diagnostic technology, and the real-world testing of model-derived experimental tasks against model-based predictions can help ensure that refinements are constrained by biological, psychological, and psychopathological realities.^20,62

Conclusions

Precise measurement of cognitive functioning in schizophrenia is critical to advancing both neuroscience and treatment studies of this disorder. However, much research on cognition in schizophrenia is confounded with psychometric artifacts, most notably the generalized deficit issue and the use of single performance indices that do not allow for a discrimination between true score variance related to the construct of interest, other sources of true score variance, and error variance. To counter this problem, it is critical to reduce measurement error as much as possible, by designing tasks so that the integrity of a cognitive process can be assessed within subject via a theory-derived prediction involving scores across two or more conditions, and where the magnitude of between-group differences are not also a function of the difficulty levels of those conditions. It is also critical to maximize the proportion of true score variance that is due to the specific cognitive process of interest and minimize the contributions of extraneous cognitive and noncognitive (eg, motivational) person-related factors. By ensuring process specificity, and that the test is designed to maximize between-group discrimination via the construct of interest, effect sizes will be maximized. A further consideration is that tests that are chosen for clinical trials should be sensitive to state-related changes in cognitive functioning. Therefore, test-retest reliability in patient samples must be balanced carefully against sensitivity to changes in mental status. The most important issue is not test-retest reliability per se, but whether we can model the changes that occur from one administration to the other (eg, understand who is changing, and how much, in terms of known factors such as preexisting characteristics or treatment conditions). However, internal consistency and/or alternate form reliability are relevant and these help ensure the construct validity of the chosen task. Finally, in assessing change over within-task conditions or over time, the use of novel data analytic strategies to characterize change can increase reliability, reduce measurement error, and increase sensitivity.

In short, when designing measures for neuroscience studies of schizophrenia, or for clinical trials, issues related to between-group discrimination are critical. As a result, researchers may find themselves in an apparent conflict with classical test theory, with its focus on maximizing individual differences and test-retest reliability. However, a balanced consideration of these issues with those raised by the need to maximize between-group discrimination and sensitivity to change is necessary to develop measures that are sensitive to both the neurophysiology of schizophrenia and to treatment effects.