An EM approach to MAP solution of segmenting tissue mixture percentages with application to CT-based virtual colonoscopy

Abstract

Electronic colon cleansing (ECC) is an emerging technique developed to segment the colon lumen from a patient’s abdominal computed tomography colonography (CTC) images. However, the residue stool and fluid tagged by contrast materials as well as mixed tissue distribution with partial volume (PV) effect impose several challenges for ECC, resulting in incomplete and overcomplete cleansings. To address the PV effect, this work investigated an improved maximum a posteriori expectation-maximization (MAP-EM) image segmentation algorithm which simultaneously estimates tissue mixture percentages within each image voxel and statistical model parameters for the tissue distribution. Given the segmented tissue mixture information beyond the image voxel level, not only the PV effect has been satisfactorily addressed as a particular case of tissue mixture problem, but incomplete and overcomplete ECC causes could also be maximally avoided. For clinical application to CTC that involves several issues transferring from theoretical analysis to practical validation, an innovative initialization procedure and refined estimation strategy were proposed to build an ECC pipeline based on the MAP-EM segmentation. The pipeline was evaluated based on 52 patient CTC studies, downloaded from the website of the Virtual Colonoscopy Screening Resource Center, by two radiologists. A noticeable improvement over the authors’ previous ECC pipeline was documented. Several typical cases were also presented to show visually the improved performance of the presented ECC pipeline.

INTRODUCTION

Colorectal carcinoma is the third most commonly diagnosed cancer and the second leading cause of death from cancer in the United States.^{1, 2} More than 90% colorectal cancers are developed from adenomatous polyps over 5 to 15 years. Since the malignant transformation usually does not show any symptom, screening programs to detect the polyps have been advocated, and several polyp detection methods, such as fecal occult blood test, sigmoidoscopy, barium enema, and fiberoptic colonoscopy (OC), have been developed over the years. Each method has its own limitations and currently OC is the gold standard. Computed tomography colonography (CTC), also known as virtual colonoscopy (VC),^{3, 4, 5} is an emerging method utilizing advanced medical imaging and computer technologies to mimic the OC navigation procedure, looking for polyps via fly-through inside a virtual colon model which is constructed from patient abdominal images.^{6, 7, 8} Considering the presence of colonic fluid and residue stool (survived after routine bowel cleansing⁹) in CT scans, finding polyps is not a trivial task in the sense that colonic fluid might “bury” polyps resulting in false negatives, while residue stool could mimic polyps and increase false positive rates, although several clinical studies have shown the great potential of VC as a mass screening modality in terms of safety, cost, and patient compliance compared to OC.^{10, 11, 12} It is admitted that scanning in both supine and prone positons can reduce the possibility of these errors, unfortunately it does not solve the problem because fluid and residue stool may not move in the way expected for their location change from supine to prone positions.¹³ Oral contrast tagging of the colonic materials could allow differentiation of colon content from colon wall.¹⁴ By the use of oral contrast, residue stool and fluid have a higher image density than the surrounding colon or polyp tissues and therefore can be cleansed electronically in the patient images for an accurate virtual colon model.^{15, 16, 17} A successful electronic colon cleansing (ECC) of tagged materials (TMs) would relieve the stress on bowel preparation that often is a limiting factor in patient compliance with colon cancer screening recommendations.^{18, 19, 20}

ECC has been explored in the past decade utilizing image segmentation and pattern recognition algorithms.^{14, 15, 16, 17, 21, 22, 23, 24} Most of these algorithms assume each image voxel is filled by a single tissue type and ignore the partial volume (PV) effect particularly around colon wall mucosa, where the details reflect very useful clinical information. Progress has been made by seeking the probability of a voxel being filled with a single tissue type rather than assuming that voxel has been fully filled by a single tissue type.²⁵ Because of the weak constraint via the probability, this indirect PV solution had shown limited gain.²⁵ Modeling tissue mixtures inside each image voxel for a direct solution to PV effect has been a research interest for many years.^{26, 27, 28} The authors have been exploring a direct PV solution,^{29, 30} utilizing the expectation-maximization (EM) algorithm³¹ to simultaneously estimate (1) tissue mixture percentages in each image voxel and (2) statistical model parameters of the acquired image data under the principle of maximum a posteriori (MAP), where the PV effect could be interpreted as a special case of tissue mixture model within each image voxel, i.e., a tissue mixture model could account for but not being limited to the PV effect. Initial clinical tests on 20 patient CTC data sets under the condition of each image voxel containing no more than two tissue types has demonstrated improved performance compared to our previous segmentation algorithms.³² Recent numerical investigations have shown the stability of the MAP-EM tissue mixture segmentation algorithm when a voxel contains more than two tissue types,³³ where each tissue type is assumed to follow a normal distribution, and all tissue types are assumed to be independent from each other. The iterative EM approach to the MAP solution is achieved by a finite number of iterations and reasonable initial estimate. Further investigation and validation of the segmentation algorithm are needed and currently under progress for application to CTC. This work represents an example of the ongoing research effort.

In current patient CTC studies, positive-contrast tagging agents are usually used to opacify the residual fecal materials and fluid for differentiation of the materials from colon wall and polyps. The use of positive-contrast tagging agents that have high radio densities tends to artificially elevate the observed CT attenuation of nearby soft tissues toward that of the TMs on Hounsfield unit scale. This artificial elevation is called pseudoenhancement (PE) according to Nappi et al.³⁴ and Nappi and Yoshida³⁵ and is an acceptable explanation to the overcomplete ECC cause where pseudoenhanced soft tissues are incorrectly identified as TMs. Moreover, the ignorance of PV effect around tissue boundaries makes ECC even more challenging by artifically altering the shape and texture information, which is believed to hamper the following detection and diagnosis tasks.²⁴ This work aims to address the PV effect in presence of PE in clinical CTC studies by improving the MAP-EM segmentation performance for estimating the tissue mixtures inside each image voxel across the entire field of view (FOV). Several implementation strategies and postsegmentation operations for construction of an ECC pipeline were proposed to transfer the theoretical analysis³³ to clinical applications in CTC. The major topics covered in this paper include (1) adequate initialization for the iterative procedure, (2) optimal neighboring system for increase or decrease of the number of tissue types at a concerned voxel, (3) iteration speed-up, and (4) innovative postsegmentation strategies for construction of an ECC pipeline with evaluation of the ECC pipeline by 52 patient CTC studies.

The remainder of this work is presented as follows. Section 2 briefly reviews the MAP-EM algorithm, followed by Sec. 3 where optimization of the algorithm implementation and construction of a corresponding ECC pipeline are detailed. Section 4 validates the ECC pipeline using 52 CTC studies with comparison to the authors’ previous results. Finally, Sec. 5 draws some conclusions and also discusses some future research topics.

BRIEF REVIEW OF THE MAP-EM ALGORITHM

In this section, the MAP-EM segmentation algorithm for simultaneously estimating both tissue mixture percentages and statistical model parameters is briefly reviewed, with more details presented in a previous work.³³

Let the acquired image Y be represented by a column vector in the form of {Y_i, i=1,…,I}, where I denotes the total number of voxels in the image and each Y_i is an observation of an individual random variable with mean ${\overline{Y}}_i$ and variance ${\sigma }_i^2$ at voxel i. Assume the image contains K tissue types. Let the contribution of tissue type k to the observation of Y_i in voxel i be denoted by X_ik, i=1,…,I; k=1,…,K, there is $Y_i={\sum }_{k=1}^K{X}_{ik}$. Each X_ik is an unobservable random variable with mean ${\overline{X}}_{ik}$ and variance ${\sigma }_{ik}^2$. Let Z_ik be the fraction of tissue type k in voxel i, contributing to Y_i, under conditions of ${\sum }_{k=1}^K{Z}_{ik}=1$, 0⩽Z_ik⩽1. Let μ_k and ν_k be the mean and variance of tissue type k fully filling in voxel i. Assume all K tissue types contribute to Y_i independently, one then has ${\overline{X}}_{ik}=Z_{ik}{\mu }_k$, ${\sigma }_{ik}^2=Z_{ik}{\nu }_k$, ${\overline{Y}}_i={\sum }_{k=1}^K{Z}_{ik}{\mu }_k$, and ${\sigma }_i^2={\sum }_{k=1}^K{Z}_{ik}{\nu }_k$.^{28, 33} Without loss of generality, it is assumed that the unobservable random variable X_ik for each tissue type k follows a normal distribution,

$$p(\mathbf{X}\mid \left\{{\mu }_k\right\},\left\{v_k\right\},\left\{Z_{ik}\right\})=\prod _{i,k=1}^{l,K}\frac{1}{\sqrt{2\pi Z_{ik}{v}_k}}\exp \{-\frac{{(X_{ik}-Z_{ik}{\mu }_k)}^2}{2Z_{ik}{\mu }_k}\}.$$ (1)

The EM algorithm³¹ then seeks the solution of tissue percentage parameters {Z_ik} and statistical model parameters {μ_k,ν_k} by maximizing the expectation of conditional probability distribution 1 of the complete data, where the E step of the EM algorithm computes the conditional expectation of the unobservable variable distribution given image {Y_i} and current iteration estimates $\{{\mu }_k^{\left(n\right)},{\nu }_k^{\left(n\right)},Z_{ik}^{\left(n\right)}\}$.³³ Thus, one has

$$Q(\Theta \mid {\Theta }^{\left(n\right)})=-\frac{1}{2}\sum _{i,k}\{\ln \left(2\pi \right)+\ln \left(Z_{ik}{\nu }_k\right)+\frac{1}{Z_{ik}{\nu }_k}[{\left(X_{ik}^2\right)}^{\left(n\right)}-2X_{ik}^{\left(n\right)}{Z}_{ik}{\mu }_k+Z_{ik}^2{\mu }_k^2]+\beta U\left(Z_{ik}\right)\},$$ (2)

where parameter set Θ represents the tissue fractions (or mixture percentages) {Z_ik} and the tissue model parameters {μ_k,ν_k}, and $X_{ik}^{\left(n\right)}$ and ${\left(X_{ik}^2\right)}^{\left(n\right)}$ are the conditional expectations of X_ik and $X_{ik}^2$, respectively,³³

$$X_{ik}^{\left(n\right)}=\mathrm{E}[X_{ik}\mid Y_i,{\Theta }^{\left(n\right)}]=Z_{ik}^{\left(n\right)}{\mu }_k^{\left(n\right)}+\frac{\left(Z_{ik}^{\left(n\right)}{\nu }_k^{\left(n\right)}\right)}{{\sum }_{j=1}^K\left(Z_{ij}^{\left(n\right)}{\nu }_j^{\left(n\right)}\right)}(Y_i-\sum _{j=1}^{\kappa }{Z}_{ij}^{\left(n\right)}{\mu }_j^{\left(n\right)}),$$ (3)

$${\left(X_{ik}^2\right)}^{\left(n\right)}=\mathrm{E}[X_{ik}^2\mid Y_i,{\Theta }^{\left(n\right)}]={\left(X_{ik}^{\left(n\right)}\right)}^2+\left(Z_{ik}^{\left(n\right)}{\nu }_k^{\left(n\right)}\right)\frac{{\sum }_{j\ne k}^K\left(Z_{ij}^{\left(n\right)}{\nu }_j^{\left(n\right)}\right)}{{\sum }_{j=1}^K\left(Z_{ij}^{\left(n\right)}{\nu }_j^{\left(n\right)}\right)},$$ (4)

where ${\left(X_{ik}^{\left(n\right)}\right)}^2$ is the square of the nth iterated estimate of $X_{ik}^{\left(n\right)}$. The last term in Eq. 2 reflects a penalty on the tissue fraction distribution {Z_ik} across the FOV for a penalized maximum likelihood or MAP solution. The usefulness of Markov random field (MRF) in modeling the distribution of label images has been evidenced by many studies, e.g., Refs. ^{36, 37}. And such continuous distribution of image label can be easily extended to the case of {Z_ik} when downsampling operations are taken infinite times. By a Gibbs functional in the well-established MRF framework,³⁶ an a priori penalty on the tissue mixture parameter Z_ik has the following quadratic form of

$$U\left(Z_{ik}\right)=\sum _{\mathrm{r}∊{\epsilon }_1}{w}_{ir}{(Z_{ik}-Z_{rk})}^2,$$ (5)

where index r indicates the neighbors ε_i and w_ir is a weighing factor for different orders of neighbors. Notation β is an adjustable parameter controlling the degree of the penalty.

The M step of the EM algorithm determines the next iteration estimates $\{{\mu }_k^{(n+1)},{\nu }_k^{(n+1)},Z_{ik}^{(n+1)}\}$, which maximize the conditional expectation 2. For the tissue model parameters $\{{\mu }_k^{(n+1)},{\nu }_k^{(n+1)}\}$, one has

$${\phantom{\mid }\frac{\partial Q}{\partial {\mu }_k}\mid }_{\mu ={\mu }^{(n+1)}}=0\Rightarrow {\mu }_k^{(n+1)}=\frac{{\sum }_i{X}_{ik}^{\left(n\right)}}{{\sum }_i{Z}_{ik}}$$ (6)

and similarly

$${\nu }_k^{(n+1)}=\frac{1}{I}\sum _i\frac{{\left(X_{ik}^2\right)}^{\left(n\right)}-2X_{ik}^{\left(n\right)}{Z}_{ik}^{\left(n\right)}{\mu }_k^{\left(n\right)}+{\left(Z_{ik}^{\left(n\right)}{\mu }_k^{\left(n\right)}\right)}^2}{Z_{ik}^{\left(n\right)}}.$$ (7)

For the tissue mixture percentages {Z_ik}, maximizing the conditional expectation 2 will be subject to the conditions of ${\sum }_{k=1}^K{Z}_{ik}=1$, 0⩽Z_ik⩽1 and will not generate a closed-form solution for $Z_{ik}^{(n+1)}$. Since the solution for $Z_{ik}^{(n+1)}$ is spatially localized to voxel i, a logic approach to the solution is to consider the neighborhood anatomical information in the acquired image, as depicted as follows.

Considering the continuity existing in both image label and {Z_ik}, if all the neighbors around voxel i are labeled as tissue type k, then central voxel i is most likely to contain tissue type k exclusively. Similarly, if all the neighbors are labeled as any two tissue types, e.g., 1 and 2 of the total K, then for central voxel i, one has $Z_{ik}^{\left(0\right)}=0$, k≠1,2. Following this argument, one can refine the estimation for voxel i containing any k tissue types up to K, provided with its neighbors’ anatomical information.

If all the neighbors at the nth iteration contain any two tissue types 1 and 2 of the total K, then the following partial differentiation operation will lead to formula 8 for calculation of the tissue mixture percentages in voxel i,³³

$${\phantom{\mid }\frac{\partial Q(\Theta \mid {\Theta }^{\left(n\right)})}{\partial Z_{i1}}\mid }_{Z_{i1}^{(n+1)}}=0\Rightarrow Z_{i1}^{(n+1)}=\frac{X_{i1}^{\left(n\right)}{\left({\sigma }_{i2}^2\right)}^{\left(n\right)}{\mu }_1^{\left(n\right)}+{\left({\mu }_2^{\left(n\right)}\right)}^2{\left({\sigma }_{i1}^2\right)}^{\left(n\right)}-X_{i2}^{\left(n\right)}{\left({\sigma }_{i1}^2\right)}^{\left(n\right)}{\mu }_2^{\left(n\right)}+2\beta {\left({\sigma }_{i1}^2\right)}^{\left(n\right)}{\left({\sigma }_{i2}^2\right)}^{\left(n\right)}{\sum }_r{w}_{ir}{Z}_{r1}^{\left(n\right)}}{{\left({\mu }_1^{\left(n\right)}\right)}^2{\left({\sigma }_{i2}^2\right)}^{\left(n\right)}+{\left({\mu }_2^{\left(n\right)}\right)}^2{\left({\sigma }_{i1}^2\right)}^{\left(n\right)}+2\beta {\left({\sigma }_{i1}^2\right)}^{\left(n\right)}{\left({\sigma }_{i2}^2\right)}^{\left(n\right)}{\sum }_r{w}_{ir}}$$ (8)

and $Z_{i2}^{(n+1)}=1-Z_{i1}^{(n+1)}$, where $X_{ik}^{\left(n\right)}$, (μ_k)⁽ⁿ⁾, and ${\left({\sigma }_{ik}^2\right)}^{\left(n\right)}=Z_{ik}^{\left(n\right)}{\nu }_k^{\left(n\right)}$ have been defined before.

If all the neighbors at the nth iteration contain any three tissue types 1, 2, and 3 of the total K, then Eq. 2 can be approximately expressed as a quadratic form for voxel i, and the associated $\left\{Z_{ik}^{(n+1)}\right\}$ could be updated by solving three linear equations, as denoted by Eqs. 9, 10, respectively,

$$Q_i\approx \frac{1}{2}\left(Z_{i1}{Z}_{i2}{Z}_{i3}\right)\left[\begin{array}{ccc}{V}_{1,1}& V_{1,2}& V_{1,3}\\ V_{2,1}& V_{2,2}& Z_{2,3}\\ V_{3,1}& V_{3,2}& V_{3,3}\end{array}\right]\left(\begin{array}{c}{Z}_{i1}\\ Z_{i2}\\ Z_{i3}\end{array}\right)-\left(b_0{b}_1{b}_2\right)\left(\begin{array}{c}{Z}_{i1}\\ Z_{i2}\\ Z_{i3}\end{array}\right),$$ (9)

$$\left[\begin{array}{ccc}1& 1& 1\\ V_{1,1}-V_{1,2}& V_{2,1}-V_{2,2}& V_{3,1}-V_{3,2}\\ V_{1,1}-V_{1,3}& V_{2,1}-V_{2,3}& V_{3,1}-V_{3,3}\end{array}\right]\left(\begin{array}{c}{Z}_{i1}^{(n+1)}\\ Z_{i2}^{(n+1)}\\ Z_{i3}^{(n+1)}\end{array}\right)=\left(\begin{array}{c}1\\ b_0-b_1\\ b_0-b_2\end{array}\right),$$ (10)

where

$$V_{1,1}=\frac{{\left({\mu }_1^{\left(n\right)}\right)}^2}{Z_{i1}^{\left(n\right)}{\nu }_1^{\left(n\right)}}+\beta \sum _r{w}_{ir},V_{2,2}=\frac{{\left({\mu }_2^{\left(n\right)}\right)}^2}{Z_{i2}^{\left(n\right)}{\nu }_2^{\left(n\right)}}+\beta \sum _r{w}_{ir},$$

$$V_{3,3}=\frac{{\left({\mu }_3^{\left(n\right)}\right)}^2}{Z_{i3}^{\left(n\right)}{\nu }_3^{\left(n\right)}}+\beta \sum _r{w}_{ir},$$

$$V_{1,2}=V_{1,3}=V_{2,1}=V_{2,3}=V_{3,1}=V_{3,2}=0,$$

$$b_0=\frac{X_{i1}^{\left(n\right)}{\mu }_1^{\left(n\right)}}{Z_{i1}^{\left(n\right)}{\nu }_1^{\left(n\right)}}+\beta \sum _r{w}_{ir}{Z}_{r1}^{\left(n\right)},$$

$$b_1=\frac{X_{i2}^{\left(n\right)}{\mu }_2^{\left(n\right)}}{Z_{i2}^{\left(n\right)}{\nu }_2^{\left(n\right)}}+\beta \sum _r{w}_{ir}{Z}_{r2}^{\left(n\right)},b_2=\frac{X_{i3}^{\left(n\right)}{\mu }_3^{\left(n\right)}}{Z_{i3}^{\left(n\right)}{\nu }_3^{\left(n\right)}}+\beta \sum _r{w}_{ir}{Z}_{r3}^{\left(n\right)}.$$

If all the neighbors at the nth iteration contain any four tissue types 1, 2, 3, and 4 of the total K, then Eq. 10 becomes

$$\left[\begin{array}{cccc}1& 1& 1& 1\\ V_{1,1}-V_{1,4}& V_{1,2}-V_{2,4}& V_{1,3}-V_{3,4}& V_{1,4}-V_{4,4}\\ V_{1,2}-V_{1,4}& V_{2,2}-V_{2,4}& V_{2,3}-V_{3,4}& V_{2,4}-V_{4,4}\\ V_{1,3}-V_{1,4}& V_{2,3}-V_{2,4}& V_{3,3}-V_{3,4}& V_{3,4}-V_{4,4}\end{array}\right]\left(\begin{array}{c}{Z}_{i1}^{(n+1)}\\ Z_{i2}^{(n+1)}\\ Z_{i3}^{(n+1)}\\ Z_{i4}^{(n+1)}\end{array}\right)=\left(\begin{array}{c}1\\ b_0-b_3\\ b_1-b_3\\ b_3-b_3\end{array}\right).$$ (11)

Similarly,

$$V_{4,4}=\frac{{\left({\mu }_4^{\left(n\right)}\right)}^2}{Z_{i4}^{\left(n\right)}{\nu }_4^{\left(n\right)}}+\beta \sum _r{w}_{ir},b_3=\frac{X_{i4}^{\left(n\right)}{\mu }_4^{\left(n\right)}}{Z_{i4}^{\left(n\right)}{\nu }_4^{\left(n\right)}}+\beta \sum _r{w}_{ir}{Z}_{r4}^{\left(n\right)},$$

$$V_{1,2}=V_{1,3}=V_{1,4}=V_{2,3}=V_{2,4}=V_{3,4}=0.$$

If the neighbors contain all the K tissue types, a set of K linear equations can be derived for the K tissue mixture percentages in voxel i. In this VC application, the authors consider four tissue types of (i) air inside the colon and lungs, (ii) fat, (iii) muscle, and (iv) bone and TMs in the abdominal CTC images. Therefore, Eqs. 8, 9, 10, 11 are sufficient to compute the (n+1)th iteration results.

IMPLEMENTATION OF THE MAP-EM ALGORITHM

Initialization of the MAP-EM algorithm

Two kinds of parameters are needed to be initialized to start the MAP-EM iteration process: tissue model parameters {μ_k,ν_k}, which reflect the image data distribution across the FOV, and tissue mixture percentages {Z_ik} of tissue type k inside voxel i. Comprehensive numerical experiments demonstrated that the MAP-EM algorithm was immune to $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)}\}$, i.e., even if the initial $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)}\}$ deviated more than 90% away from their true values, the MAP-EM iteration still converged to good stable results.³³ On contrary, its convergence appeared to be relatively more sensitive to the initial $\left\{Z_{ik}^{\left(0\right)}\right\}$. In patient CTC studies, the presence of PE, which is fully illustrated in Fig. 1 by drawing CT density profiles along vertical direction based on partially and fully pseudoenhanced tissues, is problematic for appropriately initializing $\left\{Z_{ik}^{\left(0\right)}\right\}$. More specifically, the pseudoenhanced soft tissues could be easily labeled as TMs from the initial, and therefore it could take a much longer time for the MAP-EM iteration to converge to desirable solutions and sometimes the worst cases could occur that even lead to incorrect $\left\{Z_{ik}^{\left(n\right)}\right\}$ without any chance of steering back. Improving the initial $\left\{Z_{ik}^{\left(0\right)}\right\}$ by the use of neighboring voxels and anatomic information would be a promising approach to overcome PE via the MAP-EM iterations, and is expected to be better than a blind initialization solely based on the CT image density values.

Figure 1.

Illustration of pseudoenhancement effect. The left-hand side shows a partially pseudoenhanced soft tissue (top) and profile (bottom) along the vertical arrow; and the right-hand side shows a fully enhanced soft tissue (top) and profile (bottom) along the vertical arrow.

As an image processing technique, vector quantization (VQ) has received considerable interest and has found various applications in image∕voice compression and classification, statistic pattern recognition, etc.³⁸ As its name implied, VQ has limited use in CT since each voxel has only one density value. The authors have been exploring strategies to reinterpret and reform CT images to fit the VQ’s framework. One example is the novel method of grouping each voxel’s 22 neighboring voxels to form a 23-dimensional (23D) local density vector and then classifying all the vectors based on the density similarity within certain spatial range.²¹ As a result, each voxel is uniquely reinterpreted as a 23D local density vector to catch the local anatomical information. To reduce the computing burden, principal component analysis (PCA) was applied to the local vector series to determine the dimension of their feature vectors.²¹ By applying PCA on a large database, it was observed that a reasonable dimension of the feature vectors was five, where the summation of the first five principle components’ variances was more than 92% of the total variance. In this work, the authors adapted the VQ strategy to initialize $\left\{Z_{ik}^{\left(0\right)}\right\}$ for those image density ranges affected by PE solely. This is expected to provide more useful CT density information about the pseudoenhanced soft tissues and TMs from the viewpoint of quantization under the assumption that even pseudoenhanced soft tissues would still have relatively smaller CT density values than TMs. If the density information about the pseudoenhanced soft tissues is not completely missed in the initial $\left\{Z_{ik}^{\left(0\right)}\right\}$, then the statistical model fitting mechanism built in the MAP-EM algorithm would segment those PE voxels as mixture of soft tissues and TMs. The authors’ VQ∕PCA based initial labeling procedure prior to the assignment of $\left\{Z_{ik}^{\left(0\right)}\right\}$ can be summarized as follows.

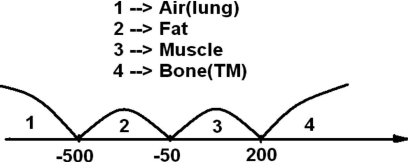
• (a)First of all, all image voxels were roughly divided into four tissue types of air, fat, muscle, and bone (including TMs and pseudoenhanced soft tissues) via thresholds adaptive to the image histogram,²⁵ which were simply determined as those local optima by taking derivative along the image histogram. In other words, different histogram shape would lead to different thresholds with typical density values illustrated in Fig. 2.
• (b)Each voxel of bone class was reformatted to be a 23D local density vector, followed by PCA through eigen-value decomposition where the first five principle components were chosen to reinterpret the original bone class voxel as 5D feature vectors.
• (c)By using an unsupervised self-adaptive VQ classification,²¹ the collection of 5D feature vectors of bone-only class voxels were further classified into ten subdivided bone classes, where the number of “10” was determined based on the criterion of maximal differentiation among the subdivided bone classes. Considering the inhomogeneous CT density distribution, it is sufficient to claim that the ten subdivided bone classes can capture the characteristics of bone, TMs, and pseudoenhanced soft tissues.
• (d)Instead of obtaining a single mean value for bone class as the authors did before, ten mean values associated with the ten subdivided bone classes, denoted by m_k, k=1,2,…,10, were calculated and sorted in an increasing order. Ten classification labels were therefore assigned to these subdivided bone class voxels with a smaller label corresponding to a smaller m_k. More specifically, if the authors originally labeled air class as 1, fat class as 2, muscle class as 3, and bone class as 4, then label 4 was subdivided via the combination of PCA and VQ strategy into ten new labels, resulting in 13 labels all together as depicted in Table 1.

Figure 2.

Typical example of three thresholds for the tissue classes of air, fat, muscle, and bone.

Table 1.

Initially classified labels by the adaptive threshold strategy on the data histogram, followed by VQ classification of the bone class.

	Before VQ	After VQ
Air	1	1
Fat	2	2
Muscle	3	3
Bone and TM	4	Subdivided class 1	5
		Subdivided class 2	6
		Subdivided class 3	7
		Subdivided class 4	8
		Subdivided class 5	9
		Subdivided class 6	10
		Subdivided class 7	11
		Subdivided class 8	12
		Subdivided class 9	13
		Subdivided class 10	14

Because of their distinct natures, those voxels with label 5 have the smallest sample mean and therefore are highly likely to be the pseudoenhanced soft tissues. In contrast, those voxels of label 14 have the largest sample mean which are highly likely to belong to the class of dense bone or TMs. For any label between 5 and 14, it serves as an indicator to provide a “second opinion” of current voxel toward either pseudoenhanced soft tissues or bone∕TMs. Figure 3 illustrates how Table 1 works via VQ∕PCA, where in Fig. 3b the brighter the area, the larger the subdivided class labels, and vice versa.

Figure 3.

Illustration of how PCA and VQ further divide the bone class into ten subclasses, (a) the original CT images, (b) the subdivided class labels from 5 to 14 for the bone class only, and (c) the enlarged TM area with pseudoenhanced soft tissue.

In CTC studies, four different tissue types are observed in the CT images, i.e., air, fat, muscle, and bone (possibly with TMs). By grouping each voxel’s 22 neighbors together in the 3D case, a picture of how this voxel is locally mixed by four tissue types is provided, and 15 mixture combinations are fully depicted in Table 2 and visually illustrated in Fig. 4 for a 2D case, where only the surrounding eight-connected neighbors were considered to preserve the simplicity and the letters “B,” “F,” “M,” and “A” represent bone, fat, muscle, and air classes, respectively.

Table 2.

Eight possible tissue mixture combinations related to the bone class.

Index	Tissue mixture combination	Index	Tissue mixture combination
1	Air only	9	Tissue and bone
2	Tissue only	10	Muscle and bone
3	Muscle only	11	Air, tissue, and muscle
4	Bone only	12	Air, muscle, and bone
5	Air and tissue	13	Air, tissue, and bone
6	Air and muscle	14	Tissue, muscle, and bone
7	Air and bone	15	Air, tissue, muscle, and bone
8	Tissue and muscle

Figure 4.

Illustration of how to determine local mixture index of each voxel in the 2D case. (a) Voxel i contains purely bone; (b) voxel i contains mixtures of two tissue types: Bone and muscle. (c) Voxel i contains mixtures of three tissue types: Bone, muscle, and fat; and (d) voxel i contains mixtures of four tissue types: Bone, air, muscle, and fat.

For example, if a voxel’s 22 neighbors are all labeled as bone class, then the voxel is linked to index 4 of Table 2 as “bone only,” otherwise it is not pure and will be linked to another index from 5 to 15. Combining Tables 1, 2, the initialization of $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)},Z_{ik}^{\left(0\right)}\}$ was treated differently. Since the MAP-EM algorithm is proven to be relatively robust to the deviation of $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)}\}$, roughly computing $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)}\}$, k=1,2,3,4 individually from the initially labeled voxels as described by step (a) turns out to serve well in our studies. However, the initial $\left\{Z_{ik}^{\left(0\right)}\right\}$ is rather sophisticated and summarized as follows:

• (1)Each voxel i, which is initially labeled as bone∕TM, is represented by two indicators so far, a subdivided class label SL_i from Table 1, and a local mixture index LMI_i from Table 2. To determine $\left\{Z_{ik}^{\left(0\right)}\right\}$ of tissue type k within voxel i, one needs to inspect its 22 neighbors whose SL_j, j=i₁,…,i₂₂ is between 5 and 14, and compute the averaged ${\mathrm{SL}}_i^{*}$ to substitute its own SL_i based on the assumption that the properties of voxel i could be uniquely characterized by its neighbors. Therefore, if ${\mathrm{SL}}_i^{*}=14$ while LMI_i=4, then voxel i is determined to be 100% bone∕TM and the corresponding $Z_{ik}^{\left(0\right)}=1$ for bone class and all other tissue classes set to 0. As ${\mathrm{SL}}_i^{*}$ goes down or LMI_i alters away from 4, $Z_{ik}^{\left(0\right)}$ is linearly decreased for bone class while proportionally increased for other tissue types subject to the constraint of ${\sum }_{k=1}^4{Z}_{ik}=1$, considering the interaction and tradeoff between ${\mathrm{SL}}_i^{*}$ and LMI_i.
• (2)For each voxel i not initially labeled as bone∕TM, we define $\left\{Z_{ik}^{\left(0\right)}\right\}$ as the normalized frequency of tissue type k occurring among neighboring voxels.

Concluding this section, it is worthwhile to emphasize the point that the versatility of PE has been observed^{39, 40} that PE depends upon various factors such as CT scan parameters, administration of tagging agent, and how the tagging agent is mixed with the fluids in the gastrointestinal tract. The initialization scheme proposed here attempts to catch part of the PE distribution range in CTC application via VQ∕PCA strategies. It could be extended to other imaging applications beyond CTC as long as differences in density value distribution exist between pseudoenhanced soft tissue and TM, such as in MRI-based virtual cystoscopy where the efficiency of VQ∕PCA in initialization procedure has been evidenced for segmentation of the bladder wall.⁴¹

Utility of neighborhood information to refine iterated estimate

Given $\{{\mu }_k^{\left(0\right)},{\nu }_k^{\left(0\right)},Z_{ik}^{\left(0\right)}\}$ as initials, $\{{\mu }_k^{\left(n\right)},{\nu }_k^{\left(n\right)}\}$ are updated iteratively by Eqs. 6, 7, respectively, while $\left\{Z_{ik}^{\left(n\right)}\right\}$ are updated by Eqs. 8, 9, 11 for voxels containing two, three, and four tissue types, respectively.

To allow the number of tissue types inside each voxel i adaptive to each individual iteration, the authors propose to inspect the first- and second-order neighbors of voxel i after each iteration. If voxel i contains more than one tissue type and the observed tissue type k in this voxel satisfies

$$\left(\frac{Z_{ik}^{\left(n\right)}+{\sum }_{j∊N_i}{\omega }_j{Z}_{jk}^{\left(n\right)}}{Z_{ik}^{\left(n\right)}+{\sum }_{k=1}^K{\sum }_{j∊N_i}{\omega }_j{Z}_{jk}^{\left(n\right)}}\right)⩽\delta ,$$ (12)

then $Z_{ik}^{\left(n\right)}=0$ and the total number of tissue types in voxel i decreases by 1, where N_i denotes the first- and second-order neighborhood system centered at voxel i, ω_j is a scale factor reflecting the difference among different orders of the neighboring voxels, and δ is a predefined small value (e.g., 0.05 or 5%). Figure 5 depicts how the first- and second-order neighbors are defined.

Figure 5.

Illustration of how to define the first- and second-order neighborhood systems for voxel i: (a) The first-order neighbors and (b) the second-order neighbors.

Similarly, if voxel i does not contain tissue type k from its neighbors the following condition holds:

$$\left(\frac{{\sum }_{j∊N_i}{\omega }_j{Z}_{jk}^{\left(n\right)}}{{\sum }_{k=1}^K{\sum }_{j∊N_i}{\omega }_j{Z}_{jk}^{\left(n\right)}}\right)>\delta ,$$ (13)

then the number of tissue types in voxel i increases by 1 and all the percentages $\left\{Z_{ik}^{\left(n\right)}\right\}$ are recalculated for the changed number of tissue types.

More comments on Eqs. 12, 13 are worthwhile. First of all, Eq. 12 was derived to exclude those tissue types which are playing negligible roles in forming current tissue mixture in voxel i, and the ratio of {Z_ik} in Eq. 12 for a given tissue type in voxel index i just acts as such an indicator, i.e., the higher the ratio, the more significant the tissue type k, and vice versa. Therefore, when such ratio is small enough compared to a predefined threshold, it is appropriate to claim its uselessness in shaping voxel i. Consequently, the number of tissue types in voxel i shall be decreased by 1. The same arguments could be easily extended to Eq. 13 for the case of increasing the number of tissue types in voxel i. In general, the thresholds defined in Eqs. 12, 13 are set to be equivalent for consistency. Second, the scale factors {w_j} were applied to reflect different roles of neighboring voxels, i.e., it is in inverse proportion to the distance between central voxel i and its neighbors. The most common way is to set 1 and $1∕\sqrt{2}$ for first- and second-order neighbors, respectively. Finally, in terms of the robustness of Eqs. 12, 13, comprehensive experiments were conducted and the following observations were obtained. Without the regulation of Eq. 12 in decreasing the number of tissue types, the segmentation results were prone to be impaired by spot noise. In other words, the initially induced spot noise (in the iterative initialization) would remain or even propagate over to its neighbors. Similarly, the use of Eq. 13 was particularly designed to compensate for the case where tissue mixture percentage is overestimated (i.e., the number of tissue types is underestimated). After an initial guess of tissue types in a voxel, Eqs. 12, 13 are considered to be “dual examinations” for refining purpose.

In doing so, $\left\{Z_{ik}^{\left(n\right)}\right\}$ is smoothly changed in an adaptive manner as iteration proceeds, either decreasing or increasing as regularized by Eqs. 12, 13. Because of the sophisticated initialization, condition 13 is observed to rarely occur compared to condition 12 in the authors’ studies. Considering the fact that computation complexity is significantly reduced as the number of tissue types in a voxel decreased, condition 12 plays an important role in boosting the efficiency. Finally as the MAP-EM iteration moves on, convergence is assumed when the following stopping rule is satisfied:

$$\mathrm{Max}\left({\mid \frac{{\mu }_k^{(n+1)}}{{\mu }_k^{\left(n\right)}}-1\mid }_{k=1,2,3,4}\right)⩽\eta ,$$ (14)

where the maximum ratios of class mean difference between (n+1)th and nth iterations to the nth class mean itself among four different tissue types is less than the prespecified threshold η. The threshold η was set to be 0.05 throughout our study.

Electronic colon cleansing procedure based on tissue mixture fractions {Z_ik}

Given the estimated $\{{\mu }_k^{\left(n\right)},{\nu }_k^{\left(n\right)},Z_{ik}^{\left(n\right)}\}$, a $\left\{Z_{ik}^{\left(n\right)}\right\}$ distribution map of bone∕TM can be obtained by extracting {Z_i4} only. Sometimes, a voxel i with 0<Z_i4⩽1 is actually filled by TM rather than bone because of their similar CT densities. In such cases, TM can still be identified and separated from bone to achieve the goal of ECC via the following two steps.

• (1)Gravity ensures the existence of a flat interface between air and TM, and by setting this interface as seeds, a 3D growable area of TM in terms of {Z_i4} can be built up via region growing. The remaining voxels with mixture fraction 0<Z_i4⩽1 and location outside the identified TM region are then labeled as bone.
• (2)For voxel i inside the region of TM, adding its Z_i4 back to Z_i1, i.e., Z_i4+Z_i1→Z_i1, and then changing its CT density as $Z_{i1}^{\left(n\right)}{\mu }_1^{\left(n\right)}+Z_{i2}^{\left(n\right)}{\mu }_2^{\left(n\right)}+Z_{i3}^{\left(n\right)}{\mu }_3^{\left(n\right)}$.

Removal of small bowel by connected-components and morphology analysis

Since colon is not the only air-filled structure in the abdomen, incomplete ECC cases inevitably exist because of the presence of small bowel in the segmentation results, resulting in more false positives particularly when the folds inside the small bowel mimic polyps inside the colon. A connected-component and morphology analysis-based postprocessing pipeline for small bowel removal, as well as other peripheral structures such as lung, is developed complementary to the MAP-EM image segmentation based on the extracted distribution map of {Z_i4}.

• (1)Taking the central colon lumen without PV effect as a seed region, i.e., those voxels whose Z_i4=1, the whole colon is categorized into two regions, with and without PV effect via region growing. Figure 6 illustrates a typical PV distribution nearby the colon wall in two colors.
• (2)Connected-component analysis is then applied to pure colon voxel (the central area in Fig. 6) to form clustered patches whose {Z_i4} are all equivalent to 1’s. In doing so, the central area is divided into separate connected components of different sizes.
• (3)In the perfect case that colon is connected as a whole and is the largest connected component in the abdomen, the easiest way to remove peripheral structures is to select the largest connected component and discard all the remains. However, in the authors’ studies on the 52 patient CTC data sets downloaded from the website of the VC Screening Resource Center, which are to be presented in Sec. 4, it was found that there are nearly 30% cases with collapsed colon, and for the purpose of keeping colon integrity, the total number of components to be selected should be no more than three in 99% of the collapsed cases.
• (4)Finally, after colon and small bowel are satisfactorily divided apart, the PV distribution around the lumen border is recovered through morphological dilation, i.e., the outer area in Fig. 6 is recovered by empirically dilating the central area three to five layers, which is the average thickness of the mucosa layer. During dilation, only those voxels pointing to the direction of decreasing {Z_i4} are candidates to be considered. Otherwise, neighboring patches belonging to different entities (e.g., small bowel) could be erroneously included.

Figure 6.

Typical PV distribution around the border of the colon lumen.

Steps (1)–(4) have been proven to work well in terms of removing not only small bowel, but also remaining bone and even noise-induced streak artifacts. Most important, the tissue mixture details, which are recovered by the MAP-EM algorithm and the postsegmentation strategies, are well preserved during the removal of the small bowel and others. The constructed ECC pipeline consisting of the MAP-EM segmentation and the postsegmentation strategy was evaluated, as presented in the following.

EXPERIMENTAL DESIGN

The newly improved ECC pipeline, including the fully automated low-level MAP-EM mixture-based segmentation and high-level postprocessing strategies, was evaluated on 52 patient CTC studies downloaded from the website of the VC Screening Resource Center. Each patient was scanned at supine and prone positions, and each scan at a view is represented by a volume image data set of more than 300 slices of 512×512 array size with spatial resolution roughly at 0.66 mm×0.66 mm×1 mm. The authors’ previous ECC pipeline with restriction of no more than two tissue types³² was also applied to these 104 data sets as a reference for a fair comparison, where two radiologists participated in the visual judgments.

How radiologists participated in the data evaluation procedure, and how they got access to the data with hundreds of slices each, were two major issues to be solved. Considering the fact that radiologists’ clinical training and experiences were deemed as the ground truth and a well-designed blinded display system was the bridge to the ground truth, an agreement on a three-step evaluation procedure was reached among the radiologists.

• (1)For each scan, two ECC results from the authors’ current and previous pipelines were displayed and compared on the same screen slice-by-slice with randomized display position, i.e., one on the left and the other on the right. The corresponding raw CT images were also displayed on the side for reference.
• (2)Radiologists started to review the slices of the highest prioritization scores, which were assigned to indicate the presence of true polyps given ground truth map. During inspection, radiologists evaluated the paired slices (one for each ECC pipeline) by the criterion of best representing polyps’ shape and texture. In reference to the original data, radiologists scored “1” representing the poorest, “2” in the middle, and “3” the best. For more than one polyp involving multiple slices, the scores for each polyp were averaged to get a final one under this particular criterion.
• (3)After step (2), radiologists were guided to the slices of the second highest priority scores, which were assigned to indicate the presence of noticeable TM, small bowel, or pseudoenhanced soft tissues based upon data characteristics. Under this circumstance, three criteria were raised, which were (i) which side on the display (either left or right in each scan) showed better cleansing of the residual fecal∕fluid or TM; (ii) which side better preserved the shape and texture information of the folds, and (iii) which side better distinguished small bowel from the colon. Similarly, three final scores were generated for the above-mentioned three criteria by averaging the individual scores if multiple cases occurred for a certain criterion. Even though no formal inter-rater reliability was calculated, based on the authors’ ad-hoc evaluation during the training sessions, the scoring agreement between the two experienced radiologists was high.

Although ECC is more useful in 3D fly-through reading modes, the appearance of the 3D images alone does not necessarily correlate to the accuracy of the ECC in preserving the true underlying structure of the colon. A smoothing algorithm after ECC could appear to give a pleasing image to the interpreting radiologist even though key structures such as folds have been thinned or removed. In this study, the 2D images allowed the radiologist evaluator to determine the underlying structures of the colon and the accuracy of preservation. The use of 3D fly-through mode to determine the efficacy of preservation of folds while determining the complete removal of tagged material is not readily possible since the 3D images only evaluate the interface. If one compared the 3D images prior to ECC and following ECC, the pre-ECC images in three dimensions would not show the underlying structures and one could not assess the accuracy of ECC in preservation of the structures. This analysis requires the use of 2D images. The authors have looked at their algorithm in three dimensions and some minor “corner effects” are present which can be removed through the application of smoothing algorithms which will be the subject of future research. This was not the purpose of this project.

RESULTS

Evaluation results

The evaluation results of each ECC pipeline were summarized by the mean scores and standard deviations for each of the four evaluation criteria as shown in Table 3. To meet the goal of comparing two different ECC pipelines using the same set of samples, the paired t-tests were employed in this study because of their effectiveness in comparing the mean difference between two populations when one believes that some dependency exists in terms of p value.^{42, 43} For the two different pipelines, the higher the mean value in Table 3, the better the corresponding ECC pipeline performance. For three out of the four criteria, the new ECC pipelines showed statistically significantly better results (p value <0.001). Even though “cleanse residuals or tagged materials” was not statistically significant, the current ECC pipeline also scored better than the old ECC pipeline.

Table 3.

Comparison of the two different ECC pipelines according to the four comparison criteria stated earlier, where score is any value from [1, 2, 3] with “1” and “3” indicating the worst and best cases. The number N in the left column indicates the number of samples collected for the evaluation of each criterion.

Criterion (N)	ECC	Mean	s.d.	p value
Cleanse residuals or tagged materials (31)	Previous ECC	2.61	0.81	0.33
	Current ECC	2.81	0.60
Preserve shape and texture of polyps (52)	Previous ECC	1.60	0.85	<0.001
	Current ECC	2.73	0.60
Preserve shape and texture of folds (32)	Previous ECC	1.03	0.18	<0.001
	Current ECC	2.78	0.49
Differentiate the small bowel from colon (66)	Previous ECC	1.06	0.35	<0.001
	Current ECC	2.95	0.21

Convergence performance of the MAP-EM segmentation algorithm

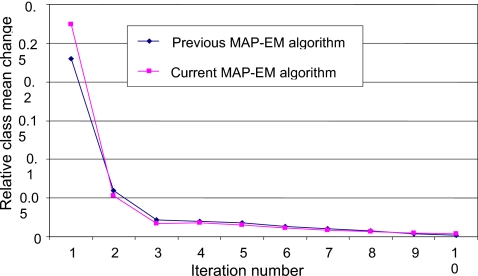
In the authors’ studies, the threshold η for convergence in Eq. 14 was set to 0.05. Taking the data set (numbered 043 at the website of the VC Screening Resource Center) at the prone position as an example, Fig. 7 reflects the converging speed of the MAP-EM algorithm as iteration proceeds.

Figure 7.

Comparison between the authors’ current and previous MAP-EM segmentations in terms of converging speed.

Capacity of overcoming pseudoenhanced soft tissues

Figures 89 illustrate examples of partially and fully pseudoenhanced soft tissues, respectively, which are exactly located on the border between air and TM where significant PV effect is present. The raw CT images on the leftmost sides of Figs. 89, as well as the image density profiles along vertical direction are shown in Fig. 1. For highlighting purpose, the small boxes of white dots indicate the location of the concerned soft tissue. It is therefore concluded that by taking sophisticated initialization procedure and other implementation optimization, the differences in CT density between TMs and pseudoenhanced soft tissues have been satisfactorily captured via the combination of VQ∕PCA strategy, such that good $\left\{Z_{ik}^{\left(0\right)}\right\}$ ensures much better segmentation performance of the MAP-EM algorithm compared to the authors’ previous version in terms of overcoming the PE distribution.

Figure 8.

Comparison between the authors’ current and previous MAP-EM algorithms in segmenting partially pseudoenhanced soft tissues: (a) The original CT images, (b) the segmentation results from the previous algorithm, and (c) the segmentation results obtained by the current algorithm.

Figure 9.

Comparison between the authors’ current and previous MAP-EM algorithms in segmenting fully pseudoenhanced soft tissues: (a) The original CT images, (b) the segmentation results from the previous algorithm, and (c) the segmentation results obtained by the current algorithm.

Capacity of removing small bowel and other peripheral structures

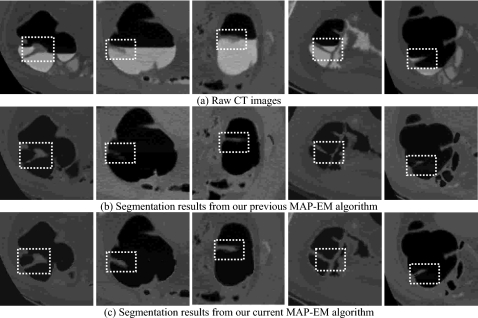
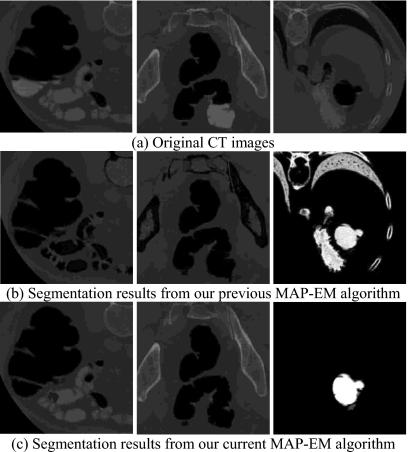
Small bowel, in the vicinity of colon as illustrated by the left picture in Fig. 10a, is sometimes incorrectly segmented as part of colon, i.e., an example of incomplete ECC cases. Although such problem could be avoided under the inspection of radiologists, it still imposes challenges for computers to automatically divide them apart. In addition, segmentation of colon even suffers from remaining bone which encompasses the colon, as well as lung and stomach represented by the middle and right pictures in Fig. 10a. The authors’ previous segmentation results shown in Fig. 10b fully describe such incomplete ECC cases which are worthy to be solved. By the use of the authors’ improved ECC pipeline coupled with effective postprocessing procedure, a noticeable difference is observed as depicted in Fig. 10c, successfully discarding all other peripheral structures.

Figure 10.

Comparison between the authors’ current and previous ECC pipelines in overcoming incomplete cleansing problem: (a) The original CT images, (b) the segmentation results from the previous algorithm, (c) and the segmentation results obtained by the current algorithm.

Computational complexity

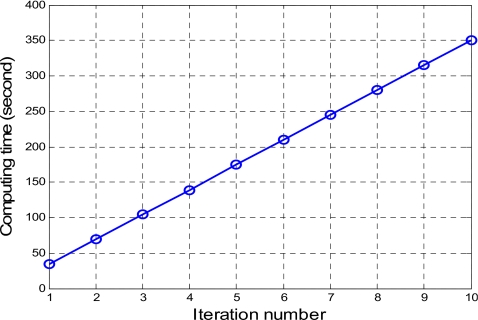
For clinical applications in CTC, the MAP-EM algorithm has to adjust the number of tissue types in each voxel at each iteration, although the total number of tissue types is four. By the introduced conditions of Eqs. 12, 13, the authors eliminated those cases of estimating the fractions of zero value. Only those fractions of nonzero values were computed in a voxel. This resulted in a speed-up of convergence. The computing efficiency is seen by Fig. 11, where the average computing time for each MAP-EM iteration is approximately 35 s, which is believed to be acceptable for clinical use. The algorithm was directly programmed using C++ language and the source code was complied in a Visual C++ environment on a HP XW8000 PC platform (2.4 GHz CPU and 2.0 Gbytes RAM) and run up to ten iterations to ensure a stable solution is achieved.

Figure 11.

Computing time for running the MAP-EM algorithm of Eqs. 10, 11, 13 for K=1,2,3,4, respectively, based on the patient CTC data sets.

DISCUSSION AND CONCLUSION

As a concluding remark, Eqs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 briefly reviewed the theoretical part of this presented MAP-EM mixture-based segmentation algorithm, which has been described mathematically in detail and analyzed numerically in Ref. 33. For CTC studies, several significant issues remain to be addressed, including parameter initialization, strategy to maximally preserve the consistency between nth and (n+1)th iterations, update on the number of tissue types in a voxel at each iteration, etc., in addition to the postsegmentation operations for removal of the small bowel and other interfering structures in the segmented results.

By relieving the constraint of the authors’ previous segmentation algorithm³² that each voxel contains no more than two tissue types, improving the parameter initialization, and utilizing both the neighboring anatomical information for update iterated results, this current ECC pipeline has shown noticeable improvement over the previous one.³² In addition, the postprocessing procedure of employing connected-components and morphology analysis has achieved great success in distinguishing small bowel from colon, improving the efficiency for following 3D fly-through navigation, quantitative analysis, and computer aided detection (CAD) studies.

The presented MAP-EM algorithm was evaluated by two radiologists’ subjective assessment on the segmented results. Quantitative improvement over the authors’ previous MAP-EM algorithm was documented. Further evaluation on polyp detection by both radiologists (human observer) and CAD (computer observer) will involve a significant effort and is currently in progress. The authors intend that the theoretical solution to the PV effect and the innovative strategy to recover the pseudoenhanced soft tissues will benefit computer-aided polyp detection, which is currently one of the major research topics in developing VC toward a screening modality.

One point the authors would like to emphasize in this application work is the effect of the PV segmentation for polyp detection and quantification. In the PV layer between air and colon wall∕polyps, the size of a polyp could be overestimated because the PV effect goes from the polyp border to the air. In the PV layer between tagged material and colon wall∕polyps, the size of a polyp could be underestimated because the PV effect goes from the border of the tagged material to the polyp, i.e., part of the polyp will be submerged inside the tagged material. Only the PV effect is accurately resolved, the under- and overestimation can be corrected consistently. In the authors’ PV segmentation, the percentage of each tissue type in a voxel is computed by a statistical MAP principle. If a voxel contains 10% polyp tissue type, then this voxel has 10% volume inside the polyp. Since the PV effect occurs on the border of a polyp, the volume of the polyp V is proportional to the third power of the radius r (assuming a sphere), i.e., V≈r³. A small error on the measure of the border will render a huge error on the measure of the volume.