Predicting human resting-state functional connectivity from structural connectivity

Abstract

In the cerebral cortex, the activity levels of neuronal populations are continuously fluctuating. When neuronal activity, as measured using functional MRI (fMRI), is temporally coherent across 2 populations, those populations are said to be functionally connected. Functional connectivity has previously been shown to correlate with structural (anatomical) connectivity patterns at an aggregate level. In the present study we investigate, with the aid of computational modeling, whether systems-level properties of functional networks—including their spatial statistics and their persistence across time—can be accounted for by properties of the underlying anatomical network. We measured resting state functional connectivity (using fMRI) and structural connectivity (using diffusion spectrum imaging tractography) in the same individuals at high resolution. Structural connectivity then provided the couplings for a model of macroscopic cortical dynamics. In both model and data, we observed (i) that strong functional connections commonly exist between regions with no direct structural connection, rendering the inference of structural connectivity from functional connectivity impractical; (ii) that indirect connections and interregional distance accounted for some of the variance in functional connectivity that was unexplained by direct structural connectivity; and (iii) that resting-state functional connectivity exhibits variability within and across both scanning sessions and model runs. These empirical and modeling results demonstrate that although resting state functional connectivity is variable and is frequently present between regions without direct structural linkage, its strength, persistence, and spatial statistics are nevertheless constrained by the large-scale anatomical structure of the human cerebral cortex.

Populations of neurons in the mammalian cerebral cortex are continuously active during purposeful behavior, as well as during resting and sleep (1). Activity levels are modulated across time by the internal dynamics of each neuronal population and by signals received from cortical, subcortical, and peripheral elements of the nervous system. In the past decade, there has been intense interest in the patterns of correlated activity [“functional connectivity” (2)] in the human brain, because these patterns are believed to reflect the patterns of interaction between neuronal populations. A set of functionally connected regions is referred to as a “functional network.” Some functional networks are most commonly detected when participants are not performing any demanding task (in the resting state); others are observed in the context of task-focused behavior; and some networks persist across both behavioral states (3–6). A set of regions including posterior medial, anterior medial, and lateral parietal cortices comprise the default mode network (DMN) (7, 8), a functional network that is particularly robust across participants and cognitive states. It has been suggested that the more persistent functional networks may be involved with ongoing organizational processes in the brain (9, 10), and that disruptions in reliably present correlations are indicative, and potentially diagnostic, of neuropathology (11, 12).

Because the propensity for 2 areas to interact should vary in proportion to the density and efficacy of the projections connecting them, it is widely assumed that the repertoire of functional configurations assumed by the cerebral cortex is reflective of underlying anatomical linkage (13- 18). However, the nature of this structure-function relationship is only beginning to be revealed. A general correspondence between functional connectivity (measured using functional MRI) and structural connectivity (measured using diffusion tractography) has previously been demonstrated in adjacent gyri in a single axial slice (19) and across the cortex in a 66-region parcellation (20). However, several questions remain. First, given that structural and functional connectivity are correlated, is it possible to infer structural connectivity from functional connectivity? Second, how does the structure-function relationship vary as we increase the distance between neuronal populations, and what are the contributions of indirect structural connections to functional connectivity? Third, to what extent does functional connectivity vary across time, and which anatomical features distinguish persistent functional networks from those that are more transient? To address these questions, we compared structural and functional connectivity maps to one another. We then used the structural connectivity maps as couplings in a computational model of the large-scale dynamics of the cerebral cortex (21, 22), and from these dynamics we extracted simulated blood-oxygenation level dependent (BOLD) signals and functional connectivity, which could be quantitatively compared against empirical observations.

Structural connectivity was measured noninvasively in 5 individual participants using diffusion spectrum imaging (DSI). Resting neural activity was then recorded in the same participants on two separate occasions using functional MRI (fMRI). Structural connectivity (SC) maps were constructed using streamline tractography and resting state functional connectivity (rsFC) maps were based on the Pearson correlations between the BOLD time series in all possible pairs of 998 cortical regions.

We hypothesized that, in both empirical and simulated data, more strongly connected region-pairs would exhibit stronger signal correlations, but that underlying SC would not be necessary for the observation of strong rsFC (19). We expected, further, that the SC-rsFC relationship would be mediated by distance and by indirect anatomical connections, although only partially, and that this effect would also be observed in our model. Finally we expected that rsFC would be most reliable where SC is strongest.

Results

We report results using 2 cortical parcellations, called the “low resolution” and the “high resolution.” In the low-resolution parcellation [supporting information (SI) Fig. S1A], 66 cortical regions (33 per hemisphere) of varying size are identified and matched across participants using an automated landmark-based algorithm (23). The high-resolution parcellation (Fig. S1B) is a refinement of the low-resolution surface partition, and is composed of 998 regions of interest (ROIs) of approximately equal area (≈1.5 cm²) (L.C., X.G, J.P.T, K. Q Do, P. Maeder, R.M., P.H., unpublished data).

SC between two ROIs was derived from the number of fibers found by the tractography algorithm that link those ROIs. rsFC was calculated using pairwise Pearson's correlation coefficients of BOLD time series obtained for each ROI by averaging across voxels within an ROI. Both SC and rsFC were calculated at the high resolution (998 ROIs) and then down-sampled by averaging across ROIs within each of the 66 predefined anatomical regions. For comparison with experimental data, we simulated a nonlinear neural mass model (21, 22) composed of 998 nodes, whose time evolution is governed by a set of differential equations. The strength of connections between nodes was determined by the empirical high-resolution SC, and simulated functional connectivity was then calculated from the simulated BOLD time series. See Methods for further details for each of these steps. All correlations we report are P ≪ 1e-3.

Overall Structure-Function Relationship

Low Resolution (66 Regions).

As described previously (20), after averaging low-resolution data across participants, the SC and rsFC strengths across all region-pairs were found to be highly significantly correlated (r = 0.66). When excluding ROI-pairs with absent or inconsistent structural connections (see Methods), this correlation strengthens to r = 0.82.

High Resolution (998 ROIs).

Because of interparticipant variability in cortical morphology, averaging data at the high resolution did not produce as much of a de-noising effect as at the low resolution. For data averaged across participants (Fig. S2), the SC-rsFC correlation was r = 0.36 and increased to r = 0.53 when excluding absent or inconsistent structural connections. For individual participants, the SC-rsFC correlations ranged from r = 0.39 to 0.48 (Fig. 1A).

Fig. 1.

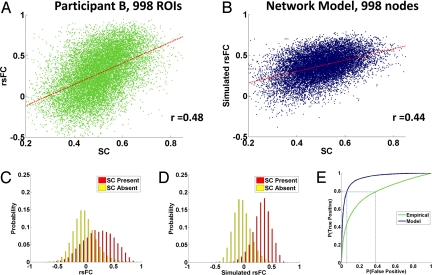
Overall SC-rsFC relationships. (A) Scatter plot (single acquisition, 20 min) of rsFC against SC at high resolution for participant B, showing edges with nonzero SC. (B) Scatter plot (single run, 16 min) of simulated rsFC against SC (from participant B) at high resolution, showing edges with nonzero SC. (C) The probability densities of rsFC values between structurally connected and unconnected region pairs, data for participant B at the high resolution. (D) Same as (C), but for simulated rsFC. (E) ROC curves, indicating the signal detection performance when inferring SC by thresholding empiricial (green) and simulated (dark blue) rsFC maps at the high resolution.

Computational Model (998 Nodes).

A comparison of empirical SC (from participant B) and simulated rsFC derived from a single run of the computational model is shown in Fig. 1B. For individual participants, the SC-rsFC correlations (single simulation) ranged from r = 0.32 to 0.44 when excluding absent connections. For data averaged across participants, the overall correlation between SC and simulated rsFC was r = 0.46 and increased to r = 0.52 when excluding absent or inconsistent structural connections. For high- and low-resolution correlations in individual participants and in the model, see Table S1.

Inference of Structure from Function.

When structural connections are present, the relationship between the strength of SC and rsFC is robust in both the empirical data and computational model. When direct structural connectivity is absent, however, the rsFC values will still vary over a wide range (Fig. 1 C and D), a finding consistent with ref. 19. Thus, although the presence of strong SC at an edge is predictive of strong rsFC, the reverse inference is less reliable. When inferring SC by thresholding rsFC, one obtains, for each given threshold value, some number of false-positives and some number of true-positives. The receiver-operating characteristic (ROC) curves in Fig. 1E show how the false-positive and true-positive rates vary as this threshold is adjusted. The area under the ROC curve is greater for the modeled data than the empirical data (0.95 versus 0.79). However, in both cases, thresholding of rsFC yields highly inaccurate prediction of SC. For example, in the empirical data, the threshold at which 80% of structural connections are correctly detected is one at which more than 40% of the unconnected region pairs are incorrectly detected (see Fig. 1E). Because structurally unconnected pairs are about 30 times as numerous as connected pairs within our high-resolution data, only ≈6% of inferred structural connections would be genuine at this threshold. This percentage is improved in the computational model, but still too low for practical inference. For the threshold at which 80% of structural connections are correctly detected, only ≈28% of the inferred SC would correspond to the true structural couplings that underlie the model dynamics.

The Role of Distance.

On average, both structural connectivity (24, 25) and functional connectivity (26) between cortical regions decrease with the distance between those regions. This effect could result from a combination of factors, including (i) spatial autocorrelation of cortico-cortical connectivity, (ii) spatial autocorrelation of subcortico-cortical projections, (iii) activation spread along the surface of the cortex via local circuitry (27, 28), (iv) spatial blurring of the BOLD signal because of vascular drainage, and (v) MRI acquisition or data preprocessing artifacts (29).

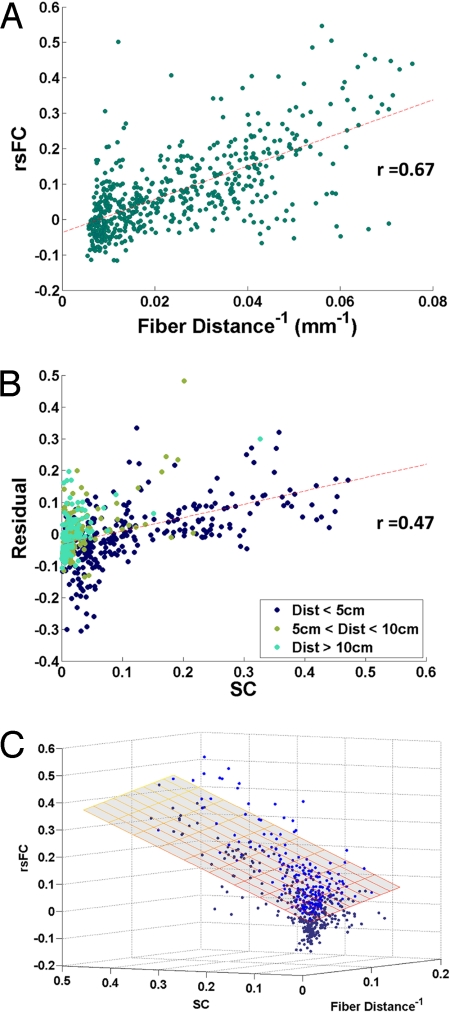
Because most of the structural connectivity we observe is short-range (20), the structure-function relationship we report here could result artifactually if both SC and rsFC are spatially autocorrelated, but for entirely unrelated reasons. To rule out this possibility we first confirmed that average rsFC is linearly related to the inverse of the fiber distance between regions (r = 0.67) (Fig. 2A, low resolution). Then, after regressing rsFC on fiber distance, we checked that structural connectivity is robustly related to the residuals of that rsFC-fiber distance relationship (r = 0.47) (Fig. 2B). This is equivalent to calculating a partial correlation between SC and rsFC, controlling for interregional fiber distance. Although the SC-rsFC relationship is weaker when we control for distance, it remains highly significant in all participants in both high- and low-resolution analyses. A bivariate linear regression using SC and (inverse) fiber distance to predict rsFC can explain 69% of the variance in participant-averaged rsFC at the low resolution, and 30% at the high resolution (see Table S1 and Fig. 2C). In the computational model, 29% of the variance in rsFC is explained by the combination of SC and inverse fiber distance at high resolution.

Fig. 2.

Role of distance. (A) Scatter plot of interregional rsFC against the inverse of the inter-regional fiber distance. (B) Scatter plot of residuals from (A) plotted against SC, at the low resolution. (C) Three-dimensional scatter plot, showing the relationship between SC, rsFC, and inverse fiber distance. The superimposed plane shows the fit of the bivariate linear model. Points above the plane of best-fit are light blue, points below are dark blue.

Indirect Connections and Network Effects.

We next sought to examine the potential role of multisynaptic anatomical structures in explaining the presence of rsFC between ROIs without direct SC. We assigned indirect connections to region-pairs that were not directly connected, but for which there existed at least one 2-edge path connecting them. For each such region pair ij, the indirect structural connection had strength equal to the sum of all of the multiplicatively weighted SC paths from i to j (i.e., Indirect SC_ij = Σw_ikw_kj where w_ab is the direct SC between regions a and b). When we consider only region pairs linked by a shortest path of 2 edges, the Pearson correlation between the indirect-SC values and rsFC values was found to r = 0.29 for the average data at the high resolution (Fig. S3). This effect could not be accounted for by the Euclidean distance between region pairs, and was significant in each individual. These data suggest that indirect cortico−cortical linkage does induce some of the rsFC seen between regions lacking direct linkage.

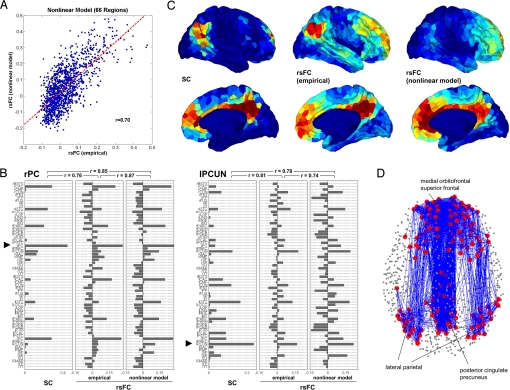
Within the computational model, indirect connections were also observed to induce functional connectivity. When considering participant-averaged rsFC matrices, the correlation between simulated rsFC and empirical rsFC at direct links in the high-resolution network was at r = 0.46, and for indirectly connected nodes was at r = 0.37, indicating that the model was capturing network-level influences of SC on rsFC. In the low-resolution networks, the correlation between simulated and empirical rsFC increased to r = 0.70 for directly linked pairs (Fig. 3A), but dropped to r = 0.23 between indirectly linked edges.

Fig. 3.

Computational model of functional connectivity. (A) Scatter plot of empirical rsFC versus simulated rsFC obtained from the nonlinear model, down-sampled to the low resolution. (B) Comparison of SC, rsFC (empirical), and rsFC (nonlinear model) for 2 single-seed regions, the posterior cingulate in the right hemisphere (rPC) and the precuneus in the left hemisphere (lPCUN). The plot displays SC and rsFC values for the seed regions in relation to all 66 regions within the corresponding low-resolution matrices. (C) Mapping of SC, rsFC (empirical), and rsFC (modeled) within the DMN. Warmer colors indicate stronger SC and rsFC. Within the posterior cingulated/precuneus, medial orbitofrontal cortex and lateral parietal cortex in both hemispheres we selected a cluster of 5 ROIs at positions that most closely matched the coordinates of peak foci of the DMN (31). These 30 ROIs served as the seeds from which SC and rsFC were determined. (D) Structural connectivity within the DMN. We selected the top 200 most correlated ROIs within the DMN (see Fig. S5D) and plotted all structural connections among them.

Reliability of rsFC.

As rsFC was acquired from each participant on two separate occasions (20- and 15-min scans), we were able to examine the reliability of rsFC. Reliability was operationalized as the correlation between 2 sets of rsFC values. For individual participants at the high resolution, reliability across scans ranged from r = 0.38 to r = 0.69, and reliability across two 10-min windows within the first scan ranged from r = 0.39 to r = 0.61. Unexpectedly low reliability is also observed in our computational model: across two consecutive 8-min windows within a single run, the simulated rsFC reliability ranged from r = 0.69 to r = 0.80 for individual maps at the high resolution.

In models and in data the observed reliability is lower than would be expected based on the sample size (at least 200 time points per window) and distributions of rsFC. Some of the empirical variability is likely because of acquisition and registration artifacts. However, we note that both empirical (30) and simulated rsFC time series exhibit very long-range temporal autocorrelations (or, equivalently, substantial power in very low frequencies), which effectively reduce the number of independent measurements captured within a time window. The values of rsFC measured in this study, as well as more generally in the field, may therefore not reflect a static underlying entity.

We also note that ROI pairs with SC exhibit significantly less variability in empirical rsFC (both across and within sessions) than do ROI pairs without SC (see SI Appendix, Fig. S4). In the present data we cannot distinguish whether rsFC between these ROIs is more persistent because it is stronger (and therefore, statistically, less subject to sampling variability in finite samples), or whether it is stronger because it is more persistent (that is, because the underlying interaction is more stable). In either case, the effect is mediated by the strength of the anatomical connections between pairs.

SC and rsFC in the DMN.

On an area-by-area basis (Fig. 3B and Fig. S5), correlations between simulated and empirical rsFC were highest for many regions located in the posterior medial cortex, including the precuneus and posterior cingulate cortex, and the medial orbitofrontal cortex. Using previously published focal coordinates of the DMN (31) within the precuneus/posterior cingulate, the medial prefrontal cortex, and the lateral parietal cortex as seed points, we extracted a subset of ROIs most strongly correlated with ROIs located in the DMN (see Fig. S5D). Figs. 3 C and D portray the relationship of SC to rsFC within the DMN. We find strong SC linking the 2 medial portions of the precuneus/posterior cingulate and medial prefrontal cortex, both interhemispherically and along the medial walls of the cerebral cortex. Lateral parietal cortex is linked through parieto-frontal pathways, while anatomical links to medial parietal cortex are less dense (see Fig. 3D). Connections between lateral and medial aspects of the posterior parietal cortex are observed in tracer studies (32), and the weakness of this connection in the DSI data likely reflects the difficulty of tracking fibers perpendicular to bundles such as the superior longitudinal fasciculus. Consistent with the structural DSI data supplied to the model, the simulated rsFC seeded in the DMN reproduces empirical rsFC patterns along the medial axis, but largely fails to include lateral parietal cortex.

Discussion

Computational work has suggested that the underlying anatomical architecture of the cerebral cortex, including its cluster structure, shapes resting-state functional connectivity on multiple time scales (22, 33). Advances in diffusion imaging (34–36) now enable us to empirically examine this structure-function relationship in individual humans at high spatial resolution across the cerebral cortex, and to compare a variety of systems-level features of resting-state functional connectivity against the predictions of computational models informed by the underlying anatomical network.

Earlier work had shown that interhemispheric rsFC is diminished in cases of callosal agenesis (37), is related to callosal integrity in healthy individuals (38), and is almost entirely abolished acutely after callosotomy (39, 40). Structural and functional connectivity were also shown to be correlated in adjacent cortical regions in a single axial slice (19) and across 66 regions of the cerebral cortex (20). The robust SC-rsFC relationship we now report at high spatial resolution provides further evidence that functional connectivity is reflective, at least in part, of interactions between distant neuronal populations. However, because anatomically unconnected edges exhibit a wide range of rsFC values, one cannot simply infer SC by thresholding maps of rsFC. The difficulty of inferring SC from rsFC arises because (i) rsFC can result from mechanisms other than direct SC, and (ii) the base rate of direct SC between 2 randomly selected ROIs at the high resolution is very low. This difficulty is not simply a reflection of the practical limitations of fMRI, because inference was nearly as difficult within our computational mode—in which SC provided the exact coupling matrix—as in empirical data.

Our second finding is that both SC and rsFC tend to decrease with interregional distance [consistent with previous studies of SC (24, 25) and rsFC (26)] and that a significant portion of the rsFC variance unexplained by SC alone is explained when distance information is combined with SC information in a bivariate model. Because interregional distance can be expected to influence sources of rsFC that are neuronal [e.g., the strength of SC, and activation spread across the cortical surface (27)] as well as nonneuronal [e.g., cardiac, vascular, acquisition and preprocessing artifacts (29)], we cannot definitively determine the origin of this distance-related residual variability in rsFC. We note, however, that although our computational model incorporates only topological (and not explicitly spatial) coupling, it exhibits a distance-associated decrease in rsFC that resembles the empirically observed fall-off. It is therefore not necessary to invoke mechanisms beyond the topology of cortico-cortical projections in explaining the distance effects.

None of the results we report in this study can be fully accounted for by interregional distance, but many are mediated by it, and the prevalence of nearest-neighbor (i.e., lattice-like) anatomical connectivity of the cerebral cortex is fundamental to its small-world (20, 36, 41–43) and hierarchical (44, 45) properties. Another factor contributing to the local clustering in rsFC networks is that indirect SC induces rsFC between region pairs that lack direct anatomical linkage. The relationship between indirect SC and rsFC is weaker than that between direct SC and rsFC, but is highly significant. Previous work (15) suggested that interhemispheric rsFC between the visual cortices most likely requires polysynaptic connectivity, and we note here that indirect cortico-cortical SC is an especially strong predictor of rsFC between the visual cortices of each hemisphere (see Fig. S3).

Our third finding is that rsFC exhibits unexpectedly low reliability within and across scanning sessions. This phenomenon is observed in each participant, as well as in our model, which is not susceptible to physiological or acquisition artifacts. In empirical data, we also observe that ROI pairs linked by SC exhibit more reliable rsFC, so that highly interconnected systems such as the DMN are nevertheless quite persistent. Within our data we cannot determine whether the shifts in rsFC reflect reconfiguration of neuronal interactions, are the result of low-frequency signal components of unknown origin, or result from a combination of the two (see SI Appendix). It is clear, however, that the proportion of the variance in rsFC that is explained by SC must be understood in light of the fact that fMRI rsFC is not static on the timescales used in this and other resting-state fMRI experiments. Studies, which compare fMRI FC against FC in modalities with higher sampling rates (16, 46, 47) remain crucial in determining the potential cognitive and behavioral significance of slow correlated fluctuations in the BOLD signal.

The rsFC of some highly connected regions was matched with high fidelity (see Fig. 3B), and this was found in particular within the posterior medial components of the default mode network (see Fig. 3 C and D). This is likely a consequence of the fact that there is a dense anatomical subnetwork linking DMN member regions (see SI Appendix) (48, 49). In future modeling work it may be fruitful to investigate how dynamical properties of individual nodes vary as a function of the node's network embedding. Large-scale cortical models will also be improved when we have access to interregional physiological efficacies, rather than fiber strengths, which only approximate the effective couplings between neuronal populations. It is also important that future models include the thalamus (50, 51) as well as the basal ganglia, which likely mediate diverse cortico-cortical interactions. By limiting ourselves in the present model to aggregate neural dynamics at each node, and by only including cortico-cortical couplings, we have been able to identify systems-level features of empirical rsFC that can be explained without recourse to subcortical input or specialized local circuitry.

The robust correspondence between SC and rsFC measured in independent imaging modalities provides a degree of mutual methodological validation for our SC and rsFC acquisition methods. Nevertheless, the potential for interregional variability in the reliability of these methods limits our ability to examine interregional differences in the strength of the structure-function relationship. While DSI tractography is often successful in resolving crossing fibers, the detection of relatively small fiber bundles running perpendicular to major fasciculi, as well as the reliable detection of very long fiber bundles, remains a technical challenge. Functional MRI is subject to susceptibility artifacts, especially in baso-temporal regions and near the frontal pole, and BOLD correlations can be contaminated by vascular, respiratory, and preprocessing artifacts (30). Preliminary conclusions about regional differences in the strength of the SC-rsFC relationship are presented in the SI Appendix, along with considerations of rsFC anti-correlations (see SI Appendix and Fig. S3B) and interparticipant differences (see SI Appendix and Table S2).

Structural connectivity of the adult mammalian brain is essentially constant from day to day, but functional connectivity can substantially reconfigure (41) within a few hundred milliseconds. In this study we confirm (19, 20, 22) at high resolution that the organizations of SC and of rsFC are strongly interrelated: structurally connected cortical regions exhibit stronger and more consistent rsFC than structurally unconnected regions. However, we also demonstrate, and capture in quantitative models, the fact that robust functional connectivity can be found between regions not linked by cortico-cortical projections, that spatial auto-correlation in functional connectivity likely results from underlying anatomy, and that functional networks continually reconfigure around the underlying anatomical skeleton. The timescales on which rsFC changes, and the relation of these changes to cognition, are important questions for future inquiry.

Methods

Extraction and Topology of Structural Networks.

DSI Acquisition.

The study protocol was reviewed and approved by the Institutional Review Board at the University of Lausanne. After obtaining written informed consent in accordance with institutional guidelines, 5 healthy right-handed male participants (age 29.4 ± 3.4 years) were scanned on an Achieva 3T Philips scanner. A high-resolution T1-weighted gradient echo sequence was acquired in a matrix of 512 × 512 × 128 voxels of isotropic 1-mm resolution.

Diffusion spectrum was performed using a diffusion-weighted single-shot echo planar imaging sequence (TR = 4,200 ms; TE = 89 ms) encoding 129 diffusion directions over a hemisphere. The maximum diffusion gradient intensity was 80 mT/m, the gradient duration δ was 32.5 ms, and the diffusion time Δ was 43.5 ms, yielding a maximal b-value of 9,000 s/mm². The acquisition matrix was 112 × 112, with an in-plane resolution of 2 × 2 mm. Thirty-six contiguous slices of 3-mm thickness were acquired in 2 blocks, resulting in an acquisition time of 18 min. The reconstruction of the data followed ref. 52. Following diffusion spectrum and T1-weighted MRI acquisitions, the segmented gray matter was partitioned into 66 anatomical regions according to anatomical landmarks using Freesurfer (surfer.nmr.mgh.harvard.edu) and 998 ROIs (see Fig. S1) as described in ref. 20. White matter tractography was performed with a custom streamline algorithm and finally, fiber connectivity was aggregated across all voxels within each of the 998 predefined ROIs. Further details are available in refs. 20 and 34.

Resampling.

The fiber strengths produced by the streamline tractography algorithm were exponentially distributed and spanned several orders of magnitude. Reasoning that interregional physiological efficacies would not span such a large range, we resampled the fiber strengths into a Gaussian distribution as follows: given N raw data values x₁, x₂, …, x_N, we generated N random samples r₁, r₂, … r_N, from a unit Gaussian distribution. We then replaced the smallest raw data value with the smallest randomly sampled value, the second-smallest raw data value with the second-smallest randomly sampled value, and so on until all raw data values are replaced. This produced a set of N resampled data values distributed according to a standard Gaussian, which we then rescaled to a mean of 0.5 and a standard deviation of 0.1 dimensionless units. The empirical results we report in this article remain strongly significant when SC is not resampled (Table S3).

Fiber Distance and Euclidean Distance.

The fiber distance between two ROIs is calculated as the average length of all of the connecting fibers found using streamline tractography. The Euclidean distance between two ROIs is calculated using the mean Talairach coordinates of voxels comprising an ROI. We used the fiber distance where possible, as it more closely reflects the distance along the cortical surface. However, fiber distance is only known where SC is present, and so for analyses in which we compare the effects of SC absence and presence while controlling for distance (see SI Appendix) we used Euclidean distance. The results in Fig. 2 remain robust and significant when Euclidean distance is used.

Extraction and Topology of Functional Networks.

BOLD Acquisition.

The same 5 participants were scanned in eyes-closed resting state using a Siemens Trio 3T system using a gradient echo EPI sequence (TR = 2,000 ms, TE = 30 ms). An axial plane was used with a field of view of 211 × 211 mm (64 × 64 voxels, each 3.3 × 3.3 mm in-plane). Thirty-five slices of 3-mm thickness with a 0.3-mm gap were acquired. All participants were scanned twice on separate days (scan 1 = 20 min, scan 2 = 15 min). Scan 1 and 2 rsFC were averaged for Fig. 3 and for some SI Appendix data as indicated. Participants were instructed to keep their eyes closed and to remain alert.

Signal Preprocessing and Correlations.

Raw BOLD signals were registered and resampled onto the b₀ image of the diffusion scan using rigid-body registration (SPM5, www.fil.ion.ucl.ac.uk/spm). Following slice-time correction BOLD time series were then computed for each of the 998 ROIs by averaging across all voxels within the ROI mask. ROI BOLD time series were then piecewise-linearly detrended (every 50 s) and mean cortical, ventricular, and white matter signals were regressed from each time series. The results we report are essentially unchanged if we regress out only the white matter and ventricular signals, and not the global mean. Finally, Pearson correlations were calculated between all ROI-pairs. Although the data and figures shown in this article are based on the raw correlation maps, the results are essentially unchanged when the 998-ROI correlation maps are Fisher z-transformed and normalized to zero-mean and unit variance within each participant (Table S4).

High- and Low-Resolution Matrices.

The 66 anatomical regions were defined according to an automated landmark-based registration algorithm (23). The 998 ROIs were chosen to provide a roughly uniform tiling of the cerebral cortex (each ROI ≈ 1.5 cm²) so that their borders aligned with those of the 66 anatomical regions. BOLD and DSI-fiber counts were captured at voxel resolution and then voxel-averaged to provide ROI-average values. BOLD correlations were calculated using the ROI time series and then down-sampled to the 66-region map by averaging across all ROIs with a region.

When averaging SC, structural connections were deemed absent overall if they were absent in more than 3 participants (high resolution) or more than 1 participant (low resolution). The SC map for Participant A was an average of 2 separate DSI scans (20).

Computational Model.

Neuronal population dynamics were simulated at 0.2-ms resolution for 16 min using a system of 998 neural masses with coupling strengths linearly proportional to the resampled fiber strengths at each edge. Each neural mass represents a population of densely interconnected excitatory and inhibitory neurons, in which the effects of both ligand- and voltage-gated membrane channels are accounted for. This model has previously been described in detail (21) and used in an anatomically informed model of large-scale functional connectivity in the macaque monkey (22). Further modeling details are provided in the SI Appendix.

Note Added in Proof.

Another article has reported correlated rsFC and SC across the whole brain (53).