Abstract
A deterministic model of dermal wound invasion, which accounts for the platelet-derived growth factor (PDGF) gradient sensing mechanism in fibroblasts mediated by cell surface receptors and the phosphoinositide 3-kinase (PI3K) signal transduction pathway, was previously described (Biophys J 2006; 90:2297–308). Here, we extend that work and implement a hybrid modeling strategy that treats fibroblasts as discrete entities endowed with heterogeneous properties, namely receptor, PI3K and 3′ phosphoinositide phosphatase expression levels. Analysis of the model suggests that the wound environment fosters the advancement of cells within the population that are better fit to migrate and/or proliferate in response to PDGF stimulation. Thus, cell-to-cell variability results in a significantly higher rate of wound invasion as compared with the deterministic model, in a manner that depends on the way in which individual cell properties are sampled or inherited upon cell division.
Key words: wound healing, chemotaxis, gradient sensing, mathematical model, stochastic, signal transduction, phosphoinositide 3-kinase, PDGF
Introduction
Dermal wound healing is a normal physiological process that exemplifies the spatiotemporal coordination of multiple cell types in vivo.1 Within minutes to hours, a fibrin-rich clot is established in the wound space, forming a provisional extracellular matrix; clotting is accompanied by the activation of platelets, and neutrophils and macrophages are subsequently recruited to the wound site to guard against infection. Over a period of several days thereafter, fibroblasts in the adjacent dermal tissue are stimulated to proliferate and migrate into the wound. These cells ultimately resolve the wound through synthesis, remodeling and contraction of the matrix.2
The cell types mentioned above communicate with each other largely through the secretion of soluble factors. Fibroblasts in particular are stimulated by the aptly named platelet-derived growth factor (PDGF) ligands, which are released as a bolus by activated platelets. PDGF has a half-life of ∼10 h in the tissue, so it seems unlikely that this initial burst of secreted PDGF is sufficient for stimulation of fibroblast invasion; however, it probably serves to prime the fibroblasts, at least in part by modulating their expression of integrins.3 Thereafter, activated macrophages and other cells provide a more sustained source of PDGF.4 Along with other factors, PDGF promotes fibroblast proliferation, but it also potently stimulates directed fibroblast migration (chemotaxis)5 as a consequence of PDGF gradients that form in the tissue. PDGF gradient sensing and spatially biased control of fibroblast motility processes are achieved through certain receptor-mediated signal transduction pathways, most notably through phosphoinositide 3-kinase (PI3K) activation, which leads to the production of specific lipid second messengers in the plasma membrane.6,7
The PDGF gradient sensing mechanism is distinct from other, well-characterized chemotactic systems, in that it does not seem to involve the rapid adaptation or amplification mechanisms that allow neutrophils and other cells to sense and respond to shallow chemoattractant gradients.7–9 Indeed, we previously showed that relatively steep gradients, spanning a certain range of PDGF concentrations, are needed to elicit robust, spatially polarized PI3K signaling.10 This finding was initially worrisome, because the mechanism could not readily explain how directed migration could be supported over large distances during wound invasion. In response, we embedded the details of PDGF receptor and intracellular signaling dynamics in a deterministic model that mathematically relates the rate of wound invasion to relevant molecular and cellular properties.11 Wound healing has been a fairly rich area for mathematical modeling, spurred by the need to explain and analyze its prescribed spatiotemporal dynamics, and a number of phenomenological models have underscored the importance of chemotaxis in this and related contexts.12–21 The distinct feature of our model is that it partially but faithfully integrated molecular-level processes. The key biological insight derived from it is that fibroblasts migrate as a population and, collectively, they are capable of eroding the PDGF concentration profile as they do so. Thus, the system of equations naturally gives rise to a traveling wave solution, provided that the PDGF concentration is sufficient for fibroblast proliferation; after a transient period of a few days, the fibroblast density profile propagates at a constant velocity and maintains a nearly constant shape, with the leading cohort of cells located in the PDGF gradient such that they experience near-optimal conditions for chemotaxis over arbitrarily long distances.11
Here, we extend the modeling framework to account for the stochastic behavior of individual cells. To do so, we implemented a hybrid continuum/discrete modeling strategy and used it to specifically address whether or not cell heterogeneity within the fibroblast population can affect the rate of wound invasion. Such hybrid models have been successfully applied to different aspects of cell dynamics in culture and in tissues.21–27 We show that enhanced invasion is achieved through a selection process by which those cells that are better fit for the task lead the infiltration of the wound. Fibroblasts with a higher expression level of PDGF receptors or of PI3K are better invaders but for different reasons; whereas high PI3K expressers (or, conversely, low 3′ PI phosphatase expressers) are more chemotactically responsive, high receptor expressers are not necessarily so but nevertheless enhance invasion because of their greater capacity for degrading PDGF. We further show that, because the cells progress through the mitotic cycle several times during the invasion process, enhanced invasion critically depends on how cell properties are inherited when a cell divides; by the same token, multiple rounds of proliferation can yield significant changes in cell-specific parameters over time, even when the range of parameter values sampled at each mitotic event is modest.
Results
Relevant details of the models and associated equations are provided under Methods. The deterministic model (DM) and its underlying assumptions are described in detail in ref. 11, and hence only the essential features and variations thereof are emphasized here. Our new hybrid model (HM) treats the PDGF concentration field as a continuum, while fibroblasts are modeled as discrete particles that behave stochastically. Both models essentially have only two macroscopic variables: the PDGF concentration, u, and the fibroblast density, v, both expressed in scaled, dimensionless terms. Aspects of intracellular signaling are related to u and its spatial gradient through algebraic expressions, invoking the quasi-steady state approximation (see Methods and ref. 11). In those expressions, we also consider here the dimensionless expression levels of PDGF receptors, PI3K, and 3′ PI phosphatase activity (rmax,i, emax,i and pmax,i, respectively) as individual cell properties, scaled relative to the base values in the DM (rmax = emax = pmax = 1). After establishing some preliminary mechanistic insights related to their effects on fibroblast chemotaxis and proliferation in the wound space, we show how variability in those properties affects the overall rate of wound invasion in the model.
Influence of individual fibroblast properties on chemotactic sensitivity.
From the standpoint of chemotaxis, the key quantity is Δm, which characterizes the intracellular gradient of PI3K signaling and determines the chemotactic velocity (Eq. 6B); this quantity depends on individual cell parameters according to Eqs. 1–4 (Fig. 1). To simplify the analysis, we assume a certain value of the relative PDGF gradient steepness, δ, and express chemotactic signaling efficiency as Δm/δ (Eq. 4).
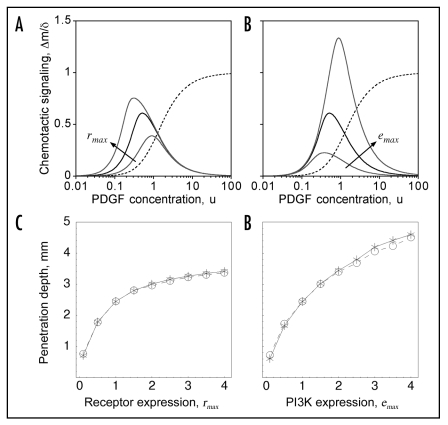
Figure 1.
Chemotactic signaling efficiency depends on PDGF concentration and individual cell properties. (A and B), the intracellular PI3K signaling gradient, Δm, is normalized by the PDGF gradient steepness δ (Eq. 4) as a measure of chemotactic signaling efficiency. The solid black curve shows Δm/δ for the base scenario, with rmax = emax = pmax = 1, and the dashed curve shows r/rmax as a function of u (Eq. 1) on the same scale. (A) the values of rmax are 1/3, 1 and 3, with emax = pmax = 1. (B) the values of emax are 1/3, 1 and 3, with rmax = pmax = 1. (C and D) effect of varying rmax and emax, homogeneously throughout the cell population, on cell invasiveness. As in ref. 11, the maximum depth into the wound where the dimensionless cell density v = 0.5 at t = 10 days is used as a metric of invasion rate. The results show good agreement between the current hybrid model (HM; circles) and the previously published deterministic model (DM; stars).
If receptor expression is increased above its base value (rmax = 1), chemotactic signaling efficiency is enhanced at low PDGF concentrations, where the number of activated receptors is limiting for formation of receptor/PI3K complexes; however, for higher PDGF concentrations (u > 1), signaling efficiency by this measure is not enhanced, because overall PI3K signaling is saturated (Fig. 1A). This is significant because the range of PDGF concentrations seen by the leading cohort of invading fibroblasts lies in this higher concentration regime. Conversely, increasing PI3K expression (emax) enhances chemotactic signaling efficiency at high but not low PDGF concentrations (Fig. 1B). Variation in the level of 3′ PI phosphatases (pmax), which oppose the action of PI3K, simply modulates the entire dose response curve by a constant factor (Eq. 4).
Based on this analysis and that of the previously published DM, it is readily understood how varying rmax or emax (uniformly throughout the population) affects wound invasion; as in ref. 11, we use the depth of penetration into the wound at t = 10 days as a measure of population invasiveness, and we demonstrate that predictions produced by the DM and HM (with homogeneous cell properties) are quantitatively consistent (Fig. 1C and D). Invasiveness is a monotonically increasing, saturable function of either receptor or PI3K expression, with the latter being more potent. Increasing rmax does not enhance chemotactic efficiency per se but nonetheless enhances chemotaxis by promoting faster erosion of the PDGF gradient profile; increasing emax, on the other hand, boosts chemotactic efficiency. These effects and their saturable nature were explored previously in the DM by varying the rate constant of receptor-mediated PDGF clearance (kv) and the chemotactic velocity (S*tax), respectively.11
Conditions are established in the wound that favor fibroblasts with higher PDGF receptor expression levels.
As explained in ref. 11, a PDGF gradient is established in the wound clot, bracketed by two characteristic concentrations: in the absence of fibroblasts, PDGF achieves its maximum concentration, umax, determined by the ratio of synthesis and basal degradation rates; in regions of the wound where a fibroblast population has been established, and the net cell migration flux is minimal, the PDGF concentration is pegged at a much lower value, u†, because the fibroblasts degrade PDGF in proportion to their density, v, and to the average number of occupied PDGF receptors per cell, r.
The value of u† and the corresponding cell density v† are determined from a classical phase-plane analysis; a similar analysis is performed here, except with varying rmax for hypothetical, homogeneous populations (Fig. 2). The results show that, because the net fibroblast proliferation rate depends explicitly on r (Eq. 6C), as does the primary PDGF degradation mechanism, the stationary value of r is insensitive to the value of rmax (Fig. 2A). That is, cells with higher rmax will reduce the PDGF concentration u† so as to establish approximately the same value of r† (≈0.11 for the base-case parameters). For rmax = 0.3, 1 and 3, the corresponding values of u† are 1.06, 0.42 and 0.22, respectively (Fig. 2B).
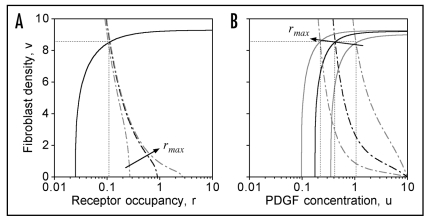
Figure 2.
Under stationary conditions, the cell population tends to maintain a certain value of the mean receptor occupancy r, regardless of the mean rmax. Plotted are the nullclines for zero net cell production (Rp = 0, Eq. 6C; solid curves) and for zero net PDGF production (ks − kuu − kvvr = 0; dot-dashed curves). Their intersection point (dotted lines) determines the steady state in the absence of spatial gradients. The black curves are for the base case, rmax = 1; other rmax values (gray curves) are 0.3 and 3. (A) plotted in (r,v) phase space. (B) plotted in (u,v) phase space.
From this analysis, it may be concluded that the presence of fibroblasts with higher rmax in the clot lowers u† and thus applies selective pressure on cells in the population with lower rmax, for two distinct reasons. For one, cells with low rmax do not sense gradients as well at lower PDGF concentrations (Fig. 1A), and so there is less of an impetus for such cells to migrate from the dermis into the clot. More importantly, in a mixed population of cells, cells with lower rmax have a distinct growth disadvantage, because the rates of cell proliferation and death for the population overall tend to be balanced; thus, cells with lower rmax that make it into the clot find themselves in an inhospitable environment for growth.
Effects of heterogeneous receptor and PI3K expression and the inheritance of those properties on wound invasion rate.
The hybrid, population-based HM allows for heterogeneity among the fibroblasts, which are modeled as discrete entities that move, proliferate and die according to probabilities consistent with the model equations (see Methods). Here and in the following sections, we use the model to analyze the impact of heterogeneity in individual cell properties, starting with the effect of varying rmax and emax, using again the depth of penetration into the wound at t = 10 days as a measure of population invasiveness (Fig. 3). It is expected that fibroblasts with higher emax are more chemotactically responsive at the leading cell front (Fig. 1B), whereas cells with higher rmax serve to advance the PDGF concentration gradient more efficiently and are favored because of their growth advantage (Fig. 2). Cells are initially seeded uniformly throughout the dermis, with one or more of their individual properties randomly sampled according to either a normal or lognormal distribution, with mean value(s) µ = 1 and various standard deviation values σ (Eqs. 12 and 13; Fig. 3A); σ = 0 corresponds to the base-case model with no cell-to-cell variability. The rationale for considering the lognormal distribution is that it is commonly observed in flow cytometric data, at least for cell surface proteins.28 Upon cell division, the properties of the two daughter cells are assigned properties according to one of three different sampling models, I, II and III (Fig. 3B). In sampling model I, each varied property is resampled without regard for the properties of the progenitor cell, that is, with µ = 1 and the same random distribution as seeded initially. Diametrically, in sampling model III, each varied property is assigned the same value as the progenitor cell; only the initial distribution is random. Thus, models I and III bookend a spectrum of cases that might be considered regarding the ‘memory’ effect associated with the inheritance of cell properties. Finally, in sampling model II, random values for the daughter cells are drawn randomly as in model I, but the value of µ is taken as the value of the progenitor cell. In the case of the normal distribution, we consider the value of σ to be a relative value, such that the standard deviation of the distribution is proportional to the mean value µ (Eq. 12); this is consistent with the biologically plausible (albeit empirical) “rich-travel-more” model of gene expression changes.29 The lognormal distribution naturally has this property, in the limit of small σ (Eq. 13).
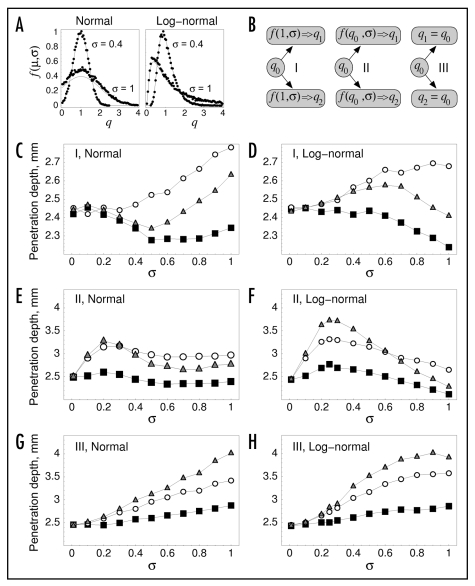
Figure 3.
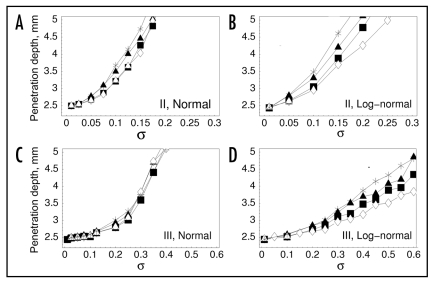
Variability in receptor and PI3K expression levels affects wound invasion rate. (A) each varied property, denoted here as q, was sampled according to a normal or lognormal distribution, based on a probability density function f(µ,σ), where µ and σ are the specified mean value and relative standard deviation, respectively (Methods). The plots show sampled averages (symbols), compared with the exact analytical expressions (solid curves), with µ = 1. The oversampling of values for the normal distribution, σ = 1 case, most noticeably close to the mean, is attributed to rejection of negative values. (B) Illustration of three distinct model variations that govern the sampling of varied cell properties when a cell divides. A varied parameter takes on values of q1 and q2 for the daughter cells, which are related in different ways to that of the progenitor cell, q0. (C–H), penetration depth, defined as in Figure 1C and D, is used as a metric of invasion rate. In each plot, either PDGF receptor expression (rmax, black squares) or PI3K expression (emax, open circles) or both parameters (gray triangles) was/were varied according to the sampling models illustrated in (B), with the standard deviation σ on the x-axis representing the degree of variability among the population. Values are averaged over 50 independent model runs, and 95% confidence intervals are within 2% of the mean. (C) model I, normal distribution. (D) model I, lognormal distribution. (E) model II, normal distribution. (F) model II, lognormal distribution. (G) model III, normal distribution. (H) model III, lognormal distribution.
Considering the variation of rmax or emax or both, we find only modest changes in fibroblast invasiveness for sampling model I (Fig. 3C and D). A modest increase (<15%) is seen when emax alone is varied, whereas varying rmax tends to yield a slight negative effect; varying both properties gives an intermediate result. This sampling model has no memory effect, and resampling upon proliferation occurs rapidly enough to limit the advantages enjoyed by a cell that happens to acquire a higher value of rmax and/or emax; indeed, in the case of rmax, those advantages tend to be outweighed by the disadvantages associated with acquisition of a lower rmax value. By comparison, sampling models II and III tend to produce gains in invasiveness, of 50% or more, when either rmax or emax is varied, and when both parameters are varied, the gains are roughly additive (Fig. 3E–H). With model II, such gains are achieved with σ values as low as ∼0.2 (Fig. 3E and F), whereas higher variability is required for model III (Fig. 3G and H). Apparently, sampling model II allows the acquisition of favorable cell properties over several cell divisions, whereas sampling model III requires the generation of exceptionally fit individuals in the initial cell seeding. These ideas are explored in further detail in the following section.
Enhanced invasiveness is accompanied by enrichment of cells expressing higher receptor and PI3K levels in the wound.
Variability in receptor and PI3K expression levels in the fibroblast population results in selective pressures and advantages that foster subpopulations with higher expression levels in the wound space (Fig. 4). For simplicity, we only consider lognormally distributed properties and the more interesting sampling models II and III, with chosen values of σ that yield significant gains in wound invasion rate (σ = 0.3 for model II and σ = 1 for model III; Fig. 3F and H).
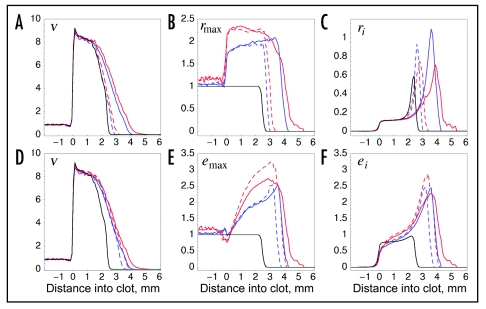
Figure 4.
Distribution of receptor and PI3K expression levels and activities in the wound space. Mean values of the cell density v (A and D) and cell-specific parameters rmax (B) and emax (E) and variables ri (C) and ei (F) are plotted as a function of location in the wound, relative to the dermis-clot interface at x = 0 (t = 10 days, as in Figs. 1 and 3). In the clot, regions containing no cells were assigned values of zero, and the results are averaged over 50 simulations. The black curve is the base case (σ = 0), blue curves were obtained using sampling model II with σ = 0.3 (lognormal distribution), and red curves were obtained using sampling model III with σ = 1 (lognormal distribution). Solid curves are for the case where both rmax and emax were sampled; dashed curves are for variation of a single parameter, either rmax (A–C) or emax (D–F).
When receptor expression is varied, the average value of rmax is high throughout the clot, with values ∼2 (Fig. 4B), reflecting the selective process by which cells with higher rmax are more likely to survive when the overall density approaches the contact-inhibited limit. Subtle differences between the observed rmax profiles reflect the nature of the property sampling; in model II, but not model III, higher average values tend to accrue as cells advance further into the wound. Although the precise values and spatial trends of rmax values differ between these two cases, they result in the same receptor occupancy value r in the region of the clot adjacent to the dermis (Fig. 4C), in accord with the analysis offered in Figure 2. Variation of emax has a greater impact on wound invasion rate than does varying rmax, and when emax is varied, its mean value shows an increasing spatial trend consistent with enhanced chemotactic migration of the higher expressers (Fig. 4E). In the region of the clot adjacent to the dermis, the range of average PI3K activation values, ei, is much less than that of emax across the different model cases (Fig. 4E and F), because PI3K recruitment becomes limited by receptor occupancy there. In a particular cell, ei is less than both αri and emax (Eq. 2B), and coincidentally the value of αri at the dermis-clot interface is constrained to be ≈1, the base value of emax (working back to model parameters, this stems from the fact that the value of α is roughly equal to the grouping kνν*/ks). At the advancing front of the fibroblast population, where receptor occupancy is higher, higher mean values of ei are achieved in tandem with the higher emax (Fig. 4F).
It should be noted that the enrichment of higher rmax and emax values in the case of model II is not an artifact associated with sampling bias. In fact, for a constant proliferation rate, this sampling produces a decreasing power-law distribution of gene expression that favors low, not high, expressers (ref. 28 and results not shown). This explains why, for sampling model II, the invasion rate shows a biphasic dependence on the relative sampling width, σ (Fig. 3E and F). In the case of the 3′ PI phosphatase, where lower expression favors fibroblast migration, sampling model II does not present the same trade-off.
Heterogeneity in 3′ PI phosphatase expression has the greatest impact on wound invasion.
Whereas the activity of PI3K tends to be limited by either receptor occupancy or PI3K expression in different regions of the wound, as illustrated in the results presented in Figures 2 and 4, the expression of 3′ PI phosphatase activity in the cell (pmax) uniformly modulates signaling through the pathway, directly affecting both random and directed migration throughout the wound. Accordingly, with sampling models II and III, selection of lower pmax values in the heterogeneous fibroblast population produces gains in invasion rate that generally exceed those seen when the other cell properties were varied (Figs. 5 and 6). In the case of sampling model II, the gains are dramatic even for σ ∼ 0.1 (Fig. 5A and B). With sampling model III, still higher values of σ are needed to achieve similar invasion rates, consistent with the results in Figure 3 (Fig. 5C and D).
Figure 5.
Modest variability in 3′ PI phosphatase expression enhances wound invasion rate. In each plot, either 3′ PI phosphatase expression pmax was varied alone (open diamonds) or together with rmax (filled squares), emax (filled triangles), or both rmax and emax (stars) according to sampling models illustrated in Figure 3B. Penetration depth is defined as in Figure 3. Values are averaged over 50 independent model runs, and 95% confidence intervals are within 5% of the mean, except where the penetration depth approaches 5 mm. (A) model II, normal distribution. (B) model II, lognormal distribution. (C) model III, normal distribution. (D) model III, lognormal distribution.
Figure 6.
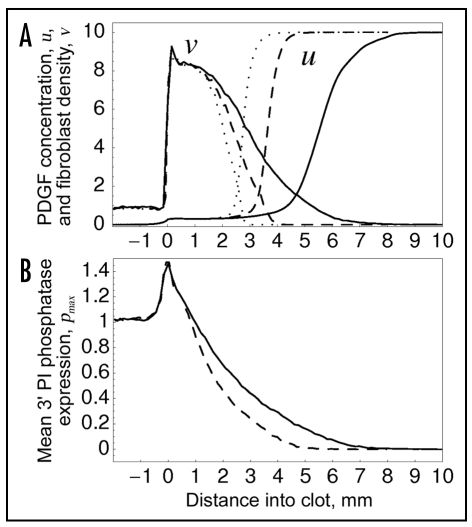
Variability in PI3K and 3′ PI phosphatase expression results in broadening of the fibroblast density and PDGF concentration profiles. Sampling model II, with lognormal distribution and σ = 0.25, was used. (A) spatial profiles of PDGF concentration and fibroblast density. Individual cell parameters were varied as follows: rmax only (dotted curves), rmax and emax (dashed curves), or rmax, emax and pmax (solid curves). (B) spatial profile of mean pmax value, with variation of pmax only (dashed curve) or all three of rmax, emax and pmax (solid curve).
Considering the plausible case of sampling model II with lognormal distribution and σ = 0.25, variation of rmax only, rmax and emax, and all three of rmax, emax and pmax shows a progressive broadening of the fibroblast density and PDGF concentration gradients in the clot (Fig. 6A), which affects the magnitude of chemotaxis. The broadening is attributed to a gradient in average cell properties, whereby the mean emax value steadily increases (Fig. 4C) and the mean pmax value steadily decreases (Fig. 6B) as the fibroblasts penetrate the wound. Thus, even as PI3K signaling (related to the ratio of emax/pmax) is enhanced by >10-fold at the leading fibroblast front, the penetration depth increases by only ∼2.5-fold.
Discussion
Cell adhesion and migration behaviors are typically characterized at the single cell level, which is challenging because of inherent cell-to-cell heterogeneity. In some cases, natural variability in a cell population can be exploited. As a case in point, in a seminal study relating adhesion strength to migration speed,30 Chinese hamster ovary cell populations expressing different average levels of α5 integrin were established by fluorescence-activated sorting; subpopulations of this sort have to be handled within a limited number of passages, because they eventually revert to the original, broad range of expression levels. Even within a well-characterized, clonal cell population under carefully controlled culture conditions, a distribution of expression levels emerges over time that affects the responsiveness of individual cells to external signals.28 This aspect of cell biology is not routinely considered in mathematical models but is expected to be important in situations where cell migration gives rise to spatially diverse cell populations,25 such as embryonic development, tumor progression, immune surveillance and, as considered here, wound healing. In our hybrid model, which treats cells as discrete entities, heterogeneity in receptor and signaling protein expression levels can significantly enhance wound invasion, and under certain conditions their effects are approximately additive. Whereas receptor expression affects the rate of PDGF erosion and has a relatively subtle effect on invasion rate, expression levels of PI3K and 3′ PI phosphatases directly impact chemotactic efficiency.
In our stochastic modeling framework, only intrinsic noise is considered, in the sense that the sampling of cell-specific signal transduction properties and certain cell decision-making processes are random. Extrinsic noise was not considered, which is notable because other work has highlighted the potential effects of ligand-receptor binding fluctuations on chemotaxis.31,32 It has been estimated that PDGF receptor activation events last for ∼4 minutes on average,33 which is significantly less than the persistence time of fibroblast migration, both on planar surfaces and in collagen and fibrin gels (∼30–60 minutes).34,35 The lateral diffusion of the lipid second messenger, with a spatial range of ∼10 µm in fibroblasts,36 would also serve to smooth out fluctuations at the level of receptor-proximal signaling, as argued previously.37 These observations suggest that, in fibroblasts, the stochastic nature of cell movement is dictated by motility processes intrinsic to the cell, rather than by fluctuations at the level of external ligand-receptor binding. The roles of membrane protrusion and retraction and cell polarization in this stochastic behavior, particularly in the context of chemotaxis, warrant further study.
A natural outcome in the hybrid model is the enrichment of cells with higher receptor or PI3K expression or lower 3′ PI phosphatase expression. Two mechanisms for achieving this were identified. In the case of variable emax or pmax, the process is simply a spatial segregation of faster and slower chemotaxing cells, whereas in the case of rmax, the process is one of selection/growth competition. The magnitudes of the effects studied here depend on the way in which individual properties are sampled or inherited upon cell division, and for this reason it would be worthwhile to explore this aspect in more detail, as in other population-based modeling efforts.38,39 Perhaps more importantly, we are interested in how external signals might influence this process. PDGF itself stimulates changes in gene expression in fibroblasts, notably the repertoire of adhesion receptors,3 and it also leads to upregulation of PDGF receptor synthesis.40 Obviously, many other locally produced factors could affect protein expression levels and/or the selection of a subset of cells with prescribed properties. Such a scenario is not unlike that which has been characterized for another invasion process—tumor metastasis—wherein the subset of cancer cells that escape the tumor differ dramatically at the level of gene expression, specifically with regard to genes that confer chemotactic responsiveness.41
Our study also highlights the potential importance of 3′ PI phosphatases in modulating random migration and chemotaxis. Although there are several such enzymes in mammalian cells, only phosphatase and tensin homolog deleted on chromosome 10 (PTEN) has been studied in detail, owing to its established role as a tumor suppressor.42–44 Consistent with its regulation of PI 3-kinase signaling, it has been demonstrated that PTEN inhibits migration of mammalian cells.45,46 We previously reported that 3′ PI lipid turnover in fibroblasts is not noticeably affected by PDGF stimulation, although there is an appreciable degree of cell-to-cell variability in the specific turnover rate,47 but further analysis suggested that the turnover rate is reduced locally in protruding regions of fibroblasts, which exhibit higher 3′ PI levels.36 Other reports have established that PTEN can be regulated or activated by reactive oxygen species,48 phosphoinositides,49 and small GTPases,50 and hence it will be important to further investigate such mechanisms in the context of fibroblast chemotaxis and wound invasion.
Finally, it is acknowledged that the relationship between PI3K signaling (and, potentially, signaling through other pathways) and cytoskeletal dynamics that govern fibroblast motility needs to be characterized in greater, more quantitative detail. Even at the level of coarse-grain modeling, it is important to know whether or not components downstream of 3′ PI lipids or perhaps energetic limitations ultimately constrain the magnitude of the chemotactic velocity if PI3K signaling is overactive. Such a constraint could serve to make the cell density profile more uniform, in contrast with the broadening of the profile predicted by the hybrid model when higher PI3K and lower 3′ PI phosphatase expressers are allowed to outpace the rest of the fibroblast population.
Methods
Deterministic model (DM).
In the DM, the PDGF concentration field is, at the tissue level, macroscopically local, whereas it is microscopically averaged at the level of a single cell (in ref. 11, microscopically averaged quantities are denoted, up to a certain point, by elbow brackets, 〈 〉). We define the degree of PDGF receptor activation, microscopically averaged, as a dimensionless variable, r. As justified previously, r and other cell-associated variables are assumed to be quasi-steady; the cellular binding/trafficking dynamics adjust the value of r relatively rapidly as the scaled PDGF concentration, u, evolves in time.
| (1) |
In the DM, rmax is set uniformly to 1, whereas we will subsequently allow rmax to vary from cell to cell, but with a population average of 1 initially. The functional form of Eq. 1, which sets the value of u = 1 as the scaled PDGF concentration that yields r = rmax/3, is an approximate analog of a more detailed description of PDGF receptor binding, dimerization and trafficking,10,11 which was based on a kinetic analysis of PDGF receptor phosphorylation.33 It should therefore be mentioned that, depending on the dimerization mechanism assumed, varying the value of rmax affects the value of the PDGF concentration that gives r = rmax/3, albeit weakly; alternatives to Eq. 1 corresponding to different plausible mechanisms were in fact explored and found to affect the results only slightly (results not shown).
The microscopically averaged, receptor-mediated recruitment of the PI3K enzyme, defined here as the dimensionless variable e, can in turn be expressed in terms of r and its maximum value emax as follows.
| (2a) |
| (2b) |
In Eq. 2A, e is expressed in implicit form to show its origin as an expression of binding equilibrium between activated receptors and PI3K; it is rearranged in explicit form in Eq. 2B. The model parameters, α = 10 and κ = 0.1, are as defined previously,10,11 and based on those definitions it is understood that emax = 1 in the DM, whereas emax is potentially heterogeneous from cell to cell. The recruited enzyme produces by phosphorylation a lipid second messenger molecule, expressed in microscopically averaged terms as m, given by
| (3) |
The new parameter here is pmax, which represents in scaled terms and for a particular cell the expression levels of phosphatases, such as PTEN, which dephosphorylate the messenger. In the DM, pmax = 1, and the basal level of m is characterized by the parameter m0 = 0.1.
In our model, the chemotactic velocity of a cell is related in a linear fashion to the gradient of PI3K-catalyzed messenger production in that cell (i.e., incorporating microscopically local information), characterized by the variable Δm; following the derivation given previously,
| (4) |
The fractional difference in u across a cell length, ε = 0.03 mm, is defined as δ. In a one-dimensional (1D) model as considered here, with spatial variable x, the PDGF gradient vector ∇u has only one component, du/dx.
In the 1D DM, the macroscopic, dimensionless PDGF concentration, u, is conserved by
| (5) |
In the base version of the model, the effective PDGF diffusivity Du = 0.01 mm2/h, the PDGF synthesis rate constant ks is equal to 0 in the dermis and 1 h−1 in the clot, the basal degradation rate constant ku = 0.1 h−1, and the fibroblast-mediated degradation rate constant kv = 1 h−1. In the absence of cells, the value of u in most of the clot approaches umax = ks/ku = 10. The macroscopic, dimension-less fibroblast density, v, is conserved by
| (6A) |
| (6B) |
| (6C) |
PI3K signaling, as defined in Eqs. 2 and 3, affects the cell migration flux, Jv, according to Eq. 6B [the corresponding Eqs. 8 and 11 of ref. 11 contain sign errors; a correction was published in Biophys J 2007; 92:696]. The migration parameters are the maximum random cell dispersion coefficient D*v = 3 × 10−4 mm2/h and the maximum chemotactic cell speed, S*tax = 0.1 mm/h. The net rate of cell proliferation, Rp, is a saturable function of receptor activation, with a maximum specific growth rate of µm = 0.05 h−1 and a dimensionless saturation constant γ = 0.1. The growth term is subject to a logistic-type function that accounts for contact inhibition as the value of v approaches v* = 10, with exponent n = 3. Rp also includes a cell death term, characterized by rate constant kd = 0.01 h−1 and which defines the resting fibroblast density in the absence of PDGF, v0; v0 is equal to 1 in the dermis and 0 in the clot, thus defining the cell density scaling. Accordingly, v = v0 in each domain initially.
Hybrid model (HM).
In the HM, implemented in the programming language C, the PDGF concentration field is solved numerically from Eq. 5 using the implicit finite difference method,51 wherein the system is discretized with constant spatial interval Δx = 0.01 or 0.015 mm and time step Δt = 0.01 h. The length of the domain is L, with the dermis region defined as 0 < × < l and the clot region defined as l < x < L; L = 15 mm and l = 2 mm were used. The PDGF concentration associated with interval j, indexed according to j = 0, 1, 2, …, J (J = L/Δx − 1), is defined as Uj(t) and assigned to the midpoint of the interval, x = Xj = (j + 0.5)Δx. The time derivative in Equation 5 was approximated by backward finite difference. The diffusion term (Laplacian) was written in a discrete form for u(x, t + Δt), whereas the reaction terms were based on discrete values obtained at time t. Zero flux boundary conditions were applied at x = 0 and x = L, and it was confirmed that u(0,t) ≈ 0 due to PDGF degradation in the dermis. A tridiagonal matrix solver was used to solve the system of equations and find discrete variables Uj(t).
In the HM, the fibroblast-mediated PDGF degradation term (analogous to kvrv in the DM) is modified to account for the discrete nature of the cells as follows. Each cell is assigned an index i, and its position in the domain is denoted x = xi, located in spatial interval j = floor(xi/Δx). In the model, individual cells do not directly interact with one another, and so each interval in 1D can represent a semi-infinite slice through the three-dimensional wound, with all of the cells in that slice stacked on top of each other in 1D. Defining the total number of cells residing in interval j as Nj(t), the associated degradation term is given by
| (7) |
where ri is the value of r associated with cell i, and N0 is a specified number of discrete cells per interval in the HM that corresponds to v = 1 in the DM. Therefore, the dermis is initially populated, in random locations, with a total of (l/Δx)N0 cells (typically, ∼1,000 cells, or ∼5 cells per interval on average, were seeded), whereas the clot does not contain cells initially. To calculate ri, ei and mi according to Eqs. 1–3, the value of u(xi) is found by linear interpolation (between the values of Uj−1 and Uj or Uj and Uj+1 as appropriate). Central differences is applied to obtain the PDGF gradient values, ∇Uj = (Uj+1 − Uj−1)/2Δx, and linear interpolation is used to estimate the value of ∇u (and, by the chain rule, that of ∇mi) at x = xi, which is needed to determine cell migration rates.
The discrete cell dynamics are simulated as follows. Migration occurs via a 1D, biased random walk, wherein each walker i is determined to move with displacement
| (8) |
The instantaneous cell speed, ci(t), is calculated from
| (9) |
where the random variable z is drawn uniformly from (0,1). According to Eq. 6C, cells also split into two (divide) and die with certain probabilities that depend on the local cell density. To evaluate those probabilities, we used a coarser spatial discretization equal to 10Δx, with intervals indexed according to k = 0, 1, 2, …, K (K = L/10Δx − 1); denoting the number of cells residing in interval k as Nk(t), the probabilities of cell division and death, respectively, during the current time interval are calculated according to
| (10) |
| (11) |
Standard tests of numerical accuracy were performed. Modest variation of Δx and Δt from their chosen values did not significantly change the model output, and a further test of model accuracy was achieved by comparing the HM, with constant rmax,i, emax,i and pmax,i, to the DM (Fig. 1C and D and results not shown).
Individual cell property sampling.
Two different probability density distributions were employed for individual cell properties: normal and lognormal. Both are consistent with the empirically based model that changes in gene expression tend to be proportional to the starting value.29 For the normal distribution, the value of a varied parameter value, referred to here as q, is determined from
| (12) |
where µ is the mean value, σ is the relative standard deviation (s.d./mean), and Gauss(0,1) is a random number generator that draws from a normal distribution with mean 0 and standard deviation 1.51 In the event that Eq. 12 produced a negative value, the sampling was performed again. For the lognormal distribution,
| (13) |
where ln µ here is the mean value of ln q and σ is its standard deviation (a value one s.d. from the mean corresponds to a 2.7-fold change from µ). Eq. 13 does not generate negative values. For both the normal and lognormal distribution, an upper limit of q = 4 was imposed; this had the effect of making the mean value of q closer to µ in the case of the lognormal distribution with larger values of σ (in general, ln〈q〉 ≠ 〈lnq〉 ).
Acknowledgements
This work was supported by grant R21-GM074711 from the National Institutes of Health.
Abbreviations
- PDGF
platelet-derived growth factor
- PI3K
phosphoinositide 3-kinase
- DM
deterministic model
- HM
hybrid model
Footnotes
Previously published online as a Cell Adhesion & Migration E-publication: http://www.landesbioscience.com/journals/celladhesion/article/6511
References
- 1.Singer AJ, Clark RAF. Mechanisms of disease: cutaneous wound healing. N Engl J Med. 1999;341:738–746. doi: 10.1056/NEJM199909023411006. [DOI] [PubMed] [Google Scholar]
- 2.Martin P. Wound healing- aiming for perfect skin regeneration. Science. 1997;276:75–81. doi: 10.1126/science.276.5309.75. [DOI] [PubMed] [Google Scholar]
- 3.Xu JH, Clark RAF. Extracellular matrix alters PDGF regulation of fibroblast integrins. J Cell Biol. 1996;132:239–249. doi: 10.1083/jcb.132.1.239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Riches DWH. Macrophage involvement in wound repair, remodeling and fibrosis. In: Clark RAF, editor. The Molecular and Cellular Biology of Wound Repair. 2nd Ed. New York: Plenum Press; 1996. pp. 95–141. [Google Scholar]
- 5.Deuel TF, Kawahara RS, Mustoe TA, Pierce GF. Growth factors and wound healing: platelet-derived growth factor as a model cytokine. Annu Rev Med. 1991;42:567–584. doi: 10.1146/annurev.me.42.020191.003031. [DOI] [PubMed] [Google Scholar]
- 6.Anand-Apte B, Zetter B. Signaling mechanisms in growth factor-stimulated cell motility. Stem Cells. 1997;15:259–267. doi: 10.1002/stem.150259. [DOI] [PubMed] [Google Scholar]
- 7.Schneider IC, Haugh JM. Mechanisms of gradient sensing and chemotaxis: conserved pathways, diverse regulation. Cell Cycle. 2006;5:1130–1134. doi: 10.4161/cc.5.11.2770. [DOI] [PubMed] [Google Scholar]
- 8.Devreotes PN, Zigmond SH. Chemotaxis in eukaryotic cells: a focus on leukocytes and Dictyostelium. Annu Rev Cell Biol. 1988;4:649–686. doi: 10.1146/annurev.cb.04.110188.003245. [DOI] [PubMed] [Google Scholar]
- 9.Van Haastert PJM, Devreotes PN. Chemotaxis: signalling the way forward. Nat Rev Mol Cell Biol. 2004;5:626–634. doi: 10.1038/nrm1435. [DOI] [PubMed] [Google Scholar]
- 10.Schneider IC, Haugh JM. Quantitative elucidation of a distinct spatial gradient-sensing mechanism in fibroblasts. J Cell Biol. 2005;171:883–892. doi: 10.1083/jcb.200509028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haugh JM. Deterministic model of dermal wound invasion incorporating receptor-mediated signal transduction and spatial gradient sensing. Biophys J. 2006;90:2297–2308. doi: 10.1529/biophysj.105.077610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Olsen L, Sherratt JA, Maini PK. A mechanochemical model for adult dermal wound contraction and the permanance of the contracted tissue displacement profile. J Theor Biol. 1995;177:113–128. doi: 10.1006/jtbi.1995.0230. [DOI] [PubMed] [Google Scholar]
- 13.Perumpanani AJ, Simmons DL, Gearing AJH, Miller KM, Ward G, Norbury J, Schneemann M, Sherratt JA. Extracellular matrix-mediated chemotaxis can impede cell migration. Proc R Soc Lond B. 1998;265:2347–2352. [Google Scholar]
- 14.Dallon JC, Sherratt JA, Maini PK. Mathematical modelling of extracellular matrix dynamics using discrete cells: fiber orientation and tissue regeneration. J Theor Biol. 1999;199:449–471. doi: 10.1006/jtbi.1999.0971. [DOI] [PubMed] [Google Scholar]
- 15.Wagle MA, Tranquillo RT. A self-consistent cell flux expression for simultaneous chemotaxis and contact guidance in tissues. J Math Biol. 2000;41:315–330. doi: 10.1007/s002850000040. [DOI] [PubMed] [Google Scholar]
- 16.Wearing HJ, Sherratt JA. Keratinocyte growth factor signalling: a mathematical model of dermal-epidermal interaction in epidermal wound healing. Math Biosci. 2000;165:41–62. doi: 10.1016/s0025-5564(00)00008-0. [DOI] [PubMed] [Google Scholar]
- 17.Dallon JC, Sherratt JA, Maini PK. Modeling the effects of transforming growth factor-β on extracellular matrix alignment in dermal wound repair. Wound Repair and Regeneration. 2001;9:278–286. doi: 10.1046/j.1524-475x.2001.00278.x. [DOI] [PubMed] [Google Scholar]
- 18.Bailón-Plaza A, van der Meulen MCH. A mathematical framework to study the effects of growth factor influences on fracture healing. J Theor Biol. 2001;212:191–209. doi: 10.1006/jtbi.2001.2372. [DOI] [PubMed] [Google Scholar]
- 19.Castro M, Molina-Paris C, Deisboeck TS. Tumor growth instability and the onset of invasion. Phys Rev E. 2005;72:041907. doi: 10.1103/PhysRevE.72.041907. [DOI] [PubMed] [Google Scholar]
- 20.Jabbarzadeh E, Abrams CF. Chemotaxis and random motility in unsteady chemoattractant fields: a computational study. J Theor Biol. 2005;235:221–232. doi: 10.1016/j.jtbi.2005.01.005. [DOI] [PubMed] [Google Scholar]
- 21.Jabbarzadeh E, Abrams CF. Simulations of chemotaxis and random motility in 2D random porous domains. Bull Math Biol. 2007;69:747–764. doi: 10.1007/s11538-006-9153-1. [DOI] [PubMed] [Google Scholar]
- 22.Dallon JC. Numerical aspects of discrete and continuum hybrid models in cell biology. Appl Numerical Math. 2000;32:137–159. [Google Scholar]
- 23.Muratov CB, Shvartsman SY. Signal propagation and failure in discrete autocrine relays. Phys Rev Lett. 2004;93:118101. doi: 10.1103/PhysRevLett.93.118101. [DOI] [PubMed] [Google Scholar]
- 24.Reeves GT, Muratov CB, Schupbach T, Shvartsman SY. Quantitative models of developmental pattern formation. Dev Cell. 2006;11:289–300. doi: 10.1016/j.devcel.2006.08.006. [DOI] [PubMed] [Google Scholar]
- 25.Anderson ARA, Weaver AM, Cummings PT, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127:905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- 26.Cai AQ, Landman KA, Hughes BD. Multi-scale modeling of a wound healing cell migration assay. J Theor Biol. 2007;245:576–594. doi: 10.1016/j.jtbi.2006.10.024. [DOI] [PubMed] [Google Scholar]
- 27.Bindschadler M, McGrath JL. Sheet migration by wounded monolayers as an emergent property of single-cell dynamics. J Cell Sci. 2007;120:876–884. doi: 10.1242/jcs.03395. [DOI] [PubMed] [Google Scholar]
- 28.Cantrell DA, Smith KA. The interleukin-2 T-cell system: a new cell growth model. Science. 1984;224:1312–1316. doi: 10.1126/science.6427923. [DOI] [PubMed] [Google Scholar]
- 29.Ueda HR, Hayashi S, Matsuyama S, Yomo T, Hashimoto S, Kay SA, Hogenesch JB, Iino M. Universality and flexibility in gene expression from bacteria to human. Proc Natl Acad Sci USA. 2004;101:3765–3769. doi: 10.1073/pnas.0306244101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Palecek SP, Loftus JC, Ginsberg MH, Lauffenburger DA, Horwitz AF. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 1997;385:537–540. doi: 10.1038/385537a0. [DOI] [PubMed] [Google Scholar]
- 31.Tranquillo RT, Lauffenburger DA, Zigmond SH. A stochastic model for leukocyte random motility and chemotaxis based on receptor binding fluctuations. J Cell Biol. 1988;106:303–309. doi: 10.1083/jcb.106.2.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Arrieumerlou C, Meyer T. A local coupling model and compass parameter for eukaryotic chemotaxis. Dev Cell. 2005;8:215–227. doi: 10.1016/j.devcel.2004.12.007. [DOI] [PubMed] [Google Scholar]
- 33.Park CS, Schneider IC, Haugh JM. Kinetic analysis of platelet-derived growth factor receptor/phosphoinositide 3-kinase/Akt signaling in fibroblasts. J Biol Chem. 2003;278:37064–37072. doi: 10.1074/jbc.M304968200. [DOI] [PubMed] [Google Scholar]
- 34.Ware MF, Wells A, Lauffenburger DA. Epidermal growth factor alters fibroblast migration speed and directional persistence reciprocally and in a matrix-dependent manner. J Cell Sci. 1998;111:2423–2432. doi: 10.1242/jcs.111.16.2423. [DOI] [PubMed] [Google Scholar]
- 35.Shreiber DI, Enever PAJ, Tranquillo RT. Effects of PDGF-BB on rat dermal fibroblast behavior in mechanically stressed and unstressed collagen and fibrin gels. Exp Cell Res. 2001;266:155–166. doi: 10.1006/excr.2001.5208. [DOI] [PubMed] [Google Scholar]
- 36.Schneider IC, Parrish EM, Haugh JM. Spatial analysis of 3′ phosphoinositide signaling in living fibroblasts, III: Influence of cell morphology and morphological polarity. Biophys J. 2005;89:1420–1430. doi: 10.1529/biophysj.105.061218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Haugh JM, Codazzi F, Teruel M, Meyer T. Spatial sensing in fibroblasts mediated by 3′ phosphoinositides. J Cell Biol. 2000;151:1269–1279. doi: 10.1083/jcb.151.6.1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liou JJ, Srienc F. Fredrickson AG, Solutions of population balance models based on a successive generations approach. Chem Eng Sci. 1997;52:1529–1540. [Google Scholar]
- 39.Mantzaris NV. Stochastic and deterministic simulations of heterogeneous cell population dynamics. J Theor Biol. 2006;241:690–706. doi: 10.1016/j.jtbi.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 40.Eriksson A, Nistér M, Leveen P, Westermark B, Heldin CH, Claesson-Welsh L. Induction of platelet-derived growth factor α- and β-receptor mRNA and protein by platelet-derived growth factor BB. J Biol Chem. 1991;266:21138–21144. [PubMed] [Google Scholar]
- 41.Condeelis J, Singer RH, Segall JE. The great escape: when cancer cells hijack the genes for chemotaxis and motility. Annu Rev Cell Dev Biol. 2005;21:695–718. doi: 10.1146/annurev.cellbio.21.122303.120306. [DOI] [PubMed] [Google Scholar]
- 42.Maehama T, Dixon JE. PTEN: a tumour suppressor that functions as a phospholipid phosphatase. Trends Cell Biol. 1999;9:125–128. doi: 10.1016/s0962-8924(99)01519-6. [DOI] [PubMed] [Google Scholar]
- 43.Cantley LC, Neel BG. New insights into tumor suppression: PTEN suppresses tumor formation by restraining the phosphoinositide 3-kinase/AKT pathway. Proc Natl Acad Sci USA. 1999;96:4240–4245. doi: 10.1073/pnas.96.8.4240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Parsons R. Human cancer, PTEN and the PI-3 kinase pathway. Semin Cell Dev Biol. 2004;15:171–176. doi: 10.1016/j.semcdb.2003.12.021. [DOI] [PubMed] [Google Scholar]
- 45.Liliental J, Moon SY, Lesche R, Mamillapalli R, Li DM, Zheng Y, Sun H, Wu H. Genetic deletion of the Pten tumor suppressor gene promotes cell motility by activation of Rac1 and Cdc42 GTPases. Curr Biol. 2000;10:401–404. doi: 10.1016/s0960-9822(00)00417-6. [DOI] [PubMed] [Google Scholar]
- 46.Lacalle RA, Gómez-Moutón C, Barber DF, Jiménez-Baranda S, Mira E, Martínez AC, Carrera AC, Mañes S. PTEN regulates motility but not directionality during leukocyte chemotaxis. J Cell Sci. 2004;117:6207–6215. doi: 10.1242/jcs.01545. [DOI] [PubMed] [Google Scholar]
- 47.Schneider IC, Haugh JM. Spatial analysis of 3′ phosphoinositide signaling in living fibroblasts: II. Parameter estimates for individual cells from experiments. Biophys J. 2004;86:599–608. doi: 10.1016/S0006-3495(04)74138-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Leslie NR, Bennett D, Lindsay YE, Stewart H, Gray A, Downes CP. Redox regulation of PI 3-kinase signalling via inactivation of PTEN. EMBO J. 2003;22:5501–5510. doi: 10.1093/emboj/cdg513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Campbell RB, Liu F, Ross AH. Allosteric activation of PTEN phosphatase by phosphatidylinositol 4,5-bisphosphate. J Biol Chem. 2003;278:33617–33620. doi: 10.1074/jbc.C300296200. [DOI] [PubMed] [Google Scholar]
- 50.Li Z, Dong XM, Wang ZL, Liu WZ, Deng N, Ding Y, Tang LY, Hla T, Zeng R, Li L, Wu DQ. Regulation of PTEN by Rho small GTPases. Nat Cell Biol. 2005;7:399–442. doi: 10.1038/ncb1236. [DOI] [PubMed] [Google Scholar]
- 51.Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C. Cambridge: Cambridge University Press; 1992. [Google Scholar]