Abstract
Motivation: Highly redundant metabolic networks and experimental data from cultures likely adapting simultaneously to multiple stresses can complicate the analysis of cellular behaviors. It is proposed that the explicit consideration of these factors is critical to understanding the competitive basis of microbial strategies.
Results: Wide ranging, seemingly unrelated Escherichia coli physiological fluxes can be simply and accurately described as linear combinations of a few ecologically relevant stress adaptations. These strategies were identified by decomposing the central metabolism of E.coli into elementary modes (mathematically defined biochemical pathways) and assessing the resource investment cost–benefit properties for each pathway. The approach capitalizes on the inherent tradeoffs related to investing finite resources like nitrogen into different pathway enzymes when the pathways have varying metabolic efficiencies. The subset of ecologically competitive pathways represented 0.02% of the total permissible pathways. The biological relevance of the assembled strategies was tested against 10 000 randomly constructed pathway subsets. None of the randomly assembled collections were able to describe all of the considered experimental data as accurately as the cost-based subset. The results suggest these metabolic strategies are biologically significant. The current descriptions were compared with linear programming (LP)-based flux descriptions using the Euclidean distance metric. The current study's pathway subset described the experimental fluxes with better accuracy than the LP results without having to test multiple objective functions or constraints and while providing additional ecological insight into microbial behavior. The assembled pathways seem to represent a generalized set of strategies that can describe a wide range of microbial responses and hint at evolutionary processes where a handful of successful metabolic strategies are utilized simultaneously in different combinations to adapt to diverse conditions.
Contact: rossc@biofilms.montana.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Microbial ecology is the study of microbial interactions with other organisms and their environment. Microbes seem to have developed a wide range of mechanisms to compete for potentially scarce resources and to survive under harsh conditions. Microbe biochemical network structure and regulation are thought to be driven by competitive adaptations to selective landscapes (e.g. Lenski and Travisano, 1994; Pfeiffer and Schuster, 2005; Pfeiffer et al., 2001). The current study seeks to deconstruct seemingly complex microbial behaviors into a combination of relatively simple, ecologically relevant stress responses using a systems biology approach known as elementary mode analysis (EMA).
Elementary modes are mathematically defined biochemical pathways that represent the simplest (hence elementary) collections of enzymes that can function at steady state with all fluxes occurring in thermodynamically permitted directions (Schuster et al., 1994, 2000, 2002). EMA is based on a branch of mathematics known as convex analysis and defines the breadth of all non-divisible biochemical fluxes within a network; therefore, all steady-state metabolite flux distributions can be represented as combinations of elementary modes. Elementary modes are usually distinct from the linear algebra concept of a basis vector. Unlike a basis set, an elementary mode set is not typically linearly independent; however, each elementary mode is genetically independent and is biologically relevant (Poolman et al., 2004). Basis vectors are mathematically defined entities which often do not have an obvious biological interpretation. For instance, a basis vector while mathematically sound may define flux directions through an enzyme catalyzed reaction which is not thermodynamically relevant given a cell's metabolite concentrations and the culturing temperature. Discussions on the stoichiometric basis of EMA and other similar methods can be found elsewhere (e.g. Klamt and Stelling, 2003; Schuster et al., 2002). Extreme pathways represent a subset of elementary modes (Klamt and Stelling, 2003).
A common aim of EMA and many other in silico methods is to predict or to explain complex behaviors using simple, tractable concepts. A few attempts have been made to explore how elementary modes can be combined to reconstruct experimental flux distributions (e.g. Carlson and Srienc, 2004b; Poolman et al., 2004; Schwartz and Kanehisa, 2005; Wiback et al., 2003; Wlaschin et al., 2006). None of these approaches considered the ecologically critical concept of resource investment and its role in competitive metabolic behaviors. The current study begins from an ecological perspective that explores the inherent challenge of investing potentially scarce resources into metabolic pathways appropriate for a given environment. For instance, each strategy requires a distinct collection of enzymes with different associated investment costs, like the amount of nutrients required to assemble the proteins. Each collection of enzymes, in turn, has an associated metabolic efficiency related to the transfer of substrate potential energy to cellular processes, such as biomass or ATP generation.
A subset of elementary modes was identified from a much larger listing of metabolic possibilities using nine competitive cost–benefit relationships. This subset was used to analyze 13C fluxome data published by the Sauer research group. The current study demonstrates that a wide distribution of cellular behaviors can be accurately described using a limited number of metabolic strategies. The results and their potential for deciphering microbial behavior were compared with another recently published study by Schuetz et al. (2007), who tested an exhaustive set of 99 different linear programming (LP) objective function/constraint pairs. These LP simulations were used to describe experimentally measured fluxes from different culturing conditions (e.g. batch, carbon-limited and nitrogen-limited chemostat growth). The culturing conditions required different objective function/constraint pairs to best describe the flux distributions. The current methodology illustrates how a single set of ecologically selected elementary flux modes, from a single simulation, can be assembled to reconstruct flux distributions with better accuracy, as defined by the Euclidean distance between prediction and experimental flux, than other current methods while providing additional ecological insight into the potential bases of cellular strategies.
2 METHODS
2.1 Metabolic models and EMA
The present study utilizes two previously described Escherichia coli central metabolism models (Carlson, 2007; Schuetz et al., 2007). The two models were selected to provide continuity with an earlier study of the anabolic requirements of metabolic pathways (Carlson, 2007) and to provide a similar in silico basis for comparing the predictions of the current methodology with alternative modeling approaches (Schuetz et al., 2007). Both models consider growth on minimal media with glucose serving as the sole electron donor and oxygen serving as the sole external electron acceptor. The metabolic models were decomposed into a complete listing of genetically independent strategies using EMA. This technique and the associated algorithms have been described previously (e.g. Schuster et al., 1994, 2000, 2002). FluxAnalyzer version 5.2 was used to identify the elementary modes (Klamt et al., 2003, 2007) and the output was processed using MATLAB (v6.5) and MS Excel.
2.2 Elementary mode cost assessment
The elementary modes were assigned anabolic and catabolic costs to assess their relative ecological fitness in different environments. The theoretical basis of the treatment has been described previously (Carlson, 2007). Briefly, two catabolic costs related to metabolite utilization were considered: one was associated with the electron donor and a second was associated the electron acceptor. They were defined as the Cmoles of glucose (electron donor) consumed per Cmole biomass produced and the moles of O2 (electron acceptor) consumed per Cmole biomass produced. Four anabolic costs were considered and were defined as the amount of anabolic resource (carbon, nitrogen, sulfur or amino acids—which can be correlated to phosphorous) required to assemble the enzymes utilized in the elementary mode. It was assumed that each elementary mode is a distinct entity with its own enzymes and the relative relationship between enzyme flux and enzyme concentration can be approximated using saturation kinetics arguments.
The present approach avoids absolute enzyme concentrations, which can be difficult to measure, and instead considers the relative ratio of enzyme concentrations. At a substrate (electron donor) concentration very low relative to the half-saturation constant (a.k.a. Monod or Michaelis–Menten constant), the pathway kinetics can be approximated by a first-order expression. Under these conditions, the ratio [Ei]/[Ej] between any pair of enzymes (Ei and Ej) utilized was assumed to be one. At the scarcity extreme, where substrate collisions with the cell limit flux through an elementary mode, an enzyme concentration ratio different than one would potentially represent an unproductive investment of anabolic resources. For purposes of this study, these pathway costs were referred to as the first-order anabolic investment costs (Carlson, 2007).
For the other extreme, when substrate concentration is high relative to the half-saturation constant, pathway kinetics can be approximated by a zeroth-order kinetic expression. Under these conditions, the ratio [Ei]/[Ej] is assumed to be proportional to the enzyme flux ratio vi/vj where Ei and Ej are enzymes participating in an elementary mode, while vi and vj are the fluxes through these enzymes, respectively. For purposes of this study, these pathway costs are referred to as the zeroth-order anabolic investment costs.
Metabolic networks are complex systems; this methodology is designed to bracket a solution space of possible relationships between metabolic flux and relative enzyme concentrations.
Consideration of free energy changes and activation energy barriers associated with each enzyme catalyzed reaction is neglected in this analysis. Conventional thought might suggest that some reactions with larger driving forces (large negative ΔG) could have faster rates and would therefore require lower enzyme concentrations than reactions with near equilibrium or small free-energy changes to maintain the same flux (Pfeiffer et al., 2001; Stucki, 1980). Likewise enzyme catalyzed reactions with lower activation energies may require fewer enzymes than those with higher activation energies to maintain the same flux. The incorporation of these concepts and spatial concentration effects like metabolite channeling will be considered elsewhere.
The catabolic costs and the first-order anabolic investment costs were calculated from the EMA output file using MATLAB and previously described techniques (Carlson, 2007). The zeroth-order anabolic investment costs for each mode were calculated by multiplying the absolute value of each flux by the investment costs for the associated enzymes. In matrix form, this operation is:
| (1) |
where Z is the matrix with each row containing the zeroth-order investment requirements for an elementary mode, A is the elementary mode matrix with rows populated by the positive magnitude of reaction fluxes in a given mode and I is the investment matrix with each row comprised of carbon, nitrogen, sulfur and amino acid costs for a specific model reaction. To create a standard basis for comparison, the reported zeroth-order investment requirements were normalized with respect to flux through the biomass synthesis reaction. The anabolic investment matrix I can be found in Carlson (2007), or in the Supplemental Material (Table S1) accompanying this article.
2.3 Minimization envelope analysis
Decomposition of robust networks into elementary modes often results in millions of genetically independent strategies (Carlson, 2007). Efficient data mining techniques are required to separate ecologically relevant solutions from the numerous mere mathematical solutions. The current study assumes that E.coli has evolved under competition for resources. Therefore, the selected solutions involve the economical use of finite anabolic and catabolic resources to produce biomass and cellular energy.
All elementary modes representing cellular growth were data mined for metabolic strategies that minimized pairwise combinations of pathway associated costs. The continuous range of strategies is referred to as a minimization envelope (MinE) (Carlson, 2007; Carlson and Srienc, 2004a; Vijayasankaran et al., 2005). Nine MinEs were considered. For each of the nine cases, the abscissa was the electron donor catabolic cost (Cmoles of glucose consumed per Cmole biomass produced), while the ordinate was varied to consider the electron acceptor catabolic cost (moles O2 consumed per Cmole biomass produced) or one of the eight anabolic investment cost scenarios.
The presented approach is analogous to industrial design processes where competing designs are compared on both investment (anabolic) costs and operating (catabolic) costs. The most competitive design is a function of numerous factors including location-dependent considerations like construction costs, labor costs, raw material, utility costs and local tax laws. Likewise, the most competitive metabolic strategy may change as a function of culturing conditions as well as the availability of electron donor, electron acceptor or anabolic resources like nitrogen or phosphorous.
2.4 Generation of artificial experimental flux distributions
Artificial metabolic flux distributions, which have not been optimized by evolution, were generated using two different strategies. Prior to generation of artificial fluxes, the elementary modes were normalized to a glucose uptake reaction flux of one. The first approach selected a random number of the total possible biomass producing modes (1–197 018) and then assigned a random weighting factor to each mode. The weighted modes were summed to create a flux vector. To replicate experimental error, each of the fluxes in the vector was then randomly and independently perturbed by a value between ±5%. The second approach randomly selected between 1 and 100 elementary modes with carbon yields that were greater than or equal to the smallest carbon yield identified on a MinE (see below). Each mode was then assigned a random weight and summed to create an artificial flux distribution. As with the previous case, each of the fluxes was then randomly and independently perturbed by a value between ±5%.
3 RESULTS
3.1 Identification of ecologically competitive metabolic strategies based on zeroth-order anabolic investment costs
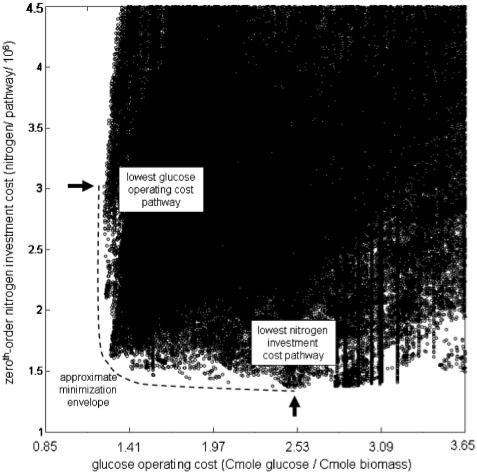
Analysis of pathway resource requirements was expanded beyond the previously described first-order investment approximation (Carlson, 2007). Four zeroth-order anabolic investment MinEs were calculated. Figure 1 illustrates the MinE for the zeroth-order treatment of nitrogen investment as a function of electron donor operating costs. Modes along the MinE minimize the combined costs and therefore represent a competitive cost–benefit relationship between nitrogen investment into enzymes and the efficiency of the resulting pathway to convert glucose into biomass. The network's highest carbon yielding strategy requires a relatively large investment of nitrogen to assemble the required enzymes. The elementary mode with the smallest requirement for nitrogen is not very efficient at converting glucose into biomass. Figure S1 in the Supplementary Material includes plots which highlight the MinE region in more detail. All modes not on the MinE represent less competitive metabolic strategies for the considered culturing conditions. It is assumed that E.coli toggles between different MinE strategies based on the availability of resources like electron donors, electron acceptors and anabolic nutrients. The large number of points near the MinE represents the robustness of the network and illustrates the huge number of alternative strategies with very comparable investment and operating properties. Figure S2 in the Supplementary Material highlights enzyme usage patterns as a function of doubling time and anabolic resource availability for the zeroth-order investment assumption.
Fig. 1.
MinE analysis. The approximate MinE is highlighted with the dashed line for the electron donor operating costs (Cmole glucose per Cmole biomass) versus zeroth-order nitrogen investment (nitrogen atoms per pathway) cost–benefit case. Each circle represents one unique elementary mode. The x-axis coordinate represents the efficiency of the elementary mode at converting glucose into biomass. Small costs represent high efficiency. The y-axis coordinate plots the nitrogen required to assemble the enzymes utilized by the elementary mode assuming a zeroth-order dependence on substrate concentration (see text for more details). Modes along the MinE minimize the combined costs and therefore represent a competitive cost–benefit relationship between nitrogen investment into enzymes and the efficiency of the resulting pathway for converting glucose into biomass. The arrow in the upper left highlights the network's most efficient strategy (lowest operating cost), which has a relatively high nitrogen requirement. The arrow in the lower right highlights the pathway with the smallest nitrogen requirement, which has a relatively high glucose operating cost. The plot scale permits approximately 1.5 million of the 2.6 million possible pathways to be shown. Pathways not shown have uncompetitive nitrogen investment and glucose operating costs.
3.2 Assembly of ecologically competitive pathway subset
The primary goal of this study was to assemble a subset of metabolic pathways which can be used to describe and interpret a range of metabolic behaviors. The subset was assembled using the elementary modes located on the nine MinEs. If the current methodology is to be seriously considered, it needs to offer advantages over existing techniques. To facilitate the comparison of the current approach with other in silico methods, the model from Schuetz et al. (2007), with a few modifications, was adopted. The reaction file can be found in the Supplementary Material along with the anabolic requirements for each model reaction.
The Schuetz-based model contained 284 864 elementary modes with 197 018 representing cellular growth. MinE analysis of the growth modes using the nine envelopes identified a subset of elementary modes which represent an ecologically competitive usage of the network. Because of fixed amino acid elemental ratios, there were numerous pathway redundancies on the nine MinEs. The redundancies were removed resulting in 38 unique pathways. These modes are listed in the Supplementary Material (Table S2). The Supplementary Material also contains a hierarchical clustering of the 38 pathways which illustrates the overlap found between the different investment strategies (Figure S3).
The experimentally measured carbon metabolism in Schuetz et al. has 10 systematic degrees of freedom. Therefore, the carbon flux distribution can be described using 10 split ratios at pivotal branch points. The split ratio approach permits a reasonable comparison of flux distributions, which often vary widely. The 10 split ratios were calculated for each of the elementary modes found along the MinEs and are listed in the Supplementary Material. For the considered model, 23 reactions define the 10 experimental split ratios.
3.3 Non-negative least squares assembly of a physiological state
It is hypothesized that the ecologically competitive subset of elementary modes can be used to predict and describe a wide variety of cellular behaviors based on linear combinations. Given a physiological flux distribution v and the subset of ecologically competitive elementary modes E [note: matrix E is arranged in a transpose fashion relative to A described in Equation (1)], a weighting vector w is sought which satisfies the following expression:
| (2) |
Before solving Equation (2) for the weighting vector w, the problem was recast in terms of the 23 reactions that define the model's carbon metabolism. The E and v elements from Equation (2) were condensed into the reactions required to define the system split ratios and renamed with an (s). For the considered model, the vector vs is comprised of the 23 experimentally reported 13C fluxes and the matrix Es is the listing of the 38 elementary modes condensed into the carbon metabolism defining reactions.
| (3) |
Linear regression analysis was performed to identify the vector w using MATLAB and the Lawson and Hanson (1974) non-negative least squares algorithm. The algorithm iteratively solves the following relationship for the weighting vector w:
| (4) |
Elements of w were constrained to non-negative values because the growth elementary modes are not reversible. The least squares analysis weighting factors represent the contribution of each mode to the overall system physiology. The results represent a best fit; a statistical analysis is given below. The weighting factor vectors (w) for the experimental culturing conditions are listed in Supplementary Table S4. The best fit for each experimental growth condition requires only three or four vectors from the set of 38.
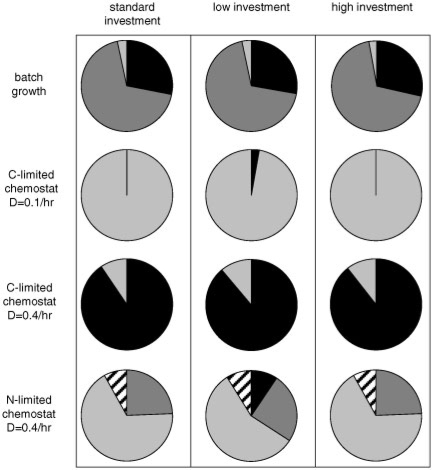
This approach was used to decompose four experimentally reported physiologies, representing batch growth, carbon-limited chemostat growth (dilution rate (D)=0.1/h and 0.4/h), and nitrogen-limited chemostat growth (D=0.4/h), into fluxes that can be assigned to different competitive resource usage strategies. Figure 2 plots the percentage of the overall flux distribution that can be assigned to the different ecological strategies. Percentages are based on flux through the glucose transport reaction. The results suggest that under many growth conditions, microbes simultaneously respond to multiple stresses. For instance, the batch growth case suggests that the overall metabolism is a combination of the optimal biomass yielding strategy combined with oxygen and anabolic resource stress.
Fig. 2.
Resource-based stress adaptation to four culturing conditions. Fluxes from four culturing conditions were decomposed into different resource-based stress responses. The graph area is proportional to the percentage of the fluxes (based on glucose transport) associated with the different stress responses (dark gray = oxygen stress; light gray = first-order investment stress; striped = zeroth-order investment stress; black = highest yielding growth). Three different metabolic model investment scenarios were considered based on different isozymes. The standard investment analysis considered isozymes deemed most likely to be utilized based on current literature. The low investment analysis utilized the isozyme with the fewest amino acids, while the high investment analysis considered the isozyme with the most amino acids. See text for more details.
The flux distribution for the carbon limited (D=0.4/h) case suggests these culturing conditions are close to ideal permitting the acquisition of the required nutrients in appropriate ratios for this E.coli strain. Approximately 91% of the flux can be assigned to the highest biomass yielding network usage, while the balance is associated with first-order anabolic investment stress. Culturing conditions that result in the expression of the highest yielding metabolism are likely strain specific. Therefore, the contributions from each of the 38 ecological modes would likely differ, at least slightly, between strains for identical culturing conditions.
The accuracy of the presented approach was compared to the best results from the 99 LP simulations considered in Schuetz et al. (2007). The LP output from that study was kindly provided by R. Schuetz and U. Sauer. The current method exceeds the accuracy of the LP-based methods for all four considered growth conditions, based on Euclidean distance between the reconstructed split ratio vectors and the experimental split ratio vectors (Table 1).
Table 1.
Accuracy of in silico descriptions of experimental fluxes
| Euclidean distance |
||
|---|---|---|
| Growth conditions | Ecological costs based | LP-based |
| Batch growth | 0.152 | 0.478 |
| Glucose limited chemostat (D=0.1/hr) | 0.267 | 0.700 |
| Glucose limited chemostat (D=0.4/hr) | 0.196 | 0.287 |
| Nitrogen limited chemostat (D=0.4/hr) | 0.251 | 0.440 |
Smaller Euclidean distances represent a more accurate description of measured fluxes. The current ecological costs-based analysis was compared with LP-based methods using 13C fluxome data found in Schuetz et al. (2007). The LP methods are presented there as well. The Euclidean distances are measured between dimensionless split ratios and do not have units.
Least squares analysis has been applied previously to metabolic flux analysis in the classic Vallino and Stephanopoulos(1990; 1993) papers. In these studies, experimentally measured metabolite accumulation rates were mapped to intracellular reactions using least squares analysis. The current study utilizes more recent experimental and computational approaches. 13C-based intracellular flux measurements are used with mathematically defined biochemical pathways to describe a cellular metabolism as a combination of different ecological cost-based strategies.
3.4 Statistical significance of calculated flux distributions
Elementary modes do not typically form a linear basis for a metabolic network's permitted flux space (Poolman et al., 2004; Schwartz and Kanehisa, 2005). Solutions presented above represent a best fit of E to v by minimizing the error found in Equation (4). To assess the biological relevance of the assembled subset, the current results were tested for statistical significance by comparing their accuracy against randomly assembled subsets of elementary modes.
MATLAB was used to construct 10 000 elementary mode subsets each comprised of 38 randomly selected modes. The modes were taken from the 197 018 growth modes identified for this biochemical model. The random sets were condensed into the 23 reactions which define the carbon metabolism (Rs). The ability of these random subsets to accurately describe the experimentally reported fluxes was assessed using the same procedure described above except that the random matrix (Rs) was substituted for the ecological cost-based matrix (Es). Briefly, non-negative least squares analysis was used to find the best fit of the random subset to the experimental fluxes, the best fit metabolism was used to calculate the 10 system split ratios, and the Euclidean distance between this computational split ratio vector and the experimental split ratio vector was calculated.
Of the 10 000 randomly assembled subsets, ∼0.6% outperformed the ecological set's accuracy at describing the batch data, ∼2.9% outperformed the ecological set's accuracy at describing glucose-limited chemostat growth (D=0.1/h), ∼5.2% outperformed the ecological set's accuracy at describing glucose-limited chemostat growth (D=0.4/h) and ∼1.7% outperformed the ecological set's accuracy at describing nitrogen-limited chemostat growth (D=0.4/h) (Table 2). Considering a P≤0.05 to represent statistical significance, the ecologically based subset is statistically significant with three of the four experimental datasets. The glucose-limited chemostat (D=0.4/h) data with a P-value of 0.052 represents a special case; ∼91% of the flux distribution can be assigned to a single elementary mode. The randomly selected subsets which by chance contain this elementary mode would achieve ∼91% of the flux distribution from a single mode. The additional 37 modes would then permit additional refinement. None of the 10 000 randomly assembled sets had an accuracy that met or exceeded the ecologically based subset on all four growth conditions. If all four culturing conditions are considered, the statistical significance of the assembled subset is at least 99.99%. The random subset fits utilized linear combinations of more pathways than the ecological costs-based subset (Table 2). The random subsets that out performed the costs-based subset utilized on average between 7.1 and 8.7 pathways. In comparison, the ecological costs-based subsets used either three or four pathways. The accuracy of the observed flux descriptions seems to confirm the biological relevance of the cost-based subset.
Table 2.
Biological significance of flux descriptions
| Growth conditions | P-value | Average no. pathways, random | No. pathways, costs-based |
|---|---|---|---|
| Batch growth | 0.0056 | 8.7±1.1 | 4 |
| Glucose limited chemostat (D=0.1/hr) | 0.0288 | 7.1±1.2 | 3 |
| Glucose limited chemostat (D=0.4/hr) | 0.0515 | 8.0±1.3 | 4 |
| Nitrogen limited chemostat (D=0.4/hr) | 0.0172 | 7.5±1.2 | 4 |
| All four conditions | ≤0.0001 | n.a. | n.a. |
The ecological costs-based flux descriptions were compared with 10 000 random pathway sets for accuracy. The P-value is based on the occurrence of random pathway subsets which outperformed the costs-based subset at describing experimental data. None of the 10 000 random sets outperformed the costs-based descriptions with all four culturing scenarios. The number of pathways required for the least squares analysis best fit is shown for both the random subsets and the costs-based subset, n.a.=not applicable.
Some of the randomly assembled subsets that surpassed the ecologically based subset at describing the batch growth, data were analyzed for their properties with regard to the MinEs. Not surprisingly, the well-performing randomly assembled subsets had numerous elementary modes that plotted near the MinEs (data not shown).
3.5 Sensitivity analysis of investment costs
The sensitivity of the presented results to the anabolic investment matrix was tested by varying the considered isozymes. Three separate investment matrices were constructed based on the anabolic requirements of different isozyme sets. The standard investment matrix was assembled using current literature to select the isozyme most likely to be utilized. A high investment matrix was assembled by selecting the isozymes with the highest amino acid count per functional enzyme complex and a low investment matrix was assembled by selecting the isozyme with the smallest amino acid count per functional enzyme. For example, there are two considered phosphofructokinase enzymes (FbaA and FbaB). Each of these homomultimeric enzymes has a different amino acid sequence and FbaA is thought to be comprised of four identical subunits, while FbaB is thought to be comprised of two identical subunits (Keseler et al., 2005). A functional FbaA enzyme requires 1280 amino acids, while a functional FbaB enzyme requires 618 amino acids. FbaA was considered in the standard cost investment matrix (Keseler et al., 2005) and in the high cost investment matrix. FbaB was considered for the low cost investment matrix. The investment matrices are given in the Supplementary Material (Tables S1 and S5).
The elementary mode output was processed to calculate the anabolic investment costs for each of the 197 018 modes using the three investment scenarios. The nine MinEs were determined for each investment scenario and the datasets were processed as described above. The low investment scenario resulted in a subset of 39 unique pathways, while the high investment scenario resulted in a subset of 44 pathways. The contribution of highest yielding fluxes, first-order anabolic investment stress, zeroth-order anabolic investment stress and oxygen stress are shown in Figure 2. The contributions from each stress category are very similar for all three investment scenarios. The results suggest that the analysis is reasonably insensitive to the different isozyme investment considerations.
3.6 Perturbation analysis of experimental flux vector
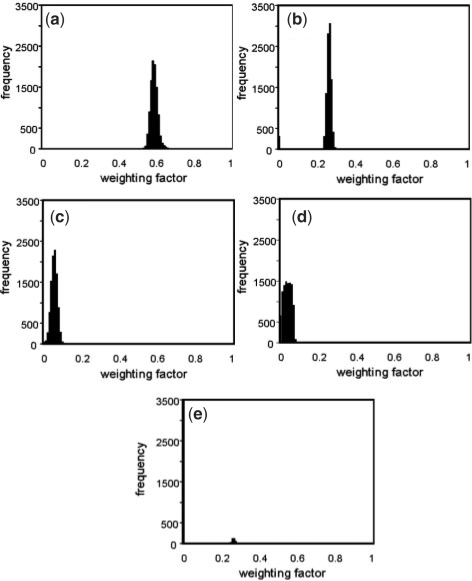
The numerical stability of the reported weighting vectors was tested by randomly and independently perturbing each of the fluxes in the experimental flux vector vs within the reaction's experimental confidence range [values given in Supplementary Material of Schuetz et al. (2007)]. The perturbed vector was then analyzed with non-negative least squares analysis. This process was repeated 10 000 times. The weighting factors for the batch growth case are shown in Figure 3 as histograms. Occasionally, different modes would be utilized for the least squares fitting. This occurrence was rare and Figure 3 shows the histogram of the mode with the highest average weighting factor besides the four previously identified best fit modes. The simulations indicate that the weighting vector elements are quite stable to perturbations, suggesting that measurement error had little impact on the results of this study.
Fig. 3.
Perturbation analysis of non-negative least squares weighting factors. The sensitivity of the predicted weighting factors was tested using the batch growth data. Each measured flux was randomly perturbed independently within the experimental confidence range. Least squares analysis was then performed using the perturbed fluxes and the ecologically competitive pathways. The analysis was repeated 10 000 times. The weighting coefficients are plotted as a histogram. (a) Primary oxygen stress pathway weighting factor, (b) optimal carbon yielding metabolism pathway weighting factor, (c) secondary oxygen stress pathway weighting factor and (d) first-order investment stress pathway weighting factor. Occasionally additional modes would be utilized during the least squares analyses. (e) Highlights the mode with the highest average value. The ordinate in (e) has been truncated for consistency with the other plots a–d.
3.7 Null hypothesis testing
The presented studies suggest the experimentally measured fluxes are the result of competitive cost–benefit tradeoffs. To further strengthen this argument, a null hypothesis experiment was formulated that explores artificial metabolic flux distributions that have not been optimized by evolution. Two separate strategies were used to generate sets of 1000 artificial null hypothesis flux distributions (see Section 2). The same analysis as described above was performed except the artificial flux distributions (n) replaced the measured physiological fluxes (v). For each of the 1000 artificial flux vectors, the accuracy of the ecological set to describe the fluxes was compared to 1000 sets of 38 randomly selected elementary modes.
Using the flux distributions generated from the entire set of elementary modes, the random sets more accurately described the artificial flux distributions almost without exception. The ecological set outperformed the random set on only 26 comparisons out of the 1 million scenarios. Using the flux distributions generated from 1–100 modes with carbon yields at least as good as the modes identified from the MinE analysis revealed that the random sets still out competed the ecologically relevant set 97.7% of the time. The ecological set of elementary modes is sufficient to describe the natural metabolite fluxes but is not sufficient to describe the artificial flux distributions.
4 DISCUSSION
A method was developed to mine the genomic potential of an organism for its ability to competitively adapt to simultaneous anabolic and catabolic pressures. The current study utilizes a single simulation and identifies a small subset of pathways from the inclusive EMA output file. The presented methodology uses this single set of strategies to describe a number of culturing conditions removing the need to test an exhaustive set of LP simulations with different objective functions and constraints for each growth condition. The accuracy of the presented metabolic flux descriptions were compared with an existing LP method and found to be more accurate. The statistical significance of the cost-based pathway subset was assessed by comparing their accuracy to 10 000 random subsets of pathways. None of randomly assembled subsets beat the ecologically competitive subset at describing all four considered growth scenarios. In addition, the random subsets required approximately two times more pathways to create a best fit as compared with the ecologically selected subset. The ecologically competitive pathways seem to be biologically significant.
The identified pathways provide an ecological explanation for overflow metabolisms observed at both nutrient starvation and nutrient excess conditions (Majewski and Domach, 1990; Teixeira de Mattos and Neijssel, 1997). Many enzymes utilized in high-yielding pathways, which efficiently oxidize glucose to CO2, are anabolically expensive to assemble. For example, the complete oxidative tricarboxylic acid cycle (TCA) requires the expensive α-ketoglutarate dehydrogenase complex. Under conditions of nutrient limitation, the current study suggests it is more competitive to utilize pathways with enzyme sets that require less resources to assemble. Under conditions of nutrient excess, a condition of nutrient stress is likely created by the unbalanced uptake of the various anabolic resources. It is hypothesized that the anabolic stress identified during batch growth is due to a limiting rate of NH3 diffusion. In M9 minimal media, the nitrogen source NH3 must diffuse into the cell via passive transport, while all other major elements have active transport systems (Conroy et al., 2007; Neidhardt, 1996). An analysis of published experimental data indicates that adding amino acids to minimal media typically results in much higher culture growth rates (Andersen and von Meyenburg, 1980). Amino acids have active transport systems potentially permitting a higher nitrogen influx. The amino acid transport would also increase carbon flux into the cell, but this increase is not likely the reason for the increased growth rates. Aerobically growing E.coli batch cultures utilize a specific glucose consumption rate which is approximately one-fourth the rate observed during anaerobic batch growth (Hempfling and Mainzer, 1975). If carbon were limiting growth, the cell could likely increase the specific glucose transport rate.
The set of identified pathways is comprised of 38 modes however, only 12 were utilized during the analyses (Table S4). This suggests that the ecologically relevant subset can be pared down even further which would certainly improve the statistical significance. It seems E.coli has adapted to stresses in a manner that can be described by the MinE approach, but the cells may not utilize every competitive metabolic adjustment. Instead, the cells appear to adopt strategies that approximate the envelope. This could be viewed as a cost–benefit arrangement. The cost of maintaining a regulation system which permits very fine adjustments is likely not offset by the associated benefit.
High-dimensional datasets can often be accurately represented as a linear combination of a limited number of vectors identified using eigen-decomposition methods. Techniques like principle component analysis and singular value decomposition have been applied to elementary mode sets (Price et al., 2003; Van Dien et al., 2006). The current set of 197 018 biomass producing modes was decomposed into a vector set which maximized projected variance using principle component analysis. Twenty-two principle components were required to capture 99.9% of the elementary mode set variance (Figure S4). Least squares analysis was used to determine if the most significant principle components were consistent with a linear combination of the 38 ecological modes. The ecological modes were not sufficient to define any of the first 22 principle components. The principle components were also used to reconstruct the four considered experimental flux distributions using least square analysis. Unlike the study using elementary modes, the least squares study utilizing principle components was not restricted to non-negative values because the principle components do not have obvious biological meaning. The first 18 principle components were required to outperform the ecologically relevant modes at all four experimental flux distributions. As a comparison, only 12 of the ecologically relevant modes were required for this analysis. The set of ecologically relevant modes is distinct from the first 22 principle components.
EMA defines a convex cone which contains all possible steady-state flux distributions constrained to biologically relevant flux directions. Figure 1 represents a 2D bisection of that cone. The principle component of the convex cone would likely run through the center of the cone (Price et al., 2003). The arc defined by the MinE in the 2D plot would not be sufficient to define such a principle component. While principle components have a meaningful mathematical definition, the biological meaning is less clear. For instance, unlike the actual elementary modes, the principle components are not constrained to values that correspond with biologically relevant fluxes. As an example, approximately half of the identified principle components had negative glucose uptake rates which do not have a biological interpretation.
The identified metabolic pathways seem to represent a general set of strategies that are utilized in different combinations to adapt to a range of environments. The predicted enzyme usage patterns are consistent with many of the reported universal stress response adaptations (Nachin et al., 2005; Nyström and Neidhardt, 1993). Using a small set of competitive strategies selected through evolution, the cell would only need to adjust its metabolic regulation to adapt to a wide range of new environmental conditions. This would represent a fairly quick response to changing circumstances as compared with the slower ecological adaptation associated with strategies like horizontal gene transfer (Woese, 2002) or the evolution of new proteins. It has been reported that E.coli can adapt its regulation scheme in as little as 100 generations (Tagkopoulos et al., 2008).
The MinE used in this analysis has conceptual similarities to tradeoff curves used in the ecological analysis of species competition (Tilman, 1999). A common ecological application of tradeoff curves is to predict if different species are capable of coexistence or whether a new species can invade and replace another established species. The presented MinE analysis utilizes the same ideology of competition and invasiveness except the MinE analysis looks at the competitiveness of different metabolic regulation schemes. The MinE analysis predicts which regulation schemes could coexist (those that lay on the MinE) and which regulation schemes could ‘invade and replace’ other regulation schemes (the MinE could replace an alternative regulation scheme with a cost–benefit curve further from the origin). This study supports the proposition that metabolic regulation has been shaped by natural selection forces similar to those that influence macro-scale ecological landscapes.
Funding
National Institutes of Health (EB006532).
Conflict of Interest: none declared.
Supplementary Material
ACKNOWLEDGEMENTS
The author is grateful to Reed Taffs for helpful discussions and critical reading of the article as well as an anonymous reviewer for generous and helpful suggestions regarding null hypothesis testing and principle component analysis. The author would also like to thank R. Schuetz and U. Sauer for sharing their linear programming output files.
REFERENCES
- Andersen KB, von Meyenburg K. Are growth rates of Escherichia coli in batch cultures limited by respiration? J. Bacteriol. 1980;144:114–123. doi: 10.1128/jb.144.1.114-123.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson RP. Metabolic systems cost-benefit analysis for interpreting network structure and regulation. Bioinformatics. 2007;23:1258–1264. doi: 10.1093/bioinformatics/btm082. [DOI] [PubMed] [Google Scholar]
- Carlson R, Srienc F. Fundamental Escherichia coli biochemical pathways for biomass and energy production: identification of reactions. Biotechnol. Bioeng. 2004a;85:1–19. doi: 10.1002/bit.10812. [DOI] [PubMed] [Google Scholar]
- Carlson R, Srienc F. Fundamental Escherichia coli biochemical pathways for biomass and energy production: creation of overall flux states. Biotechnol. Bioeng. 2004b;86:149–162. doi: 10.1002/bit.20044. [DOI] [PubMed] [Google Scholar]
- Conroy MJ, et al. The crystal structure of the Escherichia coli AmtB-GlnK complex reveals how GlnK regulates the ammonia channel. Proc. Natl Acad. Sci. USA. 2007;104:1213–1218. doi: 10.1073/pnas.0610348104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hempfling WP, Mainzer SE. Effects of varying the carbon source limiting growth on yield and maintenance characteristics of Escherichia coli in continuous culture. J. Bacteriol. 1975;123:1076–1087. doi: 10.1128/jb.123.3.1076-1087.1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keseler IM, et al. EcoCyc: a comprehensive database resource for Escherichia coli. Nucleic Acids Res. 2005;33:D334–D337. doi: 10.1093/nar/gki108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klamt S, Stelling J. Two approaches for metabolic pathway analysis? Trends Biotechnol. 2003;21:64–69. doi: 10.1016/s0167-7799(02)00034-3. [DOI] [PubMed] [Google Scholar]
- Klamt S, et al. FluxAnalyzer: exploring structure, pathways, and flux distributions in metabolic networks on interactive flux maps. Bioinformatics. 2003;19:261–269. doi: 10.1093/bioinformatics/19.2.261. [DOI] [PubMed] [Google Scholar]
- Klamt S, et al. Structural and functional analysis of cellular networks with CellNetAnalyzer. BMC Syst. Biol. 2007;1:2. doi: 10.1186/1752-0509-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson CL, Hanson RJ. Solving Least Squares Problems. Englewood Cliffs, NJ, USA: Prentice Hall; 1974. [Google Scholar]
- Lenski RE, Travisano M. Dynamics of adaptation and diversification: a 10 000-generation experiment with bacterial populations. Proc. Natl Acad. Sci. USA. 1994;91:6808–6814. doi: 10.1073/pnas.91.15.6808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majewski RA, Domach MM. Simple constrained-optimization view of acetate overflow in E. coli. Biotechnol. Bioeng. 1990;35:732–738. doi: 10.1002/bit.260350711. [DOI] [PubMed] [Google Scholar]
- Nachin L, et al. Differential roles of the universal stress proteins of Escherichia coli in oxidative stress resistance, adhesion, and motility. J. Bacteriol. 2005;187:6265–6272. doi: 10.1128/JB.187.18.6265-6272.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neidhardt FC, editor. Escherichia coli and Salmonella: Cellular and Molecular Biology. Washington D.C: ASM Press; 1996. [Google Scholar]
- Nyström T, Neidhardt FC. Isolation and properties of a mutant of Escherichia coli with an insertional inactivation of the uspA gene, which encodes a universal stress protein. J. Bacteriol. 1993;175:3949–3956. doi: 10.1128/jb.175.13.3949-3956.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer T, Schuster S. Game-theoretical approaches to studying the evolution of biochemical systems. TIBS. 2005;30:20–25. doi: 10.1016/j.tibs.2004.11.006. [DOI] [PubMed] [Google Scholar]
- Pfeiffer T, et al. Cooperation and competition in the evolution of ATP-producing pathways. Science. 2001;292:504–507. doi: 10.1126/science.1058079. [DOI] [PubMed] [Google Scholar]
- Poolman MG, et al. A method for the determination of flux in elementary modes, and its application to. Lactobacillus rhamnosus. Biotechnol. Bioeng. 2004;88:601–612. doi: 10.1002/bit.20273. [DOI] [PubMed] [Google Scholar]
- Price ND, et al. Analysis of metabolic capbabilities using singular value decomposition of extreme pathway matrices. Biophys. J. 2003;84:794–804. doi: 10.1016/S0006-3495(03)74899-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuetz R, et al. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol. 2007;3:119. doi: 10.1038/msb4100162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuster S, et al. Detecting elementary modes of functioning in metabolic networks. Mod. trends biothermokinetics. 1994;3:103–105. [Google Scholar]
- Schuster S, et al. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000;18:326–332. doi: 10.1038/73786. [DOI] [PubMed] [Google Scholar]
- Schuster S, et al. Reaction routes in biochemical reaction systems: algebraic properties, validated calculation procedure and example from nucleotide metabolism. J. Math. Biol. 2002;45:153–181. doi: 10.1007/s002850200143. [DOI] [PubMed] [Google Scholar]
- Schwartz JM, Kanehisa M. A quadratic programming approach for decomposing steady-state metabolic flux distributions onto elementary modes. Bioinformatics. 2005;21:204–205. doi: 10.1093/bioinformatics/bti1132. [DOI] [PubMed] [Google Scholar]
- Stucki JW. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem. 1980;109:269–283. doi: 10.1111/j.1432-1033.1980.tb04792.x. [DOI] [PubMed] [Google Scholar]
- Tagkopoulos I, et al. Predictive behavior within microbial genetic networks. Science. 2008;320:1313–1317. doi: 10.1126/science.1154456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teixeira de, Mattos MJ, Neijssel OM. Bioenergetic consequences of microbial adaptation to low-nutrient environments. J. Biotechnol. 1997;59:117–126. doi: 10.1016/s0168-1656(97)00174-0. [DOI] [PubMed] [Google Scholar]
- Tilman D. The ecological consequences of changes in biodiversity: a search for general principles. Ecology. 1999;80:1455–1474. [Google Scholar]
- Vijayasankaran N, et al. Metabolic pathway structures for recombinant protein synthesis in Escherichia coli. Appl. Microbiol. Biotechnol. 2005;68:737–746. doi: 10.1007/s00253-005-1920-7. [DOI] [PubMed] [Google Scholar]
- Vallino J, Stephanopoulos G. Flux determinations in cellular bioreaction networks: applications to lysine fermentations. In: Sikdar S, et al., editors. Frontiers in Bioprocessing. Boca Raton: CRC Press; 1990. pp. 205–219. [Google Scholar]
- Vallino J, Stephanopoulos G. Metabolic flux distributions in Corynebacterium glutamicum during growth and lysine overproduction. Biotechnol. Bioeng. 1993;41:633–646. doi: 10.1002/bit.260410606. [DOI] [PubMed] [Google Scholar]
- Van Dien SJ, et al. Theoretical analysis of amino acid-producing Escherichia coli using a stoichiometric model and multivariate linear regression. J. Biosci. Bioeng. 2006;102:34–40. doi: 10.1263/jbb.102.34. [DOI] [PubMed] [Google Scholar]
- Wiback SJ, et al. Reconstructing metabolic flux vectors from extreme pathways: defining the [alpha]-spectrum. J. Theor. Biol. 2003;224:313–324. doi: 10.1016/s0022-5193(03)00168-1. [DOI] [PubMed] [Google Scholar]
- Wlaschin A, et al. The fractional contributions of elementary modes to the metabolism of Escherichia coli and their estimation from reaction entropies. Metab. Eng. 2006;8:338–352. doi: 10.1016/j.ymben.2006.01.007. [DOI] [PubMed] [Google Scholar]
- Woese CR. On the evolution of cells. Proc. Natl Acad. Sci. USA. 2002;99:8742–8747. doi: 10.1073/pnas.132266999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.