Abstract
Natural selection on codon usage is a pervasive force that acts on a large variety of prokaryotic and eukaryotic genomes. Despite this, obtaining reliable estimates of selection on codon usage has proved complicated, perhaps due to the fact that the selection coefficients involved are very small. In this work, a population genetics model is used to measure the strength of selected codon usage bias, S, in 10 eukaryotic genomes. It is shown that the strength of selection is closely linked to expression and that reliable estimates of selection coefficients can only be obtained for genes with very similar expression levels. We compare the strength of selected codon usage for orthologous genes across all 10 genomes classified according to expression categories. Fungi genomes present the largest S values (2.24–2.56), whereas multicellular invertebrate and plant genomes present more moderate values (0.61–1.91). The large mammalian genomes (human and mouse) show low S values (0.22–0.51) for the most highly expressed genes. This might not be evidence for selection in these organisms as the technique used here to estimate S does not properly account for nucleotide composition heterogeneity along such genomes. The relationship between estimated S values and empirical estimates of population size is presented here for the first time. It is shown, as theoretically expected, that population size has an important role in the operativity of translational selection.
Keywords: translational selection, tAI, tRNA, codon usage bias, population size, eukaryotes
Introduction
Different codons are used to different extents, and every genome shows particular codon preferences (Grantham et al. 1980). It is generally acknowledged that the pattern of codon usage in a given genome is given by a balance between mutational bias, random genetic drift, and the action of natural selection (Sharp et al. 1995). In highly expressed genes of fast-growing organisms, preferred codons are favorably selected to match the most abundant cognate transfer tRNAs (tRNAs), thus improving translational efficiency and accuracy (Bennetzen and Hall 1982; Ikemura 1985). A selection–mutation balance theory of codon usage (Bulmer 1991; McVean and Charlesworth 1999) has been developed to explain the forces that shape codon usage in different genomes. Organisms like the bacterium Helicobacter pylori show codon usage patterns that can be explained mainly by mutational biases and drift (Lafay et al. 2000), whereas organisms like the fast-growing bacterium Escherichia coli show patterns of codon usage that are consistent with a coadaptation to the intracellular tRNA levels (Ikemura 1981; dos Reis et al. 2003). Natural selection acting at the codon level for translational optimization is usually referred to as translational selection (Akashi and Eyre-Walker 1998). Understanding how and why translational selection acts to optimize codon usage in certain organisms is an important and active area of research.
One of the major limitations of codon usage studies is that measuring translational selection is a complicated matter. Most studies are based on the development or application of codon usage indices that intend to describe general patterns of codon usage, and any evidence of selection is indirect, with selection rarely being measured directly (see, e.g., Sharp and Li 1987; Wright 1990; Knight et al. 2001; Chen et al. 2004). Perhaps, the only group of organisms where several serious attempts to estimate selection have been made are Drosophila spp. (Akashi 1995, 1997; Akashi and Schaeffer 1997; Maside et al. 2004) with some estimates in other organisms (Hartl et al. 1994; Cutter and Charlesworth 2006; Yang and Nielsen 2008). These studies have shown that the selection coefficients affecting codon usage are very small, roughly ranging between 10−6 and 10−9. Only fairly recently, Sharp et al. (2005) conducted an extensive study of codon usage in prokaryotic organisms, utilizing a population genetic model developed by Bulmer (1991) to obtain appropriate estimates of translational selection. These workers estimated the population parameter S, which is the confounded product of the effective population size and the actual selection coefficient acting at the codon level. Regrettably, their study was not extended to eukaryotic organisms.
Because the selection coefficients affecting codon usage are so small, translational selection is expected to be operative only in large populations. In small populations, random drift effects largely determine the fate of new mutants in a population even if they are slightly advantageous (Kimura 1983). The role of effective population size on the evolution of codon usage has been well discussed in the literature (Sharp et al. 1995; Chamary et al. 2006). However, it seems no researchers have actually compared estimates of selection and population size from actual data. Perhaps, the only exception is the work by Akashi (1997), where the differences in effective population sizes and the degree of codon usage in two Drosophila species were discussed.
The objective of the present work is to utilize Bulmer's (1991) model of codon evolution as implemented by Sharp et al. (2005) to study codon selection in a small set of eukaryotic genomes, with particular emphasis on the baker's yeast, Saccharomyces cerevisiae. The relationship between estimates of translational selection and expression levels is studied in detail. Furthermore, we use published estimates of effective population sizes (Lynch and Conery 2003) to show, perhaps for the first time, the relationship between effective population size and estimates of translational selection in eukaryotic organisms.
Materials and Methods
Estimating Selection on Codon Usage
This work follows Bulmer's model of codon evolution (Bulmer 1991; McVean and Charlesworth 1999). Let us consider a diploid model with an amino acid that is encoded by only two synonymous codons, c1 and c2. The mutation rate from c1 to c2 is u and from c2 to c1 is v. The model assumes that selection acts independently at all sites and that there is genic selection, this is, c1 has selective advantage s in single dose and 2s in double dose. The frequency (P) of c1, at equilibrium, will be determined by the mutation pattern, the selection strength in favor of c1, and the effect of random drift. P is approximately given by
| (1) |
where Ne is the effective population size. Figure 1 shows the expected theoretical relationship between P and Ne for a constant selective pressure s.
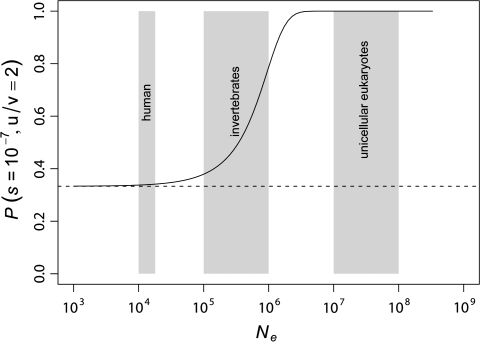
FIG. 1.—
Theoretical expected equilibrium frequency (P) of an optimal codon versus effective population size (Ne). The curve represented in the figure is from rearranging equation (1). The gray rectangles show estimated effective population size intervals for some eukaryotic groups (Sherry et al. 1997; Harpending et al. 1998; Lynch and Conery 2003). Estimates of selection on codon usage are in the order of 10−6 to 10−9 (Hartl et al. 1994; Maside et al. 2004). A value of s = 10−7 was chosen for illustrative purposes only. The dashed line shows the equilibrium frequency of the codon under no selection when u/v = 2.
In practical terms, the selection coefficient (s) cannot be estimated independently because it is confounded with the effective population number. The confounded parameter S = 4Nes (for haploid organisms S = 2Nes) can be estimated from the previous equation as
| (2) |
where k = u/v and Q = 1 – P is the frequency of the suboptimal codon (c2). If selection is absent (s = 0), equation (1) is reduced to
| (3) |
Rearranging this equation (3) gives k = (1 – P)/P. From a practical point of view, in any given genome, a value of k can be estimated from a set of genes where selection is either absent or very weak. This value of k can then be used to estimate S for a set of highly expressed genes in such genome. Formally, the estimated value of S can be expressed as
| (4) |
where the caret is used to distinguish the estimate from the model parameter and 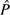 hx and
hx and 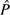 ref are the observed frequencies of optimal codons in the highly expressed and reference gene sets. Please note that the estimated k is
ref are the observed frequencies of optimal codons in the highly expressed and reference gene sets. Please note that the estimated k is 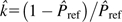 . Equation (4) was used by Sharp et al. (2005) to estimate S values in 80 bacterial genomes. Formally, this equation is simply the log-odds ratio of the relative codon frequencies of optimal over nonoptimal codons (Eyre-Walker and Bulmer 1995). If the value of k is nonhomogeneous throughout a given genome, then equation (4) cannot be used to estimate S correctly as the log-odds ratio would simply reflect different mutational patterns in different genes and not selection. This is an important issue that must be kept in mind. The crucial point is to choose the gene sets carefully and to verify that mutational patterns in both sets are similar.
. Equation (4) was used by Sharp et al. (2005) to estimate S values in 80 bacterial genomes. Formally, this equation is simply the log-odds ratio of the relative codon frequencies of optimal over nonoptimal codons (Eyre-Walker and Bulmer 1995). If the value of k is nonhomogeneous throughout a given genome, then equation (4) cannot be used to estimate S correctly as the log-odds ratio would simply reflect different mutational patterns in different genes and not selection. This is an important issue that must be kept in mind. The crucial point is to choose the gene sets carefully and to verify that mutational patterns in both sets are similar.
All nine amino acids encoded by only two synonymous codons were analyzed in this study. Values of k were estimated for each of the nine codon pairs from a suitably determined reference gene set. These k values were then used to estimate S values for each one of the nine optimal codons in genes expressed at different levels. Overall, S values for all nine amino acids were calculated as the average weighted according to the number of codons present. Bootstrap (Efron and Tibshirani 1993) confidence intervals for estimated S values were obtained by sampling with replacement codons within amino acids and expression categories. The confidence intervals are then the 2.5% and 97.5% quantiles of  b values obtained from 1,000 bootstrap samples.
b values obtained from 1,000 bootstrap samples.
The technique used here to estimate S is symmetrical for amino acids encoded by two codons. This means that if a codon c1 has a selective value S1, then the selective value against the complementary codon c2 is simply S2 = –S1. This property allows the estimation of S irrespective of whether we know beforehand which codon is the optimal one. In fact, it allows the identification of the optimal codon by computing S itself. If a negative value is obtained, then the optimal codon is the complementary one. The only exception to this rule is when S is zero, which can easily be determined by bootstrapping. Optimal codons determined this way for baker's yeast are the same as those reported in the literature (Bennetzen and Hall 1982; Percudani et al. 1997; Kanaya et al. 2001).
Sequence Data and Analysis
Sequence data for all open reading frames (ORFs) recognized in the S. cerevisiae genome were downloaded from the National Center of Biotechnology Information ftp site (ftp://ftp.ncbi.nih.gov/genomes/Saccharomyces_cerevisiae). Expression data for this organism were obtained from http://web.wi.mit.edu/young/expression/ (Holstege et al. 1998). This data set contains estimates of mRNA abundance for 5,460 genes as number of transcripts per cell, obtained from duplicated high-density oligonucleotide array experiments. This data set has already been used to study codon usage in at least three separate publications (Coghlan and Wolfe 2000; Akashi 2001, 2003). A total of 119 genes were excluded for analysis in this work because they present name discrepancies with the downloaded yeast genome or present duplicated expression values in the set. Genes were ranked according to their expression level and binned in groups containing at least 6,000 codons. Genes with the same expression level were binned together. Seventy-seven bins were obtained containing between 8 and 523 genes (there is a disproportionate amount of genes with very low expression values). This binning scheme is very similar to that used previously by Akashi (2003) for the same yeast data. Two hundred and eighty genes are depicted in the data set as having only 0.1 transcripts per cell. This represents the lowest detectable value in the array experiments. In this study, these genes were assumed to be under no translational selection, so this group was taken as the reference gene set in order to calculate codon frequencies under mutational equilibrium.
Nine more eukaryotic genomes were also analyzed: the orange bread mold (Neurospora crassa), the cryptococcosis agent (Cryptococcus neoformans), the malaria parasite (Plasmodium falciparum), the mouse-ear cress (Arabidopsis thaliana), the fruit fly (Drosophila melanogaster), a microsporidian parasite (Encephalitozoon cuniculi), a nematode worm (Caenorhabditis elegans), the common mouse (Mus musculus), and human (Homo sapiens). The 77 gene expression bins identified in the baker's yeast were collapsed into 11 expression categories sorted according to increasing expression levels. The observed number of optimal codons in a sequence is a binomial variable, and so the proportion of optimal codons has a variance inversely proportional to the total number of codons in question. Because of this, relatively large bins containing thousands of codons are desirable to obtain reliable estimates of S. These expression categories, and the genes contained within them, were used as a reference to find the corresponding orthologs in the other genomes. Best reciprocal matches obtained with BLAT (Kent J, unpublished data) were used to identify orthologous pairs of protein sequences between the baker's yeast and the nine other eukaryotic genomes. BLAT was designed to find closely related sequences and will fail to identify more distant homologs. In this sense, our approach is rather conservative as only well-conserved homologs were considered here. For general advice on the identification of orthologous sets of genes, the reader is encouraged to read Koonin (2005). If the orthologous genes are assumed to have conserved relative expression levels across species, then the technique described above can be used to estimate translational selection (S) in any of the other nine genomes given a sufficiently large number of orthologous genes can be identified. We used microarray expression data for 79 physiologically normal human tissues (Su et al. 2004; http://symatlas.gnf.org) to assess the assumption of conserved expressivity for our set of orthologs.
R scripts to calculate S with bootstrap intervals and the sets of orthologous genes analyzed here are available for download at http://people.cryst.bbk.ac.uk/∼fdosr01/Nes/.
Results
Estimates of S in the Baker's Yeast
There are approximately 15,000 transcripts in a yeast cell, with individual transcript species ranging from 0.1 to 80 transcripts per cell. The estimated S values ranged from 0 to 2.5 for the most highly expressed genes. As expected, there is a strong positive correlation between  values and expression levels for the yeast transcriptome (fig. 2), with
values and expression levels for the yeast transcriptome (fig. 2), with  values showing an asymptotic relationship with expression level for the highest expression values. Individual amino acids showed
values showing an asymptotic relationship with expression level for the highest expression values. Individual amino acids showed  values for their optimal codons ranging from 1.04 for cysteine's TGT to 4.53 for glutamine's CAA in the three most highly expressed gene bins (table 1). Interestingly, genes expressed at over one transcript per cell show noticeable, albeit small, signs of selection on codon usage. Because about 40% of yeast ORFs present more than one transcript per cell (fig. 3), this percentage of the transcriptome seems to be under the action of translational selection. All optimal codons showed the same relationship of
values for their optimal codons ranging from 1.04 for cysteine's TGT to 4.53 for glutamine's CAA in the three most highly expressed gene bins (table 1). Interestingly, genes expressed at over one transcript per cell show noticeable, albeit small, signs of selection on codon usage. Because about 40% of yeast ORFs present more than one transcript per cell (fig. 3), this percentage of the transcriptome seems to be under the action of translational selection. All optimal codons showed the same relationship of  value to expression level when all bins are taken into account (fig. 3). The trend observed in figure 2 was first noticed by Coghlan and Wolfe (2000) using the codon adaptation index (Sharp and Li 1987) compared against unbinned expression levels. This was later studied in more detail by Akashi (Akashi and Eyre-Walker 1998; Akashi 2003), comparing the relative frequency of optimal codons against binned expression data. However, our study seems to be the first comparing a formal measure of translational selection, namely
value to expression level when all bins are taken into account (fig. 3). The trend observed in figure 2 was first noticed by Coghlan and Wolfe (2000) using the codon adaptation index (Sharp and Li 1987) compared against unbinned expression levels. This was later studied in more detail by Akashi (Akashi and Eyre-Walker 1998; Akashi 2003), comparing the relative frequency of optimal codons against binned expression data. However, our study seems to be the first comparing a formal measure of translational selection, namely  , with expression levels in any organism.
, with expression levels in any organism.
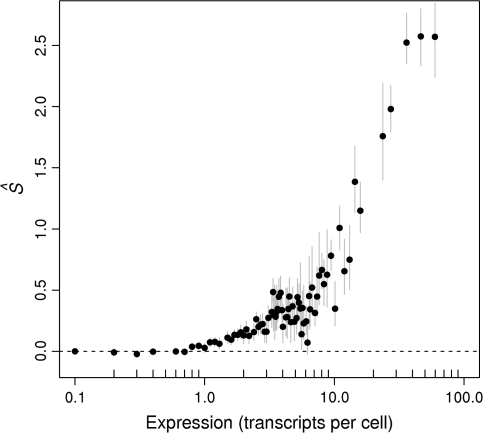
FIG. 2.—
Expression levels versus average  values on codon usage for the yeast Saccharomyces cerevisiae. Vertical bars are the bootstrap nonparametric 95% confidence intervals.
values on codon usage for the yeast Saccharomyces cerevisiae. Vertical bars are the bootstrap nonparametric 95% confidence intervals.
Table 1.
Estimated S Values Partitioned according to the Optimal Codons Analyzed for the Two Bins with Highest Expression in the Yeast Saccharomyces cerevisiae
| Codon |
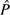 ref ref
|
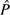 hx hx
|
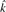 |
 (2.5%, 97.5%) (2.5%, 97.5%) |
|
| Phe | TTT | ||||
| TTC | 0.38 | 0.86 | 1.66 | 2.34 (2.08, 2.63) | |
| Tyr | TAT | ||||
| TAC | 0.41 | 0.92 | 1.41 | 2.78 (2.32, 3.43) | |
| Cys | TGT | 0.59 | 0.80 | 0.70 | 1.04 (0.50, 2.23) |
| TGC | |||||
| His | CAT | ||||
| CAC | 0.34 | 0.79 | 1.91 | 1.95 (1.59, 2.26) | |
| Gln | CAA | 0.67 | 0.99 | 0.50 | 4.53 (3.69, 5.27) |
| CAG | |||||
| Asn | AAT | ||||
| AAC | 0.37 | 0.91 | 1.67 | 2.79 (2.44, 3.16) | |
| Lys | AAA | ||||
| AAG | 0.38 | 0.87 | 1.61 | 2.39 (2.19, 2.58) | |
| Asp | GAT | ||||
| GAC | 0.34 | 0.60 | 1.95 | 1.08 (0.87, 1.27) | |
| Glu | GAA | 0.69 | 0.99 | 0.44 | 3.43 (3.03, 4.06) |
| GAG | |||||
| Overall | — | — | — | — | 2.57 (2.36, 2.78) |
NOTE.—Optimal codons are shown in boldtype face.
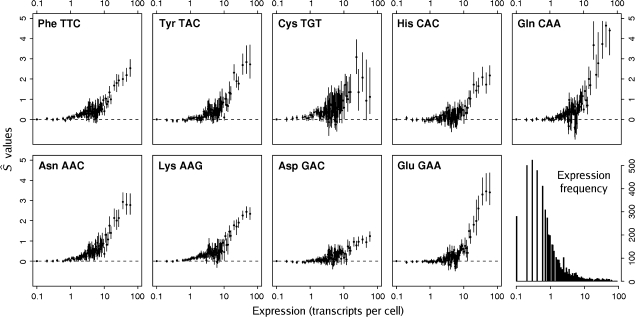
FIG. 3.—
Expression levels versus  values for each of the codons analyzed in this study for the baker's yeast. Vertical bars are the bootstrap nonparametric 95% confidence intervals. The right bottom corner depicts the frequency histogram for the expression levels of the yeast transcriptome.
values for each of the codons analyzed in this study for the baker's yeast. Vertical bars are the bootstrap nonparametric 95% confidence intervals. The right bottom corner depicts the frequency histogram for the expression levels of the yeast transcriptome.
Estimates of S in Other Eukaryotic Genomes
The following analysis of selection on codon usage in the nine other eukaryotic genomes is rather exploratory in nature. Because some of the assumptions of the analysis might be violated (specially the homogeneity of k), these results should be taken with care. They are presented here mainly to illustrate the problems faced when estimating selection. However, it is hoped that these results will help clear a path toward future research on this topic.
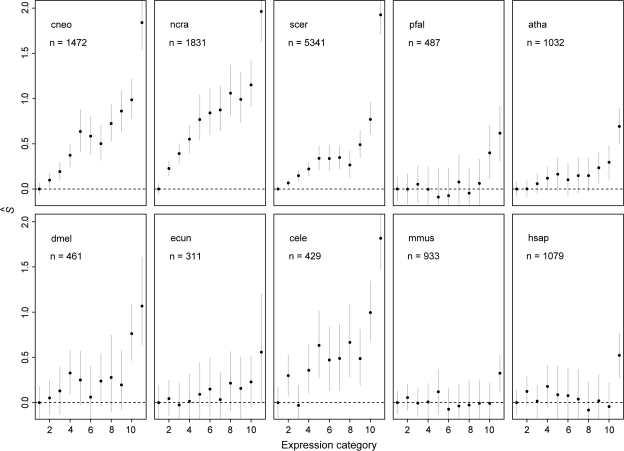
Figure 4 shows average estimated S values for all the genomes studied across expression categories. As expected,  is positively correlated with increasing expression category. What is surprising though is that the trend is strikingly similar for all species. Furthermore, orthologs belonging to the highest expression category also show the larger
is positively correlated with increasing expression category. What is surprising though is that the trend is strikingly similar for all species. Furthermore, orthologs belonging to the highest expression category also show the larger  values across all genomes analyzed. It must be stressed here again that this analysis assumes that expression levels are conserved across all species. Also it is assumed that mutation patterns between highly and lowly expressed genes are very similar, so a meaningful estimate of S can be obtained. This is why this analysis should be regarded with care. However, the results shown in figure 4 are very suggestive, and further work will be needed to confirm them.
values across all genomes analyzed. It must be stressed here again that this analysis assumes that expression levels are conserved across all species. Also it is assumed that mutation patterns between highly and lowly expressed genes are very similar, so a meaningful estimate of S can be obtained. This is why this analysis should be regarded with care. However, the results shown in figure 4 are very suggestive, and further work will be needed to confirm them.
FIG. 4.—
Estimated S values across expression categories for several eukaryotic genomes. Organism codes are: mmus, Mus musculus; hsap, Homo sapiens; pfal, Plasmodium falciparum; atha, Arabidopsis thaliana; cele, Caenorhabditis elegans; ecun, Encephalitozoon cuniculi; dmel, Drosophila melanogaster; ncra, Neurospora crassa; scer, Saccharomyces cerevisiae; and cneo, Cryptococcus neoformans. The values on the upper left corner of each panel are the number of orthologous genes analyzed.
Table 2 shows estimated S values for all the optimal codons in each of the nine amino acids being considered. The two most highly expressed bins from the original yeast analysis (fig. 2) were collapsed into one putatively highly expressed orthologous category to compute the values shown in table 2. All genomes analyzed, except mouse, show  values for the most highly expressed genes that are statistically different from zero, even after correcting for multiple testing (table 2). It is interesting to note that optimal codons are not always the same across the genomes analyzed. For example, codon CAA coding for glutamine is preferred in S. cerevisiae and P. falciparum, whereas its counterpart CAG seems to be consistently preferred by the other genomes. Estimates of S are statistically different from zero for most amino acids in most genomes. For those cases where
values for the most highly expressed genes that are statistically different from zero, even after correcting for multiple testing (table 2). It is interesting to note that optimal codons are not always the same across the genomes analyzed. For example, codon CAA coding for glutamine is preferred in S. cerevisiae and P. falciparum, whereas its counterpart CAG seems to be consistently preferred by the other genomes. Estimates of S are statistically different from zero for most amino acids in most genomes. For those cases where  is indistinguishable from zero, the optimal codon was arbitrarily chosen as the one with a positive
is indistinguishable from zero, the optimal codon was arbitrarily chosen as the one with a positive  value. This did not cause noticeable biases in the estimation of
value. This did not cause noticeable biases in the estimation of  for the genomes analyzed.
for the genomes analyzed.
Table 2.
Estimated S Values for Several Eukaryotes
|
Cryptococcus neoformans |
Neurospora crassa |
Saccharomyces cerevisiae |
Plasmodium falciparum |
Arabidopsis thaliana |
|||||||||||||||||
| Aa | Codon | tRNA | Ŝ | 2.5% | 97.5% | tRNA | Ŝ | 2.5% | 97.5% | tRNA | Ŝ | 2.5% | 97.5% | tRNA | Ŝ | 2.5% | 97.5% | tRNA | Ŝ | 2.5% | 97.5% |
| Phe | TTT | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| TTC | 5 | 1.58 | 1.19 | 2.12 | 12 | 2.41 | 1.84 | 3.12 | 10 | 2.21 | 1.99 | 2.45 | 1 | 0.53 | 0.12 | 0.92 | 16 | 0.68 | 0.34 | 1.08 | |
| Tyr | TAT | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| TAC | 4 | 2.54 | 1.78 | 4.11 | 11 | 1.73 | 1.33 | 2.29 | 8 | 2.79 | 2.36 | 3.26 | 1 | 1.23 | 0.77 | 1.60 | 76 | 1.06 | 0.63 | 1.57 | |
| Cys | TGT | 0 | 0 | 0 | 1.22 | 0.53 | 2.29 | 0 | 0 | 0.05 | −0.35 | 0.48 | |||||||||
| TGC | 3 | 0.26 | −0.22 | 0.76 | 7 | 1.92 | 1.19 | 3.53 | 4 | 0 | 1.10 | 0.52 | 1.61 | 15 | |||||||
| His | CAT | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||||||
| CAC | 4 | 2.27 | 1.59 | 3.17 | 9 | 2.05 | 1.60 | 2.78 | 7 | 1.98 | 1.68 | 2.32 | 2 | 1.03 | 0.42 | 1.58 | 10 | 0.87 | 0.43 | 1.40 | |
| Gln | CAA | 2 | 3 | 9 | 4.16 | 3.50 | 5.67 | 1 | 0.42 | −0.10 | 1.12 | 8 | |||||||||
| CAG | 3 | 1.54 | 1.18 | 1.95 | 11 | 2.89 | 2.38 | 3.64 | 1 | 1 | 9 | 0.50 | 0.16 | 0.93 | |||||||
| Asn | AAT | 4 | 10 | 10 | 1 | 16 | |||||||||||||||
| AAC | 1 | 3.11 | 2.50 | 4.26 | 2 | 3.29 | 2.67 | 4.80 | 7 | 2.83 | 2.53 | 3.16 | 2 | 1.35 | 0.98 | 1.69 | 13 | 0.88 | 0.64 | 1.14 | |
| Lys | AAA | 7 | 24 | 14 | 2 | 18 | |||||||||||||||
| AAG | 0 | 2.98 | 2.58 | 3.62 | 0 | 3.44 | 2.64 | 4.96 | 0 | 2.35 | 2.17 | 2.53 | 0 | 0.38 | 0.16 | 0.59 | 0 | 1.06 | 0.79 | 1.38 | |
| Asp | GAT | 1 | 17 | 16 | 1 | 23 | |||||||||||||||
| GAC | 3 | 2.13 | 1.78 | 2.62 | 5 | 0.38 | 0.08 | 0.73 | 14 | 1.10 | 0.92 | 1.27 | 1 | 0.29 | −0.13 | 0.62 | 12 | 0.34 | 0.03 | 0.63 | |
| Glu | GAA | 9 | 23 | 2 | 3.42 | 3.02 | 3.93 | 1 | 0.60 | 0.19 | 1.15 | 13 | |||||||||
| GAG | 0 | 1.73 | 1.48 | 2.10 | 0 | 2.67 | 2.23 | 3.28 | 0 | 1 | 0.56 | 0.23 | 0.93 | ||||||||
| Totals | 2.24* | 1.91 | 2.74 | 2.50* | 2.14 | 3.14 | 2.56* | 2.37 | 2.78 | 0.66* | 0.48 | 0.85 | 0.75* | 0.50 | 0.98 | ||||||
|
Drosophila melanogaster |
Encephalitozoon cuniculi |
Caenorhabditis elegans |
Mus musculus |
Homo sapiens |
|||||||||||||||||
| Aa |
Codon |
tRNA |
Ŝ |
2.5% |
97.5% |
tRNA |
Ŝ |
2.5% |
97.5% |
tRNA |
Ŝ |
2.5% |
97.5% |
tRNA |
Ŝ |
2.5% |
97.5% |
tRNA |
Ŝ |
2.5% |
97.5% |
| Phe | TTT | 0 | 0 | 0.06 | −0.37 | 0.64 | 0 | 0 | 0 | ||||||||||||
| TTC | 8 | 1.18 | 0.47 | 1.97 | 1 | 16 | 2.93 | 2.30 | 4.37 | 7 | 0.28 | 0.00 | 0.56 | 14 | 0.55 | 0.25 | 0.88 | ||||
| Tyr | TAT | 0 | 0 | 0.03 | −0.35 | 0.44 | 0 | 0 | 1 | ||||||||||||
| TAC | 9 | 1.30 | 0.74 | 2.04 | 1 | 19 | 2.06 | 1.51 | 2.70 | 11 | 0.26 | −0.10 | 0.71 | 11 | 0.21 | −0.08 | 0.55 | ||||
| Cys | TGT | 0 | 0 | 0.46 | −0.03 | 0.91 | 0 | 0 | 0.04 | −0.39 | 0.49 | 0 | |||||||||
| TGC | 7 | 1.28 | 0.30 | 3.42 | 1 | 13 | 1.77 | 1.20 | 2.53 | 56 | 30 | 0.16 | −0.25 | 0.63 | |||||||
| His | CAT | 0 | 0 | 0 | 0 | 0 | |||||||||||||||
| CAC | 5 | 0.58 | 0.03 | 1.35 | 1 | 0.19 | −0.26 | 0.66 | 17 | 1.45 | 1.06 | 1.87 | 10 | 0.20 | −0.21 | 0.62 | 12 | 0.85 | 0.45 | 1.26 | |
| Gln | CAA | 4 | 1 | 18 | 7 | 11 | |||||||||||||||
| CAG | 8 | 1.05 | 0.34 | 2.09 | 1 | 0.75 | −0.04 | 1.87 | 7 | 0.05 | −0.29 | 0.37 | 10 | 0.03 | −0.40 | 0.50 | 21 | 0.52 | 0.13 | 1.01 | |
| Asn | AAT | 9 | 2 | 20 | 15 | 33 | |||||||||||||||
| AAC | 7 | 1.59 | 1.03 | 2.10 | 1 | 0.48 | −0.08 | 0.91 | 16 | 2.65 | 2.14 | 3.22 | 12 | 0.22 | −0.12 | 0.56 | 16 | 0.73 | 0.39 | 1.09 | |
| Lys | AAA | 13 | 1 | 33 | 30 | 22 | |||||||||||||||
| AAG | 0 | 1.47 | 0.76 | 2.39 | 0 | 1.01 | 0.39 | 1.74 | 0 | 2.72 | 2.16 | 3.35 | 0 | 0.31 | 0.01 | 0.60 | 0 | 0.61 | 0.32 | 0.93 | |
| Asp | GAT | 11 | 1 | 22 | 16 | 0.27 | 0.02 | 0.54 | 10 | ||||||||||||
| GAC | 5 | 0.20 | −0.12 | 0.54 | 1 | 0.17 | −0.27 | 0.69 | 17 | 1.08 | 0.79 | 1.40 | 8 | 14 | 0.16 | −0.21 | 0.56 | ||||
| Glu | GAA | 12 | 1 | 20 | 11 | 8 | |||||||||||||||
| GAG | 0 | 0.79 | 0.16 | 1.38 | 0 | 0.68 | −0.27 | 1.62 | 0 | 1.48 | 1.15 | 1.80 | 0 | 0.14 | −0.20 | 0.47 | 0 | 0.48 | 0.13 | 0.87 | |
| Totals | 1.08* | 0.57 | 1.70 | 0.56* | 0.23 | 0.94 | 1.96* | 1.61 | 2.40 | 0.22 | 0.04 | 0.41 | 0.51* | 0.25 | 0.80 | ||||||
NOTE.—Aa, amino acid; tRNA, number of cognate tRNA gene copies for the given codon present in the genome (as identified with tRNAscan-SE; Lowe and Eddy 1997); 2.5% and 97.5%, are the quantiles from 1,000 bootstrap samples on  ; and *, indicates that the mean
; and *, indicates that the mean  is statistically different from zero after using Bonferroni's correction for multiple testing (P < 0.005).
is statistically different from zero after using Bonferroni's correction for multiple testing (P < 0.005).
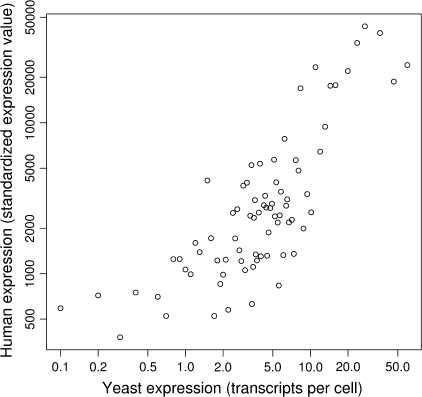
The results indicated above assume that expression levels are conserved for orthologous genes across the genomes studied. There are two problems with this. First, identifying sets of orthologous genes is a complicated matter (Koonin 2005). The organisms studied here have suffered several genome expansions during their evolutionary histories (e.g., Friedman and Hughes 2001; Maere et al. 2005). Groups of orthologous genes have led to the origin of sets of paralogous gene families through genome duplications across these genomes. For example, a single yeast gene might have several homologs in the corresponding mammalian genomes that could be considered true orthologs. The reciprocal BLAT search approach we used would simply find one of those several possible orthologous pairs. For example, once a yeast gene was matched with BLAT against the human RefSeq transcriptome (∼17,000 genes), the newly found, best match human sequence was then matched back to the yeast transcriptome. If the best reciprocal match was the original yeast sequence, then this was considered a suitable orthologous pair and was kept for further analysis, otherwise, it was discarded. Of course, each one of the selected human–yeast orthologous pairs is simply one out of several arbitrary possible pairs. It is important to note that out of ∼5,000 yeast and ∼17,000 human genes, only 1,079 were considered as suitable orthologous pairs for further analysis, so our approach attempted to be as conservative as possible. The other problem is that, even after obtaining such suitable sets of close orthologs, it is not guaranteed that their expression levels will also be conserved. We tested this for the yeast and human expression data. Figure 5 shows that, for the particular set of orthologs analyzed for these two genomes, expression levels are relatively well conserved despite 1,500 My of evolutionary divergence (Wang et al. 1999). Plotting  values versus expression for human produces essentially the same trends observed in figure 4 for this organism (data not shown). These results are encouraging and suggest that a well-conserved core of eukaryotic genes exists across the genomes analyzed with conserved expression values.
values versus expression for human produces essentially the same trends observed in figure 4 for this organism (data not shown). These results are encouraging and suggest that a well-conserved core of eukaryotic genes exists across the genomes analyzed with conserved expression values.
FIG. 5.—
Average expression levels within orthologous gene categories for Homo sapiens and Saccharomyces cerevisiae. The full 77 orthologous categories were used. The Spearman rank correlation between the two data sets is 0.76. This shows that the orthologous genes analyzed here for these organisms have reasonably conserved expression levels despite over 1,500 My of evolutionary divergence (Wang et al. 1999). Using maximum expression levels for human transcripts (i.e., the highest observed value in any tissue) leads to very similar results as reported previously (Urrutia and Hurst 2003). The human expression data were standardized so the median value per tissue equals 100 (Su et al. 2004).
Selection on Codon Usage and tRNA Adaptation
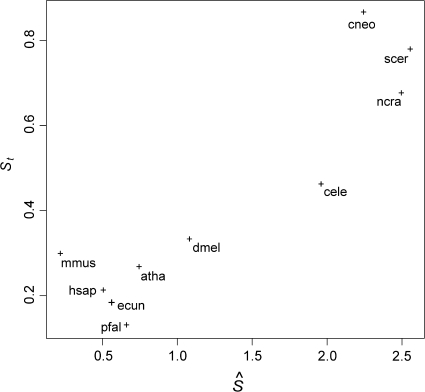
As mentioned above, estimated S values from a given genome simply reflect the log-odds values of codon frequencies between highly and lowly expressed genes. If the observed differences in codon frequencies are due to different mutational biases in both gene sets (e.g., if k is not constant throughout the genome), then misleading (and statistically different from zero) S values might be obtained. A good example of this was reported by Sharp et al. (2005) for the genomes of Xylella fastidiosa and Nitrosomonas europaea, where peculiar base compositions bias the estimation of S values. To help decide whether estimated S values are caused by translational selection and not spurious artifacts, the S values can be compared with the St values suggested by dos Reis et al. (2004). The St test is based on the relationship between the tRNA adaptation index (tAI) and the effective number of codons (Nc) used in a gene (Wright 1990). tAI quantifies how well a protein-coding sequence is adapted to the genomic tRNA pool of an organism, based on the codon frequencies observed in the gene, and how well different tRNAs recognize each codon. If a gene presents a high tAI value, it is assumed that the gene in question is finely tuned to match the tRNA composition of the genome. The correlation (St) between tAI values for a suitably chosen set of genes and their corresponding (corrected) Nc values gives an idea of how well codon usage and tRNA usage are coadapted in a given genome. Because selection for translational optimization acts through codon–tRNA coadaptation (Bulmer 1987), a high St value suggests that translational selection has been operative in the genome in question. Organisms presenting high S values averaged for highly expressed genes should also present high St values. It has been shown that S and St are moderately correlated in bacterial genomes (Sharp et al. 2005). This correlation can be substantially improved if only highly expressed genes are used to compute St (dos Reis M, unpublished data). Both, S and St values, are complementary measures that can give insight into whether true translational selection is operative or not in a given genome. Figure 6 shows that  and St values for the 10 genomes analyzed are indeed correlated. This suggests that adaptation to the genomic tRNA configuration, and not mutational patterns, drives the trends observed in table 2.
and St values for the 10 genomes analyzed are indeed correlated. This suggests that adaptation to the genomic tRNA configuration, and not mutational patterns, drives the trends observed in table 2.
FIG. 6.—
St versus  values for several eukaryotic genomes. Organism codes as in figure 4. St values were calculated as described in dos Reis et al. (2004). The correlation between phylogenetically independent contrasts (Felsenstein 1985) for the two variables is 0.95. The contrasts were calculated for hsap, dmel, cele, scer, and atha based on a phylogeny published for these organisms (Wang et al. 1999).
values for several eukaryotic genomes. Organism codes as in figure 4. St values were calculated as described in dos Reis et al. (2004). The correlation between phylogenetically independent contrasts (Felsenstein 1985) for the two variables is 0.95. The contrasts were calculated for hsap, dmel, cele, scer, and atha based on a phylogeny published for these organisms (Wang et al. 1999).
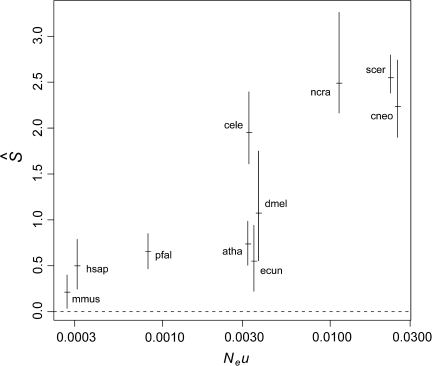
Relationship between S and Effective Population Size
Random drift causes the nonpreferential fixation of certain alleles in a population and the elimination of others. Because the time it takes for an allele to become fixed is proportional to the population size, new mutants at individual sites tend to become fixed relatively quickly in small populations, whereas individual sites tend to remain polymorphic in larger populations. Thus, random drift causes a reduction of genetic diversity, or polymorphism, in small populations (Kimura 1983). This provides a way to use molecular data to estimate population size. Using polymorphism levels from gene alignments, it is possible to estimate the quantity Neμ, which is the product between the effective population size (Ne) and the mutation rate per base pair per generation (μ). If the mutation rate is known, then it can be factored out to obtain an estimate of Ne. Recently, Lynch and Conery (2003) used this idea and gathered estimates of Neμ for several eukaryotic and prokaryotic genomes. This provides us with a unique opportunity to compare those values with estimates of selection on codon usage. This will tell us whether, as should be expected, organisms with small population sizes show signs of reduced selected codon usage bias. Figure 7 shows the estimated S values for the most putatively highly expressed orthologs in the 10 eukaryotic genomes analyzed (these are equivalent to the three most highly expressed bins out of 77 in the yeast analysis), plotted against Lynch and Conery Neμ values. As expected, there is a positive correlation between  and Neμ. The large mammalian genomes (M. musculus and H. sapiens) with low Neμ values show, as expected, low
and Neμ. The large mammalian genomes (M. musculus and H. sapiens) with low Neμ values show, as expected, low  values. On the other hand, the fast-growing fungal genomes (N. crassa, S. cerevisiae, and C. neoformans) show the largest values of
values. On the other hand, the fast-growing fungal genomes (N. crassa, S. cerevisiae, and C. neoformans) show the largest values of  and Neμ. The two multicellular invertebrates (C. elegans and D. melanogaster) and the plant genome (A. thaliana) present intermediate Neμ and
and Neμ. The two multicellular invertebrates (C. elegans and D. melanogaster) and the plant genome (A. thaliana) present intermediate Neμ and  values with large variances. The two intracellular parasites (E. cuniculi and P. falciparum) show relatively low values of
values with large variances. The two intracellular parasites (E. cuniculi and P. falciparum) show relatively low values of  despite intermediate Neμ values.
despite intermediate Neμ values.
FIG. 7.—
Estimated S values for several eukaryotic genomes versus Neμ. Organism codes as in figure 4. The horizontal bars are the mean values, and the vertical bars are the 95% nonparametric bootstrap intervals. The Spearman rank correlation for the phylogenetically independent contrasts (Felsenstein 1985) for the two variables is 0.8. The contrasts were calculated as in figure 6.
The presence of selected codon bias in mammals has been contentious, with reports in favor and against the presence of translational selection (see, e.g., Eyre-Walker 1991; Urrutia and Hurst 2001). Recent works by Urrutia and Hurst (2003), Comeron (2004), and Yang and Nielsen (2008) have shown evidence of selected codon usage in humans and other mammals. The results presented here are compatible with the findings of these authors; however, with our current analysis we cannot assert that  values are statistically different from zero in this group of organisms, until the problem of heterogeneity in k values is addressed. In any case, the general consensus seems to be that translational selection in mammals is either nonexistent or weak. This suffices to show that selection on codon bias is correlated with effective population size as displayed in figure 7. In fact, this correlation would even be stronger if the
values are statistically different from zero in this group of organisms, until the problem of heterogeneity in k values is addressed. In any case, the general consensus seems to be that translational selection in mammals is either nonexistent or weak. This suffices to show that selection on codon bias is correlated with effective population size as displayed in figure 7. In fact, this correlation would even be stronger if the  values for mouse and human were completely on the zero line at the bottom right-hand side of figure 7.
values for mouse and human were completely on the zero line at the bottom right-hand side of figure 7.
Discussion
This study highlights several important issues regarding the estimation of selection on codon usage. On the first hand, which genes are selected and how they are pooled together might have dramatic effects on selection estimates. If a cutoff of 10 transcripts per cell is used to define highly expressed genes, then overall estimates of S in the baker's yeast can range anywhere from 0.75 to 2.6 (fig. 2); because many studies use a few dozen highly expressed genes for these estimates, a lot of variation should be expected. This has important implications when comparisons between different works are made. If different studies on the same organism are based on different genes, estimates of selection could differ substantially from one another despite the fact that both studies analyzed genes that could be considered highly expressed. Recently, there has been some controversy regarding estimates of s in various species of Drosophila (Maside et al. 2004), and part of the discrepancy in the estimated s values in these studies could be explained by the fact that substantially different sets of genes were analyzed. Controlling for intragenomic heterogeneity in translational selection is of great importance in comparative studies. Furthermore, studies comparing estimates of translational selection between distant species are meaningless unless orthologous gene sets are compared. It is hoped that the approach taken in this work of using orthologous sequences to estimate S in distant species will be taken up by other workers.
An important issue is the selection of the reference (i.e., under no selection) gene set in order to estimate the relative mutational bias (k). In their work on translational selection in prokaryotic genomes, Sharp et al. (2005) used all of a genome's ORF to estimate k and then S was estimated for a small subset of 40 highly expressed genes. It is clear that if selection has been widespread in a genome, the above procedure would result in an underestimation of S in highly expressed genes. We repeated Sharp's approach to the yeast genome and found an average value of S for the two most highly expressed bins equal to 2.47, a small underestimation when compared with the value of 2.57 obtained when only the lowest expressed genes are used to estimate k. In an organism like E. coli, where the proportion of genes under selection is substantially higher (dos Reis et al. 2003), the above approach could lead to a larger error. Another problem with the estimation of k is the heterogeneity in mutational bias along genomes (Lynch 2007). In this work, it was assumed that mutational biases are homogeneous along the baker's yeast chromosomes. This is a reasonable assumption given the narrow distribution of G + C content in this genome. However, for some of the other eukaryotes analyzed, such as worm, fly, and human, the estimates of S are less reliable due to the larger variation in G + C content observed in these genomes (C. elegans Sequencing Consortium 1998; Adams et al. 2000; Lander et al. 2001).
This issue seems to be particularly important for the mammalian genomes, where the variation in genomic G + C composition is more pronounced (isochores), reflecting dramatic differences in local mutational patterns. Biased gene conversion and transcriptionally coupled mutation in these genomes could be correlated to expression levels and might produce directional biases in the estimation of S (Birdsell 2002; Duret 2002; Comeron 2004; Lynch 2007). Urrutia and Hurst (2003), Comeron (2004), and Yang and Nielsen (2008) have attempted, in various ways, to analyze the effect of expression levels on selected codon usage after taking into account various mutational effects. Urrutia and Hurst (2003) showed that expression levels in human are correlated with codon bias after correcting for local nucleotide composition, however, is not clear whether their method would account for biased gene conversion or transcriptionally coupled mutation. Comeron (2004) performed a similar analysis of human expression and codon usage and found that transcription-associated mutational bias (TAMB) is a major factor determining codon usage in humans, however, for genes expressed in tissues with no evidence for TAMB, this worker found a definite preference for a set of optimal codons. Finally, Yang and Nielsen (2008) extended well-known codon substitution models to include population genetic parameters and selection on codon usage. Their model implicitly takes into account the local nucleotide composition of a gene, and it uses the phylogenetic relationship among a set of orthologous genes to estimate the substitution parameters. They tested the model on a set of 5,639 orthologs from five mammalian genomes and found, under a likelihood ratio test, that the null hypothesis of no selection on codon bias could be readily rejected. It is not the objective of this work to present a detailed analysis of translational selection in mammals. The estimated S values we report here for human and mouse simply reflect the log-odds ratio of codon usage in lowly versus highly expressed genes. Whether the relatively modest positive deviation we observe in this ratio is due to selection as suggested by the authors above or is due to other forces such as biased gene conversion (Lynch 2007) or TAMB (Comeron 2004) is a contentious topic that requires more research.
Another issue is the meaning of S. This is a confounded parameter that contains a numerical constant (2 or 4), the effective population size (Ne), and the actual selection coefficient (s). The value of the numerical constant depends on whether the organism is haploid or diploid and, in the case of diploidy, on the selection model being considered (Crow and Kimura 1970). Nearly all studies seem to assume genic selection, if this assumption does not hold, then the exact form of S cannot be known unless a different model is explicitly specified. Furthermore, some organisms like the baker's yeast present alternating haploid and diploid phases, which could arguably lead to oscillations between 2Nes and 4Nes, with the estimated value of S being an average over the variable numerical constant. However, it is important to note that S, as defined in this work, is simply the log-odds ratio between the relative frequencies of the optimal codon in highly versus lowly expressed genes. This is, nonetheless, a useful comparative measure of selected codon usage in disparate organisms such as eubacteria, unicellular eukaryotes, or metazoans.
The results presented here show that population size has an important role affecting the operativity of translational selection. The organisms analyzed that presented the largest Neμ values also showed the largest selected codon usage bias. Although this fact was expected, this is the first time it is confirmed by empirical data. Further problems though need to be addressed before a fully clear picture can emerge. Mutation rate per base pair per generation varies from about 1 to 100 × 10−9 in eukaryotes (Lynch 2006), with the lowest rates observed in free living unicellular eukaryotes and the highest rates in vertebrates. This presupposes a negative correlation between Ne and μ (Lynch 2007), which, after being taken into account in figure 7, implies that the actual selection coefficient for codon usage, s, would be unusually high for genomes with low Ne. Another striking issue is that S for bacterial genomes ranges from 0 to 2.6 for the fastest dividing genomes (Sharp et al. 2005), which is about the same range observed here (fig. 7). Giving that average population numbers for bacteria are on the order of 108, this suggests that s would be substantially smaller for prokaryotes than eukaryotes. This paradox has been reviewed by Lynch (2007), and he has proposed that biased gene conversion in eukaryotes might have a substantial role in the overestimation of s in this group. Whether this is the case, it can only be confirmed with a more thorough analysis of mutational patterns in highly expressed genes. Yet another problem is the estimation of Neμ itself. Usually, silent sites in protein-coding gene alignments are used for this, and if translational selection has been widespread in a genome (as seems to be the case for unicellular eukaryotes and eubacteria), then Neμ itself would be underestimated. All these problems highlight the challenges that a more thorough analysis on S extended to a larger set of eukaryotic genomes will have to face.
A final future issue will be to try to understand what ecological factors or lifestyle choices affect population numbers in the organisms studied and hence their degree of selected codon bias. It is interesting to note that among the organisms studied, those with the largest genomes showed the lowest population numbers. Lynch and Conery (2003) have proposed that although prokaryotes evolved toward multicellular eukaryotes, the consequent increase in organism size was linked to a dramatic reduction in population size due to ecological constrains. Because random genetic drift is stronger in smaller populations, this allowed the accumulation of genomic features that would have been eliminated by the action of natural selection in larger populations. These features include the evolution and expansion of introns, gene duplication, and the accumulation of repetitive DNA, mechanisms that account for genome size expansion. Lynch and Conery present convincing evidence showing that indeed population size and genome size are inversely correlated from prokaryotes to eukaryotes. These findings suggest that any form of weak selection tends to be overridden by random drift in organisms with large genomes, and this must include selection on codon usage. Lynch and Conery ideas are very appealing and could provide a nice framework onto which the action of translational selection in eukaryotes could be understood. Why translational selection behaves so idiosyncratically as to optimize codon usage in certain genomes while ignoring others is a puzzling question. Achieving reliable and consistent ways to test for selection in eukaryotes is of paramount importance in order to solve this issue and to gain a deeper understanding of the processes of molecular evolution.
Acknowledgments
This work was partially supported by a studentship grant to M.d.R. by the Biotechnology and Biological Sciences Research Council, UK, and by the Medical Research Council, UK. Thanks to Paul M. Sharp and Adam Eyre-Walker for valuable comments.
References
- Adams MD, Celniker SE, Holt RA, et al. (195 co-authors) The genome sequence of Drosophila melanogaster. Science. 2000;287:2185–2195. doi: 10.1126/science.287.5461.2185. [DOI] [PubMed] [Google Scholar]
- Akashi H. Inferring weak selection from patterns of polymorphism and divergence at “silent” sites in Drosophila DNA. Genetics. 1995;139:1067–1076. doi: 10.1093/genetics/139.2.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi H. Codon bias evolution in Drosophila. Population genetics of mutation-selection drift. Gene. 1997;205:269–278. doi: 10.1016/s0378-1119(97)00400-9. [DOI] [PubMed] [Google Scholar]
- Akashi H. Gene expression and molecular evolution. Curr Opin Genet Dev. 2001;11:660–666. doi: 10.1016/s0959-437x(00)00250-1. [DOI] [PubMed] [Google Scholar]
- Akashi H. Translational selection and yeast proteome evolution. Genetics. 2003;164:1291–1303. doi: 10.1093/genetics/164.4.1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi H, Eyre-Walker A. Translational selection and molecular evolution. Curr Opin Genet Dev. 1998;8:688–693. doi: 10.1016/s0959-437x(98)80038-5. [DOI] [PubMed] [Google Scholar]
- Akashi H, Schaeffer S. Natural selection and the frequency distributions of “silent” DNA polymorphism in Drosophila. Genetics. 1997;146:295–307. doi: 10.1093/genetics/146.1.295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennetzen JL, Hall BD. Codon selection in yeast. J Biol Chem. 1982;257:3026–3031. [PubMed] [Google Scholar]
- Birdsell JA. Integrating genomics, bioinformatics, and classical genetics to study the effects of recombination on genome evolution. Mol Biol Evol. 2002;19:1181–1197. doi: 10.1093/oxfordjournals.molbev.a004176. [DOI] [PubMed] [Google Scholar]
- Bulmer M. Coevolution of codon usage and transfer RNA abundance. Nature. 1987;325:728–730. doi: 10.1038/325728a0. [DOI] [PubMed] [Google Scholar]
- Bulmer M. The selection-mutation-drift theory of synonymous codon usage. Genetics. 1991;129:897–907. doi: 10.1093/genetics/129.3.897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- C. elegans Sequencing Consortium. Genome sequence of the nematode C. elegans: a platform for investigating biology. Science. 1998;282:2012–2018. doi: 10.1126/science.282.5396.2012. [DOI] [PubMed] [Google Scholar]
- Chamary JV, Parmley JL, Hurst LD. Hearing silence: non-neutral evolution at synonymous sites in mammals. Nat Rev Genet. 2006;7:98–108. doi: 10.1038/nrg1770. [DOI] [PubMed] [Google Scholar]
- Chen S, Lee W, Hottes A, Shapiro L, McAdams H. Codon usage between genomes is constrained by genome-wide mutational processes. Proc Natl Acad Sci USA. 2004;101:3480–3485. doi: 10.1073/pnas.0307827100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coghlan A, Wolfe KH. Relationship of codon bias to mRNA concentration and protein length in Saccharomyces cerevisiae. Yeast. 2000;16:1131–1145. doi: 10.1002/1097-0061(20000915)16:12<1131::AID-YEA609>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- Comeron JM. Selective and mutational patterns associated with gene expression in humans: influences on synonymous composition and intron presence. Genetics. 2004;167:1293–1304. doi: 10.1534/genetics.104.026351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An introduction to population genetics theory. New York: Harper and Row; 1970. [Google Scholar]
- Cutter AD, Charlesworth B. Selection intensity on preferred codons correlates with overall codon usage bias in Caenorhabditis remanei. Curr Biol. 2006;16:2053–2057. doi: 10.1016/j.cub.2006.08.067. [DOI] [PubMed] [Google Scholar]
- dos Reis M, Savva R, Wernisch L. Solving the riddle of codon usage preferences: a test for translational selection. Nucleic Acids Res. 2004;32:5036–5044. doi: 10.1093/nar/gkh834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- dos Reis M, Wernisch L, Savva R. Unexpected correlations between gene expression and codon usage bias from microarray data for the whole Escherichia coli K-12 genome. Nucleic Acids Res. 2003;31:6976–6985. doi: 10.1093/nar/gkg897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duret L. Evolution of synonymous codon usage in metazoans. Curr Opin Genet Dev. 2002;12:640–649. doi: 10.1016/s0959-437x(02)00353-2. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: Chapman and Hall; 1993. [Google Scholar]
- Eyre-Walker A, Bulmer M. Synonymous substitution rates in enterobacteria. Genetics. 1995;140:1407–1412. doi: 10.1093/genetics/140.4.1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyre-Walker AC. An analysis of codon usage in mammals: selection or mutation bias? J Mol Evol. 1991;33:442–449. doi: 10.1007/BF02103136. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Phylogenies and the comparative method. Am Nat. 1985;125:1–15. [Google Scholar]
- Friedman R, Hughes AL. Gene duplication and the structure of eukaryotic genomes. Genome Res. 2001;11:373–381. doi: 10.1101/gr.155801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grantham R, Gautier C, Gouy M, Mercier R, Pave A. Codon catalog usage and the genome hypothesis. Nucleic Acids Res. 1980;8:r49–r62. doi: 10.1093/nar/8.1.197-c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harpending HC, Batzer MA, Gurven M, Jorde LB, Rogers AR, Sherry ST. Genetic traces of ancient demography. Proc Natl Acad Sci USA. 1998;95:1961–1967. doi: 10.1073/pnas.95.4.1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl DL, Moriyama EN, Sawyer SA. Selection intensity for codon bias. Genetics. 1994;138:227–234. doi: 10.1093/genetics/138.1.227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holstege FC, Jennings EG, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young RA. Dissecting the regulatory circuitry of a eukaryotic genome. Cell. 1998;95:717–728. doi: 10.1016/s0092-8674(00)81641-4. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J Mol Biol. 1981;151:389–409. doi: 10.1016/0022-2836(81)90003-6. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Codon usage and tRNA content in unicellular and multicellular organisms. Mol Biol Evol. 1985;2:13–34. doi: 10.1093/oxfordjournals.molbev.a040335. [DOI] [PubMed] [Google Scholar]
- Kanaya S, Yamada Y, Kinouchi M, Kudo Y, Ikemura T. Codon usage and tRNA genes in eukaryotes: correlation of codon usage diversity with translation efficiency and with CG-dinucleotide usage as assessed by multivariate analysis. J Mol Evol. 2001;53:290–298. doi: 10.1007/s002390010219. [DOI] [PubMed] [Google Scholar]
- Kimura M. The neutral theory of molecular evolution. Cambridge: Cambridge University Press; 1983. [Google Scholar]
- Knight R, Freeland S, Landweber L. A simple model based on mutation and selection explains trends in codon and amino-acid usage and GC composition within and across genomes. Genome Biol. 2001;2 doi: 10.1186/gb-2001-2-4-research0010. research0010.1–0010.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin EV. Orthologs, paralogs, and evolutionary genomics. Annu Rev Genet. 2005;39:309–338. doi: 10.1146/annurev.genet.39.073003.114725. [DOI] [PubMed] [Google Scholar]
- Lafay B, Atherton J, Sharp P. Absence of translationally selected synonymous codon usage bias in Helicobacter pylori. Microbiology. 2000;146:851–860. doi: 10.1099/00221287-146-4-851. [DOI] [PubMed] [Google Scholar]
- Lander E, Linton L, Birren B, et al. (255 co-authors) Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Lowe TM, Eddy SR. tRNAscan-SE: a program for improved detection of transfer RNA genes in genomic sequence. Nucleic Acids Res. 1997;25:955–964. doi: 10.1093/nar/25.5.955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M. The origins of eukaryotic gene structure. Mol Biol Evol. 2006;23:450–468. doi: 10.1093/molbev/msj050. [DOI] [PubMed] [Google Scholar]
- Lynch M. The origins of genome architecture. Sunderland (MA): Sinauer Assoc; 2007. [Google Scholar]
- Lynch M, Conery J. The origins of genome complexity. Science. 2003;302:1401–1404. doi: 10.1126/science.1089370. [DOI] [PubMed] [Google Scholar]
- Maere S, De Bodt S, Raes J, Casneuf T, Van Montagu M, Kuiper M, Van de Peer Y. Modeling gene and genome duplications in eukaryotes. Proc Natl Acad Sci USA. 2005;102:5454–5459. doi: 10.1073/pnas.0501102102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maside X, Lee A, Charlesworth B. Selection on codon usage in Drosophila americana. Curr Biol. 2004;14:150–154. doi: 10.1016/j.cub.2003.12.055. [DOI] [PubMed] [Google Scholar]
- McVean GA, Charlesworth B. A population genetic model for the evolution of synonymous codon usage: patterns and predictions. Genet Res. 1999;74:145–148. [Google Scholar]
- Percudani R, Pavesi A, Ottonello S. Transfer RNA gene redundancy and translational selection in Saccharomyces cerevisiae. J Mol Biol. 1997;268:322–330. doi: 10.1006/jmbi.1997.0942. [DOI] [PubMed] [Google Scholar]
- Sharp PM, Averof M, Lloyd AT, Matassi G, Peden JF. DNA sequence evolution: the sounds of silence. Philos Trans R Soc Lond B Biol Sci. 1995;349:241–247. doi: 10.1098/rstb.1995.0108. [DOI] [PubMed] [Google Scholar]
- Sharp PM, Bailes E, Grocock RJ, Peden JF, Sockett RE. Variation in the strength of selected codon usage bias among bacteria. Nucleic Acids Res. 2005;33:1141–1153. doi: 10.1093/nar/gki242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PM, Li WH. The codon adaptation index—a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 1987;15:1281–1295. doi: 10.1093/nar/15.3.1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherry ST, Harpending HC, Batzer MA, Stoneking M. Alu evolution in human populations: using the coalescent to estimate effective population size. Genetics. 1997;147:1977–1982. doi: 10.1093/genetics/147.4.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su AI, Wiltshire T, Batalov S, et al. (13 co-authors) A gene atlas of the mouse and human protein-encoding transcriptomes. Proc Natl Acad Sci USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrutia A, Hurst L. Codon usage bias covaries with expression breadth and the rate of synonymous evolution in humans, but this is not evidence for selection. Genetics. 2001;159:1191–1199. doi: 10.1093/genetics/159.3.1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urrutia AO, Hurst LD. The signature of selection mediated by expression on human genes. Genome Res. 2003;13:2260–2264. doi: 10.1101/gr.641103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DY, Kumar S, Hedges SB. Divergence time estimates for the early history of animal phyla and the origin of plants, animals and fungi. Proc Biol Sci. 1999;266:163–171. doi: 10.1098/rspb.1999.0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright F. The ‘effective number of codons’ used in a gene. Gene. 1990;87:23–29. doi: 10.1016/0378-1119(90)90491-9. [DOI] [PubMed] [Google Scholar]
- Yang Z, Nielsen R. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol Biol Evol. 2008;25:568–579. doi: 10.1093/molbev/msm284. [DOI] [PubMed] [Google Scholar]