Generating properly weighted ensemble of conformations of proteins from sparse or indirect distance constraints

Abstract

Inferring three-dimensional structural information of biomacromolecules such as proteins from limited experimental data is an important and challenging task. Nuclear Overhauser effect measurements based on nucleic magnetic resonance, disulfide linking, and electron paramagnetic resonance labeling studies can all provide useful partial distance constraint characteristic of the conformations of proteins. In this study, we describe a general approach for reconstructing conformations of biomolecules that are consistent with given distance constraints. Such constraints can be in the form of upper bounds and lower bounds of distances between residue pairs, contact maps based on specific contact distance cutoff values, or indirect distance constraints such as experimental ϕ-value measurement. Our approach is based on the framework of sequential Monte Carlo method, a chain growth-based method. We have developed a novel growth potential function to guide the generation of conformations that satisfy given distance constraints. This potential function incorporates not only the distance information of current residue during growth but also the distance information of future residues by introducing global distance upper bounds between residue pairs and the placement of reference points. To obtain protein conformations from indirect distance constraints in the form of experimental ϕ-values, we first generate properly weighted contact maps satisfying ϕ-value constraints, we then generate conformations from these contact maps. We show that our approach can faithfully generate conformations that satisfy the given constraints, which approach the native structures when distance constraints for all residue pairs are given.

INTRODUCTION

Three-dimensional structures of biomacromolecules (such as protein, DNA, and RNA molecules) are essential for understanding their biological functions. The primary sources of structural information of biomacromolecules are x-ray diffractions¹ and nuclear magnetic resonance (NMR) experiments.^{2, 3} In NMR studies, the assessment of chemical shifts of atomic nuclei with spins can provide information about distances between specific pairs of atoms. In addition, a number of biochemical techniques such as disulfide linking^{4, 5} and electron paramagnetic resonance labeling^{6, 7} can also provide useful partial information about distances between residues. When accurate values of distances between residue pairs are available, they can be represented by a distance matrix, where an entry (i,j) of the matrix denotes the distance between the corresponding two residues i and j. In other cases, the distance information is inexact, but can be represented by a contact map, which denotes whether the distance of each residue pair is below or above a specified distance threshold.

With distance information of various levels of details, a challenging problem is to integrate all the distance constraints into global information about the properties of ensemble structures of the biomacromolecule.^{2, 8, 9} When the distance constraints are complete and accurate, the positions of all residues can be obtained by carrying out a singular value decomposition calculation.^{10, 11} When the distance constraints are incomplete or inaccurate, one needs to solve an optimization problem and find the structures that best reproduces these distance constraints.^{9, 12, 13} If the size of the molecule is large, this is a very challenging problem.

Several previous studies address the problem of generating protein conformations from contact maps.^{14, 15} These approaches can be expanded to generate conformations when only indirect or implicit distance constraints are available. In Ref. 16, Vendruscolo et al. generated the conformations of the transition state ensemble (TSE) important in protein folding studies. In this case, no explicit distance constraints between residue pairs are given. Rather, indirect information in the form of ϕ-value constraints is known for a subset of residues. Here the ϕ-value at a residue measured experimentally is interpreted as the ratio of the average number of native contacts formed by the residue in the transition state conformations to the number of contacts formed in the native structure of ground state.

In this paper, we focus on protein structures and develop a general method to obtain ensemble of conformations that satisfy distance constraints given either in the form of an incomplete set of distance bounds, a set of binary conditions whether the distance is below or above a specific threshold, or in the indirect form of experimentally measured ϕ-values. Our approach is based on the framework of sequential Monte Carlo (SMC) method, a growth-based method in which residues are added to an existing partial chain one by one until a conformation of full length is obtained.^{17, 18, 19} In addition to generating structures, we can also estimate important physical properties of molecular ensembles. As the probabilities of growing viable conformation samples become exceedingly small because of strong distance constraints and the self-avoiding requirement, an efficient sampling strategy becomes critical in order to obtain full chain conformations consistent with all distance constraints.

This paper is organized as follows. In Sec. 2, we introduce a cubic lattice model and the incomplete and indirect distance constraints we work with. We then discuss the general approach of SMC method and a new growth potential function. Results are presented in Sec. 3.

MODEL AND METHOD

Protein model and distance constraints

Three-dimensional model for proteins

We use a three-dimensional cubic lattice model to represent a protein conformation. The sides of a cubic cell have unit length γ=1.3 Å. A length-n protein conformation is represented by a connected chain x_n=(x₁,x₂,…,x_n), where the ith C_α atom of the conformation is located at site x_i=(x_i1,x_i2,x_i3) on the cubic lattice.^{18, 20, 21}

For proteins molecules, the locations of C_α atoms satisfy certain constraints. We assume the C_α atoms in our model can only be placed on the lattice sites with the following constraints. First, the Euclidean distance between neighboring residues x_i−1 and x_i is between 3.5 and 4.1 Å. Second, the direction of the vector x_i-x_i−1 must be within 30° of four canonical directional vectors, which are specifically determined by the residue type of residue i and the locations x_i−1, x_i−2, and x_i−3. These canonical vectors are derived from a discrete four-state off-lattice model of proteins, which gives four possible locations of x_i for monomer i given the locations of x_i−1, x_i−2, and x_i−3, and the type of residue i−1. Details of obtaining optimal canonical directional vectors are given in Ref. 22. Third, we enforce the self-avoiding constraint. Specifically, non-neighboring residues are not permitted to be closer than 3.5 Å, which is the smallest distance of non-neighboring residues observed in 646 representative proteins from the Protein Data Bank (PDB).

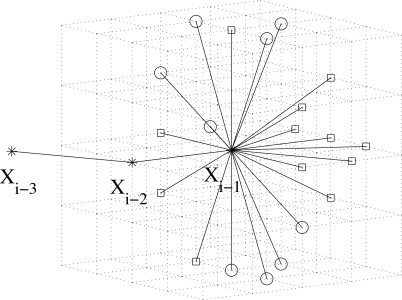
On average, there are about 23 candidate positions for placing x_i in our model, although the exact number depends on the different relative positions of x_i−3, x_i−2, and x_i−1, as well as the type of the (i−1)th residue. Figure 1 provides an illustration of this lattice model.

Figure 1.

Illustration of the cubic lattice model. We have set the cell unit length to 1.8 Å instead of 1.3 Å here for clarity. Given the locations of x_i−3, x_i−2, and x_i−1, there are 21 positions (marked by “◻” and “◯”) satisfying the first distance condition. Only nine positions (marked by “◯”) among them also satisfy the second direction condition. These positions all satisfy the third self-avoidance condition.

Direct distance constraints

Distance constraints for protein chain x_n=(x₁,…,x_n)∊R³ are written in the following general form as

$$l_{ij}\le \Vert x_i-x_j\Vert \le u_{ij}\text{for}\text{all}\left(i,j\right)∊\mathcal{D},$$

where ‖x_i−x_j‖ is the Euclidean distance between residues i and j; l_ij and u_ij are the lower and upper bounds of the distance between residues i and j. Here l_ij can be 0 and u_ij can be +∞ if only upper bound or lower bound is available, respectively. D is a given set of (i,j) residue pairs, in which such constraints are known. D is often a much smaller subset of the complete set of all residue pairs. The problem of determining the conformation x_n=(x₁,…,x_n) according to such distance constraints has been studied before.^{8, 23} In this paper, we focus on constraints of distance between C_α atoms, and we only consider the structure of C_α chain. The general principle can be applied to other types of distance constraints, and side chain repacking methods can be used to generate more detailed protein structures.^{24, 25}

Indirect distance constraints and experimentally measured ϕ-values

An important class of studies on protein folding is to characterize the properties of the TSE. TSE represents the structures around the saddle point of the potential energy surface, and these structures are often followed by a large structural change in protein unfolding process.^{26, 27, 28, 29}

It is challenging to characterize TSE due to the complexity of the folding and unfolding processes. Experimental research on this problem focuses on the measurement of ϕ-value at individual residue position, defined as the ratio of change in stability to the transition state upon mutation versus the change to the native folded state.^{27, 28, 29, 30, 31}

ϕ-value provides information about the native likeness of TSE.^{32, 33} For example, if _ϕi, the ϕ-value at residue i, is close to 1, the transition state is thought to have almost the same structure at residue i as the native state. If _ϕi is close to 0, the transition state is likely to be in the denatured state in this region. An important question therefore is to translate ϕ-value measurements into explicit conformational information of protein structures in the TSE.^{16, 31, 34}

Let ${\varphi }_i^{\text{exp}}$ be the experimentally measured ϕ-value at residue i. Based on experimental observations, it is reasonable to assume that changes in protein stability are proportional to the change in the number of contacts in a protein structure.³⁵ Based on this assumption, the calculated ϕ-value ${\varphi }_i^{\text{calc}}$, which relates to the protein structure, is defined as ${\varphi }_i^{\text{calc}}=C_i^{\text{TSE}}∕N_i^N$, where $C_i^{\text{TSE}}$ is the average number of contacts formed by residue i in the TSE and $N_i^N$ is the number of contacts formed by residue i in the native structure. In studies based on molecular dynamics simulations, Li and Daggett³¹ showed that ${\varphi }_i^{\text{calc}}$ is in good agreement with ${\varphi }_i^{\text{exp}}$. Vendruscolo et al.¹⁶ further introduced a different definition of ${\varphi }_i^{\text{calc}}$,

$${\varphi }_i^{\text{calc}}=\frac{N_i^{\text{TSE}}}{N_i^N},$$ (1)

where $N_i^{\text{TSE}}$ is taken as the average number of native contacts instead of all contacts of residue i in the TSE. In this case, the TSE is defined as the set of conformations with ${\varphi }_i^{\text{calc}}$ very close to the corresponding experimental measured ${\varphi }_i^{\text{exp}}$ at all positions. An important question is therefore how to obtain explicit conformations of TSE that satisfy these indirect distance constraints of ϕ-values. A number of studies have shown promising results.^{16, 34}

Generating conformations with various distance constraints using SMC

In general, one can aim to obtain conformations that are at the global minimum of an error function measuring deviation in distance from the lower bounds and upper bounds of the distance constraints,

$$\mathcal{E}\left({\mathit{x}}_n\right)=\sum _{i,j}\left[{\text{max}}^2\left\{l_{ij}-\Vert x_i-x_j\Vert ,0\right\}+{\text{max}}^2\left\{\Vert x_i-x_j\Vert -u_{ij},0\right\}\right]\text{for}\text{all}\left(i,j\right)∊\mathcal{D},$$ (2)

in which the distance constraints are incomplete and inaccurate.^{9, 12} Our goal is to generate a set of conformations satisfying all distance constraints and following certain target distribution π(x_n), for example, the uniform distribution of all feasible conformations satisfying the distance constraints, or the Boltzmann distribution associated with an energy function. If the true energy function was known, it could be used to estimate the thermodynamics properties of the ensemble of protein conformations following the Boltzmann distribution. In reality, one can approximate the unknown true energy function with various empirically derived energy functions, such as the Miyazaw–Jernighan potential function,³⁶ the geometric poetntial,^{37, 38} and many other potential functions as reviewed in Ref. 39.

Since our goal here is to minimize the error function E(x_n), instead of approximating the true energy function, we can set the energy function to be proportional to the error function [Eq. 2]. More details of this target distributions we use are described in Sec. 3. Let x_t=(x₁,…,x_t) be the vector for the positions of residues from 1 up to t. We recursively place residue t at position x_t following a trial distribution g_t(x_t∣x_t−1). The trial distribution proposes possible positions with different probabilities for residue t to be placed under the condition that positions x₁,…,x_t−1 for residues 1 tot−1 are given. The joint trial distribution for a chain with t residues at positions x₁,…,x_t is given by

$$g_t\left({\mathit{x}}_t\right)=g_1\left({\mathit{x}}_1\right)g_2\left(x_2\mid {\mathit{x}}_1\right)\cdots g_t\left(x_t\mid {\mathit{x}}_{t-1}\right).$$

Following the principle of importance sampling,^{40, 41, 42} the design of the trial distribution can accommodate different types of bias, which allows great flexibility for improving sampling efficiency. However, each final sample of full length chain x_n needs to be weighted to remove the bias so the original target distribution π(x_n) can be recovered. Specifically, we assign a weight

$$w\left({\mathit{x}}_n^{\left(j\right)}\right)=\pi \left({\mathit{x}}_n^{\left(j\right)}\right)∕g_n\left({\mathit{x}}_n^{\left(j\right)}\right)$$

to each conformation sample ${\mathit{x}}_n^{\left(j\right)}$, j=1,…,m, where g_n(x_n) is the trial distribution of the full chain. Then the expected mean value of physical property represented by a function h(x_n) of conformation x_n following the target distribution π(x_n) can be estimated by

$${\mathbb{E}}_{\pi }\left(h\left({\mathit{x}}_n\right)\right)\simeq \frac{{\sum }_{j=1}^{m}w\left({\mathit{x}}_n^{\left(j\right)}\right)h\left({\mathit{x}}_n^{\left(j\right)}\right)}{{\sum }_{j=1}^{m}w\left({\mathit{x}}_n^{\left(j\right)}\right)}.$$

We adopt the framework developed in Ref. 43 to generate sample conformations which minimizes the loss introduced in the resampling step when choosing a number of distinct samples from a larger sample set. It helps to maintain the diversity of the samples. Let m_t be the number of samples we retain in the tth iteration, m_max be the maximum value of m_t, the algorithm for generating samples are described in Algorithm 1.

Algorithm 1 Generating conformation

Set m1=1, $w_1^{\left(1\right)}=1.0$ and place the first residue at fixed $x_1^{\left(1\right)}$.
for t=2 to n do
Lt=0;
{Lt: number of length t chains that can be obtained from samples obtained at step t−1.}
for sample j=1:mt−1 do
Find all of the valid sites $x_t^{\left(i,j\right)}$$i=1,\cdots ,l_t^{\left(j\right)}$ for placing xt next to partial chain $x_{t-1}^{\left(j\right)}$.
{$l_t^{\left(j\right)}=\text{number}$ of available sites to place xt next to partial chain $x_{t-1}^{\left(j\right)}$}.
Generate $l_t^{\left(j\right)}$ number of t-length chain ${\tilde{x}}_t^{\left(L_t+i\right)}=\left(x_{t-1}^{\left(j\right)},x_t^{\left(i,j\right)}\right)$
${\tilde{w}}_t^{\left(L_t+i\right)}=w_{t-1}^{\left(j\right)}$. {Temporary weights for uniform distribution.}
$L_t=L_t+l_t^{\left(j\right)}$.
end for
if Lt≤mmax then
Let mt=Lt and ${\left\{\left(x_t^{\left(j\right)},w_t^{\left(j\right)}\right)\right\}}_{j=1}^{m_t}={\left\{\left({\tilde{x}}_t^{\left(l\right)},{\tilde{w}}_t^{\left(l\right)}\right)\right\}}_{l=1}^{L_t}$.
else
Let mt=mmax.
for l=1 to Lt do
Assign a priority score ${\beta }_t^{\left(l\right)}$ for chain ${\tilde{x}}_t^{\left(l\right)}$ according to the constraints.
end for
Find constant c such that ${\sum }_{l=1}^{L_t}\text{min}\left\{c{\beta }_t^{\left(l\right)},1\right\}=m_{\text{max}}$. {e.g. by binary search.}
Draw r from uniform distribution U[0,1).
for j=1:mmax do
Let rj=j−r.
Find integer Jj such that ${\sum }_{l=1}^{J_j-1}\text{min}\left\{c{\beta }_t^{\left(l\right)},1\right\}<r_j\le {\sum }_{l=1}^{J_j}\text{min}\left\{c{\beta }_t^{\left(l\right)},1\right\}$.
Select sample $x_t^{\left(j\right)}={\tilde{x}}_t^{\left(J_j\right)}$.
Set weight $w_t^{\left(j\right)}={\tilde{w}}_t^{\left(J_j\right)}∕\text{min}\left\{c{\beta }_t^{\left(J_j\right)},1\right\}$.
end for
end if
end for
for j=1:mn do
Calculate importance weight $w\left(x_n^{\left(j\right)}\right)\propto w_n^{\left(j\right)}\pi \left(x_n^{\left(j\right)}\right)$.
end for

The key step in this algorithm is to construct high quality priority scores ${\beta }_s^{\left(l\right)}$, which works as the trial distribution g_t(x_t∣x_t−1) to guide the growth of the partial chains toward more profitable regions.

In this algorithm, it is not necessary to require the growth starts from the first residue x₁. In fact, growth can start from any place, as long as the newly placed monomer is connected to the existing partial chain. For example, growth can start in one direction from a position in the middle of the primary sequence of the chain. After it reaches the end of the chain, the growth process can go back to the starting residue and continue to grow in the other direction of the primary sequence. That is, the order of placing residues can be (x_k,x_k−1,…,x₁,x_k+1,…,x_n) or (x_k,x_k+1,…,x_n,x_k−1,…,x₁) for any residue k located in the middle of the chain. The steps of adding a new residue to existed partial chain are the same as above. In this study, we choose the order of placing residues so that the fragment of the first 20 residues to be placed has the largest number of distance constraints.

Priority score

The choice of a good priority score _βt used in Algorithm 1 is very important. A carefully designed _βt can successfully guide the growth of the conformation so that the full chain will eventually obey all the distance constraints, hence increasing the sampling acceptance rate. A difficulty in the growth-based method is that when adding current residue, the distance information of future residues cannot be directly used. To solve this problem, the priority score we develop consists of three components: growth potential from upper bounds of the distance constraints, growth potential from reference points, and growth potential from lower bounds of the distance constraints. The first two components of the priority score incorporate the distance information of future residues.

Growth potential from upper bounds of the distance constraints

Given the upper bounds for the distances between residue pairs in a subset D of all residue pairs, we first develop distance upper bounds λ_ij between all residue pairs (i,j), i,j=1,…,n.

Let q(k) be an upper bound of distances between two residues that are k residues away in the protein primary sequence. For constructing the upper bounds q(k) for small sequence separation k, we enumerate self-avoiding chains on the discrete lattice model using the protein sequence of interest. We have

$$q\left(k\right)=\underset{i}{\text{max}}\underset{\mathit{x}\left(i,k\right)}{\text{max}}\left(\Vert x_{i+k}-x_i\Vert \right),$$

where x(i,k) is a self-avoiding chain of length k starting at residue i. In this study, we enumerate fragments of chains for k=1,…,5 at different starting positions i, and take the largest as q(k). When sequence separation k is large, enumeration is infeasible. We approximate q(k) by k₁q(5)+q(k₂) if k=5k₁+k₂, where k₁∊Z, k₂=0,…,4. This is an upper bound as it assumes the chain is attached at some residues without angle constraint.

Consider a complete graph G with n vertices, each vertex represents a residue. The length of edge between any two vertices i and j is set to

$$e_{ij}=\{\begin{array}{ll}\text{min}\left\{u_{ij},q\left(\mid i-j\mid \right)\right\},\hfill & \text{if}\left(i,j\right)∊\mathcal{D}\hfill \\ q\left(\mid i-j\mid \right),\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

We can use the Floyd algorithm⁴⁴ to identify the shortest path p_ij between any two vertices i and j in this complete graph G. The distance upper bound λ_ij between residues i and j is then set to the total length of the shortest path p_ij.

After obtaining the distance upper bound λ_ij and the corresponding path p_ij, we construct the potential function thatcontributes to the priority score as

$$f_1\left({\mathit{x}}_t\right)=\sum _{i<j,\left(i,j\right)∊\mathcal{P}}{h}_1\left(\Vert x_i-x_j\Vert ,{\lambda }_{ij}\right),$$ (3)

where P is a set of (i,j) pairs such that on the shortest pathp_ij between i and j, the two ends x_i and x_j are in the partial chain x_t, but none of the residues between i and j are in x_t. This is to avoid double counting of the distance constraints. The function h₁ is a loss function to measure the violation of constraint ‖x_i−x_j‖≤λ_ij. Usually, h₁(‖x_i−x_j‖,λ_ij) is set to zero when ‖x_i−x_j‖≤λ_ij, and monotonically nondecreasing as ‖x_i−x_j‖−λ_ij increases. Different types of h₁(⋅) can be chosen for different considerations, which we will discuss in detail in later sections.

Growth potential from reference points

Given a partial chain x_t, if the position of a future residue j (x_j∉x_t) is strongly constrained, e.g., there are more than four residues in the existing chain x_t having distance constraints related to residue j, then residue j can only be placed in a small spatial region. We generate candidate position for x_j on lattice sites within this small space. More specifically, if a future residue j has distance constraints,

$$l_{i_{k}j}\le \Vert x_{i_k}-x_j\Vert \le u_{i_{k}j},k=1,\dots ,K,$$

where x_ik, k=1,…,K, are in the existing chain x_t, and K≥5, we use Newton’s climbing method⁴⁵ to find a position z in R³ such that

$$z=\text{arg}\underset{x}{\text{min}}F\left(x\right)=\text{arg}\underset{x}{\text{min}}\sum _{k=1}^K{\left(\Vert x_{i_k}-x\Vert -u_{i_{k}j}\right)}^2,$$

in which z is obtained by iteratively performing z=z−(F^″(z))⁻¹F^′(z). We then search the sites on the cubic lattice around position z and choose the site x that minimizes

$$\sum _{k=1}^K\left[{\text{max}}^2\left\{l_{i_{k}j}-\Vert x_{i_k}-x\Vert ,0\right\}+{\text{max}}^2\left\{\Vert x_{i_k}-x\Vert -u_{i_{k}j},0\right\}\right]$$

as the candidate position for residue j. Denote the candidate position as $x_j^{*}$, we use it as a reference point to guide the growth of the chain. The following potential function is used to encode this:

$$f_2\left({\mathit{x}}_t\right)=\sum _{\left(i,j\right)∊{\mathcal{P}}^{\prime }}{h}_2\left(\Vert x_i-x_j^{*}\Vert ,{\lambda }_{ij}\right),$$ (4)

where P^′ is a set of (i,j) pairs such that on the shortest pathp_ij between i and j, x_i is in the partial chain x_t constructed so far, $x_j^{*}$ is the reference point, and none of the residues between i and j are in x_t. As before, h₂ is the loss function to measure the violation of constraint $\Vert x_i-x_j^{*}\Vert \le {\lambda }_{ij}$.

Growth potential from lower bounds of the distance constraints

This potential function penalizes the violation of lower bound constraint,

$$f_3\left({\mathit{x}}_t\right)=\sum _{\left(i,j\right)∊\mathcal{S}\cap \mathcal{D}}{h}_3\left(\Vert x_i-x_j\Vert ,l_{ij}\right),$$ (5)

where S is the set of residue pair (i,j) in which x_i and x_j exist in the partial chain x_t. Here h₃ is the loss function to measure the violation of constraint ‖x_i−x_j‖≥l_ij. Hence, h₃(‖x_i−x_j‖,l_ij)=0, when ‖x_i−x_j‖≥l_ij, and is monotonically nondecreasing as ‖x_i−x_j‖−l_ij decreases.

Combined priority score

The combined priority score ${\beta }_t^{\left(l\right)}$ for chain ${\tilde{\mathit{x}}}_t^{\left(l\right)}$ is set as

$${\beta }_t^{\left(l\right)}=\text{exp}\left[-\frac{{\rho }_1{f}_1\left({\tilde{\mathit{x}}}_t^{\left(l\right)}\right)+{\rho }_2{f}_2\left({\tilde{\mathit{x}}}_t^{\left(l\right)}\right)+{\rho }_3{f}_3\left({\tilde{\mathit{x}}}_t^{\left(l\right)}\right)}{{\tau }_t}\right],$$ (6)

where ρ₁,ρ₂, and ρ₃ are coefficients of the three growth potential functions, τ_t is a temperaturelike variable. The choice of loss functions h₁, h₂, and h₃ in f₁, f₂, and f₃, and coefficients ρ₁,ρ₂,ρ₃,τ_t will be described in later sections.

Generating conformations from incomplete residue distance constraints

In this section, we discuss how to use Algorithm 1 to generate protein conformations with given constraints in the form of small intervals of distances between a subset of residue pairs. The distance constraints are represented as^{12, 13}

$$d_{ij}-{ϵ}_{ij}\le \Vert x_i-x_j\Vert \le d_{ij}+{ϵ}_{ij}\text{for}\text{all}\left(i,j\right)∊\mathcal{D},$$

where d_ij is the distance of residues i and j in the native structure. The set D is assigned as follows: each non-neighboring residue pair within short range distance (SRD) in the native structure is selected in D with a certain probability, e.g., (20%, 40%,…, 100%) independently. The SRD is selected as 10 Å for residue level structure followingRef. ¹³. All residue pairs with distance d_ij>10 Å are excluded from D. Variations ϵ_ij, ϵ_ij of the bounds are randomly selected from uniform distribution U[0,1) independently, so that the distance variation is under 1 Å, about 10% of the true distance d_ij as in Ref. 13.

In this problem, the priority score in Algorithm 1 is set for Eq. 6 with

$$h_1\left(z,\lambda \right)=h_2\left(z,\lambda \right)=\{\begin{array}{cc}{\left(z-\lambda \right)}^2,& \text{if}z>\lambda \\ 0,& \text{if}z\le \lambda ,\end{array}\phantom{\}}$$

and

$$h_3\left(z,l\right)=\{\begin{array}{cc}{\left(z-l\right)}^2,& \text{if}z<l\\ 0,& \text{if}z\ge l,\end{array}\phantom{\}}$$

for f₁, f₂, and f₃, and parameters are set as ρ₁=1, ρ₂=1, ρ₃=1, and τ_t=0.5. Here z is the value of the corresponding distance.

The loss functions are chosen so that the distance between any two residues i and j in the conformational sample does not deviate too much from the given constrained interval [l_ij,u_ij], in case that not all constraints can be perfectly satisfied simultaneously. The loss functions h₁, h₂, and h₃ are concave downward functions of the distance ‖x_i−x_j‖, which increases rapidly as ‖x_i−x_j‖ departs the constrained interval [l_ij,u_ij].

Generating conformations from contact map of distance cutoff

We now describe how to generate conformations based on a given incomplete contact map, where distances between some residue pairs are known to be either above or below a cutoff value in our calculation. We use 8.5 Å as the cutoff value. This value has been used by Vendruscolo et al. in Ref. 16.

The contact map of a length n polymer chain is a n×n symmetric matrix C={c_ij}_n×n, where c_ij=1 if residues i and j are in contact, and c_ij=0 otherwise. A given contact map is equivalent to a set of distance constraints,

$$\Vert x_i-x_j\Vert \le 8.5\text{Å}\text{for}\text{all}{c}_{ij}=1,$$

$$\Vert x_i-x_j\Vert >8.5\text{Å}\text{for}\text{all}{c}_{ij}=0.$$

For this problem, we use

$$h_1\left(z,\lambda \right)=h_2\left(z,\lambda \right)=\mathbb{I}\left(z-\lambda >0\right)$$

and

$$h_3\left(z,l\right)=\mathbb{I}\left(z-l<0\right),$$

in Eqs. 3, 4, 5, respectively, to construct the priority score in Eq. 6. Here I(⋅) is the indicator function: I(⋅)=1 if the statement represented by (⋅) is true, 0 otherwise. Parameters in Eq. 6 are taken as ρ₁=1, ρ₂=1, ρ₃=0.8, and τ_t=0.2.

The loss functions are chosen in order to keep the contact map of the generate conformational samples as close to the given target contact map as possible if not completely satisfied. In particular, if the distance ‖x_i−x_j‖ violates the distance constraint, the corresponding loss function increases from 0 to 1 instantly.

Generating contact maps and conformations from indirect distance constraints by ϕ-values

In this section, we describe how to obtain contact maps based on indirect distance constraints in the form of experimentally measured ϕ-values.

Generating contact maps from indirect distance constraints

ϕ-values of TSE and contact maps. For generating conformations of the TSE, our target distribution π(x_n) is the uniform distribution of all conformations x_n satisfying the ϕ-value constraints,

$${\varphi }_i^{\text{calc}}\left({\mathit{x}}_n\right)=\frac{N_i^{\text{TSE}}}{N_i^N}\approx {\varphi }_i^{\text{exp}},i∊\mathcal{I}=\left\{I_1,\dots ,I_T\right\},$$

where I represents the set of residues whose ϕ-values have been measured experimentally, and I₁,…,I_T are the indexes of these residues. By definition, ${\varphi }_i^{\text{calc}}\left({\mathit{x}}_n\right)$ can be computed when the conformation x_n of the full chain is known. When only information of partial chains x_t−1 is available during chain growth, it is difficult to construct an effective conditional trial distribution g_t(x_t∣x_t−1).

Our approach is to translate the ϕ-value constraints into contact maps of equivalent distance constraints. These contact maps provide more direct information on distance constraints for generating conformations. We then sample conformations following the contact map constraints, which willautomatically satisfy all ϕ-value constraints. We describe briefly how to generate conformations from these ϕ-value derived contact maps in Sec. 2F2.

From ϕ-values to contact maps. Because of the intrinsic symmetry of the contact map C={c_ij}_n×n, we consider c_ij and c_ji as the same entry in C. Let N be the set of residue pairs (i,j) forming native contacts. By definition, the calculated ϕ-value ${\varphi }_i^{\text{calc}}$ for residue i of a conformation only depends on the values of c_ij in its contact map that are native contacts formed by residue i. Let

$${\mathcal{C}}_i=\left\{c_{ij}\mid \left(i,j\right)∊\mathcal{N}\right\}.$$

The size of this set, ∣C_i∣, is the number of contacts formed by residue i in native structure. Note that if (i,j)∊N, both C_i and C_j contain c_ij.

To generate contact map C satisfying the ϕ-value constraints, we only need to decide which subset of native contacts to preserve for residue i whose experimental ϕ-value is available. To satisfy the ϕ-value constraint, there needs to be $\mid {\mathcal{C}}_i\mid \cdot {\varphi }_i^{\text{exp}}$ number of native contacts preserved for residue i in the contact map. That is, we need to assign either 0 or 1 to elements in C_i,i∊I, such that there are exactly $\mid {\mathcal{C}}_i\mid \cdot {\varphi }_i^{\text{exp}}$ number of “1” s in C_i. That is, for each generated contact map we should have ${\sum }_{c_{ij}∊{\mathcal{C}}_i}{c}_{ij}=\mid {\mathcal{C}}_i\mid \cdot {\varphi }_i^{\text{exp}}$, i∊I. For simplicity, we denote ${\Psi }_i=\mid {\mathcal{C}}_i\mid \cdot {\varphi }_i^{\text{exp}}$ in the subsequent discussion.

Now we generate contact map samples properly weighted with respect to the uniform distribution of all contact maps that physically satisfy the ϕ-value constraints. Each contact map sample C generated by importance sampling via the use of a trial distribution g(C) is weighted by v=1∕g(C). Here g(C) is the probability to generate contact map C.

A similar problem has been studied in Ref. 46 for generating 0–1 tables with fixed marginal sums. Although in our problem, the contact map has to be symmetric and only part of it needs to be filled, some techniques in Ref. 46 can be used to improve the sampling efficiency.

Specifically, we proceed by assigning the proper numbers of “1’s” and “0’s” in the rows for residues with experimental ϕ-value measurement. That is, we fill 0’s and 1’s in C_i, i∊I, and repeat this position after position, until the rows corresponding to all residues with experimental ϕ-value measurement are assigned. Let m^* denote the number of contact map samples we will generate, ${\mathcal{C}}_{I_1:I_t}^k$ denote the partially filled kth contact map we have obtained thus far after finishing positions I₁ to I_t, and $v_t^{\left(k\right)}$ be the weight of the kth contact map that has been partially filled up to position I_t. The algorithm for generating contact maps from ϕ-value measurement is listed as Algorithm 2.

Algorithm 2 Generating contact map

for k=1 to m* do
${\mathcal{C}}_{I_1:I_0}^{\left(k\right)}=\stackrel{/}{0},v_0^{\left(k\right)}=1$
end for
for position index t=1 to T do
for sample k=1 to m* do
for s=t to T do
Divide CIs into disjoint sets ${\mathcal{S}}_{0,I_s}^{\left(k\right)}$, ${\mathcal{S}}_{1,I_s}^{\left(k\right)}$, and ${\mathcal{S}}_{u,I_s}^{\left(k\right)}$ based on partial contact map ${\mathcal{C}}_{I_1:I_{t-1}}^{\left(k\right)}$, where ${\mathcal{S}}_{1,I_s}^{\left(k\right)}=\left\{{\mathcal{C}}_{I_s,j}\mid \text{already}\text{filled}\text{with}1\right\}$, ${\mathcal{S}}_{0,I_s}^{\left(k\right)}=\left\{{\mathcal{C}}_{I_s,j}\mid \text{already}\text{filled}\text{with}0\right\}$, and ${\mathcal{S}}_{u,I_s}^{\left(k\right)}=\left\{{\mathcal{C}}_{I_s,j}\mid \text{unspecified}\right\}$.
end for
repeat
for s=t to T do
if $\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid >{\Psi }_{I_s}$ then
Remove this sample. {Already too many “1”s.}
else if $\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid ={\Psi }_{I_s}$ then
Fill all elements in ${\mathcal{S}}_{u,I_s}^{\left(k\right)}$ with 0.
Update ${\mathcal{S}}_{0,I_j}^{\left(k\right)}$, ${\mathcal{S}}_{1,I_j}^{\left(k\right)}$, ${\mathcal{S}}_{u,I_j}^{\left(k\right)}$, j∊{t,⋯,T}.
end if
if $\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid +\mid {\mathcal{S}}_{u,I_s}^{\left(k\right)}\mid <{\Psi }_{I_s}$. then
Remove this sample. {Already too many “0”s.}
else if $\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid +\mid {\mathcal{S}}_{u,I_s}^{\left(k\right)}\mid ={\Psi }_{I_s}$ then
Fill all elements in ${\mathcal{S}}_{u,I_s}^{\left(k\right)}$ with 1.
Update ${\mathcal{S}}_{0,I_j}^{\left(k\right)}$, ${\mathcal{S}}_{1,I_j}^{\left(k\right)}$, ${\mathcal{S}}_{u,I_j}^{\left(k\right)}$, j∊{t,⋯,T}.
end if
end for
until ${\mathcal{S}}_{u,I_t}^{\left(k\right)}=\stackrel{/}{0}$, or none of ${\mathcal{S}}_{0,I_s}^{\left(k\right)}$, ${\mathcal{S}}_{1,I_s}^{\left(k\right)}$, ${\mathcal{S}}_{u,I_s}^{\left(k\right)}$, s∊{t,⋯,T} changes.
{This step must converge because the number of unspecified positions decreases monotonically as the iteration proceeds.}
if ${\mathcal{S}}_{u,I_t}^{\left(k\right)}=\stackrel{/}{0}$ then
${\mathcal{C}}_{I_t}^{\left(k\right)}$ is completed and let weight $v_t^{\left(k\right)}=v_{t-1}^{\left(k\right)}$.
else
Fill ${\mathcal{S}}_{u,I_t}^{\left(k\right)}$ with ${\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_t}^{\left(k\right)}\mid$ “1”s following CP-distribution.
{When there are unspecified entries in this row.}
Update weight $v_t^{\left(k\right)}$ by Eq. 8.
end if
end for
Optionally resample38${\left\{\left({\mathcal{C}}_{I_1:I_t}^{\left(k\right)},v_t^{\left(k\right)}\right)\right\}}_{k=1}^{m^{*}}$ if many samples were removed.
end for

Constrained Poisson (CP) distribution. The details of CP distribution can be found in Ref. 47. Briefly, we sample 0’s and 1’s to fill each entry $s_1,\dots ,s_{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }$ of ${\mathcal{S}}_{u,I_t}^{\left(k\right)}$ described in Algorithm 2 with probability proportional to

$$g\left(s_1,\dots ,s_{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }\right)\propto \prod _{j=1}^{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }{p}_j^{s_j}{\left(1-p_j\right)}^{1-s_j},$$

and the total number of assigned 1’s is ${\sum }_{j=1}^{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }{s}_j={\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_t}^{\left(k\right)}\mid$. Here p_j∊[0,1 stretchy=’true’] are the chosen parameters to improve the sample survival probability of this distribution.

Parameters for conditional Poisson (CP) distribution. For each entry $s_j∊{\mathcal{S}}_{u,I_t}^{\left(k\right)}$ to be filled (whose corresponding entry in the contact map is c_It,Jj), we assign the parameter p_j for the CP distribution as

$$p_j=\{\begin{array}{ll}\frac{{\Psi }_{J_j}-\mid {\mathcal{S}}_{1,J_j}^{\left(k\right)}\mid }{\mid {\mathcal{S}}_{u,J_j}^{\left(k\right)}\mid },\hfill & \text{if}{c}_{I_t,J_j}∊{\mathcal{S}}_{u,I_t}^{\left(k\right)}\cap A\hfill \\ \text{max}\left\{\frac{{\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_t}^{\left(k\right)}\mid -{\sum }_{c_{I_t,i}∊{\mathcal{S}}_{u,I_t}^{\left(k\right)}\cap A}{p}_i}{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\backslash A\mid },0.1\right\},\hfill & \text{if}{c}_{I_t,J_j}∊{\mathcal{S}}_{u,I_t}^{\left(k\right)}\backslash A,\hfill \end{array}\phantom{\}}$$

where A={c_It,It+1,c_It,It+2,…,c_It,IT} are entries recording existence of contacts between residue I_t and other future residues with experimental ϕ-values.

If J_j is a position with ϕ-measurement but currently unspecified, we assign p_j as the ratio of the number of 1’s to be assigned ${\Psi }_{J_j}-\mid {\mathcal{S}}_{1,J_j}^{\left(k\right)}\mid$ and the number of unspecified positions $\mid {\mathcal{S}}_{u,J_j}^{\left(k\right)}\mid$ for residue J_j.

If J_j is a position currently unspecified but not a position with known ϕ-measurement, we assign p_j as the ratio of the number of 1 to be assigned ${\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_t}^{\left(k\right)}\mid$, minus an expected number ${\sum }_{c_{I_t,i}∊{\mathcal{S}}_{u,I_t}^{\left(k\right)}\cap A}{p}_i$ of 1’s that will be assigned for future positions with ϕ values, and the number $\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\backslash A\mid$ of unspecified positions without known ϕ-values, or the value of 0.1, which ever is larger. This choice of p_j is expected to fill ${\Psi }_{J_j}-\mid {\mathcal{S}}_{1,J_j}^{\left(k\right)}\mid$ number of 1’s in $\mid {\mathcal{S}}_{u,j}^{\left(k\right)}\mid$ for j∊{I_t,I_t+1,…,I_T}. Note that in this assignment, p_i is guaranteed to have a value between 0 and 1.

Realization of CP distribution. The overall idea for sampling from the CP distribution is to take out ${\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid$ number of elements from the set ${\mathcal{S}}_{u,I_t}^{\left(k\right)}$ one by one without following specific probability replacement. These elements will be assigned as 1’s, while the remaining ones will be 0’s.⁴⁶

Specifically, let a_j=p_j∕(1−p_j). Suppose ${\overline{\mathcal{S}}}_{u,I_t}^{\left(k\right)}\left(i\right)$ are the remaining elements after taking out i elements $\left(i=0,1,\dots ,{\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid -1\right)$. Each $s_j∊{\overline{\mathcal{S}}}_{u,I_t}^{\left(k\right)}\left(i\right)$ will be selected as next element to be taken out and assigned the value of 1 with probability

$$P\left(s_j,{\overline{\mathcal{S}}}_{u,I_t}^{\left(k\right)}\left(i\right)\right)=\frac{a_j\cdot R\left({\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid -i-1,{\overline{\mathcal{S}}}_{u,I_t}^{\left(k\right)}\left(i\right)\backslash \left\{s_j\right\}\right)}{\left({\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid -i\right)\cdot R\left({\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid -i,{\overline{\mathcal{S}}}_{u,I_t}^{\left(k\right)}\left(i\right)\right)},$$

where R(i,S) is

$$R\left(i,\mathcal{S}\right)=\sum _{\mathcal{B}\subset \mathcal{S},\mid \mathcal{B}\mid =i}\left(\prod _{j∊\mathcal{B}}{a}_j\right).$$ (7)

It is the summation of ∏_j∊Ba_j of all size i subsets B in S.

For an integer i and a subset $\mathcal{S}\subset {\mathcal{S}}_{u,I_t}^{\left(k\right)}$, R(i,S) can be calculated using the recursive formula

$$R\left(i,\mathcal{S}\right)=R\left(i,\mathcal{S}\backslash \left\{s_j\right\}\right)+a_{i}R\left(i-1,\mathcal{S}\backslash \left\{s_j\right\}\right)$$

for any s_j∊S. The initial conditions for the recursion are R(0,S)=1 for any $\mathcal{S}\subset {\mathcal{S}}_{u,I_t}^{\left(k\right)}$ and R(i,S)=0 for any ∣S∣<i.

Updating sample weight. The weight associated with a sample of contact map is updated as

$$v_t^{\left(k\right)}=v_{t-1}^{\left(k\right)}\cdot \frac{R\left({\Psi }_{I_t}-\mid {\mathcal{S}}_{1,I_s}^{\left(k\right)}\mid ,{\mathcal{S}}_{u,I_t}^{\left(k\right)}\right)}{{\prod }_{j=1}^{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }{a}_j^{s_j^{\left(k\right)}}},$$ (8)

where $s_1^{\left(k\right)},\dots ,s_{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }^{\left(k\right)}$ is a realization of $s_1,\dots ,s_{\mid {\mathcal{S}}_{u,I_t}^{\left(k\right)}\mid }$ for the kth contact map and R(i,S) is defined in Eq. 7.

Generating conformations from contact map samples derived from ϕ-values

With a set of properly weighted samples of contact map $\left\{\left({\mathcal{C}}^{\left(k\right)},v_T^{\left(k\right)}\right),k=1,\dots ,m^{*}\right\}$, we draw a subset of it. The probability for each sample to be drawn is proportional to $v_T^{\left(k\right)}$. For each selected contact map, we use it as the target contact map to generate conformations following Algorithm 1, using the priority score described in Sec. 2E. The set of the generated conformations form the TSE.

RESULTS

Result of generating conformations from incomplete residue distance constraints

This section shows the result of generating protein conformations with given constraints in the form of small intervals of distances for a subset of residue pairs as described in Sec. 2D.

Consider the Boltzmann distribution π(x_n)∝exp{−E(x_n)∕τ∣D∣}, where E(x_n)∕∣D∣ is the error function defined in Eq. 2 normalized by the number of constraints, τ is a temperaturelike parameter in the Boltzmann function. It reflects deviation from the lower and upper bounds of the distance constraints. Here we set τ=0.5. We use Algorithm 1 to estimate the expected root mean square distance (rmsd) to the native structure of conformations following this Boltzmann distribution. The algorithm is applied to 189 proteins chosen from PDB, whose lengths are between 80 and 120. The distance constraints are constructed for non-neighboring residue pairs whose distances are less than 10 Å (SRD). The percentage of SRD pairs included in the given constraint set D varies from 20% to 100%.

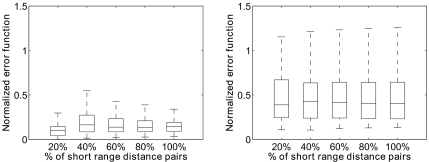
The growth priority score used in Algorithm 1 is described in Sec. 2D. We repeat the algorithm 20 times independently with at most m_max=1000 samples being kept during each computation. The corresponding estimated rmsd expectations of distance constraint set D that includes different percentages of SRDs are plotted in Fig. 2. The boxes in the figure have lines at the lower quartile, median, and upper quartile values of the estimated expectations of the 189 proteins. We can see the corresponding expectation of rmsd becomes smaller as the percentage of the constraints increases. This is expected, as the Boltzmann probabilities π(x_n) of conformations close to the native structure tend to be larger as more distance constraints are available.

Figure 2.

Box plot of expected to native structures rmsd expectations measured in Å of conformations following Boltzmann distribution of the error function π(x_n)∝exp{−E(x_n)∕τ∣D∣} for 189 proteins with length between 80 and 120. The boxes have lines at the lower quartile, median, and upper quartile values. The lines extending from each end of the boxes are to show the rest of the data. X axis is the percentage of native SRD pairs included in the constraint set D.

We can choose the conformation with the smallest error function Eq. 2 from the generated conformation samples as the recovered structure. In Fig. 3a, we plot the values of normalized error function E(x_n)∕∣D∣ of these recovered structures, compared to the values of normalized error function of the fittest native structures [Fig. 3b]. The fittest native structure is the conformation in our discrete model, whose rmsd to the native structure is the smallest. It is obtained by a greedy growth method (Ref. ¹⁹) with a local minimal rmsd to the native structure. Although the objective of our algorithm is to generate conformations following the Boltzmann distribution π(x_n)∝exp{−E(x_n)∕τ∣D∣}, we still can find conformations with smaller error function values in terms of violation of distance donstraints than the fittest native structures.

Figure 3.

Normalized error function of the recovered structure and the fittest structure. (a) Box plot of normalized error function E(x_n)∕∣D∣ of recovered structures of 189 proteins with length of 80–120; (b) box plot of normalized error function E(x_n)∕∣D∣ of the fittest native structures of 189 proteins with length of 80–120. The boxes have lines at the lower quartile, median, and upper quartile values. The lines extending from each end of the boxes are to show the rest of the data. X axis is the percentage of native SRD pairs included in the constraint set D.

The rmsd’s of the recovered structures to native structures are plotted in Fig. 4. When the distance informations of all SRD are provided, the recovered structures of 160 out of the 189 proteins have rmsd to the native structures less than 3 Å. In general, the recovered structures approach native structures as more distance constraints are incorporated. This shows that the priority score β_t we use introduces larger probability to generate conformations close to the native structure when more distance constraints are available.

Figure 4.

Box plot of rmsd’s measured in Å of recovered structures of 189 proteins with length of 80–120 to native structures. The boxes have lines at the lower quartile, median, and upper quartile values. The lines extending from each end of the boxes are to show the rest of the data. X axis is the percentage of native SRD pairs included in the constraint set D.

We compare the difficulties of recovering structures from distance constraints among different protein classes. The rmsd’s of the recovered structures to native structures of ten proteins of different classes are reported in Table 1. Compared to alpha helical proteins, the recovered structures from incomplete distance constraints for beta proteins and alpha∕beta proteins have larger rmsd’s to the native structures. Table 2 reports the normalized error function of the recovered structures and the fittest native structures (in parentheses). Although the recovered structure and the fittest structure are both fixed, depending on the choice of the constraints at different percentages, values of the error function normalized by the number of constraints will be different. We also report the number of violated distance constraints of the recovered structures and the fitted native structures in Table 3. The results show that although the recovered structures violate some of the distance constraints, values of the normalized error function can be much smaller than the fittest native structures. This is because the loss functions h₁, h₂, and h₃ we use are concave downward functions, which focus on preventing the distance between residues being far away from the given distance constraints.

Table 1.

rmsd’s measured in Å of the recovered structures and the fittest native structures to native structures of ten proteins of different classes. Number of all SRD pairs: the number of all residue pairs with distance less than 10 Å. % of SRD: the percentage of SRDs included in the constraint set D.

RMSD to native structure measured in Å
PDBID	Proteinclass	Proteinlength	# of allSRD pairs	Fittest nativestructure	Structure recovered from % of SRD
					20%	40%	60%	80%	100%
2mhr	All alpha	118	765	0.9	5.3	3.9	1.9	2.3	1.5
256b	All alpha	106	752	1.0	9.6	3.7	1.5	1.2	1.4
1cmc	All alpha	104	619	0.9	6.3	4.9	2.7	2.1	2.3
1btn	All beta	106	749	1.5	6.1	6.5	4.0	4.1	2.3
1f7d	All beta	118	796	1.4	7.9	8.4	8.0	5.1	4.5
1f86	All beta	115	816	1.2	5.5	5.3	3.4	2.6	2.3
2trx	Alpha∕beta	108	728	1.1	5.2	3.5	2.1	2.1	1.8
1bkf	Alpha∕beta	107	788	1.5	5.6	2.6	2.0	2.1	1.6
1lkk	Alpha∕beta	105	719	1.0	6.2	4.3	1.8	2.3	1.6
1puc	Alpha∕beta	101	455	0.9	10.6	8.9	7.1	7.5	4.2

Table 2.

Value of the normalized error function of the recovered structures and of the fittest native structures (in parentheses) of ten proteins of different classes. % of SRD: the percentage of SRDs included in the constraint set D.

Normalized error function
PDBID	Structure recovered from % of SRD
	20%	40%	60%	80%	100%
2mhr	0.050 (0.108)	0.117 (0.105)	0.085 (0.122)	0.092 (0.136)	0.093 (0.140)
256b	0.060 (0.237)	0.049 (0.199)	0.077 (0.203)	0.085 (0.201)	0.083 (0.202)
1cmc	0.018 (0.211)	0.071 (0.196)	0.071 (0.164)	0.068 (0.165)	0.097 (0.161)
1btn	0.072 (0.842)	0.465 (0.648)	0.478 (0.650)	0.530 (0.678)	0.370 (0.696)
1f7d	0.147 (0.669)	0.293 (0.726)	0.260 (0.648)	0.343 (0.716)	0.200 (0.688)
1f86	0.144 (0.527)	0.217 (0.469)	0.330 (0.430)	0.339 (0.415)	0.198 (0.443)
2trx	0.044 (0.564)	0.102 (0.466)	0.196 (0.471)	0.120 (0.427)	0.129 (0.418)
1bkf	0.159 (0.526)	0.117 (0.564)	0.130 (0.691)	0.131 (0.667)	0.164 (0.584)
1lkk	0.264 (0.214)	0.146 (0.216)	0.128 (0.239)	0.128 (0.246)	0.121 (0.228)
1puc	0.009 (0.181)	0.083 (0.157)	0.103 (0.134)	0.069 (0.137)	0.068 (0.132)

Table 3.

The numbers of violations of distance constraints of the recovered structures and the fittest native structures (in parentheses) of ten proteins of different classes. % of SRD: the percentage of SRDs included in the constraint set D.

Number of violated distance constraints
PDBID	Structure recovered from % of SRD
	20%	40%	60%	80%	100%
2mhr	67 (61)	158 (137)	224 (211)	288 (303)	383 (377)
256b	63 (74)	123 (143)	202 (231)	271 (313)	318 (372)
1cmc	36 (60)	92 (107)	150 (176)	211 (236)	281 (302)
1btn	62 (93)	188 (175)	267 (263)	386 (352)	427 (439)
1f7d	81 (83)	183 (184)	260 (294)	375 (383)	428 (463)
1f86	72 (96)	191 (210)	279 (302)	349 (384)	455 (504)
2trx	63 (79)	133 (156)	214 (233)	276 (313)	351 (398)
1bkf	84 (98)	160 (182)	237 (292)	311 (383)	414 (489)
1lkk	82 (79)	137 (158)	249 (242)	299 (327)	376 (402)
1puc	30 (47)	87 (88)	133 (134)	150 (180)	171 (216)

The relatively large number of constraint violation may be due to certain limitation of our discrete model. There may not exist any conformation on the lattice satisfying all of the distance constraints. To address this issue, we construct a different set of distance constraints using the fittest native structure among the conformations of the discrete model, which is obtained by a greedy method. The new set of distance constraints are

$${\tilde{d}}_{ij}-{ϵ}_{ij}\le \Vert x_i-x_j\Vert \le {\tilde{d}}_{ij}+{ϵ}_{ij}\text{for}\text{all}\left(i,j\right)∊\mathcal{D},$$

where ${\tilde{d}}_{ij}$ is the distance of residues i and j in the fittest native structure. In this case, there exists at least one conformation, the fittest native structure, in the discrete model satisfying all the distance constraints. Under this setting, the normalized error function E(x_n)∕∣D∣ of the recovered structures is plotted in Fig. 5, and the rmsd’s of the recovered structures to the fittest native structures are plotted in Fig. 6. Among 189 proteins, the recovered structures of 40 proteins can match the fittest native structures perfectly when all SRD pairs are in the constraint set D.

Figure 5.

Box plot of normalized error function E(x_n)∕∣D∣ of recovered structures of 189 proteins with length of 80–120 when distance constraints are constructed based on the fittest native structures. The boxes have lines at the lower quartile, median, and upper quartile values. The lines extending from each end of the boxes are to show the rest of the data. X axis is the percentage of native SRD pairs included in the constraint set D.

Figure 6.

Box plot of rmsd’s measured in Å of the recovered structures to the fittest native structures of 189 proteins with length of 80–120 when distance constraints are constructed based on the fittest native structures. The boxes have lines at the lower quartile, median, and upper quartile values. The lines extending from each end of the boxes are to show the rest of the data. X axis is the percentage of native SRD pairs included in the constraint set D.

Result of generating conformations from contact map of distance cutoff

This section shows the result of generating conformations based on a given contact map, where the distances between residue pairs are known to be either above or below a cutoff value (8.5 Å).¹⁶

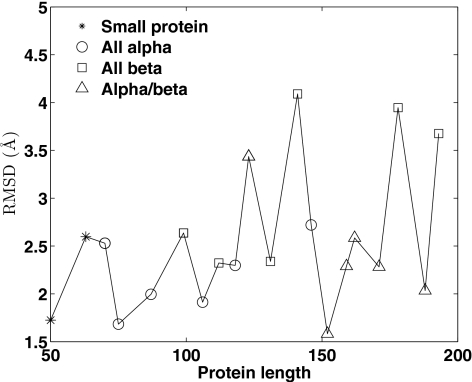
We choose 20 proteins with length of 50–200 from the Protein Data Bank and generate conformations from their complete native contact map using Algorithm 1. We repeat the computation ten times independently and at most m_max=1000 samples are kept during each computation. The conformation with the smallest numbers of missing contacts (residue pairs that form contact in the native structure but not in the generated conformation) and extraneous contacts (residue pairs that form contact in the generated conformation but not in the native structure) is chosen as the recovered structure. The number of missed contacts, extraneous contacts, and rmsd to native structures measured in angstroms of the recovered structures are reported in Table 4. Figure 7 shows rmsd of the recovered structures to native structures. Again, we found that the recovered structures of alpha helical proteins have smaller rmsd to the native structures.

Table 4.

List of proteins of different classes used to recover structures form complete native contact maps. The number of all native contacts, the number of missed contacts, the number of false positive contacts, rmsd to native structure in Å are also listed.

PDB	Protein	Protein	Number of native	Number of missed	Number of extraneous	rmsd
ID	class	length	contacts	contacts	contacts	(Å)
1ptq	Small protein	50	164	8	9	1.7
1cse	Small protein	63	172	10	11	2.6
1utg	All alpha	70	206	6	3	2.5
1hyp	All alpha	75	232	12	7	1.7
1lmb	All alpha	87	280	8	5	2.0
1plc	All beta	99	391	28	51	2.6
256b	All alpha	106	363	17	7	1.9
2mcm	All beta	112	414	36	36	2.3
2mhr	All alpha	118	352	17	17	2.3
1dz3	Alpha∕beta	123	413	22	15	3.4
1mdc	All beta	131	474	40	22	2.3
1stm	All beta	141	521	68	77	4.1
1mba	All alpha	146	530	38	53	2.7
1byr	Alpha∕beta	152	641	52	42	1.6
4dfr	Alpha∕beta	159	598	49	49	2.3
3dfr	Alpha∕beta	162	578	45	65	2.6
1v37	Alpha∕beta	171	672	60	58	2.3
1dgw	All beta	178	617	65	52	3.9
1fvk	Alpha∕beta	188	664	58	36	2.0
1o7n	All beta	193	622	77	85	3.7

Figure 7.

rmsd of structures recovered from complete native contact maps to native structures for 20 proteins of different classes with length of 50–200. X axis is the protein length, Y-axis is the rmsd value of generated conformation that best fit the contact map to the native structure measured in Å.

Result of generating contact maps and conformations from indirect distance constraints by ϕ-values

This section depicts the result of generating TSE from ϕ-value constraints.

We generate TSE of bovine acyl-coenzyme A-binding protein, a length 86 protein with experimental ϕ-values. The PDB entry of the protein is 1nvl. The experimental ϕ-values are plotted in Fig. 8. More details of the experimental ϕ-values can be found in Ref. 48. We follow Ref. 16 and define TSE as the conformations satisfying $\mid {\varphi }_i^{\text{calc}}-{\varphi }_i^{\text{exp}}\mid <0.15$ for all residue i with experimental measured ϕ-value. Hence, the target distribution is the uniform distribution of all conformations satisfying these constraints.

Figure 8.

Comparison of the experimental ϕ-values and calculated ϕ-values of the generated TSE of 1nvl. The filled circles represent the experimental ϕ-values, empty circles represent the calculated ϕ-values of the generated TSE.

We generate m^*=10 000 contact map samples using Algorithm 2, among which 1000 contact maps are chosen with probability proportional to their corresponding weights. For each chosen contact map, Algorithm 1 is used to generate conformations. At most m_max=1000 conformations are generated for each contact map. Figure 8 reports ${\varphi }_i^{\text{calc}}$ of the generated TSE. It is seen that the generated TSE can faithfully reproduce the ϕ-values. The average rmsd between TSE and the native structure of 1nvl is 11.3 Å. The result shows that the conformations of TSE can be far away from the native structure.

DISCUSSION

Obtaining molecular structures from incomplete and inaccurate distance information provided by experiments is an important problem. Several global optimization methods has been applied to solve this problem,^{9, 12, 13, 14} in which the goal is to minimize some error function derived from the provided distance information. In this study, we use SMC method to recover protein structures.

Compared to global optimization methods, an important advantage of our approach is that it can generate a set of conformations that are properly weighted with respect to a specified target distribution. Hence, in addition to recovering structures, we can also provide estimate of important physical parameters of the molecular ensemble, including thermodynamics properties such as energy and entropies under a given energy function.^{18, 19} In this paper, the average rmsd to native structure for TSE conformations is a consistent estimate of how close the native structure and TSE satisfying the distance constraints indirectly provided by ϕ-values are.

A difficulty in growth-based method, such as SMC method, is that the distance information of future residues cannot be directly used for placing current residue. To circumvent this problem, we develop a new growth potential function that can incorporate the distance information of future residues. In this potential function, we convert upper bound constraints of distance for a subset of residue pairs to global distance upper bound constraints of all possible residue pairs. In addition, we introduce reference points of future residues to be placed.

We have used this algorithm to generate protein conformations from constraints in the form of small intervals of distances between a subset of residue pairs, from contact map, and from indirect distance constraints by ϕ-values. This algorithm can effectively recover native structures and can generate conformations satisfying any given set of distance constraints. The conformations generated by this method can also be used as the initial conformations for further refinement.^{9, 10, 11, 12}

In this study, a discrete model for protein structures was used for simplicity, at the price of model accuracy.²² We expect further improvement by extending our model to continuous space, with additional steps of local move refinement, as demonstrated in Refs. ^{14, 49}.