A computational study of mother rotor VF in the human ventricles

Abstract

Sudden cardiac death is one of the major causes of death in the industrialized world. It is most often caused by a cardiac arrhythmia called ventricular fibrillation (VF). Despite its large social and economical impact, the mechanisms for VF in the human heart yet remain to be identified. Two of the most frequently discussed mechanisms observed in experiments with animal hearts are the multiple wavelet and mother rotor hypotheses. Most recordings of VF in animal hearts are consistent with the multiple wavelet mechanism. However, in animal hearts, mother rotor fibrillation has also been observed. For both multiple wavelet and mother rotor VF, cardiac heterogeneity plays an important role. Clinical data of action potential restitution measured from the surface of human hearts have been recently published. These in vivo data show a substantial degree of spatial heterogeneity. Using these clinical restitution data, we studied the dynamics of VF in the human heart using a heterogeneous computational model of human ventricles. We hypothesized that this observed heterogeneity can serve as a substrate for mother rotor fibrillation. We found that, based on these data, mother rotor VF can occur in the human heart and that ablation of the mother rotor terminates VF. Furthermore, we found that both mother rotor and multiple wavelet VF can occur in the same heart depending on the initial conditions at the onset of VF. We studied the organization of these two types of VF in terms of filament numbers, excitation periods, and frequency domains. We conclude that mother rotor fibrillation is a possible mechanism in the human heart.

sudden cardiac death is the most common cause of death in the industrialized world, and, in most cases, it is due to ventricular fibrillation (VF) (62). During VF, excitation waves are disturbed, causing the contraction of the ventricles to become rapid and uncoordinated. It has been shown in clinical and experimental studies that these turbulent wave patterns are underpinned by reentrant sources of excitation (6, 11, 56, 28, 15, 52). If VF is not halted by means of defibrillation, this condition will be lethal within several minutes.

Several mechanisms have been proposed to explain the dynamics of VF. One widely studied mechanism is known as multiple wavelet VF (26, 27) and is characterized by the presence of multiple self-sustained electrical wavelets in the heart. These wavelets may arise due to dynamical instabilities, which are associated with action potential (AP) duration (APD) restitution properties (the so-called restitution hypothesis) (34, 12, 36, 54, 40, 9, 37) and intracellular calcium dynamics (55).

Another well-established mechanism is known as mother rotor fibrillation, in which VF is driven by a dominant fast source of excitation (17, 2, 61). This rapid reentrant electrical source (i.e., the mother rotor) is responsible for maintaining VF and causes conduction block in the surrounding tissue due to heterogeneity in refractory periods (1). The activation source is so fast that it is unable to conduct in some regions, where it blocks but manages to conduct in other regions where refractoriness allows. As a result, multiple small wavebreaks and irregular activation patterns are generated (17).

Mother rotors have been observed in VF experiments in animal hearts. Samie et al. (44) reported the presence of a high-frequency rotor in the left ventricle (LV) responsible for maintaining VF in guinea pig hearts. They also demonstrated that a spatial left-right gradient provides a robust ionic mechanism for rotor stabilization in the LV and wavebreak generation in the right ventricle (RV). Mother rotor fibrillation has also been reported in rabbit hearts (2, 57). Furthermore, long-lived stationary rotors have been reported in isolated RV slabs of sheep (61). Multiple attempts to find similar mother rotor VF in pig hearts have not been successful (16, 21, 20). Although these studies showed the presence of long-lasting epicardial rotors, they were not consistently present throughout VF. The authors concluded that epicardial mother rotors did not drive VF in their experimental model; however, the presence of a transmural mother rotor could not be ruled out. In the human heart, several clinical studies have investigated VF organization on the epicardial and/or endocardial surface (31, 33, 30, 25). In particular, the study by Nash et al. (33) reported persistent epicardial rotors that lasted over 5 s, corresponding to 20 reentrant cycles or more. However, similar to studies on pig hearts (16, 21, 20), these rotors were not consistently present throughout the measured VF episodes. The study by Masse et al. (25) showed an example of a persistent rotor on the endocardium coexisting with multiple reentrant patterns occurring on the epicardium and suggested that this could be a recording of mother rotor fibrillation. However, as in the study of Nash et al. (33), this persistent rotor was not consistently present throughout the measured VF episode. Finally, both these studies (33, 25) could not determine whether these long-lasting rotors were responsible for driving VF or represented only part of the multiple wavelet activity.

One factor contributing to the plausibility of mother rotor VF is electrophysiological tissue heterogeneity (61). In heterogeneous tissue, the period of rotation varies spatially, and if a rotor is placed in a region where rotation is fastest, then it may serve as a mother rotor that drives VF (44). Recently, in clinical studies (60, 32), a large degree of electrophysiological tissue heterogeneity has also been reported in human hearts.

The primary aim of this report was to study whether the electrophysiological tissue heterogeneity recorded by Nash et al. (32) could provide a substrate to support mother rotor VF in the human heart. We define mother rotor VF as a stationary persistent source that lasts for at least 5 s and actively induces wavebreaks. In addition, elimination of the mother rotor must result in VF termination. Having identified such rotors, we also studied the organization of the resulting mother rotor VF and compared this with multiple wavelet VF in the human heart.

This study used an integrative model of human ventricles, which incorporates a detailed ionic model of the human ventricular myocyte (51, 50) combined with an anatomically realistic geometry of human ventricles that includes fiber direction anisotropy (14). Recently, this model was extended (23) to include heterogeneous APD restitution data from human ventricles obtained from Ref. 32. Our modeling framework allows us to check whether VF in the human heart can be driven by a mother rotor and to study how properties of the mother rotor (such as its frequency) affect VF excitation patterns. Performing such studies experimentally is difficult, if not impossible.

MATERIALS AND METHODS

We used a realistic model of human ventricles that contained a detailed description of cell electrophysiology, ventricular anatomy, and fiber direction anisotropy (51, 50). We extended this model to include clinically measured restitution data of human ventricles (32) using our previously developed diffusion-based algorithm (23).

The Human Ventricular Model

We modeled excitable behavior using a monodomain description of cardiac tissue (22) as follows:

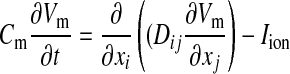(1)

where C_m is membrane capacitance, V_m is transmembrane voltage, t is time, D_ij is the diffusion tensor accounting for the anisotropy of cardiac tissue, x_i and x_j are the tensor notation of the x, y, z coordinates, and I_ion is the sum of ionic transmembrane currents describing the excitable behavior of individual ventricular cells. To represent human ventricular electrophysiological properties, we used the ionic model developed by ten Tusscher et al. (50), which we refer to as the TNNP model. This model provides a detailed description of voltage, ionic currents, and intracellular ion concentrations. This model represents intracellular calcium dynamics by including the subspace calcium dynamics that control L-type calcium channel current (I_CaL) and calcium-induced calcium release (CICR). CICR is modeled with a four-state Markov model for the ryanodine receptor, and both fast and slow voltage-gated inactivation of I_CaL are also incorporated (see Ref. 50 for detailed information). The model reliably reproduces experimentally measured APD (29, 32) and conduction velocity restitution curves (10).

Geometric data describing three-dimensional (3-D) ventricular anatomy and fiber direction field were derived from a normal healthy human heart (14) and are described in more detail in Ref. 49. Overall, the heart was represented by ∼13.5 million points with a spatial resolution of 0.25 mm. As in Ref. 49, we assumed that the transverse conductivity was the same in all directions orthogonal to the longitudinal direction of the muscle fiber axis and that local conductivity tensors can be derived from local muscle fiber directions using the following equation:

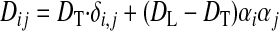(2)

where D_L and D_T are the longitudinal and transverse conductivity, respectively, and α is the muscle fiber direction. For D_L, we used 162 Ω·cm, and for D_T, we used 40.5 Ω·cm, which resulted in conduction velocities of 68 cm/s in the longitudinal direction and 32 cm/s in the transverse direction, similar to the values reported in Ref. 48. The resulting anisotropy ratio was ∼2:1, which was also consistent with clinical measurements (19).

Clinical Data on Restitution Heterogeneity

We used clinical restitution data from Ref. 32, which provided global epicardial APD restitution properties in cardiac patients undergoing aortic valve replacement or coronary artery bypass graft procedures. Activation-recovery intervals (ARIs) were recorded on the entire ventricular epicardial surface using an epicardial sock containing 256 unipolar contact electrodes (interelectrode spacing: ∼10 mm). ARI values have been shown to correlate with APD at 50% repolarization values (13). In each electrode, restitution properties were determined using a standard S1-S2 protocol. Clinical restitution data were then fitted using a least-squares monoexponential fit, and maximum restitution slopes (S_max) were determined for each electrode. For more information about the clinical data and procedures used, we refer to Ref. 32.

For this study, we used data from a single patient. This dataset contained a large degree of heterogeneity and steep slopes of measured APD restitution (see Supplemental Fig. 1). Mean ± SD S_max was 2.01 ± 1.20 based on n = 243 (95%) valid restitution curves (see Ref. 23). We assigned these restitution properties throughout the entire 3-D ventricular mass. However, data on the full 3-D organization of APD restitution in human ventricles are presently not available. Observations have been only reported for surfaces of the heart. To date, either epicardial or endocardial recordings for individual hearts have been reported (32, 60). For both epicardial and endocardial data, S_max values varied markedly between regions, and the spatial arrangement of these regions varied considerably within and between patients. It is likely that this heterogeneity has a 3-D structure.

In the absence of a 3-D restitution profile, we extrapolated the epicardial data from Nash et al. (32) across the 3-D mass. To this end, we developed a diffusion-based algorithm to smoothly extend the epicardial profile across the ventricular muscle. We first extended the 243 clinically measured surface S_max values across the entire ventricular walls by solving a diffusion problem. The variable S_max value was kept constant at each electrode position during the diffusion process. As a result, we obtained a smooth spatial interpolation of S_max across the ventricles except for regions immediately adjacent to the recording electrodes. The second step was to remove these sharp gradients by applying a 3 × 3 × 3 voxel moving average window. The third step involved linear scaling to correct all 13.5 million S_max values based on the original known 243 S_max values at the recording electrode locations. For a more extensive description of the diffusion algorithm, we refer to Ref. 23. We believe that this is a reasonable first step to qualitatively describe APD restitution heterogeneity until more detailed data on the 3-D organization of restitution in the human restitution becomes available.

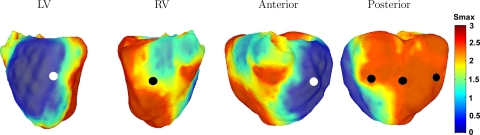
The results of this interpolation for the present dataset are shown in Fig. 1 (polar plots are shown Supplemental Fig. 1). A large region of the posterior wall contained steep restitution slopes, with S_max values up to 3. The LV contained more shallow restitution slopes, with S_max values of ∼0.5-1. Between these regions, intermediate values were present. The mean ± SD restitution slope was 2.01 ± 0.25 (n = 13.5 million).

Fig. 1.

Three-dimensional (3-D) plots of the maximum slope (S_max) values of the maximum restitution curves. Left: left ventricular (LV) view; middle left: right ventricular (RV) view; middle right: anterior view; right: posterior view. Circles show the positions of initial wavebreaks leading to the formation of the first spiral wave: black circles show positions of the first wavebreak that led to multiple wavelet ventricular fibrillation (VF) dynamics, whereas white circles show positions of the first wavebreak that led to mother rotor VF dynamics. S_max values ranged from 0.5 (blue) to 3 (red).

Numerical Approach

Equations for the gating variables in the TNNP model were integrated using a Rush and Larsen integration scheme (43). To integrate Eq. 1, we used a forward Euler scheme with a time step of Δt = 0.02 ms and a space step of Δx = 0.25 mm. No-flux boundary conditions were used so that the axial current flow from heart points to nonheart points was set to 0. For more details, we refer to Refs. 49 and 23.

Induction of VF

To initiate 3-D scroll waves, we used a S1-S2 protocol, for which the S1 stimulus was applied at either the RV or on the posterior junction of the LV and RV. The S2 stimulus was activated during the refractory tail of the S1 stimulus and was extended from the base for ∼50% of the base-apex dimension, thereby creating a single scroll wave. We varied the position of the S2 stimulus such that the core of the initial scroll wave was located in different regions of the ventricles, with either shallow or steep restitution curves (see Fig. 1). Stimulus currents were applied at twice the diastolic threshold value. We performed different simulations of VF by initiating the scroll wave at different locations (see Fig. 1, black and white circles; the difference between these black and white circles will be described later). Furthermore, we also initiated a scroll wave in the septum (not shown in Fig. 1). Simulations were run for 8 s or were terminated if there was no activity present.

Electrograms

Assuming that the medium is an infinite volume conductor, electrograms can be calculated using the dipole source density of the membrane potential in all voxel points using the following equation (38):

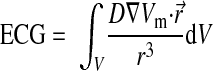(3)

where V is the domain of integration (i.e., the ventricular volume); D is the diffusion tensor; r→ is the vector from each point to the recording electrode, which was placed 10 cm from the center of the ventricles in the anterior direction of the transverse plane; and r³ is the distance from each point to the ECG electrode.

Filaments and Phase Singularities

Scroll wave filaments were detected using an algorithm proposed by Fenton and Karma (8). If there is a spiral wave in two dimensions (a scroll wave in 3-D) present, the core (filament) can be defined as the point(s) for which the excitation wavefront and waveback meet. This can be calculated as the intersection points of an isopotential line (we used −60 mV) and the dV/dt = 0 isoline. Voxel data corresponding to these intersection points were then stored. Individual filaments were detected by iteratively joining neighboring voxels that were designated as filament points. Filaments were determined at 10-ms intervals. Of these filaments, we tracked the following: time of birth, time of death, time of bifurcation, time of amalgamation, lifespan, filament from which a filament bifurcated, filament into which a filament amalgamated, and ultimate filament to which a filament could be traced back through the bifurcation events (49). Filaments were categorized based on their geometrical position and assigned to either the LV, RV, or septum.

Period Distribution and Frequency Domains

For all simulations, we calculated the interbeat interval between successive APs in every heart point (n = 13.5 million points) after the initiation of VF (i.e., after the first 2 s of simulation time). For the histograms (see Figs. 5 and 6), the mean period was calculated in every point between 2 and 6 s of simulation time. The histogram range was 0.16–0.28 s and the bin size was 1 ms. Note that this method is different from experimental methods that calculated the dominant frequency via fast Fourier transformations (FFTs) of optical AP mappings (61, 44, 57, 33). Because experimental recordings are often measured during time intervals that exceed our simulation time (minutes vs. seconds), we preferred to use direct measurement of period values.

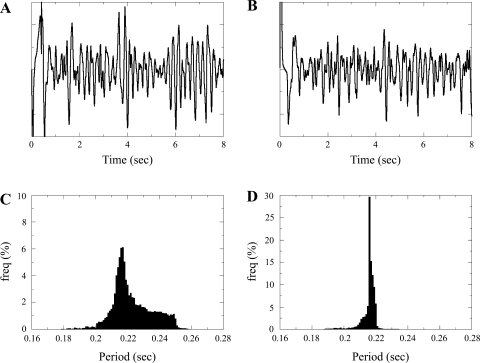
Fig. 5.

A and B: ECG. C and D: histograms of the mean period distribution measured in all heart points between 2 and 6 s of simulation time. A and C: multiple wavelet simulation. B and D: mother rotor simulation.

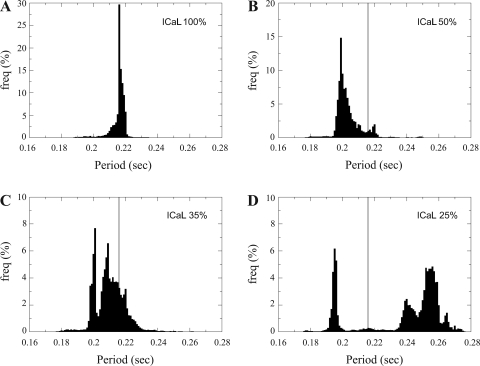
Fig. 6.

Normalized period distributions. Local mother rotor properties were changed [L-type Ca²⁺ channel current (I_CaL) times 1.0 (A), 0.5 (B), 0.35 (C), and 0.25 (D)]. The gray vertical line denotes the mean period value of I_CaL times 1.0 (A).

Implementation

All simulations were coded in C++ and MPI and were run on 16 processors of a Beowulf cluster consisting of 16 Dell 650 Precision Workstations (dual Intel Xeon 2.66 GHz). Simulating 1 s of wave propagation in the ventricles took ∼6.5 h of wall clock computation time. Ventricular geometry, wave patterns, and scroll wave filaments were visualized using marching cubes algorithms for isosurface detection in voxel data and OpenGL for isosurface rendering.

RESULTS

Multiple Wavelet and Mother Rotor VF Wavefronts

Scroll waves were initiated at different locations of the ventricles (see Fig. 1, white and black circles). After investigating the results of the different starting locations, we found that we could distinguish two different types of VF dynamics, which were dependent on the location of the first spiral.

The first type of VF dynamics we found was multiple wavelet VF, and this was investigated in our previous publication (23). The starting locations of the initial spiral for this type of VF are denoted by the black circles in Fig. 1. These initial locations were located in regions containing steep restitution slopes. Figure 2 shows a typical example of these dynamics. After initiation, we observed that the spiral wave broke up into multiple wavelets that were predominantly located in the RV, where APD restitution was steepest (slopes of 2.5–3). The chaotic spatiotemporal patterns that arose persisted throughout the simulations and were similar to the restitution-induced multiple wavelet VF dynamics we studied in Refs. 49 and 23.

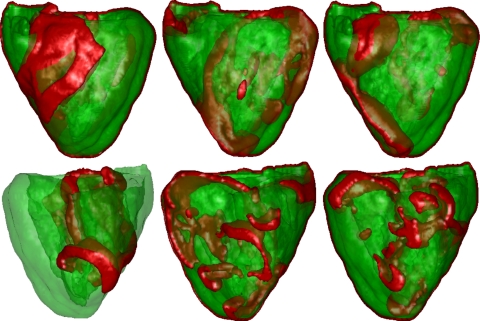
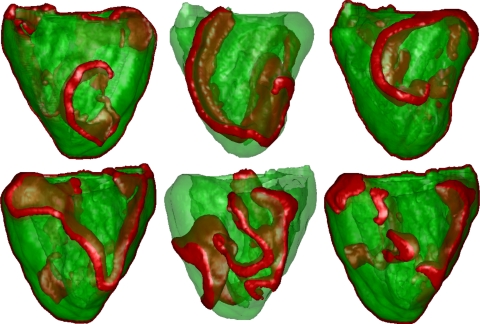
Fig. 2.

Multiple wavelet VF. Wavefronts are shown in red. Top: LV view; bottom: RV view. Left: location of the initial spiral; middle: after 5 s; right: after 7 s. Most wavebreaks occured in the RV free wall and existed independently.

The second type of VF we found was mother rotor VF. For several other initial conditions (denoted by the white circles in Fig. 1) located in regions with shallow restitution slopes, we found patterns of excitation that were different from the patterns described above. In both cases, the mother rotor was similar in size. Figure 3 shows an example of such an excitation pattern. After an initial transient, we observed a persistent (single) stable spiral wave located in the LV, where restitution slopes were shallow (slopes of 0.5–1.0). At the same time, we observed the continuous formation of wavebreaks occurring on the other side of the heart (the free wall of the RV and posterior wall), where restitution slopes were steep (slopes of 2.5–3). These wave patterns are consistent with mother rotor fibrillation. To verify this, we show below that these wavebreaks were indeed driven by the single stable spiral in the LV.

Fig. 3.

Mother rotor VF. Wavefronts are shown in red. Top: LV view; bottom: RV view. Left: location of the initial spiral; middle: after 3.5 s; right: after 10 s. Note the stable spiral in the LV free wall, whereas breaks occurred in the RV free wall. The spiral in the LV wall remained stable until the end of the simulation (up to 12 s simulated). Breaks in the RV were driven by the mother rotor spiral.

During mother rotor VF, wavebreaks were induced by dynamical heterogeneity (due to steep slopes of the APD restitution curves). Indeed, we found that wavebreaks occurred not immediately but after several cycles of mother rotor rotation. Moreover, APD alternans instability was clearly evident at the locations of onset of wavebreaks. This wavebreak mechanism differs from the mechanism of wavebreaks due to conduction blocks between regions with different refractoriness that is usually reported to underlie mother rotor fibrillation.

Ablation of the Mother Rotor

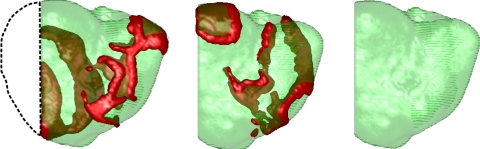
To test the hypothesis that the wavebreaks shown in Fig. 3 are driven by the mother rotor, we eliminated the mother rotor spiral 3 s after its onset by removing ∼20% of the LV free wall of the LV that contained this rotor (see Fig. 4). We found that after removal, the wavebreaks did not complete rotation and that the wavetips of the rotors ran into the refractory tails of the waves and disappeared. After 0.5 s, there was no wave activity present in the heart. Thus, the wavebreaks in the RV (Fig. 3) seemed to be driven by the stable spiral wave in the LV, implying that this is indeed mother rotor fibrillation. We tested this removal procedure further by applying it at different phases of the mother rotor rotation and by removing differently sized regions (10–20% of the LV free wall). We found that as soon as the mother rotor activity was eliminated, the wavebreaks in the RV died out.

Fig. 4.

Ablation of the mother rotor spiral in the LV (posterior view). The black dashed line denotes the portion of the ventricles that was removed. The first snapshot (left) is at ∼3 s of simulation time (i.e., the time when part of the LV was removed), the second snapshot (middle) is at 3.3 s, and the third snapshot (right) is at 3.5 s, after which there was no longer any wave activity.

Clearly, removal of part of the myocardium decreased the overall ventricular mass of the heart, which could potentially terminate wave activity during fibrillation (critical mass hypothesis). To verify that this was not the case here, we repeated the multiple wavelet simulations shown in Fig. 2 and removed the same part of the LV as we did for the mother rotor simulation. We found that multiple wavelet VF did not terminate after the removal of tissue and that the RV sustained multiple independent sources that could complete a rotation and were not terminated by the tissue removal procedure (see Supplemental Fig. 2). Thus, termination of mother rotor VF was not related to the critical mass phenomenon but to the removal of a persistent rotor that was responsible for actively inducing wavebreaks.

These results demonstrate that VF as shown in Fig. 3 is driven by a single spiral and represents mother rotor VF. Interestingly, our simulations show that multiple wavelet and mother rotor VF can occur in the same heart, depending on the initial location of the spiral.

VF Dynamics and Organization

ECG, period distribution, and frequency domains.

Figure 5 shows ECG and period distributions for both multiple wavelet and mother rotor simulations. For multiple wavelet VF (Fig. 5A), the ECG had a mean frequency of 4.4–4.5 Hz, similar to clinically recorded frequencies (4, 31, 33, 59). For the mother rotor fibrillation (Fig. 5B), the mean frequency was very similar and had a mean frequency of 4.6–4.7 Hz. Both ECGs had similar complexity. Note that the shapes of the FFT spectra for the ECGs shown in Fig. 5, A and B, were similar (see Supplemental Fig. 7), and there did not appear to be any relationship between period distribution and underlying heterogeneity profile (see Supplemental Fig. 6).

We also determined period values for every point (n = 13.5 million heart points) from 2 to 6 s and constructed a histogram of mean period values for these simulations (Fig. 5, C and D). Histograms for the mother rotor and multiple wavelet VF differed substantially. For multiple wavelet VF (Fig. 5C), there was a broad period distribution with mean period of 0.223 (4.48 Hz) (box-plot statistics: median = 0.217, interquartile range = 0.016, n = 13.5 million), whereas for mother rotor VF (Fig. 5D), the distribution had a clear peak at 0.216 s, corresponding to the period of the mother rotor, and a narrow distribution. Overall, the mean was 0.216 (4.63 Hz) (box-plot statistics: median = 0.216, interquartile range = 0.002, n = 13.5 million).

Supplemental Figure 3 shows the corresponding 3-D spatial distribution of mean period values for the multiple wavelet and mother rotor simulation measured between 2–4 and 4–6 s, respectively. Indeed, during multiple wavelet VF, period values were grouped into different domains with different frequencies (Supplemental Fig. 3A). However, these domains were not anatomically predefined but changed during the course of the simulation (Supplemental Fig. 3B), as they were determined by dynamic processes (23). For the mother rotor simulations, we did not observe distinct frequency domains for the durations between 2–4 s (Supplemental Fig. 3C) or 4–6 s. In this case, the period distribution was mainly determined by the frequency of the mother rotor.

Number of filaments.

A convenient way to quantify the complexity of excitation patterns in the ventricles of the heart is by determining the number of excitation sources (scroll wave filaments) (49, 52, 42, 41, 21, 3, 5, 35). A scroll wave filament is a line around which a 3-D spiral wave rotates. When such a filament intersects with the surface of the heart, a phase singularity manifests on the heart surface. Supplemental Figure 4 shows a comparison of the time dynamics of the total number of filaments and epicardial phase singularities for both the multiple wavelet and mother rotor simulations.

For the multiple wavelet simulation, the number of filaments varied between 10 are 30. The mean number of filaments was 11.2, and the mean number of phase singularities was 8.0. Initially, there were only filaments detected in the RV, but after ∼4.5 s of simulation time, there were also filaments detected in the LV. Most wavebreaks were found in high-restitution areas, but sometimes wavebreaks also occurred in areas with shallow restitution slopes. Additional characteristics of multiple wavelet VF organization, such as the location of breaks, have been previously discussed in Ref. 23. The ratio of the number of filaments to phase singularities was ∼1.4, consistent with previous findings (49).

For the mother rotor VF, the number of filaments varied between 2 and 8, which was lower compared with multiple wavelet VF. The mean number of filaments was 3.8, and the mean number of phase singularities was 2.3, resulting in a 1.65 ratio between filaments and epicardial phase singularities. Apart from the mother rotor filament in the LV, most filaments occurred in the RV.

Filament history.

We also analyzed filament history by tracing the events of filament creation and elimination over 8 s of time through death, birth, bifurcation, and amalgamation events. This is shown in Supplemental Fig. 5 for both the multiple wavelet and mother rotor fibrillation simulations.

For the multiple wavelet VF simulation, we detected 1,025 filaments. Most of the filaments existed for only short periods of time (<0.5 s). However, we also observed a few long living filaments, which lasted for several cycles (up to 2–3 s). The mean lifespan of a filament was 0.084 s (n = 1,025).

For the mother rotor fibrillation simulation, we detected 388 filaments. During this simulation, the mother rotor filament was stable and was present until the end of the simulation. All other filaments existed for short periods of time (<0.25–0.5 s). Similar results have been reported for rabbit hearts where VF was driven by a mother rotor (2). The mean lifespan of a filament was 0.068 s (n = 387, mother rotor filament excluded).

We found that the total number of filaments during mother rotor fibrillation was two to three times smaller compared with the multiple wavelet fibrillation. In addition, during mother rotor fibrillation, filaments have a shorter lifetime (P < 0.05, unpaired Student's t-test). Furthermore, during multiple wavelet VF, there were several filaments that lasted longer (up to 2–3 s), whereas during mother rotor fibrillation, only short-lived filaments accompanied the (long lasting) mother rotor. Similar results were found for the simulations using other initial conditions that resulted in either multiple wavelet or mother rotor VF (see Table 1).

Table 1.

Total number of filaments detected during 8 s of simulation time for different locations of the initial scroll wave

Location of the Initial Scroll Wave	Type	No. of Filaments	Average Lifespan, s
LV	MR	388	0.068
LV anterior	MR	518	0.061
LV posterior	MW	1,268	0.081
Posterior	MW	1,025	0.084
RV posterior	MW	952	0.082
RV	MW	978	0.079
Septum	MW	980	0.084

LV, left ventricle; RV, right ventricle; MR, mother rotor ventricular fibrillation; MW, multiple wavelet ventricular fibrillation.

Effect of Mother Rotor Frequency on VF Dynamics

If fibrillation is driven by a mother rotor, then influencing the frequency of the mother rotor should have a substantial effect on VF dynamics. We performed additional simulations in which we decreased the maximal conductance of I_CaL in the region in which the mother rotor resided to 50%, 35%, and 25% of its original value. This intervention increased the frequency of the mother rotor and resulted in flattening of the restitution slope in the region of the mother rotor. This did not change the type of rotation of the mother rotor, which remained stable after the intervention.

The results of these simulations are shown in Fig. 6. Figure 6A shows the same period distribution as in Fig. 5D for normal I_CaL conductance. We found a narrow unimodal period distribution with a mean period of 0.216 s. Spatially distinct frequency domains were not observed (see Supplemental Fig. 3C).

We found that for a 50% I_CaL reduction, the mean period of VF decreased to 0.204 s (see Fig. 6B). We also found that the period distribution became wider and that a small second peak arose around a period of 0.218 s. When we decreased I_CaL to 35% of its normal conductance, a bimodal period distribution arose (see Fig. 6C), with a first peak around a mean period of 0.202 s and a second peak with a mean period of 0.210 s. When we decreased I_CaL to 25% of its original conductance, the split in the period distribution became more pronounced (see Fig. 6D). The first peak had a mean period value of 0.197 s, whereas the second peak increased to a mean of 0.252 s, which was much larger than the mean period value for the original settings of 0.216 s.

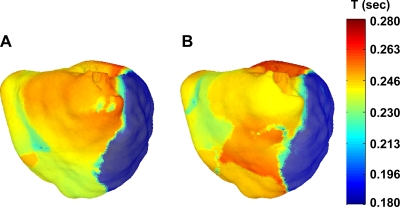
The bimodal period distributions that occured for decreased I_CaL conductance reflect an underlying 3-D spatial distribution of periods, as shown in Fig. 7, A and B, for the case where I_CaL was reduced to 25% of its original value. The heart was clearly subdivided into different frequency domains: the mother rotor area [which had a period of 0.197 s (which accounts for the left peak in Fig. 6D)] and the area around the RV where most of the wavebreaks occured and which had a much longer period of excitation (accounting for the right peak in Fig. 6D). Such domains of different frequency of excitation are similar to those reported in experimental studies of atrial and ventricular mother rotor fibrillation (18, 61). These domains arise when differences in refractory periods between different regions are large enough to cause Wenckebach-like conduction blocks, which is presumed to be the sole mechanism for wavebreak formation during mother rotor type fibrillation.

Fig. 7.

Spatial period distribution for the simulation with I_CaL times 0.25. A: 2–4 s; B: 4–6 s. The mother rotor was located in the dark blue region. Period values ranged from 0.18 s (blue) to 0.28 s (red). T, time.

We conclude that increasing the frequency of the mother rotor changes the process of the onset of breaks during VF. For normal I_CaL, the wavebreaks are caused by dynamic instability: the first breaks occured only after a number of rotations of the initial spiral, and the onset of these breaks was clearly associated with alternans in APD. This indicates that steep APD restitution-mediated alternans was the mechanism for wavebreak formation. However, since these wavebreaks only occurred in steep regions far away from the initial spiral core, they led to a mother rotor type rather than a multiple wavelet type of VF. When I_CaL was decreased to more than 50%, breaks occured straight after the formation of the initial spiral without any alternans (which is an important characteristic for wavebreaks caused by dynamic heterogeneity). This is because the frequency of the mother rotor increased so much that the differences in refractory period led to local conduction block, as was also reported in Ref. 24. Thus, anatomic (and not dynamic) heterogeneity was responsible for wavebreak formation.

In addition, we found that due to the increased frequency of the mother rotor, the total number of filaments produced during 8 s increased from 388 (I_caL times 1.0) to 538 (I_caL times 0.25). Thus, speeding up of the mother rotor not only changes the mechanism of wavebreak formation but also increases the complexity of VF.

DISCUSSION

In this study, we report on mother rotor fibrillation in an electrophysiologically heterogeneous computational model of human ventricles. We defined a mother rotor as a stationary, persistent source that actively drives VF, which terminates when the mother rotor is eliminated. However, it is also possible that a source driving VF is transient. We also call this a mother rotor if VF can be stopped by the removal of this source. It is understood that there may be special cases for which multiple wavelet VF can be eliminated by the removal of a single source. However, we think that, in most cases, true mother rotor VF will be correctly classified using this definition.

It should be noted that mother rotor-like VF can occur without tissue substrate heterogeneity. Fenton and Cherry (7) showed that mother rotor-like excitation patterns can occur as a result of discordant alternans-induced breakup far from the center of the spiral. In addition, rotors that anchor to inexcitable obstacles (45, 57, 53) (such as papillary muscles and fibrosis) may also result in mother rotor-like VF. Furthermore, additional sources of heterogeneity (such as increased fibrosis) can lead to local conduction block and the development of reentry and are also important for the initiation and organization of VF (58).

Our study shows that increased heterogeneity in the human heart can result in the onset of mother rotor VF. However, it should be emphasized that any type of heterogeneity, i.e., from local dynamic or fixed heterogeneities (including APD restitution), favors the formation of local wavebreaks and thus provides a substrate to sustain VF of any type (e.g., multiple wavelets) and not exclusively mother rotor VF.

Although our model is based on clinical data on heterogeneity and involves a detailed description of the structure of the heart and properties of cardiac cells, our conclusions should be further tested in experimental and clinical studies involving high spatial resolution recordings of wave activity in the human heart during VF.

In our model, we consistently reproduced mother rotor VF if the initial spiral wave was located in the LV where APD was shortest and APD restitution shallowest. We found multiple wavelet VF when the initial spiral was located in the RV where APD restitution was steep and APD was longer. In our model, shallow restitution curves were correlated with shorter APDs and periods, whereas steep restitution curves corresponded to longer APDs and periods (see Ref. 23). Theoretically, it should be possible to have a model in which longer periods correspond to steeper restitution curves. However, in such a case, we believe mother rotor fibrillation would not occur, since a rotor in a region of steep restitution would be unstable and would therefore lead to multiple wavelet-type VF.

To demonstrate that the mother rotor was indeed responsible for driving the wavebreaks, we mimicked local ablation to remove the mother rotor spiral. After removal of the tissue that supported the mother rotor, we found that all wavebreaks ended and the fibrillation was terminated within 0.5 s of simulation time. However, we do not think that local ablation of a mother rotor is of clinical use, as multiple mechanisms of VF can occur in the same heart depending on the initiation procedure. However, we cannot exclude the possibility that local interventions may be used to stop a specific episode of VF. Note that if the mother rotor is terminated by other means, e.g., it slows down and is overrun by other wavelets, then VF is not necessarily terminated.

We then analyzed the differences in the underlying dynamics between mother rotor and multiple wavelet fibrillation. ECG signals for mother rotor and multiple wavelet VF were similar and resembled clinically observed ECG signals during VF. During multiple wavelet VF, we observed a broad period distribution that was mainly determined by dynamic processes rather than underlying heterogeneity (see also Ref. 23). In contrast, during mother rotor VF, we observed that the periods were dominated by the period of the mother rotor, leading to a narrow distribution. Apart from the mother rotor, only short-lived wavebreaks were present during mother rotor fibrillation, whereas during multiple wavelet VF, several long-lived filaments were present. In addition, during mother rotor VF, approximately two to three fewer filaments were present compared with multiple wavelet VF. This difference is due to the fact that during mother rotor fibrillation the fast mother rotor dominates a large part of the cardiac tissue. Hence, other wavebreaks did not have enough time or space to independently persist.

For the mother rotor fibrillation with the default I_CaL settings, we found that wavebreaks in the RV occurred due to dynamic instabilities caused by steep APD restitution slopes (i.e., alternans). Wavebreaks occurred after several cycles of mother rotor rotation, and at places where the breaks occurred, there was alternans instability in APD. Excitation periods across the entire tissue were dictated by the mother rotor, and different frequency domains were not present.

We found that decreasing the period of the mother rotor (by decreasing I_CaL conductance in the mother rotor region), and thus increasing anatomic heterogeneity, led to Wenckebach-like conduction blocks due to large differences in refractory period. Wavebreaks now occurred immediately after the initiation of the mother rotor and were anatomically predefined. Consequently, different frequency domains were present, similar to experimental findings for mother rotor type VF (61).

We have thus shown that the formation of domains of different frequency is dependent on the frequency of the mother rotor and the degree of anatomic heterogeneity in refractory periods. Therefore, mother rotor-type fibrillation is not necessarily associated with different frequency domains.

For multiple wavelet fibrillation, flattening restitution slope has been proposed as a promising therapeutic intervention (9). However, for mother rotor fibrillation, besides absolute restitution slopes, heterogeneity in restitution slopes and APD is a major determinant for VF occurrence. This implies that reducing electrophysiological heterogeneity may also be a fruitful target for therapeutic intervention.

Limitations

Despite the fact that our model incorporates a detailed description of the electrophysiological properties of human ventricular cells, a realistic human ventricular geometry including fiber direction field, and a detailed description of ventricular electrophysiological heterogeneity, there are number of shortcomings of our study.

The first limitation is that clinical data were only available for the epicardial surface of the ventricles. There was no information on restitution properties in the midmyocardium or endocardium of these hearts. As a consequence, epicardial restitution slope data had to be extrapolated across the entire ventricular wall using a diffusion-based algorithm as reported in Ref. 23. The use of different parameters in our diffusion algorithm may lead to different gradients in slope values for the same set of clinical data. It remains to be investigated how these different heterogeneity profiles with different transmural slope gradients affect the results presented in this study.

Second, other heterogeneities, such as epicardial, endocardial, and M cells, Purkinje fibers, laminar sheets, and disease conditions (such as fibrosis and gap junction remodeling), were not taken into account in our model. Additional heterogeneities may further contribute to the complexity of excitation patterns during VF.

A third limitation to our study is that the ionic mechanisms responsible for the variation in APD restitution are presently unknown. It should be noted that the mapping of TNNP model parameters to restitution slope values that we used is not unique and that the same slopes may likely be obtained using other combinations of parameter settings. However, we believe that this nonuniqueness should not qualitatively affect the results of our study as long as shallow restitution curves correspond to shorter periods and steep restitution curves correspond to longer periods.

Finally, the mechanisms of VF studied in this report are not the only mechanisms that may potentially cause VF. As an example, apart from steep APD restitution, other nonlinear instabilities, e.g., in intracellular calcium dynamics (39, 46, 47), may also lead to alternans and VF.

Conclusions

In this study, we report the finding of mother rotor VF in a computational model of human ventricles. Furthermore, we showed that mother rotor and multiple wavelet VF can occur in the same heart depending on the initial location of reentry. We show that the underlying VF dynamics are markedly different between mother rotor and multiple wavelet VF. Mother rotor VF was more organized, with a smaller number of filaments and a more uniform distribution of rotor periods. Ablation of the mother rotor was sufficient to terminate VF. Studying the basic mechanisms responsible for maintaining and terminating VF in the human heart is important for understanding the pathogenesis of sudden cardiac death.

GRANTS

This research was funded by Netherlands Organization for Scientific Research Grant 814.02.014. M. P. Nash acknowledges previous support from the Marsden Fund Council from New Zealand government funding, administered by the Royal Society of New Zealand.