A structural model of latent evolutionary potentials underlying neutral networks in proteins

Abstract

A central question in molecular evolution concerns the nature of phenotypic transitions, in particular, if neutral mutations hamper or somehow facilitate adaptability of proteins to new requirements. Proteins have been found to fluctuate between different structures, with frequencies of structures being proportional to their stability. Therefore, functional promiscuity may correspond to different structures with energies close to the ground state which then represent multiple selectable traits. We here postulate that these near-ground-state structures facilitate smooth transitions between phenotypes. Using a biophysical heteropolymer model with exhaustive mappings of sequences onto structures, we demonstrate that this is indeed possible because of a smooth gradient of stability along which any structural phenotype can be optimized and also because of mutational proximity of similar phenotypes in genotype space. Our model provides a biophysical rationalization of the intriguing, and otherwise puzzling experimental observation that adaptation to new requirements, e.g., latent function of a promiscuous enzyme, can proceed while the “old,” phenotypically dominant function is maintained along a series of seemingly neutral mutations (see accompanying article). Thus pleiotropy may facilitate adaptation of latent traits before gene duplications and increase the effective adaptability of proteins.

A widely debated issue in molecular evolution concerns the relative importance of adaptive (“Darwinian”) and neutral mutations for biological innovation (Nei, 2005; Kimura, 1981; Bush, 2001). While most mutations of natural proteins reduce their stability and thus presumably compromise activity (DePristo et al., 2005), the vast majority of observable mutations is considered to be neutral (Kimura, 1981) or close to neutral as they have little or no effect on the organism’s fitness, i.e., its reproductive success. On the other hand, many indications suggest that adaptive mutations, or transitions to new phenotypes, are rare (Graur and Li, 2000; Weinreich et al., 2006). It is widely assumed that neutral mutations are instrumental for adaptation. Recently, it has been argued that neutral mutations augment the possibility for further adaptation (Wagner, 2005; Fontana and Schuster, 1998). However, our understanding of how such an enhancement is accomplished, in particular the precise nature of phenotypic transitions, is vague at best. This contribution aims to investigate, from a structural perspective, how phenotypic transitions can be facilitated in accordance with the assumption that the majority of observable mutations are neutral.

It is important to recall that protein function (and thus neutrality) is context dependent since proteins are embedded in a complex cellular network of interactions and regulations [for reviews see, e.g., Barabasi and Oltvai (2004); Pal et al. (2006); and Phillips (1998)]. To overcome the difficulties these entanglements represent for studying molecular evolution, simplified experimental setups or computer simulations for both RNA and proteins have been applied. Most of these approaches have in common that individuals in a constant population of molecules are randomly mutated and amplified proportional to one fitness criterion. While experiments mostly define fitness in terms of a specific function [see Amitai et al. (2007), and references therein], computations usually use structural similarity to a target or similar measures as a reasonable proxy for functional fitness (Huynen et al., 1996; Fontana and Schuster, 1998; Williams et al., 2001). For computational simulations the situation is simpler for RNA than for proteins since RNA molecules may represent both genotype and phenotype, efficient and more reliable structure prediction algorithms exist for RNA (Tacker et al., 1996; Hofacker et al., 1994) and many predictions can be experimentally tested for RNA viruses and viroids (Sanjuan et al., 2006; van Nimwegen, 2006; Codoner et al., 2006). For proteins, most computations employ highly simplified models, so-called “simple exact models” [SEMs; for reviews see Chan and Bornberg-Bauer (2002); Xia and Levitt (2004)] in which the thermodynamically most stable structure for a given sequence can be determined and, if exactly one such ground state exists, is considered to be a viable structural phenotype, or phenotype for short. In this simplified view of molecular evolution, mutations are considered neutral if and only if a phenotype is maintained, a mutation that changes a phenotype is referred to as a phenotypic transition, and no distinction is made between sequence and genotype.

So far, computations using simple models offered an explanation for how phenotypically neutral drift, i.e., genotypic variation without or with little phenotypic changes, is complemented by sudden adaptation, resulting in phenotypic transitions. The associated theory predicts that evolutionary landscapes of biopolymers are comprised of “neutral nets,” sets of mutationally interconnected genotypes with identical viable phenotypes. In this view, populations evolving under selection pressure can drift along neutral nets until a mutant encoding for a fitter phenotype (i.e., a sequence belonging to a different neutral net) is so close in sequence space for a phenotypic transition to occur. Soon after such a transition, the “new” neutral net which is composed of genotypes coding for fitter phenotypes becomes populated. The “old” neutral net is depopulated and this process has been proposed to correspond to selective sweeps (van Nimwegen, 2006). This picture is surprisingly robust across a range of protein-like models (Bastolla et al., 1999; Williams et al., 2001; Chan and Bornberg-Bauer, 2002,Wroe et al., 2005) and applies as well to models of RNA evolution (Fontana and Schuster, 1987; Huynen et al., 1996; Fontana and Schuster, 1998). It complies well with the view of John Maynard-Smith, who convincingly argued for the existence of a continuous phenotype space and postulated that any feasible series of point mutations must always pass through a regime of genotypes coding for functional phenotypes (Maynard-Smith, 1970). For protein models, funnel-like organizations in sequence space have been found: the mutationally most stable prototype sequence$\left({\widehat{S}}^X\right)$ in a neutral net (χ), i.e., the sequence which tolerates the largest number of neutral mutations, is generally also the thermodynamically most stable one. Sequences become gradually less stable with increasing mutational distance from ${\widehat{S}}^X$ (Bornberg-Bauer and Chan, 1999) (see also Fig. 1). This superfunnel paradigm is supported by experiments (Bloom et al., 2005; Cordes et al., 2000) and buttressed by more recent computational analyses (Wroe et al., 2005). It is important to recall that SEMs are useful for studying biophysical principles of molecular evolution but most parameters, such as chain rigidity, sequence length, or mutation rates do not directly translate into the corresponding properties of real protein molecules. It is the general principles of the landscape topology of sequence spaces and the connectivities within and between neutral nets which have been successfully predicted using SEMs in the past. In the present study, SEM approaches are further explored to understand the general biophysical requirements for phenotypic transitions.

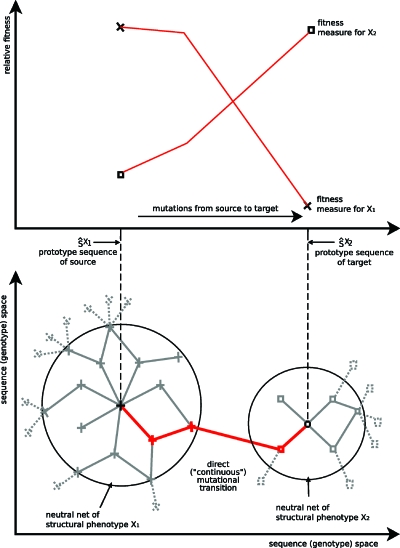
Figure 1. Schematics of evolutionary transitions between neutral nets.

Top: possible development of the relative fitness (e.g., a selected enzyme activity or structural similarity to a target) during adaptation of a population which was initially optimal for one function (×, left) and then selected for another function (target: ◻, right), similar to the situation investigated by the experiments of Aharoni et al. (2005). Bottom: an interpretation in terms of structural phenotypes according to Maynard-Smith’s idea of a continuous phenotype space (there is one direct transition from one representative of one structural phenotype to the other) and the superfunnel paradigm (genotypes depicted in the center have more neutral neighbors and code for thermodynamically most stable structures). The two big circles denote the boundaries of the neutral nets of the two structural phenotypes (× and ◻). Every genotype within one neutral net codes uniquely for the same structural phenotype and point mutations among them are indicated by solid lines; mutations that result in a sequence outside the neutral net are represented by dashed lines. Mutations along solid lines are commonly referred to as neutral as long as they stay within one neutral net. A mutation is termed adaptive at the transition, i.e., when it changes the phenotype. The top and bottom drawings are positioned to show the correspondence between the concept proposed in this work and the superfunnel paradigm. The solid red evolutionary path indicated in the bottom drawing corresponds to the fitness paths in the top drawing. Initially, evolution seems neutral because the same phenotype dominates although it becomes less frequent in the structural ensemble (the fractional population is reduced) and the phenotype which is selected for gradually becomes more frequent in the structural ensemble.

Quite unexpectedly, recent experiments (Aharoni et al., 2005) showed that, in a population of proteins optimized for one function, adaptation to new requirements can happen before the existing “native” function is lost. Here, using simple protein models, we propose a biophysical framework to reconcile these observations with a view of proteins that focuses not only on a single ground-state structure but also a multitude of near-ground-state structures. Under ambient conditions in an aqueous environment, proteins are dynamic entities that can switch between structures for different functions and thus represent multiple selectable traits (James and Tawfik, 2003). We propose that selecting for such a latent trait will steer evolving populations along neutral nets to transition points such that the probability for adaptive mutations, leading to a transition to a new phenotype, will be enhanced compared to random drift. This is further explicated in the discussion below on the implications of our results for the understanding of protein evolution in general, and for connecting with a parallel experimental study in the accompanying paper, which focuses on the changes in latent function of a pleiotropic enzyme (Amitai et al., 2007).

The present investigation focuses on the following questions: What are the biophysical properties of transitions between neutral networks? Can the selection for latent traits accelerate phenotypic transitions? Can a biophysical model offer a reasonable explanation for the observed adaptation of latent traits and thus indicate that such a mechanism could be a more general principle of adaptation?

RESULTS

First we extend Maynard-Smith’s picture of a continuous phenotype space (Fig. 1): As a protein initially drifts away from a genotype close to the optimal prototype sequence ${\widehat{S}}^{X_1}$ for an original phenotype, the original phenotype remains dominant. Meanwhile, in view of dynamic conformational interconversions and polyreactivity, another phenotype X₂ that satisfies the new fitness criterion can gradually appear more frequently in the population with every mutation. Finally, X₂ becomes the dominant phenotype of the ensemble at the expense of X₁. This picture follows directly from the original superfunnel paradigm (Bornberg-Bauer and Chan, 1999) when structure is considered a proxy for function (see also Introduction and Discussion). However, if the phenotypic transition is to be smooth, it entails two extensions of the paradigm: (i) structurally similar phenotypes are on average mutationally closer to one another than random, and (ii) adaptation toward a new structural phenotype is via a smooth increase in frequency of the new structure in the conformational ensemble while the “old” phenotype remains dominant during the “neutrality” phase.

We now ask if these properties are indeed predicted by the simple biophysical model by which the superfunnel paradigm was first developed. In our model, mappings of sequences onto structures are exhaustively constructed (see Methods). Here we consider sequences with unique (g=1) ground states as viable. For any sequence we can compute the energies of all possible structures. Given a sequence S_i we can compute the energy E_j of any structure X_j even if it is an “excited” rather than the ground state of S_i. Excited states have higher than ground-state energies and will only be populated with much lower probabilities. Therefore, in an ensemble of molecules with identical sequences, the fraction of molecules assuming one particular excited state, the “fractional population” of this structure, will be smaller the more excited the state is, i.e., the less stable the structure is (see Methods section for details). Using Eq. 2 it becomes possible to compute the fractional population of X_j, i.e., the probability that X_j is present under certain conditions such as temperature. We then define a fitness value F(S_i) with respect to a chosen target structure X_j and simulate population dynamics by applying a constant rate of mutation to populations of genotypes in which individuals’ reproductive rates are proportional to their fitness. Therefore, the more stable (less excited) and thus the larger the fractional population of the target structure becomes for a given genotype, the more offsprings it will have in the next generation.

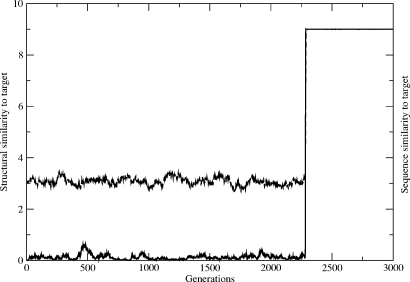
Earlier considerations showed that, under constant fitness pressure, a population on a neutral net χ tends to concentrate around the genotype with the largest number of neutral mutations (van Nimwegen et al., 1999; Wilke et al., 2001; Bornberg-Bauer and Chan, 1999) which, according to the superfunnel concept (see above), is also the thermodynamically most stable prototype sequence ${\widehat{S}}^X$. Therefore, we initiate a dynamic simulation with 1000 identical copies of ${\widehat{S}}^X$ for a given χ and subject this population to a newly imposed fitness pressure (Fig. 2). We have repeated the computations for ten simulations involving the five largest neutral nets (only one set of data is shown). Taken together, our findings allow for a common framework of interpretation, as follows. Immediately after initiation of the evolutionary dynamics, genotypic variance increases but the phenotypic distance to the target remains essentially unchanged. These results are in apparent agreement with earlier computations (Williams et al., 2001; Huynen et al., 1996; Fontana and Schuster, 1998). Note, however, that the initial evolutionary trend appears to remain neutral with respect to the originating structure only because the measure of structural similarity that has been used considers only ground-state conformations. Enrichment of the target structure in excited energy states is possible, but has not been explored, and thus remains “hidden” or “latent.” We also note a reduction in genotypic variation immediately before the steps of adaptation, while at the same time structural distance from the originating structure increases [Fig. 2b]. This pattern of behavior strongly suggests that, at the point immediately before a phenotypic transition, the sequence population has become extremely enriched around one genotype on the fringe of the originating neutral net. The fitness function in Eq. 3 (see Methods) imparts selective advantages to the fractional population of the target structure even when it is not the ground-state conformation of a given sequence. Biologically, this may correspond to having a selective advantage for a target function even when the fractional population of functioning molecules is small. Since evolutionary adaptation is more directed toward the target, it is approximately 40 times faster than in the same setup but without selection, i.e., when there is no evolutionary driving force towards the target before the model protein randomly drifts into the target neutral net (Fig. 3). In such a case, evolutionary optimization may be impeded as the dynamic process gets stuck because direct evolutionary transitions between neutral nets, i.e., point mutations inducing transformation of one phenotype into another, are rare (Cui et al., 2002).

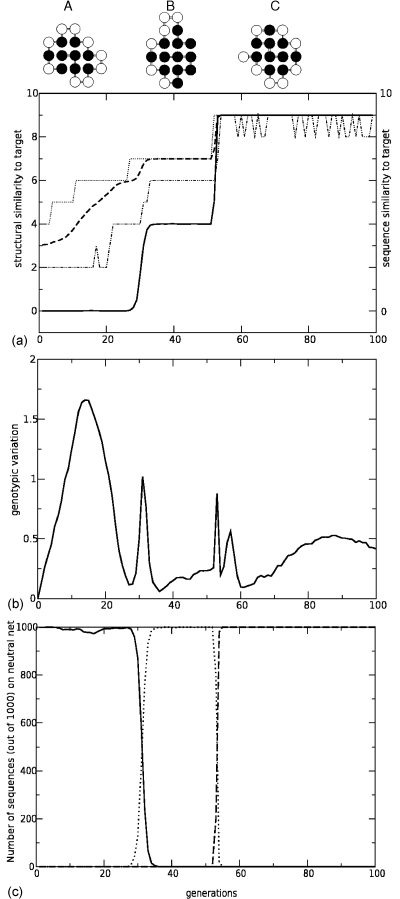
Figure 2. Population dynamics with excited-state selections for uniquely folding.

g=1 sequences. The genotypes evolve from a homogeneous starting population of identical copies of the prototype sequence for structure A toward the target neutral net for structure C. (a): phenotypes A, B, and C are modeled by structures of lattice proteins, depicted here in their corresponding prototype sequences. Black circles symbolize hydrophobic residues, which stabilize structures if and only if they are nearest neighbors on the lattice but not along the chain. The originating structure A has nine such stabilizing intrachain contacts between hydrophobic residues. Structure A has no common intrachain contact with the target structure C. For instance, the two chain ends are in contact in structure A, but one of the chain ends is not in contact with any residue in structure C. The thick solid curve shows the average structural similarity (measured by the number of shared intrachain contacts) between the target structure and the structures encoded by all of the sequences in the population as a function of evolutionary generation. In this simulation, maximum structural similarity is achieved after two major transitions (at approximately generation 32 and 52) by traversing the neutral net of structure B (top drawing, shown with its prototype sequence), which is dominantly populated at an intermediate stage of this evolutionary process (middle plateau). The thick dashed curve provides the average sequence similarity of all sequences to the target, measured by the Hamming distance $h(S_i,{\widehat{S}}^C)$ to the prototype sequence ${\widehat{S}}^C$ for target structure C. The upper and lower dotted curves give, respectively, the maximum and minimum similarity of the sequences in the population to ${\widehat{S}}^C$. While the population drifts along network A, the changing sequence similarity indicates that it is getting closer to the target but structurally the vast majority of the sequences still stay on the neutral network for structure A. (b): The average pairwise Hamming distance between all pairs of sequences in the population. (c): Number of sequences (out of 1000), which code uniquely for structure A (solid curve), B (dotted), and C (dashed) as functions of generation. All population dynamics simulations in this work were conducted using α=10⁶ for the selection gradient parameter in Eq. 1, and T=−ϵ∕0.5k_B, where ϵ is the HH contact energy in the HP model (Bornberg-Bauer and Chan, 1999).

Figure 3. Population dynamics without excited-state selections is around 40 times slower than with using excited states.

Same as Fig. 2 (middle) but now selection for the target structure is turned off unless the sequence is already in the neutral net of the target structure, i.e., F(S_i)=1 unless S_i is in the target neutral net. The average sequence and structural similarities are given, respectively, by the upper and lower trajectories in this plot.

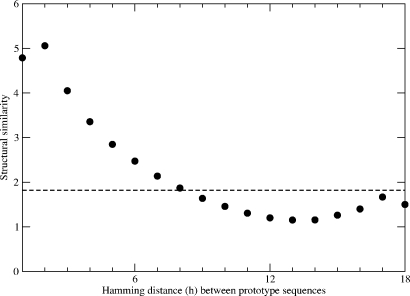
We now turn to the structural aspects of phenotypic transitions. Figure 4 provides the average structural similarity as a function of the mutational distance h between all prototype sequences. Their sequence-space proximity is well correlated with the structural similarity of their ground-state conformations. Thus, even for the rare events of direct phenotypic transitions from one neutral net to a neighboring net, structural features of the phenotype tend to be conserved to a significant degree.

Figure 4. Average pairwise structural similarity of phenotypes is measured by the number of identical intrachain contacts and shown as a function of sequence dissimilarity (Hamming distance) between the two prototype sequences that encode the pair of structures.

The dotted horizontal line here marks the level of random structural similarity obtained by averaging over all possible pairs of phenotypes.

To better understand how excited states contribute to the optimization for a chosen target, we further analyze all shortest mutational paths linking two different prototype sequences $({\widehat{S}}^{X_1},{\widehat{S}}^{X_2})$ of two neighboring neutral nets χ₁ and χ₂, encoding, respectively, for structures X₁ and X₂. Along each path considered in this analysis, the connection between χ₁ and χ₂ must be via a pair of sequences coding for two different viable (g=1) phenotypes and differing by one single point mutation, i.e., the sequences belong to different neutral nets. Then, thermodynamic stabilities of the two structures (X₁,X₂) for every sequence along the path are computed. The example in Fig. 5a shows that the thermodynamic stability (and thus the fractional population) for each of the two structures decreases almost smoothly (increasing ΔG) as the mutational distance h from its prototype sequence increases, although the ground-state structure does not change for all but one step along this path. Moreover, the fractional population of other excited states decays smoothly (free energy increases) such that any possible promiscuous function associated with those structures will also decrease. By evaluating all single-point mutational steps, we find that across the entire sequence space and for every arbitrarily chosen structural phenotype X, there is an essentially smooth gradient of increasing thermodynamic stability toward its prototype sequence ${\widehat{S}}^X$, i.e., with every mutational step decreasing the mutational distance to ${\widehat{S}}^X$, the fractional population will increase [Fig. 5b]. This is precisely how an evolving population such as that in Fig. 2 is driven toward the target prototype sequence. In other words, in the process of adaptation to a new fitness criterion, the population on average merely follows such a gradient of gradually increasing stability of the target structure in the conformational ensemble. In this perspective, even at the commencement of such an evolutionary process, when the population is mostly evolving along a neutral net (with respect to the dominant function), there can still be directional drift imposed by the new, “latent” fitness criterion.

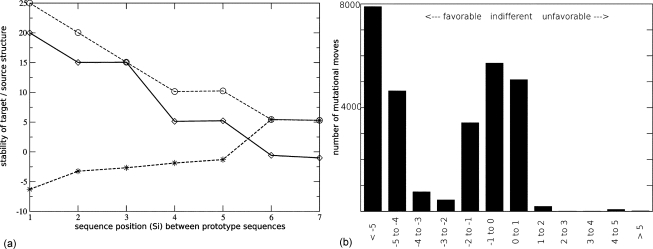
Figure 5. Relative stabilities of optimal and suboptimal structures along mutational paths from one prototype sequence to another.

(a): Relative stabilities of structures X₁ and X₂ along a typical mutational path from the prototype sequence ${\widehat{S}}^{X_1}$ (sequence position 1, left) to another prototype sequence ${\widehat{S}}^{X_2}$ (sequence position 7, right). Data points joined by solid and dashed lines denote, respectively, ΔG(X₂∣T,S_i) and ΔG(X₁∣T,S_i), in units of k_BT, where T=−ϵ∕5k_B. We refer to a single-point mutational step along a viable path from sequence S_i to sequence Si′ as a “favorable” move for a structure X_j if ${\Delta }_{i{i}^{\prime }}^j\equiv$ [ΔG(X_j∣T,S_i^′)−ΔG(X_j∣T,S_i)]≤0 and when the Hamming distance between S_i^′ and the prototype sequence ${\widehat{S}}^{X_j}$ of structure X_j is shorter than or equal to that between S_i and ${\widehat{S}}^{X_j}$, i.e., $h(S_{i^{\prime }},{\widehat{S}}^{X_j})\le h(S_i,{\widehat{S}}^{X_j})$. Otherwise, the mutational step is referred to as “unfavorable.” Only one of the 12 moves (solid and dashed lines) shown is slightly unfavorable (solid line between sequences 4 and 5). Two are essentially neutral (solid line between sequences 2 and 3, dashed line between sequences 6 and 7). All others are favorable. The increasing stability of structure X₂ toward ${\widehat{S}}^{X_2}$ and of structure X₁ toward ${\widehat{S}}^{X_1}$ correspond to typical superfunnel behaviors as in Figs. 2(a) and 5 of Bornberg-Bauer and Chan (1999). Included for comparison are the stability values (circles, joined by dotted line) of a structure that has the second lowest energy among all possible conformations that can be adopted by sequence 7 $\left({\widehat{S}}^{X_2}\right)$. Stability and fractional population of this structure decreases (free energy increases) as the sequence moves away from ${\widehat{S}}^{X_2}$. (b): Distribution of favorable, indifferent, and unfavorable moves, binned in units of ${\Delta }_{i{i}^{\prime }}^j∕k_{B}T$ (horizontal axis), among all 28,208 single-point mutational steps along all 1714 direct paths between pairs of prototype sequences. Around half (51.0%) of the moves are nearly indifferent $({\Delta }_{i{i}^{\prime }}^j\approx 0k_{B}T)$, but almost the same fraction (48.7%) are strongly favorable $({\Delta }_{i{i}^{\prime }}^j<-1k_{B}T)$ whereas only a negligible fraction (0.3%) are strongly unfavorable $({\Delta }_{i{i}^{\prime }}^j>1k_{B}T)$.

DISCUSSION

Thus, our proposed evolutionary framework is borne out in a biophysical heteropolymer model. Results here support the view that, as a general trend, phenotypic organization in genotype space permits smooth transitions (gradualistic adaptation) along any mutational path in at least two respects: (i) structurally more similar phenotypes tend to be in mutational proximity in genotype space, and (ii) excited stuctural states provide a latent and smooth path along which adaptation can proceed.

Conceivably, two issues might arise when applying these concepts to real proteins. First, our biophysical model is very simple. Although HP lattice conformations capture essential hydrophobicity-related features in folding and bear structural resemblance to real proteins, they do so only at a very coarse-grained level (Chan et al., 2004). Despite this obvious limitation, we found that the main trends predicted using simple models, e.g., regarding connected neutral nets and superfunnels, appear to be robust over a diverse set of different interaction schemes (Govindarajan and Goldstein, 1997; Williams et al., 2001; Wroe et al., 2005), and they are consistent with experiments (Bloom et al., 2005; Cordes et al., 2000). Thus, we are confident that our model is apt for the broad-stroke, evolutionary questions we are aiming to tackle in the present study.

Second, although it is widely accepted that structure begets function, the details of how excited states relate to a multitude of functions is not yet well understood. In this regard, the novel perspective offered in our modeling study and the parallel experimental investigation (Amitai et al., 2007) constitutes a first step toward a better understanding of this question. Theoretically, we expect the general trend predicted by the present model to apply to the general case of a biological function being associated with an ensemble of conformations rather than a single conformation. This is possible because our formulation can be readily extended from selecting one phenotype to selecting a given distribution of phenotypes, corresponding to different excited states.

Experimentally, as is emphasized in the “new view of protein structures,” biomolecules are dynamic entities (Mittermaier and Kay, 2006), with many minor structural fluctuations even for cooperatively folding proteins under native conditions (Bai et al., 1995). Some globular proteins may only fold noncooperatively, with an even higher population of excited states under folding conditions (Knott and Chan, 2006). Some proteins can be intrinsically disordered, lacking a folded structure altogether (Eisenmesser et al., 2005; Tompa, 2002; Gunasekaran et al., 2003; Dyson and Wright, 2005; Haynes et al., 2006). In several cases it has been argued that the evolution of new structures may be via metastable intermediates, that is, when two structures with energetically almost equally stable ground-state structures exist and conversion between the states is possible. For instance, the prion molecule, which is probably only metastable thermodynamically, was suggested to be a membrane protein, which is evolutionarily “en route” toward a globular protein (Tompa et al., 2001). For arc repressor, it was shown via mutagenesis studies that a significant part of the structure can switch between sheets and helices, depending on the HP (hydrophobic-polar) pattern (Cordes et al., 2000).

As far as protein function is concerned, enzymes have long been known to be promiscuous (James and Tawfik, 2001; Khersonsky et al., 2006). Promiscuity (polyreactivity) in function can be underlied by dynamic interconversions among energetically similar structures of a protein (James and Tawfik, 2003). As reported in the parallel experimental study (Amitai et al., 2007), the reactivity of serum paraoxonase with at least five substrates were well demonstrated. For several members of the very divergent enolase superfamily, it was recently argued that the evolution from an enzyme with one specificity toward another enzyme happened via promiscuous intermediates (Matsumura and Ellington, 2001; Glasner et al., 2006; Thoden et al., 2004). Taken together, these data support the idea that conformational intermediates between two or more different structures can correspond to evolutionary transitional forms that bridge different dominant biological functions.

The prevailing view on the emergence of new function at the molecular level stipulates that genes duplicate and the resulting redundancy facilitates adaptation since one of the gene copies becomes free to assume a new function (“neofunctionalization”), for example, via adaptive mutations (Ohno, 1970; Nowak et al., 1997; Wagner, 2005). However, several caveats have been identified. For example, the rate of adaptive mutations seems to be too low to explain the retention of genes (Graur and Li, 2000) and new environmental requirements do not necessarily occur exactly when an adaptable gene is provided by gene duplication. Several explanations have been offered such as the ability in polyploid organisms to adapt one of the two genomic alleles before gene duplication (Proulx and Phillips, 2006) or the idea of duplication/degeneration/complementation (DDC) (Lynch and Force, 2000). The latter idea already assumes that genes, ancestral to gene duplication, have multiple functions and that differential adaptation between two gene copies leads to subfunctionalization. Our results from a structural model, in conjunction with the functional studies in the accompanying paper (Amitai et al., 2007), offers a perspective on how molecular adaptation to new requirements can be accomplished while a dominant phenotype is maintained. The novelty here lies in the fact that, under the pressure to acquire a new function, specific latent traits can be selected for and that our simple structural model suggests a general principle of how optimization of latent traits expedites adaptation although adaptive mutations per se are extremely rare. Under ambient or physiological conditions, statistical mechanics stipulates that a certain degree of protein conformational fluctuation resulting in nonzero populations of excited states is inevitable. Hence all proteins have potential for functional promiscuity. Acting on excited states representing latent traits, adaptive evolution can proceed to optimize for an alternative function even while the gene retains the dominance of its original function associated with the ground state of the protein. Then, when the gene duplicates, since the alternate function has already been partially optimized, it would have a head start toward dominance of the new function. In light of our simulation results, an evolving population is expected to first concentrate at the transition point toward the neighboring neutral net [note the decrease in genetic variation shortly before the transition from net A to B in Fig. 2b]. As soon as the gene duplicates, one copy then becomes free to follow the trajectory to the most optimal phenotype for the new function while the other is released from that adaptive pressure. This biophysical perspective extends Maynard-Smith’s idea of a continuous phenotype space to a concept of proximal networks with nearby transition points through which evolutionary trajectories are funnelled. Furthermore, this view reconciles the ideas of adaptive and neutral mutations, thus providing a conceptual framework to rationalize pertinent experimental results reported in the companion article (Amitai et al., 2007) and elsewhere (Aharoni et al., 2005).

MATERIALS AND METHODS

Biopolymer model

For consistency with earlier computations we represent phenotypes as structures which are self-avoiding chains of length 18 on a square lattice (Bornberg-Bauer and Chan, 1999; Wroe et al., 2005) (see also structures on top of Fig. 2). We place special emphasis on the density of states (DOS) g(E_j), which is the set of numbers of conformations with energy E_j for a given sequence S_i. The DOS is determined exactly for all unique (g=1) sequences, where the degeneracy g is the number of conformations with ground-state energy E_N; all other conformations are called “excited” states. Using the DOS, we can compute the partition function

$$Z(S_i;T)=\sum _{E_j}g\left(E_j\right)\exp (-E_j∕k_{B}T)$$ (1)

of sequence S_i (where k_BT is Boltzmann constant times absolute temperature) and the thermodynamic stability

$$\mathrm{\Delta }G(X_j\mid T,S_i)=E_j+k_{B}T\ln [Z(S_i;T)-\exp (E_j∕k_{B}T)]$$ (2)

of any structure X_j. This stability, which is a free energy, is directly related to the fractional population exp[−ΔG(X_j∣T,S_i)∕k_BT]∕{1+exp[−ΔG(X_j∣T,S_i)∕k_BT]} of X_j in the conformational ensemble of S_i. It depends on the energy E_j of the structure X_jand the conformational population of all other energy levels.

Population dynamics

We simulate population dynamics among uniquely folding sequences, similar to earlier approaches (Fontana and Schuster, 1987; Huynen et al., 1996; Cui et al., 2002). Genotypes corresponding to a large protein family are taken and, to produce the next generation, a uniform mutation rate of 0.1 is randomly applied. Mutations to g>1 sequences are considered lethal but the number of mutations per sequence is not limited and back mutations are permitted. Fitness values F(S_i) with respect to a chosen target structure X_j are assigned to every sequence S_i based on the fractional population of X_j in the conformational ensemble of S_i as follows:

$$F\left(S_i\right)=\exp [\alpha e^{-(E_j∕k_{B}T)}∕Z\left(S_i\right)],$$ (3)

where α is a tunable selection gradient and E_j is computed by mapping S_i onto X_j (see above). We set the rate of reproduction of each sequence S_i proportional to F(S_i). The functions F and Z are T dependent, although this dependence is not explicitly indicated in the above equation for notational simplicity. By normalizing the overall population after each reproduction cycle, population size is kept constant, as we assume resources are limited. This process is repeated until convergence, i.e., either all genotypes arrived at the target phenotype or the overall population fitness stagnates.