Transistor analogs of emergent iono-neuronal dynamics

Abstract

Neuromorphic analog metal-oxide-silicon (MOS) transistor circuits promise compact, low-power, and high-speed emulations of iono-neuronal dynamics orders-of-magnitude faster than digital simulation. However, their inherently limited input voltage dynamic range vs power consumption and silicon die area tradeoffs makes them highly sensitive to transistor mismatch due to fabrication inaccuracy, device noise, and other nonidealities. This limitation precludes robust analog very-large-scale-integration (aVLSI) circuits implementation of emergent iono-neuronal dynamics computations beyond simple spiking with limited ion channel dynamics. Here we present versatile neuromorphic analog building-block circuits that afford near-maximum voltage dynamic range operating within the low-power MOS transistor weak-inversion regime which is ideal for aVLSI implementation or implantable biomimetic device applications. The fabricated microchip allowed robust realization of dynamic iono-neuronal computations such as coincidence detection of presynaptic spikes or pre- and postsynaptic activities. As a critical performance benchmark, the high-speed and highly interactive iono-neuronal simulation capability on-chip enabled our prompt discovery of a minimal model of chaotic pacemaker bursting, an emergent iono-neuronal behavior of fundamental biological significance which has hitherto defied experimental testing or computational exploration via conventional digital or analog simulations. These compact and power-efficient transistor analogs of emergent iono-neuronal dynamics open new avenues for next-generation neuromorphic, neuroprosthetic, and brain-machine interface applications.

The complex dynamics emergent from spatiotemporal interactions of ionic signals in neurons (Koch, 1999) present great challenges for experimental investigation or computer simulation, and become intractable at the network or system level. To break the computation barrier limiting large-scale neural network simulations of emergent behaviors, various drastic measures using dedicated supercomputers or high-performance distributed computing (Markram, 2006) or digital gate arrays (Mak et al., 2006; Weinstein and Lee, 2006) have been proposed. High-speed computing has also penetrated new experimental approaches that employ brain-machine interfaces (BMIs) for neuroscience and neuroprosthetics applications (Wise, 2005). For example, a combined experimental-simulation paradigm called “dynamic clamp” tests emergent neuronal dynamics by creating virtual membrane or synaptic conductances in biologic neurons (Prinz, 2004). For such applications, advances in high-speed computational platforms and procedures are critical for the realization of increasingly complex and realistic neuron-computer interfaces that can operate in “hard real time” (Dorval, 2001).

The current quest for high-speed digital simulation of large-scale neuronal dynamics at high bit-resolution and low noise misses the point that neuronal computations are inherently analog and, furthermore, are noisy and subject to parameter variations even though neuron-to-neuron communication is digital and deterministic via all-or-none spiking. From the theory of computation, a fundamental tradeoff between digital and analog computing (and for any computational platform in general) is that of high precision vs high speed for given space and power budgets. The brain’s unique analog-digital hybrid architecture provides an intricate balance of computational speed and resolution with impressively high space- and power-efficiency and scalability to complex problems (Sarpeshkar, 1998; Herz et al., 2006).

The advent of neuromorphic “silicon neuron” models using metal-oxide silicon (MOS) transistors makes it possible to emulate such hybrid computations with analog very-large-scale-integrated (aVLSI) circuits technology (Mahowald and Douglas, 1991; Van Schaik, 2001; Farquhar and Hasler, 2005). The computational advantage of the aVLSI approach lies in its inherent spatially dense, parallel, and real-time nature (Mead, 1989; Hopfield, 1990). This approach has led to many spike-based aVLSI neuromorphic modeling, sensory signal processing and neuroprosthetic device applications at the network or system level (Jung et al., 2001; Lewis, 2001; Chicca et al., 2003; Still et al., 2006; Bartolozzi and Indiveri, 2007; Shi and Horiuchi, 2007).

However, extending aVLSI technology to emulate passive and active membrane conductances in complex or large-scale networks has proved to be fraught with many difficulties. Silicon transistors are subject to inherent structural heterogeneity and, hence, functional variability across nominally identical units within a finite chip area (Tsividis, 2003). Traditional neuromorphic aVLSI circuits are particularly susceptible to such device variability because they have a limited input voltage dynamic range (<±100 mV) for emulating biologic ion-channel current-voltage (I-V) relationships. Although such susceptibility to device nonidealities may not present a serious problem for the purpose of mimicking simple neuronal behaviors such as spiking, it could create a major hurdle when emulating more sophisticated iono-neuronal dynamics that necessitate extensive post-fabrication tuning of circuit parameters in order to correct for variabilities in transistor threshold voltages, making their aVLSI implementation impractical. Such intrinsic parameter sensitivity precludes robust emulation of complex neuronal behaviors beyond simple spiking or specific ion channel dynamics with limited computational capabilities. For this and other reasons, most current aVLSI neural networks resort to using simple integrate-and-fire models with non-conductance-based synaptic dynamics (Indiveri et al., 2006) instead of conductance-based models of spiking neurons and synapses as the basic computational units.

Here we present novel wide voltage dynamic range (>1 V) and low-power aVLSI circuit designs that allow robust emulation of emergent iono-neuronal dynamics at a computational speed that is limited only by device physics. These iono-neuromorphic transistor analogs provide the basic building blocks that can be readily configured on-chip to robustly emulate intricate synaptic and intracellular computations with little or no parametric tuning across the fabricated circuits necessary. As a prime example of the power of this advanced neuromorphic computation approach, the versatility of our on-chip interactive simulation capability enabled our prompt discovery of a minimal model of chaotic pacemaker bursting, an emergent iono-neuronal behavior of fundamental importance that has hitherto defied conventional digital or analog simulations. This new benchmark for neuromorphic computation demonstrates the feasibility and promise of compact, low-power, high-speed, and wide dynamic range aVLSI implementation of complex iono-neuronal models. Future applications of this approach include monolithic integration with MOS compatible iono-electronic devices to interface directly with biologic neurons in vitro (Zeck and Fromherz, 2001; Sorensen et al., 2004) with an eye towards real-time closed-loop control of neuronal processes for implantable neuroprosthetic or BMI applications.

Results

Robust iono-neuromorphic transistor circuits

Voltage dynamic range of biologic ion channels and their transistor analogs. Iono-neuromorphic transistor circuits compute macroscopic ion-channel currents of the form I_OUT=g(x_i)(V_MEM–E_REV), where V_MEM is the membrane potential, E_REV is the reversal potential of the channel, and the conductance term g(x_i) describes the cumulative effects of various voltage- and∕or ligand-dependent (or other biophysical) gating variables x_i. The inherently sigmoidal transistor I-V transconductance relationship (for MOS transistors biased in the weak-inversion regime (Tsividis, 1999) provides the computational primitives for all the g(x_i) terms.

A major limitation of all analog circuits is the intrinsic variabilities of the transistor threshold voltage and dark current (or current factor) due to fabrication inaccuracy, device noise, etc. (Kinget, 2005). Variabilities of the transistor dark current translate linearly to inaccuracies in the bias current and resultant simulated ion-channel currents. Such physical variabilities of the ion-channel currents are unavoidable in neuromorphic or biologic neurons alike. By contrast, physical or noise-induced mismatch of the transistor threshold voltages in an iono-neuromorphic circuit may result in much larger errors in the simulated ion-channel currents because of the sigmoidal (exponential) transconductance relationship. Indeed, significant departure of the effective driving potential (V_MEM–E_REV) from the intended linear region (input voltage dynamic range) of the sigmoidal relationship may render the ion channel totally malfunctional.

For this reason, membrane potentials in biologic neurons are generally regulated much more tightly than are ionic currents. Biologic ion channels are responsive to changes in V_MEM that span a 150 mV range (from −100 to +50 mV). This range is slightly wider than those of traditional neuromorphic analog circuits, which attempt to scale the biological voltage range using a 1:1 ratio. However, biologic ion channels are designed using proteins that all have very similar activation parameters and are capable of responding to a very small voltage change. In biologic neurons the sigmoidal I-V relationship is highly reproducible across all ion channels of the same family to within a narrow window.

Unfortunately, the threshold voltage of weak-inversion transistors in present MOS technology and device dimensions of interest is liable to variabilities in the mV range, making traditional neuromorphic analog circuits highly susceptible to transistor mismatch, device noise and other nonidealities. Thus, in order to emulate emergent iono-neuronal dynamics each sub-circuit must be accurately tuned to the desired ion channel linear region and correct for fabrication inaccuracies. Such nonrobustness to threshold voltage variability makes it rather difficult and time-consuming to select the correct parameter values pre- or post-fabrication for proper circuits operation especially when the parameter space has many dimensions and the emergent behavior of interest is specific to a small section of the parameter space. More importantly, because such parameter tuning may vary considerably from transistor to transistor, circuits fabricated on the same die (and especially those on different chips) may not share a consistent calibration of the electronic-biologic potentials (such as membrane potentials) and cannot be directly connected across the chip. Therefore, it is impractical to put a plurality of such circuits on the same silicon die for aVLSI implementation. Although biasing the transistors in the strong-inversion regime may increase the input voltage dynamic range thereby allowing consistent linear calibrations throughout, this approach also increases the power consumption by several orders of magnitude thus precluding its aVLSI implementation or applications to implantable biomimetic devices (Simoni, 2004).

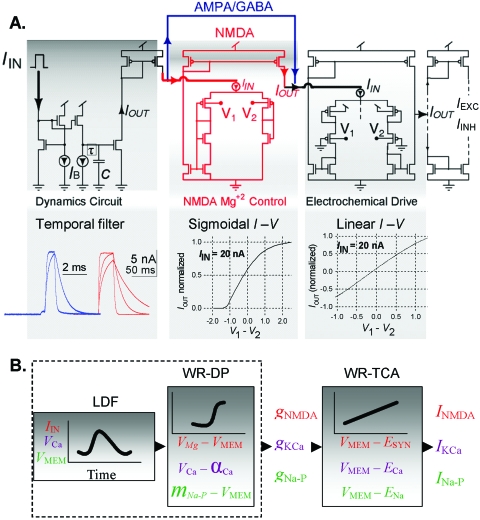
Wide dynamic range iono-neuromorphic aVLSI circuits design. To circumvent these difficulties, we introduce the following current-mode low-power MOS circuit designs for robust neuromorphic modeling [Fig. 1A]: wide-range transconductance amplifier (WR-TCA) (Sarpeshkar, 1997) and custom-designed wide-range differential pair (WR-DP), which increase the corresponding dynamic range by an order of magnitude to >±1 V, the highest attainable for a 5 V supply voltage; and log-domain filter (LDF) (Frey, 1993), a current-mode filter with input and output currents tunable over five orders of magnitude, which can interface directly with other wide-range current-mode circuits. WR-TCA is used to realize the electrochemical gradient (V_MEM–E_REV) portion of the channel equation. Sigmoidal input-output relations, such as activation or inactivation of voltage-gated channels or the [Mg⁺²]-dependent block of the N-methyl-D-aspartate (NMDA) channel, are emulated with WR-DP. Temporal dynamics of synaptic transmission processes including neurotransmitter diffusion, receptor binding, ion channel kinetics, intracellular ion buffering and second messenger kinetics (for metabotropic synapses) are modeled as an α-function at the whole-cell level (Koch, 1999) by a cascade of LDFs or lumped into a single LDF. The novel combination of these state-of-the-art circuit designs makes it possible to extend the dynamic range of the weak-inversion transistor circuits to near maximum without encroaching on the strong-inversion regime, thus keeping these building-block circuits extremely power efficient (<100 nW) (Tsividis, 1999) with operating currents in the pico- to nanoampere range and a supply voltage (V_DD) as little as 1.2 V (Rachmuth, 2005).

Figure 1. Wide dynamic range ion-channel circuits architecture.

(A) Building block circuits and input-output curves. Left: Log-domain filter (LDF) (Frey, 1993). Plots show several possible I_O-LDF of AMPA (blue) and NMDA (red) conductance dynamics. Middle: wide-range differential pair (WR-DP) implementing a sigmoidal I_O-DP–V_IN relation. V_IN=V₁−V₂; Right: a wide-range transconductance amplifier (WR-TCA) implementing a linear I_O-TCA–V_IN relation. I_IN-DP=I_IN-TCA=20 nA DC current (upper limit of I_O amplitude) AMPA/GABA channel design (blue line); NMDA channel includes a WR-DP (red circuit). (B) Block diagram representations of circuits from (A), and realizations of voltage-gated and calcium-dependent channels can be implemented with the same architecture as the NMDA channel.

Each circuit module can be tailored to specific ion channels by setting only 1–2 tunable voltages which are linearly mapped to specific biopotential parameters (such as E_REV). The wide voltage range increases the error tolerance of circuit parameters by more than an order of magnitude such that standard ion-channel biopotential parameter values can be hard-wired into the microchip without the need for separate tuning or storage. (Alternatively, these parameters can be left programmable post-fabrication for modeling flexibility.) To preserve biological realism and consistency across all on-chip circuits, all relevant biopotentials are linearly mapped to specific transistor input voltages with the same calibration throughout, which is critical for aVLSI implementation (see Methods).

The resultant transistor output currents (current-mode output) emulate changes in ion-channel currents potentially covering several orders of magnitude, which are typical of biologic neurons. Similarly, the effects of transistor thermal noise—the dominating noise source in transistors biased in weak-inversion—are reduced in the wide-range circuits compared to conventional circuits [by at least 8.5 dB (Sarpeshkar, 1997)]. These advantages allow for robust high-speed simulation of large-scale iono-neuromorphic models using aVLSI technology operating at relatively low power and small size compared to digital simulation platforms.

For example, to realize excitatory AMPA or inhibitory GABA_A ligand-gated channels, one or more LDFs are cascaded with a WR-TCA [Fig. 1A]. An input current pulse (I_in, modeling a presynaptic spike) to the LDF produces a time-varying conductance signal in the form of an α-function which, in turn, is multiplied by the electrochemical gradient in the WR-TCA to generate an I_OUT with similar time course as biologic AMPA or GABA_A channels. For NMDA channel, a WR-DP is added after the LDF to model the effect of voltage-dependent [Mg⁺²] block on the conductance. The resultant channel current can be made excitatory (I_AMPA,I_NMDA) or inhibitory (I_GABAA) by connecting I_OUT to a current source or a current sink, respectively [Fig. 1A].

Figure 1B illustrates the general circuit architecture for modeling any excitatory or inhibitory ionotropic or metabotropic receptor-gated channels. Similar architecture also applies to Ca⁺²-dependent ion channels or other ion channels that are coupled to neuromodulators, except that the input to the LDFs would be an intracellular Ca²⁺ or extracellular neuromodulator signal instead of presynaptic spike. Hodgkin-Huxley type voltage-dependent ion channels can also be modeled in a similar fashion (Mahowald and Douglas, 1991; Simoni, 2004) with additional LDFs and WR-DPs to simulate the activation and inactivation kinetics.

Two examples of coincidence detection

Coincident spikes detection. Coincident neuronal activity at the cellular or network levels is an important form of Boolean computation in the brain (Koch, 1999). To test the versatility of our microchip, we first constructed a network model of coincidence spike detection via monosynaptic excitation and disynaptic feedforward inhibition in a hippocampal pyramidal cell (Pouille, 2001) [Fig 2A]. Such coincidence detection is thought to enhance neuronal synchrony in brain systems (Konig, 1996). Similar feedforward inhibition network architecture is also shown to sharpen visual information transmission between retinal ganglion cells and thalamocortical neurons in the lateral geniculate nucleus (Blitz, 2005). Because most experimentally induced disynaptic inhibition protocols necessarily activate multiple fibers which may not be coactivated by normal physiological inputs, it is difficult to determine how the dynamics of such feedforward inhibition are related to those occurring physiologically (Blitz, 2005). We, therefore, examined the role of feedforward inhibition in regulating temporal integration and coincidence detection computations in a single pyramidal neuron by systematically varying the strengths and timings of two convergent stimuli over a wide range in our model.

Figure 2. Wide dynamic range aVLSI microchip emulation of coincidence detection via feedforward inhibition.

(A) Network arrangement and synaptic compartment. Left top: A hippocampal network architecture (Pouille, 2001) of Schaffer collateral inputs (S1 and S2) on to a pyramidal cell (PC); IN–interneuron; ●–inhibitory synapse; ◁–excitatory synapse. Left bottom: A membrane node of PC designed with a follower integrator circuit (Mead, 1989). Right top: Excitatory I_AMPA and inhibitory I_GABAA responses to presynaptic AP stimulation recorded from excitatory and inhibitory synapses, respectively. Right bottom: Somatic response to a stimulation pulse to S1 recorded from the PC membrane node circuit results in EPSP+IPSP complex. A stimulation pulse to S2 results in EPSP only. (B) Somatic EPSP recordings in response to pairing two input pulses (Pulse1 to S1; Pulse2 to S2, respectively) with various delays. Left: the response of the intact network. Right: same experiment on a network with IN removed. (C) Spiking responses to the above stimulation protocol recorded from a somatic compartment implemented by an integrate-and-fire neuron (Van Schaik, 2001). Left: intact network. Right: IN removed. Identical results were recorded in Pouille et al. (2001).

The excitatory-inhibitory network fabricated on aVLSI technology produced a stereotypical sequential excitatory-inhibitory postsynaptic potential (EPSP-IPSP) response for a primary input and EPSP response for a second input [Fig. 2A]. For weak stimuli, temporal summation of the resulting EPSPs was suppressed in the intact network if the second input did not arrive prior to the initiation of the IPSP [Fig. 2B]. When the inhibitory connection was blocked, temporal summation occurred over a much wider time window determined by the membrane time constant [Fig. 2B].

For strong stimuli, coincidence detection was achieved in the intact network such that the postsynaptic neuron fired an action potential only when the second input arrived within a narrow time window after the first input; this time window became much wider after the inhibitory connection was blocked [Fig. 2C].

These findings support a possible role for feedforward inhibition in ensuring precise coincidence detection, by limiting temporal summation of inputs within a small time window (Pouille, 2001). Thus, coincidence detection can be thought of as an analog version of the familiar digital AND gate, with feedforward inhibition performing a delayed veto operation. Together, these analog operations can be used to bind temporally coincident but spatially separate input signals, without the need for power-inefficient clocked digital circuits. An aVLSI circuit realization of this motif in a 2D pixel-based architecture can be used to perform spatial pattern recognition tasks in real time and in a compact, low-power environment for advanced biomimetic sensory signal processing applications.

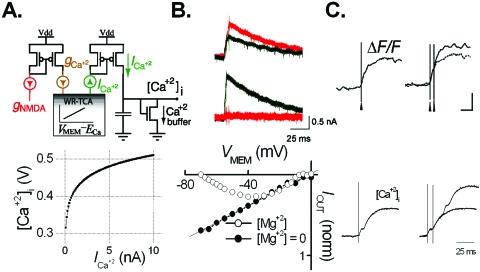
Coincident pre- and postsynaptic activities. We next tested our iono-neuromorphic circuit model of the NMDA channel—the most sophisticated ionotropic synaptic channel known to date due to its exquisite co-dependence on both neurotransmitter gating and voltage-dependent Mg⁺² block. We tuned the circuit to reflect the relatively low magnitude and slow dynamics of the NMDA channel found in hippocampal neurons and, furthermore, reproduced the dependence of channel conductance on both presynaptic activation and V_MEM (Fig. 3). This on-chip embodiment of the NMDA channel’s well-known function as coincidence detector for pre- and post-synaptic activities circumvents certain deficiencies of previous silicon NMDA conductance models via conventional circuit designs (Rasche and Douglas, 1999).

Figure 3. Wide dynamic range aVLSI microchip emulation of NMDA receptor-mediated calcium dynamics.

(A) Top: the NMDA-dependent calcium circuit. The NMDA conductance g_NMDA (red) is scaled to generate calcium conductance g_Ca. This signal is sent to a WR-TCA to generate $I_{\mathrm{Ca}}^{+2}$. $I_{\mathrm{Ca}}^{+2}$ is sent to a current-voltage converter circuit to generate [Ca⁺²]. Bottom: the I_IN-V_OUT steady-state V-I curve of the current-voltage converter circuit. (B) Top: I_NMDA (red) and I_Ca (green) responses to a presynaptic AP at V_MEM=−40 and 0 mV, showing the NMDA channel voltage dependence and the presence of $I_{\mathrm{Ca}}^{+2}$ while I_NMDA≈0. Bottom: I_NMDA-V_MEM curve of the NMDA circuit in the presence (○) or absence (●) of [Mg⁺²] block. (C) Top: biological recording of [Ca⁺²] integration in response to a single or a pair of presynaptic pulses [adapted by permission from MacMillan Publishers Ltd.: Nature (Mainen 1999), copyright 1999]. Bottom: the circuit response to the same stimulation protocol (time scale apply to both top and bottom.)

Because the NMDA channel is a non-selective cation channel, the resultant calcium current $\left(I_{\mathrm{Ca}}^{+2}\right)$ is distinct from the net NMDA current (I_NMDA). We employ a separate WR-TCA to generate $I_{\mathrm{Ca}}^{+2}$ independent of I_NMDA and integrate it on a current-voltage converter circuit to yield an intracellular calcium concentration ([Ca⁺²]_i) signal [Fig 3A]. Figure 3B shows that $I_{\mathrm{Ca}}^{+2}$ is distinct from the net NMDA current (I_NMDA) for different membrane potentials. The resultant circuit emulated differing [Ca⁺²]_i accumulation patterns following single or paired-pulse stimulation similar to intracellular imaging results in a single dendritic spine (Mainen, 1999) [Fig. 3C]. Interestingly, the temporal summation of [Ca⁺²]_i following a paired-pulse input evidences a temporal integrator even though the NMDA channel itself acts as a coincidence detector.

NMDA coincidence detection and postsynaptic intracellular calcium integration are widely believed to be the key steps underlying the induction of many forms of Hebbian synaptic plasticity, a putative cellular correlate of learning and memory behaviors in central neurons. The present transistor analogs of these processes will pave the way for future development of NMDA receptor-mediated Hebbian synaptic plasticity models on similar silicon substrates (Rachmuth, 2006).

Chaotic bursting in pacemaker model

Bursting in pacemaker cells is a profound emergent behavior at the single-neuron level and is fundamental to a variety of biologic rhythms (heartbeat, respiration, thalamic rhythm, gastric movement, locomotion, etc.) and to some forms of sensory encoding (Destexhe and Sejnowski, 2003; Krahe, 2004). The dynamics of the opposing inward and outward currents that control phase transitions during bursting are shaped by a myriad of ionic mechanisms that may vary in differing pacemakers. For example, burst initiation has been variously ascribed to voltage-gated persistent sodium (Na_v–P) current, sustained inward current, T- and L-type Ca⁺² currents, Ca⁺²-activated nonspecific cation current, or hyperpolarization-activated cation current (Harris-Warrick, 2002; Destexhe and Sejnowski, 2003; Del Negro, 2005). In all, a wide array of K⁺ conductances is thought to mediate burst termination.

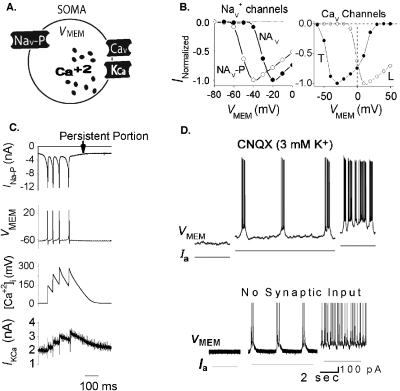
Iono-neuromorphic model of pacemaker bursting. To set a new benchmark for neuromorphic computation, we programmed the microchip to realize a minimal model of neuronal bursting [Fig. 4A] consisting of an integrate-and-fire soma circuit (Van Schaik, 2001) and circuit models of Na_v–P, voltage-gated Ca⁺² (Ca_v) and Ca⁺²-dependent K⁺ (K_Ca) channel dynamics for controlling burst initiation and termination [Fig. 4B]. The Na_v–P channel was set at a relatively low activation threshold of approximately −60 mV, which provided a depolarizing current at resting V_MEM to initiate the bursting. The resultant Ca⁺² influxes via the Ca_v channel activated the K_ca channel incrementally until it terminated the burst [Fig. 4C]. Increasing the leak current of the soma circuit abolished the bursting, whereas subsequent application of a depolarizing bias current restored it, as observed experimentally (Del Negro, 2005) [Fig. 4D]. Similar on-chip bursting behaviors have been reproduced previously but with circuit designs that required many more parameters and much higher operating currents (Simoni, 2004).

Figure 4. Wide dynamic range aVLSI microchip emulation of pacemaker bursting behavior.

(A) Somatic compartment with Na_v–P–persistent Na_v channel; Ca_v–voltage-gated calcium channel; K_Ca—calcium-dependent potassium channel. V_MEM is connected to an integrate-and-fire (I-F) soma circuit for spike generation. (B) Left: I_OUT-V_MEM curves of Na_v channels and of L-type Ca_v channel and T-type Ca_v channel (T-spice simulation). (C) Fabricated chip recording of ionic signals during a burst. (D) Top: Biological recording of a pacemaker neuron [reproduced with permission from Del Negro et al. (2005), Copyright 2005 by the Society for Neuroscience]. Bottom: fabricated chip recording from circuit V_MEM node. Same scales for both top and bottom.

The wide-range circuit design allowed us to conveniently generate various bursting or non-bursting patterns, tune the burst frequency over three orders of magnitude (0.1–10 Hz), as well as vary the number of spikes per burst by simply adjusting, in real time, certain ion-channel circuit parameters that affected neuronal excitability, channel dynamics, and persistent depolarizing current at resting potential (see supplemental online text). For a wide range of parameter values, the bursting exhibited a decrementing pattern early in the burst—with gradually increasing interspike intervals (ISIs)—as observed experimentally in synaptically isolated rat pre-Bötzinger and crustacean pyloric pacemakers (Elson, 1999; Del Negro et al., 2001) and in computer simulations (Del Negro et al., 2001). Other bursting patterns, such as the accelerating-decelerating pattern observed in thalamic reticular cells (Destexhe and Sejnowski, 2003) or some invertebrate pacemakers, could also be readily reproduced with proper parameter tuning (see supplemental online text).

Previous attempts to enhance the dynamic range of neuromorphic analog circuits in order to emulate pacemaker bursting have resorted to biasing the transistors in the strong-inversion regime, a practice that is bound to increase power consumption by several orders of magnitude making them non-ideal for aVLSI implementation or implantable biomimetic device applications (Simoni, 2004). In contrast, all three building blocks of our wide-range neuromorphic analog circuits are designed to operate in power-efficient weak-inversion regime, all in current mode. Importantly, analysis of our on-chip minimal pacemaker model revealed a novel chaotic bursting pattern, an emergent property of pacemaker iono-neuronal dynamics that had eluded previous analog or digital simulations.

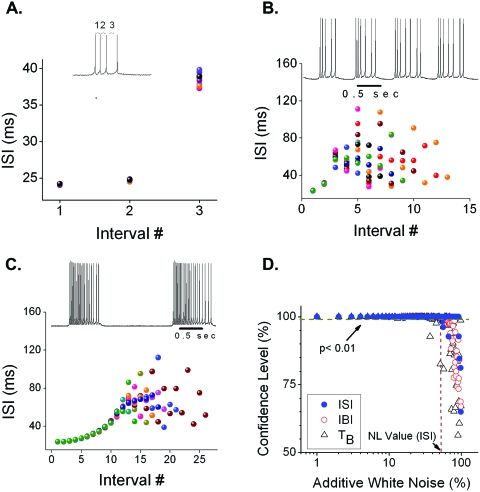
Minimal model of chaotic pacemaker bursting. Irregular bursting has been observed in some pacemakers with decrementing bursting pattern, such that the ISIs are sharply defined at burst onset but become increasingly variable as the burst continues (Elson, 1999). The decrementing pattern in our on-chip minimal pacemaker model displayed similar irregularity, which was evident even in bursts with as few as 3–4 spikes [Fig. 5A] and became full-blown in longer bursts thus causing highly irregular burst durations (TBs) and interburst intervals (IBIs) from burst to burst [Fig. 5B]. For bursts with a longer initial decrementing regime the ISI series displayed sensitive dependence on initial conditions [Fig. 5C]—a defining signature of deterministic chaos (Abarbanel, 1996; Poon and Barahona, 2001). Application of a chaos-specific numerical titration test (see Methods) (Barahona and Poon, 1996; Poon and Barahona, 2001) to the simulation data verified the presence of strong chaotic dynamics in the ISI series as well as the IBI and TB series [Fig. 5D].

Figure 5. Chaotic ISIs revealed by on-chip simulations of minimal pacemaker model with varying ionic parameters.

(A) Short bursts showing a decrementing firing pattern as indicated by a plot of ISI vs spike interval # (defined in inset). Each color represents a different burst in the same run. (B) Longer bursts showing highly irregular ISIs that quickly diverged from burst to burst. (C) Even longer bursts showing the ISIs’ sensitive dependence on their initial conditions. (D) Results of noise limit (NL) test for chaos (Poon and Barahona, 2001) for simulation shown in (C) The corresponding NL values (indicated by vertical dotted line) averaged over three runs for IBI series, ISI series, and T_B series were 68%, 25%, and 37%, respectively with (p<0.01), indicating that all three series were chaotic (see Methods).

Previous pacemaker bursting models ascribed the irregularities in TB and IBI to either stochastic ion-channel fluctuations (Carelli, 2005) or nonlinear interaction of ionic signals with slow intracellular processes (Falcke, 2000). All these models involved at least five different types of ion channels and other mechanisms for irregular bursting. The present microchip results show that chaotic dynamics in intraburst ISI and, hence, in TB and IBI, could emerge from a pacemaker model with as few as three types of ion channels (one for burst initiation and two for burst termination) without the need for any intrinsic or extrinsic stochastic influences or other complex intracellular processes. Although the effects of small ambient or thermal noise cannot be ruled out even in our low-noise wide-range circuits as with biologic neurons, our finding of sensitive dependence on initial conditions and noise titration provide unequivocal proofs that the irregular ISI pattern in our minimal model of pacemaker bursting was largely an emergent property of nonlinear iono-neuronal dynamics instead of random fluctuations. This discovery is highly significant in that chaotic pacemaker bursting is one of the most fundamental forms of chaotic dynamics at the single cell level, which may contribute to many other forms of irregular rhythmic activities ranging from heart rate variability (Poon and Merrill, 1997) to epileptic seizure (Martinerie et al., 1998). These novel observations were made possible by the present wide-range transistor analog, which provides a robust, versatile, and highly interactive computational platform for the modeling, simulation, and exploration of complex iono-neuronal dynamics in real time (see supplemental online text).

DISCUSSION

The present results demonstrate the feasibility of wide dynamic range aVLSI neuromorphic circuits in offering a compact simulation environment with excellent power efficiency for real-time emulation of emergent iono-neuronal dynamics at the subcellular, single-neuron and network levels. Compared to traditional neuromorphic aVLSI circuits, the present use of wide dynamic range building-block circuits significantly increases their robustness to parameter variability and decreases their sensitivity to thermal noise. The latter advantages make it practicable to build complex iono-neuromorphic models that emulate emergent iono-neuronal behaviors, and to implement these models using aVLSI technology such that a uniform calibration of electronic-biologic potentials can be consistently applied across all circuits on the same chip (or between different chips) with little post-fabrication tuning of individual circuits necessary. Our strict adherence to the weak-inversion regime ensures exceedingly low-current (pico- to nanoampere) transistor operation throughout, thus circumventing the high power consumption limitations of previous wide dynamic range neuromorphic circuit designs that resorted to the strong-inversion regime (Simoni, 2004). The demonstrated ability of this approach to emulate complex emergent behaviors such as chaotic pacemaker bursting in a tiny silicon chip operating at extremely low power (presently set to 2–20 nA×5 V per ion channel) sets a new benchmark for neuromorphic computation.

Our wide dynamic range circuit designs include a MOS-based LDF building block for modeling temporal events such as synaptic α-functions or ion channel activation∕inactivation kinetics. For these ionic dynamics, the robustness requirements for emulation are generally not as critical as for the corresponding I-V relationships and, hence, other current-mode temporal filters may be substituted as desired. In contrast, recently proposed neuromorphic models capture the characteristic voltage dependence of ion channel activation∕inactivation time constants in conformance with the Hodgkin–Huxley formalism but the I-V characteristics of these models are again nonrobust to fabrication inaccuracies (Hynna and Boahen, 2007). A challenge in future is to extend the present wide dynamic range circuit designs to the modeling of such voltage-dependent ion channel activation and inactivation dynamics in accordance with the Hodgkin–Huxley formalism, although the choice of the latter vs simpler phenomenological models is often determined by a fine balance of detail and abstraction in practice (Meunier and Segev, 2002; Herz et al., 2006).

Additionally, although the wide dynamic range circuits as embodied here are relatively large compared with traditional narrow dynamic range circuits (with 20–25 vs 6–10 transistors), it is still more compact than traditional designs since the latter would have required a hundred-fold increase in transistor size (for a ten-fold decrease in variability of threshold voltage) in order to match a similar ten-fold increase in robustness (measured by the input voltage dynamic range relative to the variability of transistor threshold voltage). While no attempt was made to optimize circuits size in our proof of concept, future refinements of this approach should allow smaller circuits design for greater large-scale integration. In any case, judicious tradeoffs between circuit complexity, realism, and desired performance are key to neuromorphic systems operability and scalability. The latter is dependent on voltage dynamic range at the circuit level, device fabrication density at the chip level as well as chip-to-chip communication bandwidth at the system level. For a conservative 1.5 μm fabrication process, a standard 20 mm² die may accommodate approximately 200 ligand-gated channels, 80 Ca⁺²-dependent (or 40 voltage-dependent) channels or 275 integrate-and-fire somatic compartments, whereas the use of a 0.35 μm process and 1 cm² die will increase the chip capacity by ∼100 fold. (For comparison, current Pentium 4D Intel processors are built using a 0.065 μm process on a 1.62 cm² die.) At the system level, efficient inter-chip communication schemes (Boahen, 2000) may be used to build large-scale iono-neuronal network models on a multi-chip circuit board where >40 neuromorphic chips can be interconnected using state-of-the-art digital communication protocols (Merolla et al., 2007).

The computational speed of iono-neuromorphic circuits is governed by the integration rate of currents on circuit capacitors to mimic iono-neuronal dynamics. In keeping with convention, we designed the wide dynamic range circuits with time constants that operate on biological timescales (2–80 ms) by including capacitors that range from 1–30 pF, such that they can interact with biologic neurons in real time. Alternatively, by using smaller capacitors (on the order of fF), iono-neuromorphic circuits time constants can reach “accelerated time” of up to 10⁶× biological time (Mahowald and Douglas, 1991). Custom digital implementations of conductance-based models using field programmable gate array (FPGA) or digital signal processing (DSP) devices could in theory achieve similar speeds for specific small networks (Mak et al., 2006; Weinstein and Lee, 2006) but these digital devices are fundamentally limited due to their algorithmic computational approach, bounded computational resources, as well as relatively large physical size and power consumption compared to neuromorphic MOS circuits.

An important extension of the present wide dynamic range circuits is an iono-neuromorphic aVLSI implementation of passive and active dendritic compartments in order to investigate the complex spatiotemporal dendritic dynamics that shape intra-neuronal signaling. These iono-neuromorphic circuits may be fabricated alongside other silicon devices, such as micro-electromechanical multielectrode recording arrays or other iono-electronic systems to fashion a monolithic neuron-computer interface (Zeck and Fromherz, 2001) for real-time closed-loop neuroprosthetic applications.

METHODS

Circuit design and layout

Circuits were simulated with T-spice simulation engine (Tanner Research), running direct (level 49) model simulations using parameters downloaded from a public foundry (MOSIS). Corner simulations were run to assess worst-case performance. The circuits were laid out using L-Edit (Tanner Research) in a double poly, double metal process and were fabricated by MOSIS. All circuits employed large transistors to minimize mismatch errors and second-order effects. Transistors used for current mirrors were laid out in cross-connected pattern to further improve matching. To allow testing of individual circuit nodes, the overall circuit layouts were not optimized for area consumption in this prototyping run. Circuit area values are given in λ units, which is equal to $\frac{1}{2}$ minimum transistor lengths for a given process. An AMPA or GABA_A channel circuit with two LDFs and WR-TCA is 300λ×250λ; an NMDA circuit with one LDF (and a large capacitor), one WR-DP, and two WR-TCA, and the calcium dynamics circuit of Fig. 3C is 1540λ×380λ; an integrate-and-fire soma circuit is 280λ×245λ; a follower-integrator V_MEM circuit [Fig 2A] is 175λ×90λ; and current mirrors are 65λ×65λ. Once circuit operation is verified, optimal layout techniques can be used to reduce circuit sizes by a factor of 2–4. Microchips were fabricated by MOSIS in the AMI 1.5 μm process, where λ=0.8 μm. The overall chip area is 4.6 mm×4.7 mm with 116 analog I∕O pins.

Calibration

For V_DD=5 V, the circuits’ electronic voltages were offset and scaled according to V_Electronic=3 V+10 V_Biological. Thus the biological V_MEM signal (which can go from −100 to50 mV) was mapped to a nominal electronic operating range of 2 V to 3.5 V (with biological 0 mV=3 V electronic). The 10× biological-to-electronic voltage scaling with a 1.5 V (instead of 0.15 V) electronic operating range was made possible by our wide dynamic range neuromorphic circuit design. To allow for aVLSI implementation, the above linear calibration was universally applied across all on-chip iono-neuromorphic circuits.

An integrate-and-fire circuit (Van Schaik, 2001) was used to generate an action potential with an amplitude of approximately 1.1–1.2 V (electronic scale) and a half width of 1.5 ms. For simplicity, the action potential signal was mapped to the iono-neuromorphic electronic range by capacitively coupling the integrate-and-fire circuit’s output node to the ionic circuits’ V_MEM node. Such capacitive coupling may be obviated if the integrate-and-fire circuit is configured to conform with the scaling of other iono-neuromorphic circuits.

Iono-neuromorphic simulation studies

Neuronal and ionic networks were simulated by connecting circuit outputs modeling ionic signals and V_MEM nodes to each other using an external programmable chip containing a matrix of low-leak, low noise switches on a custom-designed testing board (layout: PCAD, Altrium Inc.; fabrication: Advanced Circuits). The board was carefully designed to minimize crosstalk and noise. The switch-matrix connectivity is controlled by a customized LABVIEW program (National Instruments); reprogramming neuronal model architecture was achieved by changing parameters on the LABVIEW program. Voltage parameters of building-block circuits modeling channel dynamics, reversal potentials, and ionic concentrations were tuned using low-current potentiometers.

Chaos detection

To detect chaos in experimentally recorded analog data, we employed a noise-resistant, chaos-specific numerical titration technique previously described (Poon and Barahona, 2001). Briefly, ISI series is fit with a family of linear and nonlinear Volterra–Wiener autoregressive models (Barahona and Poon, 1996). The technique identifies nonlinear determinism if nonlinear models predict the data better than linear models, as measured by a cost function C(r)=−ln ε(r)+r∕N, where r is the number of polynomial terms, ε(r) is the residual error, and N is the number of data points. To quantify the chaos, we titrated the data with additive white noise of increasing standard deviation (σ) until its nonlinearity goes undetected (within a prescribed level of statistical confidence, here p<0.01) at a limiting value of σ=noise limit (NL). In this scheme, NL>0 provides a sufficient proof of chaos, and the value of NL gives an estimate of its relative intensity (Poon and Barahona, 2001).

SUPPORTING INFORMATION

Transistor Analogs Supplementary Material.doc