Abstract
I attempt to reconcile apparently conflicting factors and mechanisms that have been proposed to determine the rate constant for two-state folding of small proteins, on the basis of general features of the structures of transition states. Φ-Value analysis implies a transition state for folding that resembles an expanded and distorted native structure, which is built around an extended nucleus. The nucleus is composed predominantly of elements of partly or well-formed native secondary structure that are stabilized by local and long-range tertiary interactions. These long-range interactions give rise to connecting loops, frequently containing the native loops that are poorly structured. I derive an equation that relates differences in the contact order of a protein to changes in the length of linking loops, which, in turn, is directly related to the unfavorable free energy of the loops in the transition state. Kinetic data on loop extension mutants of CI2 and α-spectrin SH3 domain fit the equation qualitatively. The rate of folding depends primarily on the interactions that directly stabilize the nucleus, especially those in native-like secondary structure and those resulting from the entropy loss from the connecting loops, which vary with contact order. This partitioning of energy accounts for the success of some algorithms that predict folding rates, because they use these principles either explicitly or implicitly. The extended nucleus model thus unifies the observations of rate depending on both stability and topology.
Keywords: nucleation-condensation, diffusion-collision, SH3, CI2, loops
To understand pathways of protein folding, experimentalists and theoreticians have, over the past decade, focused their efforts on analyzing small proteins. Many of these fold very rapidly with simple two-state kinetics. The structures of the rate-determining transition states have been analyzed in increasing numbers at atomic resolution by protein engineering and Φ-values and by various types of computer simulation. A recent development has been to correlate rate constants of folding (k) of the two-state proteins with their topology by using the gross parameter of the contact order (CO) defined by:
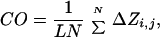 |
1 |
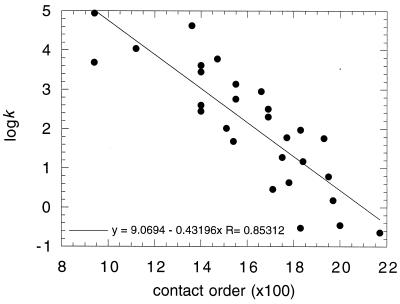
where N is the total number of contacts in the protein, ΔZi.j is the number of residues separating contacts i and j, and L is the number of residues in the protein. In a protein with low contact order, residues interact, on average, with others that are close in sequence. A high contact order implies that there is a large number of long-range interactions (1). That is, residues interact frequently with partners that are far apart in sequence. There is a statistically significant correlation between lnk and CO, whereby the rate constant of folding decreases with increasing contact order (Fig. 1). This correlation points to topology being an important factor in the rate of folding. The questions are why and what does it tell us?
Figure 1.
Plot of logk vs. 100 × CO for two-state folding proteins listed in Table 18.1 of ref. 3 and unpublished data from this laboratory.
The structure of the rate-determining transition state in protein folding can be derived by Φ-value analysis (2, 3). This procedure uses protein engineering to make suitable mutants of the protein, and changes in the free energy of activation (ΔΔG‡) and equilibrium (ΔΔG) on mutation are measured. Φ is defined by ΔΔG‡/ΔΔG. A value of Φ for folding of 0 means that the interaction measured is as poorly formed in the transition state as it is in the denatured state. A value of one means that it is as well formed in the transition state as in the native structure. Exactly the same approach had been used previously (4, 5) to understand changes in enzyme-substrate reactions during binding and catalysis, and the analogous equation was used to define the equivalent of Φ (5).
Very recently, Φ-value analysis has been applied to three proteins to support the contact order theory and the role of topology (6–8). But, in apparent contradiction, it has been found that three members of a family of the same topology fold with rate constants that correlate with stability and not contact order (9). There is strong evidence that many proteins fold by a nucleation mechanism, whereas arguments have been made in favor of hierarchical (framework) mechanisms in which preformed elements of secondary structure associate (10, 11). I wish now to present arguments that there are no real conflicts among these proposals, and that each of these mechanisms is accommodated in existing schemes that invoke general features of transition states for folding determined by Φ-value analysis.
Nature of Transition State for Protein Folding.
Φ-Value analysis of CI2 (12, 13) shows that:
(i) The protein folds around an extended nucleus that is composed of a contiguous region of structure (for CI2, an α-helix) and long-range native interactions with groups distant in sequence.
(ii) The transition state for folding is a distorted form of the native structure, which appears to be more distorted and weakened the further away from the nucleus. There is a gradation of Φ-values, the ones in the nucleus tending to be 0.5–0.7 and the more distal ones, from 0.1 to 0.3.
(iii) It was reasoned that the mechanism did not involve the association of preformed elements of secondary structure, but that the secondary and tertiary interactions are formed in parallel because the Φ-values in the nucleus were significantly less than 1. A mechanism was proposed, nucleation-condensation (or nucleation-collapse), that involves the simultaneous collapse or condensation of the tertiary structure around the extended nucleus as it is formed.
(iv) Mutations, especially in the folding nucleus, affect the folding rate, and there is a relation between folding rate and stability [a Brønsted plot (14)].
The rate-determining transition state in the multistep pathway for the folding of barnase is more polar (15). Many of the Φ-values are very close to 0 or 1, and so the rate-determining step is the docking of preformed structural domains. Mutations in the regions of barnase that are unstructured in the transition state have folding rates that are insensitive to mutation. The transition state structures of many small proteins may be classified into “CI2” (a gradation of Φ-values) or “barnase” (polarized, with a significant number of Φ-values close to 0 or 1) and are listed in ref. 3, Table 19.2. Nucleation-condensation appears to be a widespread mechanism. Indeed, lattice simulations independently showed that a specific nucleus is an optimal mechanism for folding model proteins (16).
Implications of a Native-Like Transition State.
The transition state resembles native-like structural elements with the connecting loops tending to be poorly structured (some structured loops are formed in the rate-determining transition state for barnase). A consequence of the extended nucleus is that the overall topology of the transition state must resemble that of the native structure. The correlation between folding rate constant, which depends on transition state structure, and contact order of the native state for a large number of proteins (Fig. 1) implies that the topology of the transition state resembles the topology of the native chain in general.
Relationship of Contact Order to Loop Length and Configurational Entropy.
It has been speculated that the dependence of rate constant on contact order may be a consequence of the relative importance of short-range and long-range interactions, or it might somehow relate to the length of the connecting loops in proteins (17). To resolve this, I derive a simple equation relating contact order and loop length for a specific case and then apply this to kinetic data. The analysis is done for just that specific case, but it illustrates the general principles.
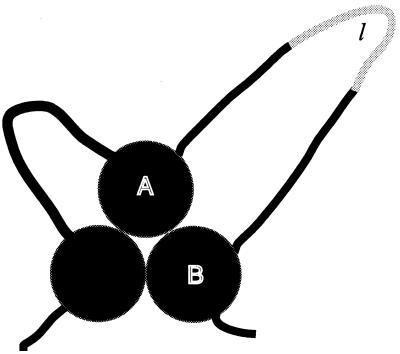
Suppose two segments of a protein, A and B, are connected by a loop of length nl, and that there are NA/B interactions across the A/B interface. Suppose we insert l residues in the loop that makes no interaction with other residues (Fig. 2). The total number of interactions in the protein does not change, but the value of Z for the interaction across the A/B interfaces increases by l ⋅ NA/B, because each of the NA/B interactions is displaced by l residues in sequence. Thus:
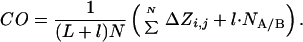 |
2 |
Thus, contact order increases with increasing loop size.
Figure 2.
Cartoon of the extended (specific) nucleus mechanism of the nucleation-condensation mechanism. This is for the extreme case of the connecting loops being unstructured. The filled circles represent native-like elements of secondary structure that interact mainly by native tertiary interactions. The shaded part of the loop illustrates an insertion of length l.
The loss of configurational entropy of closing an unstructured loop of nl + l residues relative to one of nl residues is calculated from standard polymer theory to be:
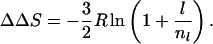 |
3 |
Eqs. 2 and 3 show that changes in contact order and configurational entropy are directly related. The relationship becomes simpler when l ≪ nl. Then
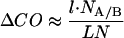 |
4 |
and
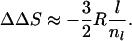 |
5 |
To a first approximation:
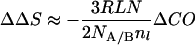 |
6 |
or
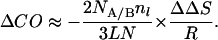 |
7 |
There are several assumptions in Eq. 3 that cause considerable uncertainty in the exact relationship between ΔΔS and CO. As discussed (18), the exact value of nl is not known, and interactions within the loop and with neighboring residues will alter its energy. Further, the numerical term 3/2 may be an underestimate, and values up to 2.4 may be appropriate, depending on the nature of the side chains. Conversely, if the loop is partly structured in the transition state, then 3/2 will be an overestimate.
Effect of Unstructured Closed Loop on Folding Kinetics.
A simple way of analyzing reaction kinetics is the application of transition state theory or analogous theories that assume that a transition state or activated complex is in (virtual) rapid equilibrium with the ground state. The rate constant is then given by an equation that is the product of the virtual equilibrium constant and the frequency (ν) and transmission coefficient (κ) of passing over the energy barrier. Suppose that the transition state has a free energy that is higher than the ground state by ΔΔG‡, then the rate constant is given by:
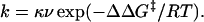 |
8 |
Energies that affect the equilibrium are directly manifested in the activation energy, ΔΔG‡. The product κν cancels out when comparing rates of reaction under identical conditions, as in Φ-value analysis. We can calculate the effect of loop entropy on rate by assuming that folding follows Eq. 8. Suppose that the loop of nl residues is unstructured in the transition state but is closed at either end by tertiary interactions made as two elements of structure associate in the transition state. Increasing the loop by l residues increases the loss of configurational entropy by ΔΔS according to Eq. 3. The increase in free energy of activation because of loop size is given by TΔΔS, and the change in lnk by −ΔΔS/R. Thus, according to Eq. 6,
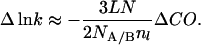 |
9 |
This equation predicts an approximately linear relationship between changes in k and changes in contact order resulting from changes in loop size. The equation is derived for a specific case for changes within a single protein, but it does illustrate some general points. Importantly, the slope is a function of the number of interactions between the elements connected by the loop and the nature and degree of structure formation within the loop in the transition state, which will alter the factor of 3/2. The slope is thus unlikely to be a constant.
Diffusion Control of Protein Folding?
The effects of inserting residues into loops of CI2 and the α-spectrin SH3 domain have been systematically analyzed and have provided an excellent system for benchmarking the above equations (18, 19). Before applying Eq. 9 to the data, the question has to be addressed of whether the folding reaction is diffusion controlled. The usual meaning of “diffusion control” in chemical kinetics is that a reaction is limited by the rate of diffusion together of molecules. The characteristics of such a diffusion-controlled reaction are that it has a low activation energy, the rate decreases with increasing viscosity (k α 1/η), and the reaction rate is not affected by the activation energy of the chemical steps. It was proposed from the effects of viscogenic agents that the folding of CspB is diffusion controlled, that is, compaction of the polypeptide chain is rate determining because the rate constant for folding is inversely proportional to viscosity (20). Plaxco and Baker showed that folding of the 62-residue IgG binding domain of protein L is not diffusion controlled (21), as did Bhattacharya and Sosnick the α-helical GCN4-p2′ (22). The kinetics was analyzed by Kramers' theory (23), a more fundamental version of Eq. 8 that does not invoke a fixed value of ν. Kramers' theory invokes an inverse dependence of κν on viscosity under “high-viscosity” conditions because of frictional effects on passage over the transition state barrier. At “high viscosity,” the system moves many times back and forth over the top of the barrier in a diffusion-like way before it can escape to give products, and the rate constant becomes inversely proportional to viscosity. Under these conditions, the rate constant varies with both viscosity and the change in chemical activation energy. Plaxco and Baker (21) pointed out that the interpretation of the observed inverse dependence of folding rate on viscosity is ambiguous and is consistent both with diffusion-limited chain collapse and frictional effects on the transition state, because both predict that rates vary as 1/η. But numerical simulation demonstrated that the effects of viscosity were at the transition state and not at the early diffusive steps (21). The assertions of Baker and Plaxco are directly supported from observations on CI2 that the folding of wild-type and loop insertion mutants of CI2 is on a much longer time scale (>10 ms) than chain compaction events, which are on a time scale of 100 μs or less (24). Indeed, one mutant of CI2 (RF48) folds some 40 times faster than wild type, with a half life of 0.3 ms, showing directly that diffusional events per se are not rate limiting for wild type. Similarly, some mutants of the SH3 domain fold faster than wild type (120 s−1 vs. 3 s−1; Luis Serrano, personal communication) so that its folding is not diffusion limited. Further, a compact transition state is not consistent with an early transition state that is expected from collapse being rate determining (21, 24).
Experimental Tests of the Contact Order Relationships.
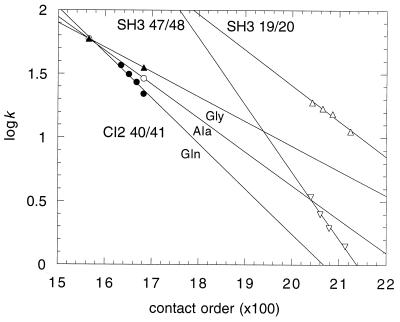
Plotted in Fig. 3 are the logarithms (log10) of the rate constants vs. 100 × CO for mutants of CI2 containing 7, 9, 11, and 13 residues that are mainly Gln, and 13 residues that are predominantly Ala or Gly inserted between residues 40 and 41 of its loop. The slopes are −0.36, −0.26, and −0.19, respectively, compared with a value of −0.12 calculated from Eq. 9 (converted to log10), assuming a value of nl of 15, which is the length of the loop in the native protein. Also plotted are data for 2, 4, 6, 10 residues inserted between residues 19 and 20 or 47 and 48 of α-spectrin SH3. The slopes are −0.28 and −0.53, respectively, compared with values of −0.07 and −0.47 calculated from Eq. 8 and the native loop lengths. These values span that of −0.43 found for the proteins plotted in Fig. 1. Given the uncertainties in the theory behind Eq. 3 and the assumptions about the nature of the loops in the transition state, the agreement is probably as good as can be expected. Nevertheless, the observations that logarithms of folding rate constants are linear with contact order for these specific systems, and that the slopes are of the right order of magnitude and vary qualitatively as predicted, are consistent with and lend strong support for the importance of contact order in protein folding.
Figure 3.
Plots of logk vs. 100 × CO for loop insertion mutants of CI2 and the α-spectrin SH3 domain.
How Precise Is the Dependence of lnk on Contact Order?
The rate constant for folding depends on all the energy differences between the transition and ground states. The energies first analyzed are those caused by direct interactions of residues, especially those in the folding nucleus. These can dominate the rate equation. For example, the rate constants for the folding of CI2 span three orders of magnitude: wild type folds at 25°C at 56 s−1, the double mutant AG16/IA57 in the folding nucleus at 2.4 s−1, and RF48 at 2300 s−1. Consequently, the contact order equation cannot by itself accurately predict rate constants. But the correlation between logk and contact order is truly remarkable and points to general principles about the nature of folding that must be included in simulations. Further, the correlation also implies that the free energy of forming the nucleus in the transition state has the component from direct interaction constant within a few kcal/mol so that the entropy terms from contact order appear above the “noise” level from differences in specific interactions.
Pathway to the Extended Nucleus: Nucleation-Condensation vs. Diffusion-Collision.
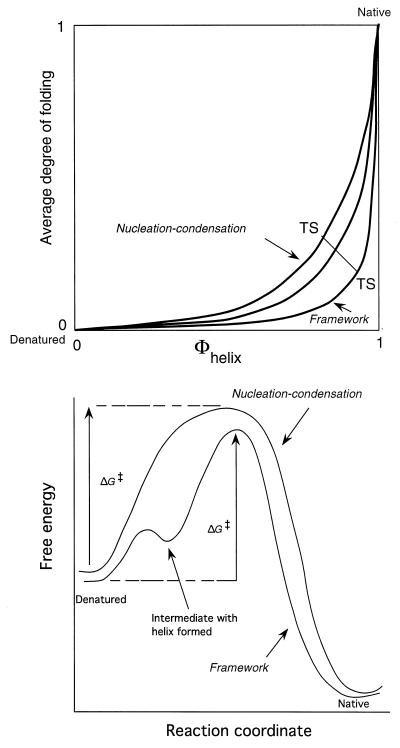
The increasing accumulation of Φ-value data and the correlation of the contact order plot with native state topology are strong evidence for the mechanism involving an extended nucleus in the transition state being quite general. There is persuasive evidence both for the nucleation-condensation mechanism for CI2 and allied proteins with simultaneous formation of secondary and tertiary interactions and some evidence for a diffusion-collision model for the folding of the small α-helical fragment of λ repressor by preformed elements of secondary structure associating (25, 26). The strict diffusion-collision model predicts that local interactions everywhere in helices and strands define the folding rate. Nucleation-condensation predicts that some native tertiary interactions are crucial as well as the native interactions' secondary structure in the nucleus. In practice, the transition states for both processes involve extended structures with a mixture of tertiary and secondary interactions, the secondary structural elements in the diffusion-collision mechanism forming the tertiary interactions as the secondary structures coalesce. Nucleation-condensation and diffusion-collision mechanisms are basically extremes of the same process, with the elements of secondary structure being inherently more stable and better formed in the diffusion model than in nucleation-condensation (27) (Fig. 4).
Figure 4.
(Lower) Simplified energy diagrams for true two-state folding via nucleation-condensation and apparent two-state kinetics for a framework mechanism that involves the formation of, say, an α-helix, at a higher energy than the denatured state. If both mechanisms involve an extended network of long-range native-like tertiary interactions around the helix, then the free energy of activation, ΔG‡, responds to changes in structure in a similar manner for both mechanisms, because ΔG‡ depends just on the difference in energy between similar transition states and the denatured state. (Upper) Two-dimensional representation of the merging of the nucleation-condensation and framework mechanisms. In the framework mechanism, the Φ-values for the formation of the helix are close to 1, because it is relatively stable and can form to an appreciable extent in the absence of tertiary interactions. As the helix becomes less stable, it requires more tertiary interactions to become stable in the transition state, and so the formation of helix is coupled with that of tertiary structure. The Φ-values for formation of the helix can then be appreciably less than 1.
The transition states for the stepwise and nucleation mechanisms are thus qualitatively similar, which leads to a dilemma in interpreting kinetic data and simple models of folding. According to the transition state equation (Eq. 8), the rate folding constant depends on just the energy difference between the transition state and the ground state, provided any preequilibria are rapid (Fig. 3). Thus, kinetic data relating changes in structure and kinetics respond in a qualitatively similar manner to changes in structure. But they can be distinguished between by quantitative data: the diffusion-collision mechanism is predicted to have Φ-values of 1 for the relevant secondary structure, which is found for a model system (28), whereas nucleation-condensation has mainly fractional values that can tend to 1.0 for especially stable elements.
Baldwin and Rose (10, 11) have argued that all proteins fold in a hierarchical model, with the successive docking of elements of native structure. But the predictive success of their hierarchical model does not have implications for the kinetic mechanism, because any mechanism that invokes rapid preequilibria and an extended nucleus containing native-like secondary structure will fit the observed kinetics.
Simulations of Folding.
The mechanistic features of an extended folding nucleus that is stabilized directly by native-like secondary-structure interactions and destabilized by loop entropy are explicitly or implicitly included in the simple algorithms for folding of Muñoz and Eaton (29) and Baker and coworkers (6). Muñoz and Eaton successfully calculated the folding rate constants of 22 proteins using an elementary statistical mechanical model and the known distribution of interactions in their three-dimensional structures. They assumed residues come into contact only after all of the intervening chain is in the native conformation, and that native structure grows from localized regions that then fuse to form the complete native molecule. The relative success of their calculations suggested that folding rate constants are largely determined by the distribution and strength of contacts in the native structure, that is, topology is important. The Baker model invokes similar features and is successful in predicting structures as well as rates (6, 30). Very recently, Debe and Goddard (31) have calculated accurately the rates of folding of 21 of the two-state folding proteins, on the basis of the nucleation-condensation mechanism. The extended nucleus mechanism of the nucleation-condensation mechanism is clearly a very robust basis for calculating folding rate constants.
Although there is no single mechanism for protein folding, the extended transition state provides a unifying feature in the two-state folding of small domains. An extended nucleus is necessary for the folding of these domains, because a large number of interactions have to be made for an energetically downhill passage after the transition state.
Acknowledgments
I thank David Baker, Hans Frauenfelder, Kevin Plaxco, Luis Serrano, and Eugene Shakhnovich for helpful discussion, Kevin Plaxco for the computer program for calculating contact orders, and Eugene Shakhnovich for the suggestion of Fig. 2.
References
- 1.Plaxco K W, Simons K T, Baker D. J Mol Biol. 1998;277:985–994. doi: 10.1006/jmbi.1998.1645. [DOI] [PubMed] [Google Scholar]
- 2.Matouschek A, Kellis J T, Jr, Serrano L, Fersht A R. Nature (London) 1989;340:122–126. doi: 10.1038/340122a0. [DOI] [PubMed] [Google Scholar]
- 3.Fersht A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. New York: Freeman; 1999. [Google Scholar]
- 4.Fersht A R, Leatherbarrow R J, Wells T N C. Nature (London) 1986;322:284–286. [Google Scholar]
- 5.Fersht A R, Leatherbarrow R, Wells T N C. Biochemistry. 1987;26:6030–6038. doi: 10.1021/bi00393a013. [DOI] [PubMed] [Google Scholar]
- 6.Riddle D S, Grantcharova V P, Santiago J V, Alm E, Ruczinski I, Baker D. Nat Struct Biol. 1999;6:1016–1024. doi: 10.1038/14901. [DOI] [PubMed] [Google Scholar]
- 7.Martinez J C, Serrano L. Nat Struct Biol. 1999;6:1010–1016. doi: 10.1038/14896. [DOI] [PubMed] [Google Scholar]
- 8.Chiti F, Taddei N, White P M, Bucciantini M, Magherini F, Stefani M, Dobson C M. Nat Struct Biol. 1999;6:1005–1009. doi: 10.1038/14890. [DOI] [PubMed] [Google Scholar]
- 9.Clarke J, Cota E, Fowler S B, Hamill S J. Structure (London) 1999;7:1145–1153. doi: 10.1016/s0969-2126(99)80181-6. [DOI] [PubMed] [Google Scholar]
- 10.Baldwin R L, Rose G D. Trends Biochem Sci. 1999;24:26–33. doi: 10.1016/s0968-0004(98)01346-2. [DOI] [PubMed] [Google Scholar]
- 11.Baldwin R L, Rose G D. Trends Biochem Sci. 1999;24:77–83. doi: 10.1016/s0968-0004(98)01345-0. [DOI] [PubMed] [Google Scholar]
- 12.Otzen D E, Itzhaki L S, elMasry N F, Jackson S E, Fersht A R. Proc Natl Acad Sci USA. 1994;91:10422–10425. doi: 10.1073/pnas.91.22.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Itzhaki L S, Otzen D E, Fersht A R. J Mol Biol. 1995;254:260–288. doi: 10.1006/jmbi.1995.0616. [DOI] [PubMed] [Google Scholar]
- 14.Fersht A R, Itzhaki L S, elMasry N F, Matthews J M, Otzen D E. Proc Natl Acad Sci USA. 1994;91:10426–10429. doi: 10.1073/pnas.91.22.10426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fersht A R. FEBS Lett. 1993;325:5–16. doi: 10.1016/0014-5793(93)81405-o. [DOI] [PubMed] [Google Scholar]
- 16.Abkevich V I, Gutin A M, Shakhnovich E I. Biochemistry. 1994;33:10026–10036. doi: 10.1021/bi00199a029. [DOI] [PubMed] [Google Scholar]
- 17.Goldenberg D P. Nat Struct Biol. 1999;6:987–990. doi: 10.1038/14866. [DOI] [PubMed] [Google Scholar]
- 18.Ladurner A G, Fersht A R. J Mol Biol. 1997;273:330–337. doi: 10.1006/jmbi.1997.1304. [DOI] [PubMed] [Google Scholar]
- 19.Viguera A R, Serrano L. Nat Struct Biol. 1997;4:939–946. doi: 10.1038/nsb1197-939. [DOI] [PubMed] [Google Scholar]
- 20.Jacob M, Schindler T, Balbach J, Schmid F X. Proc Natl Acad Sci USA. 1997;94:5622–5627. doi: 10.1073/pnas.94.11.5622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plaxco K W, Baker D. Proc Natl Acad Sci USA. 1998;95:13591–13596. doi: 10.1073/pnas.95.23.13591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bhattacharyya R P, Sosnick T R. Biochemistry. 1999;38:2601–2609. doi: 10.1021/bi982209j. [DOI] [PubMed] [Google Scholar]
- 23.Kramers H A. Physica. 1940;7:284–304. [Google Scholar]
- 24.Ladurner A G, Fersht A R. Nat Struct Biol. 1999;6:28–31. doi: 10.1038/4899. [DOI] [PubMed] [Google Scholar]
- 25.Burton R E, Huang G S, Daugherty M A, Fullbright P W, Oas T G. J Mol Biol. 1996;263:311–322. doi: 10.1006/jmbi.1996.0577. [DOI] [PubMed] [Google Scholar]
- 26.Burton R E, Huang G S, Daugherty M A, Calderone T L, Oas T G. Nat Struct Biol. 1997;4:305–310. doi: 10.1038/nsb0497-305. [DOI] [PubMed] [Google Scholar]
- 27.Fersht A R. Curr Opin Struct Biol. 1997;7:3–9. doi: 10.1016/s0959-440x(97)80002-4. [DOI] [PubMed] [Google Scholar]
- 28.Kippen A D, Fersht A R. Biochemistry. 1995;34:1464–1468. doi: 10.1021/bi00004a042. [DOI] [PubMed] [Google Scholar]
- 29.Munoz V, Eaton W A. Proc Natl Acad Sci USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Simons K T, Bonneau R, Ruczinski I, Baker D. Proteins Struct. Funct. Genet. 1999. Suppl. 3, 171–176. [DOI] [PubMed] [Google Scholar]
- 31.Debe D A, Goddard W A. J Mol Biol. 1999;294:619–625. doi: 10.1006/jmbi.1999.3278. [DOI] [PubMed] [Google Scholar]