Abstract
MR diffusion tensor imaging (DTI) can measure and visualize organization of white matter fibre tracts in vivo. DTI is a relatively new imaging technique, and new tools developed for quantifying fibre tracts require evaluation. The purpose of this study was to compare the reliability of a novel clustering approach with a multiple region of interest (MROI) approach in both healthy and disease (schizophrenia) populations. DTI images were acquired in 20 participants (n=10 patients with schizophrenia: 56 ± 15 years; n=10 controls: 51 ± 20 years) (1.5 Tesla GE system) with diffusion gradients applied in 23 non-collinear directions, repeated three times. Whole brain seeding and creation of fibre tracts were then performed. Interrater reliability of the clustering approach, and the MROI approach, were each evaluated and the methods compared. There was high spatial (voxel-based) agreement within and between the clustering and MROI methods. Fractional anisotropy, trace, and radial and axial diffusivity values showed high intraclass correlation (p<0.001 for all tracts) for each approach. Differences in scalar indices of diffusion between the clustering and MROI approach were minimal. The excellent interrater reliability of the clustering method and high agreement with the MROI method, quantitatively and spatially, indicates that the clustering method can be used with confidence. The clustering method avoids biases of ROI drawing and placement, and, not limited by a priori predictions, may be a more robust and efficient way to identify and measure white matter tracts of interest.
Keywords: diffusion tensor imaging, tractography, streamline, clustering, region of interest, schizophrenia
Introduction
Magnetic resonance diffusion tensor imaging (DTI) is the most powerful and currently the only way to measure and to visualize the organization of white matter fibre tracts in vivo (Alexander and Lobaugh 2007). Diffusion tensor tractography takes advantage of underlying large scale features of the diffusion data to estimate the direction of white matter fibre tracts in the brain (Basser et al. 2000). In addition, tractography permits the calculation of quantitative measures of the tensor along white matter fibre tracts. For DTI, particularly tractography, new tools and applications are being developed that require evaluation. Our group has published an innovative method (O'Donnell et al. 2006; O'Donnell and Westin 2007) that automatically clusters white matter tracts together based on tract shape and similarity. This method thus offers an alternative to the multiple region of interest method (MROI) that is commonly used in streamline tractography (Wakana et al. 2007).
Most common methods for isolating fibre bundles based on streamline tractography require the manual placement of multiple regions of interest. These MROI methods include: 1) an approach that starts from seed points within a predefined region of interest, and then calculates and preserves only traces that touch other predefined ROIs (Mori and van Zijl 2002) or 2) an alternative approach that creates seed points throughout the entire brain (whole brain tractography). Only tracts that pass through the ROIs are then included (Wakana et al. 2007). Our recently published method eliminates the need to manually place ROIs to identify fibre bundles. Importantly, this method is able to differentiate fibre bundles which would be difficult to define and separate using MROI approaches. This clustering approach is fully automatic, unguided, and takes advantage of the similarity of fibre paths. Collections of fibre trajectories are also analyzed in 3D and separated into bundles or clusters that contain paths with similar shape and spatial position. Fibre paths are thus grouped on the basis of shape and location using spectral clustering (O'Donnell et al. 2006). We have also recently created a high dimensional white matter atlas using automatic tractography segmentation whereby whole brain tractography was performed (O'Donnell and Westin 2007). In that study, the entire brain was seeded and a collection of several hundred clusters were produced that represent white matter fibre tracts of the brain (O'Donnell and Westin 2007).
Our clustering method is an efficient and high throughput approach that produces a whole brain model of white matter tracts. White matter tracts of interest can then be visualized in their correct anatomic location and selected to evaluate tract-specific diffusion parameters. For this study, diffusion parameters included fractional anisotropy (FA), related to fibre density and/or myelination and reflecting the degree to which diffusion is directionally dependent, and trace (diffusion magnitude). Axial (DL) and radial diffusivity (DR) were also included, as they may be specific to myelination (Song et al. 2005) and axonal degeneration (Song et al. 2002), respectively, and therefore may provide useful information in neuropsychiatric disorders.
Fibre tracking algorithms may behave differently in disease populations (Ciccarelli et al. 2008). Therefore, we believe that it is important to perform methodological studies in both healthy and disease populations. The importance of successful segmentation of corresponding white matter tracts across subjects and across hemispheres is that neuroscientific hypotheses can be tested regarding group differences and questions of symmetry (O'Donnell and Westin 2007). Since our group is particularly interested in the study of schizophrenia, where white matter changes using DTI have been shown (Kubicki et al. 2007), we examined our clustering method both in healthy controls and in individuals with schizophrenia. Evaluation of this method in both a healthy and schizophrenia population, if successful, will allow for greater confidence in future studies in both populations.
The present study seeks to establish: 1) that the clustering method is reliable, and 2) comparable to the MROI approach both spatially (voxel overlap), and quantitatively, using four scalar indices of the diffusion tensor (fractional anisotropy, FA; trace, axial diffusivity, DL; radial diffusivity, DR).
Methods
Image Acquisition
DTI images were acquired using an eight-channel head coil on a 1.5 Tesla GE Echospeed system (General Electric Medical Systems, Milwaukee, WI), which permits maximum gradient amplitudes of 40 mT/m. A single shot spin echo planar sequence was used with diffusion gradients applied in 23 non-collinear directions and b=1000 s/mm2. Two b=0 images were obtained. Fifty seven to sixty two slices were acquired for whole brain coverage oblique to the axial plane. Slice thickness was 2.6 mm, and voxels were isotropic. The field of view was 330 mm and the size of the acquisition matrix was 128 x 128 mm, with echo time (TE) = 85.5 ms, and repetition time (TR) = 15,000 ms. To improve the signal to noise ratio, the entire sequence was repeated three times. Inversion recovery prepped spoiled gradient recall and fast spin echo T2 weighted images were also acquired in the event of need for registration and to ensure anatomical accuracy.
Study Participants
Participants were recruited at the Centre for Addiction and Mental Health. All participants had DSM-IV Structured Clinical Interview for Diagnosis performed (First M 1995; First MB 1995), and were interviewed by a psychiatrist to ensure diagnostic accuracy. Any subject with a recent history of substance abuse or dependence was excluded, as were those subjects with previous head trauma with loss of consciousness, or neurological disorders. All subjects were between the ages of 25 and 80, with verbal IQ greater than 71. Study participants included (n=10) patients with schizophrenia: 56 ± 20 years, 6M, 4F; and (n=10) healthy controls: 51 ± 15 years, 6M, 4F; all right handed, as assessed by the Edinburgh handedness inventory (Oldfield 1971). All subjects provided informed, written consent, and the study was approved by the Centre for Addiction and Mental Health Ethics Review Board.
Image Analysis and Tractography
DTI data were transferred to a workstation and reconstructed. A diffusion-weighted image was created for each of the three repetitions. The three DTI repetitions were co-registered to the first b=0 image in the first repetition using FSL (v. 4.0) www.fmrib.ox.ac.uk to produce a new averaged image, with gradients re-oriented. Registration corrects eddy current distortions and subject motion, important artifacts that can affect the data, and averaging improves the signal to noise ratio. A brain ‘mask’ was then generated. Points were seeded throughout each voxel of the brain.
Whole-brain tractography was performed with a deterministic (streamline) approach (Runge-Kutta order two tractography with a fixed step size of 0.5 mm). The three threshold parameters for tractography were: Tseed, Tstop, and Tlength. Tseed and Tstop are anisotropy thresholds based on the linear anisotropy measure CL (Westin et al. 2002), where CL = (λ1 -λ2)/ λ1 and, λ1 and λ2 are the two largest eigenvalues of the diffusion tensor sorted in descending order. The goal of the anisotropy thresholds is to limit tractography to the white matter. Thresholds were based on the CL rather than on FA, because FA can be relatively high in regions of planar anisotropy which may indicate tract crossings or branching (Ennis and Kindlmann 2006). The Tlength threshold is used to eliminate very short fibres from being generated. The parameters chosen for this study were (in mm): Tseed = 0.3, Tstop =0.15, and Tlength = 20. Tractography and creation of white matter fibre tracts using both the clustering and multiple region of interest approach were performed using 3D Slicer (open source software www.slicer.org) and Matlab 7.0 (www.mathworks.com).
1. Clustering approach
As previously described (O'Donnell et al. 2006), pairwise fibre trajectory similarity was quantified by first computing a pairwise fibre distance. The mean closest point distance was employed, which is defined as the mean distance between pairs of closest points on two fibres. The directed distances between fibres ‘A’ and ‘B’ are converted to a symmetric pairwise fibre distance by taking the mean of the distance from A to B and from B to A. Each distance is then converted to an affinity measure suitable for spectral clustering via a Gaussian kernel (Wij) = e ^ (−d2ij/σ2), a method that is employed in the clustering literature (Shi and Malik 2000). The role of σ(σ=60 mm used in the present study) is to define the size scale of the problem by setting the distance over which fibres can be considered similar (O'Donnell and Westin 2007).
A spectral embedding of fibres is then created based on the eigenvectors of the fibre affinity matrix. In our clustering application, we used the top 15 eigenvectors of the fibre similarity matrix to calculate the most important shape similarity information for each fibre. The clustering algorithm used was k- way normalized cuts, as it produces clusters with high within-cluster similarity and low between-cluster similarity (Ng et al. 2002).
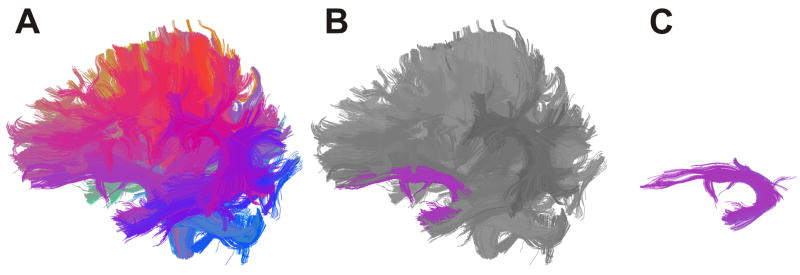
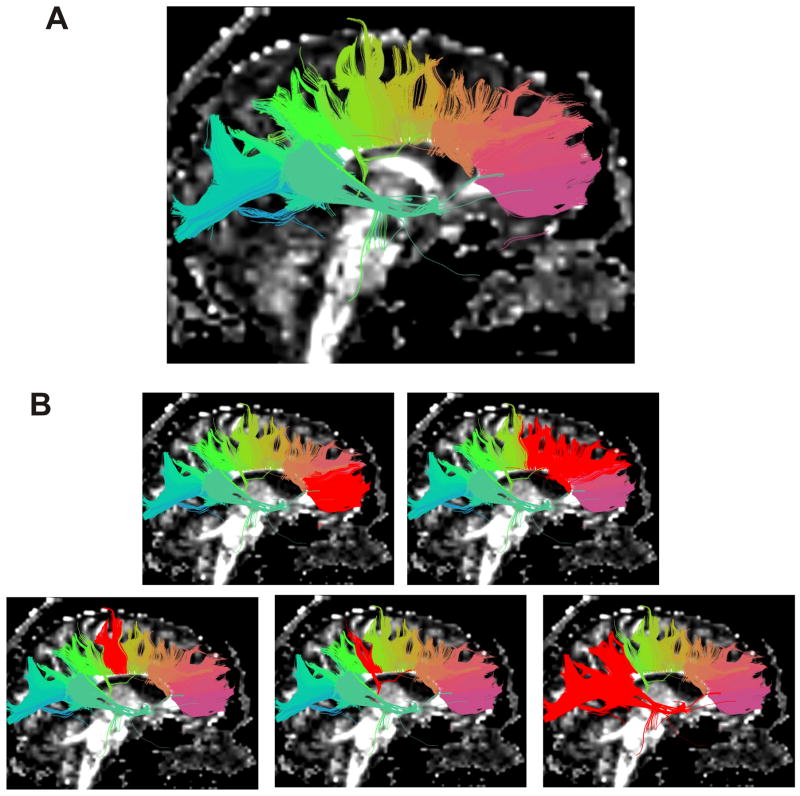
Once the whole brain cluster model is produced, the operator combines the clusters that correspond to a given fibre tract. Clusters of the same anatomical tract tend to have similar weights, thus facilitating selection (Figure 1). In this study, the left and right uncinate fasciculus, left and right inferior occipitofrontal fasciculus, left and right cingulum bundle left and right inferior longitudinal fasciculus, left and right arcuate fasciculus, left and right corticospinal tract, and genu of corpus callosum were selected. The remainder of the corpus callosum was segmented using the clustering method, and selection of neuroanatomical subdivisions were made according to a previously demonstrated DTI based topographical study of the corpus callosum (Hofer and Frahm, 2006). Specifically, following selection of the genu, premotor and supplementary motor projections (CC2), motor projections (CC3), sensory projections (CC4), and finally parietal, temporal, and occipital projections (CC5) were selected. Correct selection of tracts was verified by superimposing clusters on both the FA and T1 images (Mori et al. 2005). Two individuals, blind to participant information, performed the entire clustering procedure to generate two complete sets of cluster models for each dataset.
Figure 1.
(A,B,C). Whole brain clustering result and example of how white matter tract is selected (left uncinate fasciculus). Tracts are grouped into clusters according to similarity of shape and location and are colour coded accordingly. This facilitates neuroanatomical selection of tracts of interest.
2. Multiple Region of interest approach
Regions of interest were drawn on the baseline image of the DTI scans. All ROIs were placed bilaterally. For uncinate fasciculus, two ROIs were drawn on each side on the same coronal slice, one just anterior to the temporal stem, where the frontal cortex begins and one in the temporal pole. For inferior occipitofrontal fasciculus, the same ROI on the coronal slice anterior to the temporal stem for uncinate fasciculus was used, and one coronal ROI was drawn in temporal cortex, just anterior to the occipital cortex. For the cingulum bundle, three ROIs were drawn in the antero-posterior direction on consecutive coronal slices around the cingulum on each side, five slices posterior to where the genu joins at the midline, and three ROIs were drawn on consecutive coronal slices starting five slices anterior to where the splenium joined at the midline. For the inferior longitudinal fasciculus, two ROIs were drawn on coronal slices. The anterior ROI was drawn in temporal cortex on the slice where the corticospinal tract is seen to decussate. The posterior ROI was drawn in occipital cortex, below the inferior occipitofrontal fasciculus, one slice posterior to where the forceps major separates. For the arcuate fasciculus, three ROIs were drawn on consecutive axial slices. These ROIs were placed on the FA image. Since there is great interindividual variability in the anatomy of the AF (Catani and Mesulam 2008), it was necessary to visualize the tract cross sectionally for accurate ROI placement. The first ROI was drawn once the cingulum bundles were visible. Placement of the ROI was lateral to where the corticospinal tract was visible and was made around the visible part of the arcuate fasciculus. The second and third ROIs followed on successive descending axial slices where the arcuate fasciculus was visible. The first ROI includes the shorter fibres of the anterior indirect segment, the second ROI includes the long fibres, and the third ROI includes the shorter fibres of the posterior indirect segment (Catani and Mesulam 2008). For the corticospinal tract, three ROIs were drawn on axial slices. One ROI was drawn around the border of the midbrain. The other ROI was drawn just lateral to the corpus callosum, beside the motor projections of the corpus callosum. In order to ensure no crossing fibres from other tracts were obtained, an ROI was placed liberally in the contralateral hemisphere at the level of the anterior commissure. Any fibre penetrating this ROI was removed. For the genu of the corpus callosum, one ROI was drawn on the midsagittal slice on the corpus callosum. The remainder of the corpus callosum using an MROI approach was not segmented, since reliable segmentation is not easily achieved using this approach (Wakana et al. 2007), and identifying a specific protocol to reproducibly identify 2D slices for ROI drawing is challenging. Tracts generated from whole brain seeding had to pass through all ROIs that corresponded to those drawn for each fasciculus or bundle. Two individuals, blind to participant information, drew ROIs on the dataset to generate two complete sets of ROIs and white matter fibre tracts for each individual scanned.
Quantifying the tensor
Four tensor measures were obtained for each white matter fibre tract: FA and trace (Basser & Pierpaoli 1996), DL (λ1) (Song et al. 2005) and DR ([λ2+λ3]/2) (Song et al. 2002). These values were calculated for each of the thirteen tracts for each operator and fibre segmentation method (clustering, MROI). Matlab (v. 7.0) was used to make the calculations. Data presented represent the mean values along the selected tracts.
Statistical Analysis
Spatial agreement
Cohen’s kappa (k) was used to compare pixels covered by the selected white matter tracts generated by each operator for the two fibre segmentation methods (Landis and Koch 1977). This metric measures the proportion of voxels that are covered between two white matter tracts. A recent evaluation of the MROI method used this measure as their primary measure of reliability as described by Wakana et al. (Wakana et al. 2007). Pixels occupied by the tracts were assigned a value of 1 and non-occupied pixels a value of 0. Four pixel categories were created: 1) pixels that did not contain the tract in both trials (nn), 2) pixels that contained the tract in only one of the two trials (pn, np), and 3) pixels that contained the tracts in both trials (pp). For the calculation, only pixels with FA>0.2 were included. Expectation values (Enn, Enp, Epn, and Epp) for each class were then calculated as follows:
Where N = nn + np + pn + pp is the total number of pixels for that particular fibre.
Observed agreement = (nn + pp)/N × 100
Expected agreement = (Enn + Epp)/N × 100
k = (observed agreement – expected agreement) / (100 – expected agreement)
Higher values of k indicate stronger agreement between the two methods. The Landis and Koch (Landis and Koch 1977) criteria for interpretation of Cohen’s kappa (k) coefficient was employed, where k = 0.61–0.8 indicates ‘substantial’ agreement, and k = 0.81–1.0 ‘almost perfect’ agreement.
Inter-rater reliability (defined as comparison of identical methods between two operators) was first calculated within each fibre identification method for each of the thirteen tracts for each participant. Mean and standard deviation of inter-rater reliability values were then calculated. Inter-method reliability (defined as comparison between fibre identification methods by the same operator) was then calculated for each of the thirteen tracts for each participant, followed by mean and standard deviation calculations. Only inter-rater reliability was calculated for the subdivisions of the corpus callosum (except for the genu, where inter-rater and inter-method reliability were calculated)
Scalar indices of the tensor
Intraclass correlation coefficients were calculated for each of the scalar indices of diffusion (FA, trace, DL, DR) for each fibre identification method using SPSS vr 15. To compare the clustering and MROI methods, the percent difference of the clustering method from the MROI method was calculated for each tract for each study participant. Mean percent difference (of all study participants) for each tract was then calculated.
Results
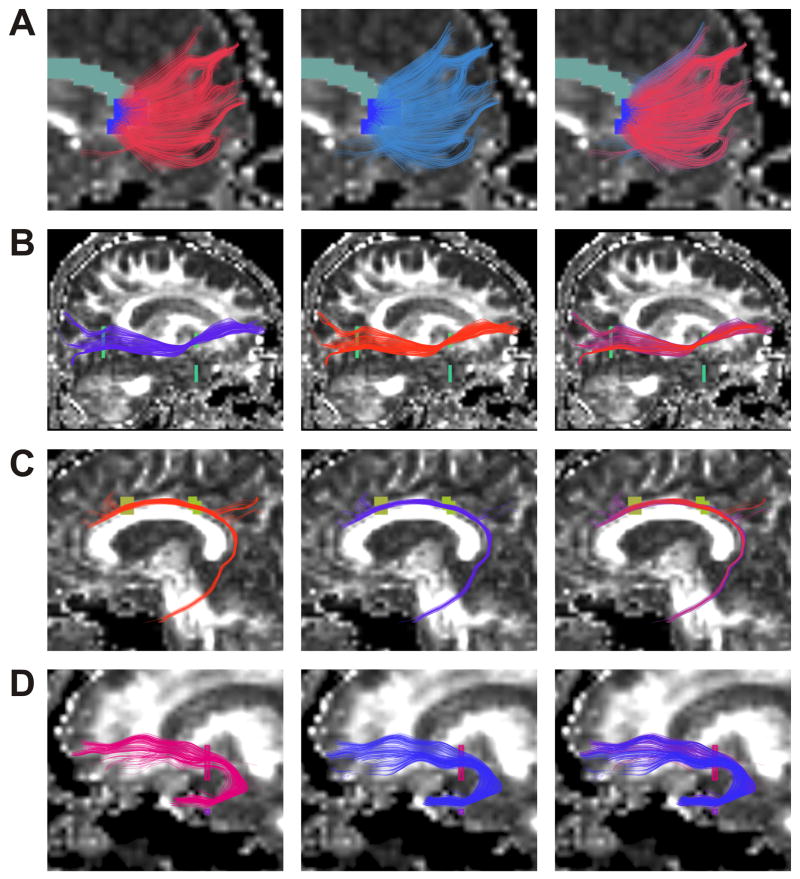
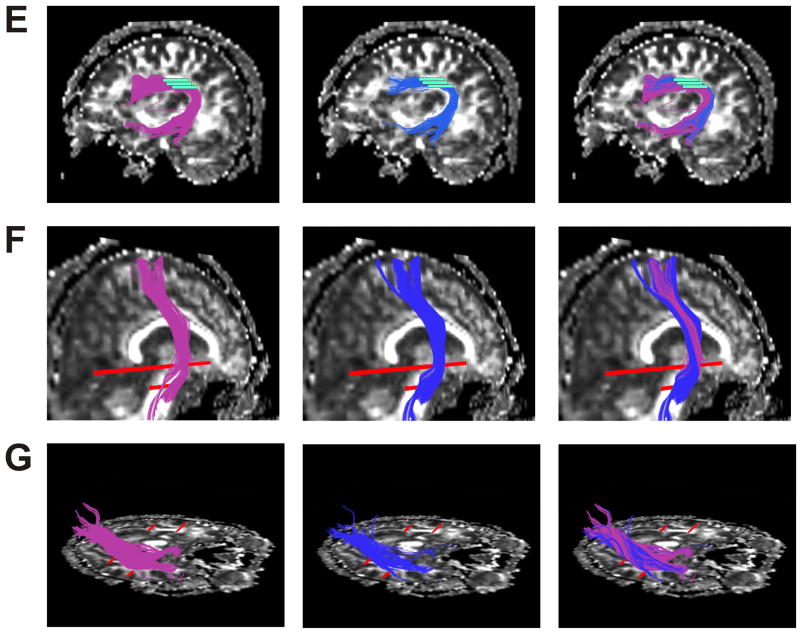
The result of whole brain clustering and the process of selection of a white matter tract (left uncinate fasciculus) is shown in Figure 1, where similar colours indicate tract similarity. Results for each anatomical tract are overlaid on a FA map in Figure 2. Tracts generated using the clustering method (Fig 2, left) and the MROI method (Fig 2, centre) were quite similar, and the high spatial agreement is apparent in Fig 2 (right), where the tracts are superimposed. Successful segmentation of the corpus callosum, and its subdivisions, as previously explained, is also shown (Fig 3).
Figure 2.
(A,B,C,D,E,F,G). Genu of corpus callosum (A), Right inferior occipitofrontal fasciculus (B), Left cingulum bundle (C), Left uncinate fasciculus (D), Left arcuate fasciculus (E), Right corticospinal tract (F), Right inferior longitudinal fasciculus (G) For each tract output of clustering method (on left), MROI method (centre), and both methods superimposed (right) each displayed on a sagittal slice
Figure 3.
(A,B). Segmentation of corpus callosum, and selection of subdivisions. Tracts are grouped into clusters according to similarity of shape and location and are colour coded accordingly (A). Clusters are then selected (B), red highlighted from left to right, as genu, premotor and supplementary motor projections, motor projections, sensory projections, and finally parietal temporal and occipital projections.
Spatial agreement
Mean k criterion results across the sample are presented in Table 1. The clustering method had excellent reliability, with ‘substantial’ or ‘almost perfect’ agreement for each white matter tract studied. The MROI method also had excellent reliability. The two fibre identification methods were also similar within rater. That is, for each rater, the clustering method showed either ‘substantial’ or ‘almost perfect’ agreement with the MROI method, indicating a high degree of voxel overlap. When the schizophrenia group and healthy control group were separated, both the clustering and MROI method still showed high reliability for each group (Table 2). For the remainder of the corpus callosum (where only the clustering method was used) there was high reliability for each subdivision across all participants, and, high reliability for both the schizophrenia group and healthy control group (Table 3).
Table 1.
| CLUST 1 | MROI 1 | CLUST 1 | CLUST 2 | |
|---|---|---|---|---|
| CLUST 2 | MROI 2 | MROI 1 | MROI 2 | |
| (n=20) | (n=20) | (n=20) | (n=20) | |
| L CB | 0.86 ± 0.09 | 0.72 ± 0.10 | 0.76 ± 0.12 | 0.74 ± 0.14 |
| R CB | 0.90 ± 0.05 | 0.78 ± 0.12 | 0.82 ± 0.11 | 0.72 ± 0.12 |
| Genu | 0.88 ± 0.05 | 0.81 ± 0.07 | 0.82 ± 0.07 | 0.79 ± 0.08 |
| L IFOF | 0.83 ± 0.11 | 0.88 ± 0.10 | 0.77 ± 0.09 | 0.81 ± 0.11 |
| R IFOF | 0.81 ± 0.13 | 0.86 ± 0.07 | 0.72 ± 0.14 | 0.73 ± 0.09 |
| L UF | 0.90 ± 0.08 | 0.87 ± 0.08 | 0.69 ± 0.11 | 0.72 ± 0.12 |
| R UF | 0.92 ± 0.06 | 0.88 ± 0.07 | 0.72 ± 0.12 | 0.70 ± 0.14 |
| L ILF | 0.87 ± 0.12 | 0.80 ± 0.08 | 0.72 ± 0.08 | 0.69 ± 0.08 |
| R ILF | 0.92 ± 0.08 | 0.76 ± 0.06 | 0.74 ± 0.06 | 0.71 ± 0.11 |
| L AF | 0.76 ± 0.15 | 0.69 ± 0.06 | 0.65 ± 0.12 | 0.66 ± 0.06 |
| R AF | 0.81 ± 0.08 | 0.74 ± 0.08 | 0.69 ± 0.09 | 0.74 ± 0.10 |
| L CST | 0.84 ± 0.15 | 0.71 ± 0.09 | 0.71 ± 0.09 | 0.69 ± 0.08 |
| R CST | 0.77 ± 0.15 | 0.73 ± 0.06 | 0.68 ± 0.11 | 0.67 ± 0.10 |
k = 0.61–0.80 is considered ‘substantial agreement and k = 0.81–1.0 is considered ‘almost perfect’ agreement.
CLUST 1 = clustering result by operator 1; CLUST 2 = clustering result by operator 2; MROI 1 = MROI result by operator 1; MROI 2 = MROI result by operator 2
CB = cingulum bundle, Genu (of corpus callosum), IFOF = inferior occipitofrontal fasciculus, UF= uncinate fasciculus, ILF = inferior longitudinal fasciculus, AF = arcuate fasciculus, CST = corticospinal tract
Table 2.
Spatial (voxel) agreement using k criteriona by diagnosis
| b SZ CLUST1 | HC CLUST1 | SZ MROI1 | HC MROI1 | SZ CLUST | HC CLUST | |
|---|---|---|---|---|---|---|
| SZ CLUST2 | HC CLUST2 | SZ MROI2 | HC MROI2 | SZ MROI | HC MROI | |
| (n=10) | (n=10) | (n=10) | (n=10) | c(n=10) | c(n=10) | |
| L CB | 0.88 ± 0.07 | 0.84 ± 0.10 | 0.69 ± 0.13 | 0.74 ± 0.08 | 0.76 ± 0.16 | 0.73 ± 0.13 |
| R CB | 0.88 ± 0.07 | 0.90 ± 0.04 | 0.79 ± 0.11 | 0.76 ± 0.12 | 0.81 ± 0.10 | 0.83 ± 0.12 |
| Genu | 0.89 ± 0.05 | 0.87 ± 0.05 | 0.80 ± 0.05 | 0.82 ± 0.09 | 0.80 ± 0.07 | 0.85 ± 0.06 |
| L IFOF | 0.73 ± 0.14 | 0.91 ± 0.11 | 0.86 ± 0.09 | 0.90 ± 0.10 | 0.81 ± 0.13 | 0.84 ± 0.09 |
| R IFOF | 0.80 ± 0.10 | 0.83 ± 0.15 | 0.85 ± 0.05 | 0.86 ± 0.08 | 0.76 ± 0.15 | 0.76 ± 0.10 |
| L UF | 0.82 ± 0.08 | 0.97 ± 0.08 | 0.85 ± 0.08 | 0.89 ± 0.07 | 0.75 ± 0.14 | 0.67 ± 0.11 |
| R UF | 0.94 ± 0.05 | 0.91 ± 0.07 | 0.90 ± 0.09 | 0.85 ± 0.06 | 0.70 ± 0.10 | 0.75 ± 0.09 |
| L ILF | 0.93 ± 0.09 | 0.82 ± 0.15 | 0.79 ± 0.08 | 0.80 ± 0.08 | 0.73 ± 0.08 | 0.70 ± 0.08 |
| R ILF | 0.96 ± 0.05 | 0.87 ± 0.10 | 0.74 ± 0.07 | 0.78 ± 0.05 | 0.71 ± 0.10 | 0.72 ± 0.07 |
| L AF | 0.78 ± 0.17 | 0.74 ± 0.12 | 0.70 ± 0.05 | 0.69 ± 0.07 | 0.68 ± 0.06 | 0.63 ± 0.10 |
| R AF | 0.79 ± 0.11 | 0.82 ± 0.06 | 0.77 ± 0.05 | 0.70 ± 0.10 | 0.71 ± 0.07 | 0.75 ± 0.10 |
| L CST | 0.86 ± 0.14 | 0.82 ± 0.15 | 0.75 ± 0.11 | 0.67 ± 0.08 | 0.69 ± 0.10 | 0.72 ± 0.08 |
| R CST | 0.70 ± 0.17 | 0.84 ± 0.13 | 0.76 ± 0.04 | 0.71 ± 0.07 | 0.70 ± 0.11 | 0.68 ± 0.10 |
k = 0.61–0.80 is considered ‘substantial agreement and k = 0.81–1.0 is considered ‘almost perfect’ agreement
Inter rater reliability for each method calculated separately in schizophrenia (SZ) and healthy control (HC) groups
Averaged values for rater 1 and rater 2; intermethod reliability calculated separately for each rater initially for each subject, then averaged.
Table 3.
| CLUST1 | SZ CLUST1 | HC CLUST1 | |
|---|---|---|---|
| CLUST2 | SZ CLUST2 | HC CLUST2 | |
| (n=20) | (n=10) | (n=10) | |
| a CC2 | 0.88 ± 0.09 | 0.84 ± 0.12 | 0.92 ± 0.07 |
| b CC3 | 0.76 ± 0.18 | 0.76 ± 0.15 | 0.75 ± 0.20 |
| c CC4 | 0.81 ± 0.12 | 0.72 ± 0.11 | 0.79 ± 0.12 |
| d CC5 | 0.74 ± 0.11 | 0.76 ± 0.11 | 0.71 ± 0.11 |
premotor and supplementary motor projections
motor projections,
sensory projections,
parietal, temporal, and occipital projections
Scalar indices of the tensor
Scalar indices of the diffusion tensor (FA, trace, axial diffusivity, radial diffusivity) had high intraclass correlation coefficients for both the clustering and MROI methods. The intraclass correlation coefficient for all tracts using the clustering method was 0.93 (p<.001), and for the MROI method was 0.91 (p<.001). Percent differences between the clustering method and the MROI method for the four measures were small, as can be seen in Table 4 (shown for one operator).
Table 4.
Impact of Tract Segmentation Method on Diffusion Measures*
| Region | FA | Trace | Radial Diffusivity | Axial Diffusivity |
|---|---|---|---|---|
| L CB | 1.19 ± 1.2 | 0.49 ± 1.2 | 0.05 ± 0.3 | 0.03 ± 0.8 |
| R CB | 1.73 ± 2.3 | 0.67 ± 1.7 | 0.11 ± 0.4 | 0.21 ± 0.9 |
| Genu | 1.57 ± 1.8 | 0.25 ± 1.3 | 0.49 ± 0.7 | 0.48 ± 0.8 |
| L IFOF | 0.22 ± 1.6 | 0.84 ± 1.6 | 0.11 ± 0.4 | 0.76 ± 1.8 |
| R IFOF | 0.89 ± 1.4 | 0.36 ± 2.8 | 0.15 ± 0.7 | 0.88 ± 2.9 |
| L UF | 2.37 ± 2.3 | 1.22 ± 2.0 | 0.72 ± 0.5 | 1.87 ± 1.7 |
| R UF | 0.28 ± 1.3 | 0.87 ± 0.7 | 0.21 ± 0.4 | 0.62 ± 0.8 |
| L ILF | 1.72 ± 2.1 | 1.13 ± 2.7 | 0.69 ± 0.8 | 1.29 ± 1.3 |
| R ILF | 2.61 ± 2.9 | 1.20 ± 2.9 | 0.91 ± 0.9 | 1.65 ± 0.9 |
| L AF | 2.13 ± 2.4 | 0.50 ± 1.7 | 0.75 ± 1.3 | 1.07 ± 2.7 |
| R AF | 2.42 ± 1.8 | 0.68 ± 2.3 | 0.86 ± 1.7 | 0.97 ± 2.1 |
| L CST | 0.69 ± 1.7 | 0.03 ± 1.9 | 0.10 ± 0.4 | 0.08 ± 1.1 |
| R CST | 0.82 ± 1.9 | 1.80 ± 1.6 | 0.12 ± 0.6 | 0.29 ± 0.8 |
|
| ||||
| All regions** | 1.43 ± 2.2 | 0.77± 1.9 | 0.41 ± 0.7 | 0.78 ± 1.3 |
Mean and SD of the percent difference between the clustering and MROI methods.
The value for ‘All regions’ is simply the mean of the all the regional means.
Discussion
Our results indicated that the clustering method has excellent reliability. The present study also confirmed the reliability of the MROI method, that has recently been shown (Wakana et al. 2007). For all of the tracts studied, only minimal differences between the clustering method and the MROI method were found when comparing quantitative measures of diffusion and in the specific voxels included in the segmented tracts. We have previously shown that the clustering method is useful for grouping fibres based on their shape and similarity (O'Donnell et al. 2006) and for constructing a white matter atlas (O'Donnell and Westin 2007). The present study extends that work to demonstrate the suitability of the clustering method for the study of a wide range of quantitative measures of the diffusion tensor in white matter tracts in both healthy and diseased populations (schizophrenia).
The clustering method and the MROI method for segmenting whole-brain streamline tractography represent a significant advance over other approaches for quantifying diffusion, such as drawing ROIs on individual brain slices and taking measurements from the voxels covered by the ROIs alone (Alexander and Lobaugh 2007). Due to their construction via streamline tractography based methods, the clustering and MROI methods allow for calculation of quantitative properties of the diffusion tensor along white matter tracts in the brain.
Reproducibility values (k) of the clustering method exceeded 0.75 for all white matter tracts studied. The clustering method may present an advantage over the MROI method in segmenting those tracts that require the placement of several ROIs. It is possible that the placement of each successive ROI increases the potential for error. The k values for reproducibility of the MROI method for the right and left cingulum bundle were less than 0.8. However, in the case of the genu of the corpus callosum, or the UF or IFOF, where only one, two, and two ROIs were placed respectively, k values for the MROI method fell in the highest range of reproducibility (i.e. greater than 0.8). Variability in the clustering method is due to the operator’s decision regarding which clusters to choose following initial selection of the main cluster(s) that clearly comprise the bulk of the neuroanatomic tract of interest. A small number of clusters, usually consisting of short fibres, can be subsequently selected by the operator. When both operators do not select the same short fibres, voxel overlap drops below 100%, and variability is introduced. For instance, the arcuate fasciculus, consists of short as well as long fibres (Catani and Mesulam 2008), and voxel overlap between operators in our study show, as expected, more variability than in the uncinate fasciculus, where fewer clusters of short fibres are present. Superimposing the clusters on the FA and T1 image allows for confirmation that the correct clusters are chosen.
Less opportunity for user bias exists with the clustering method since it is impossible for the user to visualize the properties of the tensor of that tract when selecting clusters corresponding to the white matter tract of interest. Conversely, using the MROI method, bias can occur in several situations, such as deciding on the size of the ROI, the number of ROIs drawn, and the slice(s) on which the ROIs are drawn. Limiting user bias is especially important for studies comparing disease populations to healthy populations, where investigators are usually interested in finding a difference between groups. In addition, ROI analyses of DTI data may be more sensitive to bias created by ROI placement in the presence of disease or atrophy (Alexander and Lobaugh 2007). The clustering method may also be more suitable for longitudinal studies, since opportunities for interrater discrepancies are minimized.
A limitation of streamline fibre tractography that has an impact on both the clustering and MROI methods is that it can be difficult to accurately map white matter pathways in regions with crossing or converging fibres (such as the limbic projection of the cingulum bundle). Streamline (deterministic) tractography, in particular, poses challenges in resolving fibres in such regions (Alexander and Lobaugh 2007). Limbic system segmentation can produce challenges for the clustering method, since there is a general ‘noisiness’ in this area. For example, the fibres in the fornix region may, at times, cross structures to follow part of the corona radiate. Image resolution affects the size scale of tracts that may be traced (both tract width and radius of curvature should be larger than the voxel scale). Therefore, smaller tracts such as the posterior commissure, fimbria, and stria terminalis may not be appropriate for standard streamline tractography techniques (Wakana et al. 2007). The reliability of the clustering method for the fornix is not high, due to errors of tractography (trajectories crossing into corpus callosum and anterior commissure for example) and due to the fact that trajectories are often "broken" along the course of the structure. These issues are better addressed by improvements in acquisition, tractography, and/or fiber distribution modeling (such as multiple tensors, etc) rather than at the clustering stage. A potential limitation of the clustering method is that it may include small, short, white matter fibre tracts that the MROI method may not. For instance, the inferior occipito-frontal fasciculus was created by drawing two ROIs using the MROI method. Any white matter fibres not sufficiently long to pass through both ROIs would not have been included. However, our data (not shown) indicate that the clustering method might include such shorter fibres, particularly if they are similar in shape and location to the longer fibres and meet the selected distance threshold. As a result, mean fibre length for each tract is slightly shorter in the clustering method, but mean fibre number slightly larger. While it is unclear if these additional fibres create a more or less ‘anatomically correct’ white matter tract, the virtually identical scalar measures of the diffusion tensor between the clustering and MROI method, and the strong spatial overlap results, indicate that there is little to no effect of these additional smaller fibres on average values across the whole bundle.
In conclusion, our clustering algorithm presents an alternative to the more commonly used MROI method. Since it eliminates some forms of user bias, it may be especially useful when characterizing multiple white matter fibre tracts or studying disease populations. It is a robust method in both a healthy and disease population and produces easily visualized and highly reliable quantifiable white matter tracts with diffusion tensor tractography.
Acknowledgments
The authors would like to acknowledge the Canadian Institutes of Health Research Clinician Scientist Award (ANV), National Institutes of Health (NIH) U41-RR019703 (LJO’D), the Brain Science Foundation (LJO’D), NIH R01 MH074794 (CFW, MES), NIH P41 RR13218 (CFW), R01 MH 50740 (MES), NIH 1P50 MH08272 (MES), U54GM072977-01 NIG/HS NIH (MES), VA MERIT (MES), VA Schizophrenia Center Grant (MES), and the Sandra A. Rotman Research Institute (BGP).
The authors would also like to thank Dielle Miranda for her assistance in this project.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander A, Lobaugh N. Insights into Brain Connectivity Using Quantiative MRI Measures of White Matter. Springer; Springer: 2007. [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44:625–32. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Catani M, Mesulam M. The arcuate fasciculus and the disconnection theme in language and aphasia: History and current state. Cortex. 2008;44:953–61. doi: 10.1016/j.cortex.2008.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciccarelli O, Catani M, Johansen-Berg H, Clark C, Thompson A. Diffusion-based tractography in neurological disorders: concepts, applications, and future developments. Lancet Neurol. 2008;7:715–27. doi: 10.1016/S1474-4422(08)70163-7. [DOI] [PubMed] [Google Scholar]
- Ennis DB, Kindlmann G. Orthogonal tensor invariants and the analysis of diffusion tensor magnetic resonance images. Magn Reson Med. 2006;55:136–46. doi: 10.1002/mrm.20741. [DOI] [PubMed] [Google Scholar]
- First MSR, Williams J, Gibbon M. Structured Clinical Interview for DSM-IV -Non-Patient Edition (SCID-NP, Version 1.0) American Psychiatric Press, American Psychiatric Pres; 1995. [Google Scholar]
- First MBSR, Gibbon M, Williams JBW. Strucutured Clinical Interview for DSM-IV Axis I Disorders, Patient Edition (SCID-P), version 2. Biometrics Research, Biometrics Research; 1995. [Google Scholar]
- Hofer S, Frahm J. Topography of the human corpus callosum revisited--comprehensive fiber tractography using diffusion tensor magnetic resonance imaging. Neuroimage. 2006;32(3):989–94. doi: 10.1016/j.neuroimage.2006.05.044. [DOI] [PubMed] [Google Scholar]
- Kubicki M, McCarley R, Westin CF, Park HJ, Maier S, Kikinis R, Jolesz FA, Shenton ME. A review of diffusion tensor imaging studies in schizophrenia. J Psychiatr Res. 2007;41:15–30. doi: 10.1016/j.jpsychires.2005.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–74. [PubMed] [Google Scholar]
- Mori S, van Zijl PC. Fiber tracking: principles and strategies - a technical review. NMR Biomed. 2002;15:468–80. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]
- Mori S, Wakana S, Negae-Poetscher L, Zijl PCv. MRI Atlas of Human White Matter. Elsevier, Elsevier; 2005. [Google Scholar]
- Ng A, Jordan M, Weiss Y. On Spectral Clustering: Analysis and an Algorithm. MIT Press, MIT Press; 2002. [Google Scholar]
- O'Donnell LJ, Kubicki M, Shenton ME, Dreusicke MH, Grimson WE, Westin CF. A method for clustering white matter fiber tracts. AJNR Am J Neuroradiol. 2006;27:1032–6. [PMC free article] [PubMed] [Google Scholar]
- O'Donnell LJ, Westin CF. Automatic tractography segmentation using a high-dimensional white matter atlas. IEEE Trans Med Imaging. 2007;26:1562–75. doi: 10.1109/TMI.2007.906785. [DOI] [PubMed] [Google Scholar]
- Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Shi J, Malik J. Normalized cuts and image segmentation. IEEE Trans Pattern Anal Mach Intell. 2000;22:888–905. [Google Scholar]
- Song SK, Sun SW, Ramsbottom MJ, Chang C, Russell J, Cross AH. Dysmyelination revealed through MRI as increased radial (but unchanged axial) diffusion of water. Neuroimage. 2002;17:1429–36. doi: 10.1006/nimg.2002.1267. [DOI] [PubMed] [Google Scholar]
- Song SK, Yoshino J, Le TQ, Lin SJ, Sun SW, Cross AH, Armstrong RC. Demyelination increases radial diffusivity in corpus callosum of mouse brain. Neuroimage. 2005;26:132–40. doi: 10.1016/j.neuroimage.2005.01.028. [DOI] [PubMed] [Google Scholar]
- Wakana S, Caprihan A, Panzenboeck MM, Fallon JH, Perry M, Gollub RL, Hua K, Zhang J, Jiang H, Dubey P, Blitz A, van Zijl P, Mori S. Reproducibility of quantitative tractography methods applied to cerebral white matter. Neuroimage. 2007;36:630–44. doi: 10.1016/j.neuroimage.2007.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westin CF, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R. Processing and visualization for diffusion tensor MRI. Med Image Anal. 2002;6:93–108. doi: 10.1016/s1361-8415(02)00053-1. [DOI] [PubMed] [Google Scholar]