Abstract
Escherichia coli HUαβ, a major nucleoid associated protein (NAP), organizes the DNA chromosome and facilitates numerous DNA transactions. Using isothermal titration calorimetry (ITC), fluorescence resonance energy transfer (FRET) and a series of DNA lengths (8, 15, 34, 38 and 160 base pairs) we establish that HUαβ interacts with duplex DNA using three different nonspecific binding modes. Both the HU to DNA mole ratio ([HU]/[DNA]) and DNA length dictate the dominant HU binding mode. On sufficiently long DNA (≥ 34 base pairs), at low [HU]/[DNA], HU populates a noncooperative 34 bp binding mode with a binding constant of 2.1 (± 0.4) × 106 M−1, and a binding enthalpy of +7.7 (± 0.6) kcal/mol at 15 °C and 0.15 M Na+. With increasing [HU]/[DNA], HU bound in the noncooperative 34 bp mode progressively converts to two cooperative (ω ~ 20) modes with site sizes of 10 bp and 6 bp. These latter modes exhibit smaller binding constants (1.1 (± 0.2) × 105 M−1 for the 10 bp mode, 3.5 (± 1.4) × 104 M−1 for the 6 bp mode) and binding enthalpies (4.2 (± 0.3) kcal/mol for the 10 bp mode, −1.6 (±0.3) kcal/mol for the 6 bp mode). As DNA length increases to 34 bp or more at low [HU]/[DNA], the small modes are replaced by the 34 bp binding mode. FRET data demonstrate that the 34 bp mode bends DNA by 143 ± 6° whereas the 6 and 10 bp modes do not. The model proposed in this study provides a novel quantitative and comprehensive framework for reconciling previous structural and solution studies of HU, including single molecule (force extension measurement, AFM), fluorescence, and electrophoretic gel mobility shift assays. In particular, it explains how HU condenses or extends DNA depending on the relative concentrations of HU and DNA.
Keywords: HU protein, isothermal titration calorimetry, DNA binding mode, DNA bending, fluorescence resonance energy transfer
Introduction
The organization of genomic DNA influences critical cellular processes in all organisms. In bacteria, nucleoid-associated proteins (NAPs) fold chromosomal DNA into a compact structure with distinct topological domains that in turn are dynamically altered during various DNA transactions (replication, transcription, recombination).1; 2 As cells approach and enter stationary phase, the morphology of the nucleoid undergoes a distinct change, becoming more compact.1; 3; 4; 5; 6 As part of the reprogramming to this low energy state (i.e. low [ATP]/[ADP]), the numbers and relative amounts of NAPs dramatically shift.7 Expression of FIS (factor inversion stimulation), the most abundant NAP in exponential growth (~ 3 × 104 dimers per cell), is severely down regulated to only ~ 100 dimers per cell in stationary phase. The amount of Dps (DNA protection from starvation) increases dramatically from < ~ 100 dodecamers per cell to over ~ 104 dodecamers per cell in the transition from exponential growth to early stationary phase. Also, in this transition, E.coli replaces large amounts of the “histone-like” protein HU with its structural homolog IHF (Integration Host Factor). This exchange appears to semi-quantitatively conserve the total amount of these homologs: the amount of HU per cell decreases from ~ 3 × 104 to ~ 1.5 × 104 dimers; concurrently, the amount of IHF per cell increases from ~ 6 × 103 to ~ 2.7 × 104 dimers.7 To understand the roles of HU, IHF and other NAPs in the mechanism of growth phase dependent nucleoid organization (and regulation of DNA transactions), biophysical information about their interactions with DNA is needed.
How do changes in the population distributions of NAPs over different growth conditions alter the structure of the nucleoid? A logical scenario is that differences in folds and subunit assemblies of the various NAPs induce different changes in local DNA structure, leading to global changes in the packing of the E. coli chromosome. FIS, functioning as a dimer,8; 9; 10 binds specifically and locally compacts DNA by introducing 50 – 90° DNA bends.11; 12; 13; 14; 15 In contrast, dodecameric Dps assemblies are proposed to form three-dimensional hexagonally packed arrays which thread nonspecifically bound DNA through the pores, sequestering it in the interstices.5; 6; 16; 17; 18 However, the growth-phase-dependent switch between the small, basic HU and IHF proteins is not as easily rationalized in terms of structure or assembly. HU and IHF share 30 – 40 % sequence identity and identical folds in compact heterodimers: an N-terminal alpha helical “body” connected to two extended beta strand arms by a beta-strand “saddle”. 1; 19; 20; 21; 22; 23; 24 Nonetheless, despite their superimposable architecture, IHF and HU exhibit distinct differences in DNA binding mode. IHF interacts with intact duplex DNA both specifically and nonspecifically whereas no DNA sequence dependence of HU binding has been identified.1; 18; 23
IHF binds its target sequence (H’ site) with a binding constant of approximately 107 M−1 (ITC determined) and a site size of 34 bp at 0.22 M K+ (in KCl) and 20 °C.25 Extrapolated to 0.1 M K+, the H’ DNA binding constant is approximately 109 M−1.25 Nonspecific DNA binding of IHF exhibits a site size of 5 ~ 10 bp and binding constant of 104 – 105 M−1 at 0.1 M K+,26 (JK, unpublished) giving rise to a specificity ratio of approximately 104 – 105. Fluorescence anisotropy and electrophoretic mobility shift (EMSA) assays of the binding of HU to 20 ~ 42 bp DNA oligomers have been interpreted in terms of a single non-cooperative or cooperative binding mode with a site size of 9 ~ 11 bp and a binding constant in the range ~105 – 106 M−1 (0.015 ~ 0.2 M Na+ and 5 ~ 10 °C).27; 28; 29; 30 Other fluorescence anisotropy measurements and EMSA studies provide evidence for a 2:1 complex of HU with a 13 bp DNA oligomer and 3:1 complex of HU with a 19 bp DNA, respectively, indicating a binding mode with a site size of ~ 6 bp.29; 31 Studies of supercoiling of plasmid DNA induced by HU indicate the existence of a binding mode with a site size of ~ 34 bp,32; 33 and EMSA studies with nicked and gapped 30 ~ 40 bp DNA revealed the formation of a 1:1 complex with a significantly larger binding constant than that observed for intact DNA (~ 108 M−1 at 0.015 M Na+ and ~ 107 M−1 at 0.2 M Na+).28; 34; 35; 36 Steric considerations based on the trajectory of the highly bent DNA in the crystal structures of complexes of Anabena HU with 17 bp mismatched DNA oligomers22 suggest that bound HU could occlude 25 to 35 bp.1; 22 The population distribution of these various binding modes on DNA in vitro and in vivo and their roles in DNA compaction or expansion, nucleoid organization and DNA transactions in vivo remain to be determined.
Recent single molecule force – extension measurement studies observed that the end-to-end length of 10 and 48.5 kbp linearized plasmid DNA molecules decreased with increasing HU concentration at constant force, demonstrating HU-induced compaction of the plasmid flexible coil.37; 38 At higher HU concentrations, however, the end-to-end length increased, becoming greater than that of uncomplexed DNA.37; 38 The ability of HU to stiffen DNA seems highly surprising given its presumed role in condensing the bacterial nucleoid 39. To reconcile these data, it occurred to us that changes in the properties of HU-DNA complexes formed at different HU concentrations may reflect changes in HU binding mode. Shifts in binding modes with protein concentration and other solution variables (e.g. [salt]) characterize the single-stranded DNA binding interactions of E. coli SSB40; 41; 42; 43 and DNA polymerase beta44; 45. Like SSB43, the multiple functions of HU in DNA processes in vivo likely involve distinct binding modes22, with each mode inducing a unique DNA structure.
To characterize the binding modes and transitions between modes as a function of HU/DNA mole ratio, we performed ITC (isothermal titration calorimetry) studies, complemented by a fluorescence energy transfer (FRET) binding assay, with 5 different lengths of DNA (8, 15, 34, 38, and 160 bp) at 15°C and moderate salt concentration ([Na+] = 0.15 M). The complexities of these ITC isotherms provide strong quantitative evidence for three different binding modes (binding site sizes of 6, 10, and 34 bp) on the longer DNA oligomers (34, 38, 160 bp), two binding modes (binding site sizes of 6 and 10 bp) on 15 bp DNA, and a single binding mode (binding site size of 6 bp) on 8 bp DNA. For the longer oligomers, increases in HU/DNA mole ratio drive transitions from a 34 bp noncooperative mode to cooperative modes with site sizes of 10 bp and 6 bp. Based on the FRET results, we propose that the 34 bp mode involves DNA bending to form a complex similar to that seen in the cocrystal of Anabena HU with distorted DNA,22 in which the DNA is less bent and wrapped than in the complex of IHF with its specific H’ site.21 Conclusions drawn from the quantitative HU binding mode analysis presented here are consistent with results of previous, more qualitative studies and provide insight into the thermodynamic interpretation of single molecule studies and into the physiological function of HU in nucleoid organization and in regulation of various DNA transactions.
Results and analysis
ITC Titrations of DNA Oligomers (8 bp to 160 bp) with E. coli HUαβ: Evidence for Multiple Nonspecific Binding Modes and Transitions between Binding Modes as a Function of HU Concentration
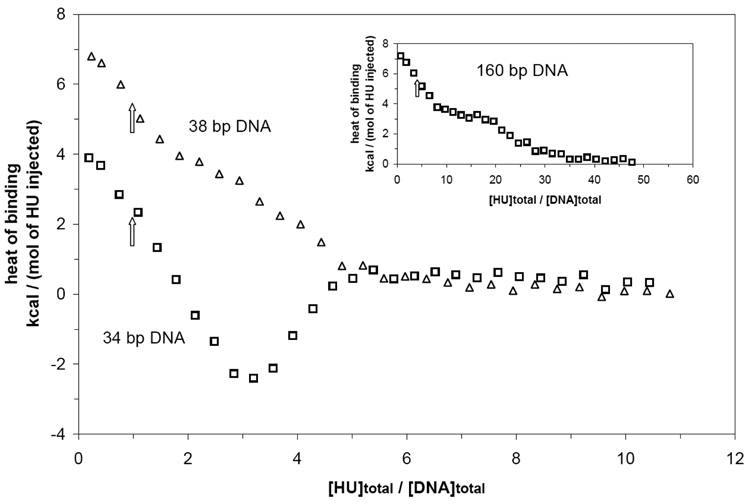
To identify and characterize the binding modes used by HU in its nonspecific interactions with duplex DNA, we titrated five DNA oligomer duplexes spanning a 20-fold range of lengths (8 – 160 bp) with HU and monitored the resulting binding isotherms and binding enthalpies using ITC. Representative data for forward ITC titrations of 34 bp and of 160 bp DNA with HU are shown in Figure 1a, where the rate at which heat is absorbed by or evolved from the sample cell, as compared to a reference cell, is plotted for each injection of HU into DNA. Experimentally-determined heats of binding per mol of HU injected into solutions of 8, 15, 34, 38, and 160 bp DNA are shown in Fig. 1b as a function of the HU/DNA bp mole ratio.
Figure 1.
Interaction between HU and different lengths of double-stranded DNA at 15 °C and 0.15 M Na+ investigated by isothermal titration calorimetry (ITC). (A) Representative raw heat signals for titrations of 34 bp DNA (lower trace: 2.5 µM in reaction cell) and 160 bp DNA (upper trace: 0.5 µM) with 10 µL injections of HU (100 M in injection syringe) with 240 s equilibration time. The heat of dilution detected in control injections of the same amount of HU into buffer is also plotted (middle trace). (B) Heat signals for representative HU titrations of 8 bp (x; 12 µM), 15 bp (circle; 3.8 µM), 34 bp (square: 2.5 µM), 38 bp (cross; 2.5 µM), and 160 bp (open triangle: 0.5 µM; filled triangle: 1 µM) DNA. Heats of binding, corrected for the heat of dilution and normalized per of mole of HU injected, are plotted as a function of the molar ratio [HU]/[DNA bp]. Inset: Initial binding heats from Fig. 1B are plotted as a function of DNA length for 34, 38, and, 160 bp DNA. The continuous line represents a simulation of the initial binding heat as a function of DNA length using the binding mode transition model (see Results and Analysis).
For the binding of any ligand to DNA in a single binding mode, the initial enthalpy of binding per mol of ligand injected (characteristic of binding the first ligand to an unoccupied DNA oligomer) would be independent of DNA length. However, Fig. 1b (and Inset) shows that the initial heat of binding increases strongly with increasing DNA length from a value which is indistinguishable from zero for binding to 8 bp DNA to approximately 4.0 kcal/mol for binding to 34 bp DNA and 6.3 kcal/mol for binding to 38 bp DNA. With a further increase to 160 bp, the initial binding enthalpy increases only modestly to 7.3 kcal/mol.
For noncooperative single-mode binding, the heat signal (either endothermic or exothermic) would decay monotonically (with an inflection point corresponding to the binding site size) to zero with increasing ligand concentration as saturation of the DNA lattice is approached. However, the isotherms for DNA lengths in the range 15 bp to 160 bp show at least two different phases over the range of [HU]total/[DNA]total ([HU]/[DNA] below) examined. In particular, as [HU]/[DNA] increases, both the 15 and 34 bp isotherms exhibit unusual transitions from endothermic to exothermic binding, and subsequent broad minima late (near saturation) in the titration (The FRET-detected binding isotherm (Fig. 8 below) with an analogous 34 bp DNA also provides evidence for two different phases with a broad breakpoint at [HU]/[DNA] of 1 ~ 2). For 160 bp DNA, a weak but reproducible plateau at [HU]/[DNA bp] ~ 0.08 separates two distinct decays in the endothermic heat signal.
Figure 8.
FRET monitored titrations of 34 bp DNA with HU at 15 °C and 0.15 M Na+. (A) Representative fluorescence emission spectra (500 ~ 615 nm) for end – labeled (FAM, TAMRA at each 5’ end) 34 bp DNA (120 nM) with an excitation wavelength of 490 nm in the absence of HU (black) and in the presence of 120 nM HU (red). (B) Titration of 34 bp DNA with HU, plotted as the observed transfer efficiency as a function of [HU]/[DNA]. Black solid curve represents the fit with macroscopic quantities determined from ITC experiments (Table 1) and with the intrinsic transfer efficiency for each binding mode given in Results and Analysis. Corresponding population distributions of the 34 (green), 10 (blue), and 6 (red) bp modes are plotted on right ordinate.
The effects of DNA length on the initial heat of binding and the dependence of the shape of the isotherm on [HU]/[DNA] are not consistent with a single mode of binding. Instead these data indicate that multiple binding modes are populated during the titration. Inspection of these isotherms and comparison with isotherms for the same DNA lengths obtained at lower salt concentration (see Fig. 2 and 3) allow us to estimate the binding site sizes of the various modes as follows.
Figure 2.
Representative binding isotherms obtained by ITC for 34 bp (square), 38 bp (triangle), and 160 bp DNA (inset) at 15 °C and 0.125 M Na+. Normalized heats of binding are plotted as a function of [HU]/[DNA]. Arrows indicate inflection points in the first phase of the isotherms for these three lengths of DNA, as expected for the binding mode with a site size of ~ 34 bp.
Figure 3.
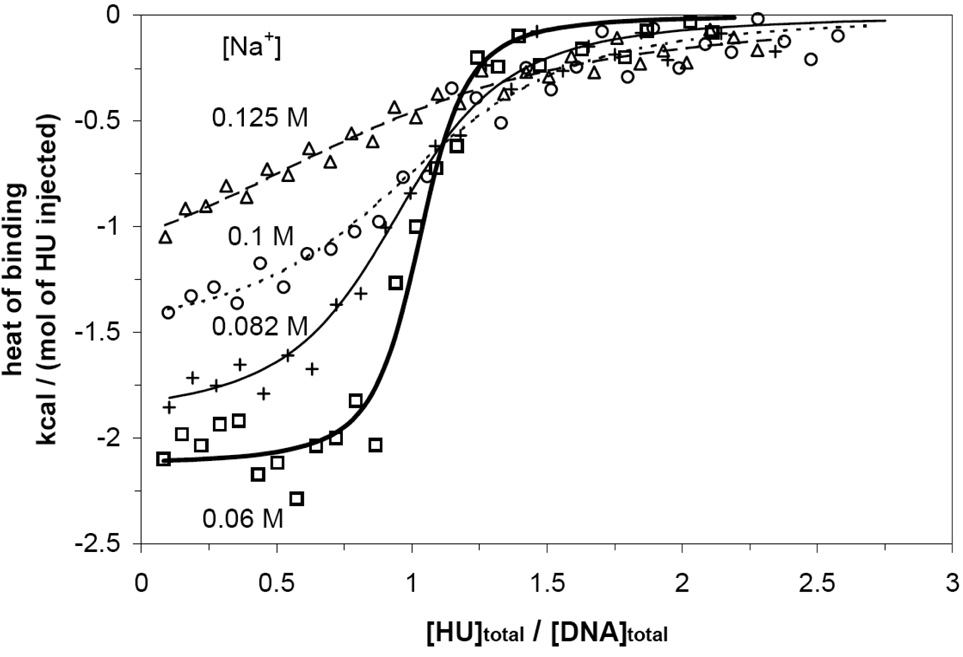
Representative binding isotherms obtained by ITC for 8 bp DNA at 0.06 M (square), 0.082 M (cross), 0.1 M (circle), and 0.125 M (triangle) Na+ at 15 °C. All isotherms show a 1:1 binding stoichiometry and exothermic binding enthalpies. Fitted curves at each salt concentration are for a single site binding model.81
The transition from endothermic to exothermic binding with increasing [HU]/[DNA] is particularly abrupt for 34 bp DNA. The weak inflection point/midpoint of this transition (at [HU]/[DNA bp] ~ 0.03 or [HU]/[DNA] ~ 1) indicates the existence of a large-site size mode (necessarily in the range 18 bp to 34 bp) on 34 bp DNA. The modest inflection point in the first phase of titration of 160 bp DNA (near [HU]/[DNA bp] = 0.03 or [HU]/[DNA] = 5) provides additional evidence for a binding mode with a large site size (27 to 32 bp). Lowering the salt concentration in the binding buffer from 0.15 M to 0.125 M Na+ makes the inflection points of the 34 and 160 bp isotherms (at [HU]/[DNA] ~ 1 and 5, respectively) more pronounced by increasing the macroscopic HU-DNA binding constants (Fig. 2 and inset therein). At the lower salt concentration, the isotherm of 38 bp DNA also exhibits an inflection point at [HU]/[DNA] ~ 1, confirming the existence of a large-site-size binding mode. The transition from endothermic to exothermic binding heat with increasing [HU]/[DNA] on 34 bp DNA demonstrates the transition from an initial large-site-size mode (approximately 34 bp) to one or more small-site-size modes with different thermodynamic properties (binding enthalpy, binding constant, cooperativity).
Use of shorter DNA duplexes (8 and 15 bp) eliminates the contribution from the large site size mode and allows better characterization of the small site size modes. No significant heat signal (above background) is detected in titrations of 8 bp DNA with HU at 0.15 M Na+ (Fig. 1b). However, a 1:1 binding isotherm is observed (Fig. 3) in ITC titrations of 8 bp DNA with HU at lower salt concentrations ([Na+] = 0.06 ~ 0.125 M). In this case, only a single exothermic phase is observed, in contrast to the behavior of longer (15, 34, 38, and 160 bp) fragments. The 1:1 stoichiometry observed for 8 bp DNA indicates a binding site size of 5 ~ 8 bp, which we interpret to be the same binding mode (~ 6 bp) as observed in previous fluorescence assays using 13 bp DNA (2:1 stoichiometry at saturation)29 and in EMSA using 19 bp DNA (3:1 stoichiometry at saturation).31 With increasing salt concentration, both the binding constant and the magnitude of the binding enthalpy decrease, so that the isotherm of 8 bp DNA is not directly detectable by ITC at 0.15 M Na+.
The observed binding isotherm of 15 bp DNA clearly deviates from what would be expected for the 6 bp binding mode, exhibiting an endothermic heat of binding at low [HU]/[DNA] where no more than one HU is bound per DNA molecule. Therefore, another binding mode with a site size in the range of 9 ~ 15 bp is required. This binding mode is likely to be that observed in previous fluorescence and EMSA with a site size of ~10 bp.27; 28; 29; 30
We therefore propose that HU interacts with intact duplex DNA using at least three different binding modes (34, 10 and 6 bp mode) with different structures and thermodynamics (binding site size, binding constant, binding enthalpy, cooperativity). For the set of DNA oligomers examined, there is no indication that the binding constants and enthalpies of these three modes depend significantly on DNA sequence or length. Below we demonstrate that an analysis of the ITC data using three binding modes satisfactorily describes the observed complexity of the binding behavior of HU with intact duplex DNA, both qualitatively and quantitatively; increasing [HU]/[DNA] for a given length of DNA (or decreasing DNA length for a given [HU]/[DNA]) drives transitions from the large to the small site size modes. Figure 4 illustrates these transitions with increasing [HU]/[DNA] for a given DNA length, and with increasing DNA length at constant [HU]/[DNA]. While the increase in the initial heat of binding with an increase in DNA length above 34 bp superficially argues for a binding mode with a site size larger than 34 bp, we show that the 34 bp mode is sufficient to explain this feature. Indeed, the surprisingly large increase in initial binding heat from 34 to 38 bp DNA with only a 4 bp increase in DNA length provides strong evidence for our model (see below).
Figure 4.
A) Schematic description of HU binding mode transitions. For a given length of DNA, as [HU]/[DNA] increases, HU converts from a large to a small site size binding mode. At low [HU]/[DNA], where no more than one HU binds to DNA, if the ratio of the binding constants of the large and small site size modes exceeds the ratio of statistical factors (i.e. numbers of available binding sites on a DNA molecule), the large site size mode is the principal mode. At high [HU]/[DNA], the small site size mode is preferred because the ratio of populations of the large and small site size modes varies with [HU]Δg in this limit, where Δg is the difference (Δg < 0) between the maximum number of HU that can be bound in the large and small site size modes (see Discussion). (B) For a given (low) [HU]/[DNA], as DNA length increases, the HU binding mode converts from the small to the large site size mode because the ratio of statistical factors (large site size to small site size mode) increases with increasing DNA length, becoming unity for infinitely long DNA.
Binding of HU to 8 and 15 bp DNA: Quantifying the Thermodynamics of the 10 and 6 bp Modes and the Transition from the 10 bp to 6 bp Mode on 15 bp DNA with Increasing [HU]/[DNA]
The features of a forward titration of 15 bp DNA with HU (Fig. 1b and 5) described above are most simply interpreted as initial endothermic binding in a larger site size (≤ 15 bp) binding mode, followed by a transition with increasing [HU]/[DNA] to exothermic binding of a smaller site size mode. To fit the 15 bp binding isotherms in Fig. 5, we used two (model-independent) macroscopic binding constants (K1, K2; the subscripts represent the number of HU dimers bound per DNA lattice) and two corresponding binding enthalpies (ΔH1, ΔH2). The quantities K1 and ΔH1 dominate the first half of the isotherm whereas K2 and ΔH2 dominate the second half. As shown in Fig. 5a, the best-fit binding constants (K1 = 9.9 (± 2.4) × 105 M−1 and K2 = 1.2 (± 0.5) × 1011 M−2) and binding enthalpies (ΔH1 = 2.2 (± 0.3) kcal/mol and ΔH2 = − 3.6 (± 1.0) kcal/mol) describe the experimental isotherm very well (Table 1).
Figure 5.
Noncompetitive and competitive binding isotherms of 15 bp DNA at 15 °C and 0.15 M Na+. (A) Representative isotherms for noncompetitive (closed squares: from Fig. 1B) and competitive binding of HU (open squares; 4.2 µM 15 bp DNA with 20 µM 8 bp DNA). For the noncompetitive isotherm, the fitted curve (Eq. 7 – 9) yields the model independent macroscopic binding constants and enthalpies in Table 1. For the competition isotherm, the fitted curve (Eq. 1–5 and 10) yields the microscopic thermodynamic quantities in Table 2. The dashed line represents the simulation of competition isotherm based on an alternative interpretation of macroscopic quantities in terms of single site, cooperative binding model (see Discussion). (B) Global minimum of the sum of square of residuals from fitting the competitive isotherm for choices of ω ranging from 1 to 103, demonstrating the uniqueness of the fit for ω = 24. (C) Population distribution (from a simulation using quantities in Table 2; see Methods and Materials) of 10 bp mode (thick), 6 bp mode (thin), and of two HU molecules cooperatively bound (dot) on 15 bp DNA (contact point between two HU, each bound in the 6 bp mode) as a function of [HU]/[DNA] corresponding to Fig. 5a. (D) Dissection of the observed heat signal of noncompetitive isotherm (solid curve) into the heat of 10 bp mode formation (circles), the heat of 6 bp mode formation (squares), and the heat of HU-HU contact point formation (triangles).
Table 1.
Macroscopic binding constants and binding enthalpies used in fitting the ITC binding isotherms of 15 bp and 34 bp DNA (errors were determined from at least 3 independent measurements)
| 15 bp DNA | 34 bp DNA | |
|---|---|---|
| K1 (M−1) | 9.9 (± 2.4) × 105 | 5.9 (± 0.7) × 106 |
| K2 (M−2) | 1.2 (± 0.5) × 1011 | 1.0 (± 0.4) × 1013 |
| K3 (M−3) | - | 3.5 (± 1.3) × 1018 |
| ΔH1 (kcal/mol) | 2.2 (± 0.3) | 4.4 (± 0.3) |
| ΔH2 (kcal/mol) | −3.6 (± 1.0) | 7.5 (± 1.0) |
| ΔH3 (kcal/mol) | - | −2.2 (± 0.6) |
nHU + DNA ↔ (HUn – DNA) Kn, ΔHn
We interpret these macroscopic binding constants and enthalpies using nonspecific ligand – DNA binding theory46; 47; 48 in terms of the microscopic quantities characterizing each binding mode i: intrinsic (microscopic) binding constant (ki), site size (ni), enthalpy (Δhi), cooperativity (ωi) and cooperativity enthalpy (Δhωi). The cooperativity ωi is defined as the ratio of binding constants for adjacent binding and isolated binding of HU.
The macroscopic K1 is an ensemble-averaged binding constant for the binding of the first HU molecule to a DNA lattice; K1 is therefore the sum over microscopic binding constants ki for all possible binding modes weighted by the statistical factors N − ni + 1, which represent the number of distinctive configurations of the N bp DNA lattice with one HU bound as mode i with site size ni:
| (1) |
Two binding modes with site sizes of 6 and 10 bp are used to interpret the macroscopic thermodynamic quantities obtained from 15 bp data for the reasons discussed in the previous section. An analysis based on only these two site sizes provides an excellent fit to the forward titrations of 15 bp DNA for a range of salt concentrations (0.06 to 0.15 M Na+) and temperatures (5 to 25 °C) (JK, in preparation), including the conditions reported here (0.15 M Na+, 15 °C). For binding of one HU, using either 10 or 6 bp mode, to a 15 bp DNA (N = 15; ki = 0 for all i except i = 6 and 10), the specific expression for K1 for 15 bp DNA is:
| (2) |
If the only two binding modes are the 10 bp and 6 bp modes, then the binding of two HU molecules to a 15 bp DNA lattice must involve only the 6 bp mode, and the interpretation of the macroscopic binding constant K2 is:
| (3a) |
The statistical factors PN(k,j) represent the number of distinct ways to distribute k HU molecules on a N bp DNA lattice with j contact points between nearest neighbors. (For the 6 bp mode on 15 bp DNA, there can be no more than one contact point.) The general equation for this statistical factor is given by46:
| (3b) |
From Eq. 3b, or from a direct enumeration of configurations, P15(2,0) = 6 and P15(2,1) = 4.
The temperature derivatives of Eq. 1 and 2 dissect the two macroscopic enthalpies, ΔH1 and ΔH2, into the same microscopic parameters.
| (4) |
| (5) |
Since Eq. 2 – 5 contain six unknown microscopic thermodynamic quantities (k10, k6, Δh10, Δh6, ω6, and Δh6), at least two of these must be obtained from independent experiments. Optimally, we would obtain k6 and Δh6 from titration of a DNA lattice shorter than 10 bp to which HU binds only in the noncooperative (isolated) 6 bp mode. However, the small binding constant and binding enthalpy of the 6 bp mode for the experimental conditions used here preclude direct determination of these quantities (see Fig. 1b and Fig. 3 for HU titration of 8 bp DNA). Instead, competition assays in which mixtures of 8 and 15 bp DNA were titrated with HU were used to detect the relatively weak interaction of HU with 8 bp DNA and to characterize the 6 bp mode (Fig. 5a). The competition isotherm is clearly displaced in the exothermic direction from the 15 bp DNA isotherm, demonstrating that the 6 bp mode on 8 bp DNA competes with the 10 bp and the 6 bp modes on 15 bp DNA with a small exothermic binding enthalpy, consistent with the behavior observed directly with 8 bp DNA at low salt concentrations (Fig. 3).
Six microscopic quantities (k6, Δh6, ω6, Δhω6, k10, Δh10) are obtained from the fit to the 8 bp – 15 bp competition isotherm (Fig. 5a). Only two (ω6, Δh6) parameters are floated in this fit; the other four are constrained by the macroscopic quantities obtained from the 15 bp isotherm and Eq. 2 – Eq. 5 (i.e. k6 = [K2,15bp / (6 + 4ω6)]0.5, k10 = (K1,15bp − 10k6) / 6, Δh10 = (ΔH1,15bpK1,15bp − 10k6Δh6) / 6k10, and Δhω6 = (ΔH2,15bp − 2Δh6) (6 + 4ω6) / 4ω6). Uniqueness of the fit was assessed by plotting the global minimum for the sum of squares of the residuals of the fit as a function ofω6 (Fig. 5b). The best-fit values of the microscopic binding constants are k10 = 1.1 (± 0.2) × 105 M−1 and k6 = 3.5 (± 1.4) × 104 M−1. As expected from the transition from endothermic to exothermic binding at higher [HU]/[DNA], Δh10 is positive and Δh6 is negative: Δh10 = 4.2 (± 0.3) kcal/mol and Δh6 = −1.6 (± 0.3) kcal/mol. Since the binding constant ratio, k10/k6 = 3.1, exceeds the inverse of the corresponding initial ratio of the number of potential binding sites ((s10/s6)−1= 1.7), the 10 bp mode dominates at low [HU]/[DNA]. The small magnitudes of k6 and h6 at this salt concentration are consistent with the inability to detect binding of HU to 8 bp DNA in a direct (noncompetitive) titration (Fig. 1b). The binding cooperativity for the 6 bp mode is positive (ω6 = 24 ± 11); this moderately large cooperativity enhances the replacement of the 10 bp mode by the 6 bp mode on 15 bp DNA as [HU]/[DNA] increases. The cooperative interaction between two adjacent HU bound in the 6 bp mode has a small, apparently exothermic enthalpy (Δhω6 = − 0.3 (± 1.0) kcal/mol). The large uncertainties in ω6 and Δhω6 result from the scatter in the data in the region of the isotherm at high [HU]/[DNA] that best characterizes ω6 and Δhω6. Table 2 reports the microscopic thermodynamic quantities for all of the observed binding modes.
Table 2.
Microscopic thermodynamic quantities from interpretation of macroscopic binding constants and enthalpies (Table 1) in terms of the binding mode transitions between different binding modes (on 15 bp DNA: 10 and 6 bp mode, on 34 bp DNA: 34, 10, and 6 bp mode)
| k34 (M−1) | 2.1 (± 0.4) × 106 |
| k10(M−1) | 1.1 (± 0.2) × 105 |
| k6 (M−1) | 3.5 (± 1.4) × 104 |
| Δh34 (kcal/mol) | 7.7 (± 0.6) |
| Δh10 (kcal/mol) | 4.2 (± 0.3) |
| Δh6 (kcal/mol) | −1.6 (± 0.3) |
| ω6 | 24 (± 11) |
| Δhω6 (kcal/mol) | −0.3 (± 1.0) |
Using the results above, the average number of HU bound to 15 bp DNA in the 10 bp mode, in the 6 bp mode, and bound cooperatively in the 6 bp mode were calculated as a function of [HU]/[DNA] for the titrations in Fig. 5a. These distributions are plotted in Fig. 5c. The observed heat signal was then dissected into the contribution from each component in Fig. 5d by differentiating the calculated equilibrium population distribution and multiplying the corresponding enthalpies. In the noncompetitive 15 bp DNA isotherm (in the absence of 8 bp DNA), HU binds primarily in the 10 bp mode up to an occupancy of ~ 0.4 HU per DNA molecule (Fig. 5c, [HU]/[DNA] ~ 1 for the concentration of DNA investigated), giving rise to the endothermic phase of the isotherm (Fig. 5d). As [HU]/[DNA] further increases, a transition from the 10 bp to 6 bp mode occurs (Fig. 5c), and the observed binding becomes exothermic (Fig. 5d). As the population of the 6 bp mode increases, the cooperativity between bound HU dimers becomes increasingly significant; for the population of 15 bp complexes with two HU dimers bound, ~ 95 % have HU bound adjacently. In the competition experiment, binding of HU to 8 bp DNA in the 6 bp mode makes the isotherm more exothermic, reducing both the apparent endothermicity and the binding constant relative to the isotherm for 15 bp DNA alone.
Analysis of HU Binding to an Intact 34 bp DNA: Demonstration of a Large Site Size (~34 bp) Binding Mode
The binding isotherms for 15 and 34 bp DNA are qualitatively similar; both exhibit a transition from an endothermic to an exothermic phase with increasing [HU]/[DNA]. However, the quantitative analysis of the 34 bp DNA isotherm (also 38 and 160 bp) given below requires the introduction of a large site size mode (i.e. 34 bp mode) in addition to the two small site size modes (10 and 6 bp) observed in the binding isotherms of 8 and 15 bp DNA. Using a similar model-independent macroscopic analysis to that described for the 15 bp DNA isotherm, we find that a minimum of three macroscopic binding constants and three enthalpies are required to describe the isotherm for the 34 bp DNA (Fig. 6a), indicating that at least three HU dimers can bind per 34 bp DNA under these conditions.
Figure 6.
Analysis of 34 bp DNA binding isotherm at 15 °C and 0.15 M Na+. (A) Solid curve through representative data for the 34 bp DNA binding isotherm (from Fig. 1B) represents the fit to Eq. 7, 9, and 11 and yields the model independent macroscopic binding constants and enthalpies in Table 1. (B) Population distribution of 34 bp mode (thick), 10 bp mode (thin), and 6 bp mode (dot) on 34 bp DNA as a function of [HU]/[DNA] showing the transitions between the three modes (see Methods and Materials for details of simulation).
The fitted values for the macroscopic binding constants are K1,34bp = 5.9 (± 0.7) × 106 M−1, K2,34bp = 1.0 (± 0.4) × 1013 M−2 and K3,34bp = 3.5 (± 1.3) × 1018 M−3 (Table 1). The corresponding binding enthalpies are ΔH1,34bp = 4.4 (± 0.3) kcal/mol, ΔH2,34bp = 7.5 (± 1.0) kcal/mol and ΔH3,34bp = − 2.2 (± 0.6) kcal/mol. If HU bound to 34 bp DNA using only the 6 and 10 bp modes, then K1,34bp would be interpreted as 25k10 + 29k6 which is equal to 3.8 × 106 M−1. This predicted K1,34bp, while greatly exceeding K1,15bp (9.9 × 105 M−1), is significantly less than the experimentally-observed value (K1,34bp = 5.9 × 106 M−1). A similar discrepancy is found for ΔH1 if only the 10 and 6 bp modes are considered; the predicted ΔH1,34bp is 2.5 kcal/mol while the observed value is ΔH1,34bp = 4.4 kcal/mol. The simplest explanation for these differences is that another binding mode with a larger binding constant, site size and enthalpy, absent on 8 to 15 bp DNA oligomers, is occupied at low [HU]/[DNA] on 34 bp DNA. Based on previous observations of nucleosome-like structures at [DNA bp]/[HU] ~ 3032; 33 and the formation of the specific 34 bp H’ DNA complex with the HU homolog IHF,21; 25; 26 we propose that HU exhibits a nonspecific 34 bp binding mode on large duplex DNA fragments. If binding modes with 34, 10, and 6 bp site sizes are populated in the 34 bp DNA oligomer titrations, then the binding constant and enthalpy for the 34 bp mode are: k34 = K1 − 25k10 – 29k6 = 2.1 (± 0.4) × 106 M−1 and Δh34 = (ΔH1K1 − 25k10Δh10 − 29k6Δh6) / k34 = 7.7 (± 0.6) kcal/mol (Table 2), respectively.
In principle, interpretations of K2,34bp and K3,34bp provide quantitative information about the cooperativities of various modes (10 bp mode and inter-mode) on 34 bp DNA. However, interpretations of K2,34bp and K3,34bp are much more complicated than the interpretation of K1 because of the greater number of microscopic thermodynamic quantities involved. K2, for example, is a sum of statistical weights for all possible configurations of the DNA lattice with two HU bound, including configurations from two HU bound in the 10 bp mode with or without cooperativity (ω10), two HU bound in the 6 bp mode with or without cooperativity (ω6) and two HU bound in the 10 and 6 mode with or without cooperativity (ω10/6):
| (6) |
(The 34 bp mode is not included in any configuration for DNA with two bound HU.) In addition to the large number of parameters involved, the enumeration of each configuration described above is complicated, especially for K3. Semi-quantitative information about the cooperativity of the 10 bp mode and of the 6 and 10 bp inter-mode is deduced by comparing the observed K2,34bp with the predicted K2,34bp based on the previously determined thermodynamic quantities (k10, k6, and ω6). Numerically, K2 calculated from Eq. 5 (K2,calc) is much smaller than the observed value (K2,calc = 3.8 × 1012 M−2 vs. K2,obs = 1.0 × 1013 M−2), indicating that cooperativity of the 10 bp mode and/or of the inter-mode significantly contribute to the overall binding isotherm. Although the data set here does not allow a unique determination of the cooperativity of each mode, using the simplistic assumption that the cooperativity determined above for the 6 bp mode (ω6 = 24) also describes the 10 bp and inter-mode cooperativities (ω10 = ω10/6 = 24), we find that K2,calc = 1.1 × 1013 M−2. This value agrees well with K2,obs (1.0 (± 0.4) × 1013 M−2).
The population distribution of all three modes on 34 bp DNA was calculated from the thermodynamic quantities obtained above (Table 2, ω10 = ω10/6 = 24) using a modified sequence generating function (SGF) method. Here the single-site binding of HU to 34 bp DNA (in the 34 bp mode) is incorporated into the SGF describing multiple-site binding of HU (in the 10 and 6 bp modes) to 34 bp DNA (Fig. 6b; see Methods for the derivation of the modified SGF). However, due to the ambiguity in the determination of the 10 bp and inter-mode cooperativities as described above, Fig. 6b neglects any contribution from mode-specific cooperativity effects, which would be most significant at high concentrations of HU. This analysis predicts that initial occupancy ([HU]/[DNA] < 1) of 34 bp DNA utilizes the 34 and 10 bp modes, replaced at higher [HU]/[DNA] by the 10 and 6 bp modes.
Additional Evidence for the 34 bp Binding Mode from Analysis of the Initial Heat Signal for HU Binding to 160 bp DNA
Fig. 1b indicates that the initial endothermic heat signal is much larger for the binding of HU to 160 bp DNA (~7.3 kcal/mol of HU injected) than to 34 bp DNA (~4.0 kcal/mol of HU injected). Is the existence of a 34 bp binding mode consistent with this observation or are larger site size modes involved? By analogy with the specific binding of IHF, we propose that 34 bp is the maximum site size that an HU dimer can occupy. The observed differences in the initial binding heat must then reflect the combined effects of DNA length-dependent statistical factors (see Eq. 1), intrinsic binding constants, and site sizes on the partitioning of HU between different binding modes. In the initial part of the titration, if all of the injected HU binds DNA and if no more than one HU is bound per DNA molecule, then the initial population ratio of a 1:1 complex bound in the 34 bp mode to that in the 10 bp mode for N bp DNA is This relationship, combined with the values of k34 and k10, predicts that dramatically increases from 0.8 for the population of 1:1 complexes with 34 bp DNA to 16.1 for the population of 1:1 complexes with 160 bp DNA. This analysis requires that all of the initial injection of HU is bound to DNA. To test this, we examined the effect of DNA concentration on the initial heat of binding HU. Over the ranges that were feasible to study (2 to 6 µM 34 bp DNA and 1 to 3 µM 160 bp DNA in the reaction cell), the initial heats of binding were independent of DNA concentration ([DNA] > 20(K1,obs)−1), demonstrating that all of the initially injected HU is bound when titrating 34 and 160 bp DNA (SFig. 1).
The fractional population of 1:1 complexes in each binding mode in the initial part of the titration was calculated from fi = (N – ni + 1) ki / [∑i=6,10,34 (N – ni + 1) ki] for each DNA length studied (Table 3). As expected, almost all HU (~92 %) bound in a 1:1 complex on 160 bp DNA is in the 34 bp mode, compared to only ~36 % on 34 bp DNA. The fractional population of 1:1 complexes in the 6 bp mode is small on the 160 and 34 bp DNA, but significant on 15 bp DNA. Calculation of the initial binding heat (Q = ΔH34f34 + ΔH10f10 + ΔH6f6) from these fractional values yields results that agree with experimental values of Qobs as a function of DNA length (Table 3 and inset of Fig. 1b). We conclude that the large difference in site size (and the corresponding difference in statistical factors) and in binding enthalpy between the 34 bp and the two small site size modes is the origin of the difference in the observed initial binding heats (see below for additional discussion).
Table 3.
Analysis of the dependence of initial heat of binding on DNA length in terms of the binding mode transitions. Qobs are the experimentally observed initial heat signals for 4 lengths of DNA.
| 15bp DNA | 34bp DNA | 38bp DNA | 50bp DNA | 160bp DNA | |
|---|---|---|---|---|---|
| f34 | - | 0.36 | 0.72 | 0.86 | 0.92 |
| f10 | 0.65 | 0.46 | 0.21 | 0.10 | 0.06 |
| f6 | 0.35 | 0.18 | 0.07 | 0.04 | 0.02 |
| Qcalc (kcal/mol) | 2.2 | 4.4 | 6.3 | 7.0 | 7.3 |
| Qobs (kcal/mol) | 1.9 (± 0.2) | 4.2 (± 0.3) | 6.5 (± 0.2) | n. d. | 7.3 (± 0.4) |
In principle, an independent fit of the 160 bp isotherm should not only yield the same values of the microscopic thermodynamic quantities (K, ΔH,ω) for the three binding modes as deduced from the 15 bp and 34 bp isotherms, but also resolve whether the 34 bp mode exhibits any cooperativity. In practice this fitting problem involves at least 18 microscopic quantities and thus is not possible. As an alternative approach, we investigated how well the 160 bp isotherm could be described by considering only the 34 and 10 bp modes (K and ΔH in Table 2; Fig. 7). The 34 bp mode was first assumed to be noncooperative (ω34 = 1) while varying the cooperativity of the 10 bp mode (ω10) from 1 to 100. The initial phase of the isotherm ([HU] / [DNA] < 3) is well described by this simplified model regardless of the value of cooperativity of the 10 bp mode chosen (Fig. 7a) whereas the introduction of cooperativity of the 34 bp mode (ω34 = 20 ~ 100) significantly displaces the simulated isotherm from the observed one (Fig. 7b).
Figure 7.
Simulation of 160 bp DNA binding isotherm using sequence generating function method (see Methods and Materials) with k34 = 2.1 × 106 M−1, k10 = 1.1 × 105 M−1, Δh34 = 7.7 kcal/mol, and Δh10 = 4.2 kcal/mol. Experimental binding isotherms at 0.45 µM 160 bp DNA (open triangle) and 1 µM (closed triangle) are also plotted. (A) No cooperativity for the 34 bp mode (ω34 = 1) and cooperativities of 1, 20, 50, and 100 for the 10 bp mode (ω10). (B) Cooperativities of 1, 20, 50, and 100 for the 34 bp mode with ω10 = 20 for the 10 bp mode. Population distribution of the 34 (blue) and 10 bp (magenta) modes on 160 bp DNA for each case is plotted in the inset.
These results suggest that the 34 bp mode is not highly cooperative and that the occupancy of the 6 bp mode in the initial phase is indeed insignificant. The population distributions (insets) also show that the 34 bp mode is much more significant on 160 bp DNA than on 34 bp DNA (Fig. 6b) in the initial phases of the isotherms (i.e. [HU]/[DNA]<1 for 34 bp DNA and [HU]/[DNA]<4 for 160 bp DNA). However, as [HU]/[DNA] increases, the theoretical and observed isotherms quickly diverge, suggesting that binding in the 6 bp mode contributes and/or cooperative effects (and their enthalpies) between modes exist at higher concentrations of HU.
Testing the Proposed Model: Binding of HU to 38 bp DNA Is More Like Binding to 160 bp DNA than to 34 bp DNA
The statistical nature of the distribution of binding modes as a function of DNA length predicts that increasing the length of the 34 bp DNA by only 4 bp will increase the fraction of 1:1 HU/DNA complexes bound in the 34 bp binding mode by almost two-fold (from 36% to 72%, Table 3) while decreasing the fraction in the 10 bp mode by a corresponding factor (46 % to 21%, Table 3). This redistribution occurs because the increase in N from 34 to 38 bp adds four to the statistical factors (N − ni + 1) for all binding modes, resulting in a 5-fold increase (from 1 to 5) in this factor for the 34 bp mode but only 1.2- and 1.1-fold increases for the 10 and 6 bp modes. This analysis also predicts that the magnitude of the initial heat signal should plateau at ~ 50 bp DNA, far before 160 bp DNA. We therefore tested the counter-intuitive but unambiguous prediction that the initial binding behavior of HU on a 38 bp DNA should be more similar to the 160 bp DNA than to the 34 bp DNA. Fig. 1b shows that the ITC data for the 38 bp DNA are clearly distinct from the 34 bp DNA data, falling strikingly close to the 160 bp DNA data as predicted. The value of the initial heat signal (6.5 (± 0.2) kcal/mol; Fig. 1b) is within experimental uncertainty of the calculated value (Table 3). These results further confirm that a 34 bp binding site size provides the best fit to the data set obtained in this work. They also rule out any hypothesis that would attribute the large difference in the initial heat signal between 34 and 160 bp DNA to possible effects of nicks or sequence differences between the mono-nucleosomal 160 bp DNA and the shorter synthetic DNA oligomers.
FRET Studies: Estimation of DNA Bending Angle Induced by HU Bound in the 34 bp Mode
The site size of the 34 bp binding mode implies a large HU/DNA interface. Given the relatively small size of HU and its similarity to IHF, this binding mode likely involves DNA bending, as seen in the co-crystal structure of the specific 34 bp H’-DNA/E.coli IHF complex and of 17 bp mismatched and gapped DNA/Anabena HU complexes.21; 22; 23 Because tight wrapping of the H’-DNA site on IHF brings the DNA ends into close proximity, bending by IHF is readily detected in solution by fluorescence energy transfer experiments.25; 49; 50; 51 To examine the extent of DNA bending by HU in the 34 bp mode, we end-labeled 34 bp DNA with donor (FAM) and acceptor (TAMRA) probes and monitored the resulting transfer efficiency from the reduction in the donor fluorescence emission intensity in the presence of HU (Fig. 8a). Fig. 8b plots the observed transfer efficiency (TE) as a function of [HU]/[DNA]. Although the observed TE is small, it is highly reproducible and exhibits non-monotonic (biphasic) behavior. At low [HU]/[DNA], TE increases as [HU] increases, reaching a broad maximum of ~ 0.03 at [HU]/[DNA] of 1 ~ 2. At higher [HU]/[DNA], TE decreases with increasing [HU].
The biphasic behavior observed in the FRET-determined binding isotherm was analyzed using the macroscopic binding constants (K1, K2, and K3, Table 1) obtained from the ITC experiments and assuming that only the 34 bp mode involves sufficient DNA bending to allow energy transfer (i.e. TE = 0 for free 34 bp and for DNA with more than one bound HU). In this case, the observed TE is equal to (TE34k34 / K1) f1, where f1 represents the fractional population of DNA with one HU bound (in any mode). Global fitting of all FRET data yields an intrinsic transfer efficiency for the 34 bp mode (TE34) of 0.16 (± 0.06). The fraction of HU bound in each binding mode is also calculated in Fig. 6 using the same method described in previous sections. Based on our model, the observed biphasic TE behavior is well explained by initial occupancy of the DNA in the 34 and 10 bp mode. As [HU]/[DNA] increases, the 34 bp mode is replaced by the 10 and 6 bp modes, eliminating any FRET. The transitions between the binding modes as a function of [HU]/[DNA] are broader than the transitions observed in the ITC isotherm (compare population distributions in Fig. 6b and 8b) because the concentration of DNA used in the FRET experiments (120 nM) is much lower than that used in the ITC experiments (2.5 µM). The intrinsic TE34 of 0.16 (± 0.06) corresponds to a end-to-end distance d = 66 (± 5) Å for 34 bp DNA with HU bound in the 34 bp mode (using a Foster distance Ro of 50 Å, obtained by assuming rapid randomization of the relative orientation of the donor and acceptor so that the orientation factor κ2 = 2/3).50; 52; 53 A DNA bending angle of 143 (± 6)° was calculated from this end-to-end distance as described in Methods and Materials.
Discussion
E.coli HUαβ Binds Intact Linear Duplex DNA with at least 3 Different Binding Modes at Moderate Salt Concentration and Temperature ([Na+] = 0.15 M and 15 °C)
Taken together, studies of HU-DNA interactions over the past three decades provide evidence that HU has at least three different nonspecific binding modes: a large (~ 34 bp) mode observed on nicked or gapped DNA oligomers and on supercoiled plasmid DNA; and two smaller modes (6 and 10 bp) observed on short DNA oligomers. The ITC data presented here demonstrate that these modes coexist on the same DNA molecule. Appreciable differences between the three modes in site size (34, 10, and 6 bp), binding constant (K34 = 2.1 × 106 M−1, K10 = 1.1 × 105 M−1, and K6 = 3.5 × 104 M−1 at 0.15 M Na+, 15 °C and, pH 7.5), and cooperativity (ω34 ~ 1 and ω10 ~ ω6 = 24) underlie the complexity of behavior observed in the ITC isotherms. In these titrations, HU switches between modes both as functions of both [HU]/[DNA] and DNA length. The ITC data, together with the direct demonstration by FRET that the 34 bp mode bends DNA (whereas the 10 and 6 bp modes do not), explain how HU can act to either condense or extend DNA depending on HU concentration as observed in single molecule studies. Our work predicts that transitions between binding modes may occur in vivo in response to growth phase dependent changes in mole ratio of HU to DNA.
E.coli HUαβ Binds and Bends DNA, Occluding 34 bp at Low [HU]/[DNA]
The initial heat of binding as a function of DNA length detected by ITC, together with FRET measurements, provides direct thermodynamic and structural evidence for a highly bent DNA binding mode with a site size of ~ 34 bp and a DNA bending angle of ~143° in the interaction between E.coli HUαβ nd “intact” linear duplex DNA in solution. Because the 34 bp mode has a larger binding constant and site size than the 10 and 6 bp modes, the 34 bp mode is most significant at low [HU]/[DNA] (for concentrations where on average there is less than one HU bound to 34 or 38 bp DNA, and less than four HU bound to 160 bp DNA). Moreover, in comparisons at a given low extent of binding, the statistical factor (N − n + 1) predicts an increase in the population of the 34 bp mode and a decrease in the population of the small site size modes with increasing DNA length above 34 bp since the ratio of statistical factors between two different modes becomes more insignificant on longer DNA. (i.e. for infinitely long DNA, since (N – nx + 1) / (N – ny + 1) ~ 1.) The observed increase in the initial heat of binding as well as the observation of a more pronounced inflection point corresponding to a site size of ~ 34 bp with increasing DNA length is consistent with this prediction.
Considering the dimensions of HU and DNA, the site size of 34 bp necessarily requires the bending of DNA toward HU as detected by FRET. The DNA bending angle for the 34 bp mode obtained from the FRET measurement (143 ± 6°) is consistent with the bend angles observed in co-crystal structures (105° – 140°, depending on crystal form) of Anabena HU and duplex DNA molecules with mismatched base pairs and extra-helical bases (T). In these structures, like the IHF-H’ complex21, two invariant proline residues on HU insert between base pairs, stabilizing a sharp DNA bend.22
Both the ITC and FRET results are consistent with early studies of supercoiling induced by E.coli HU on plasmid DNA which indicated the existence of a large site size binding mode.33 Supercoiling assays at low salt concentrations (25 ~ 50 mM NaCl) showed a maximum in the effect of HU on superhelical density (ΔLk) at [DNA]/[HU] ~ 30 bp/HU. A subsequent nuclease digestion study of HU-DNA complex (at the same DNA/HU mole ratio) provided additional evidence for a large site size binding mode which bent DNA.32 A periodicity of nicking of 8.5 base pairs was observed for both strands of DNA, interpreted as a reduction in DNA helical pitch from 10.5 to 8.5 bp per helical turn of DNA induced by HU, proposed to be compensated by ~ 180° of negative writhe introduced by wrapping of DNA around one HU dimer to generate a net negative change in linking number.32 Although no direct information regarding binding site size and binding constant was obtained in the supercoiling studies, the 34 bp mode observed in our calorimetric study is likely responsible for the observed supercoiling of DNA caused by significant DNA bending at low [HU]/[DNA]. Similarly, the observed decrease in end-to-end distance of linearized plasmid flexible coil DNA with increasing [HU]/[DNA] at low [HU]/[DNA] and constant force in recent single molecule studies37; 38 and the bending of DNA by HU detected by AFM38; 39 likely result from the 34 bp mode. Extensive binding of HU to a DNA flexible coil in the DNA-bending 34 bp mode will reduce the through-space end-end distance, compact the flexible coil and reduce the apparent persistence length, as proposed.37; 38; 39
Given the evidence for a large site size binding mode on plasmid length DNA and the significance of this mode expected in DNA compaction and modulation of transcription activation or repression in vivo,1; 54; 55; 56; 57; 58 it is initially puzzling that this mode was not detected in previous fluorescence and EMSA with intact DNA oligomers in the size range 30 ~ 42 bp.27; 28; 29 However, for this range of DNA lengths, the 34 bp mode is only significantly populated over a very narrow, low range of [HU]/[DNA] due to competition from the 10 and 6 bp modes (see the population distribution analysis in Fig. 6B). Because each binding mode appears to have a unique binding enthalpy, ITC allows the thermodynamically “transient” population of the 34 bp mode to be observed (see below for further discussion).
Structural and Thermodynamic Properties of the HU 34 bp Binding Mode
It is noteworthy that the 34 bp nonspecific mode of HU and the specific binding mode of IHF with 34 bp H’ DNA exhibit different DNA bending angles as deduced from FRET measurements in solution (143 ± 6° and 162 ± 4°, respectively) or from the cocrystal structures (105° – 140° and 163°). [The above DNA bending angle for IHF has been obtained from FRET experiments with exactly the same DNA construct and method of analysis as used in this study (Vander Meulen et al., in preparation).] The DNA bending angle of 143° for HU must be large enough to sterically occlude 34 bp from any additional binding of HU. Why isn’t the angle as large as IHF, which also occludes 34 bp? For IHF, binding the H’ site involves an extensive interaction with residues on the beta arms and the alpha helical core, resulting in a tightly wrapped DNA molecule. These wrapping interactions presumably make a net favorable contribution (together with specific interactions in consensus sequence) to the binding constant, which is ~50 fold larger for IHF than for HU at 0.15 M Na+ (2.1 × 106 M−1 for HU vs. 1.2 × 108 M−1 for IHF25). We hypothesize that unlike IHF, E. coli HU does not position a sufficient number of arginines and lysines on its core to drive additional DNA bending and wrapping. For example, Arg46 in the beta subunit of IHF which interacts with the conserved TTR (R = A or G) in the 3’ end of the H’ site1; 21; 22; 23; 25 is replaced by valine both HUαand HUβ Similarly, at the 5’ end of the H’ site, the symmetry-related Lys45 in IHF which contacts the H’ phosphate backbone corresponds to a glutamine and alanine in HUαand HUβ, respectively.
Binding of HU in the 34 bp mode is endothermic (+7.7 kcal/mol) and entropically driven (56 cal/K/mol) at 15 °C. In the temperature range 5 ~ 25 °C, other nonspecific minor groove DNA binding proteins that bend DNA (HMG-D74, HMG-D100, and Sac7d) also exhibit endothermic binding enthalpies and favorable (positive) binding entropies. These favorable binding entropies have been attributed to the release of counterions and water upon protein binding.59; 60; 61 Endothermic binding enthalpies and high characteristic temperatures TH (where ΔH°=0) for DNA bending proteins are predicted based on the intrinsic enthalpic penalty of base pair unstacking and bending of DNA helical axis.59; 62; 63; 64 Release of ordered water molecules from the DNA minor groove has also been proposed to contribute to endothermic binding enthalpies of minor groove binding proteins.61
However, the 34 bp mode of HU, which has a larger DNA bending angle and binding site size (e.g. larger amount of surface area buried upon binding) than the above proteins, does not have a correspondingly large enthalpic penalty of binding at 15°C (HMG-D74: 18 kcal/mol, 94° bend angle65; HMG-D100: 14 kcal/mol, 120° bend angle65; Sac7d: 11 kcal/mol, 70° bend angle60). Similarly, the binding enthalpy for the specific binding of IHF to the H’ site is estimated to be ~ −10 kcal/mol at 15 °C and is −20 kcal/mol at 20 °C25; a value far less positive (even exothermic!) than other minor groove, bending proteins that bind DNA specifically (HMG-Sox5: 3 kcal/mol, 100° bend angle;65; 66 Lef-86: 4 kcal/mol, 117° bend angle;61 Lef-79: 5 kcal/mol, 88° bend angle61). Clearly differences in the amount and type of interface formed/disrupted in DNA binding and bending (e.g. salt bridge disruption26; 67) may be one of many factors contributing to differences in the DNA binding enthalpy of HU, IHF and other minor groove binding proteins. Other coupled processes such as folding of theβ– arms of HU/IHF and coupled protonation should be also considered.
Increase in HU/DNA Mole Ratio Drives Binding Mode Transitions from 34 to 10 to 6 bp: Comparison with Other Nonspecific Protein – DNA Interactions
Statistical thermodynamic analysis of the non-monotonic behavior of the ITC – determined binding isotherms of 8 bp, 15 bp, and 34 bp DNA demonstrates that HU transitions from a 34 to 10 to 6 bp mode with increasing [HU]/[DNA] (10 to 6 bp mode on 15 bp DNA). Smaller site size or larger maximum number of HU bound on DNA molecules (≡ g) results in dominance of this mode at higher [HU]/[DNA] because the statistical weight (~ g PN(g) (K[HU])g) of each binding mode varies with [HU]free g regardless of binding constant, cooperativity, or statistical factor (i.e. Rx/y ~ [HU]free gx−gy at [HU]free -> ∞). Cooperativities of the 10 and 6 bp mode enhance the replacement of the 34 bp mode at high HU concentrations. The decrease in TE at high [HU]/[DNA] provides compelling evidence that these small site size modes do not bend DNA. The binding mode transitions as a function of [HU]/[DNA] proposed in our study are consistent with the biphasic features (transition from DNA compaction to extension with increasing HU concentration) observed in single molecule studies.37; 38; 39 The extension of DNA at high concentrations of HU in those studies likely reflects the effects of the 10 and 6 bp modes on DNA conformation. These small site size modes could increase the end-to-end distance of a flexible DNA coil over its “free solution” value as observed in single molecule experiments37; 38 in two possible ways. Binding of HU could locally stiffen the DNA helix and/or thicken it (increase the DNA diameter and therefore its excluded volume), thereby increasing the radius of gyration of the chain and its through-space end-to-end distance. Similar biphasic behavior was observed in HU – induced DNA supercoiling studies, where superhelical density of plasmid DNA decreased as [HU]/[DNA] increased after a maximum superhelical density at ~ 30 bp / HU.32; 33
Transitions between different binding modes have been observed for other nonspecific protein – DNA interactions. E.coli SSB exhibits at least four distinct binding modes (33, 40–42, 55 and 65 nucleotides of ss DNA) depending on solution conditions and DNA lattice, each with distinct binding constants and cooperativities. 40; 41; 42; 68; 69; 70; 71 At low to moderate [NaCl] ([NaCl] < 0.2 M), SSB binds ss DNA using large (65 and 55 nucleotides) binding site size modes at low binding density that converts into smaller binding site size modes at high binding density.41; 42; 71 Interconversions between modes also occur as a function of salt concentration, type, pH, and temperature. For HU, the binding mode transitions seem to be more sensitive to [HU]/[DNA] (i.e. binding density) than to temperature or salt concentration (JK, in preparation). Human DNA polymerase β binds to ss DNA using a 16 base mode at low [protein]/[DNA] and a 5 base mode at high [protein]/[DNA].45 These binding modes are thought to be used to fill single stranded gaps of different lengths. For IHF, as the mole ratio of IHF to 34 bp H’ DNA is reduced, small site size nonspecific binding modes convert to the 34 bp specific binding mode26 [Our preliminary studies of nonspecific binding of IHF to different lengths of DNA provide evidence for similar nonspecific binding mode transitions of IHF to that of HU]. We are currently investigating the thermodynamic and structural properties of the nonspecific binding modes of IHF.
Transitions between binding modes as a function of [HU]/[DNA] are revealed by ITC because each binding mode has a distinct magnitude and in some cases a unique sign of its binding enthalpy. The incremental or differential nature of the ITC isotherm, where each addition of HU changes the heat signal, enhances the ability of this method to detect [HU]/[DNA]-dependent transitions. Transitions between modes as a function of [HU]/[DNA] or DNA length may have escaped detection in previous spectroscopic studies29; 30 and EMSA studies27; 28; 29 due to the insensitivity of the cumulative signal to the [HU]/[DNA]-dependent behavior of this system. Similar spectroscopic properties of the different binding modes may have also prevented identifying the different binding modes and/or detecting switches in mode. Nevertheless, the binding site sizes measured at high [HU]/[DNA] in those studies (6 ~ 10 bp) are qualitatively consistent with our calorimetric results. Quantitative comparisons of binding constants and cooperativities between results here and previous studies are not straightforward due to the different experimental conditions (e.g. salt concentration and temperature) and the different models used in each analysis.
Structural and thermodynamic properties of the HU 10 and 6 bp binding modes
The 10 bp and 6 bp modes exhibit comparable standard binding free energies at the conditions investigated here ( and ); both are less favorable than the 34 bp mode ( ). However, these two small site size modes exhibit very different thermodynamic origins of their ΔG° values. The 10 bp mode is entropically driven ( ) and enthalpically unfavorable ( ) whereas the 6 bp mode is favorable both enthalpically () and entropically ( ) at 15 °C (c.f. ). Counterion release likely makes a favorable contribution to the binding entropy of all modes at low salt concentrations72; 73; to test this hypothesis, the [salt]-dependences of the nonspecific modes are being determined.
Further understanding of the different thermodynamic behaviors of the two modes (and the 34 bp mode) requires structural information not available yet. The small site size modes may represent part of the 34 bp mode interface, possibly utilizing one of two β arms and half turn of DNA helix in the 6 bp mode, and two β arms and one helical turn of minor groove of DNA in the 10 bp mode as proposed previously.23; 27; 29 Alternatively, they may involve interactions between the folded regions of both β arms (the “saddle”) and the narrow minor groove (6 bp mode) or the wider major groove (10 bp mode). The moderately large cooperativities for the 10 and 6 bp modes (ω~ 24) indicate that binding of HU to a site adjacent to an already bound HU is more favorable than to an isolated site. The origin of cooperativity is primarily entropic (TΔS° ~ 1.5 kcal/mol, ΔS° ~ 5.3 eu) at 15 °C, possibly reflecting a protein-protein interaction (hydrophobic or electrostatic) and/or a DNA conformational change that facilitates the subsequent binding of another HU dimer.46; 47; 74
Other alternative models cannot describe the complexities observed in ITC binding isotherms
A minimum of three different binding modes (34, 10, and 6 bp) and cooperativity of the two small site size modes are required to describe all of the features observed in the ITC binding isotherms investigated here (8 – 160 bp DNA, 0.15 M Na+, 15 °C). Below we explore whether alternative models (e.g. fewer binding modes or other coupled processes) could explain the ITC data, and whether the large site size mode could be appreciably smaller than 34 bp.
i) Are two small site size binding modes needed to fit the 8 and 15 bp DNA isotherms?
The [HU]/[DNA]-dependent biphasic feature (endo- to exothermic heat) observed for the titration of 15 bp DNA could be modeled as a single cooperative binding model with an endothermic binding enthalpy (e.g. for 6 bp mode) and exothermic cooperativity enthalpy for binding two adjacent HU. In this model, one HU binds DNA with an endothermic heat signal at low [HU]/[DNA], whereas an exothermic cooperativity enthalpy significantly contributes to the isotherm at high [HU]/[DNA]. This alternative model provides a unique interpretation of macroscopic thermodynamic quantities obtained from fitting the 15 bp noncompetitive DNA binding isotherm; K1,15bp = 10 k6 (assuming a site size of 6 bp), K2,15bp = (6 + 4ω6) k6 2, ΔH1,15bp = Δh6, and ΔH2,15bp = 2Δh6 + (4ω6 Δhω6) / (6 + 4ω6). The corresponding model-dependent microscopic binding parameters are 9.6 × 104 M−1, 2.3 kcal / mol, 0.6 and - 31.0 kcal / mol for k6, Δh6,ω6 and Δhω6, respectively.
However, the 8/15 bp competition isotherm rules this alternative model out (Fig. 5a). In the competition experiment, binding of HU to 8 bp DNA decreases the concentration of two HU bound adjacently in the 6 bp mode on 15 bp DNA (i.e. the concentration of contact point). Because the cooperativity enthalpy of the single site model is highly exothermic, any decrease in the number of HU bound cooperatively predicts a net (large) endothermic change. Consequently, the magnitude of the simulated competition isotherm (dashed line; Fig. 5a) is highly endothermic for the entire titration, in sharp contrast to what is experimentally observed.
ii) Could a conformational change in HU explain some of the complexities of the 15 and 34 bp DNA isotherms?
In principle, the [HU]/[DNA]-dependent behavior of the 15 and 34 bp binding isotherms could arise from coupling DNA binding (in a single mode) to a conformational change in E. coli HU.24 However, no detectable transition (αβ → I or I → α + β) is observed in preliminary temperature scans of 50 µM HU (same buffer used in the ITC experiments) by either circular dichroism or differential scanning calorimetry until 25 °C (Tm = 37 °C for αβ → I) (data not shown).
iii) Could the large site size mode be significantly smaller than 34 bp?
The macroscopic binding constant K1,34bp in the analysis of the isotherm of 34 bp DNA could be interpreted by choosing a smaller site size n (e.g. 15 < n < 34) for the largest site size mode. In this case, fits to K1,34bp for site size n < 34 decrease the intrinsic binding constant (ki) due to an increase in the statistical factor (unity for n = 34 bp on 34 bp DNA, see Eq. 1). However, the binding enthalpy is constant regardless of the choice of site size (Table 4). The inflection point of the initial phase in the isotherm of 160 bp DNA corresponds approximately to the stoichiometry of the large site size mode. The inflection point (Fig. 2) is between ~ 5 and ~ 8 [HU]/[DNA], indicating a site size of 20 to 34 bp.
Table 4.
The dependence of the initial binding heat of 38/160bp DNA on the choice of the binding site size of a large site size mode
| 20 bp | 25 bp | 30 bp | 34 bp | |
|---|---|---|---|---|
| ki (M−1) | 1.4 × 105 | 2.1 × 105 | 4.3 × 105 | 2.1 × 106 |
| (i = 20, 25, 30 or 34) | ||||
| ΔHi (kcal/mol) | 7.7 | 7.7 | 7.7 | 7.7 |
| fi,160bp / fi,38bp | 0.48 / 0.39 | 0.57 / 0.41 | 0.72 / 0.48 | 0.92 / 0.72 |
| f10,160bp / f10,38bp | 0.39 / 0.45 | 0.32 / 0.43 | 0.21 / 0.38 | 0.06 / 0.21 |
| f6,160bp / f6,38bp | 0.13 / 0.16 | 0.11 / 0.16 | 0.07 / 0.14 | 0.02 / 0.07 |
| Qcalc,160bp / Qcalc,38bp | 5.1 / 4.6 | 5.6 / 4.7 | 6.3 / 5.0 | 7.3 / 6.3 |
| Qobs,160bp / Qobs,38bp | 7.3 / 6.5 | 7.3 / 6.5 | 7.3 / 6.5 | 7.3 / 6.5 |
In Table 4, several alternative choices for the large site size mode are presented. For any choice of n smaller than 34 bp, the predicted initial heat signal for both 38 and 160 bp DNA decreases relative to the experimentally observed heat. This discrepancy results from a statistical decrease in the fractional population of the large site size mode relative to the smaller modes on 38 or 160 bp when n < 34 (Table 4 and SFig. 2). (The dependence of fractional population of the large site size mode (fi = (N – ni + 1)ki / [∑i=6,10,34 (N – ni + 1)ki]) on DNA length is ∂fi/∂N = [ki∑j=6,10 kj(ni – nj)] / [∑all modes (N – ni + 1) ki]2.) The difference between the large site size ni and the small 6, 10 bp site sizes (ni − nj) is greatest when ni = 34, and predicts the largest increase in the fractional population of the large site size mode and in the initial heat signal as DNA length increases from 34 to 38 or 160 bp DNA. Since this change provides the best fit to the observed increase in the initial heat signal with increasing DNA length (see Table 4), we conclude that the large site size is ~ 34 bp.
Possible Implications of Different Binding Modes of HU for In Vivo Function
Models for the roles of HU in regulation of genetic expression1; 54; 55; 56; 57; 58; 75 typically invoke local large-scale (140 degree) bending of DNA, observed in crystal structures of specific complexes of HU with nicked or gapped DNA. Here, we demonstrate that bending is also characteristic of the nonspecific 34 bp binding mode on intact duplex DNA. Expression of many genes in actively replicating cells is activated or repressed by interactions at a distance between DNA-bound proteins; these interactions require conformational distortions (looping and/or bending) of DNA between promoters and upstream regions.55 HU bound in the 34 bp mode should facilitate formation of, and/or stabilize, DNA loops and bends in these regulatory complexes. For example, HU-assisted DNA looping highly favors formation of nucleoprotein complexes in the gal54 and lac76 operons. Similarly, HU promotes binding of lac repressor and CRP – cAMP complex to their specific sites.77 In contrast, binding of HU in its small site size, cooperative modes should disfavor interactions at a distance involving looping or bending of the intervening DNA.37;38;39
DNA bending induced by the 34 bp mode of HU, which is relatively weak and therefore presumably rapidly reversible in vitro, may also contribute to DNA compaction/nucleoid organization (as observed in single molecule studies in vitro37,38) and to the greatly enhanced apparent flexibility of DNA in vivo observed in quantitative studies of DNA looping by lac repressor using expression assays.76 Decondensed nucleoids have been observed in hupAB mutants lacking both subunits of HU.56
In E. coli, how prevalent is the 34 bp bending-binding mode of HU in exponential growth? If the other abundant DNA binding proteins (FIS, H-NS, IHF, RNA polymerase and CAP) are assumed to be all bound and randomly distributed on the nucleoid, we estimate an average gap size of at least 160 bp and an in vivo ratio [HU]/[160 bp DNA gaps] ~ 0.6. Based on the analysis of titrations of 160 bp DNA with HU (Fig. 7), we predict that that HU binds DNA primarily in the 34 bp mode at these in vivo concentrations.
In regions of the nucleoid where the gap sizes are less than 34 bp, the small site size modes should be dominant binding modes. The moderate cooperativity observed for these modes is presumably necessary to fill these gaps at the physiological HU concentration and binding constant. As cooperative assemblies, such gap-filling complexes are more stable than isolated complexes, but their stability is not large. It is probable that these cooperative small-site-size complexes, like the 34 bp binding mode, form and dissociate frequently on the in vivo time scale (derepression/expression time scale ~ 1 second), unless stabilized by interactions with other proteins in an assembly on DNA.
The changes in absolute and relative amounts of HU and other NAPs in the transition from exponential to stationary phase (see Introduction) may greatly change the parameters of the above estimates and result in a different binding-mode distribution of HU in stationary phase cells. Although the amount of HU decreases from 30,000 to 15,000 dimers per cell as a cell enters the stationary phase,7 the chromosome copy number in stationary phase is also less than that in exponential growth phase. Thus, the amount of HU per DNA bp may not be significantly less than in exponential growth. The large amount of Dps (and presumably IHF) which coat and compact the nucleoid in stationary phase cells 3; 4; 5; 6 are expected to decrease the average gap size available for HU and increase the effective HU/DNA ratio, favoring the small site size modes.
Materials and Methods
Chemicals
Anhydrous Na2HPO4 (99.4 % pure, FW 141.96), NaCl (99.9 % pure, FW 58.43), and Na2EDTA (> 99 % pure, FW 372.23) used in binding buffer preparation were obtained from Fisher Scientific (Pittsburgh, PA). Phenylmethylsulfonyl fluoride (PMSF, > 99 % pure, FW 174.2), benzamidine hydrochloride hydrate (> 98 % pure, FW 156.51), and polyethyleneimine (PEI) solution (50 % w/v in water) used in HU preparation were obtained from Sigma (St. Louis, MO).
Purification of HUαβ
HUαβ was purified from E. coli strain RJ5814 (a generous gift from R. Johnson, UCLA) containing the plasmid, pPL-hupAB ApR, which codes for the overexpression of both α and β subunits of HU. The purification procedure, provided by R. Johnson, was followed with slight modifications for large scale production. Cells were grown on a 10 L scale at 30°C in LB broth in a fermentor and induced at mid to late log phase by shifting the temperature to 42°C for 30 min. Cells were harvested by centrifugation at 3,000 g for 15 min. The harvested cell pellet was resuspended in lysis buffer (0.05 M Tris pH 7.5, 0.2 M NaCl, 0.01 M EDTA and 10% v/v glycerol). Immediately prior to lysis, PMSF and benzamidine were added to concentrations of 0.001 M and 0.002 M, respectively. The cell suspension was lysed by sonicating for 30 s followed by 60 s on ice, repeated ten times. The cell lysate was centrifuged at 27,000 g for 15 min. 10% PEI (0.35% final concentration) was added to the supernatant with NaCl (0.75 M final concentration), incubated at 4°C for several hours to precipitate any nucleic acid and centrifuged at 17,000 g for 20 min. Ammonium sulfate ((NH4)2SO4; 50% saturation; 320 g/L) was added to the supernatant, incubated at 4°C for an hour and centrifuged at 17,000 g for 15 min. After this step, the pellet contains a very small amount of HU (IHF and nuclease activity are removed at this step5451). The remaining supernatant was then completely saturated with NH4SO4 to precipitate HU and centrifuged at 17,000 g for 30 min.
The (NH4)2SO4 precipitate was then dissolved in buffer A (0.02 M Tris pH 7.5, 0.001 M EDTA, 0.1 M NaCl and 10% v/v glycerol) and dialyzed in the same buffer for 36 hours with three buffer changes. Dialysate was loaded onto 5 mL SP (strong cationic exchanger) - sepharose column (Amersham-Pharmacia) and eluted in buffer A with a step gradient of NaCl (0.1 M initial wash, 0.2 M elution, 0.25 M elution and 1 M final wash). Significant amounts of proteins other than HU were eluted in the 0.1 M NaCl wash and in the first 1 ~ 2 column volumes of 0.2 M NaCl wash. After 5 column volumes of 0.2 M NaCl were added, HU was eluted along with a small amount of other proteins (the same species as those that eluted in the early 0.2 M NaCl step; 4 ~ 5 bands on a 15% SDS PAGE). Elution of HU was completed with 0.25 M NaCl. The final 1 M elution contained a large amount of proteins other than HU. Late 0.2 M and 0.25 M eluents were collected and loaded onto 5mL CM (weak cationic exchanger) - sepharose column (Amersham-Pharmacia). A 100 mL gradient from 0.1 M to 1 M NaCl was run to remove the minor bands from previous column eluents; HU eluted at ~0.25 M NaCl. The final pooled fraction appeared to be ~ 95 % (single band) pure as judged by coomassie staining of fractions run on a 15% SDS-polyacrylamide gel. The total yield of protein was > 60 mg. Because HU lacks any tryptophan or tyrosine residue, the concentration of HU was determined by far-UV absorbance at 230 nm using a calculated molar extinction coefficient at 230 nm of 3.75×104 M−1cm−1.29
DNA
All oligonucleotides were obtained HPLC-purified (> 90% pure) from Integrated DNA Technologies (Coralville, IA) with sequences designed to minimize formation of secondary structure (e.g. hairpins) in the single strands: 8 bp (5’- CTCGCGAG -3’; self complementary), 15 bp (5’-CGGTCAGTTCAAGGC-3’and its complementary strand), 34 bp (5’- CCAAAAAAGCATTGCTTATCAATTTGTTGCACC-3’ and its complementary strand; the H’-DNA binding site of IHF, used for convenience due to availability from contemporaneous IHF studies in the laboratory) and 38 bp DNA (5’- CGGTCAGTTCAAGCCCTTCTAAGTTTGTAGACACCAGC-3’and its complementary strand). After dissolving in buffer (0.025 M Na2HPO4, 0.1 M NaCl, and 0.0025 M Na2EDTA, pH 7.5), oligomers were annealed by mixing equimolar quantities of the complementary single strands, increasing the temperature to 85°C (greater than the melting temperature Tm of all DNA oligomers at this salt concentration), and cooling the samples to room temperature overnight in a large water bath. To assess the degree of annealing, samples were loaded on a DMAE (dimethyl amino ethyl) column and separated using HPLC with a salt gradient of 0 to 1.5 M NaCl and a flow rate of 1.5 mL/min. Successful annealing was confirmed by observation of a single dominant peak corresponding to double-stranded DNA for all oligonucleotides. Concentrations of the annealed duplexes were determined using calculated molar extinction coefficients at 260 nm of 1.1 × 105, 2.0 × 105, 4.2 × 105, and 5.0 × 105 M−1cm−1 for 8, 15, 34, and 38 bp DNA, respectively.26; 78 The 160 bp calf thymus DNA fragments were prepared following the procedure79 and their concentration was determined using molar extinction coefficient at 260 nm of 1.32 × 104 M−1 cm−1 in base pairs80. The stabilities of all duplex DNA molecules were confirmed by a temperature scan in UV spectrophotometer.
FRET studies were performed using a donor-acceptor labeled 34 bp oligomer. Purchased HPLC-purified from IDT, the single strands were identical to the 34 bp DNA above except for the addition of a pyrimidine (dT and dC) to each 5’ end. Oligos were 5’ end-labeled with 6 – carboxyfluorescein (FAM) or tetramethylrhodamine (TAMRA) through a six carbon phosphoramidite linker (100 % labeling efficiency) 25. The same annealing procedure as above was used to prepare duplex DNA, the concentration of which was determined from molar extinction coefficient at 260 nm of 4.8 × 105 M−1cm−1.25
ITC titrations
Samples for ITC experiments were extensively dialyzed (3 changes, > 36 hours total) against binding buffer (0.010 M Na2HPO4, 0.001 M Na2EDTA, and 0.128 or 0.103 M NaCl, pH 7.5) using Spectra/Pore membrane tubing (3500 MWCO for HU and 500 MWCO for DNA). Forward ITC titrations (HU injected into the cell containing DNA) were performed using a VP-ITC (MicroCal, LLC, Northhampton, MA). Prior to titration, all samples were centrifuged at 30,000 g for 30 min at 4°C and completely degassed in vacuum system provided from MicroCal at 11 °C. The typical concentration of HU was 50 ~ 100 µM in the injection syringe. The concentration of DNA in the reaction cell varied, depending on the DNA length and on the magnitude of heat effect upon injection of HU (8 bp: 6 ~ 13µM, 15 bp: 2.2 ~ 4.5µM, 34, 38 bp: 1.2 ~ 2.8µM and 160 bp: 0.25 ~ 1.0 µM). To confirm that degassing did not affect concentration, concentrations of HU and DNA were measured before and after degassing for every titration experiment. Because the heat signal from binding was very small for some cases (8 bp, 15 bp and 8/15 bp competition titration), baselines were monitored until they were sufficiently stable without any drift; only then were samples injected. The slightly overfilled reaction cell (1.4 mL) containing DNA was titrated with HU (50 ~ 100 uM) using ~ 30 injections (10 µL) and an equilibration time of 240 seconds at a stirring rate of 307 revolutions per min (RPM) in most experiments. All experimental parameters (e.g. concentration of materials, injection volume (6 to 10 µL), equilibration time (180 to 300 s) and stirring rate (307 to 412 RPM)) were varied, and no systematic dependence on any of these was observed. At least three titrations were performed for each DNA length and two different preparations of HU were used in titration to verify the reproducibility. Heat contributions other than binding in each injection (e.g. heat of dilution, mechanical heat of injection) were determined in control experiments. Titrations of buffer and buffer containing a trace amount of DNA (but saturable based on the observed binding constant) with HU were performed. In the latter experiment, the first 3 or 4 points yield the heat signal from binding and subsequent injections (reaching plateau) correspond to the heat of dilution. Two different controls showed the consistent average heat of dilution, which was subtracted from the experimental HU – DNA titration data.
ITC binding isotherms were analyzed using the standard heat equation 81 for each injection point. This equation takes into account the volume displacement in reaction cell using the nonlinear regression program NONLIN82:
| (7) |
In Eq. 7, ΔH° = standard enthalpy for formation of any complex S, Vcell = volume of reaction cell, [HU] = molar concentration of HU in injection syringe, Vinj = injection volume, and [S]i = the concentration of any complex formed after ith injection (expressions for S, which differ for the different DNA oligomers, are given in subsequent analysis section). Values of [S]i used in fitting or simulation of binding isotherms and population distributions were obtained by numerically solving the appropriate system of equation involving total concentrations of HU and DNA and thermodynamic quantities (e.g. binding constant) for each length of DNA as given in following sections.
Fitting and simulation of 15 bp DNA binding isotherms (and competition isotherms)
The binding isotherm for 15 bp DNA was fit to macroscopic binding constants K1 and K2 (also ΔH1° and ΔH2°), describing binding of one and two HU to a 15 bp DNA molecule respectively. Here [S] is the total concentration of DNA molecules with one or two bound HU. For a DNA molecule (N bp) that can be maximally bound two HU dimers, the binding polynomial or partition function is given by:
| (8) |
Given the mass balance equation for total HU concentration and fit values of K1 and K2, [HU] can be solved for, which in turn allows the calculation of concentrations of HU – DNA complexes:
| (9a) |
| (9b) |
Based on the interpretation of Z(N bp) in terms of binding mode transition between the 10 and 6 bp mode (see Eq. 1 and 2) on 15 bp DNA, the population distribution of HU bound in those two modes on 15 bp DNA was calculated from appropriate derivatives of Z(15 bp):
| (10a) |
| (10b) |
In the analysis of competition isotherm (8 + 15 bp), the 1:1 complex between HU (bound in 6 bp mode) and 8 bp DNA is introduced in mass balance equation for total HU concentration:
| (10c) |
where the factor of 3 is the statistical factor representing the three possible configurations of the 1:1 complex.
Fitting and simulation of 34 bp DNA binding isotherm
The binding isotherm of 34 bp DNA was fit using the same approach taken in fitting the 15 bp DNA binding isotherm, but with three macroscopic binding constants. Here [S] is the total concentration of DNA molecules with one, two, or three bound HU. The macroscopic partition function for DNA molecule that can bind a maximum of three HU is given by:
| (11) |
The same mass balance equation for total HU concentration described in Eq. 9a, b was used to calculate free HU concentration, thereby yielding concentrations of DNA with 1 to 3 bound HU.
Since it is complicated to derive the exact closed form of Z(34 bp) in terms of binding mode transitions between three binding modes (see Results and Analysis) using the same combinatorial method used in Z(15 bp), we derived a modified sequence generating function (SGF) method to describe both the 1:1 binding interaction between 34 bp DNA and HU (bound in the 34 bp mode) and binding of HU in the 10 and 6 bp mode. This modified SGF allowed us to simulate the population distribution of all three modes. The equilibrium for interaction between HU (free and bound in the 10 and/or 6 bp mode) and DNA (free and occupied by HU in the 10 and/or 6 bp mode) is described by the secular equation f(x) derived from the SGF developed by Lifson83 and Schellman84 and further extended and applied by Lohman, Bujalowski and co-workers41; 45; 68; 85:
| (12) |
The largest root of Eq. 12 for ×(≡ x1) corresponds to the partition function of DNA base pair with the reference state of free base pair, so x134 is the partition function for 34 bp DNA. Concentration of HU bound in the 10 or 6 bp mode is calculated from the derivative of the partition function with respect to statistical weight for the 10 or 6 bp mode (k10 or 6 [HU]):
| (13a) |
| (13b) |
[DNA] and [DNA]b, 10/6 are free and occupied form (by the 10 and/or 6 bp mode), respectively. Note that DNA occupied by HU in the 34 bp mode is not included in this calculation, but is separately described by a simple 1:1 binding equilibrium, [HU]b, 34bp mode = [DNA]b,34 = k34[HU][DNA]. [DNA] can be also described in terms of partition function x. Since the statistical weight for free DNA is (1/x)34,
| (14a) |
And using the mass balance equation for total DNA concentration ([DNA]tot = [DNA] + [DNA]b,10/6 + [DNA]b,34), [DNA] (also [DNA]b,10/6 and [DNA]b,34) is expressed in terms of total DNA concentration:
| (14b) |
Finally, the mass balance equation of total HU concentration ([HU]tot = [HU] + [HU]b,6 + [HU]b,10 + [HU]b,34) can be expressed in terms of [HU] and x:
| (15) |
[HU] and × (thereby, all the possible complexes) are obtained by simultaneously and numerically solving Eq. 12 and 15 for a given set of binding constants and cooperativities; × is varied until [HU], which can be solved from the quadratic Eq. 12, satisfies the mass balance Eq. 15. However, since the effect of finite DNA length is not considered in SGF, our approach in the calculation of population distribution on 34 bp DNA should be considered as approximate, especially at high concentrations of HU.
Simulations of 160 bp DNA binding isotherm
The simulation of the binding isotherm of 160 bp DNA with the 34 and 10 bp modes was performed using the same SGF method as described above. Here [S] represents the total concentration of HU bound in either 10 or 34 bp mode. Binding constants and cooperativities in Eq. 12 were changed to appropriate ones corresponding to the 34 and 10 bp mode. Power terms to × were also changed according to the site sizes of 34 and 10 bp.
FRET titration and analysis
FRET titrations were performed in the same buffer as that used in ITC studies with the addition of 100 µg/ml of BSA (to reduce adherence of HU to the cuvette wall). Doubly (FAM – TAMRA) or singly (FAM) labeled DNA in the 180 µL cuvette (typically 120 nM) was titrated by adding a concentrated stock solution of HU (5 µM) sequentially to minimize systematic pipetting errors. The reaction mixture was equilibrated for ~ 4 minutes before measurement. Fluorescence emission intensity of the donor (FAM) for each titration point was measured in a L – shaped QuantaMaster C – 60/2000 spectrofluorometer (Photon Technology Instruments, Birmingham, NJ) at magic angle conditions. The temperature was maintained at 15°C by a circulating water bath. Fluorescence emission spectra of the donor (FAM) were obtained from 500 to 615 nm with an excitation wavelength of 490 nm. The integration time was 4 seconds with a step size of 1 nm. No time dependence of the donor emission spectra was confirmed by incubating HU – DNA mixture (the range of HU/DNA mole ratio 0 ~ 10) for > 2 hours.
FRET efficiency (TE) was determined from a comparison of the donor emission intensity of doubly labeled DNA (IDA) and singly labeled DNA (ID) at the same HU/DNA mole ratio. Donor emission intensity was obtained from integration of emission spectra from 510 to 530 nm. Then, TE is given by50; 52; 86:
| (16) |
End-to-end distance (d) of doubly labeled 34 bp DNA was calculated with fitted TE34 (see Results and Analysis) using the following equation52:
| (17) |
where Ro is the Foster distance at which 50% of energy transfer occurs. Knowledge of the end-to-end distance (d) allows one to estimate DNA bending angle (θ) by
| (18) |
10 bp corresponds to the distance occluded by two arms of HU in minor groove region and 12 bp corresponds to the length of each DNA segment flanking DNA bending point. The length of chemical linker was assumed to be 10 Å. In this calculation, DNA bending is modeled using the crystal structures of IHF21 and Anabena HU22 (in which bending occurs almost symmetrically at the two kinking points).
Supplementary Material
Acknowledgements
We thank Tim Lohman (Washington University) for valuable discussion, Reid Johnson (UCLA) for providing the E. coli strain for over-expressing HU and its purification protocol, Wlodek Bujalowski (UTMB) for helping initial computational set up in SGF analysis, Kirk Vander Muelen (UW-Madison) for providing end-labeled DNA oligomer used in FRET studies and helpful discussions, Mike Capp (UW-Madison) for assistance in HU over-expression and preparation of 160 bp calf thymus DNA, and Darrel McCaslin (UW-Madison, Biophysics Instrumentation Facitlity) for technical advice. This work was supported by NIH grant GM23467.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Johnson RC, Johnson LM, Schmidt JW, Gardner JF. Major Nucleoid Proteins in the Structure and Function of the Escherichia coli Chromosome. In: Higgins NP, editor. The Bacterial Chromosome. Washington, D.C: ASM Press; 2005. pp. 65–132. [Google Scholar]
- 2.Stavans J, Oppenheim A. DNA-protein interactions and bacterial chromosome architecture. Phys Biol. 2006;3:R1–R10. doi: 10.1088/1478-3975/3/4/R01. [DOI] [PubMed] [Google Scholar]
- 3.Frenkiel-Krispin D, Levin-Zaidman S, Shimoni E, Wolf SG, Wachtel EJ, Arad T, Finkel SE, Kolter R, Minsky A. Regulated phase transitions of bacterial chromatin: a non-enzymatic pathway for generic DNA protection. Embo J. 2001;20:1184–1191. doi: 10.1093/emboj/20.5.1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kim J, Yoshimura SH, Hizume K, Ohniwa RL, Ishihama A, Takeyasu K. Fundamental structural units of the Escherichia coli nucleoid revealed by atomic force microscopy. Nucleic Acids Res. 2004;32:1982–1992. doi: 10.1093/nar/gkh512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wolf SG, Frenkiel D, Arad T, Finkel SE, Kolter R, Minsky A. DNA protection by stress-induced biocrystallization. Nature. 1999;400:83–85. doi: 10.1038/21918. [DOI] [PubMed] [Google Scholar]
- 6.Frenkiel-Krispin D, Ben-Avraham I, Englander J, Shimoni E, Wolf SG, Minsky A. Nucleoid restructuring in stationary-state bacteria. Mol Microbiol. 2004;51:395–405. doi: 10.1046/j.1365-2958.2003.03855.x. [DOI] [PubMed] [Google Scholar]
- 7.Ali Azam T, Iwata A, Nishimura A, Ueda S, Ishihama A. Growth phase-dependent variation in protein composition of the Escherichia coli nucleoid. J Bacteriol. 1999;181:6361–6370. doi: 10.1128/jb.181.20.6361-6370.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kostrewa D, Granzin J, Koch C, Choe HW, Raghunathan S, Wolf W, Labahn J, Kahmann R, Saenger W. Three-dimensional structure of the E. coli DNA-binding protein FIS. Nature. 1991;349:178–180. doi: 10.1038/349178a0. [DOI] [PubMed] [Google Scholar]
- 9.Yuan HS, Finkel SE, Feng JA, Kaczor-Grzeskowiak M, Johnson RC, Dickerson RE. The molecular structure of wild-type and a mutant Fis protein: relationship between mutational changes and recombinational enhancer function or DNA binding. Proc Natl Acad Sci U S A. 1991;88:9558–9562. doi: 10.1073/pnas.88.21.9558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Johnson RC, Bruist MF, Simon MI. Host protein requirements for in vitro site-specific DNA inversion. Cell. 1986;46:531–539. doi: 10.1016/0092-8674(86)90878-0. [DOI] [PubMed] [Google Scholar]
- 11.Dame RT. The role of nucleoid-associated proteins in the organization and compaction of bacterial chromatin. Mol Microbiol. 2005;56:858–870. doi: 10.1111/j.1365-2958.2005.04598.x. [DOI] [PubMed] [Google Scholar]
- 12.Gille H, Egan JB, Roth A, Messer W. The FIS protein binds and bends the origin of chromosomal DNA replication, oriC, of Escherichia coli. Nucleic Acids Res. 1991;19:4167–4172. doi: 10.1093/nar/19.15.4167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McLeod SM, Xu J, Cramton SE, Gaal T, Gourse RL, Johnson RC. Localization of amino acids required for Fis to function as a class II transcriptional activator at the RpoS-dependent proP P2 promoter. J Mol Biol. 1999;294:333–346. doi: 10.1006/jmbi.1999.3262. [DOI] [PubMed] [Google Scholar]
- 14.Pan CQ, Finkel SE, Cramton SE, Feng JA, Sigman DS, Johnson RC. Variable structures of Fis-DNA complexes determined by flanking DNA-protein contacts. J Mol Biol. 1996;264:675–695. doi: 10.1006/jmbi.1996.0669. [DOI] [PubMed] [Google Scholar]
- 15.Thompson JF, Landy A. Empirical estimation of protein-induced DNA bending angles: applications to lambda site-specific recombination complexes. Nucleic Acids Res. 1988;16:9687–9705. doi: 10.1093/nar/16.20.9687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ceci P, Cellai S, Falvo E, Rivetti C, Rossi GL, Chiancone E. DNA condensation and self-aggregation of Escherichia coli Dps are coupled phenomena related to the properties of the N-terminus. Nucleic Acids Res. 2004;32:5935–5944. doi: 10.1093/nar/gkh915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Grant RA, Filman DJ, Finkel SE, Kolter R, Hogle JM. The crystal structure of Dps, a ferritin homolog that binds and protects DNA. Nat Struct Biol. 1998;5:294–303. doi: 10.1038/nsb0498-294. [DOI] [PubMed] [Google Scholar]
- 18.Luijsterburg MS, Noom MC, Wuite GJ, Dame RT. The architectural role of nucleoid-associated proteins in the organization of bacterial chromatin: a molecular perspective. J Struct Biol. 2006;156:262–272. doi: 10.1016/j.jsb.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 19.Drlica K, Rouviere-Yaniv J. Histonelike proteins of bacteria. Microbiol Rev. 1987;51:301–319. doi: 10.1128/mr.51.3.301-319.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Guo F, Adhya S. Spiral structure of Escherichia coli HUalphabeta provides foundation for DNA supercoiling. Proc Natl Acad Sci U S A. 2007;104:4309–4314. doi: 10.1073/pnas.0611686104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rice PA, Yang SW, Mizuuchi K, NAsh HA. Crystal structure of an IHF-DNA complex: A protein-induced DNA u-turn. Cell. 1996;87:1295–1306. doi: 10.1016/s0092-8674(00)81824-3. [DOI] [PubMed] [Google Scholar]
- 22.Swinger KK, Lemberg KM, Zhang Y, Rice PA. Flexible DNA bending in HU-DNA cocrystal structures. Embo J. 2003;22:3749–3760. doi: 10.1093/emboj/cdg351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Swinger KK, Rice PA. IHF and HU: flexible architects of bent DNA. Curr Opin Struct Biol. 2004;14:28–35. doi: 10.1016/j.sbi.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 24.Ramstein J, Hervouet N, Coste F, Zelwer C, Oberto J, Castaing B. Evidence of a thermal unfolding dimeric intermediate for the Escherichia coli histone-like HU proteins: thermodynamics and structure. J Mol Biol. 2003;331:101–121. doi: 10.1016/s0022-2836(03)00725-3. [DOI] [PubMed] [Google Scholar]
- 25.Vander Meulen KA, Saecker RM, Record MT., Jr Formation of a wrapped DNA-protein interface: experimental characterization and analysis of the large contributions of ions and water to the thermodynamics of binding IHF to H' DNA. J Mol Biol. 2008;377:9–27. doi: 10.1016/j.jmb.2007.11.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holbrook JA, Tsodikov OV, Saecker RM, Record MT., Jr Specific and non-specific interactions of integration host factor with DNA: thermodynamic evidence for disruption of multiple IHF surface salt-bridges coupled to DNA binding. J Mol Biol. 2001;310:379–401. doi: 10.1006/jmbi.2001.4768. [DOI] [PubMed] [Google Scholar]
- 27.Bonnefoy E, Rouviere-Yaniv J. HU and IHF, two homologous histone-like proteins of Escherichia coli, form different protein-DNA complexes with short DNA fragments. Embo J. 1991;10:687–696. doi: 10.1002/j.1460-2075.1991.tb07998.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pinson V, Takahashi M, Rouviere-Yaniv J. Differential binding of the Escherichia coli HU, homodimeric forms and heterodimeric form to linear, gapped and cruciform DNA. J Mol Biol. 1999;287:485–497. doi: 10.1006/jmbi.1999.2631. [DOI] [PubMed] [Google Scholar]
- 29.Wojtuszewski K, Hawkins ME, Cole JL, Mukerji I. HU binding to DNA: Evidence for multiple complex formation and DNA bending (vol 40, pg 2588, 2001) Biochemistry. 2001;40:4892–4892. doi: 10.1021/bi002382r. [DOI] [PubMed] [Google Scholar]
- 30.Wojtuszewski K, Mukerji I. HU binding to bent DNA: A fluorescence resonance energy transfer and anisotropy study. Biochemistry. 2003;42:3096–3104. doi: 10.1021/bi0264014. [DOI] [PubMed] [Google Scholar]
- 31.Benevides JM, Danahy J, Kawakami J, Thomas GJ., Jr Mechanisms of specific and nonspecific binding of architectural proteins in prokaryotic gene regulation. Biochemistry. 2008;47:3855–3862. doi: 10.1021/bi7009426. [DOI] [PubMed] [Google Scholar]
- 32.Broyles SS, Pettijohn DE. Interaction of the Escherichia coli HU protein with DNA. Evidence for formation of nucleosome-like structures with altered DNA helical pitch. J Mol Biol. 1986;187:47–60. doi: 10.1016/0022-2836(86)90405-5. [DOI] [PubMed] [Google Scholar]
- 33.Rouviere-Yaniv J, Yaniv M, Germond JE. E. coli DNA binding protein HU forms nucleosomelike structure with circular double-stranded DNA. Cell. 1979;17:265–274. doi: 10.1016/0092-8674(79)90152-1. [DOI] [PubMed] [Google Scholar]
- 34.Castaing B, Zelwer C, Laval J, Boiteux S. HU protein of Escherichia coli binds specifically to DNA that contains single-strand breaks or gaps. J Biol Chem. 1995;270:10291–10296. doi: 10.1074/jbc.270.17.10291. [DOI] [PubMed] [Google Scholar]
- 35.Kamashev D, Balandina A, Rouviere-Yaniv J. The binding moti recognized by HU on both nicked and cruciform DNA. Embo J. 1999;18:5434–5444. doi: 10.1093/emboj/18.19.5434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kamashev D, Rouviere-Yaniv J. The histone-like protein HU binds specifically to DNA recombination and repair intermediates. Embo J. 2000;19:6527–6535. doi: 10.1093/emboj/19.23.6527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Skoko D, Wong B, Johnson RC, Marko JF. Micromechanical analysis of the binding of DNA-bending proteins HMGB1, NHP6A, and HU reveals their ability to form highly stable DNA-protein complexes. Biochemistry. 2004;43:13867–13874. doi: 10.1021/bi048428o. [DOI] [PubMed] [Google Scholar]
- 38.van Noort J, Verbrugge S, Goosen N, Dekker C, Dame RT. Dual architectural roles of HU: Formation of flexible hinges and rigid filaments. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:6969–6974. doi: 10.1073/pnas.0308230101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dame RT, Goosen N. HU: promoting or counteracting DNA compaction? FEBS Lett. 2002;529:151–156. doi: 10.1016/s0014-5793(02)03363-x. [DOI] [PubMed] [Google Scholar]
- 40.Bujalowski W, Lohman TM. Escherichia coli single-strand binding protein forms multiple, distinct complexes with single-stranded DNA. Biochemistry. 1986;25:7799–7802. doi: 10.1021/bi00372a003. [DOI] [PubMed] [Google Scholar]
- 41.Ferrari ME, Bujalowski W, Lohman TM. Co-operative binding of Escherichia coli SSB tetramers to single-stranded DNA in the (SSB)35 binding mode. J Mol Biol. 1994;236:106–123. doi: 10.1006/jmbi.1994.1122. [DOI] [PubMed] [Google Scholar]
- 42.Lohman TM, Overman LB. Two binding modes in Escherichia coli single strand binding protein-single stranded DNA complexes. Modulation by NaCl concentration. J Biol Chem. 1985;260:3594–3603. [PubMed] [Google Scholar]
- 43.Lohman TM, Ferrari ME. Escherichia coli single-stranded DNA-binding protein: multiple DNA-binding modes and cooperativities. Annu Rev Biochem. 1994;63:527–570. doi: 10.1146/annurev.bi.63.070194.002523. [DOI] [PubMed] [Google Scholar]
- 44.Jezewska MJ, Rajendran S, Bujalowski W. Transition between different binding modes in rat DNA polymerase beta-ssDNA complexes. J Mol Biol. 1998;284:1113–1131. doi: 10.1006/jmbi.1998.2252. [DOI] [PubMed] [Google Scholar]
- 45.Rajendran S, Jezewska MJ, Bujalowski W. Human DNA polymerase beta recognizes single-stranded DNA using two different binding modes. J Biol Chem. 1998;273:31021–31031. doi: 10.1074/jbc.273.47.31021. [DOI] [PubMed] [Google Scholar]
- 46.Epstein IR. Cooperative and non-cooperative binding of large ligands to a finite one-dimensional lattice. A model for ligand-oligonucleotide interactions. Biophys Chem. 1978;8:327–339. doi: 10.1016/0301-4622(78)80015-5. [DOI] [PubMed] [Google Scholar]
- 47.McGhee JD, von Hippel PH. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogeneous lattice. J Mol Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- 48.Schwarz G, Stankowski S. Linear cooperative binding of large ligands involving mutual exclusion of different binding modes. Biophys Chem. 1979;10:173–181. doi: 10.1016/0301-4622(79)85037-1. [DOI] [PubMed] [Google Scholar]
- 49.Kuznetsov SV, Sugimura S, Vivas P, Crothers DM, Ansari A. Direct observation of DNA bending/unbending kinetics in complex with DNA-bending protein IHF. Proc Natl Acad Sci U S A. 2006;103:18515–18520. doi: 10.1073/pnas.0608394103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lorenz M, Hillisch A, Goodman SD, Diekmann S. Global structure similarities of intact and nicked DNA complexed with IHF measured in solution by fluorescence resonance energy transfer. Nucleic Acids Res. 1999;27:4619–4625. doi: 10.1093/nar/27.23.4619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sugimura S, Crothers DM. Stepwise binding and bending of DNA by Escherichia coli integration host factor. Proc Natl Acad Sci U S A. 2006;103:18510–18514. doi: 10.1073/pnas.0608337103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Clegg RM. Fluorescence resonance energy transfer and nucleic acids. Methods Enzymol. 1992;211:353–388. doi: 10.1016/0076-6879(92)11020-j. [DOI] [PubMed] [Google Scholar]
- 53.Stuhmeier F, Welch JB, Murchie AI, Lilley DM, Clegg RM. Global structure of three-way DNA junctions with and without additional unpaired bases: a fluorescence resonance energy transfer analysis. Biochemistry. 1997;36:13530–13538. doi: 10.1021/bi9702445. [DOI] [PubMed] [Google Scholar]
- 54.Aki T, Adhya S. Repressor induced site-specific binding of HU for transcriptional regulation. Embo J. 1997;16:3666–3674. doi: 10.1093/emboj/16.12.3666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dorman CJ, Deighan P. Regulation of gene expression by histone-like proteins in bacteria. Curr Opin Genet Dev. 2003;13:179–184. doi: 10.1016/s0959-437x(03)00025-x. [DOI] [PubMed] [Google Scholar]
- 56.Huisman O, Faelen M, Girard D, Jaffe A, Toussaint A, Rouviere-Yaniv J. Multiple defects in Escherichia coli mutants lacking HU protein. J Bacteriol. 1989;171:3704–3712. doi: 10.1128/jb.171.7.3704-3712.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Paull TT, Johnson RC. DNA looping by Saccharomyces cerevisiae high mobility group proteins NHP6A/B. Consequences for nucleoprotein complex assembly and chromatin condensation. J Biol Chem. 1995;270:8744–8754. doi: 10.1074/jbc.270.15.8744. [DOI] [PubMed] [Google Scholar]
- 58.Perez-Martin J, de Lorenzo V. The sigma 54-dependent promoter Ps of the TOL plasmid of Pseudomonas putida requires HU for transcriptional activation in vivo by XylR. J Bacteriol. 1995;177:3758–3763. doi: 10.1128/jb.177.13.3758-3763.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jen-Jacobson L, Engler LE, Jacobson LA. Structural and thermodynamic strategies for site-specific DNA binding proteins. Structure. 2000;8:1015–1023. doi: 10.1016/s0969-2126(00)00501-3. [DOI] [PubMed] [Google Scholar]
- 60.Peters WB, Edmondson SP, Shriver JW. Thermodynamics of DNA binding and distortion by the hyperthermophile chromatin protein Sac7d. J Mol Biol. 2004;343:339–360. doi: 10.1016/j.jmb.2004.08.042. [DOI] [PubMed] [Google Scholar]
- 61.Privalov PL, Dragan AI, Crane-Robinson C, Breslauer KJ, Remeta DP, Minetti CA. What drives proteins into the major or minor grooves of DNA? J Mol Biol. 2007;365:1–9. doi: 10.1016/j.jmb.2006.09.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gray HB, Jr, Hearst JE. Flexibility of native DNA from the sedimentation behavior as a function of molecular weight and temperature. J Mol Biol. 1968;35:111–129. doi: 10.1016/s0022-2836(68)80041-5. [DOI] [PubMed] [Google Scholar]
- 63.Harrington RE. DNA chain flexibility and the structure of chromatin nu-bodies. Nucleic Acids Res. 1977;4:3519–3535. doi: 10.1093/nar/4.10.3519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Holbrook JA, Capp MW, Saecker RM, Record MT., Jr Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 1999;38:8409–8422. doi: 10.1021/bi990043w. [DOI] [PubMed] [Google Scholar]
- 65.Dragan AI, Klass J, Read C, Churchill ME, Crane-Robinson C, Privalov PL. DNA binding of a non-sequence-specific HMG-D protein is entropy driven with a substantial non-electrostatic contribution. J Mol Biol. 2003;331:795–813. doi: 10.1016/s0022-2836(03)00785-x. [DOI] [PubMed] [Google Scholar]
- 66.Privalov PL, Jelesarov I, Read CM, Dragan AI, Crane-Robinson C. The energetics of HMG box interactions with DNA: thermodynamics of the DNA binding of the HMG box from mouse sox-5. J Mol Biol. 1999;294:997–1013. doi: 10.1006/jmbi.1999.3285. [DOI] [PubMed] [Google Scholar]
- 67.Saecker RM, Record MT., Jr Protein surface salt bridges and paths for DNA wrapping. Curr Opin Struct Biol. 2002;12:311–319. doi: 10.1016/s0959-440x(02)00326-3. [DOI] [PubMed] [Google Scholar]
- 68.Bujalowskiq W, Lohman TM. Limited co-operativity in protein-nucleic acid interactions. A thermodynamic model for the interactions of Escherichia coli single strand binding protein with single-stranded nucleic acids in the "beaded", (SSB)65 mode. J Mol Biol. 1987;195:897–907. doi: 10.1016/0022-2836(87)90493-1. [DOI] [PubMed] [Google Scholar]
- 69.Lohman TM, Bujalowski W. Negative cooperativity within individual tetramers of Escherichia coli single strand binding protein is responsible for the transition between the (SSB)35 and (SSB)56 DNA binding modes. Biochemistry. 1988;27:2260–2265. doi: 10.1021/bi00407a002. [DOI] [PubMed] [Google Scholar]
- 70.Lohman TM, Overman LB, Datta S. Salt-dependent changes in the DNA binding co-operativity of Escherichia coli single strand binding protein. J Mol Biol. 1986;187:603–615. doi: 10.1016/0022-2836(86)90338-4. [DOI] [PubMed] [Google Scholar]
- 71.Bujalowski W, Overman LB, Lohman TM. Binding mode transitions of Escherichia coli single strand binding protein-single-stranded DNA complexes. Cation, anion, pH, and binding density effects. J Biol Chem. 1988;263:4629–4640. [PubMed] [Google Scholar]
- 72.deHaseth PL, Lohman TM, Record MT., Jr Nonspecific interaction of lac repressor with DNA: an association reaction driven by counterion release. Biochemistry. 1977;16:4783–4790. doi: 10.1021/bi00641a004. [DOI] [PubMed] [Google Scholar]
- 73.Record MT, Jr, Lohman ML, De Haseth P. Ion effects on ligand-nucleic acid interactions. J Mol Biol. 1976;107:145–158. doi: 10.1016/s0022-2836(76)80023-x. [DOI] [PubMed] [Google Scholar]
- 74.Tanaka I, Appelt K, Dijk J, White SW, Wilson KS. 3-A resolution structure of a protein with histone-like properties in prokaryotes. Nature. 1984;310:376–381. doi: 10.1038/310376a0. [DOI] [PubMed] [Google Scholar]
- 75.Lavoie BD, Shaw GS, Millner A, Chaconas G. Anatomy of a flexer-DNA complex inside a higher-order transposition intermediate. Cell. 1996;85:761–771. doi: 10.1016/s0092-8674(00)81241-6. [DOI] [PubMed] [Google Scholar]
- 76.Becker NA, Kahn JD, Maher LJ., 3rd Bacterial repression loops require enhanced DNA flexibility. J Mol Biol. 2005;349:716–730. doi: 10.1016/j.jmb.2005.04.035. [DOI] [PubMed] [Google Scholar]
- 77.Flashner Y, Gralla JD. DNA dynamic flexibility and protein recognition: differential stimulation by bacterial histone-like protein HU. Cell. 1988;54:713–721. doi: 10.1016/s0092-8674(88)80016-3. [DOI] [PubMed] [Google Scholar]
- 78.Bloomfield VA, Crothers DM, Tinoco I. Nucleic Acids: Structures, Properties, and Functions. University Science Books; Sausalito, CA: 2000. [Google Scholar]
- 79.Wang L, Ferrari M, Bloomfield VA. Large-scale preparation of mononucleosomal DNA from calf thymus for biophysical studies. Biotechniques. 1990;9(24):26–27. [PubMed] [Google Scholar]
- 80.Ausubel FM. Current Protocols in Molecular Biology. 1997 Suppl. 44 [Google Scholar]
- 81.Microcal I. ITC Data Analysis in Origin. 2004:104–106. [Google Scholar]
- 82.Johnson ML, Frasier SG. Nonlinear least-squares analysis. Methods Enzymol. 1985;117:301–342. [Google Scholar]
- 83.Lifson S. Partition functions of linear-chain molecules. J. Chem. Phys. 1964;40:3705–3710. [Google Scholar]
- 84.Schellman JA. Cooperative multisite binding to DNA. Isr. J. Chem. 1974;12:219–238. [Google Scholar]
- 85.Bujalowski W, Lohman TM, Anderson CF. On the cooperative binding of large ligands to a one-dimensional homogeneous lattice: the generalized three-state lattice model. Biopolymers. 1989;28:1637–1643. doi: 10.1002/bip.360280912. [DOI] [PubMed] [Google Scholar]
- 86.Clegg RM, Murchie AI, Zechel A, Lilley DM. Observing the helical geometry of double-stranded DNA in solution by fluorescence resonance energy transfer. Proc Natl Acad Sci U S A. 1993;90:2994–2998. doi: 10.1073/pnas.90.7.2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.