Counting the number of releasable synaptic vesicles in a presynaptic terminal

Abstract

Synaptic transmission depends on the continued availability of neurotransmitter-filled synaptic vesicles (SVs) for triggered release from presynaptic boutons. Surprisingly, small boutons in the brain, that already contain comparatively few SVs, are thought to retain the majority of these SVs in a “reserve” pool that is not mobilized under physiological conditions. Why such a scarce synaptic resource is normally inaccessible has been a matter of debate. Here, we readdress this issue by developing an electrophysiological approach for counting SVs released from boutons formed by a single, isolated neuron on itself (“autapses”). We show that, after treatment with Bafilomycin A1 to prevent reloading of discharged SVs with glutamate, each SV is counted only once on first-time release. Hence, by integrating all autaptic currents as they run down over time, we can estimate the total number of SVs released by a single neuron. This total can be normalized to the number of boutons on the neuron, giving the mean number of SVs released per bouton. We estimate that up to ≈130 vesicles can be released per bouton over ≈10 min of stimulation at 0.2 Hz. This number of vesicles represents a substantial proportion of the total number of SVs (100–200) that have been counted in these boutons by using electron microscopy. Thus, mild electrical stimulation, when maintained for sufficient time, causes the eventual release of many of the SVs in a bouton, including those in the putative reserve pool. This result suggests that SVs are functionally homogeneous in that the majority can contribute to basal synaptic transmission.

Information flow in the nervous system depends on the triggered release of packets of neurotransmitter contained in small synaptic vesicles (SVs) in the presynaptic terminal. This mechanism relies on the continued availability of release-ready SVs, particularly during periods of stronger synaptic activity (see ref. 1 for review). Small presynaptic boutons in the brain contain 100–200 SVs (2, 3) yet, paradoxically, only a small fraction of these seems to be available for release under normal conditions (1, 4), the remainder being held in reserve. This notion seems puzzling because it requires neurons to invest in a resource that is only rarely used. Here, we address this paradox by developing a method for counting the number of releasable SVs at small, central synapses in hippocampal cultures.

Classically, SVs are thought to belong to 3 distinct pools, often referred to as the readily releasable pool (RRP), the recycling pool, and the reserve pool (1, 5). The RRP, which comprises ≈10 vesicles at excitatory hippocampal synapses (≈5% of the total) (1, 2), is the pool that is immediately available for release, whereas the recycling pool (≈15% of the total) is released with moderate ongoing stimulation (1, 4). The reserve pool, containing the bulk of SVs, seems to be released only in response to intense stimulation. Thus, reserve vesicles may be seldom or never recruited during physiological activity (1, 6, 7), raising questions about their functional importance.

Three main techniques have been used to study SV pools in small, central synapses (1). Electron microscopy, often used with endocytic markers to label recycling vesicles, offers high spatial resolution but can only provide a static snapshot (2, 6, 8, 9). Fluorescent labeling of SVs (e.g., with FM dyes or synaptopHluorin) can provide excellent spatial and temporal information, but the assay is somewhat indirect, fueling controversy (4, 10–12). Finally, electrophysiology provides a direct readout of SV release, but the data can be model-dependent and difficult to interpret (13, 14).

Here, we readdress this issue by developing an electrophysiological approach that allows us to unambiguously count functional SVs at synapses in culture. We conclude that a majority of SVs, even those in the putative reserve pool, can be released with mild stimulation over ≈10 min.

Results

Our approach involves recording excitatory postsynaptic currents (EPSCs) from autapses on an isolated cultured hippocampal pyramidal neuron after applying bafilomycin A1 (Baf) to prevent refilling of empty vesicles with glutamate (15). Baf is a cell-permeant blocker of the V-type ATPase, a proton pump that is required for SV reacidification after endocytosis (16). Thus, after a Baf-poisoned vesicle discharges its “quantum” of glutamate, it is unable to reload and becomes functionally silent. This ensures that each vesicle is counted only once. By counting the total number of quanta released (by summing all EPSCs as they decline in amplitude) (Fig. 1), we arrive at the total number of functional SVs. This approach depends on 3 critical requirements, which we tested in turn.

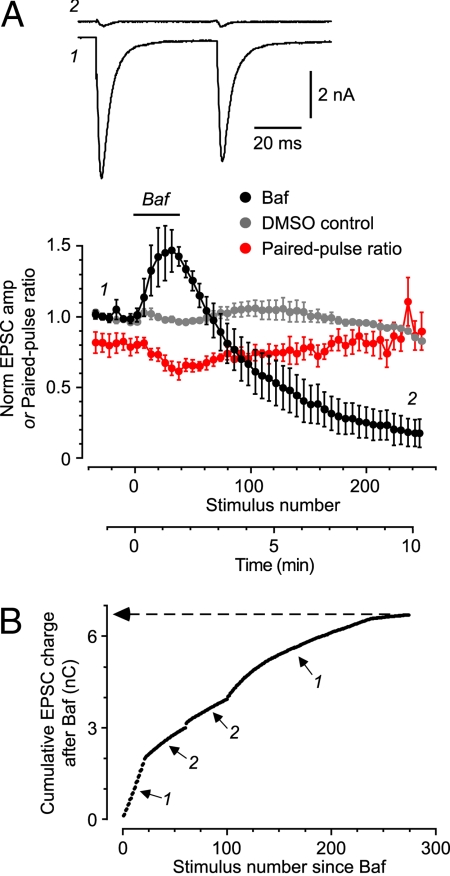
Fig. 1.

Acute Baf treatment causes irreversible, stimulus-dependent loss of glutamate-containing SVs and can be used to count the total number of SVs that are released. (A Upper) Typical pairs of EPSCs measured before Baf treatment (trace 1) and after stimulating for 8.5 min after Baf application (trace 2). Stimulus transients have been blanked. (Lower) Mean normalized EPSC amplitude (Baf-treated, black circles; DMSO control, gray circles) or paired-pulse ratio for Baf-treated EPSCs (red circles) plotted against stimulus number (average of n = 4 cells, all with paired stimuli repeated at 0.2 Hz). Baf and/or DMSO was applied by puffer during the period indicated by the horizontal bar. The numbers on the plot indicate the times at which the example EPSCs were recorded. (B) Cumulative EPSC charge measured in a typical cell after Baf treatment, plotted against stimulus number. Periods 1: paired stimulation at 0.2 Hz; periods 2: 2-s, 20 Hz train. Asymptotic level is indicated (6.70 nC, dashed line).

Baf-Treated Vesicles Cycle Normally Within the Presynaptic Terminal.

If we wish to count SVs under conditions of normal synaptic transmission, it is essential to ensure that Baf does not disrupt the synaptic vesicle cycle. Acute application of Baf caused a drug-specific rundown of the EPSC amplitude (Fig. 1A, black circles for Baf cf., gray circles for control). However, the paired-pulse ratio (PPR; ratio of the amplitudes of 2 EPSCs elicited in quick succession) remained constant as the EPSC amplitude declined (Fig. 1A, red circles). PPR is thought to reflect vesicular release probability, which in turn correlates with the RRP size (17). Hence, our data suggest that RRP size remains constant, presumably because of the maintenance of a normal SV cycle.

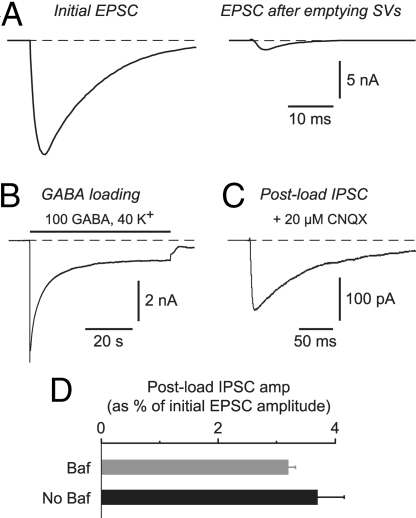
In a second kind of experiment, we used the endocytosis and exocytosis of an exogenous neurotransmitter (GABA) as an assay for the correct functioning of the SV cycle. We have shown that bath-applied GABA can be endocytosed by glutamate-containing SVs at autapses on isolated pyramidal neurons (18), just like FM dyes, which are widely used as fluorescent tracers of the SV cycle (19). After washout of GABA from the bath, subsequent electrical stimulation causes exocytosis of the loaded GABA onto postsynaptic GABA_A receptors, giving rise to a “postload” inhibitory postsynaptic current (IPSC) in the pyramidal cell (Fig. 2 A–C). If Baf disrupts the SV cycle, endocytosis and exocytosis of GABA will be altered, affecting the amplitude of the postload IPSC. This did not occur. We found that the postload IPSC amplitude (normalized to the amplitude of the native EPSC measured in the same cell before treatment) was similar for control vesicles and emptied Baf-treated vesicles (Control: 3.7 ± 0.5%, n = 20; Baf: 3.2 ± 0.1%, n = 3; P = 0.69) (Fig. 2D). This supports the conclusion that Baf-treated SVs cycle normally within the terminal, in agreement with other reports (15, 20).

Fig. 2.

The SV cycle functions normally after Baf-produced depletion of vesicular glutamate, as confirmed by the ability to load a normal amount of exogenous GABA into SVs by endocytosis and to release it again by exocytosis. (A) Autaptic EPSC measured at the beginning of the experiment (Left) and after puffing on Baf and stimulating for 10 min at 0.2 Hz to empty glutamate from the SVs (Right). (B) Response of the same cell (after emptying SVs) to a 60-s application of GABA loading solution containing 100 mM GABA. An inward current was produced because the internal solution contained high chloride. (C) Postload IPSC recorded in the same cell as in A and B after washing out the GABA loading solution and blocking any residual EPSC with 20 μM CNQX. This postload IPSC is due to the evoked release of endocytosed GABA onto postsynaptic GABA_A receptors. (D) Amplitude of the postload IPSC, expressed as a percentage of the initial EPSC amplitude (e.g., A Left), for experiments in which SVs were first depleted of glutamate (Baf), or for control experiments in which Baf was not applied (No Baf). The two measures are not significantly different (P = 0.69), suggesting that vesicular endocytosis and exocytosis is unaffected by prior treatment with Baf.

Baf Irreversibly Blocks Glutamate Reloading in All Functional SVs.

For our approach to be useful, it is critical that Baf irreversibly silences SVs that have already been released, ensuring that all vesicles are counted only once. This requirement appears to be satisfied. After an acute application of Baf, evoked EPSCs ran down to near 0 (Figs. 1A and 3A). Moreover, EPSCs did not recover after prolonged cessation of stimulation (>5 min; data not shown) (20).

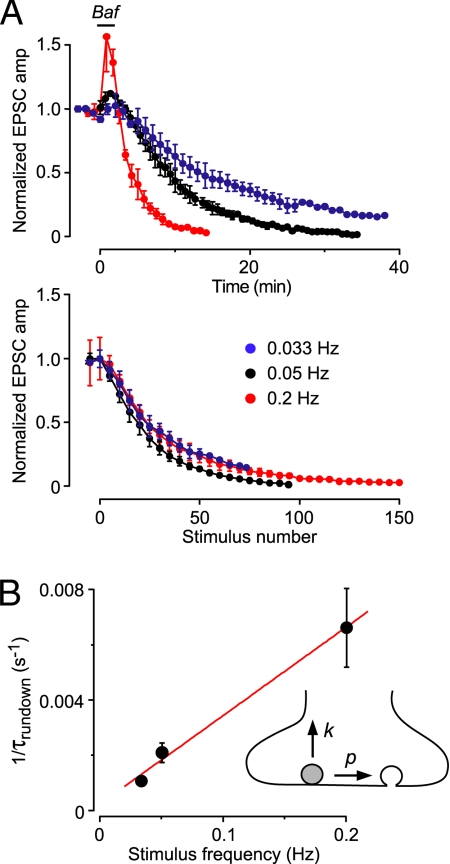
Fig. 3.

Baf-treated SVs do not passively leak out glutamate. (A Upper) EPSC amplitudes evoked at different stimulus frequencies, normalized to the amplitude before Baf application, plotted against time (n = 2–5 cells). (Lower) The same EPSC amplitudes, normalized to the peak amplitude during Baf application to facilitate comparison, plotted against stimulus number. The plots vs. stimulus number all overlie, implicating a stimulus–dependent loss of glutamate from SVs. (B) The data in A can be described by a simple model that incorporates a stimulus-dependent probability of exocytosis (p, Inset) and a time-dependent passive leak of glutamate from SVs (k, Inset). A plot of the reciprocal of the time constant of rundown at different stimulus frequencies (from A Upper) vs. stimulus frequency can be fitted to Eq. 2 in the text (superimposed red line) to yield p = 0.032 and k = 0.00024 s⁻¹. Thus, passive leakage of glutamate from SVs is very slow. Error bars are ±SD (smaller than symbol at 0.033 Hz).

Baf-Treated SVs Do Not Passively Leak Out Glutamate.

Our final requirement is that Baf-treated vesicles maintain their native vesicular glutamate concentration before exocytosis, i.e., there is no passive leakage of glutamate out of the vesicles. This ensures that, when it is finally released, each SV contributes a full-sized postsynaptic quantal response and will be counted correctly. This assumption was tested in two ways. In the first experiment, we measured the stimulus dependence of the Baf-induced rundown of evoked EPSCs (stimulation frequencies 0.2, 0.05, 0.033 Hz) (Fig. 3A). When EPSC amplitude was plotted against stimulus number, rather than time, all rundown plots overlay (Fig. 3A Lower), suggesting that vesicular glutamate is lost by a stimulus-dependent process rather than by leakage. This leakage was quantified by developing a simple model that incorporated 2 free parameters (Fig. 3B Inset): stimulus-dependent probability (p) of releasing a vesicle by exocytosis and stimulus-independent rate (k) of leakage of glutamate out of vesicles (Eq. 2 and 3, Materials and Methods). These equations were fitted to a plot of the reciprocal of the time constant of EPSC amplitude rundown vs. the stimulation frequency (Fig. 3B), yielding p = 0.032 ± 0.003 and k = 0.00024 ± 0.00033 s⁻¹. Thus, the rate of leakage is negligible. The fitted value of p is close to that estimated by using a completely different approach (≈0.03) (2).

In a second experiment, we measured miniature EPSCs (mEPSCs) before and after Baf-induced rundown of the EPSC. If leakage occurs, smaller mEPSCs should appear over time (because of the release of “partially filled” vesicles). This was not observed. Rundown was accompanied by a significant reduction in mEPSC frequency, with no effect on mEPSC amplitude (Fig. 4 A and B) (15, 21). This suggests that Baf-treated SVs are either completely full (i.e., they yield mEPSCs of normal amplitude) or completely empty (i.e., there is a reduction in mEPSC frequency). Again, this is compatible with the absence of leakage.

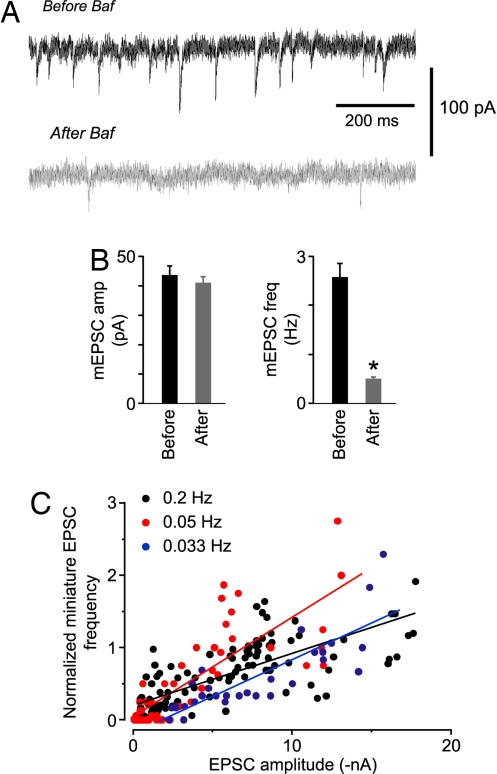
Fig. 4.

Properties of mEPSCs suggest that, after Baf application and stimulation, SVs are either completely full or completely empty. Moreover, evoked EPSCs and mEPSCs appear to draw from the same pool of SVs. (A) Typical mEPSCs recorded in the same cell before (Upper) or ≈10 min after (Lower) stimulation after the acute application of Baf. (B) Mean mEPSC amplitude (Left) and frequency (Right) measured before and after Baf-induced rundown of evoked EPSCs. Only the frequencies were significantly different (n = 6 cells; P = 0.015). (C) Normalized frequency of mEPSCs plotted against the amplitude of the immediately preceding EPSC, recorded during Baf-induced rundown of the EPSC amplitude. For any one cell, the points initially lie in the upper right corner of the plot then move toward the origin as rundown proceeds. Points of the same color are the merged data from a number of cells that were stimulated at the indicated frequency (0.2 Hz: n = 4; 0.05 Hz: n = 2; 0.033 Hz: n = 2). Superimposed straight lines are fits to all points of the same color. Their slopes are not significantly different (P > 0.1).

These data also allow us to ask whether SVs that contribute to evoked release and mEPSCs are drawn from a common pool. This point is controversial, with evidence both for (22) and against (21) the existence of such a pool. We found that the evoked EPSC amplitude and the mEPSC frequency declined together after Baf treatment and the proportionality constant relating these two measures was the same in different cells, even when the EPSCs were evoked at different rates (slopes of fitted straight lines: 0.2 Hz, 0.072; 0.05 Hz, 0.137; 0.033 Hz, 0.101; P > 0.1) (Fig. 4C). This is expected if SVs that contribute to both the evoked EPSCs and the mEPSCs are drawn from the same depleting pool.

Counting the Total Number of SVs That Are Released.

Having validated the requirements of our approach, we next estimated the total number of released SVs as follows. For each EPSC evoked after Baf treatment, the charge was calculated by integrating the current; this ensured that asynchronous release of vesicles was included in the measurement (14). The cumulative sum of these charges was plotted vs. stimulus number, generating a curve that approached a plateau as the EPSC amplitude declined to 0 (Fig. 1B, arrow). The plateau value represents the total charge carried by all of the EPSC quanta resulting from the release of all functional SVs in that cell, with each SV being counted only once. This number was converted to a total number of SVs by dividing by the average quantal charge (227 ± 39 fC, n = 9 cells), yielding a mean functional pool size of 27,600 ± 6,800 vesicles (±SEM, n = 7 cells).

To make this value meaningful, we also need to know the number of autaptic boutons to enable us to calculate the number of functional SVs released from each bouton. The most direct bouton count would use a morphological approach, e.g., immunolabeling and microscopy. However, the small size of the microdots on which our isolated neurons were grown produced a high density of boutons, precluding morphological methods (23). Instead, we used two kinds of electrophysiological assay.

Estimating the Number of Autaptic Boutons by Using Trains and Hypertonic Sucrose.

The first method makes use of a standard train protocol for estimating the RRP size across all boutons. A 2-s, 20-Hz train of stimuli was applied to each cell before exposure to Baf (e.g., Fig. 5A Upper). The RRP size was estimated by linearly extrapolating a plot of the cumulative EPSC charge during the train vs. time (Fig. 5A Lower) then dividing the extrapolated charge by the quantal charge (13). This yielded a mean total RRP size of 1780 ± 550 vesicles (n = 7).

Fig. 5.

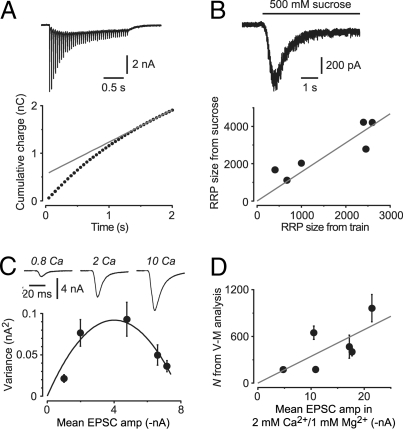
Two methods can be used for estimating the number of synaptic boutons per cell, to enable calculation of the number of SVs released per bouton. (A and B) Method using train and sucrose application to estimate the total size of the RRP of vesicles and hence the number of boutons. (A Upper) EPSCs evoked by a train of 40 stimuli at 20 Hz (cell not exposed to Baf). Stimulus transients have been blanked. (Lower) Cumulative EPSC charge plotted against time during the train for the data shown in the Upper image. The superimposed straight line (gray) is fitted to the points after 1.5 s. Extrapolated to 0 time, the intercept yields one estimate of the total RRP size for this cell. (B Upper) Response of the cell in A to a 6-s application of external solution made hypertonic by the addition of 500 mM sucrose. The area of the transient part of this response provides another estimate of the total RRP size. (Lower) Plot of RRP size estimated from the sucrose method vs. that from the train method. Each point is from a different cell (n = 6). The superimposed gray line is a linear fit constrained through the origin with a slope of 1.56. This provides a scale factor for estimating the number of synaptic boutons from trains (see Results). (C and D) Method using the variance-mean (V–M) fluctuation analysis technique to estimate the number of synaptic release sites, N. (C) Data from a typical V-M experiment. (Upper) representative EPSCs recorded from the same cell in bath solution containing the indicated Ca²⁺ concentration (in mM). Stimulus transients have been blanked. (Lower) Plot of the variance of fluctuations in EPSC amplitude vs. the mean amplitude of EPSCs recorded in each Ca²⁺ concentration. The superimposed smooth curve is a parabola (Eq. 1), which gives N (175 ± 27 for this cell). Error bars are ±SD. (D) Plot of N estimated amplitude measured in the same cell in external solution containing 2 mM Ca²⁺ and 1 mM Mg²⁺. Each point is from a different cell (n = 6). Superimposed gray line is a linear fit constrained through the origin with a slope of 34.4. This provides a scale factor for estimating the number of synaptic release sites, knowing the mean EPSC amplitude before Baf.

It has been reported that the train method underestimates the RRP size, perhaps because of the presence of “reluctantly releasable” vesicles (13, 14). Accordingly, in a separate series of experiments, we compared the train estimate with an estimate based on the application of hypertonic sucrose solution (Fig. 5B Upper). In the sucrose method, the charge carried by the transient component of the sucrose response is due to release of the RRP and, as before, can be converted to a number of SVs by dividing by the quantal charge (24). RRP size was estimated by using both the sucrose and train methods in the same cell. A plot of these two estimates was linearly correlated with a slope of 1.56 (n = 6 cells) (Fig. 5B Lower). This result now allows us to apply a correction factor (1.56) to the RRP sizes that were estimated by using the train method in the Baf-treated cells, yielding a (corrected) mean total RRP size of 2770 ± 850 vesicles (n = 7). A similar result was obtained if EPSC amplitude, rather than charge, was measured in the train experiments.

The actual number of SVs in the RRP at each bouton in hippocampal cultures has been estimated to be ≈10 by using several approaches (reviewed in ref. 1). Hence, the mean number of boutons in our Baf-treated cells is equal to the corrected RRP count across all boutons (2770 ± 850) divided by the RRP count at each bouton (≈10), giving ≈277 ± 85 boutons per cell. Finally, dividing the total number of SVs in the functional pool by the number of boutons on each cell gives 133 ± 44 SVs released per terminal (n = 7 cells).

Estimating the Number of Boutons by Using Variance-Mean Analysis.

Because the above estimate depends on a chain of arguments, each of which may introduce errors, we sought another method to independently verify our bouton counts. Hence, in a separate series of experiments, we used the variance-mean (V-M) method of fluctuation analysis to estimate the number of release sites (25). In these experiments, the EPSC amplitude was first measured in the normal 2 mM Ca²⁺/1 mM Mg²⁺ bath solution used for the Baf experiments. Then, the bath was changed to a series of solutions containing different Ca²⁺ and Mg²⁺ concentrations to vary the synaptic release probability, P_r, over a wide range (Fig. 5C Upper). For each solution, the mean and variance of EPSC amplitudes were calculated and plotted, as in Fig. 5C Lower. A fit of this plot to the V-M parabola (Eq. 1) yielded estimates for the mean quantal amplitude, Q, and the number of release sites, N, for that cell.

A general expression for the mean synaptic current, I, is I = N × P_r × Q. That is, the net current scales with the number of release sites, the probability of release, and the size of the postsynaptic response to each release (25). In our V-M experiment, only P_r was altered by changing Ca²⁺ and Mg²⁺ concentrations. Hence, if we always measure I in the same 2 Ca²⁺/1 Mg²⁺ solution at the beginning of the experiment (constant P_r), the I measured in this solution should be proportional to N when I and N are compared across different cells. As shown in Fig. 5D, this appears to be approximately the case (slope = 34.4 release sites per nA of synaptic current measured in 2 Ca²⁺/1 Mg²⁺). Thus, knowing the EPSC amplitude measured in 2 Ca²⁺/1 Mg²⁺ in the Baf experiments before Baf application, the correlation in Fig. 5D allows us to estimate the number of release sites for each cell. This was done for each cell in our Baf dataset (mean N = 363 ± 74 sites).

Finally, assuming that there is one release site per bouton (Discussion), we arrive at an estimate of 81 ± 20 functional SVs released from each bouton (n = 7 cells). This is smaller than the estimate using the train method (133 ± 44) but, because of between-cell variability, the difference is not significant (P = 0.14).

Discussion

In this paper, we have developed an approach by using Baf, an inhibitor of synaptic vesicle refilling, to count the total number of SVs that can be released from a presynaptic bouton with mild stimulation. Our method is an electrophysiological version of the “alkaline trapping” optical technique in which the accumulation of fluorescence of synaptopHluorin after Baf treatment is used to measure properties of vesicular exocytosis (16, 20). An advantage of our electrophysiological version is that it provides a direct functional readout of release.

We first confirmed 3 critical requirements of our approach (Figs. 1–4) that ensure that each released SV is counted fully and only once. To express the vesicle count as a number per bouton, we also needed an estimate of the number of boutons on each cell. This was done in 2 ways: by using a train to estimate the total RRP size then dividing this by the known RRP size per bouton (Fig. 5 A and B) and by using the variance-mean method of fluctuation analysis to measure directly the number of vesicle release sites (Fig. 5 C and D). The first method estimated that a total of ≈130 functional SVs are released per glutamatergic bouton during mild, prolonged electrical stimulation whereas the second method gave an estimate of ≈80 SVs per bouton.

Accuracy of the Estimates.

Why do these two estimates differ? Of relevance is the fact that the V-M method provides the number of vesicle release sites, not the number of boutons (25). It is well established in this culture system that multivesicular release occurs, meaning that two or more SVs may be released from separate functional release sites at some boutons (23, 26), especially under the high-Ca²⁺ conditions used in the V-M method to determine N (25). This leads to an overcounting of boutons and, hence, to an underestimate of the SV count per bouton. Therefore, we feel that the true number of SVs released per bouton is likely to be closer to 130 than 80.

Note that our estimates depend on a number of simplifying assumptions that are implicit in both the train and V-M approaches. For example, the train/sucrose method depends on the definition of the RRP, which has been controversial (13, 14). Moreover, the V-M method assumes the existence of a fixed population of noninteracting release sites, which may sometimes be incorrect (25). Future experiments would use a strictly morphological approach, such as serial electron microscopy (2), to count unambiguously the number of boutons on the same cell in which Baf-induced rundown was measured.

Comparison with Other Estimates of Functional Pool Size.

Two main kinds of experiment have been used to estimate the recycling pool size in cultured hippocampal boutons. One approach analyzes labeling of SVs by fluorescent markers such as FM dyes and pHluorins (4, 5, 7). Counts using this method are variable but often surprisingly small [31 ± 18 (7); 25 ± 11 (27); 64 ± 14 (28); 127 (29)]. A second approach uses electron microscopy to count SVs that have been labeled with endocytic markers (6, 7). These also suggest that the recycling pool is comparatively small [≈50 (3); 30–45 (7)].

Why should our estimate (up to ≈130 cycling SVs per bouton) be larger than many previous estimates? An explanation may lie with the stimulation protocol. The studies mentioned above typically applied a single 10–30 Hz train for 1 or 2 min. It has been claimed that such a brief, intense protocol is sufficient to load >90% of the recycling pool (16, 30). However, it is clear from electrophysiological recordings that high-frequency trains lead to profound depression of EPSCs (e.g., Fig. 5A), raising the possibility that mobilization of SVs from the reserve pool becomes rate-limiting, minimizing its participation during just 1–2 min of activity (4, 31, 32). In contrast, our stimulation was much milder and more prolonged (paired electrical stimuli at 0.2 Hz for ≈10 min, with occasional 2-s trains at 20 Hz) (Fig. 1B). This may allow time for reserve pool vesicles to participate in release.

In conclusion, we have described a simple method of counting the functional pool size at autapses in cell culture. We have found that low-frequency stimulation is capable of releasing up to ≈130 of the 100–200 morphologically identified SVs in the same culture system. Thus, our data suggest that a large proportion of SVs, even those in the putative reserve pool, do eventually find their way to being released under conditions that are compatible with mild physiological activity.

Materials and Methods

Cell Culture.

Hippocampal autaptic cultures were prepared by using standard methods, as described (18). Briefly, single isolated CA1 rat pyramidal neurons were grown on small diameter (≈50–100μm) microdots of permissive substrate. Cultures were used after 14–18 days in vitro, by which time the isolated neurons had formed abundant autaptic connections.

Electrophysiology.

Whole-cell patch clamp recordings were made from isolated pyramidal neurons, as described (18, 23). In brief, autaptic EPSCs were evoked by a 2-ms voltage clamp step to 0 mV from a holding potential of −60 mV. In many experiments, pairs of stimuli (at 50-ms interval) were applied. EPSCs were confirmed from their fast decay kinetics (time constant ≈5 ms) and blockade by 10–20 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX). Electrode series resistance (3.5–7 MΩ) was monitored continuously for stability, with compensation adjusted to 70–85%. All experiments were done at room temperature (22–25°C).

Baf (5 μM; Tocris) was applied via a puffer pipette (2–3-μm tip diameter) driven with brief pressure pulses (10 psi, 0.5 s at 1 Hz) provided by a Picospritzer (Parker Valve). Pressure pulses were applied for 100 s while moving the pipette around the microdot. In control experiments, external solution containing the same concentration of DMSO alone (0.5%) was applied (Fig. 1A). At all times, apart from during Baf application, the cell was continuously perfused with external solution by using a glass flowpipe, the internal diameter of which (500 μm) was larger than the diameter of the microdot, ensuring that all autapses were uniformly bathed with external solution. GABA loading solution was applied for 60 s by switching rapidly to a second flowpipe containing this solution. Hypertonic sucrose solution was applied for 6 s in a similar way, by using a motorized micromanipulator (MP-285, Sutter Equipment) under software control to move the flowpipes. Control experiments showed that the switch was complete within 100 ms.

V-M experiments were done as described (23). Autaptic EPSCs were first evoked in normal 2 mM Ca²⁺/1 mM Mg²⁺ external solution (see Solutions) to obtain a reference EPSC amplitude. The cell was then bathed consecutively in a series of 4 or 5 modified external solutions containing a range of Ca²⁺ concentrations (0.8–10 mM) to vary the release probability. EPSCs (n = ≈30–60) were evoked at 0.1–0.2 Hz in each bath solution with bracketing to check stability.

Solutions.

The normal external solution comprised: 125 mM NaCl, 3 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 25 mM Hepes (pH 7.4 with NaOH), and 10 mM glucose, adjusted to 300 mOsm with sorbitol. The bath solutions for V-M experiments were the same, except they contained x mM Ca²⁺ and y mM Mg²⁺, with x + y = 11 mM to maintain a constant divalent concentration. The GABA loading solution comprised: 100 mM GABA, 40 mM NaCl, 40 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 25 mM Hepes (pH 7.4 with NaOH), and 10 mM glucose, adjusted to 310 mOsm with sorbitol. The hypertonic sucrose solution comprised normal external solution supplemented with 500 mM sucrose and 0.5 μM tetrodotoxin (Tocris). The pipette solution comprised: 135 mM KCl, 7 mM NaCl, 1 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, 0.3 mM Na₃GTP, 20 mM Na₂-phosphocreatine, and 10 mM Hepes (pH 7.2 with KOH), adjusted to 330 mOsm with sorbitol. Baf was prepared as a 1 mM stock solution in DMSO, aliquoted and stored at −70°C. On the day of the experiment it was diluted in external solution to a final concentration of 5 μM. This working solution was kept on ice until just before use.

Data Analysis.

Only cells in which the series resistance remained stable (±10%) over the entire experiment were used for analysis. For each EPSC, the charge was calculated by integrating from the foot of the EPSC over a 50-ms time window. The cumulative EPSC charge, used to estimate total vesicle exocytosis (Fig. 1B), was calculated for EPSCs recorded from the end of Baf application (Fig. 1A). The transient increase in EPSC amplitude observed during Baf application at some stimulation frequencies (Fig. 3A Upper) was accompanied by a reduction in PPR (Fig. 1A), implicating a transient increase in release probability. The mechanism of this effect is unclear, but it should not affect our results. mEPSCs (Fig. 4) were captured by using the mini detection algorithm in Axograph (Axograph Scientific). The mean mEPSC frequencies plotted in Fig. 4C were normalized to the mean frequency measured in the same cell before Baf application. The 20 Hz train data (Fig. 5A) were analyzed by calculating the cumulative integral of each EPSC in the train (including the asynchronous plateau current). A straight line was fitted to the last 1.5 s of the plot of cumulative EPSC charge vs. time and extrapolated back to time 0 to get the RRP charge. This was divided by the mean mEPSC charge measured in the same cell or, if unavailable, by the average of mEPSC charges measured in all other cells in the dataset (0.227 ± 0.039 pC, n = 9). Sucrose responses (Fig. 5B) were integrated to find the area under the transient portion of the response, then this was converted to number of vesicles by dividing by the appropriate mean mEPSC charge.

V-M data were analyzed as described (23). Briefly, for each Ca²⁺ solution, the mean and variance of EPSC amplitudes were calculated and plotted as in Fig. 5C. The V-M plot was then fitted to the parabola

where σ² is the variance, I is the mean EPSC amplitude, Q is the quantal amplitude, and N is the number of release sites. The fit provides estimates of Q and N for each cell. Similar results were obtained with a more complex version of this equation that includes additional sources of variance (23).

The plot in Fig. 3B was fitted to the equation

where

Here, τ is the time constant for rundown of the EPSC amplitude after Baf, f is the frequency of stimulation, p is the probability that a vesicle will undergo exocytosis on each stimulus, and k is the rate constant for leakage of glutamate out of the vesicles. The derivation of these equations is given in the SI Text.

Statistical significance was assessed by using Student's t test (paired or unpaired two-tailed) or ANOVA. Unless stated otherwise, errors are given as ± SEM, with n = number of cells.